Blood flow redistribution and ventilation-perfusion mismatch during embolic pulmonary arterial occlusion

Abstract

Acute pulmonary embolism causes redistribution of blood in the lung, which impairs ventilation/perfusion matching and gas exchange and can elevate pulmonary arterial pressure (PAP) by increasing pulmonary vascular resistance (PVR). An anatomically-based multi-scale model of the human pulmonary circulation was used to simulate pre- and post-occlusion flow, to study blood flow redistribution in the presence of an embolus, and to evaluate whether reduction in perfused vascular bed is sufficient to increase PAP to hypertensive levels, or whether other vasoconstrictive mechanisms are necessary. A model of oxygen transfer from air to blood was included to assess the impact of vascular occlusion on oxygen exchange. Emboli of 5, 7, and 10 mm radius were introduced to occlude increasing proportions of the vasculature. Blood flow redistribution was calculated after arterial occlusion, giving predictions of PAP, PVR, flow redistribution, and micro-circulatory flow dynamics. Because of the large flow reserve capacity (via both capillary recruitment and distension), approximately 55% of the vasculature was occluded before PAP reached clinically significant levels indicative of hypertension. In contrast, model predictions showed that even relatively low levels of occlusion could cause localized oxygen deficit. Flow preferentially redistributed to gravitationally non-dependent regions regardless of occlusion location, due to the greater potential for capillary recruitment in this region. Red blood cell transit times decreased below the minimum time for oxygen saturation (<0.25 s) and capillary pressures became high enough to initiate cell damage (which may result in edema) only after ~80% of the lung was occluded.

INTRODUCTION

Acute pulmonary embolism (APE) is characterized by full or partial occlusion of one or more pulmonary arteries, resulting in a redistribution of blood to the non-occluded vessels. This leads to ventilation/perfusion (V/Q) matching abnormalities which includes extremely high or infinite V/Q values in the embolized region(s) but also potentially decreased V/Q units in the non-occluded tissue, hence impaired gas exchange, hypoxemia and hypocapnia can result.[1] Tsang et al.[2] and Altemeier et al.[3] concluded that the changes in V/Q after APE are determined primarily by the redistribution of pulmonary blood flow, with a minor contribution from ventilation redistribution; however this blood flow redistribution has not been studied in detail. It is not clear what happens to V/Q, or oxygen levels, within the non-occluded region alone, where the lung must attempt to achieve sufficient oxygenation in a reduced volume. The degree of vascular recruitment, distension, and other changes in hemodynamics in these non-occluded regions are also not well described in the literature.

APE can also result in pulmonary hypertension (PH) which is defined clinically by a mean pulmonary artery pressure (mean PAP) ≥25 mmHg at rest[4] (normal resting mean PAP is ~14 mmHg with an upper limit of normal of ~20 mmHg[5]). While it is apparent that thromboembolic occlusion increases pulmonary vascular resistance (PVR) via mechanical obstruction of distal vascular beds, there is evidence to suggest that additional mechanisms are required to increase pulmonary pressures to levels observed in patients presenting with APE. Subjects with inert (non-thromboembolic) vascular occlusion of ~50% of the lung (as observed in patients undergoing unilateral pneumonectomy) often have normal pulmonary arterial pressures; however patients with thromboembolic occlusions of ~25% of the lung may experience PH.[6,7] The contribution of vasoconstriction via neural reflexes and the release of humoral factors (i.e., serotonin, endothelin-1, thromboxane-A2) in APE is relatively well established in animals.[6,8] Data are more difficult to obtain within human subjects; however, some studies have shown preliminary evidence for endothelin abnormalities and the role of vasoconstriction in human APE.[9–12] Hypoxic pulmonary vasoconstriction resulting from hypoxemia has also been suggested as a mechanism for the increase in PVR in APE.[6]

In this study, we used a structure-based computational model of the human pulmonary circulation[13] to determine how cardiac output is accommodated post-occlusion, and what impact this would have on V/Q matching and oxygen transfer from air to blood if ventilation distribution remained unchanged post-embolus. A secondary question was to determine whether direct obstruction of a blood vessel by itself can be sufficient to elevate PAP to a level that is indicative of PH. The model used here incorporates an anatomically-based geometry of the extra-acinar blood vessels, the effect of axial and radial tissue tethering on vascular geometry, and accounts for the zonal flow mechanisms[14] that occur in the micro-circulation.

MATERIALS AND METHODS

This study uses a previously published multiscale computational model of blood flow through the distensible vessels of the full pulmonary circulation (arteries, veins, and intra-acinar circulation) coupled to parenchymal tissue deformation.[13] Only a brief description of the methods of this model will be given here: additional detail may be found in the Multiscale Model given below (following our Conclusions, and before the Acknowledgments), as well as in the corresponding references.

The perfusion model

Specific details of the components of the model can be found in references.[13,15–17] A summary of the most important model features is provided here and in the Multiscale Model. To summarize, this model includes the following.

First, it includes anatomically-based geometry of the lung surface and central blood vessels,[18,19] and computationally-generated, morphometrically-consistent models of the “accompanying” arterial and venous vessels (i.e., not including supernumerary vessels) to the level of the acini.[20] There are approximately 64,000 each arterial and venous branches in the model, and each terminal vessel supplies a single pulmonary acinus (31,800 in the whole lung model). Diameters were defined using a Strahler-diameter ratio.[13,15]

Second, it includes an intra-acinar circulation model[16] linking each of 9 symmetric branches of arterioles and venules via a “sheet” flow model of the capillaries[21] that crosses between each generation of arteriole and venule, forming a ladder-like configuration.

Third, it includes a model of parenchymal tissue deformation under gravity,[19] to which the vascular networks are tethered. Tissue deformation influences perfusion via shift in the vessel locations (the “Slinky” effect,[22]) by elastic recoil pressures acting to distend the extra-capillary vessels, and by the effect of alveolar inflation on capillary sheet distensibility.[13,15] Tissue deformation was simulated for a supine lung at functional residual capacity (FRC).

Steady blood flow through the full model was simulated after applying boundary conditions for pressure or flow at the “inlet” and “outlet” vessels: this corresponded to an inlet flow (Q_RV) of 5 l/min. at the pulmonary trunk, and left atrial pressure (LAP) of 5 mmHg. These values were used for all simulations unless otherwise stated. By solving equations for Poiseuille resistance including gravity, conservation of mass, vessel elasticity, and a microcirculatory model (see Multiscale Model and Clark et al.,[13]) predictions were obtained for the regional distribution of blood flow, blood and transmural pressures, capillary recruitment, red blood cell (RBC) transit time, and vessel radius. An output of the simulation was mean pulmonary arterial pressure (PAP), and therefore pulmonary vascular resistance (PVR=(PAP-LAP)/Q_RV) was calculated across the full circulation.

Simulating occlusions

Post-occlusion simulations were performed by setting vessel radius at the occlusion site to 10% of its initial radius which, in general, was sufficient to reduce flow to ~5% of baseline in the occluded region.

Emboli vary in size and shape, and an embolus traveling into the lung via the pulmonary trunk could deposit in numerous locations. Studying the relationship between embolic arterial obstruction, PAP, and hemodynamics therefore first requires assessment of the likely distribution of emboli. All potential sites and their probability of occlusion were calculated for three sizes of emboli (5, 7, or 10 mm radius). The probability of occlusion was assumed to be proportional to the baseline flow rate to the occluded vessel (i.e., regions of higher flows more likely to occlude). The emboli were assumed to occlude the first vessel that they encountered that was smaller in radius than the embolus, and they did not deform within the artery. Flow distribution was simulated for each site of occlusion.

To quantify the relationship between volume of obstructed tissue and hemodynamic outcomes in the model, emboli of a single size (either 5, 7, or 10 mm radius) were added cumulatively (in random order) and flow distribution re-calculated, until there were emboli in blood vessels that feed nearly all capillary beds. The number of acini distal to the occlusion and PAP were recorded. Lung occlusion was defined as the percentage of acinar units distal to occlusions (relative to total number of acini). To assess the impact of obstruction on microcirculatory flow in the unobstructed tissue, for the 10 mm simulations the capillary sheet flow-rate, capillary pressures, and capillary recruitment were calculated. To quantify the relationship between PAP and cardiac output in the PE model, simulations were repeated for increased cardiac output.

Estimating alterations in oxygen transfer

To estimate alterations in regional oxygen transfer post occlusion, a 3%/cm linear gradient of ventilation was assumed along the gravitational axis (compared with 2.7-5.2 %/cm in the supine posture for healthy humans[23–25]) with total alveolar ventilation of 5 l/min. such that mean V/Q=1. Oxygen transfer from air to blood was estimated using a simple model based on Kapitan and Hempleman[26] describing oxygen (O₂) partial pressure balance in each acinus.

where V_I is the inspired ventilation (l/min.); V_A is expired or alveolar ventilation (l/min.); Q is blood flow to the acinar compartment (l/min.); and P_kO₂ is the O₂ partial pressure (mmHg) of oxygen in humidified inspired air (k=I), alveolar air (k=A), end-capillary blood (k=C), or the mixed venous blood that enters the lungs from the systemic circulation (pulmonary arterial blood) (k=v). P_IO₂ was 150 mmHg (for all cases), and P_vO₂ was set to 40 mmHg (baseline level). For post-occlusion simulations retaining P_vO₂ at 40 mmHg assumes that oxygen uptake in the systemic circulation adapts (reduces) and so this will likely overestimate oxygen partial pressures. More likely, oxygen consumption by the body remains close to baseline levels and P_vO₂ reduces; therefore, lower values of 30 mmHg and 20 mmHg were also considered in simulations.

The perfusion model and ventilation distribution gives Q and V (=V_I =V_A) in each acinus, with unknowns P_AO₂ and P_CO₂. Assuming that blood remains in the capillaries for long enough for O₂ to equilibrate between alveolar air and capillary blood, then at end inspiration P_AO₂=P_CO₂. This assumption is likely to be valid except at very high levels of occlusion (as discussed later). These assumptions reduce equation (1) to

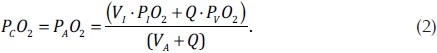
Equation (2) was solved for each acinus to predict P_CO₂ and P_AO₂. The ventilation-weighted sum of P_AO₂ was calculated as an estimate of expired O₂ partial pressures from the full lung. As most capillary O₂ is bound to Hemoglobin, to calculate arterial (pulmonary venous) O₂ partial pressures P_CO₂ was converted to O₂ content (C_CO₂) and an acinar perfusion-weighted sum of C_CO₂ was calculated before conversion back to partial pressure units. To do this we used the formula

where ρ(P_CO₂) is the oxygen saturation—a function of P_CO₂. The first term on the right hand side represents the O₂ in hemoglobin, and the second term represents dissolved O₂ concentration in blood plasma. Hemoglobin has an oxygen binding capacity of 1.34 ml O₂ per gram of hemoglobin, and 15 g of hemoglobin per 100 ml of blood. Dissolved O₂ concentration was calculated from Henry's Law (for each mmHg of partial pressure there is 0.03 ml of O₂ in 100 ml of whole blood).

Oxygen saturation was in turn calculated using the Monod-Wyman-Changeux (MWC) model[27]

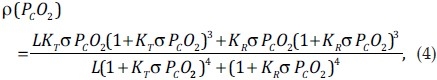
where K _T =10×10³L mol⁻¹, K_R =3.6×10⁶Lmol⁻¹, L=171.2×10⁶, and the O₂ solubility, σ is 1.4×10⁻⁶ M mmHg⁻¹.[28]

RESULTS

The baseline lung model

A full comparison of the baseline lung model to literature data is given in Clark et al.[13] In brief, PAP for the baseline model was 15.8 mmHg (a PVR of 2.2 mmHg/l/min.) in the upright posture, 16.8 mmHg (a PVR of 2.4 mmHg/l/min.) in the prone posture and 18.2 mmHg (a PVR of 2.6 mmHg/l/min.) in the supine posture. In the supine posture (used in this study) a mean RBC transit time of 1.76±0.53 sec. (range 0.30-9.89 sec.) was calculated in the model at baseline.

Predicted variability in the sites of occlusion

Sites of occlusion, their probability of occlusion, and all distal vessels that are affected by a single 5, 7, or 10 mm radius embolus are illustrated in the supine lung model in (Fig. 1). The number (and percentage of total) of acinar units affected by each occlusion are given in (Table 1) (column 2). The 10 mm emboli occluded lobar level arteries, the 7 mm emboli predominantly occluded segmental vessels, and the 5 mm emboli were distributed within the segmental and sub-segmental arterial level. A slight preference for occlusion of the gravitationally dependent regions was predicted, consistent with the flow distribution. Emboli had an almost identical probability of occluding the left (49.5%) or right (50.5%) lung. For the 5 mm emboli, the probability of lobar deposition was 19.2%, 5.0%, and 26.3% for the right upper, mid, and lower lobes, respectively; and 23.4% and 26.2% in the left upper and lower lobes, respectively. This anatomical distribution of emboli compares well with measurements in humans.[29]

Figure 1.

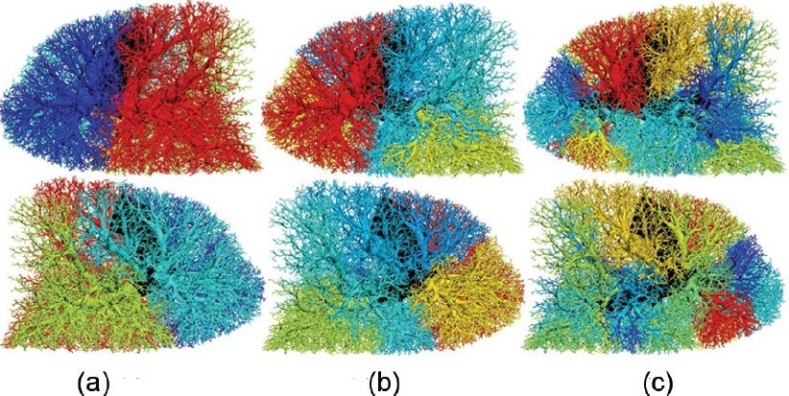
Visualization of all potential occluded regions for emboli of (a) 10, (b) 7, or (c) 5 mm in radius. Images are oriented in the supine posture and show right (upper panel) and left (lower panel) lung side views. Color range indicates the probability of each occlusion (vessels distal to occlusion have the same color). The color spectrum ranges from most likely (red) to least likely (dark blue) occlusion (ranges: 0.31 to 0.19, 0.19 to 0.014, and 0.059 to 0.011 for 10, 7, and 5 mm emboli). Non-occluded, central vessels shown in black. Flow solution is obtained in the supine posture at FRC.

Table 1.

Mean hemodynamic outcomes after a single occlusion from the range of occlusion locations with emboli of 10, 7, and 5 mm in radius

The probability of occlusion had a strong linear correlation with the volume of tissue distal to the occlusion (not shown). This is expected as larger regions of tissue will typically receive a higher flow of blood. The larger emboli occluded flow to larger volumes of tissue and therefore resulted in greater mean increases in PAP and PVR (Table 1). The gravitationally dependent flow gradient decreased after all occlusions, regardless of occlusion size or location.

Relationship between vascular obstruction and PAP

The effect of cumulative vascular occlusions on PAP is plotted in (Fig. 2) for each embolus size, with emboli added sequentially until almost all acinar units were occluded (simulations are not conducted for 100% occlusion). The clinical definition for PH (mean PAP ΃25 mmHg) was not reached until approximately 55% of the vascular tissue was occluded. Both clinical[30] and animal studies[31] have shown that a mean PAP of approximately 40 mmHg is the maximum pressure that an initially non-hypertrophied right ventricle can sustain acutely before progressing to right ventricular failure (RVF)—this pressure was not reached in the model until ~90% of the lung was occluded. These results were consistent for the different sized emboli in this study. Response to embolization in human and animal studies is typically heterogeneous. It has been shown that only 25-30% total vascular occlusion can lead to hypertension, with hypoxemia, embolus location, and post-embolus release of vasoactive mediators each playing a role in the heterogeneity of response.[7,30,32] Inert occlusion studies have demonstrated that more than half of the lung (~60-70%) may be occluded before PH is reached.[6,8,33] The model is representative of an inert (nonhematogenous) obstruction—given that no vasoconstriction is included in the model—and, given the slightly higher than average baseline PAP, predicts a level of occlusion very similar to these measurements.

Figure 2.

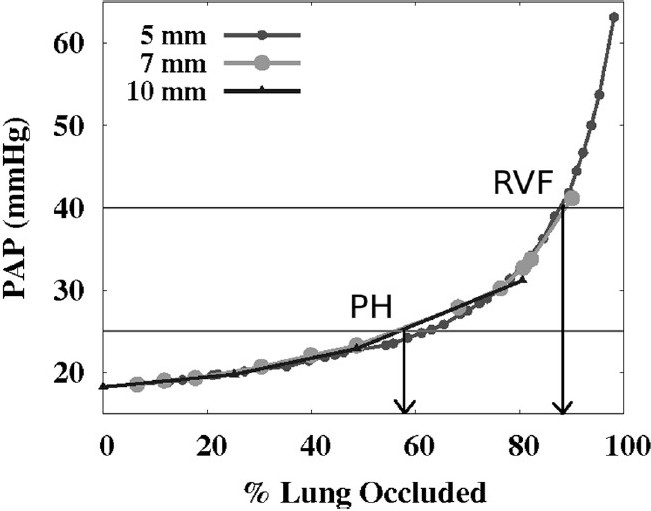
The effect of increasing the amount of vascular obstruction on mean PAP (mmHg) shown for 5, 7, and 10 mm emboli. Pulmonary hypertension (PH) is defined clinically as PAP >25 mmHg,[4] and right ventricular failure (RVF) is considered likely at pressures >40 mmHg[30,31].

Contribution of capillary recruitment, and capillary pressures

Capillary sheet flow-rate, pressure, and recruitment (Fig. 3a–c respectively) are shown as a function of gravitationally-dependent height for cumulative levels of occlusion with 10 mm emboli (other embolus sizes gave similar results, so are not shown). Values are averaged within 10 mm iso-gravitational slices. Each hemodynamic measure increased as the proportion of occluded tissue increased, because the same cardiac output (constant Q_RV) was accommodated through an effectively smaller vascular circuit. Mean overall capillary recruitment increased from 70% at baseline to 73.2, 77.2, and 89% recruited after 25.2, 48.7, and 80.5% of the tissue was occluded. Note that for the 80.5% occlusion, the model was only perfused in the right upper lobe hence the solution does not extend to the full gravitationally dependent height (maximum height ~92.5% of the total dorso-ventral height).

Figure 3.

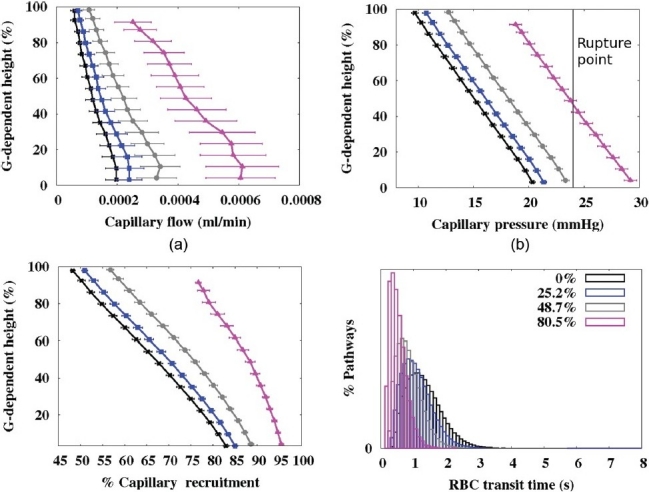
Micro-circulatory results at different levels of occlusion (0%, 25.2%, 48.7%, and 80.5%) with emboli 10 mm in radius. (a) Capillary flow rate (ml/ min.), (b) capillary pressure (mmHg), (c) % capillary sheet recruited. Each plot displays mean values in 10 mm isogravitational slices plotted with respect to gravitationally-dependent lung height (dorsoventral axis, %). In (b) the pressure (~24 mmHg) when the blood gas barrier may start to become compromised35 is included. (d) RBC transit time distribution for each occlusion level. All occluded capillary ‘sheets’ were removed from this analysis.

Experimental studies have shown that the endothelium begins to break at transmural pressures of approximately 24 mmHg (24-40 mmHg for as little as 4 min. leads to cell rupture)[34] and the level of damage is increased at higher lung volumes.[35] The model predicts that once perfusion is occluded to ~20% of the tissue (without additional vasoconstriction) capillary pressures begin to reach a high enough level to cause this destruction which would result in fluid filtration and alveolar edema. However, it is not until perfusion is occluded to ~80% of the tissue that a significant proportion of capillaries reach this limit (as illustrated in Fig. 3b).

Relationship between PAP and cardiac output, pre- and post-occlusion

The relationship between PAP and cardiac output (flow) is shown in (Fig. 4) at baseline and for two levels of occlusion (~48% and ~80%) using emboli of 7 mm in radius. For the 48% occlusion the PAP remained below the PH level up to a Q _RV of ~8 l/min. When vascular obstruction was ~80% the PH level was reached at ~3 l/min. A slightly curvilinear relationship between PAP and Q is predicted due to vessel distension (limited by the distensibility parameter α, see Multiscale Model Equation A1) and the potential for increased capillary surface area via recruitment (R, see Equation A6 in the Multiscale Model) under increased pressure/flow.

Figure 4.

Relationship between flow into the pulmonary circuit and resultant mean pulmonary arterial pressure (PAP) at baseline (0% obstruction) and two levels of vascular obstruction (~49% and ~80% vascular obstruction using emboli of size 7 mm in radius). At the standard flow used in this study (5 l/min.) PH (PAP >25 mmHg) is not present with ~48% of vascular bed occluded, but is present when flow exceeds ~3 l/min. with 80% vascular obstruction.

Redistribution of blood flow within non-occluded regions

Blood flow was found to redistribute preferentially to non-dependent lung regions following occlusion. (Fig. 5a) shows the ratio of post-occlusion to baseline flow (Q_occluded/Q_baseline) in the full lung model, for a single embolus occlusion of radius 10 mm. (Fig. 5c) shows the same ratio within acini (averaged within 10 mm slices) as a function of gravitationally-dependent height for each of the four possible occlusion sites for 10 mm embolus. For all occlusions, regardless of the location (and size, data not shown), the flow was preferentially redistributed to the gravitationally non-dependent region of the lung via increased capillary recruitment (Fig. 5d). The gravitationally non-dependent tissue is the region where there is the most potential for increased flow through the capillary bed (as has previously been shown in an isolated acinar model[16]) due to low baseline recruitment (Fig. 3c). The relationship used to determine capillary recruitment as a function of capillary pressure is illustrated in (Fig. 5b) (from Equation A6 in the Multiscale Model and Equation 6 in Clark et al.[13]) The relationship was derived from the experimental measurements of Godbey et al.,[36] who measured the percentage of capillary pathways perfused in five dog lungs, with intact thorax, perfused over a range of capillary pressures. (Fig. 5b) illustrates that in lower pressure regions (such as in the non-dependent lung) the same increase in pressure results in a proportionately larger increase in capillary recruitment than in higher pressures (gravitationally dependent) regions. This gravitationally influenced redistribution of flow has implications on V/Q matching and gas exchange after occlusion (discussed below).

Figure 5.

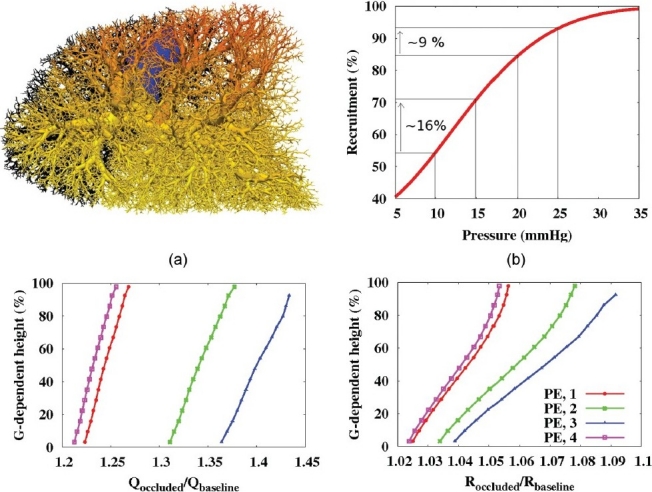
Flow redistribution after occlusion with 10 mm emboli. (a) Supine model with 1 occlusion (PE, 1), occluded vessels in black, color spectrum represents Q_occluded/Q_baseline (red=1.3, dark blue=1.0). (b) Plot of the capillary recruitment function (Eqn A6). (c) Acinar flow values (Q_occluded/Q_baseline) and (d) capillary recruitment post-occlusion normalized by baseline values (R_occluded/R_baseline). (b-d) show all 4 potential occlusions. (c,d) Values averaged in 10 mm slices, plotted with respect to gravitationally dependent height (%). All occluded capillary ‘sheets’ removed from this analysis.

Oxygen transfer

A common clinical outcome of APE is some degree of hypoxemia and most (>90%) of APE patients present with a higher than normal alveolar-arterial oxygen partial pressure difference (P(A-a)O₂).[1] (Fig. 6a) shows the reduction in arterial (blood leaving the lungs) oxygen partial pressures (P_aO₂) with increasing occlusion. Only the 7 mm radius emboli are shown, as similar results were found for 5 and 10 mm emboli. These results are presented for three different values of P_vO₂ (40, 30, and 20 mmHg); P_vO₂ has been found to range between 21-35 mmHg in APE[37] compared to 40 mmHg in normals, suggesting that to maintain sufficient oxygen transfer in the systemic circulation P_vO₂ must drop from baseline levels. At the higher level of P_vO₂, P_aO₂ in the model did not fall below the normal range (reported to be between 80-100 mmHg)[38] until ~49% of the lung was occluded. However, when P_vO₂ was dropped to the lower level measured in APE (20 mmHg) P_aO₂ was reduced below normal when as little as 12% of the lung was occluded. This prediction is more aligned with measurements that have shown that P_aO₂ may be depressed with as little as 13% of lung tissue occluded.[7] The P(A-a)O ₂ difference provides a measure of the efficiency of gas exchange and is found to be ~8- 12 mmHg in normal healthy subjects.[39] This difference is attributable partly to venous admixture of shunted blood and partly to V/Q mismatch, if diffusional limitation is assumed to be negligible. A normal shunt of 2% of cardiac output accounts for 4 mmHg of the difference,[40] this amount was added explicitly to the value of P(A-a)O₂ calculated by the model in this study. P(A-a)O₂ increased notably with embolization, with values exceeding the normal limit with as little as 10% tissue occlusion (Fig. 6b).

Figure 6.

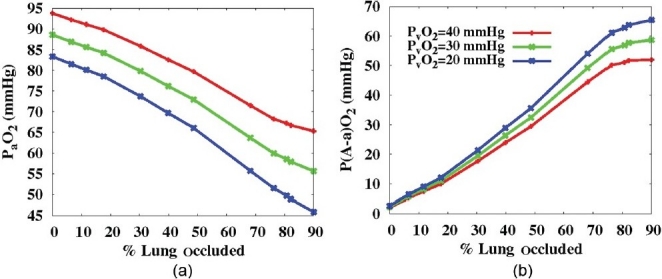
(a) The reduction in arterial (blood leaving the lung) oxygen partial pressures (P_aO₂) and (b) the difference between alveolar and arterial oxygen partial pressures (P(A-a)O₂, mmHg). Both plotted with respect to increasing occlusion indicating three different levels of mixed venous oxygen partial pressure (P_vO₂=40, 30, or 20 mmHg) for emboli of 7 mm in radius. P_aO₂ reduced and P(A-a)O₂ increased with increasing occlusion and decreasing P_vO₂.

It is known that APE can result in bimodal distributions of V/Q ratios[41,42] and so by inference must have an impact on oxygen partial pressure at the alveolar level. (Fig. 7) shows a transverse view through the supine lung model at FRC, for 40% vascular occlusion resulting from the insertion of multiple 7 mm emboli. Each acinus in the section is colored to show the distribution of (A) Q, (B) V/Q, and (C) P_AO₂ (=P_cO₂). Baseline distributions of P_AO₂ in the upright model (not shown) were consistent with estimates from the literature (~89 mmHg at the base and ~132 mmHg in the apex of the lung.[40]) The post-occlusion results in the supine model show a clear bimodal distribution of P_AO₂ (Fig. 7c), with a shift to high P_AO₂ in most of the left (occluded) lung, and a shift to low P_AO₂ in the right lung. P_AO₂ < 80 mmHg developed in the posterior of the right lung, with some heterogeneity in its distribution. These low values for P_AO₂ indicate regions where hypoxia could theoretically develop. The emergence of this distribution of P_AO₂ is explained by the V/Q distribution in (Fig. 7b): regions of V/Q > 1 develop high P_AO₂ due to flow occlusion (Fig. 7a) and therefore low O₂ uptake by the blood; redistribution of Q to the non-occluded tissue results in a lower than baseline V/Q, and the preferential gravitational redistribution establishes lowest V/Q in the dependent tissue such that the O₂ uptake to the blood is enhanced, thereby reducing P_AO₂ to low levels. In the absence of any V redistribution to optimize the matching of post-occlusion V and Q, it is clear that localized hypoxia could theoretically occur with relatively small levels of vascular occlusion.

Figure 7.

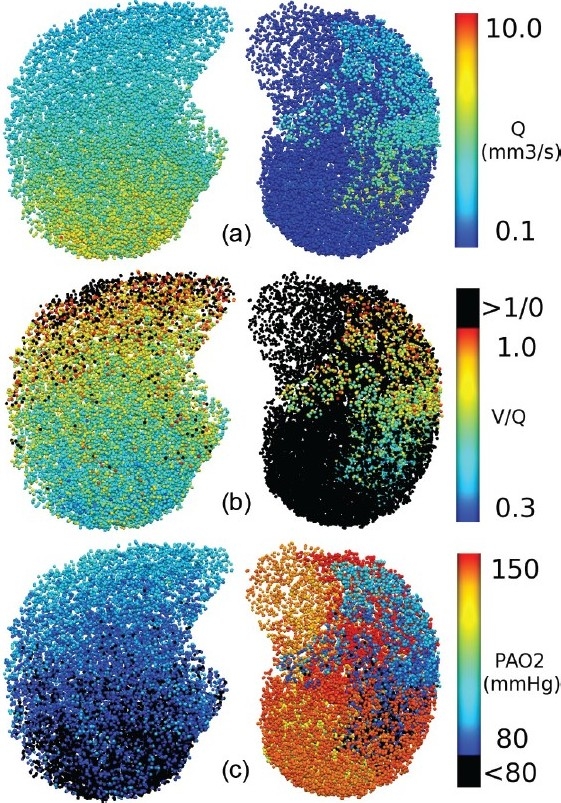
Acinar values of (a) blood flow (Q, mm3/s), (b) V/Q matching, and (c) P_AO₂ (mmHg), shown in a transverse section (caudal view) through a supine lung model at FRC with 40% tissue occlusion by multiple 7 mm emboli. The color spectrum ranges are indicated to the right of each image. V/Q >1 in (b) and P_AO₂<80 mmHg in (c) are colored black to highlight regions of poor perfusion and regions where hypoxic pulmonary vasoconstriction could theoretically be occurring, respectively.

DISCUSSION

This study used an anatomically-based, integrated functional model of blood flow through the full pulmonary circuit to investigate the redistribution of pulmonary blood flow, elevation of PAP, and micro-circulatory hemodynamics after occlusions of arteries of various size and location. The main outcomes from this study are: the prediction that blood flow preferentially redistributes to the (gravitationally) non-dependent regions after vessel occlusion; evidence and explanation that the effect of mechanical occlusion alone does not increase PAP to hypertensive levels without significant vascular occlusion; and evidence that significant (particularly localized) hypoxia could occur as a direct result of mechanical occlusion.

Physiological consistency of the model

Comparison of baseline model outputs with physiological measurements and a detailed sensitivity analysis of all model parameters has previously been conducted by Clark et al.[13] This prior study demonstrated that the model predicts physiologically consistent distributions of blood flow and PAP under “normal” conditions.

Oser et al.[29] observed that emboli were distributed anatomically, with 53% in the right lung (16% in the upper, 9% in the mid, and 25% in the lower lobe) and 47% in the left lung (14% in the upper and 26% in the lower lobe). Similar distributions were predicted in the current model, suggesting that emboli preferentially distribute in proportion to flow rates. In the human experimental studies the emboli could have lodged while the subject's lung was in any position, whereas here we studied only the supine lung. However for both the upright and the supine lung the flow was preferentially distributed to the lower lobes, and this was also the region of greatest probability for embolus location in both the experiments and the model.

Relationship between proportion of vascular occlusion and PAP

Pulmonary hypertension triggered by PE is believed to primarily be a result of the combined effect of mechanical obstruction and exacerbation in the presence of underlying cardiopulmonary disease. Another factor that has been found to play an important role in the immediate response to embolus occlusion in animal studies is pulmonary vasoconstriction, initiated by neural reflexes or via the release of vasoactive mediators from platelets or plasma (for example, serotonin and thromboxane A ₂.[9,10,32,41]) Several studies have demonstrated that larger portions of the lung need to be occluded by inert occlusions (such as balloon catheters) to induce the same rise in pulmonary arterial pressure seen during embolic occlusion,[6–8,33,43] which is indicative of vasoconstriction playing a role in elevating PVR. The extent and course of this constriction, however, does not appear to have been characterized in detail and is still a topic of debate. Vasoconstriction was neglected in this study; therefore the results are indicative of outcomes induced by “passive” occlusions such as balloon catheters or glass beads. Model results indicate that ~55% of the vascular tissue needs to be occluded before hypertensive pressure levels are reached—this is in agreement with inert occlusion studies that obstructed an entire lung before PH developed.[6,32] McIntyre and Sasahara[7,30] estimated the degree of obstruction in multiple patients with no prior cardiopulmonary disease and with variable levels of tissue obstruction using selective pulmonary angiography. The data showed a reasonably good correlation between mean PAP and obstruction level, however a fairly large amount of heterogeneity was evident across subjects. Mean PAP values in that study were, on average, slightly higher than the model for similar embolic obstructions. The clinical data indicates a rapid rise in PAP with occlusion size which may be a result of the additional effect of pulmonary vasoconstriction; the level of this response may vary across subjects which could partly explain the variability of values. Indeed the oxygen transfer model presented here suggests that localized hypoxia post-embolus is a potential contributor to increased PVRs.

Relationship between PAP and cardiac output, pre- and post-occlusion

Both experimental[41,42,44] and modeling[45] studies have assessed the effect of embolization on the relationship between PAP and flow. Each study has demonstrated an increase in the gradient of pressure against flow and the linearly interpolated pressure intercept following embolization. The current model predicts behavior that is consistent with these previous studies, showing that increasing the size of the occluded region results in an increase in both the gradient and pressure intercept (Fig. 4). The model did not predict a strictly linear relationship between PAP and Q, but instead displayed a slight curve as a result of vessel distension and recruitment during increased flow. This type of curved relationship has also been measured in murine lungs.[46]

Redistribution of blood flow within non-occluded regions

Preferential redistribution of blood flow to the (gravitationally) non-dependent regions was predicted, regardless of embolus size or location. This was demonstrated via decreased gradients of blood flow (Table 1, column 6), and the ratio of post-occlusion flow to baseline flow with respect to gravitationally dependent height (Fig. 5a,c). This pattern of redistribution occurred because of the greater potential for capillary recruitment (Fig. 5b) in the non-dependent tissue. The additional flow was therefore distributed more evenly to the non-occluded region than if it were distributed in proportion to the baseline flow.

Oxygen transfer

Measurements have shown that, under normal conditions, there is a gravitationally-dependent gradient of V/Q, both in animals[47] and in humans,[48] whereby V/Q decreases from (>1) in non-dependent to (<1) in dependent regions. This is because of the relatively steeper gradient of blood flow compared to air. This distribution results in a gradient of P_AO₂;[40] the model of oxygen transport employed here was consistent with these findings at baseline.

Assuming that ventilation distribution is unchanged post-embolization[3,49] we can estimate the effect of emboli on V/Q and gas exchange from the predictions of blood flow redistribution in this study. In each case considered, embolization reduced the gas exchange capacity of the lung. In occluded regions high V/Q ratios predominate due to minimal blood flow distal to the occlusion. Where there is complete vascular occlusion these distal regions would have an infinite V/Q ratio and would contribute to physiological dead space. As little oxygen is taken up from air to blood in these regions, they develop higher than normal alveolar oxygen partial pressures (P_AO₂, Fig. 7c).

The blood flow that would otherwise have supplied the occluded region has to be redistributed to the non-occluded tissue (Fig. 7a). (Figure 7c) shows a significant reduction in P_AO₂ in the non-occluded regions due to increased oxygen uptake by the blood; the level of reduction (to < 80 mmHg) could lead to localized hypoxia, even when whole lung gas exchange is sufficient to maintain arterial blood gases. This is a particularly important consideration as hypoxic pulmonary vasoconstriction (HPV) in these regions has the potential to increase overall PVR, although it has been observed that the potential for HPV may be reduced in PE.[9] The model has also shown that it is possible for the arterial (pulmonary venous) oxygen level to reduce significantly post-embolus, before the development of hypertension.

Model limitations

We have followed the paradigm of using as simple a model as possible for our study; the model used in the current study is considerably more complex (in particular with the extra-acinar vessel representation) than previous models used to study PE, however this has been necessary to enable predictions about the regional variation in perfusion parameters both at the macro- and micro-scale level within the pulmonary vascular circuit that have not previously been possible. Steady-state, laminar blood flow is assumed: turbulent flow is unlikely to occur in any but the largest pulmonary blood vessels. Most other models of pulmonary perfusion also use this approximation, and it is considered sufficient for studies of PVR and perfusion distribution.[50] The model represents vessels as 1D ′elements′ so it cannot account for alterations in 3D flow profiles arising from different geometries of emboli. This is most likely to have a localized effect, with minimal influence on the redistribution of blood flow. We maintained a constant flow rate into the pulmonary circuit. Cardiac output (CO) may, in reality, be reduced; however, a decrease in CO is unusual without at least a 50% obstruction.[7] If the flow was to reduce post-occlusion the same distributions would be predicted but with a smaller magnitude than in the current study. Our oxygen transfer model assumes alveolar-capillary oxygen equilibration. This requires RBC transit times to be > 0.25 s, a condition that is met in most of the lung except during very severe (>80%) occlusion. At this level capillary blood pressures are such that vessel rupture and edema would occur, causing diffusional limitation. In this situation the model would underestimate the impact of embolus occlusion on gas exchange.

CONCLUSION

This structure-based computational modeling study provides evidence that passive obstruction down to the level of the sub-segmental pulmonary arteries in the human lung is insufficient to raise PAP to PH levels, until ~55% of the capillary bed is distal to occlusions. Elevation of PAP to a critical level for smaller levels of obstruction is therefore most likely due to vasoconstriction that is initiated by localized hypoxia or via vasoactive mediators. Redistribution of blood flow in the non-occluded regions of the lung model followed a gravitationally-preferential distribution, which could improve V/Q matching in some cases of minor occlusions, and hence be protective of gas exchange.

The Multiscale Model

The following model description summarizes the integrated model for the pulmonary circulation that was presented by Clark et al.[13]

Extra-acinar vessels

Each extra-acinar blood vessel was defined using a one dimensional (1D) finite element positioned within the anatomical 3D lung geometry, represented by a centerline and a numeric value for its unstrained diameter (at zero transmural pressure, P_tm). The diameters of the left pulmonary artery (14.80 mm) and right pulmonary vein (12.97 mm) were assigned based on measurements by Huang et al.[51] All other arteries and veins down to the level of the acinus were assigned diameters based on a constant rate of decrease in diameter with decreasing vessel order (the Strahler diameter ratio R_DS), where R_DS was 1.53 in the arterial tree and 1.54 in the venous tree.[13]

Intra-acinar vessels

Each acinar circulatory ‘unit’ connects a single artery and a single vein. Within each unit the intra-acinar vessels were explicitly represented with nine symmetric bifurcations each of arteries and veins. These intra-acinar vessels are joined at each generation by a capillary bed that covers the alveoli present at that generation, forming a ‘ladder-like’ structure, described previously by Clark et al.[16]

Vessel radius as a function of pressure

Radial deformation of the extra-capillary (extra- and intra-acinar) blood vessels is related to P_tm by a linear relationship

where D is the strained vessel diameter and α is a compliance constant (baseline model compliance, α = 1.50 ×?10^-4 Pa^-1.[13]) In the larger blood vessels P_tm≈P_b-P_e (where P_b is the average blood pressure across the length of the vessel and P_e is the elastic recoil pressure acting on the vessel - values are derived from a soft tissue mechanics model.[15,19]) In the smallest vessels (diameter <200 μm) the dominant pressure acting externally to the blood vessel is assumed to be alveolar pressure (P_a), so P_tm≈P_b-P_a (P_a=0 in this study). Capillary sheet thickness is defined using a relationship analogous to Eqn. A1.[16] Eqn. A1 is assumed valid for P_tm < 32 cmH₂O, beyond which the vessel is maximally extended in the radial direction.

The blood flow equations

Blood flow in the extra-acinar vessels was described by the Poiseuille equation incorporating the effect of gravity acting on the blood in the direction of the vessel centerline. Thus flow in an artery or vein was described by

where ΔP is the pressure drop along the vessel, μ is the viscosity of blood in the vessel (μ=3.36×10 ^-3 Pa.s), Q is the volumetric blood flow rate, ρ_b is the blood density in the vessel (ρ_b =1.05×10^-6 kg.mm^-3), g represents gravitational acceleration (9.81 m.s^-2), L is the length of the vessel, and Θ is the angle that the vector along the centerline of the blood vessel makes with the direction of gravity. The gravity vector is oriented either along the craniocaudal axis (upright) in this study.

Gravity in the acinar arterioles and venules is neglected; therefore flow in the arterioles and venules was described by Poiseuille's equation

Finally, blood flow in a capillary sheet is described using the sheet flow model of Fung and Sobin[52]

where S is the proportion of alveolar surface area comprised of capillaries (S=0.86 (no units)), A is alveolar surface area (A=73 m² - at TLC), μ_C is the apparent viscosity of blood in the capillaries (μ_C =1.92×10^-3 Pa.s), f is a numerical friction factor (f= 21.6 (no units)), l_C is the average path length from an arteriole to a venule through the capillary network (l_C = 1186×10^-6 m - at TLC) and H is the height of the capillary sheet. In the above equations (A2-4) we solve for ΔP and Q. D (or H) is then updated based on the pressure values and the solution is iterated until convergence is reached.

Mean red blood cell (RBC) transit times (TT) through capillary sheets can also be calculated using the theory of Fung and Sobin[53] using the formula

The different forms of Equations A4-5 describing Q and TT through the alveolar sheet as a function of alveolar and blood pressures are provided in the Appendix of Clark et al.[16]

Capillary recruitment

A model of capillary recruitment is incorporated into the sheet flow model. This model predicts the proportion of capillary bed perfused (R) as a function of capillary blood pressure (P _cap) as follows

where the constants F_rec =0.65 and σrec =22.7 cmH₂ O (2.23 kPa) were fitted to the raw data of.[54] Capillary surface area (A in Eqn. A4) was scaled by R in the flow and pressure calculations.