NNScore 2.0: A Neural-Network Receptor–Ligand Scoring Function

Abstract

NNScore is a neural-network-based scoring function designed to aid the computational identification of small-molecule ligands. While the test cases included in the original NNScore article demonstrated the utility of the program, the application examples were limited. The purpose of the current work is to further confirm that neural-network scoring functions are effective, even when compared to the scoring functions of state-of-the-art docking programs, such as AutoDock, the most commonly cited program, and AutoDock Vina, thought to be two orders of magnitude faster. Aside from providing additional validation of the original NNScore function, we here present a second neural-network scoring function, NNScore 2.0. NNScore 2.0 considers many more binding characteristics when predicting affinity than does the original NNScore. The network output of NNScore 2.0 also differs from that of NNScore 1.0; rather than a binary classification of ligand potency, NNScore 2.0 provides a single estimate of the pK_d. To facilitate use, NNScore 2.0 has been implemented as an open-source python script. A copy can be obtained from http://www.nbcr.net/software/nnscore/.

Introduction

Initial ligand identification is a critical step in modern drug discovery. Currently, high-throughput screens are the gold standard.(1) These screens take advantage of well-developed biochemical assays, advanced robotics, and parallelization to test tens of thousands of compounds for potential target binding. Unfortunately, high-throughput screening is often very expensive and time consuming, placing it beyond the reach of many scientists in both academia and industry.

Consequently, many researchers are turning increasingly to computational techniques for ligand identification and optimization. While some advanced computational techniques like thermodynamic integration,(2) single-step perturbation,(3) and free-energy perturbation(4) in some cases approach experimental assays in accuracy,(5) in practice these techniques are currently too time consuming and resource intensive for high-throughput applications.

Faced with this challenge, researchers have developed other computational techniques that sacrifice some accuracy for increased speed. These techniques, which include computer docking programs and their associated scoring functions, are typically not accurate enough to properly characterize any single ligand; however, when applied to many thousands of potential ligands, they can enrich a pool of candidate compounds for true binders. Subsequent biochemical testing is required to verify binding.

Recently, Durrant et al. introduced a neural-network scoring function called NNScore(6) designed to aid the computational characterization of predocked small-molecule ligands. While the test cases included in the original NNScore paper demonstrated the utility of the program, the application examples were limited. The purpose of the current work is to further confirm that neural-network scoring functions are effective, even when compared to the scoring functions of state-of-the-art docking programs, such as AutoDock,(7) the most commonly cited program,(8) and AutoDock Vina, thought to be two orders of magnitude faster.(9) Additionally, we here present a second neural-network scoring function, NNScore 2.0. To facilitate use, NNScore 2.0 has been implemented as an open-source python script. A copy can be obtained from http://www.nbcr.net/software/nnscore/.

Materials and Methods

Database of Receptor–Ligand Complexes

The database of receptor–ligand complexes used in the current study has been described previously.^6,10 In brief, crystallographic and NMR structures with corresponding experimentally measured K_d values were identified using the MOAD(11) and PDBbind-CN^12,13 online databases. These structures were then downloaded from the Protein Data Bank.(14) Published binding affinities are biased toward potent binders; to compensate, we used AutoDock Vina(9) to dock ligands from the National Cancer Institute’s Developmental Therapeutics Program (DTP) repository into the downloaded crystal structures. Those compounds whose best-predicted pose had a docking score between 0 and −4 kcal/mol were retained as examples of weakly binding ligands. For the purpose of training the neural networks, these docked complexes were assumed to have K_d values of 1 M.

Docking Parameters

Two computer docking programs, AutoDock Vina (Vina)(9) and AutoDock 4.2 (AutoDock),(7) were used to dock ligands into nine protein receptors obtained from the directory of useful decoys (DUD) database.(15) In all cases, the docking-box dimensions and location provided by the database were used. Vina default parameters were selected, as this program has limited user-specified options. In contrast, AutoDock has many modifiable parameters; consequently, we used two AutoDock docking protocols for each ligand. One docking protocol, AutoDock_Fast, was designed to test lax parameters optimized for speed. Parameter defaults were employed, except ga_num_evals was set to 2 500 000, and ga_run was set to 10. A second docking protocol, AutoDock_Rigorous, was designed to test more thorough parameters. Aside from the default parameters, ga_num_evals was set to 10 000 000, and ga_run was set to 50.

The Vina-docked poses were reevaluated with the original version of NNScore.(6) The default 24 networks that come with the program were used. For each docked ligand, Vina proposed several possible poses. Rather than calculating the NNScore of the top Vina-predicted pose alone, we rescored all poses and selected the best-scoring pose as judged by NNScore itself. A similar protocol was used for rescoring with NNScore 2.0.

Measuring Docking-Protocol Utility: Receiver Operating Characteristic Curves

Receiver–operator characteristic (ROC) curves(16) were used to judge the utility of the virtual screens. Following docking, a moving cutoff was established, beginning at the best docking score and sweeping through to the worst. At each cutoff value, the selectivity (Se) and specificity (Sp) were calculated, as given by

where TP is the true-positive rate, FN is the false-negative rate, TN is the true-negative rate, and FP is the false-positive rate. The ROC curve was generated by plotting all pairs of (1 – Sp, Se), and the area under this curve (AUC) was calculated using the composite trapezoidal rule as implemented in SciPy.(17)

Measuring Docking-Protocol Utility: Enrichment Factors

A common virtual-screening technique is to dock a large library of potential ligands into a receptor of interest and then to recommend the best-predicted small molecules for experimental validation. An enrichment factor describes how much better this set of recommended compounds performs than a set of equal size selected at random from the entire database. The enrichment factor is given by

where E is the factor itself, Hits_rec and Inactives_rec are the number of true hits and inactive compounds among those recommended for experimental validation, respectively, and Hits_total and Inactives_total are the number of true hits and inactive compounds present in the entire compound database, respectively. For a given virtual screen, E is a simple function of the number of top-predicted compounds recommended for experimental testing.

Network Structure/Setup

The new neural networks described in the current study are similar in many ways to those described previously(6) in that they are feed-forward networks created using the FFNET python package.(18) However, there are a number of important differences between NNScore 1.0 and NNScore 2.0. For example, NNScore 1.0 characterizes receptor–ligand complexes using five metrics in its attempts to identify potent ligands: close-contact (receptor–ligand atoms within 2 Å), semiclose-contact (within 4 Å), electrostatic-interaction, ligand–atom-type, and number-of-ligand-rotatable-bonds counts are all tallied. These five characterizations ultimately serve as network input.

In contrast, the receptor–ligand characterizations used by NNScore 2.0 are more numerous. The binding characteristics encoded on the networks’ input layers are derived from two sources. First, Vina 1.1.2 (but not 1.1.1!) correctly outputs the individual term values used to calculate Vina docking scores. These values include three steric terms, labeled “gauss 1,” “gauss 2,” and “repulsion,” a hydrophobic term, and a hydrogen-bond term. Second, a recently published algorithm called BINANA(10) provides 12 distinct binding characteristics, ranging from the number of hydrogen bonds to rough metrics of active-site flexibility.

BINANA counts the number of receptor–ligand atoms that come within 2.5 Å of each other and tallies them by their AutoDock atom types. When this binding characterization was used as network input, the following atom-type pairs were permitted: (A, A), (A, C), (A, CL), (A, F), (A, FE), (A, HD), (A, MG), (A, MN), (A, N), (A, NA), (A, OA), (A, SA), (A, ZN), (BR, C), (BR, HD), (BR, OA), (C, C), (C, CL), (C, F), (C, HD), (C, MG), (C, MN), (C, N), (C, NA), (C, OA), (C, SA), (C, ZN), (CD, OA), (CL, FE), (CL, HD), (CL, MG), (CL, N), (CL, OA), (CL, ZN), (F, HD), (F, N), (F, OA), (F, SA), (F, ZN), (FE, HD), (FE, N), (FE, OA), (HD, HD), (HD, I), (HD, MG), (HD, MN), (HD, N), (HD, NA), (HD, OA), (HD, P), (HD, S), (HD, SA), (HD, ZN), (MG, NA), (MG, OA), (MN, N), (MN, OA), (N, N), (N, NA), (N, OA), (N, SA), (N, ZN), (NA, OA), (NA, SA), (NA, ZN), (OA, OA), (OA, SA), (OA, ZN), (S, ZN), (SA, ZN). All juxtaposed receptor–ligand atoms that did not correspond to these pairs were ignored.

BINANA also sums the energy of the electrostatic interaction between receptor–ligand atoms that come within 4 Å of each other and tallies this sum by atom-type pairs. When this characterization was used as input for the neural networks, the same atom-type pairs permitted for the 2.5 Å close-contact metric were again allowed, with the exception of (CD, OA). Additionally, the following atom-type pairs were also permitted for the electrostatic characterization: (A, BR), (A, I), (A, P), (A, S), (BR, N), (BR, SA), (C, FE), (C, I), (C, P), (C, S), (CL, MN), (CL, NA), (CL, P), (CL, S), (CL, SA), (CU, HD), (CU, N), (FE, NA), (FE, SA), (I, N), (I, OA), (MG, N), (MG, P), (MG, S), (MG, SA), (MN, NA), (MN, P), (MN, S), (MN, SA), (N, P), (N, S), (NA, P), (NA, S), (OA, P), (OA, S), (P, S), (P, SA), (P, ZN), (S, SA), (SA, SA). All juxtaposed receptor–ligand atoms that did not correspond to these pairs were again ignored.

BINANA also counts the number of receptor–ligand atoms that come within 4.0 Å of each other and tallies them by the AutoDock atom type. When this characterization was used as network input, the same atom-type pairs allowed for the electrostatic characterization were again permitted, except (F, ZN). Additionally, (A, CU) and (C, CD) were also permitted. All juxtaposed receptor–ligand atoms that did not correspond to these pairs were again ignored.

In the original NNScore, a single hidden layer of five neurodes was employed. As preliminary analysis suggested that an expanded hidden layer might perform better, we use a single hidden layer of ten neurodes in NNScore 2.0. As before, each of the neurodes of the input layer is connected to each of the neurodes of the hidden layer.

The network output of NNScore 2.0 also differs from what was used previously. The output layer consists of a single neurode corresponding to the predicted pK_d. In contrast, the original NNScore was a binary classifier that only distinguished between good and poor binders. As before, all hidden neurodes are connected to all output neurodes.

Each neurode had a log-sigmoid activation function, given by

where t is the input sum of the respective node. All input and output values were normalized using a linear mapping to the range (0.15, 0.85) so that each variable was given equal importance independent of its magnitude.

Different paradigms were used to train the networks; the number of inputs was varied, as was the training set used. Regardless, in all cases 1000 networks were trained for each paradigm. The weights on the network connections were initially randomized and then optimized/trained by applying 10 000 steps of a truncated Newton algorithm,(19) as implemented in SciPy.(17) The scores used for analysis were obtained by taking the average predicted score of the top 20 trained networks.

Calculating R²

To judge the predictive accuracy of the neural networks, we first plotted the known vs the neural-network predicted pK_d values. A linear regression was then performed, and the associated R² value was used to judge goodness of fit.

Results and Discussion

The current study, in which we expand upon our previous work developing a neural-network scoring function (NNScore),(6) can be divided into two parts. First, we compare the accuracy of the NNScore,(6) AutoDock 4 (AutoDock),(7) and AutoDock Vina (Vina)(9) scoring functions by docking both known ligands and physically similar decoys into nine distinct protein receptors. Second, we describe the development of a second neural-network scoring function called NNScore 2.0.

Comparing NNScore, AutoDock, and Vina

To compare the NNScore, AutoDock, and Vina scoring functions, we turned to the DUD database.(15) The DUD database contains 40 protein targets, each with numerous known ligands. Each of these true ligands is associated with 36 decoy molecules. These decoys are not chosen at random; they are rather carefully selected to be physically similar to the known binders. Consequently, distinguishing between the ligands and decoys of the DUD database using computational methods is likely to be more difficult than distinguishing between the active and inactive compounds present in large databases of diverse small molecules. This challenging set of compounds/receptors is thus useful for robustly testing novel scoring functions.

Of the 40 available DUD targets, 9 were associated with over 100 known ligands: acetylcholinesterase (AChE); cyclooxygenase-2 (COX-2); dihydrofolate reductase (DHFR); epidermal growth factor receptor, tyrosine kinase domain (EGFr); fibroblast growth factor receptor 1, tyrosine kinase domain (FGFr1); coagulation factor Xa (FXa); p38 map kinase platelet-derived growth factor receptor kinase (P38); β-type platelet-derived growth factor receptor (PDGFrb); and tyrosine-protein kinase c-src (SRC). These nine receptors were used for subsequent analysis.

All ligand and decoy molecules were docked into their respective structures using AutoDock and Vina. Vina-docked poses were rescored with NNScore. Two AutoDock docking protocols were used: AutoDock_Fast was designed to test AutoDock with lax docking parameters optimized for speed, and AutoDock_Rigorous was designed to test AutoDock with more thorough parameters.

Several metrics to judge the effectiveness of virtual screens have been used. One technique is to calculate the area under a ROC curve.(16) ROC curves seek to simultaneously measure two important characteristics of a virtual screen: the ability to correctly identify true ligands and to discard decoys. The area under a ROC curve (AUC) is thought to correspond to the probably that a randomly picked known ligand will rank better than a randomly picked decoy molecule. If the AUC is 0.5, the screen has performed no better than selecting potential ligands at random. If the AUC is 1.0, the virtual screen is optimal.

With the remarkable exception of DHFR, AutoDock performed poorly as judged by the ROC AUC, regardless of whether or not the AutoDock_Fast or AutoDock_Rigorous protocol was used (Table 1). The AUC of the AutoDock screens was generally less than 0.5, meaning identifying true ligands by random selection would have been more effective. Vina performed somewhat better, with an average AUC of 0.58 over the nine proteins. The original NNScore algorithm, however, was the most effective, with an average AUC of 0.64. Clearly the best scoring function for a given project is highly system dependent; however, in the absence of specific evidence that would recommend a particular function, docking with Vina and rescoring with NNScore is often the best choice.

Table 1. Virtual screen AUC ROC values corresponding to nine protein targets and five distinct docking programs/scoring functions. ^a.

	NNScore 1.0	NNScore 2.0	AutoDockFast	AutoDockRigorous	Vina
AChE	0.55	0.57	0.48	0.53	0.67
COX-2	0.74	0.49	0.38	0.43	0.31
DHFR	0.72	0.83	0.83	0.95	0.76
EGFr	0.47	0.51	0.51	0.49	0.61
FGFr1	0.58	0.55	0.41	0.35	0.46
FXa	0.76	0.52	0.44	0.47	0.63
P38	0.75	0.58	0.40	0.37	0.54
PDGFrb	0.60	0.62	0.50	0.36	0.53
SRC	0.58	0.63	0.65	0.58	0.69
Average	0.64	0.59	0.51	0.50	0.58

^aItalic indicates ROC AUC less than 0.5. Bold indicates that the given docking program/scoring function is best suited to the corresponding receptor.

While ROC curves are certainly useful metrics, in practice one is rarely interested in the results of an entire virtual screen from the best-predicted binder to the worst. Often, researchers are more interested in only the best-predicted binders, the compounds that will ultimately be recommended for experimental validation. An enrichment factor is a useful metric that indicates how many times better a recommended set of docked compounds performs than a set of the same size selected at random from the entire small-molecule library. For example, suppose a library of 100 compounds containing 10 true ligands were docked into a receptor of interest. Further suppose that the top 20 compounds were recommended for subsequent experimental validation; among these, 5 were ultimately shown to be true ligands. Given that 10% of the entire library contained true ligands, one would expect 2 of the 20 recommended compounds to be actives by chance alone. Because 5 were in fact active, the enrichment factor is 5/2 = 2.5. Thus, for a given virtual screen, the enrichment factor can be expressed as a function of the number of top-predicted ligands selected for subsequent experimental validation.

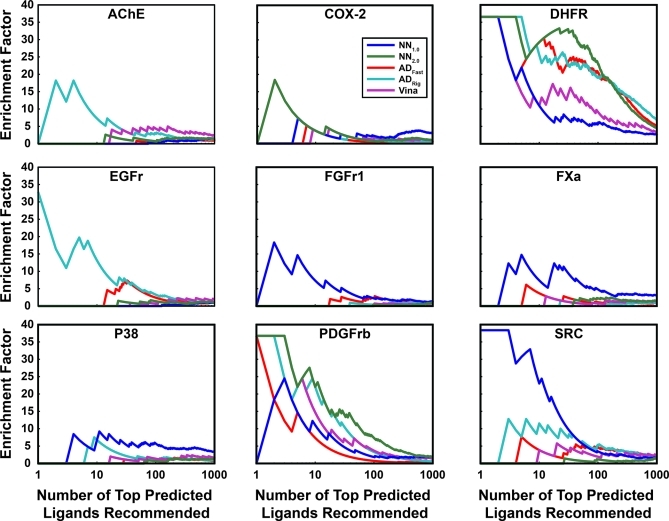
Judged by this metric, the scoring function best suited for a given project appears to be highly system dependent. Among the previously published scoring functions tested, NNScore 1.0 was arguably the best choice for docking into P38, FGFr1, FXa, and SRC. AutoDock_Rigorous appears to be best suited for docking into AChE, EGFr, PDGFrb, and DHFR. These two functions performed comparably when docking into COX-2. We note, however, that AutoDock_Rigorous is by far the slowest of the docking protocols tested. When a single processor is used to dock a single ligand, Vina takes at most a few minutes, and rescoring a Vina-docked pose with NNScore takes only seconds. In contrast, AutoDock_Fast and AutoDock_Rigorous take 11.4 min and 3.5 h on average, respectively. For projects where many thousands of ligands need be docked, Vina docking with NNScore rescoring may be the most reasonable protocol (Figure 1).

Figure 1.

Virtual-screen enrichment factors. Enrichment factors are shown as a function of the number of top-predicted ligands recommended for experimental testing. NN_1.0 corresponds to the original NNScore scoring function, NN_2.0 corresponds to the NNScore 2.0 scoring function, AD_Fast corresponds to AutoDock 4.2 using parameters optimized for speed, AD_Rig (AD_Rigorous) corresponds to AutoDock 4.2 using more rigorous parameters, and Vina corresponds to AutoDock Vina. Note that the independent variable is shown on a logarithmic scale.

As Vina is a new docking program/scoring function, its reasonable performance against AChE, COX-2, DHFR, and PDGFrb, even in the absence of NNScore rescoring, is also noteworthy (Figure 1).

NNScore 2.0: Neural-Network Setup

Encouraged by the success and utility of the original NNScore, we have developed a second neural-network scoring function called NNScore 2.0. The original NNScore function accepted as input a limited number of binding characteristics, including tallies of close-contact atoms, close-contact electrostatic-interaction energies, ligand atom types, and rotatable bonds. However, many more binding characteristics can be imagined. Consequently, a far greater number of binding characterizations were considered when training the neural networks of NNScore 2.0 (see the Material and Methods Section).

The network output of NNScore 2.0 also differs from what was used previously. The original version of the scoring function was a binary classifier; the output layer included two neurodes, where (1,0) represented strong binding and (0,1) represented weak binding. In contrast, NNScore 2.0 contains only one output neurode corresponding simply to the predicted pK_d of binding. We believe these changes will significantly improve the usability of the program.

As described below, different paradigms were used to train the neural networks. Specifically, the number of input neurodes was varied according to the binding characteristics considered, and different subsets of a database of receptor–ligand complexes that has been described previously^6,10 were used for training and validation.

NNScore 2.0: Which Binding Characteristics Should Serve as Network Inputs?

A number of programs can analyze receptor–ligand binding; the output of these programs can potentially serve as the input for a neural-network scoring function. The first program, Vina 1.1.2 (but not 1.1.1!), can correctly output the individual terms used to calculate Vina docking scores, without redocking. These values include three steric terms, labeled “gauss 1”, “gauss 2”, and “repulsion”, a hydrophobic term, and a hydrogen-bond term. Second, a recently published algorithm called BINANA(10) provides twelve distinct binding characteristics, ranging from the number of hydrogen bonds to rough metrics of active-site flexibility. Importantly, BINANA includes binding metrics similar to all those used in the original NNScore algorithm.

To prevent overtraining, it is in theory best to use as few network inputs as possible while still maintaining the network’s ability to accurately predict pK_d. Overtraining can occur when the networks manage to identify small quirks in the data set that allow for accurate prediction that is not generally applicable to other, albeit similar, data sets. By keeping the number of network inputs to a minimum, any inductive bias is likely to be based on true principles of molecular recognition.

Given that Vina has been used successfully to identify novel ligands in the past (see, for example, ref (20)), we first allowed the neural networks to consider Vina output alone in attempting to predict the pK_d values of 4284 receptor–ligand complexes.^6,10 One thousand neural networks were trained using the Vina score and its five constituent terms as input; a single score was then calculated for each receptor–ligand complex by averaging the predicted pK_d values of the 20 best-performing individual networks.

The importance of the BINANA metrics was less certain. We therefore initially trained 12 sets of 1000 neural networks, again using all the receptor–ligand complexes of the database. As input, the networks of each set considered a different BINANA binding characteristic, always together with the six Vina-derived terms. A single composite score for each receptor–ligand complex was again determined by calculating the average score of the 20 best-performing individual networks. For each set of networks, an R² value was obtained from a linear regression describing the correlation between predicted and known pK_d values. The best set of inputs was considered to be that which led to the greatest improvement in R².

Once the best set of inputs was thus determined, 11 more networks were created using these same inputs plus an additional BINANA descriptor. This process was repeated in a stepwise fashion, adding with each round the BINANA characterization that had the largest impact on goodness of fit.

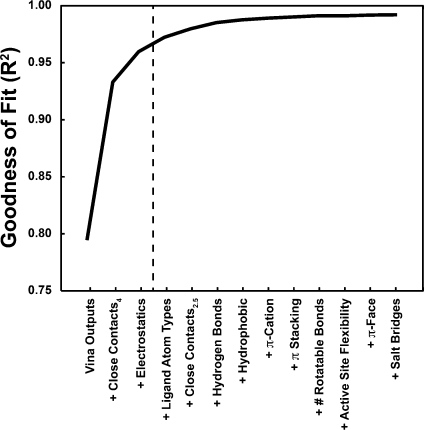
The results of this analysis are given in Figure 2. The ability of the networks to accurately predict pK_d values rose quickly when, in addition to the Vina binding characteristics, the networks were also “told” about the receptor–ligand atoms that came within 4 Å of each other and about the electrostatic energy between those atoms; indeed, with only these characterizations, the R² value rose above 0.95. With the addition of other binding characteristics, R² continued to improve, albeit more modestly.

Figure 2.

R² values improve as the networks are allowed to consider additional binding site characteristics, suggesting the development of a genuine inductive bias based on learned principles of molecular recognition.

NNScore 2.0: Verifying that the Networks Are Not Overtrained

The networks described in the previous section were trained on all the database receptor–ligand complexes available; there was no validation set, so it was not possible to assess for overtraining. We could not verify that the inductive bias was based on true principles of molecular recognition, rather than the random, isolated quirks of our particular data set.

To test for overtraining, we partitioned the database of receptor–ligand complexes into training and validation sets. Training sets of 500, 1000, 1500, 2000, 2500, 3000, 3500, and 4000 complexes were created by selecting crystallographic and docking-derived structures at random. For each training set, a corresponding validation set was created from the remaining crystallographic complexes only. The networks were subsequently trained on the complexes in the training set; to determine predictive accuracy, the trained networks were then used to evaluate the complexes of the validation set, complexes that the networks had never “seen” before.

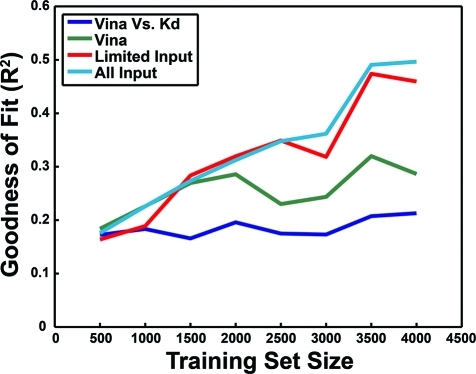
Figure 3 shows the results of this analysis. As a baseline, each of the complexes in the validation sets was evaluated with Vina, and the linear-regression R² value of the correlation between the docking score and the pK_d value was plotted in blue. As no training took place, this R² was understandably independent of the training-set size. Interestingly, simply feeding the Vina score and its constituent five terms into the neural networks led to significant improvements in predictive accuracy (Figure 3 in green), suggesting that the neural networks may be better suited for combining these terms into a single score than is the weighted sum currently employed by Vina.(9)

Figure 3.

The database of receptor–ligand complexes was divided into multiple partitions of training and validation sets. The networks were trained on the complexes in the training set; the R² values shown correspond to predictions on the validation set. In blue, the R² value associated with the correlation between the Vina docking score and the known pK_d. In green, the performance of the neural networks when only the Vina score and its constituent five terms were considered. In red, the same, with tallies of receptor–ligand close contacts (4 Å cutoff) and electrostatic interactions also included. In light blue, the same, but with all Vina and BINANA binding characterizations considered.

Additional networks that considered not only Vina binding characteristics but also tallies of the receptor–ligand atoms that came within 4 Å of each other and the electrostatic energy between those atoms fared even better (Figure 3 in red). Furthermore, networks that considered all the Vina and BINANA binding characteristics performed better still (Figure 3 in light blue).

Importantly, in all cases there was little evidence of widespread overtraining. As the training-set size increased, the accuracy with which the networks predicted the pK_d values of the complexes in the validation set improved; as the networks were exposed to more examples of receptor–ligand complexes, they became better able to predict the pK_d values of complexes they had never “seen.” If anything, one wonders if the accuracy could have been improved even further had more examples of complexes with known binding affinities been available.

Additionally, the validation-set accuracy of the networks also improved as they considered more and more binding characteristics; the inductive bias is likely based on an improved “understanding” of the principles of molecular recognition rather than overtraining. Consequently, the 20 best networks trained on all the receptor–ligand complexes of the database, using as input all Vina and BINANA characteristics, were selected for further analysis and were subsequently incorporated into the published version of NNScore 2.0.

NNScore 2.0: Use as a Docking Scoring Function

To verify that NNScore 2.0 can serve as a useful scoring function, we used the new neural networks to analyze the same DUD data set described above. The original NNScore still performed best as measured by the ROC-AUC metric (Table 1). However, NNScore 2.0 arguably performed better than any other scoring function tested, including NNScore 1.0, when docking into COX-2, PDGFrb, and DHFR. The performance in the DHFR screen was particularly notable.

Identifying the Best Docking Program for a Given Project is Highly System Dependent

The current study confirms that no single docking program/scoring function is perfectly suited for all receptor systems. While the neural-network scoring functions arguably performed better on average, they were not consistently the best scoring functions for all systems. For example, the AutoDock_Rigorous docking protocol had a remarkable ROC AUC of 0.95 in the screen against DHFR, a performance superior to that of the neural-network scoring functions. However, in general the ROC AUC of the AutoDock screens was less than 0.5, suggesting that selecting random compounds from the library would have been a better way of identifying true ligands.

Similarly, while NNScore 2.0 performed remarkably well against DHFR and other receptors, it performed poorly against targets like AChE and FGFr1. Clearly, using known ligands (positive controls) to validate a docking program/scoring function for a given receptor is critical. Only when a scoring function has been confirmed effective can a virtual screen of a diverse molecular library be reasonably undertaken. Fortunately, the neural-network scoring functions here described appear to be well suited for many protein receptors.

Conclusion

The purpose of the current work was two-fold. First, we confirmed that neural networks can be effective scoring functions by comparing NNScore(6) directly to AutoDock(7) and Vina(9) using two different metrics for docking efficacy and nine distinct receptor systems. Second, we developed a new neural-network scoring function called NNScore 2.0. To facilitate use, NNScore 2.0 has been implemented as an open-source python script. A copy can be obtained from http://www.nbcr.net/software/nnscore/.

Funding Statement

National Institutes of Health, United States