Dynamic testing of regional viscoelastic behavior of canine sclera

Abstract

Intraocular pressure (IOP) fluctuations have gained recent clinical interest and thus warrant an understanding of how the sclera responds to dynamic mechanical insults. The objective of this study was to characterize the regional dynamic viscoelastic properties of canine sclera under physiological cyclic loadings. Scleral strips were excised from the anterior, equatorial, and posterior sclera in ten canine eyes. The dimensions of each strip were measured using a high resolution ultrasound imaging system. The strips were tested in a humidity chamber at approximately 37°C using a Rheometrics Systems Analyzer. A cyclic strain input (0.25%, 1 Hz) was applied to the strips, superimposed upon pre-stresses corresponding to an IOP of 15, 25, and 45 mmHg. The cyclic stress output was recorded and the dynamic properties were calculated based on linear viscoelasticity. Uniaxial tensile tests were also performed on the same samples and the results were compared to those reported for human eyes. The results showed that the sclera’s resistance to dynamic loading increased significantly while the damping capability decreased significantly with increasing pre-stresses for all regions of sclera (P<0.001). Anterior sclera appeared to have a significantly higher damping capability than equatorial and posterior sclera (P=0.003 and 0.018, respectively). The secant modulus from uniaxial tensile tests showed a decreasing trend from anterior to posterior sclera, displaying a similar pattern as in the human eye. In conclusion, all scleral regions in the canine eyes exhibited an increased ability to resist and a decreased ability to dampen cyclic stress insults at increasing prestress (i.e., increasing steady-state IOP). The regional variation of the dynamic properties differed from those of uniaxial tensile tests. Dynamic testing may provide useful information to better understand the mechanical behavior of the sclera in response to dynamic IOP.

1. Introduction

Elevated intraocular pressure (IOP) is a primary risk factor for glaucomatous optic neuropathy; however, the mechanistic details of pressure-associated optic nerve damage are not fully understood. The biomechanical theory proposes axonal compromise, connective tissue mechanical failure, and blood flow and nutrient diffusion impairment in the optic nerve head (ONH), attributed to pathological mechanical stresses and strains associated with an increased IOP (Burgoyne and Downs, 2008; Burgoyne et al., 2005; Downs et al., 2008; Quigley and Anderson, 1977). Finite element analysis has suggested that the geometric and mechanical properties of the peripapillary sclera are important factors that influence the biomechanical states of the optic nerve head (Bellezza et al., 2000; Sigal et al., 2005; Sigal et al., 2009).

Past experimental measurements of scleral biomechanics have focused on the quasi-static elastic and viscoelastic properties. Tensile, compression, biaxial, and inflation tests (Battaglioli and Kamm, 1984; Downs et al., 2005; Eilaghi et al., 2010; Elsheikh et al., 2010; Girard et al., 2009; Mortazavi et al., 2009; Myers et al., 2010; Woo et al., 1972; Curtin, 1969; Schultz et al., 2008; Friberg and Lace, 1988; Asejczyk-Widlicka and Pierscionek, 2008) have been conducted, yielding useful information in understanding the biomechanical behavior of sclera. These studies have demonstrated that sclera is mechanically nonlinear, heterogeneous, and viscoelastic. Significant regional variations in thickness and stiffness also exist in sclera (Elsheikh et al., 2010; Norman et al., 2010), likely due to the heterogeneous distribution and organization of collagen fibers and proteoglycans.

The viscoelastic properties of sclera have been investigated using stress-relaxation and creep tests (Downs et al., 2005; Ku and Greene, 1981; McBrien et al., 2009). Dynamic mechanical analysis (DMA) is another approach to examine the viscoelastic properties of a tissue, using harmonic excitation to mimic the cyclic/dynamic loading that the tissue is often subjected to in its natural physiologic state. This method has been performed on many types of soft tissues including blood vessels, brain, cartilage, ligaments, and vocal folds (Bergel, 1961; Fallenstein et al., 1969; Patel et al., 1970; Tanaka et al., 2007; Wiikmann et al., 2009), as well as ocular tissues such as vitreous humor, eye lens and cornea (Bettelheim and Wang, 1976; Kaplan and Bettelheim, 1972; Soergel et al., 1995; Weeber et al., 2005).

To our knowledge, the regional dynamic viscoelastic properties of the sclera have not been characterized in the past. These properties may be of particular relevance to the pathophysiology of the eye due to the dynamic nature of IOP. In healthy adults IOP pulsates with a peak-to-peak amplitude of a few mmHg, caused by the systolic bolus of blood entering the eye at each heart beat (Kaufmann et al., 2006).

The ocular pulse has drawn increasing interest, due to its implication to ocular blood flow and also the physiologic states of ocular tissue. For example, in vitro studies have shown that the addition of a small cyclic component to IOP (mimicking ocular pulse) decreased trabecular outflow by an average of 30% as compared to static IOP (Ramos and Stamer, 2008; Ramos et al., 2009). The dynamic strain on the ONH and lamina cribosa has been shown to influence the gene expression of lamina cribosa cells within the extracellular matrix (Quill et al., 2011). These studies indicate that the dynamic mechanics of the eye may play a role in IOP control and ocular tissue remodeling, and thus are an important element of understanding eye physiology and pathology.

The objective of this study was to examine the dynamic mechanical properties of the sclera in response to cyclic loadings. These properties were measured at different regions (i.e., anterior, equatorial, and posterior) of the sclera by applying a small cyclic strain superimposed to different levels of pre-stresses that mimicked clinically relevant steady-state IOP. Our hypotheses are: (1) the sclera’s ability to resist and dampen dynamic loadings will change when the steady-state IOP (i.e., pre-stress) increases; and (2) the different regions of the sclera have different abilities to dampen dynamic stress/strain inputs. We also performed standard uni-axial tensile tests on the canine scleral samples and compared the results with those reported for the human eye to evaluate the suitability of canine as an animal model for studying ocular biomechanics.

2. Materials and Methods

2.1 Tissue sample preparation

Ten canine eyes from five animals were collected within 30 minutes of euthanasia from a local animal shelter. The globes were transported and stored in a sealed container on ice. All experimentation was performed within 24 hours of euthanasia.

The diameter of the sclera was measured with an electronic caliper prior to tissue dissection. The average diameter measured from the three main axes of the eye (i.e., the superior-inferior axis, the optical axis, and the nasal-temporal axis) was used. After dissecting the corneal button, the intraocular contents including lens, vitreous humor, retina, and choroid were removed. The remaining scleral shell was fit on a polybutadiene ball to maintain tissue geometry while excising scleral strips. Rectangular tissue strips with a gage width of approximately 3.7 mm and length of 16 mm were extracted in the circumferential direction from superior to inferior in the predetermined regions of the eye using a custom made excision device composed of parallel cutting blades.

Tissue strips from the anterior sclera, equatorial sclera, and posterior sclera were prepared from each eye. The posterior, equatorial, and anterior strips were cut from the nasal side of the eye directly adjacent to the optic nerve head, along the equator, and 1 mm posterior to the canine eye’s extended limbus, respectively. A representation of the scleral cutting positions is seen in Figure 1.

Figure 1.

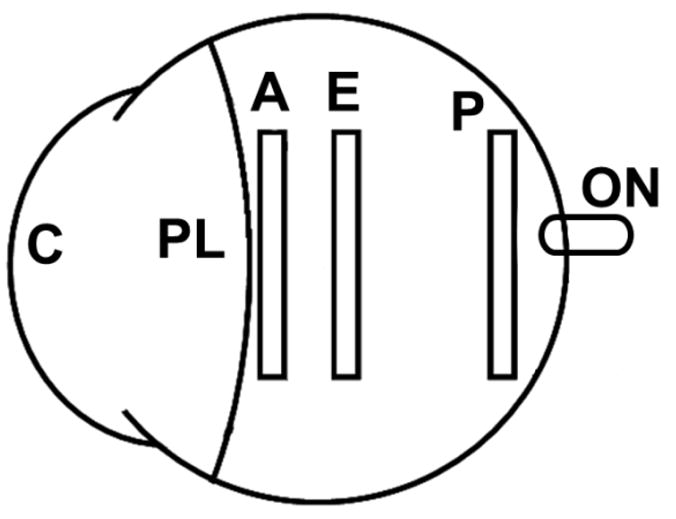
Schematic of the regions in which rectangular scleral strips were taken from the canine eye (C: cornea; PL: perilimbal region; A: anterior sclera; E: equatorial sclera; P: posterior sclera; ON: optic nerve).

It is of importance to note that the limbus and perilimbal tissue directly posterior to the limbus of the canine eye demonstrated a stepwise increase in thickness for about a 5 mm width of circumferential tissue posterior to the corneoscleral junction. Preliminary testing on this perilimbal tissue demonstrated markedly different dynamic mechanical properties compared to the rest of the canine sclera. For this reason, the cutting location for the anterior strips for this experiment was moved posteriorly, past the step-wise change in thickness, in order to provide a more homogenous representation of the scleral tissue. Anatomically, this perilimbal tissue is most likely a combination of sclera, conjunctiva, episclera, and muscular attachments that are difficult to separate for measurements.

The gage thickness and width of each strip was measured using high frequency B-mode ultrasound (Vevo660, VisualSonics, Toronto). Three B-mode image thickness measurements and one width measurement were taken at each of three spots along the central gage length. The averages of the nine total thickness measurements and three width measurements were used in further analysis. Figure 2 shows a representative B-mode image of the cross-sectional sclera with concurrent thickness and width measurements. Prior to testing, the scleral strips were kept at 4ºC and stored in phosphate buffered saline (PBS) solution. All mechanical testing was performed within 4 hours of strip excision and with a randomized order of eye regions.

Figure 2.

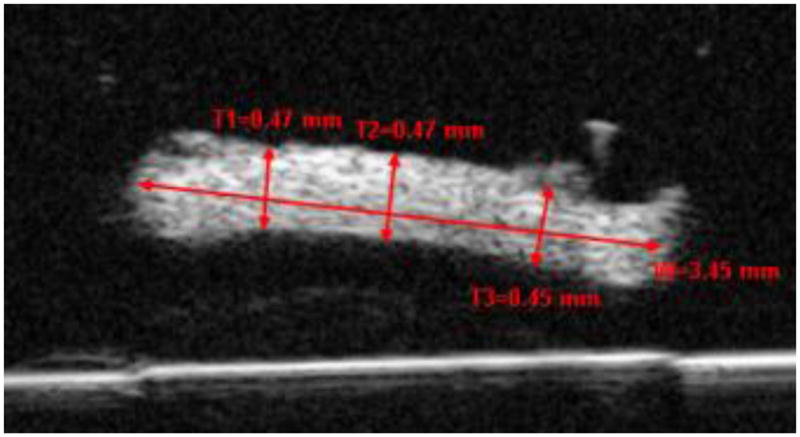
A high-frequency B-mode ultrasound image showing the cross-section of a scleral strip. Three thickness measurements and one width measurement using the VisualSonics image processing software (recalibrated for a speed of sound = 1640 m/s) are shown. W=Width; T=Thickness.

2. 2 Dynamic Testing Method and Protocol

Dynamic mechanical analysis (DMA) is one of the standard methods to determine the viscoelastic properties of a material by applying a small amplitude, cyclic strain and observing the cyclic stress response. For a given sinusoidal strain input with the form:

$$\epsilon ={\epsilon }_{\circ }sin(\omega t+{\delta }_{\epsilon }),$$ (1)

the resulting stress response will be sinusoidal if the applied strain is small enough so that the tissue can be approximated as linearly viscoelastic (Ferry, 1980; Fung, 1993). The sinusoidal stress output may differ in phase from the applied strain depending on the viscoelastic properties of the tissue:

$$\sigma ={\sigma }_{\circ }sin(\omega t+{\delta }_{\sigma })$$ (2)

where σ_∘, ε_∘, δ_σ, δ_ε, and ω, are the peak stress amplitude, peak strain amplitude, stress phase shift, strain phase shift, and angular frequency of the harmonic excitation, respectively. For a purely elastic material, the sinusoidal stress and strain are perfectly in phase (i.e., δ_σ = δ_ε). For a viscoelastic material there is a phase lag, δ, between the strain input and the stress response,

$$\delta ={\delta }_{\epsilon }-{\delta }_{\sigma }$$ (3)

where 0° (purely elastic) < δ < 90° (purely viscous). Representation of the parameters can be seen in Figure 3.

Figure 3.

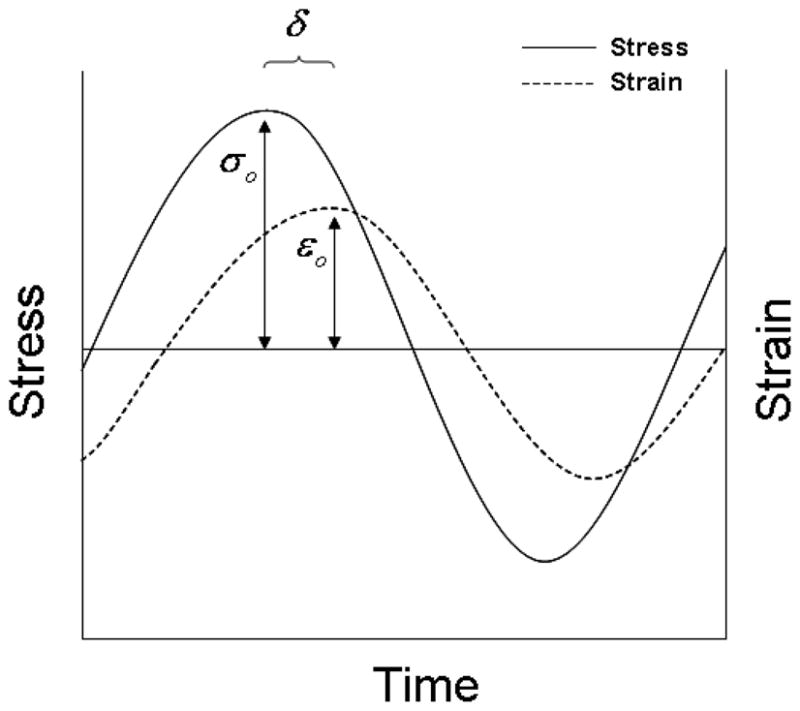
Schematic representation of the measured parameters used in calculating the dynamic properties.

The dynamic mechanical properties are quantified with the complex modulus, which can be thought of as an overall resistance to deformation under dynamic loading. The complex modulus has two components: the storage modulus (elastic component) and the loss modulus (viscous component) that are additive using the linear theory of viscoelasticity. Using complex numbers, the complex dynamic modulus E^* is defined as

$$E^{\ast }=\frac{\sigma }{\epsilon }=E^{\prime }+{iE}^{″}$$ (4)

where E′ is the storage modulus, and E″ the loss modulus. The loss modulus represents the energy dissipated from the tissue, typically as heat, while the storage modulus is proportional to the amount of elastic energy conserved. By definition, the storage modulus and loss modulus are related to the complex dynamic modulus and the phase lag δ between the stress and strain by equations

$$E^{\prime }=E\ast ·cos(\delta )$$ (5)

and

$$E^{″}=E\ast ·sin(\delta )$$ (6)

By measuring the phase lag one can achieve the separation of the real (elastic) and imaginary (viscous) components of the complex modulus, providing insight into the dynamic viscoelastic characteristics of the tissue. A simple physics analogy involves the dropping of a rubber ball in which the ball returns to a height below which it is dropped because of energy losses due to friction. The storage modulus is analogues to the height that the ball reaches while the loss modulus is analogues to the reduction in return height.

Other important viscoelastic parameters can be derived from the storage and loss moduli. One such parameter is the tan(δ), which represents the damping ability of the tissue and can be quantified by the ratio of the loss modulus to storage modulus:

$$\frac{E^{″}}{E^{\prime }}=tan(\delta )$$ (7)

Another often cited dynamic property is the dynamic viscosity, which can be found as

$${\eta }^{\prime }=\frac{E^{″}}{\omega }$$ (8)

The protocol of the dynamic testing used in the present study is given below.

Preliminary strain sweeps were first conducted on a group of canine sclera specimens to identify the strain amplitude range for the DMA testing. The samples were tested at increasing oscillating strain amplitudes at 1.0 Hz superimposed upon different pre-stress levels. The strain sweep was used to determine the strain amplitude range in which the storage modulus was independent of strain amplitude, which is a prerequisite for the application of the linear viscoelasticity theory in the analysis of dynamic properties. If the strain amplitude is outside of the linear range, a harmonic strain will not result in a harmonic stress response preventing the analysis based on linear viscoelasticity.

DMA testing was performed using a Rheometrics System Analyzer (RSA III, TA Instruments, New Castle, DE) with a displacement resolution of 0.05 μm and a force resolution of 2 μN. Scleral strips were carefully mounted to ensure good alignment and prevent grip slippage. All samples were kept moist using a custom humidifying chamber and at a temperature of approximately 37°C. The specimens were stretched from a relaxed state to a load between 0.001 N and 0.002 N to flatten the curvature and ensure full contact between sample and grips. The tissue was then allowed to equilibrate in the moist environment for 5 minutes. The gage distance between the tissue grips was approximately 9.0 mm according to the displacement readings from the RSA III device.

The harmonic excitations were superimposed on static pre-loads that corresponded to different levels of steady-state IOP. Specifically, the pre-stresses corresponding to the desired IOP levels were calculated using the tissue dimensions measured for each strip and the Laplace equation:

$$\sigma =\frac{P·r}{2·T}$$ (9)

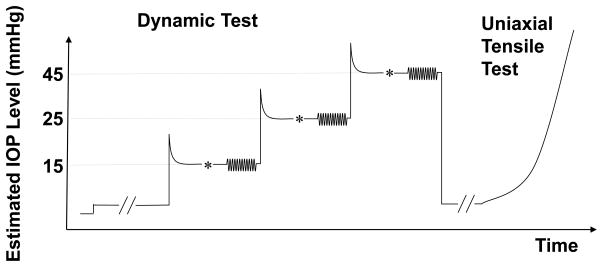
where P, r, and T are the desired steady-state IOP, radius of curvature, and thickness, respectively. It is noted that the above conversion was an estimate, which did not take into account the nonlinear, heterogeneous and viscoelastic properties of the tissue. This estimation should thus not be considered as the exact measurement of the tangential stresses caused by IOP. The tissue was first brought to a stress level approximately 45% above the desired stress, allowed to relax for five minutes, and then manually adjusted to achieve the desired pre-stress level. The tissue was again allowed to equilibrate for three minutes. The change in stress during the additional three minute equilibration time was observed to be within 10% in all sclera specimens. The DMA testing was then performed with 12 cycles of a sinusoidal strain input at an angular frequency of 1.0 Hz. A strain amplitude of 0.25% was chosen based on the preliminary strain sweep results to ensure a linear tissue response. The evolution of the stress and strain over time was recorded for the last eight cycles. The Lissajous loop (i.e., the stress-strain diagram) for each dynamic test was plotted to distinguish any large deviations from the expected ellipsoid-shaped loops dictated by the linear theory of viscoelasticity. When deviation from the expected ellipsoid-shape occurred, which suggested that the strain amplitude was outside the linear range for that tissue sample, the corresponding data point was removed from further analysis (one data point of the posterior region was removed in the present study due to this reason). This dynamic protocol was performed in the same manner at three increasing static pre-stress levels that corresponded to IOP levels of 15, 25, and 45 mmHg. Following all DMA testing, each strip was brought to the initial preload, allowed to relax for 5 minutes, and then tested up to 6% strain at a strain rate of 0.1%/s. An illustration of the testing protocol is presented in Figure 4.

Figure 4.

The DMA and tensile testing protocol for each specimen strip. (* indicated the small manual adjustments to fine tune the desired pre-stress levels which occurred between the 5-min tissue relaxation and the 3-min tissue equilibrium).

The stress/strain data obtained from the tensile tests was fit to Fung’s standard exponential model (Fung, 1993):

$$\sigma =A·(1-e^{B\epsilon })$$ (10)

The constants A and B were fitted by a least squares method. The tangent modulus (E) to stress (σ) relationship can be found by taking the derivative of Equation 10 with respect to strain,

$$E=\frac{d\sigma }{d\epsilon }=AB·e^{B·\epsilon }=B\sigma +BA.$$ (11)

This relationship provides a physical meaning to the parameters A and B, where B is reflective of the slope of the “tangent modulus/stress” curve and the product A*B represents an initial modulus of the tissue. The secant modulus at 1.0% strain was also calculated as a stiffness measure for comparison among different regions and with literature reports.

2. 3 Statistical analysis

All statistical analysis was performed using SAS 9.2 software package (SAS Institute Inc., Cary, NC). Regional differences for tan(δ), dynamic viscosity, and complex modulus, as well as the influence of the pre-stress level (corresponding to 15, 25, and 45 mmHg IOP), were tested using linear mixed models to account for the correlation in the same eye. A sensitivity analysis indicated that the models treating the ten eyes as independent and the models considering “animal” as covariate yielded the same outcome. The reported results were based on the models assuming the ten eyes were independent. The tensile test data was analyzed similarly to compare values of B, A*B, and the 1.0% secant modulus across the three regions of the sclera. Additionally, an exploratory analysis was conducted to assess for any correlations of the properties across the different scleral regions. P-values less than 0.05 were considered significant.

3. Results

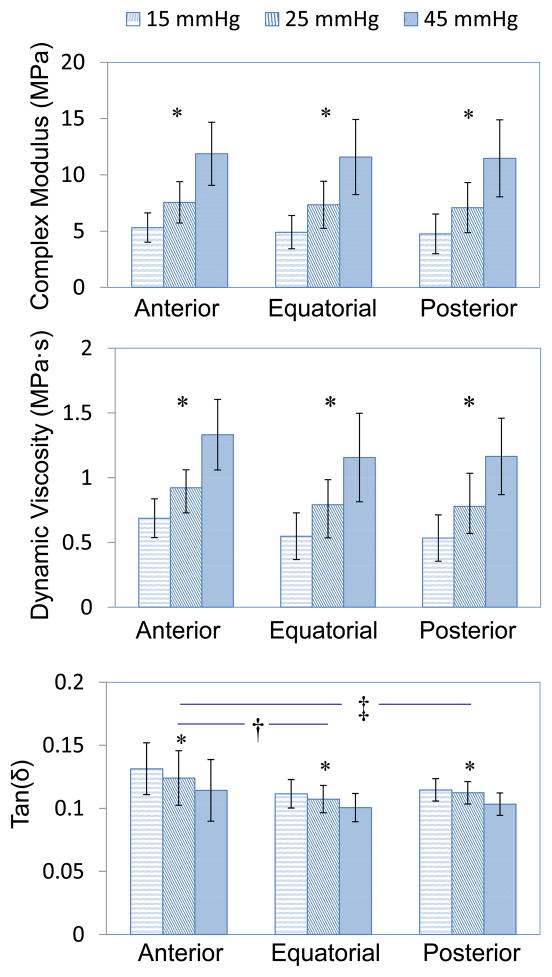
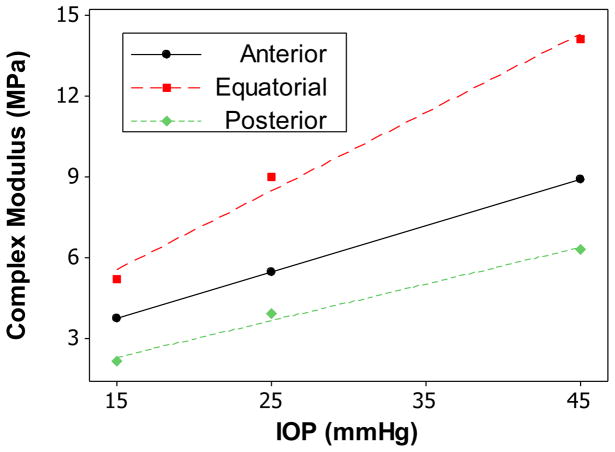
The mean thickness found using B-mode ultrasound images for the anterior, equatorial, and posterior sclera were 0.58 ± 0.08 mm, 0.47 ± 0.05 mm and 0.68 ± 0.11 mm, respectively. The average radius of curvature for the scleral shell was 11.3 ± 0.4 mm. Table 1 and Figure 5 summarize the complex modulus, tan(δ), and dynamic viscosity of the three regions of the canine sclera at different pre-stresses (equivalent to IOP levels of 15, 25, and 45 mmHg). There was significant linear relationship between the complex modulus/tan(δ)/dynamic viscosity and the pre-stress (all P’s<0.001). Figure 6 is an example showing the linear relationship between complex modulus and pre-stress in the three scleral regions of one tested eye. This linear relationship was also evident in our initial tests when five pre-stress levels (i.e., 10, 15, 25, 45, and 55 mmHg) were used (data not shown). Both complex modulus and dynamic viscosity were not significantly different among the three regions of the sclera (all P’s>0.20).

Table 1.

Complex modulus, tan(δ), and dynamic viscosity of the three regions of sclera measured at increasing pre-stresses.

	Equivalent IOP (mmHg)	Anterior (n=10)	Equatorial (n=10)	Posterior (n=9)
Complex Modulus (MPa)	15	5.32 ± 1.30	4.91 ± 1.47	4.76 ± 1.76
	25	7.56 ± 1.83	7.35 ± 2.09	7.09 ± 2.23
	45	11.9 ± 2.80	11.58 ± 3.34	11.47 ± 3.42
tan(δ)	15	0.131 ± 0.011	0.112 ± 0.009	0.115 ± 0.015
	25	0.124 ± 0.011	0.107 ± 0.009	0.112 ± 0.016
	45	0.114 ± 0.011	0.101 ± 0.009	0.103 ± 0.010
Dynamic Viscosity (MPa *s)	15	0.69 ± 0.15	0.55 ± 0.18	0.53 ± 0.18
	25	0.92 ± 0.19	0.79 ± 0.26	0.78 ± 0.21
	45	1.33 ± 0.27	1.16 ± 0.34	1.16 ± 0.30

Figure 5.

Regional mean and standard deviation of complex modulus, tan(δ), and dynamic viscosity measured at pre-stresses equivalent to IOP loadings of 15, 25, and 45 mmHg. Error bar represents standard deviation. Complex modulus and dynamic viscosity increased significantly while tan(δ) decreased significantly with increasing pre-stress levels across all sclera regions (P<0.001, indicated by *). Tan(δ) was significantly higher in anterior sclera than equatorial and posterior sclera (P=0.003 and 0.018, indicated by † and ‡, respectively). There was no significant regional difference of the sclera in terms of complex modulus or dynamic viscosity (P=0.60).

Figure 6.

Complex modulus vs. pre-stress (at equivalent IOP) for anterior, equatorial, and posterior sclera from one canine eye. The regression lines showed strong linear relationships.

When the pre-stress increased, tan(δ) significantly decreased in all three regions of the sclera (P<0.001). The anterior sclera had a significantly higher tan(δ) than the equatorial and posterior sclera (P=0.003 and 0.018, respectively). There was no difference in tan(δ) comparing the equatorial and the posterior sclera (P=0.60).

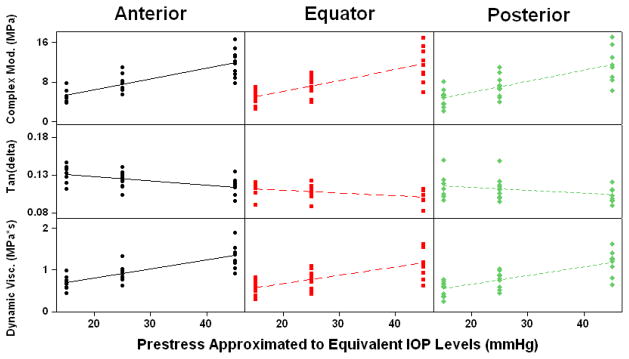
Overall trends and data ranges for complex modulus, tan(δ), and dynamic viscosity can be seen in Figure 7. No significant pairwise correlations were found for any dynamic properties between the different regions of the sclera.

Figure 7.

Scatter plots showing the range and trends of complex modulus, tan(δ), and dynamic viscosity with increasing pre-stress levels.

Table 2 contains the results from uni-axial tensile tests, including the mean and standard deviation for B, A*B, and the secant modulus at 1.0% strain. The secant modulus of the posterior sclera at 1.0% strain was significantly lower compared to that of the equator (P=0.004) and anterior (P=0.012) sclera. The equatorial sclera had smaller mean secant modulus (1.0%) than the anterior sclera, but the difference was not statistically different in this study (P=0.14). All stress-strain data fit the standard exponential model with an R² value greater than 0.98. In addition, a significant correlation of 0.89 was found for the 1.0% strain secant modulus between the equatorial and posterior sclera (P=0.008, Pearson correlation).

Table 2.

The 1.0% strain secant modulus and curve fitting parameters using the standard exponential model for the uni-axial tensile tests data from the three regions of the canine sclera.

Region	1.0% Secant Modulus (MPa)	B	A*B (MPa)
Anterior (n=10)	2.93 ± 2.21	44.67 ± 10.85	4.38 ± 2.79
Equatorial (n=9)†	1.72 ± 1.20	45.63 ± 9.54	2.96 ± 1.85
Posterior (n=8)†	0.74 ± 0.66	49.81 ± 9.77	1.88 ± 0.97

^†Data from one equatorial and two posterior specimens were discarded due to tissue-clamp slippage prior to reaching the desired strain level.

4. Discussion

The primary findings of this study include: (1) the damping ability (i.e., tan(δ)) of the anterior sclera appeared to be significantly higher than the other regions, and there was no significant difference in the complex modulus and dynamic viscosity between different regions of the sclera; (2) when the pre-stress increased (as in an elevated IOP), complex modulus (the ability to resist dynamic loading) significantly increased while tan(δ) (the damping ability) significantly decreased in all regions of sclera. The dynamic properties demonstrated a distinct regional pattern as compared to the quasi-static properties: the secant modulus (at 1.0% strain) of the posterior sclera was significantly lower than that of the anterior and equatorial sclera, while the complex modulus remained essentially the same across different regions. In addition, the uni-axial tensile properties in canine sclera were in good agreement with the reported data on human sclera within physiologic strain levels (i.e., lower than 5.0%). These findings are elaborated below.

The dynamic damping of canine sclera found in the present study (0.101 to 0.134 in average) fits into the range of past reports on soft tissue. Arteries have been shown to have tan(δ) values between 0.07 and 0.17 in the longitudinal and radial directions.(Bergel, 1961; Patel et al., 1970) Human cornea was reported to have tan(δ) values ranging from 0.05 to 0.07 when the dynamic oscillations were superimposed upon a static strain of 18–20%.(Kaplan and Bettelheim, 1972) The tan(δ) values indicate that the sclera, similar to other viscoelastic biological tissue, is considerably more elastic than viscous.

The complex modulus and dynamic viscosity both increased significantly with increases in pre-stress levels at all three scleral regions. This result indicates that the dynamic properties of the sclera have a strong dependence on the pre-stress level. Physiologically, this result suggests that the sclera is capable of increasing its resistance to cyclic loadings at increasing IOP levels, protecting the eye from large and potentially destructive dynamic strains. The increase of the complex modulus with increasing pre-stress was reminiscent of the familiar nonlinearity of collagenous tissue in response to quasi-static loadings (i.e., increased tensile modulus at increased loading). However, the complex modulus is not equivalent to the tensile modulus because the former represents how “stiff” a material is in response to a dynamic loading. For very viscous materials, the complex modulus could have a significant component due to viscosity that may or may not have the same positive association with pre-stress.

There was evidence of a decreasing trend of tan(δ) with increasing pre-stress. This inverse relationship represents an increase in the ratio of the conserved mechanical energy to energy lost as heat in the sclera tissue during cyclic loadings superimposed upon an elevated pre-stress. This change may be due to an alteration in the interactions between proteoglycans, water, and collagen fibers at increased pre-stress (Silver et al., 2001a; Silver et al., 2001b). Elevated tension on the collagen fibers and cross-links between collagen fibers may allow for a greater storage of mechanical energy during dynamic loading. However, as indicated by the decreasing tan(δ), the energy dissipation may not increase by the same magnitude, likely due to a combination of a decrease in collagen fibril sliding and an increase in water expulsion from the collagen matrix (Silver et al., 2001a; Silver et al., 2001b). It is noted that the current study only involved acute increases in pre-stress. Long-term exposure to increased pressure may induce tissue remodeling in sclera and potentially lead to changes in the dynamic properties different from what was found in the present study.

Together, the decrease in tan(δ) and the increase in complex modulus with increased pre-stress indicate that at higher IOP levels the canine sclera may resist overall deformation better but loses some capability to dampen dynamic mechanical inputs, such as from ocular pulse or other IOP fluctuations. This loss of scleral damping at higher IOP levels may redistribute the mechanical energy to other tissue (cornea, vitreous humor, or ONH) in a different manner as compared to lower IOP levels. The detailed implications of these dynamic properties at the tissue, cellular and molecular levels have yet to be elucidated.

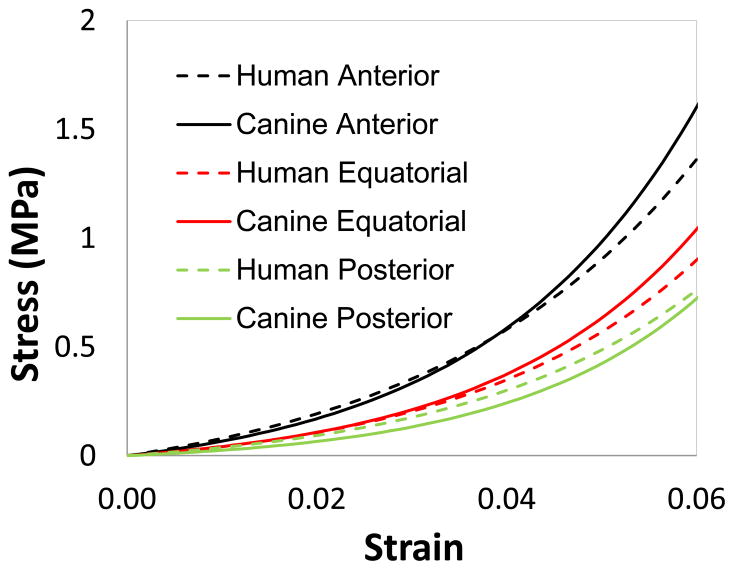
Based on quasi-static tensile tests of human scleral strips, it was reported that on average the anterior sclera had the highest secant modulus followed by the equatorial sclera and the posterior sclera (Elsheikh et al., 2010; Friberg and Lace, 1988; Curtin, 1969). Our uni-axial tensile tests on canine sclera showed similar results in both the trend and the modulus values compared to those found in human sclera. This result provides evidence of the soundness of the testing techniques and sample conditions in the present study. Figure 8 contains the exponential fit of the canine scleral quasi-static tensile test data from the present study compared to data reported by ElSheikh et al. on human sclera (Elsheikh et al., 2010). The stress-strain relationship was quite similar at low strain levels but began to deviate as strain increased beyond 4–5%. Our experimental results only contained data up to 6% strain because the physiological strains in sclera are largely within this range. The overall uni-axial tensile properties of the canine sclera appeared to be similar to that of humans, indicating the suitability of using canine eyes as an animal model for certain biomechanical experimentation. Future studies are needed to compare the dynamic properties between these two species.

Figure 8.

The exponential fit for canine sclera at the anterior, equatorial, and posterior regions as compared to that reported for human sclera (Elsheikh et al., 2010).

Regionally, the dynamic complex modulus of the canine sclera did not show the same trend from anterior to posterior as the quasi-static elastic modulus that this study and previous human tissue studies demonstrated (Curtin, 1969; Elsheikh et al., 2010; Friberg and Lace, 1988). This may be explained from two perspectives. First, the microstructural constituents that govern the quasi-static mechanical properties may be different in form and degree than those that govern the dynamic properties. The regional difference in the tensile modulus is believed to arise from the differences in regional microstructure, including the collagen fiber size, compactness, and the angle of weave of the collagen fiber bundles (Curtin, 1969). Dynamic properties also have strong dependence on microstructure, but involve different aspects of the microstructure. For example, the collagen fiber sliding and internal friction between collagen fibers and matrix were believed to influence the dynamic properties of skin and arterial wall (Silver et al., 2001a; Silver et al., 2001b). Second, the dynamic testing in this study was performed at a pre-stress level calculated for individual tissue samples at an equivalent IOP. Thus, the pre-stress varied from sample to sample due to the difference in sample thickness. Nonetheless, a theoretical prediction of the complex modulus at a common pre-stress is feasible because of the strong linear relationship between complex modulus and the normalized pre-stress across all scleral regions observed in this study (Figure 6). Our analysis showed that at the same pre-stress, the posterior sclera, due to its greater thickness, would have the largest complex modulus, followed by the anterior sclera, and finally the equatorial sclera which was the thinnest. This trend was still different than that found for the quasi-static tensile modulus. It is also of interest to note that the dynamic modulus did not exhibit correlations between different regions in the same eye; however, we found a strong correlation in the secant modulus between equatorial and posterior sclera. These results emphasized the distinct nature of the dynamic properties of sclera.

The regional pattern seen in the present study was also different than that obtained from inflation tests in monkey eyes (Girard et al, 2009), where the regions with thinner sclera were found to have higher stiffness. Although the species difference and the microstructural factors previously discussed may have contributed to this outcome, there was a third factor that warranted consideration. The study of the monkey sclera (Girard et al, 2009) used a different loading condition, i.e., inflation of the scleral shell. The multi-axial loading during inflation tests may have elicited different mechanical responses in the scleral tissue than uni-axial tensile tests in strips. Because inflation tests better resembles the in vivo situation, future dynamic testing should consider the implementation of this loading condition.

This study has the following limitations. First, the sample size (n=10) was small, which may be partially responsible for not detecting significant regional differences in dynamic viscoelastic properties of the sclera. The current results serve as a starting point for future studies in human sclera which may or may not exhibit the same dynamic properties as canine sclera. Secondly, the use of excised strips has multiple drawbacks as noted in previous studies with excised corneas (Elsheikh and Anderson, 2005; Hoeltzel et al., 1992). The sclera is stressed along multiple axes and also curved in vivo. The uni-axial pre-stresses in combination with the severed collagen fibrils in the strips may have aligned the collagen in the loading direction, altering the natural microstructure and mechanical properties of the tissue. The results in the present study may be most relevant for relative comparisons between the different scleral regions. Future work should attempt to perform dynamic tests on the whole globe using a pressure-controlled system to identify how the corneoscleral shell handles multi-axial physiologic dynamic loads. Third, the viscoelastic properties of soft tissues can be significantly altered with varying degrees of hydration (Chan and Tayama, 2002; Chimich et al., 1992; Haut and Haut, 1997). A moist chamber with temperature and humidity control was used in this study to maintain hydration during dynamic and quasi-static tensile tests. Tissue handling such as mounting onto the mechanical grips may have introduced uncontrolled hydration changes in the test samples. This change however should be fairly consistent from sample to sample. Fourth, linear viscoelasticity was assumed in the analysis of the dynamic testing data. A small strain amplitude (i.e., 0.25%) was adopted in the present study so that the linearity assumption was likely fulfilled in most tested samples. The data from a sample that showed obvious deviation from this assumption was removed from analysis. Last, we have selected one frequency (1.0 Hz) in the current study for the dynamic testing. Ocular pulse and other physiologic dynamic loadings such as blinking, eye rubbing, and eye movement, contain a broader range of loading frequencies. Frequency sweeps should be included in future work to understand the frequency dependence of the sclera’s dynamic viscoelastic properties. Frequency sweep testing may also provide data for theoretical comparisons with other viscoelastic models such as stress-relaxation and creep tests (Chan and Tayama, 2002; Fung, 1993).

5. Conclusions

In summary, we examined the dynamic mechanical properties of the sclera in response to cyclic loadings. Our results indicated that the sclera’s ability to dampen dynamic mechanical loading may decrease at higher IOPs, and there was a detectable, albeit small, difference in the damping capabilities from anterior to posterior sclera. In addition, the dynamic complex modulus exhibited distinct regional features as compared to the quasi-static tensile modulus. These results provide a better understanding of the mechanical behavior of the sclera in response to dynamic loading.

Research Highlights.

• To our best knowledge, this is the first report on regional dynamic mechanical properties of sclera.

• Sclera’s ability to resist dynamic loadings increased at higher pre-stress (i.e., higher steady-state IOP).

• Sclera’s ability to dampen dynamic loadings decreased at higher pre-stress (i.e., higher steady-state IOP).

• Dynamic properties had a distinct regional pattern compared to quasi-static properties.

• Canine sclera had similar quasi-static properties as reported for human sclera.