Abstract
The purpose of this study was to explore individual patterns of strengths and weaknesses in children’s mathematical knowledge about common fractions. Tasks that primarily measure either conceptual or procedural aspects of mathematical knowledge were assessed with the same children in their fourth and fifth grade years (n = 181; 56% female). Procedural knowledge was regressed on levels of conceptual knowledge, and vice versa, to obtain residual scores. Residual scores capture variability in each kind of math knowledge that is not shared with the other type of knowledge. Cluster analysis using residuals indicated four distinct knowledge profiles in fourth graders: a) higher than expected conceptual knowledge and relatively lower procedural knowledge, b) relatively lower conceptual knowledge and higher procedural knowledge, c) lower concepts but expected levels of procedural knowledge, and d) relatively higher than expected levels of both procedural and conceptual knowledge. In fifth grade, another cluster emerged that showed lower procedures but expected levels of conceptual knowledge. In general, students with relatively lower than expected conceptual knowledge showed poorer accuracy on measures used to form the clusters and also word problem set-ups and estimation of sums. Implications for explaining seemingly conflicting results from prior work across studies were discussed.
Keywords: Conceptual and procedural knowledge, Fraction skills, Mathematical development, Mathematical knowledge
Mathematics involves a variety of related types of knowledge (e.g. Bransford, Brown, & Cocking, 2000; Greeno, 1991; Hecht, 1998). Two distinct types of knowledge that is essential for mathematical competence is conceptual understanding and procedural skill (Hiebert & Lefevre, 1986; Moss & Case, 1999;National Mathematics Advisory Panel, NMAP, 2008; Schneider & Stern, 2010). Conceptual knowledge involves meaningful understandings about underlying principles that govern a domain, and procedural knowledge is awareness of the processing steps or algorithms for solving a problem (Bisanz & LeFevre, 1990; Rittle-Johnson, Siegler, & Alibali, 2001). Conceptual understanding could be used during the process of solving 1/2 + 1/4 by shading corresponding regions of a circle or using a number line (Cramer, Wyberg, & Leavitt, 2008). Procedural knowledge could be used to convert the addends into common denominators and then add the numerators. Procedural steps can be carried out either with or without understanding why the algorithm works. Indeed, some children might have poor representations of the magnitudes of fraction symbols, and therefore resort to using procedures in a mechanical way (Geary, 1994; Rittle-Johnson & Siegler, 1998). Little is understood about how these types of knowledge are related to each other, such as how children’s performance on one type of mathematical knowledge corresponds to their accuracy on the other type of knowledge. It is also unclear whether particular strengths and weaknesses in mathematical knowledge are related to achievement. Such understanding would provide insight concerning the nature of mathematical knowledge and practical guidance about how to identify and treat children with math difficulties. The purpose of the present study was to explore individual patterns of strengths and weaknesses in children’s procedural and conceptual knowledge. We examined this issue with respect to emerging fraction skills, a domain of math that children and adults find particularly difficult (Hecht & Vagi, 2010; NMAP, 2008).
The ability to accurately represent number magnitudes is a central characteristic of conceptual knowledge about numbers (Hecht, Vagi, & Torgesen, 2007; Hiebert & Lefevre, 1986; Kilpatrick, et al. 2001; Siegler, Thompson, & Schneider, in press). For example, 1/2 can refer to a pie with half of it eaten, two pies with one of them eaten, and so on. Part-whole knowledge can also be used to determine the relative size of fraction numerals (Cramer, Post, & del Mas, 2002), such as ordering fractions from lowest to highest (e.g. Hecht, Close, & Santisi, 2003; Mazzocco & Devlin, 2008; Smith, Solomon, & Carey, 2005). Computation can be used to measure procedural knowledge because a step-by-step procedure is presumably the dominant approach for finding the exact answer (cf. Byrnes & Wasik, 1991; Hallett et al. 2010; Hecht, 1998; Hiebert & Lefevre, 1986; Kerslake, 1986; Rittle-Johnson & Siegler, 1998).
Despite considerable research focusing on conceptual and procedural knowledge in mathematical cognition (Canobi, 2004; Gilmore & Papadatou-Pastou, 2009; Rittle-Johnson & Siegler, 1998), there has not yet emerged a universal and agreed upon way to measure each type of knowledge independently of the other type. That is, performance on a task that presumably measures one type of knowledge may involve to some extent the other kind of math knowledge (Schneider & Stern, 2010). Accordingly, associations between concepts and procedures are reported within the .4 to .6 range (e.g. Byrnes & Wasik, 1991; Hallett et al. 2010; Hecht, 1998) and performance on each type of knowledge predicts growth in the other type (e.g. Hecht & Vagi, 2010; Rittle-Johnson & Alibali, 1999). Conceptual knowledge might be used when performing step-by-step procedures, such as by using knowledge about fraction symbol magnitudes to check whether or not the answer to a problem is plausible (Hiebert & Lefevre, 1986). Likewise, conceptual knowledge tasks might involve rotely learned procedural steps, such as memorizing the rule to determine the number of regions to shade based on the size of the denominator or combining the amounts depicted by two area models by converting each picture into a fraction symbol and then using a procedure to add up the fractions. Consequently, methods are needed to estimate student’s ability on one type of knowledge that is independent of the other kind of knowledge.
Hallett et al. (2010) demonstrated a means to obtain purer estimates of procedural and conceptual knowledge based on residual scores obtained from regression analysis. The goal was to obtain a conceptual knowledge variable that was maximally different from the procedural knowledge task, and vice versa. Conceptual items were judged by two of the authors of Hallett et al. (2010) to index student’s understandings about the magnitude of fractions. Computation problems were judged to be solved by applying a taught algorithm that can be implemented without concern for the meaning of the numerals. They also deemed items that were assumed to have not been taught to the children as conceptual items. It is noted that the present study adopted the first two criteria for identifying tasks as procedural or conceptual. Performance on the procedural knowledge task was regressed on levels of performance on the conceptual knowledge variable (and grade), and vice versa, to obtain the residual scores. This allows for estimation of one type of mathematical knowledge while statistically controlling for shared components of performance with the other type of knowledge.
Hallett et al. (2010) employed a cluster analysis on residual scores from a concurrent sample of fourth and fifth graders. The residuals for procedural and conceptual knowledge were compared to determine student’s strengths and weaknesses. The first cluster (lower procedures) included children whose procedural knowledge was relatively worse than expected by performance on the conceptual knowledge task, while conceptual knowledge was neither better nor worse than expected by performance on the procedural knowledge task. The second cluster (lower conceptual) included those who scored relatively worse than expected on concepts while procedural knowledge was at expected levels. The third cluster (higher) scored relatively better than their peers on both types of knowledge. The fourth cluster included children who scored relatively worse than expected on concepts and relatively better than expected on procedures (higher procedural-lower conceptual). The fifth cluster scored better than expected on concepts and lower than expected on procedures (higher conceptual-lower procedural). Another interesting finding was that there was an advantage for students who exhibited relatively better conceptual knowledge than procedural knowledge – these students demonstrated better accuracy on a fraction computation task than students with relatively lower than expected conceptual knowledge.
Existence of children with differing profiles of conceptual and procedural knowledge ability provides an explanation for seemingly contradictory findings reported in prior work (Hallett et al. 2010;Rittle-Johnson & Siegler, 1998). One line of work suggests that, during initial learning of fractions, students tend to have better conceptual knowledge than procedural knowledge (Byrnes & Wasik, 1991). Byrnes and Wasik (1991) found that conceptual knowledge tasks were easier than procedural knowledge variables during initial learning of fractions. Presumably this is the case because conceptual knowledge is either more basic and easier to apprehend than procedures or because students are provided more frequent, and perhaps earlier, instructional time focused on fraction concepts than procedures. Indeed, even three- to seven-year olds can add and subtract fractional amounts in a nonsymbolic task, suggesting very early number sense for rational quantities (Mix, Levine, & Huttenlocher, 1999). In contrast, others have documented students who accurately carried out procedures, but had very little conceptual understanding about why the operation worked (Kerslake, 1986; Mack, 1990; Peck & Jencks, 1981). This pattern of results suggests that at least some students should perform relatively better on measures of procedures than concepts. Still others have proposed that both procedural and conceptual knowledge develop together (i.e., Rittle-Johnson & Alibali, 1999; Rittle-Johnson & Siegler, 1998; Rittle-Johnson, et al. 2001). In particular, learning of one type of knowledge can lead to rather immediate gains in the other type of knowledge. Rittle-Johnson and Alibali (1999) reported that learning of the concept of mathematical equivalence with whole numbers generalized to enhanced performance on an immediate test of procedural skill. Thus, if gains in conceptual knowledge lead to immediate improvements in procedures (and vice versa) then comparable levels of difficulty might be found on both types of knowledge at any given point in the learning process. Hallett et al. (2010) proposed that in any given sample, some children may learn more conceptual than procedural knowledge, some may have acquired more procedural than conceptual knowledge, and still others may learn both types of knowledge in tandem. Thus, existence of these coherent patterns of individual differences can provide an explanation for the seemingly conflicting results in the prior literature (cf. Hallett et al. 2010).
Overview of Current Study
The purpose of this study was to extend prior work by examining two related questions concerning relations between procedural and conceptual knowledge in the case of fractions. Our first research question asked whether or not clusters of different learning profiles for procedural and conceptual knowledge would emerge in the present sample. As part of this research question, we were also interested in the degree of stability of obtained learning profiles from fourth to fifth grade. A student’s pattern of strengths and weaknesses in mathematical knowledge may change over time. Presumably, as children become more effective fraction problem solvers, they will demonstrate increases in the types of mathematical knowledge that are associated with improvements in fraction skills (Hiebert & Wearne, 1989; Siegler, 2000; Wearne & Hiebert, 1986). On the other hand, difficulties with fractions may be due to persistent usage of the same inefficient strategies for problem solving. Thus, individual patterns of strengths and weaknesses in mathematical knowledge may persist over time. In summary, we attempted to replicate and extend the main findings from Hallett et al. (2010) in several ways: 1) we used other measures of conceptual knowledge that have been shown to be unique predictors of growth in fraction skills and are commonly taught to children (see Byrnes & Wasik, 1991; Hecht & Vagi, 2010), 2) we examined stability of cluster membership, and 3) our sample was from the United States, while Hallett et al.’s was from the United Kingdom.
Our second research question asked whether or not obtained clusters of students systematically differed with respect to raw accuracy on our fraction measures. It seems unclear which types of mathematical knowledge should be given priority during instruction so that students will develop greater accuracy. The dominant view appears to be that rote memorization of procedures without similar focus on conceptual understanding during initial learning is inefficient (Kilpatrick, et al. 2001; Rittle-Johnson & Siegler, 1998). Thus, it is possible that children who have relatively better conceptual than procedural knowledge also perform at higher levels of accuracy on fraction tasks, including those that were not included in the determination of clusters. By including tasks that were not included in the cluster analysis, we were able to provide an independent test of whether or not there were meaningful differences between the individual profiles (cf. Milligan & Cooper, 1987). We included both a word problem set-up and an estimation of sums task. The set-up task required students to provide the correct fraction computation problem, but not to solve it. There is evidence that prior levels of conceptual knowledge about fraction magnitudes are associated with growth in word problem set-up and estimation of sums accuracy (Hecht & Vagi, 2010). Thus, we expected that students with relatively better concepts would be more accurate on word problem set-ups and estimation tasks than students who scored relatively poorer than their peers on measures of conceptual knowledge. It is also possible that students with relatively stronger procedures then concepts will perform better on word problem and estimation tasks. Neither estimation nor word problem set-ups require using procedural knowledge to find the exact answer. However, that does not preclude some students from using procedural knowledge to find the exact answer (e.g. checking the accuracy of a word problem set-up by using an algorithm to actually solve it or calculating the exact answer for an estimation of sums problem by using procedures).
To examine our two research questions, we calculated residualized conceptual and procedural knowledge scores for each student and then used cluster analysis to obtain distinct knowledge profiles for groups of children. We tested the same children during their fourth and fifth grade school years, and then compared the results of our cluster analysis to Hallett et al. (2010). Our longitudinal data allowed for examination of the stability of membership in the knowledge clusters. Also, we determined if there were any differences between the learning profiles with respect to fraction estimation of sums and word problem set-up accuracy.
Method
Participants
We tested 260 fourth-grade students who were recruited from nine schools in South East Florida. All participating children returned an affirmative parent permission form. There were 181 (70%) of the original sample who also participated the next school year. This final sample involved 31 fourth grade and 39 fifth grade classrooms from the same nine schools (mean age in fourth grade = ~10 years and 3 months). Attrition analyses (repeated measures) revealed that the 181 children with complete data did not differ from the 79 children who did not participate in fifth grade on the study variables at baseline (i.e., all p’s >.05). This supports the assumption that data were missing at random. The racial/ethnic composition was 72 (40%) African American, 69 (38%) White, 36 (20%) Hispanic, and 4 (2%) other. There were 24 (13%) children eligible for free/reduced lunch, and 12 (7%) had a school identified disability. Age-based standard scores for full scale intelligence on the Wechsler Abbreviated Scales of Intelligence (WASI; Wechsler; 1999; 2-form version; which is normed to have a mean of 100 and standard deviation of 15) placed all children within both groups at the normal range in general intelligence (i.e., age-based standard score of at least 80 - the 9th percentile - or above) in fourth grade. Children’s mean estimated Full Scale IQ score at the fall of fourth grade was 101.36 (SD = 11.51). The mean age-based standard score on the Woodcock-Johnson III Calculation composite (WJIII; Woodcock, McGrew, & Mather, 2001) in fourth grade was 104.45 (SD =15.58) and the mean percentile rank was 61.09 (SD = 31.31). The Calculation composite is based on both the Calculation and Math Fluency measures.
Measures
For all fraction measures, total correct was used to index performance.
Procedural Knowledge
Fraction computation
Several kinds of fraction computation problems were included to measure a wide variety of problems that were potentially taught to the students. There were 12 addition and 12 multiplication fraction computation problems. For each operation, there were two items for each of six item types: (a) proper fractions, same denominators; (b) proper fractions, different denominators; (c) one term mixed fraction and the other term a proper fraction with same denominators (e.g. 2 3/5 + 1/5); (d) one term a proper fraction and the other term a whole number (e.g. 2 + 1/4), (e) one term a proper fraction and the second term a proper fraction with a zero numerator (e.g. 1/4 + 0/4); and (f) one term mixed fraction and the other term a proper fraction with different denominators (e.g. 2½ + 1/4). There were also two fraction division problems involving proper fractions with same denominators. Coefficient alpha on this sample was .80 and .87 in fourth and fifth grade, respectively.
Conceptual Knowledge
Picture-symbol
For each item, students indicated the fraction of a polygon, or set of polygons, that was shaded. Students wrote the indicated fraction in symbolic form (e.g. ½). There were 13 items. Coefficient alpha on this sample was .91 and .90 in fourth and fifth grade, respectively.
Symbol-picture
For each item, participants were presented a fraction symbol (e.g. ¾). Beside each fraction symbol there was a polygon figure or set of figures. Students shaded the polygon(s) in the amount indicated by the fraction symbol. There were 18 items. Coefficient alpha on this sample was .85 and .86 in fourth and fifth grade, respectively.
Size of fraction
For each item, students were presented a pair of numbers (e.g. ½ and 1). Students indicated which of the two numbers was the largest. There were 24 items. Coefficient alpha on this sample was .89 and .91 in fourth and fifth grade, respectively.
Picture computation
For each item, participants were presented two circles, or two squares or two rectangles (all equal in size). Part of each figure was shaded. Next to each pair of pictures was a blank picture that was the same sized shape (or shapes) as the preceding two. Students were instructed to add the amount shaded in the two pictures and draw the answer using the provided blank pictures. For example, if one picture depicted a square with ¼ shaded, and another square with 2/4 shaded, students would need to shade ¾ of the provided blank square to get this item correct. Thus, this task measures the understanding of how rational quantities depicted in pictorial form (as opposed to mathematical symbol form) can be combined. There were 13 items, with six items adding up to one or less and the remaining items with sums greater than one whole. Coefficient alpha on this sample was .88 and .84 in fourth and fifth grade, respectively.
Fraction Skills
Word problems
This test was composed of 18 word problems. Six problems were correctly solved by addition of the quantities, six by multiplying, and six by dividing. Within each set of six problems, there were two problems with whole numbers only, two involving one fraction and one whole number, and two with fractions only. Students were instructed to provide the correct mathematical equation to determine the answer to the word problem. Students were not told to provide the actual answer. Coefficient alpha on this sample was .81 and .85 in fourth and fifth grade, respectively. The total correct mathematical equation setups were recorded.
Estimation of sums
This test was composed of 12 items. Students were presented a fraction computation problem (e.g. 99/100 + 99/100 = ) with four alternatives (1, 10, 100, 1000), and circled the closest whole number to the correct sum. Coefficient alpha on this sample was .84 and .91 in fourth and fifth grade, respectively. The total correct answers were recorded.
Estimated Intelligence
WASI
This is the Wechsler Abbreviated Scales of Intelligence (WASI; Wechsler; 1999; 2-form version). The WASI is a nationally standardized screening instrument for intellectual functioning. The two-form version is based on the Vocabulary and Matrix Reasoning subtests, which are administered in approximately 15 minutes.
Procedure
Participants completed the fraction tasks in the winter of fourth grade and again in the spring of fifth grade. Fourth graders were individually administered both the WJIII Calculation and Math Fluency measures and the WASI Vocabulary and Matrix Reasoning measures which were used to create the overall full scale IQ estimate in the late fall of fourth grade. The remaining fraction-related measures were stapled together in a test booklet for group administration: fraction computation, fraction word problems, fraction estimation, picture symbol, picture computation, symbol picture, and size of fractions. Directions for each measure in the test booklet were printed at the beginning of each measure. The test booklet measures were arranged in one of six different random orders. For the group administered tasks, participants were told to complete the test booklet at their own pace and were encouraged to ask questions when necessary. Group administration was done in a vacant classroom, library, or the cafeteria. Students completed the group session test booklet in approximately 45 to 60 min.
Results
Descriptives and preliminary analyses
We created a weighted composite variable for conceptual knowledge. Principal components factor analysis across the observed conceptual knowledge variables was employed. The principal components factor analysis yielded only one factor, and therefore no rotation was necessary. A confirmatory factor analysis for the conceptual knowledge factor yielded a good fit to the data for both fourth grade (χ2= 5.13, p > .05; CFI=991) and fifth grade (χ2 = 4.17, p > .10; CFI = .993). Thus, performance on the conceptual knowledge tasks is substantially influenced by a common latent ability, which is presumably the quality of student’s representations about the magnitudes of fractions. Bivariate correlations among all of the variables are reported in Table 1. It is noted that the bivariate correlation between the conceptual knowledge factor and the procedural knowledge task (fraction computation) was .67 and .69, in fourth and fifth grades respectively. Similar correlations have been reported in some prior work, including Byrnes and Wasik (1991) who used comparable tasks at immediate posttest (r’s ranged from .38 to .55 across tasks and experiments) and also Hallett et al. (2010; r = .675).
Table 1.
Bivariate correlations among the variables
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Tasks used for the cluster analyses | ||||||||
| 1. Fraction computation – 4th | -- | |||||||
| 2. Fraction computation – 5th | .66 | -- | ||||||
| 3. Conceptual composite – 4th | .67 | .67 | -- | |||||
| 4. Conceptual composite – 5th | .61 | .69 | .84 | -- | ||||
| Tasks used for external validity | ||||||||
| 5. Word problems – 4th | .55 | .50. | .67 | .69 | -- | |||
| 6. Word problems – 5th | .60 | .59 | .72 | .73 | .76 | -- | ||
| 7. Estimation of sums - 4th | .43 | .39 | .50 | .48 | .44 | .41 | -- | |
| 8. Estimation of sums - 5th | .54 | .57 | .63 | .59 | .53 | .57 | .52 | -- |
Table Note: All correlations signt (p < at most .05).
Residualized conceptual and procedural knowledge values were obtained using linear regression in accordance with procedures described in Hallett et al. (2010). Residuals for conceptual knowledge were obtained by regressing conceptual knowledge on procedural knowledge. Residuals for procedural knowledge were obtained by regressing procedural knowledge on conceptual knowledge. Residuals provide a purer estimate of student’s conceptual knowledge by controlling for redundancy with procedural knowledge, and vice versa (cf., Cohen, Cohen, West, & Aiken, 2003). The residuals are scaled with a mean of zero and standard deviation of one. Thus, positive values indicate that those children learned relatively more about that type of knowledge than what would be expected by performance on the other type of knowledge. Negative values reflect that those children learned relatively less about that type of knowledge than what would be predicted by performance on the other type of knowledge. A residual of zero indicates that those students scored comparable to what would be predicted by the other variable.
Identification and stability of clusters
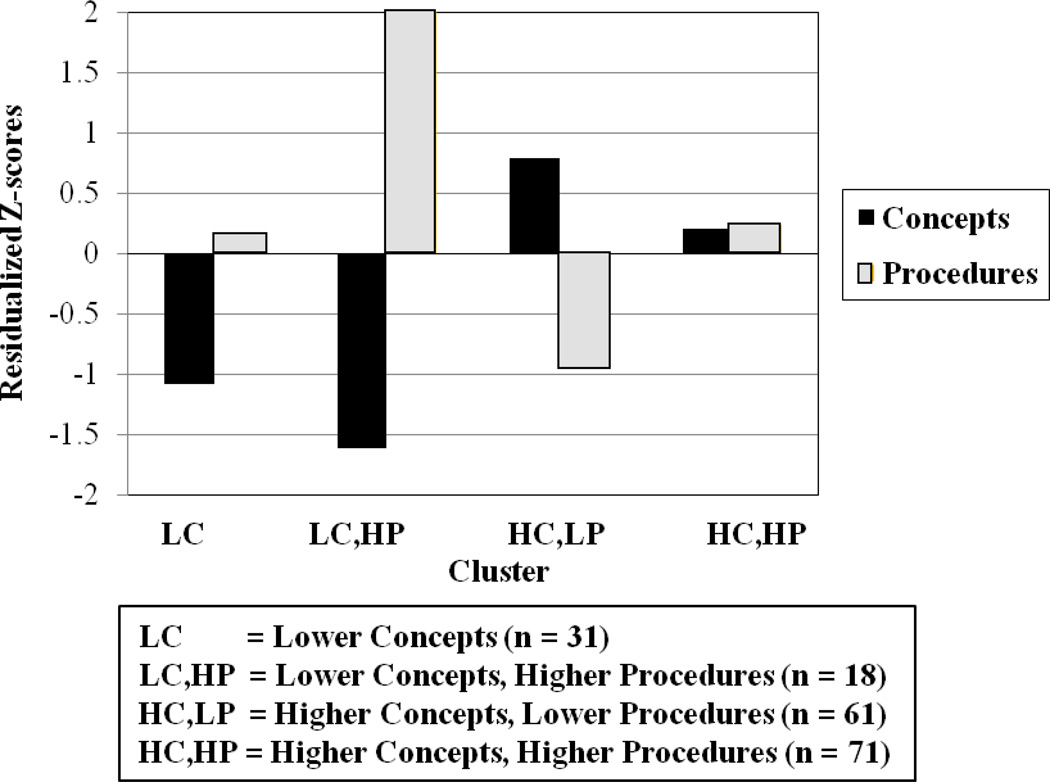
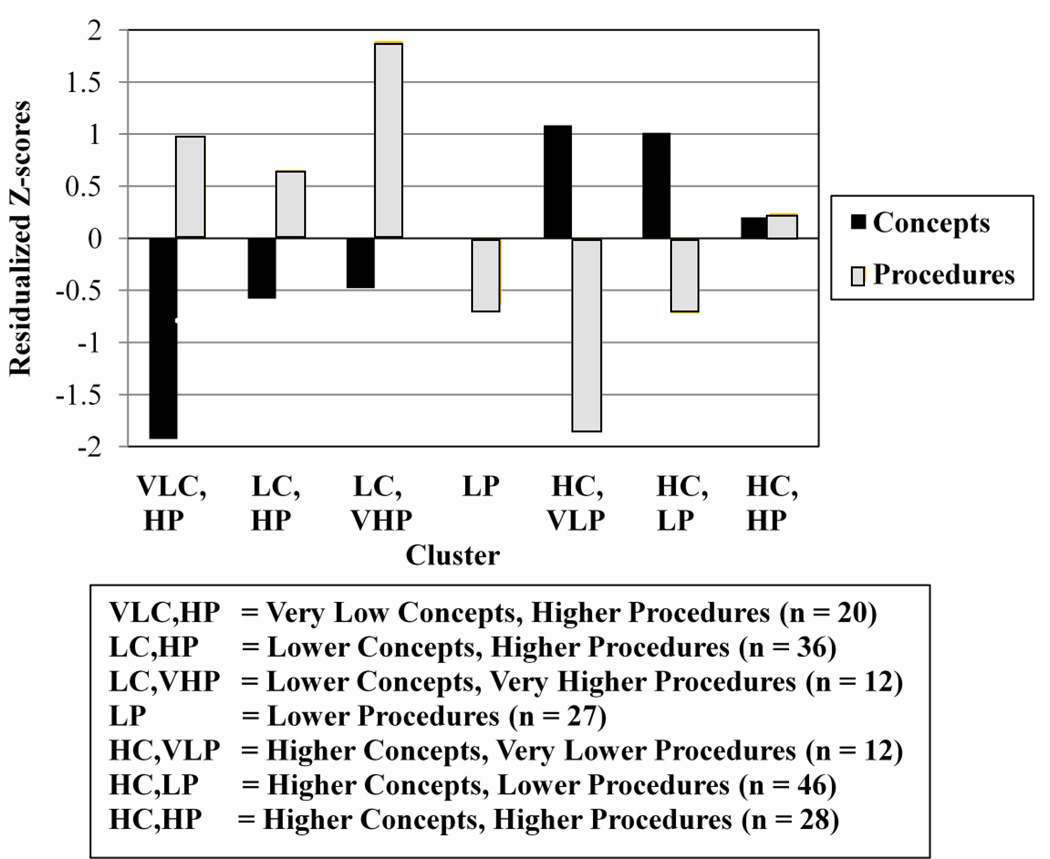
Our first research question asked what individual learning profiles were present in the sample during the fourth and fifth grades. As part of this research question, we were also interested in the stability of obtained learning profiles. Following Hallett et al (2010), cluster analysis was performed on the two residualized variables (one for conceptual and one for procedural knowledge). Also, the Ward’s method was used for the cluster analysis because it tends to reduce the number of small splinter clusters (Everitt, Landau, & Leese, 2001). Consistent with the Duda and Hart (1973) ratio criterion, a two cluster solution is a better fit to the data than a no-cluster solution. The number of clusters that potentially fit the data better than a two cluster solution was determined based on the method devised by Calinski and Harabasz (1974). The ideal number of clusters is obtained by computing the ratio between the mean sum of squared distances between each of the kth clusters and the other k - 1 clusters and the mean internal sum of squared errors for the k clusters. The mean sums of squares between the clusters is divided by the mean within cluster sums of squares to obtain the ratio, which is comparable to the F-statistic ratio (Milligan & Cooper, 1985). For both the fourth and fifth grade years, we obtained this ratio for cluster solutions ranging from two clusters to eight clusters. The cluster solution that yields the greatest ratio is chosen. As can be seen in Table 2, the Calinski and Harabasz (1974) ratios indicate that a four cluster solution was ideal for fourth graders, and a seven cluster solution had the best fit to the data for fifth grade performance. The average procedural and conceptual knowledge residuals per cluster are depicted in Figures 1 and 2. For each cluster, mean residuals for conceptual and procedural knowledge that were opposite in sign were significantly different (i.e., p < at most .05). All residuals were significantly different from the mean of zero, except for procedural knowledge in the fourth grade lower concepts cluster, and conceptual knowledge in the fifth grade lower procedures cluster.
Table 2.
Ratio of between by within mean sums of squares for determining the optimal number of clusters, segregated by grade.
| Solution | Fourth Grade | Fifth Grade |
|---|---|---|
| Two clusters | 111.436 | 64.558 |
| Three clusters | 138.049 | 40.893 |
| Four clusters | 142.734* | 48.069 |
| Five clusters | 141.352 | 54.821 |
| Six clusters | 134.708 | 59.797 |
| Seven clusters | 135.542 | 78.032* |
| Eight clusters | 139.718 | 70.790 |
Indicator values based on Calinski & Harabasz (1974). Asterisk indicates the optimal indicator value, which is the point where the ratio is maximized.
Figure 1.
Frequency and mean procedural and conceptual residual scores, segregated by cluster for fourth grade.
Figure 2.
Frequency and mean procedural and conceptual residual scores, segregated by cluster for fifth grade.
The fourth grade cluster analysis replicated four of the five individual learning profiles reported in Hallett et al. (2010). Some children showed relatively worse performance than expected for conceptual knowledge while procedural knowledge was at expected levels (lower concepts). Some students scored better than expected in conceptual knowledge and lower than expected for procedures (higher concepts and lower procedures cluster), while others showed the opposite pattern (the lower concepts and higher procedures cluster). Finally, a cluster emerged with higher than expected performance on both types of knowledge (the higher cluster). The findings in fifth grade were evidently more complex, with the best fitting cluster analysis solution involving seven clusters. For fifth graders, some children showed lower than expected procedures while conceptual knowledge was at expected levels. There were two clusters that showed higher concepts and lower than expected procedures. Also, there was one cluster of students who learned more than expected on both types of knowledge. Finally, three clusters showed lower than expected concepts, with varying degrees of higher than expected procedures.
We also examined the cluster solutions obtained using actual performance (converted to z−scores) for the procedural and conceptual knowledge variables instead of residuals. Cluster analysis was performed in the exact same manner as we used for residual scores, using Wards method. Based on the Calinski and Harabasz (1974) procedure, the optimal number of clusters was two for both fourth and fifth grade. The ratio of within to between mean sums of squares ranged from 162.258 to 220.89 and 209.073 to 229.614 for fourth and fifth graders, respectively. In both grades, one cluster had mean residuals for both procedural and conceptual knowledge that indicated lower performance than expected by performance on the other variable. The other cluster had residual means that were better than expected for both procedures and concepts. Essentially, the two cluster solution produced mean levels of procedural and conceptual performance that would be obtained with roughly a mean split of the data. It is noted that Hallett et al. (2010) reported the lack of a useful cluster solution with raw scores as well.
There were three substantive patterns in the cluster analysis solutions with residual scores that were consistent with patterns found in prior work. In fourth grade, 49 students, or 27% of the sample, showed significantly lower than expected conceptual knowledge and expected or better than expected levels of procedural knowledge t(48)=9.88, p < .001), which is consistent with prior data suggesting that some students tend to carry out procedures successfully without demonstrating substantial understanding of why the steps work. Also, 61 children, or 34% of the sample, scored higher than expected for conceptual knowledge and lower than expected for procedural knowledge (t(60)=13.53, p < .001), which is consistent with prior data suggesting that some students demonstrate substantially more conceptual than procedural knowledge. Finally, 71 (39% of sample) scored comparably high on both conceptual and procedural knowledge tasks, which is consistent with the view that learning of math knowledge occurs in tandem; t(70)=324, p > .05). In fifth grade, the same three profiles persisted, with students exhibiting either higher than expected procedural than conceptual knowledge, higher conceptual than procedural knowledge, or higher than expected performance on both types of knowledge. Thus, consistent with Hallett et al. (2010), each of the patterns of individual differences suggested by prior work was demonstrated by the current data.
Stability of cluster membership
As part of the first research question, we were interested in examining the degree to which cluster membership was stable from fourth to fifth grade. To examine this issue, we first combined the fifth grade clusters that had the same interpretation with respect to relative conceptual and procedural knowledge ability into one cluster. Specifically, three of the clusters showed lower than expected conceptual knowledge and higher than expected procedural knowledge. Also, two of the clusters showed higher than expected concepts and lower than expected procedures. Cramer’s V indicated a small, yet significant, association between cluster memberships in fourth grade and the clusters that students were placed into in fifth grade (i.e., .258, p < .001). Most of the students (i.e., n = 130 or 72% of the sample) changed category membership from fourth to fifth grade.
Although we found only a small degree of stability in cluster membership, it is noted that three of the same substantive clusters identified in fourth grade were also obtained in fifth grade (i.e., lower concepts and higher procedures, higher concepts and lower procedures, and higher concepts and higher procedures). We compared the frequency of members in each of these clusters in fourth and fifth grade. The frequencies were 18 and 68, 61 and 58, and 71 and 28, for lower concepts and higher procedures, higher concepts and lower procedures and higher concepts and higher procedures in fourth and fifth grade, respectively. Cramer’s V values for the low concepts higher procedures, higher concepts lower procedures, and higher both concepts and procedures were .24, .09, and .13 (only the first value was significant, p < .001). Thus, only the first cluster of students that showed relatively better procedures and relatively worse conceptual knowledge showed greater than chance levels of stability in learning profile membership. In all, these findings suggested modest stability of cluster membership.
Clusters and accuracy on fraction related measures
The second research question asked whether or not obtained clusters of students in fourth grade systematically differed with respect to raw (i.e., absolute) levels of accuracy on our fraction-related measures. On the one hand, mean accuracy may not be related to profiles of relative performance on procedural and conceptual knowledge tasks. For example, members of clusters with higher than expected concepts may not necessarily show more accuracy on conceptual knowledge tasks than students assigned to clusters with relatively lower than expected conceptual knowledge. On the other hand, relative performance in procedural and conceptual knowledge may indeed reflect absolute levels of accuracy. We also examined cluster differences with respect to variables not included in the determination of clusters in order to provide an independent test of whether or not there were meaningful differences between the clusters (cf. Milligan & Cooper, 1987).
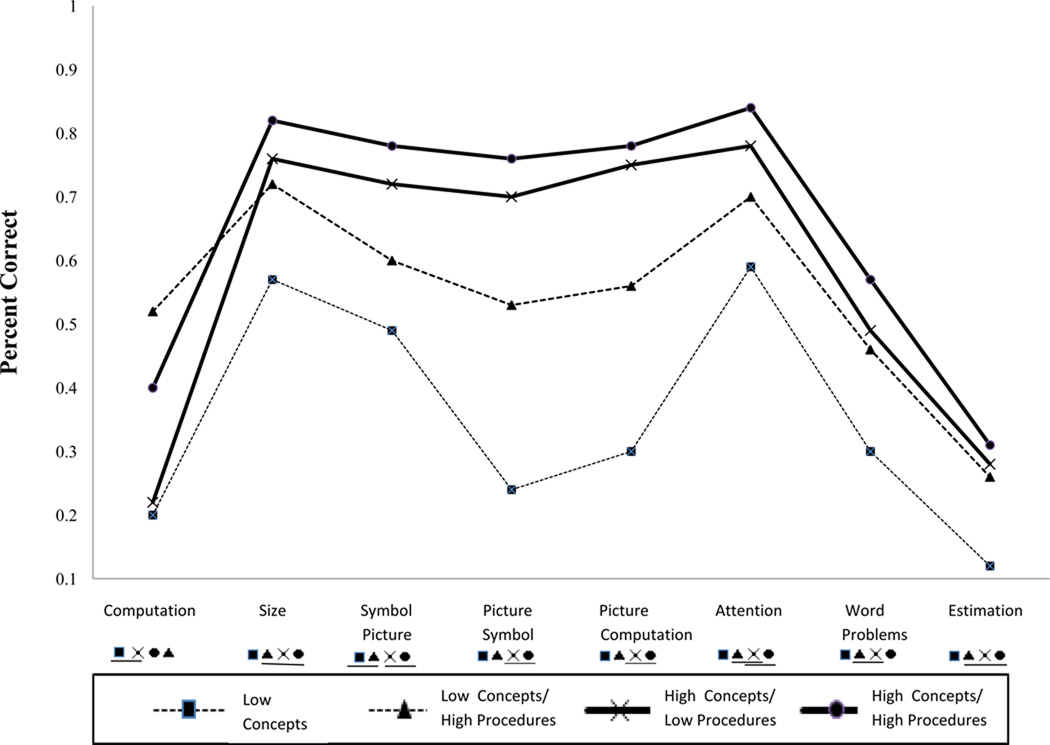
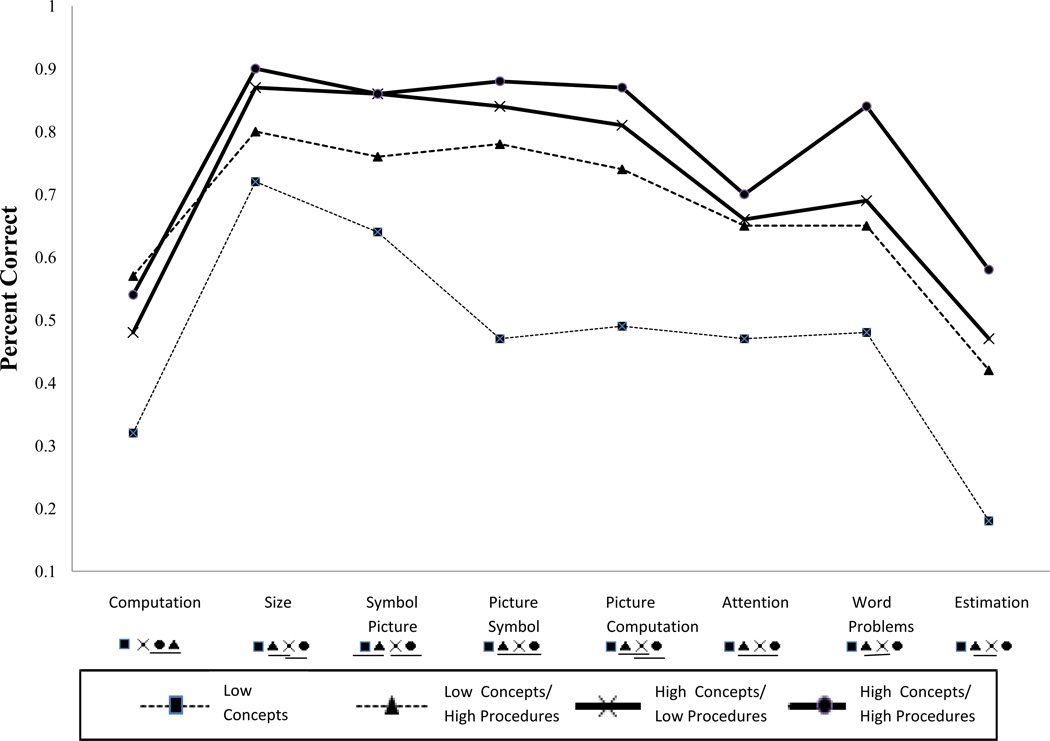
We first compared the four clusters obtained in fourth grade with respect to accuracy on tasks used to measure procedural and conceptual knowledge and also word problem and estimation of sums. To account for the dependency among observations (students) within groups (i.e., classrooms), we conducted all inferential analyses using the “complex analysis” feature in Mplus, Version 4.21 (Muthen & Muthen, 2007), in which the models were estimated via the maximum likelihood estimation method with robust standard errors (Williams, 2000). In Table 3 we show means and standard deviations for each of the observed variables segregated by the four individual learning profiles obtained in fourth grade. All of the omnibus F−values (not reported in Table 3) were significant (p < at most .01), which indicates significant differences among the clusters on all of our measures. Figures 3 and 4 depict the means reported in Table 3, along with follow-up tests. We compared univariate differences between the clusters using Fisher least significant difference tests (Seaman, Levin, & Serline, 1991). Results of the follow-up tests are depicted in each figure under the horizontal axis labels. Symbols for the four clusters (see key) are provided underneath each of the clusters. Clusters joined by a horizontal line underneath the symbols were not significantly different from one another.
Table 3.
Mean Performance Segregated by Fourth Grade Cluster Membership (SD’s in parentheses).
| Cluster |
||||
|---|---|---|---|---|
| Lower concepts (n = 31) |
Lower concepts/ higher procedures (n = 18) |
Higher concepts/ lower procedures (n = 61) |
Higher concepts Higher procedures (n = 71) |
|
| Measure | ||||
| Tasks Used in the Cluster Analysis | ||||
| 1. Fraction computation | ||||
| 4th grade | .20(.09) | .52(.20) | .22(.14) | .40(.09) |
| 5th grade | .32(.16) | .57(.22) | .48(.22) | .54(.16) |
| 2. Size | ||||
| 4th grade | .57(.25) | .72(.31) | .76(.20) | .82(.15) |
| 5th grade | .72(.15) | .80(.27) | .87(.11) | .90(.12) |
| 3. Symbol picture | ||||
| 4th grade | .49(.23) | .60(.34) | .72(.20) | .78(.16) |
| 5th grade | .64(.24) | .76(.25) | .86(.18) | .86(.11) |
| 4. Picture symbol | ||||
| 4th grade | .24(.18) | .53(.37) | .70(.27) | .76(.23) |
| 5th grade | .47(.20) | .78(.38) | .84(.30) | .88(.23) |
| 5. Picture computation | ||||
| 4th grade | .30(.16) | .56(.34) | .75(.20) | .78(.19) |
| 5th grade | .49(.20) | .74(.30) | .81(.19) | .87(.15) |
| Tasks Used for External Validity | ||||
| 6. Word problems | ||||
| 4th grade | .30(.18) | .46(.30) | .49(.22) | .57(.21) |
| 5th grade | .48(.21) | .65(.31) | .69(.24) | .84(.22) |
| 7. Estimation of sums | ||||
| 4th grade | .12(.11) | .26(.30) | .28(.25) | .31(.25) |
| 5th grade | .18(.14) | .42(.33) | .47(.32) | .58(.31) |
Figure 3.
Mean levels of accuracy by cluster for fourth graders.
Figure 4.
Mean levels of accuracy by cluster for fifth graders.
For all variables except procedural knowledge (computation), there was better performance for the cluster with higher than expected levels of both concepts and procedures, followed by the higher concepts and lower procedures cluster, then the lower concepts and higher procedures cluster, and finally the lower concepts cluster (F’s < .05 at most). The means for procedural and conceptual knowledge obtained from actual performance were consistent with the pattern of means obtained from residual scores. That is, for the measure of procedural knowledge, both clusters with higher than expected procedures were more accurate than those clusters with lower than expected or expected levels of procedural knowledge. Also, for accuracy on measures of conceptual knowledge, both clusters with higher conceptual knowledge performed better than the other clusters. For both word problem set-up and estimation of sums accuracy, both clusters with higher than expected procedures scored better than the lower concepts cluster. Thus, relatively higher than expected procedural knowledge can also enhance accuracy when conceptual knowledge is relatively low. Evidence for cluster differences with respect to accuracy on two fraction tasks that were not used in the cluster analysis (i.e., estimation of sums and word problems) provided external validation for the obtained clusters (cf. Milligan & Cooper, 1987).
Clusters and frequency of students with math difficulties
One implication of the current findings of cluster differences in mean accuracy on our fraction tasks might be that students with math difficulties are more prevalent in the lowest performing individual learning profiles. We investigated this issue by looking at the frequency of participants with math difficulties that were included in each of the individual learning profiles. Math difficulty status was based on the cutoff criteria used by Siegel and Ryan (1989; see also Barnes, Smith-Chant, & Landry, 2005; Geary, 2004). The sample included 55 students with math difficulties (MD), who scored at or below the 25th percentile on the Woodcock-Johnson III Calculation composite (WJIII; Woodcock, McGrew, & Mather, 2001) in the fall of fourth grade. Table 4. shows the Chi-Square contingency table with both obtained and expected frequency values. The chi square test of independence indicated that MD status varied with cluster in both grade four (χ2 = 51.241, p < .001, N = 181) and grade five (χ2 = 29.551, p < .001, N = 181). Significant differences between the obtained and expected frequencies for each cell in the contingency table are reported in Table 4 as well. Briefly, for fourth grade there was a significantly greater than expected proportion of children with math difficulties in the lower concepts group (χ2 = 10.282, p < .001, N =55), and significantly fewer than expected proportion of typical achievers in that same lowest performing cluster (χ2 = 10.043, p < .001, N = 126). There were also significantly fewer than expected MD children in the higher concepts, higher procedures group (χ2 = 10.121, p< .001, N = 55). In fifth grade, there was a significantly greater than expected proportion of MD students in the lower procedures group (χ2 = 3.983, p < .05, N = 55), and significantly less than expected proportion of MD students in the higher concepts and lower procedures cluster (χ2 = 3.976, p < .05, N = 55) and the higher concepts, higher procedures group (χ2 = 4.640, p < .05, N = 55). In all, these results indicate that there were substantially more children with math difficulties in the lowest performing clusters than expected by chance and fewer than expected children with MD in the highest performing cluster.
Table 4.
Observed and Expected Frequencies of Children in Cluster, Segregated by Grade and Ability Group
| MD (n = 55) |
TA (n = 126) |
|||||
|---|---|---|---|---|---|---|
| Cluster | Observed | Expected | O-E | Observed | Expected | O-E |
| Panel 1. Fourth Grade | ||||||
| 1. | LC | 25 | 9.42 | 15.58*** | 6 | 21.58 |
| −15.58*** | ||||||
| 2. | LC, HP | 5 | 5.47 | −.47 | 13 | 12.53 |
| .47 | ||||||
| 3. | HC, LP | 18 | 18.54 | −.54 | 43 | 42.46 |
| .54 | ||||||
| 4. | HC, HP | 7 | 21.58 | −14.58*** | 64 | 49.43 |
| 14.57+ | ||||||
| Panel 2. Fifth Grade | ||||||
| 1. | LP | 17 | 8.20 | 8.8* | 10 | 18.70 |
| −8.70+ | ||||||
| 2. | LC, HP | 27 | 20.66 | 6.34 | 41 | |
| 47.34 | −6.34 | |||||
| 3. | HC, LP | 9 | 17.62 | −8.62* | 49 | |
| 40.38 | 8.62 | |||||
| 4. | HC, HP | 2 | 8.51 | −6.51* | 26 | 19.49 |
| 6.51 | ||||||
Table Notes: MD = children with math difficulties. TA = Typical achievers. O-E = the difference between observed and expected frequencies. Negative differences indicate observed frequency was less than expected frequency; positive differences indicate observed frequency was greater than expected frequency. LC = lower concepts; LC, HP = lower concepts, higher procedures; HC, LP = higher concepts, lower procedures; HC, HP = higher concepts, higher procedures; HP = Higher procedures
= p < .001;
= p < .05;
= p < .10
Clusters and growth in word problem and estimation skills
We next examined whether or not there were reliable cluster differences with respect to growth in estimation of sums and word problem performance. Multiple regression analyses were carried out using hierarchical regression procedures (i.e., variables entered in steps). In all analyses, we included the autoregressive effects of fourth grade fraction skills, estimated full scale IQ, and word reading. Autoregressive refers to models where a variable is regressed on itself at a prior time period. By including fourth grade fraction skills in the first step of these analyses, we were able to predict changes in relative ordering of participant’s fraction skills (i.e., growth) during the time points under consideration (Gollob & Reichardt, 1987; Hecht, Torgesen, Wagner, & Rashotte, 2001). Fourth grade estimates of IQ and word reading were included to rule out general learning mechanisms as an underlying reason for correlations between our predictors and criterion (Bull & Johnston, 1997; Hecht, 1998). Table 5 shows the regression coefficients and total proportion of variance captured by our measures. We first entered fourth grade levels of performance on our fraction skills and control measures. In the second step, we entered three dummy variables that represented cluster membership. Dummy1 represents the contrast between the lower concepts cluster with the higher concepts and higher procedures cluster. Dummy 2 represents the contrast between lower concepts and higher procedures cluster with the higher concepts higher procedures cluster. Dummy3 represents the contrast between the higher concepts and lower procedures cluster with the higher concepts and higher procedures cluster. These analyses indicated that there were some significant differences among the clusters with respect to growth in word problem and estimation of sums skills after accounting for the control variables. Follow-up analyses were conducted to determine the significance of each pair-wise contrast (See Table 6). There were some consistent effects. Students in the lower concepts cluster tended to show less growth in word problem and estimation of sums skills than students with both higher than expected procedures and concepts. Also, there was more growth in word problem and estimation of sums skills for those with both higher than expected conceptual and procedural knowledge than those with relatively lower concepts and higher than expected procedures.
Table 5.
Growth in Fraction Skills Explained by Fourth Grade Predictors (standard errors in parentheses).
| Word Problem |
Estimation |
|||
|---|---|---|---|---|
| Step and predictor | B(SE) | Total R2 | B(SE) | Total R2 |
| 1a. Autoregressor | .73(.07)*** | .44(.05)*** | ||
| 1b. Word reading | .06(.02)** | .18(.06)*** | ||
| 1c. Estimated IQ | .04(.02)* | .61*** | .13(.06)* | .32*** |
| 2a. Dummy1 | −2.31(.70)*** | −3.06(.59)*** | ||
| 2b. Dummy2 | −1.83(.66) | −1.35(.60)*** | ||
| 2c. Dummy3 | −1.39(.42)*** | .65*** | −.81(.63) | .39*** |
Note: Autoregressor refers to the same variable as the criterion measured in fourth grade. B refers to regression coefficient. Our procedural knowledge variable used in the cluster analysis was fraction computation. Dummy1 represents the contrast between lower concepts and the higher concepts/higher procedures cluster. Dummy2 represents the contrast between lower concepts/higher procedures and the higher concepts/higher procedures cluster. Dummy3 represents the contrast between higher concepts/lower procedures and the higher concepts/higher procedures profile cluster.
Table 6.
Pairwise Contrasts between Each Profile Cluster with Respect to Growth in Fraction Skills (standard errors in parentheses).
| Variable | |||||
|---|---|---|---|---|---|
| Word Problem | Estimation | ||||
| Contrast | B(SE) R2 | B(SE) R2 | |||
| Lower concepts versus: | |||||
| Lower concepts/higher procedures | −.48(.54) | .00 | −.71(.65)** | .02 | |
| Higher concepts/lower procedures | −.91(.77) | .00 | −2.26(.51)*** | .05 | |
| Higher concepts/higher procedures | −2.31(.70)*** | .04 | −3.06(.59)*** | .09 | |
| Lower concepts/higher procedures versus: | |||||
| Higher concepts/lower procedures | 44(.71) | .00 | −.55(.62) | .00 | |
| Higher concepts/higher procedures | −1.83(.66)** s: | .01 | −1.35(.60)* | .01 | |
| Higher concepts/lower procedures versus: | |||||
| Higher concepts/higher procedures | −1.39(.42)*** | .02 | −.81(.63) | .00 | |
Table Note: Values are unique estimates after controlling for estimated full scale IQ, reading, and prior ability (i.e., the autoregressor). All regression coefficient values negative in sign.
Discussion
The current results support the usefulness of exploring individual learning profiles for procedural and conceptual knowledge (see e.g. Canobi, 2004 for the case of whole numbers). As did Hallett et al. (2010), we identified individual learning profiles that were consistent with patterns of relative strengths and weaknesses reported in prior work. The individual learning profiles suggest that it is common for some children to learn relatively more about one type of knowledge than the other type. Other children will have learned relatively more than their peers about both types of knowledge. Thus, the current study provides additional support for the possibility that seemingly conflicting results in prior work can be explained by considering individual learning profiles for procedural and conceptual knowledge.
We also found some, albeit modest, evidence for cross-age consistency in individual learning profile membership. Children’s reliance on procedural and conceptual knowledge about fractions appears to be in large part a dynamic process over time. Indeed, only the frequencies for the lower concepts and higher procedures cluster showed any consistency in membership from fourth to fifth grade. There was a tendency for some children to show relatively higher than expected levels of procedural knowledge than conceptual knowledge as they gained experience with fractions in school (cf. Byrnes & Wasik, 1991). That is, there was a larger proportion of children in the lower concepts and higher procedures clusters in fifth grade (i.e., .38) than in fourth grade (χ2 = 38.10, p < .001, N =181).
Some of the current findings can be explained by the iterative learning hypothesis (see e.g. Rittle-Johnson et al., 2001). The iterative learning view assumes that children have a pattern of development in which they make particular conceptual advances that lead to a set of procedural advances that, in turn, lead to other conceptual advances, and so on. But it remains unclear whether or not the iterative process occurs gradually over time or if gains in one type of knowledge lead to immediate gains in the other kind. If the iterative process is gradual, then cluster membership should be substantially unstable over a period of time, as we found here, and depend most on where in the learning cycle the child is at during the assessment. Meanwhile, increases in one type of knowledge in response to increments in another type of knowledge may be more immediate, as was found by Rittle-Johnson & Alibali (1999). Only the cluster with both relatively higher procedural and conceptual knowledge suggested that these types of math knowledge can develop in tandem for some students. Further work is needed to determine with more direct evidence whether or not immediate or gradual iterative learning mechanisms might lead to any of the obtained clusters found here.
The answer to our second research question replicated findings from Hallett et al. (2010), who also found that students with relatively lower concepts scored worse than any of the other obtained learning profiles on both measures used to establish external validity. We also found that students with lower than expected concepts but relatively better procedural knowledge scored higher on the measures than students with poorer concepts and expected levels of procedural knowledge. Thus, students with better than expected procedures were able to compensate to some extent for relatively poorer conceptual knowledge. The identification of individual learning profiles reported here are also useful for describing the strengths and weaknesses in mathematical knowledge for students with math difficulties. Prior work also suggests distinct individual learning profiles of children with math difficulties (e.g. Fuson & Abrahamson, 2005; Geary, 1993; Robinson, Menchetti, & Torgesen, 2002). We found more children with math difficulties to be in the lowest performing clusters (i.e., lower concepts or lower procedures) than expected by chance, and fewer than expected children with MD were found in the higher concepts and higher procedures cluster. We note, however, that children with MD were also found in the other clusters as well. Future research is needed to determine if interventions might be enhanced when the curriculum is tailored to struggling student’s strengths and weaknesses in conceptual and procedural knowledge.
Another avenue of future research is to determine if the current pattern of results occur using other methods to obtain purer estimates of procedural and conceptual knowledge. In the current study, students were allowed to choose whatever strategy they wanted to solve the conceptual and procedural knowledge items. We then statistically controlled for shared variance among these tasks to obtain purer estimates of each kind of math knowledge. Another way to obtain purer estimates of knowledge is to ask students to solve problems using a particular strategy. For example, students could be asked to solve each fraction computation problem by using either a procedural or conceptual strategy (e.g. using an area model) and then performance could be compared in these two conditions with another choice-allowed condition wherein students choose their own strategy (see e.g. Siegler & Lemaire, 1997 for an example of this “choice/no-choice” method involving whole numbers). It is possible that some students will demonstrate substantially higher levels of procedural or conceptual knowledge when constrained to use these kinds of knowledge to solve the problems than a choice-allowed condition like that currently used (see e.g. Hecht, 2006, Siegler, 1988 for a related case with whole number simple arithmetic).
A potential source for relative strengths and weaknesses in procedural and conceptual knowledge ability is classroom instruction, which may include more emphasis on one kind of knowledge than another type of knowledge. For example, fewer children may have relatively higher procedural and relatively lower conceptual knowledge in classrooms that emphasize conceptual instruction. One study documents how classroom instruction might influence whether or not procedural or conceptual knowledge about fractions are learned best by students. Rittle-Johnson & Koediger (2008) experimentally manipulated the order in which children were taught conceptual and procedural knowledge in the domain of decimal fractions with sixth graders. In the concepts-first condition, students were provided three place-value concept lessons and then three decimal arithmetic procedure lessons. In the iterative-process condition, another group of students were provided a place value concept lesson, followed by a decimal procedures arithmetic lesson, followed by concept instruction. In two experiments, the iterative-process students made significantly greater gains on a decimal arithmetic procedural knowledge test than students assigned to the concepts-first condition. With respect to conceptual knowledge, in both experiments, students in the iterative condition produced consistently higher scores for novel conceptual knowledge items than the concepts-first students. Findings from the Rittle-Johnson & Koediger (2008) study suggest that student’s emerging procedural and conceptual knowledge can be at least partially determined by order that math knowledge is taught.
In conclusion, the obtained clusters are consistent with the only other study that examined individual student’s strengths and weaknesses in fraction-related procedural and conceptual knowledge in children (i.e. Hallett et al. 2010). Focusing on individual patterns of performance helps to inform theory by reconciling seemingly contradictory findings from prior studies. Further, distinguishing between students who demonstrate stronger conceptual knowledge and those who demonstrate stronger procedural knowledge is likely to have practical importance. Remedial instruction should be most effective when teachers tailor instruction to address the specific weaknesses of individual students (see e.g. Connor, Piasta, Glasney, et al., 2009, who found this approach effective for reading instruction).
Highlights.
> In this study we compare relative performance in two kinds of knowledge concerning fractions. > Measures of conceptual and procedural knowledge were obtained. > Cluster analysis identified several patterns of strengths and weaknesses. > We conclude that prior conflicting results can be explained by our findings.
Acknowledgments
This research was supported by Eunice Kennedy Shriver National Institute of Child Health and Human Development grant 5R03HD044599-02 awarded to Steven A. Hecht. We are very grateful to the research assistants and the children and teachers who participated in this project for their generous cooperation. The contents of the article are solely the responsibility of the authors and do not necessarily represent the official views of the National Institutes of Health. All involvement by Kevin J. Vagi in the conduct of this study occurred while he was a graduate student at Florida Atlantic University.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Steven A. Hecht, Abraham S. Fischler School of Education, Nova Southeastern University
Kevin J. Vagi, Department of Psychology, Florida Atlantic University
References
- Anderson JR, Bothell D, Byrne MD, Douglass S, Lebiere C, Qin Y. An integrated theory of mind. Psychological Review. 2004;111:1036–1060. doi: 10.1037/0033-295X.111.4.1036. [DOI] [PubMed] [Google Scholar]
- Ball DL, Peoples B. Assessing a student’s mathematical knowledge by way of interview. In: Schoenfeld A, editor. Assessing mathematical Proficiency. Vol. 53. MSRI Publications; 2007. pp. 213–267. [Google Scholar]
- Barnes MA, Smith-Chant S, Landry H. Number processing in neurodevelopmental disorders: Spina bifida myelomeningocele. In: Campbell JID, editor. Handbook of mathematical cognition. New York: Psychology Press; 2005. pp. 299–314. [Google Scholar]
- Behr M, Post T. Estimation and children’s concept of rational number size. In: Schoen H, Zweng M, editors. Estimation and mental Computation: 1986 yearbook. Reston, V A: National Council of Teachers of Mathematics; 1986. pp. 103–111. [Google Scholar]
- Bisanz J, LeFevre J. Strategic and nonstrategic processing in the development of mathematical cognition. In: Bjorklund DF, editor. Children's strategies: Contemporary views of cognitive development. Hillsdale, NJ: Erlbaum; 1990. [Google Scholar]
- Bransford JD, Brown AL, Cocking RR, editors. How people learn: Brain, mind, experience, and school. Washington, DC: National Academy Press; 2000. [Google Scholar]
- Bull R, Johnston RS. Children’s arithmetical difficulties: Contributions from processing speed, item identification, and short-term memory. Journal of Experimental Child Psychology. 1997;65:1–24. doi: 10.1006/jecp.1996.2358. [DOI] [PubMed] [Google Scholar]
- Byrnes JP, Wasik BA. Role of conceptual knowledge in mathematical and procedural Learning. Developmental Psychology. 1991;27:777–786. [Google Scholar]
- Calinski T, Harabasz J. A dendrite method for cluster analysis. Communications in Statistics: Theory and Methods. 1974;3:1–27. [Google Scholar]
- Canobi KH. Individual differences in children’s addition and subtraction knowledge. Cognitive Development. 2004;19:81–93. [Google Scholar]
- Case R, Sowder JT. The development of computational estimation: A neo- Piagetian analysis. Cognition and Instruction. 1990;7:79–104. [Google Scholar]
- Cohen J, Cohen P, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. 3rd ed. Mahwah, NJ: Erlbaum; 2003. [Google Scholar]
- Connor CM, Piasta SB, Glasney S, Schatschneider C, Fishman B, Underwood P, et al. Individualizing student instruction precisely: Effects of child by instruction interactions on first graders’ literacy development. Child Development. 2009;80:77–100. doi: 10.1111/j.1467-8624.2008.01247.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cramer K, Wyberg T, Leavitt S. The Role of Representations in Fraction Addition and Subtraction. Mathematics Teaching in the Middle School. 2008;13:490–496. [Google Scholar]
- Demaray MK, Ruffalo SL, Carlson J, Buss RT, Olson AE, McManus SM, Leventhal A. Social skills assessment: A comparative evaluation of six published rating scales. School Psychology Review. 1995;246:48–671. [Google Scholar]
- Duda RO, Hart PE. Pattern classification and scene analysis. New York, NY: Wiley; 1973. [Google Scholar]
- Everitt BS, Landau S, Leese M. Cluster analysis. 4th ed. London, England: Oxford University Press; 2001. [Google Scholar]
- Flavell JH. Cognitive development: Children’s knowledge about the mind. Annua Review of Psychology. 1999;50:21–45. doi: 10.1146/annurev.psych.50.1.21. [DOI] [PubMed] [Google Scholar]
- Fuchs LS, Fuchs D, Compton DL, Powell SR, Seethaler PM, Capizzi AM, Schatschneider C, Fletcher JM. The cognitive correlates of third-grade skill arithmetic, algorithm computation, and arithmetic word problems. Journal of Educational Psychology. 2006;98:394–409. [Google Scholar]
- Fuson K. Children’s counting and concepts of number. New York, NY: Springer-Verlag; 1988. [Google Scholar]
- Fuson KC, Abrahamson D. Understanding ratio and proportion as an example of the Apprehending Zone and Conceptual-Phase problem-solving models. In: Campbell J, editor. Handbook of mathematical cognition. New York: Psychology Press; 2005. pp. 213–234. [Google Scholar]
- Fuson K, Willis G. Second graders’ use of schematic drawings in solving addition and subtraction word problems. Journal of Educational Psychology. 1989;81:514–520. [Google Scholar]
- Gagne RM. Some issues in the psychology of mathematics instruction. Journal for Research in Mathematics Education. 1983;14:275–282. [Google Scholar]
- Geary DC. Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin. 1993;114:345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC. Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association; 1994. [Google Scholar]
- Geary DC. Mathematics and learning disabilities. J. of Learning Disabilities. 2004;37:4–15. doi: 10.1177/00222194040370010201. [DOI] [PubMed] [Google Scholar]
- Gilmore CK, Bryant P. Individual differences in children’s understanding of inversion and arithmetical skill. British Journal of Educational Psychology. 2006;76:309–331. doi: 10.1348/000709905X39125. [DOI] [PubMed] [Google Scholar]
- Gollob HF, Reichardt CS. Interpreting and estimating indirect effects assuming time lags really matter. In: Collins LM, Horn LJ, editors. Best Methods for the Analysis of Change: Recent Advances, Unanswered Questions, Future Directions. Washington, DC: American Psychological Association; 1991. pp. 243–259. [Google Scholar]
- Green KD, Forehand RL, Beck SJ, Vosk B. An assessment of the relationship among measures of children’s social competence and children’s academic achievement. Child Development. 1980;51:1149–1156. [Google Scholar]
- Greeno JG. Number sense as situated knowing in a conceptual domain. Journal for Research in Mathematics Education. 1991;22:170–218. [Google Scholar]
- Gresham FM, Elliott SN. Social skills rating system. Circle Pines, MN: American Guidance Service; 1990. [Google Scholar]
- Hallett D, Nunes T, Bryant P. Individual Differences in Conceptual and Procedural Knowledge When Learning Fractions. Journal of Educational Psychology. 2010;102:395–406. [Google Scholar]
- Hecht SA. Toward an information-processing account of individual differences in fraction skills. Journal of Educational Psychology. 1998;90:545–559. [Google Scholar]
- Hecht SA. Group differences in adult simple arithmetic: Good retrievers, not-so-good retrievers, and perfectionists. Memory and Cognition. 2006;34:207–216. doi: 10.3758/bf03193399. [DOI] [PubMed] [Google Scholar]
- Hecht SA, Close L, Santisi M. Sources of individual differences in fraction skills. Journal of Experimental Child Psychology. 2003;86:277–302. doi: 10.1016/j.jecp.2003.08.003. [DOI] [PubMed] [Google Scholar]
- Hecht SA, Greenfield DB. Comparing the predictive validity of first grade teacher ratings and reading related tests on third grade levels of reading skills in young children exposed to poverty. School Psychology Review. 2001;30:50–69. [Google Scholar]
- Hecht SA, Torgesen JK, Wagner RK, Rashotte CA. The relations between phonological processing abilities and emerging individual differences in mathematical computation skills: A longitudinal study from second- to fifth-grade. Journal of Experimental Child Psychology. 2001;79:192–227. doi: 10.1006/jecp.2000.2586. [DOI] [PubMed] [Google Scholar]
- Hecht SA, Vagi K. Sources of Group and Individual Differences in Emerging Fraction Skills. Journal of Educational Psychology. 2010;102:843–859. doi: 10.1037/a0019824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecht SA, Vagi KJ, Torgesen JK. Fraction skills and proportional reasoning. In: Berch DB, M. Mazzocco MM, editors. Why is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities. New York: Brookes Publishing; 2007. pp. 121–132. [Google Scholar]
- Hedges LV, Olkin I. Statistical methods for meta-analysis. Orlando, FL: Academic Press; 1985. [Google Scholar]
- Hegarty M, Kozhevnikov M. Types of visual-spatial representations and mathematical problem solving. Journal of Educational Psychology. 1999;91:684–689. [Google Scholar]
- Hegarty M, Mayer RE, Monk CA. Comprehension of arithmetic word problems: A comparison of successful and unsuccessful problem solvers. Journal of Educational Psychology. 1995;87:18–32. [Google Scholar]
- Hiebert J. Conceptual and procedural knowledge: The case of mathematics. Mahwah, NJ: Lawrence Erlbaum Associates; 1986. [Google Scholar]
- Hiebert J, Lefevre P. Conceptual and procedural knowledge in mathematics: An introductory analysis. In: Hiebert J, editor. Conceptual and procedural knowledge. Mahwah, NJ: Lawrence Erlbaum Associates; 1986. pp. 1–27. [Google Scholar]
- Hiebert J, Wearne D. Procedures over concepts: The acquisition of decimal number knowledge. In: Hiebert J, editor. Conceptual and procedural knowledge: The case of mathematics. Hillsdale, NJ: Erlbaum; 1986. pp. 199–223. [Google Scholar]
- Kail RV. Cognitive development includes global and domain specific processes. Merrill-Palmer Quarterly. 2004;50:445–455. [Google Scholar]
- Karmiloff-Smith A. Beyond Modularity. Cambridge, MA: MIT Press; 1992. [Google Scholar]
- Kerslake D. Fractions: Children’s strategies and errors. A report of the strategies and errors in secondary mathematics project. Windsor, England: NFER-Nelson; 1986. [Google Scholar]
- Kieren TE. Personal knowledge of rational numbers: Its intuitive and formal development. In: Hiebert J, Behr M, editors. Number concepts and operations in the middle grades. Reston, VA: National Council of Teachers of Mathematics; 1988. pp. 162–181. [Google Scholar]
- LeFevre J, Greenham S, Waheed N. The development of procedural and conceptual knowledge in computational estimation. Cognition & Instruction. 1993;11:95–132. [Google Scholar]
- Mack N. Learning fractions with understanding: Building on informal knowledge. Journal for Research in Mathematics Education. 1990;21:16–32. [Google Scholar]
- Milligan GW, Cooper MC. Methodology review: Clustering methods. Applied Psychological Measurement. 1987;11:329–354. [Google Scholar]
- Mix KS, Levine SC, Huttenlocher J. Early fraction calculation ability. Developmental Psychology. 1999;35:164–174. doi: 10.1037//0012-1649.35.1.164. [DOI] [PubMed] [Google Scholar]
- Moss J, Case R. Developing children’s understanding of the rational numbers: A new model and experimental curriculum. Journal for Research in Mathematics Education. 1999;30:122–147. [Google Scholar]
- Muthen LK, Muthen BO. Mplus user’s guide. 4. Los Angeles, CA: Muthen & Muthen; 2007. [Google Scholar]
- National Mathematics Advisory Panel. Foundations for success: The final report of the national mathematics advisory panel. Washington, DC: U.S. Department of Education; 2008. [Google Scholar]
- Peck DM, Jencks SM. Conceptual issues in the teaching and learning of fractions. Journal for Research in Mathematics Education. 1981;12:339–348. [Google Scholar]
- Piaget J. Success and understanding. Cambridge, Mass: Harvard University Press; 1978. [Google Scholar]
- Resnick LB, Omanson SF. Learning to understand arithmetic. In: Glaser R, editor. Advances in instructional psychology. Vol. 3. Hillsdale, NJ: Lawrence Erlbaum; 1987. pp. 41–95. [Google Scholar]
- Rittle-Johnson B, Koedinger KR. Iterating between lessons on concepts and procedures can improve mathematics knowledge. British Journal of Educational Psychology. 2008;79:483–500. doi: 10.1348/000709908X398106. [DOI] [PubMed] [Google Scholar]
- Rittle-Johnson B, Siegler RS. The relations between conceptual and procedural knowledge in learning mathematics: A review. In: Donlan C, editor. The development of mathematical skill. Hove, England: Psychology Press; 1998. pp. 75–110. [Google Scholar]
- Rittle-Johnson B, Siegler RS, Alibali MW. Developing conceptual understanding and procedural skill in mathematics: An iterative process. Journal of Educational Psychology. 2001;93:346–362. [Google Scholar]
- Robinson CS, Menchetti BM, Torgesen JK. Toward a Two-Factor Theory of One Type of Mathematics Disabilities. Learning Disabilities: Research & Practice. 2002;17:81–89. [Google Scholar]
- Schneider M, Stern E. The developmental relations between conceptual and procedural knowledge: A multimethod approach. Developmental Psychology. 2010;46:178–192. doi: 10.1037/a0016701. [DOI] [PubMed] [Google Scholar]
- Seaman MA, Levin JR, Serlin RC. New developments in pairwise multiple comparisons: Some powerful and practical problems. Psychological Bulletin. 1991;110:577–586. [Google Scholar]
- Siegel LS, Ryan EB. The development of working memory in normally achieving and subtypes of learning disabled children. Child Development. 1989;60:973–980. doi: 10.1111/j.1467-8624.1989.tb03528.x. [DOI] [PubMed] [Google Scholar]
- Siegler RS. Individual differences in strategy choices: Good students, not-so-good students, and perfectionists. Child Development. 59:833–851. [PubMed] [Google Scholar]
- Siegler RS. In young children’s counting, procedures precede principles. Educational Psychology Review. 1991;3:127–135. [Google Scholar]
- Siegler RS. The rebirth of children’s learning. Child Development. 2000;71:26–35. doi: 10.1111/1467-8624.00115. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Lemaire P. Older and younger adults’ strategy choices in multiplication: Testing predictions of ASCM via the choice/no choice method. Journal of Experimental Psychology, General. 1997;126:71–92. doi: 10.1037//0096-3445.126.1.71. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Thompson CA, Schneider M. An integrated theory of whole number and fractions development. Cognitive Psychology. doi: 10.1016/j.cogpsych.2011.03.001. (in press). [DOI] [PubMed] [Google Scholar]
- Skemp RR. Relational understanding and instrumental understanding. Mathematics Teaching. 1976;77:20–26. [Google Scholar]
- Sophian C. Beyond competence: the significance of performance for conceptual development. Cognitive Development. 1997;12:281–303. [Google Scholar]
- Spelke ES, Kinzler KD. Core knowledge. Developmental Science. 2007;10:89–6. doi: 10.1111/j.1467-7687.2007.00569.x. [DOI] [PubMed] [Google Scholar]
- Stafylidou S, Vosniadou S. The development of students’ understanding of the numerical value of fractions. Learning and Instruction. 2004;14:503–518. [Google Scholar]
- VanLehn K. Mind bugs: The origins of procedural misconceptions. Cambridge, MA: MIT Press; 1990. [Google Scholar]
- VanLehn K, Brown J. Planning nets: A representation for formalizing analogies and semantic models of procedural skills. In: Snow RE, Federico PA, Montague WE, editors. Aptitude, learning, and instruction. Hillsdale, NJ: Lawrence Erlbaum; 1980. pp. 95–137. [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. NY: Psychological Corp; 1999. [Google Scholar]
- Wearne D, Hiebert J. Cognitive changes during conceptually based instruction on decimal fractions. Journal of Educational Psychology. 1989;81:507–513. [Google Scholar]
- Wentzel KR. Social competence at school: Relation between social responsibility and academic achievement. Review of Educational Research. 1991;61:1–24. [Google Scholar]
- Williams RL. A note on robust variance estimation for cluster-correlated data. Biometrics. 2000;56:645–646. doi: 10.1111/j.0006-341x.2000.00645.x. [DOI] [PubMed] [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson III: Complete Battery Tests of Achievement. Itasca, IL: Riverside Publishing; 2001. [Google Scholar]