Penalized Fisher Discriminant Analysis and Its Application to Image-Based Morphometry

Abstract

Image-based morphometry is an important area of pattern recognition research, with numerous applications in science and technology (including biology and medicine). Fisher Linear Discriminant Analysis (FLDA) techniques are often employed to elucidate and visualize important information that discriminates between two or more populations. We demonstrate that the direct application of FLDA can lead to undesirable errors in characterizing such information and that the reason for such errors is not necessarily the ill conditioning in the resulting generalized eigenvalue problem, as usually assumed. We show that the regularized eigenvalue decomposition often used is related to solving a modified FLDA criterion that includes a least-squares-type representation penalty, and derive the relationship explicitly. We demonstrate the concepts by applying this modified technique to several problems in image-based morphometry, and build discriminant representative models for different data sets.

1. Introduction

In biology and medicine, morphology refers to the study of the form, structure and configuration of an organism and its component parts. Clinicians, biologists, and other researchers have long used information about shape, form, and texture to make inferences about the state of a particular cell, organ, or organism (normal vs. abnormal) or to gain insights into important biological processes [1, 2, 3]. Earlier quantitative works often focused on numerical feature-based approaches (e.g. measuring size, form factor, etc.) that aim to quantify and measure differences between different forms in carefully constructed feature spaces [3, 4]. In recent times, many researchers working in applications in medicine and biology have shifted to a more geometric approach, where the entire morphological exemplar (as depicted in an image) is viewed as a point in a carefully constructed metric space [5, 6, 7], often facilitating visualization. When a linear embedding for the data can be assumed, standard geometric data processing techniques such as principal component analysis can be used to extract and visualize major trends in the morphologies of organs and cells [8, 9, 10, 11, 7, 12, 13, 14, 15]. While representation of summarizing trends is important, so is the application of discrimination techniques for elucidating and visualizing trends that differentiate between two or more populations [16, 17, 18, 19, 20, 21].

In part due to its simplicity and effectiveness, as well as its connection to the Student’s t-test, Fisher Linear Discriminant Analysis (FLDA) is often employed to summarize discriminating trends [21, 22, 23]. When employed in high dimensional spaces, the technique is often adapted and a regularized version of the associated generalized eigenvalue problem is used instead of the original eigenvalue problem, in order to avoid ill conditioning problems [24, 25, 26, 27]. The geometric meaning of such adaptation, to the best of our knowledge, is not fully understood [28]. Here we show that even in problems where ill conditioning does not exist, the straightforward application of the FLDA technique can lead to erroneous interpretation of the results. We show that a modified FLDA criterion that includes a representation penalty error can be used in such cases to extract meaningful discriminating information. We show the solution of the modified problem is related to the commonly used regularized eigenvalue problem, and derive the relationship explicitly. In contrast to the standard FLDA technique, the combination of a discrimination term with a data representation term allows for a decomposition whereby, in a two class problem, several discriminating trends can be computed and ranked according to their discrimination power (together with a least squares-type representation penalty), and discriminant representative models can be built accordingly. We also describe a kernalization of the procedure, similar to the one described in [28]. Finally, we apply the modified FLDA technique to several example problems in image-based morphometry, and contrast the technique to the straightforward FLDA method, as well as a method that combines PCA and FLDA serially [29, 24].

2. Methods

The method we describe can be applied whenever a linear embedding for the image data can be assumed and obtained. That is, given an image I_i depicting one structure to be analyzed, a function f can be used to map the image to a point in a linear subspace. This point may or may not be unique, depending on the embedding method being used. Mathematically: f(I_i) = x_i, with x_i ∈ ℛ^m, with m the dimension of the linear subspace. In addition, it is important for the linear embedding to be able to represent well the morphological structure present in I_i. Though other linear embeddings could also be utilized [12, 14, 15], in this work we utilize the landmark-based approach as described by [30, 31]. Briefly each image I_i is reduced to a set of landmarks, stored in a vector x ∈ ℛ²ⁿ (we use two dimensional images, and n is the number of landmarks). Although an inverse function does not exist (one cannot recover the image I_i from the set of landmarks x_i), the set of landmarks is densely chosen, so that visual interpretation of morphology is possible. Given two images I₁ and I₂, with landmarks x₁, x₂, the landmarks are stored in corresponding order.

In some of the examples shown below we use contours to describe a given structure. In these examples, the correspondence between two sets of points describing two contours is not known a priori. We use a methodology similar to the one described in [9, 30], where the points in the contour are first converted to a polar coordinate system, with respect to the center of the contour. The contour is then sampled at n equidistant angles evenly distributed between angles 0 and 2π (n landmarks). This procedure maps each image I_i to a point x_i in the standard ℛ²ⁿ vector space. Finally, we note that in all examples shown below, the sets of landmarks were first aligned by setting their center of mass to zero. Each set of landmarks was also aligned such that its principal axis aligned with the vertical axis.

2.1. Fisher discriminant analysis

Given a set of data points x_i, for i = 1,⋯, N, with each index i belonging to class c, the problem proposed by Fisher [3, 32] relates to solving the following optimization problem

$${\mathbf{w}}^{*}=\text{arg }\underset{\mathbf{w}}{\text{max}}\frac{{\mathbf{w}}^T{S}_B\mathbf{w}}{{\mathbf{w}}^T{S}_W\mathbf{w}}$$ (1)

where S_B = Σ_c N_c(μ_c − x̄)(μ_c − x̄)^T represents the ’between class scatter matrix’, S_W = Σ_cΣ_i∈c(x_i − μ_c)(x_i − μ_c)^T represents the ’within classes scatter matrix’, $\overline{\mathbf{x}}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N}{\mathbf{x}}_i$ represents center of the entire data set, N_c is the number of data in class c and μ_c is the center of class c. As usually done, we subtract each data point by this mean ${\mathbf{x}}_i^{\prime }={\mathbf{x}}_i-\overline{\mathbf{x}}$ before computing the scatter matrices S_W, S_B. The solution for the FLDA problem can be computed by solving the generalized eigenvalue problem [32]

$$S_B\mathbf{w}=\lambda S_W\mathbf{w}.$$ (2)

We note that for a two class problem, maximizing the Fisher criterion is related to finding the linear one dimensional projection that maximizes the t-statistic for the two-sample t-test. Let the mean and variance of the two classes be denoted by (m₁,m₂) and $\left(C_1^2,C_2^2\right)$ respectively. When the variances are unequal, usually Welch’s adaptation of the t-test [33] is used:

$$t=\frac{m_1-m_2}{\sqrt{\frac{C_1^2}{N_1}+\frac{C_2^2}{N_2}}}$$ (3)

Recall the objective function of FLDA defined in equation (1):

$$\frac{{\mathbf{w}}^T{S}_B\mathbf{w}}{{\mathbf{w}}^T{S}_W\mathbf{w}}=\frac{\frac{N_1{N}_2}{N}{[{\mathbf{w}}^T({\mu }_1-{\mu }_2)]}^2}{{\displaystyle {\sum }_{i\in c_1}}{[{\mathbf{w}}^T(x_i-{\mu }_1)]}^2+{\displaystyle {\sum }_{i\in c_2}}{[{\mathbf{w}}^T(x_i-{\mu }_2)]}^2},$$

where μ₁, μ₂ represent the mean vectors of the two classes, and c₁, c₂ represent the different class labels, N₁,N₂ represent the number of samples in classes c₁, c₂ respectively, and N = N₁ + N₂. Let $m_1^{\prime }(\mathbf{w})={\mathbf{w}}^T{\mu }_1=m_2^{\prime }(\mathbf{w})={\mathbf{w}}^T{\mu }_2,\text{ and }{C}_1^{\prime 2}(\mathbf{w})={\displaystyle {\sum }_{i\in c_1}}{[{\mathbf{w}}^T(x_i-{\mu }_1)]}^2,C_2^{\prime 2}(\mathbf{w})={\displaystyle {\sum }_{i\in c_2}}{[{\mathbf{w}}^T(x_i-{\mu }_2)]}^2$ be the sample means and standard deviations over the projection w. We rewrite the Fisher criterion as:

$$\frac{\frac{1}{N}{(m_1^{\prime }(\mathbf{w})-m_2^{\prime }(\mathbf{w}))}^2}{\frac{C_1^{\prime 2}(\mathbf{w})}{N_1{N}_2}+\frac{C_2^{\prime 2}(\mathbf{w})}{N_1{N}_2}}$$

When the number of data points in the two classes are the same, the Fisher criterion is equal to the scaled t²(w). We believe that in part due to its simplicity and its connections to the t-test (which are widely used in image-based morphometry [21, 22, 23]), FLDA-related techniques can play an important role in morphometry problems, especially in biology and medicine. As we show next, however, the FLDA technique must be modified before it can be used meaningfully in arbitrary morphometry problems.

2.2. A simulated data example

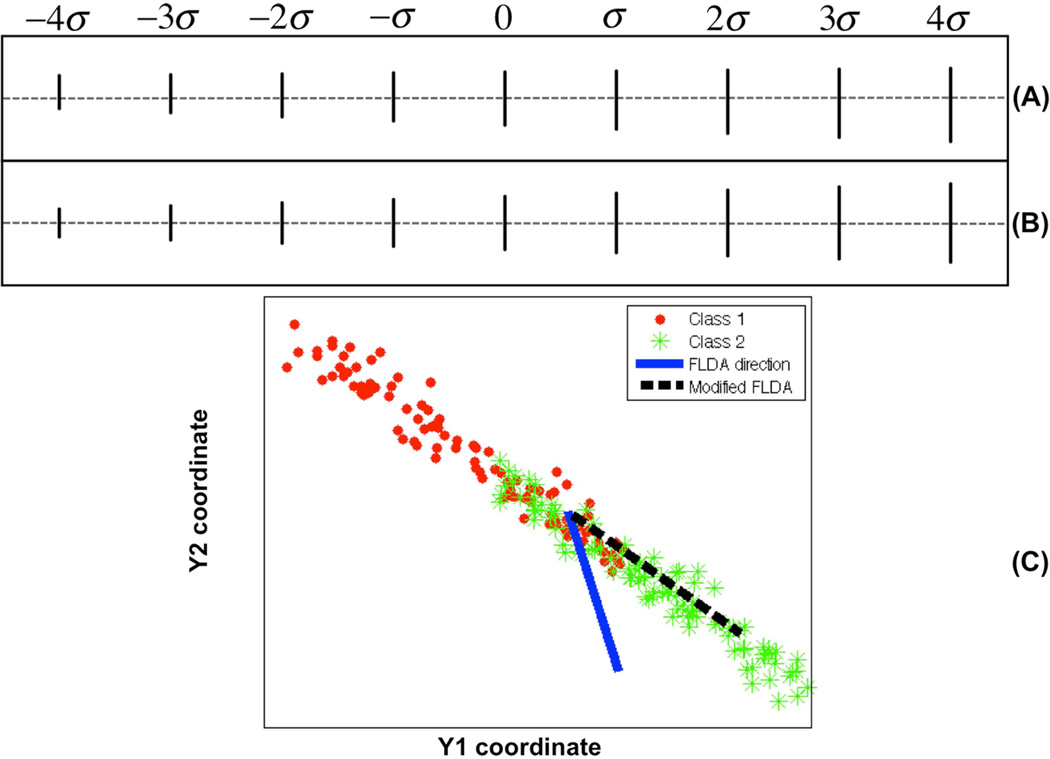
Here we show that the straightforward application of the FLDA method may not lead to a direction that represents real differences present in the data. In this example, two classes of two-dimensional vertical lines (each class with 100 lines) were generated. The lengths for the lines in class 1 ranged from 0.42 to 0.62, while lengths in class 2 ranged from 0.28 to 0.48. We aligned the center of each line to a fixed coordinate. Because the horizontal coordinates of each line do not change, for the purpose of visualizing the concepts we are about to describe, we characterize each simulated line by taking the vertical coordinates of upper and bottom-most points, where the Y 1 coordinate represents the y coordinate of the upper sample point on the line, while the Y 2 represents the y coordinate bottom-most sample point. Each line can then be uniquely mapped to a point in the two dimensional space R². The data (set of all lines), however, occupies a linear one-dimensional subspace of R², because only one parameter (length) varied in our simulation. From the coordinates x_i = (Y 1_i, Y 2_i)^T any line can be reconstructed. In order to avoid the ill-conditioning of the data covariance matrix, independent Gaussian noise was added to Y 1_i, Y 2_i (see Fig 1 (C)).

Figure 1.

Discriminant information computed for a simulated data set. A: Visualization of computed most discriminant direction by applying the standard FLDA method. B: Visualization of computed most discriminant direction by applying the penalized FLDA method. C: Plot of two sample points on the contour for the whole data set. See text for more details.

The solution w* of the FLDA problem discussed above can be visualized by plotting x_γ = x̄ + γw* for some range of γ. Fig 1(A)(B) contains the lines corresponding to x_γ for −4σ ≤ γ 4σ, where σ is the standard deviation (square root of the largest eigenvalue from eq. (2)). Visual inspection of the results in Fig 1(A) quickly reveals the problem. The method indicates that line translation in combination with a change in length is the geometric variation that best separates the two distributions according the Fisher criterion. While such a direction may allow for high classification accuracy, by construction, the data contained no variation in the position (translation) of the lines. We can therefore understand that such results are misleading, since the translation effect is manufactured by the FLDA procedure and does not exist in the data. The problem is further illustrated in part C of the figure, where the two distributions are plotted. The short lines (red dots) will have relatively bigger Y 1 and smaller Y 2 coordinates compared with the long lines (green dots). The solid blue line corresponds to the solution computed by FLDA. While this direction may be good for classifying the two populations (long vs short lines), it is not guaranteed to be well populated by data. If a visual understanding is to be obtained, the FLDA solution can thus provide misleading information (as shown in Fig 1 (A)).

2.3. A modified FLDA criterion

The FLDA criterion can be modified by adding a term that ’penalizes’ directions w that do not pass close to the data. To that end, we combine the standard FLDA criterion with a penalty term that measures, on average, how far the data is from a given direction w. Mathematically, an arbitrary line in the shape space R^m can be represented as λw + b, with line direction and offset w, b ∈ R^m, λ ∈ R. The squared distance $d_i^2$ from a data point x_i in the shape space R^m to the line can be represented as [32]:

$$d_i^2=\mathit{\text{tr }}[(\mathbf{b}-{\mathbf{x}}_i){(\mathbf{b}-{\mathbf{x}}_i)}^T(\mathbf{I}-\frac{{\mathbf{\text{ww}}}^T}{{\mathbf{w}}^T\mathbf{w}}\left)\right].$$

For a data set of N points, the mean of squared distances from each point in that data set to that line is:

$$\frac{1}{N}{\displaystyle \sum _{i=1}^N}{d}_i^2=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\mathit{\text{tr }}[(\mathbf{b}-{\mathbf{x}}_i){(\mathbf{b}-{\mathbf{x}}_i)}^T(\mathbf{I}-\frac{{\mathbf{\text{ww}}}^T}{{\mathbf{w}}^T\mathbf{w}}\left)\right]$$ (4)

We note that the term defined in equation (4) contains b that multiplies the terms containing w. Since it should be minimum for all possible choices of w, b can be chosen independently of w and can be shown to be (see section Appendix A for details): ${\mathbf{b}}^{*}={\displaystyle {\sum }_{i=1}^N}{\mathbf{x}}_i/N$ (this is equivalent to normalizing the data set by the mean, and, in that case, we could just assume b = 0). This indicates that this line must go through the center of the data set. Equation (4) can then be rewritten as:

$$\underset{\mathbf{w},\mathbf{b}={\mathbf{b}}^{*}}{\text{min}}\frac{1}{N}{\displaystyle \sum _{i=1}^N}{d}_i^2=\underset{\mathbf{w},\mathbf{b}={\mathbf{b}}^{*}}{\text{min}}\frac{1}{N}\mathit{\text{tr }}\left[S_T\right(\mathbf{I}-\frac{{\mathbf{\text{ww}}}^T}{{\mathbf{w}}^T\mathbf{w}}\left)\right]=\underset{\mathbf{w}}{\text{min}}\{\frac{1}{N}\mathit{\text{tr}}(S_T)-\frac{1}{N}(\frac{{\mathbf{w}}^T{S}_T\mathbf{w}}{{\mathbf{w}}^T\mathbf{w}}\left)\right\}.$$ (5)

where $S_T={\displaystyle {\sum }_{i=1}^N}({\mathbf{x}}_i-\overline{\mathbf{x}}){({\mathbf{x}}_i-\overline{\mathbf{x}})}^T$ represents the ’total scatter matrix’. The optimization problem defined in equation (5) is equivalent to:

$$\underset{\mathbf{w}}{\text{min}}\{-(\frac{{\mathbf{w}}^T{S}_T\mathbf{w}}{{\mathbf{w}}^T\mathbf{w}}\left)\right\}$$ (6)

Recall that our goal is to maximize the Fisher criterion defined in equation (1) while minimizing the mean of squared distances defined in equation (4) (or (6)) to guarantee the discriminating direction found is well populated by the data. First we note that equation (1) is equivalent to the following optimization problem [32]

$${\mathbf{w}}^{*}=\text{arg }\underset{\mathbf{w}}{\text{max}}J(\mathbf{w})=\frac{{\mathbf{w}}^T{S}_T\mathbf{w}}{{\mathbf{w}}^T{S}_W\mathbf{w}}$$ (7)

where S_T is the ’total scatter matrix’ as defined in equation (5), and S_T = S_B +S_W. The criterion is then optimized by solving the generalized eigenvalue problem [32] S_Tw = λS_Ww, and selecting the eigenvector associated with the largest eigenvalue.

We note that maximizing the Fisher criterion defined in equation (7) is equivalent to maximizing $-\frac{1}{J(\mathbf{w})}$ [3, 32]. Since our goal is to maximize the Fisher criterion and at the same time minimize the penalty term defined in equation (6) (or maximize the reciprocal of it), we combine both terms and define

$$E(\mathbf{w})=\frac{1}{J(\mathbf{w})}+\alpha *\mathit{\text{penalty}}$$ (8)

$$=-\frac{{\mathbf{w}}^T{S}_W\mathbf{w}}{{\mathbf{w}}^T{S}_T\mathbf{w}}-\alpha \frac{{\mathbf{w}}^T\mathbf{w}}{{\mathbf{w}}^T{S}_T\mathbf{w}}$$ (9)

where α is a scalar weight term, as the criterion to optimize. Maximizing equation (9) is equivalent to

$$\underset{\mathbf{w}}{\mathit{\text{max}}}\left\{\frac{{\mathbf{w}}^T{S}_T\mathbf{w}}{{\mathbf{w}}^T(S_W+\alpha \mathbf{I})\mathbf{w}}\right\}$$ (10)

where I is the identity matrix. The solution for the problem above is also given by the well-known generalized eigenvalue decomposition S_Tw = λ (S_W + αI)w. This solution is similar to the solution to the traditional FLDA problem, however, with the regularization provided by αI. We note once again that although the regularized eigenvalue problem has been utilized in the past, to our best knowledge, the geometric meaning of such regularization is not well understood. According to the derivation above, the geometric meaning of the regularization is the minimization of the least squares-type projection error, in combination with the Fisher criterion. Moreover the rank of the generalized eigen decomposition problem defined in eq. (2) [34] is one. This means that, for two-class problem, only one discrimination direction is available. On the other hand, the minimization of the objective function (9) allows for a PCA-like decomposition, yielding a decomposition with as many directions as allowed by the rank of S_T (assuming a large enough α). All directions are orthogonal to each other, and each direction in this decomposition maximizes the objective function (9), with the constraint of being norm one and orthogonal to other directions.

2.4. Relationship with FLDA and PCA

It is clear that if we set the parameter α = 0, the objective function defined in equation (9) will be the same as optimizing the traditional FLDA criterion. On the other hand, when the parameter α → ∞, the generalized eigenvalue decomposition problem for equation (10) $S_T\mathbf{w}=\lambda \alpha \left(\frac{S_W}{\alpha }+\mathbf{I}\right)\mathbf{w}$ can be rewritten as S_Tw = λ′w (because $\underset{\alpha \to \mathrm{\infty }}{\mathit{\text{lim}}}\left(\frac{S_W}{\alpha }+\mathbf{I}\right)=\mathbf{I}$ ), which is the well-known PCA solution with the same eigenvectors (with eigenvalues multiplied by α). By changing the penalty parameter α from 0 to ∞, the solution of the modified FLDA problem described in (9) ranges from the traditional FLDA solution to the PCA one.

2.5. Parameter selection for α

The discriminant direction computed by equation (10) can be regarded as a function w(α) of the parameter α. For a given problem or application, one must select an appropriate value for α to ensure meaningful results. Too low a value for α and problems related to poor representation (as well as ill-conditioning in the associated eigenvalue problem) can occur. Too high a value and little or no discrimination information will be contained in the solution. We propose to select α such that it is close to the value of zero and that also is stable in the sense that a small variation in α does not yield a large change in the computed direction w(α). To that end, in each problem demonstrated below we compute $\mathit{\text{dw}}(\alpha )/d\alpha \sim \frac{\Vert \mathbf{w}(\alpha +\mathrm{\Delta }\alpha )-\mathbf{w}(\alpha )\Vert }{m\mathrm{\Delta }\alpha }$ (m is the dimensionality of w) numerically and compare it to a fixed threshold (10⁻⁴ in this paper). Several values of α are scanned starting from zero (or close to zero when the system is ill conditioned), and the first value of alpha for which dw(α)/dα < 10⁻⁴ is true is chosen as the α for that dataset.

2.6. ”Kernelizing” the modified FLDA

Morphometry problems, in particular in biology and medicine, can often involve high-dimensional data analysis (e.g. three dimensional deformation fields [20, 21]). Computation of the full covariance matrices involved in such problems is often infeasible. To address this problem, the technique we propose above can be ”kernelized,” in an approach similar to the one described in [28]. Assume Φ be a mapping function to higher that Φ : Rⁿ → R^m. The modified FLDA defined in equation (9) can be transformed to:

$$J(w)=\underset{\mathbf{w}}{\mathit{\text{max}}}\{-\frac{{\mathbf{w}}^T{S}_W^{\mathrm{\Phi }}\mathbf{w}}{{\mathbf{w}}^T{S}_T^{\mathrm{\Phi }}\mathbf{w}}-\alpha \frac{{\mathbf{w}}^T\mathbf{w}}{{\mathbf{w}}^T{S}_T^{\mathrm{\Phi }}\mathbf{w}}\}$$ (11)

where $S_W^{\mathrm{\Phi }}={\displaystyle {\sum }_c}{\displaystyle {\sum }_{i\in c}}(\mathbf{\Phi }(x_i)-{\mu }_c^{\mathrm{\Phi }}){(\mathbf{\Phi }(x_i)-{\mu }_c^{\mathrm{\Phi }})}^T,\text{ and }{S}_T^{\mathrm{\Phi }}={\displaystyle {\sum }_i}(\mathbf{\Phi }(x_i)-{\mu }^{\mathrm{\Phi }}){(\mathbf{\Phi }(x_i)-{\mu }^{\mathrm{\Phi }})}^T,\text{ with }{\mu }_c^{\mathrm{\Phi }}=\frac{1}{N_c}{\displaystyle {\sum }_{i\in c}^{N_c}}\mathbf{\Phi }(x_i),{\mu }^{\mathrm{\Phi }}=\frac{1}{N}{\displaystyle {\sum }_i^N}\mathrm{\Phi }(x_i)$ . If we assume $\mathbf{w}={\displaystyle {\sum }_i^N}{\upsilon }_i\mathbf{\Phi }(x_i)$ , equation (12) can be transformed to:

$$J(\upsilon )=\underset{\upsilon }{\mathit{\text{max}}}\{-\frac{{\upsilon }^T[\mathbf{Q}+\beta \mathbf{G}]\upsilon }{{\upsilon }^T[\mathbf{T}]\upsilon }\}$$ (12)

where G = (G)_i,j := Φ(x_i)^TΦ(x_j) is a N × N matrix, $\mathbf{Q}={\displaystyle {\sum }_c}{K}_c(\mathbf{I}-1_{N_c})K_c^T,K_c$ is a N × N_c matrix with (K_c)_i,j := Φ(x_i)^TΦ(x_j∈c), T = G(I − 1_N)G^T is a N × N matrix, and 1_N is a matrix with all entries 1/N. Although the computational examples we show below are of low enough dimension and do not require such an approach, we anticipate that the kernel version of our method will be useful in higher dimensional morphometry problems.

3. Results

3.1. Simulated experiments

We tested the modified FLDA method above on the simulated dataset depicted in Figure 1. We compared the result of applying the FLDA method Fig 1 (A) with our modified FLDA method (α = 500) in Fig 1 (B). As mentioned above, the value of α was chosen automatically as the one that satisfied dw(α)/dα < 10⁻⁴. The same criterion was used for all the experiments described in this section. We can see the method we propose does indeed recover the correct information that discriminates between the two populations (in this case, the length of each line). While this is not necessarily the most discriminating information in the FLDA sense, it is the most discriminating information that is well populated by the data, in the sense made explicit by equation (9). In this specific simulation the modified FLDA method yields the same result as the standard PCA method would. However, as shown in other examples below, that is not a general rule.

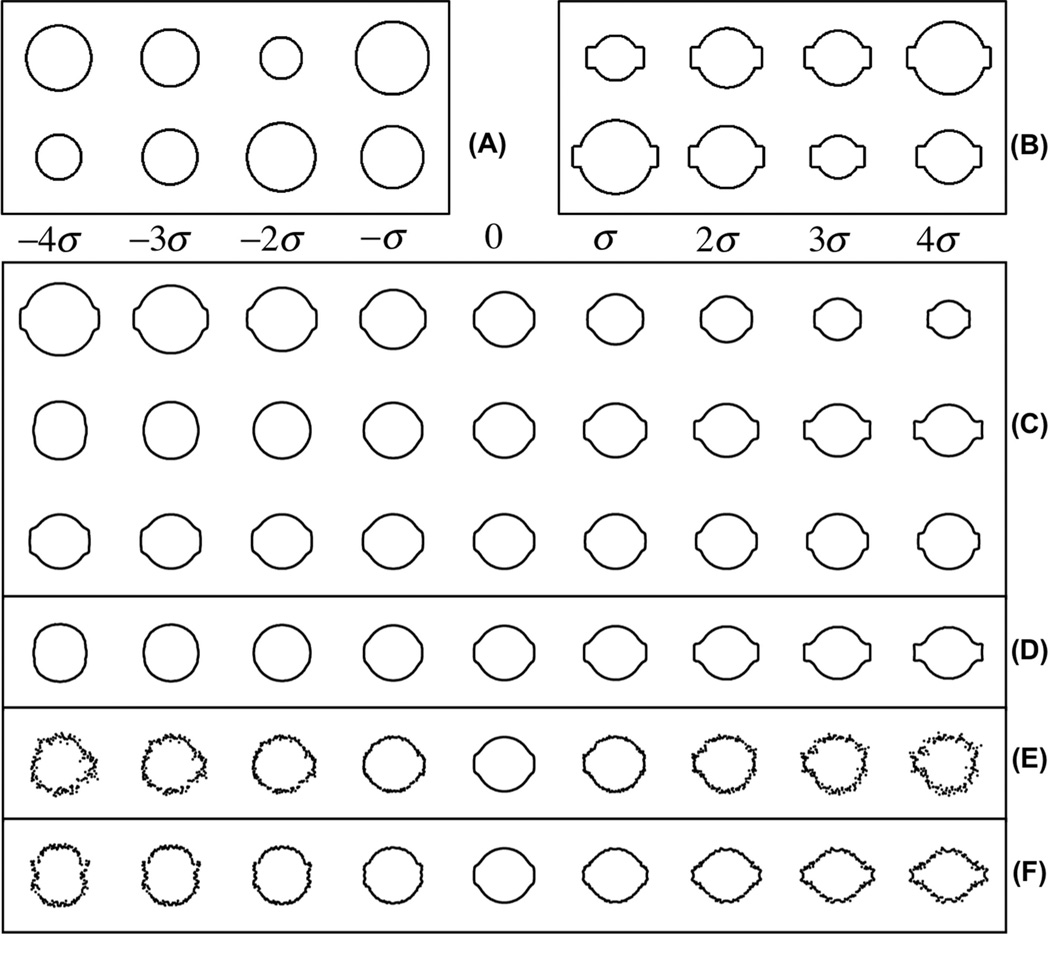
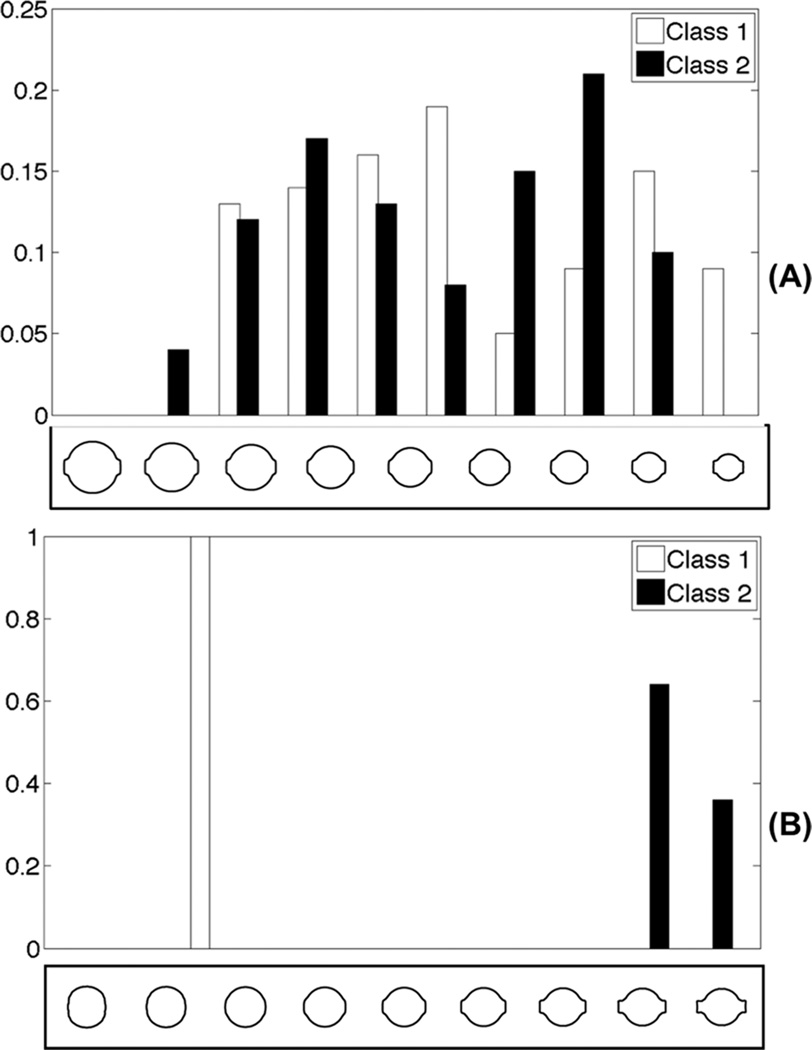
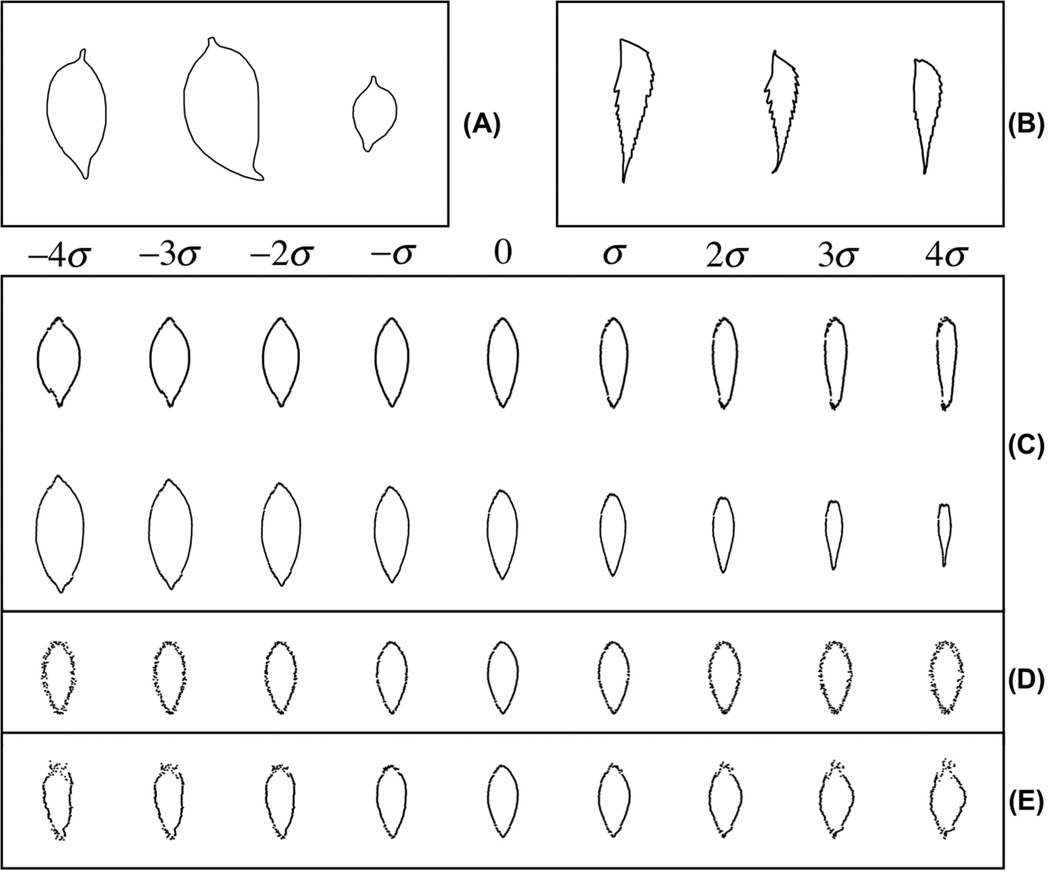
We also tested the modified FLDA method on another simulated data set, where two classes of shapes were analyzed. One class was composed of circles (as shown in Fig 2(A)), and the other class was composed of circles with square protrusions emanating from opposite sides (as shown in Fig 2(B)). We used 100 samples for each class, and in each class the radii of circles ranged uniformly from 0.2 to 0.8. We generated these images in the way that we expect the discriminating information for this simulated data to be the rectangular protrusion. We used the contour-based metric to extract 90 sample points along the contour of each image, and used both [X,Y] coordinates of the sample points. Each image was thus mapped to a point in a 180 dimensional vector space. In Fig 2(C), the first three PCA modes (computed using both classes) are shown. The first mode of variation is related to circle size and the second seems to show the difference in shape. In Fig 2(D), we demonstrate the discriminating mode computed by the modified FLDA (α = 800) method. We can see that the method successfully recovers the discriminating information in the data set, without being confused by the misleading information such as size and the shape of the ovals. To verify that indeed the projection recovered by the modified FLDA is more discriminant than the size (radii) of the circles, we project the data onto the directions found by PCA (the first mode) and the modified FLDA (Fig 3(A) and (B)). As can be seen from this figure, by construction, the differences in shape (rectangular protrusions) are more discriminating than differences in size. We also applied the traditional FLDA (without regularization) on this simulated data. Results are shown in part (E) of Fig. 2. As can be seen, although the generalized eigenvalue problem can be solved and some discriminant information can be detect, the data cannot be easily visualized. The contours start to break and sample points along the contour start to move irregularly. In addition, we compare the methods mentioned in [29, 24], where PCA and FLDA are used sequentially. In the PCA step, we discard all the eigen-vectors whose corresponding eigen-value is smaller than a threshold (set at 0.1% of the biggest eigen-value). The result, shown in Fig 2(F), indicates that although some interpretable discriminant information can be detected, the direction provided also suffers from similar artifacts as the traditional FLDA method. We also compared the classification accuracy obtained by the three difference methods (traditional FLDA, sequential PCA and FLDA, and our penalized FLDA method). We used a K-fold (K = 10) cross-validation strategy [32] to separate the whole data set into 10 parts. In each fold, one part was left out and the remaining parts were used for training to compute the discriminant directions by the three methods, and these directions were used to classify the testing set. We repeated the procedure until each part has been selected once, and computed the final classification accuracy. The classification accuracies obtained were: 90% (traditional FLDA), 98% (PCA plus FLDA) and 100% (penalized FLDA).

Figure 2.

Principle variations and discriminant information computed for a simulated data set. A: Sample images from the first class. B: Sample images from the second class. C: First 3 principle variations computed by Principle Component Analysis (PCA). D: Discriminant variation computed by the penalysed FLDA method. E: Discriminant variation computed by directly applying the traditional FLDA on this simulated data. F: Discriminant variation computed by sequentially applying PCA then FLDA on this simulated data.

Figure 3.

Histograms of data projected onto different directions. A: projection histogram on direction computed by the PCA method. B: projection histogram onto the direction computed by the modified FLDA method.

3.2. Real data experiments

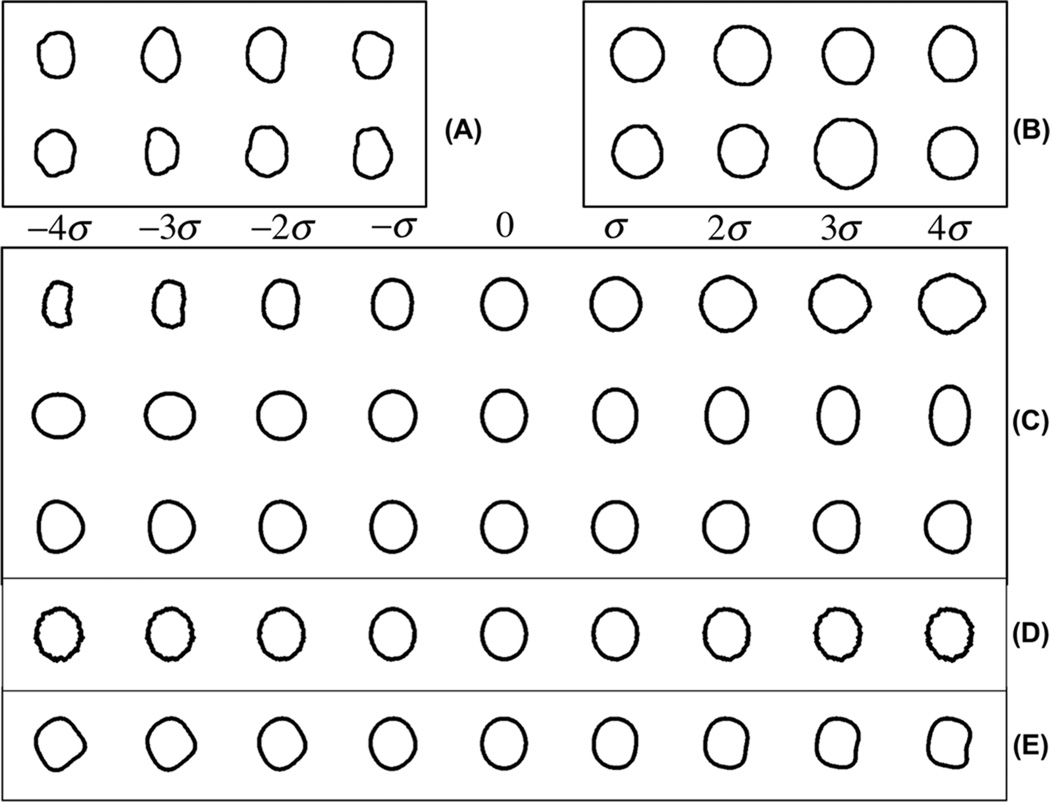
We applied the modified FLDA method on a real biomedical image data set to quantify the difference in nuclear morphology between normal versus cancerous cell nuclei. The raw data consisted of histopathology images originating from five cases of liver hepatoblastoma (HB), each containing adjacent normal liver tissue (NL). The data was taken for the archives at the Children’s Hospital of Pittsburgh, and is described in more detail in [18, 35]. The data set is available online at [36]. Briefly, the images were segmented by a semi automatic method involving a level set contour extraction. They were normalized for translation, rotations, and coordinate inversions (flips) as described in our earlier work [11, 18, 35]. The dataset we used consisted of a total of 500 nuclear contours: 250 for (NL), and 250 for (HB). Some sample images are shown in Fig 4(A)(B) for HB and NL classes. The contours of each image were mapped to a 180 dimensional vector x_i as described earlier.

Figure 4.

Discriminant information computed for real liver nuclei data. A: Sample nuclear contours from the cancerous tissue (HB). B: Sample nuclear contours from normal tissue (NL). C: First three discriminating modes computed by the modified FLDA method. D: Discriminant variation computed by directly applying the traditional FLDA method on this data. E: Discriminant variation computed by sequentially applying PCA then FLDA on this data. See text for more details.

Fig 4(C) contains the first three discriminating modes computed by the modified FLDA method (with α = 600). For this specific cancer, we can see that a combination of size differences and protrusions is the most discriminating directional information. The elongation of nuclei is the second most discriminant morphological information (that is orthogonal to the first). The third direction contains a protrusion effect. The p values of the t-test for each direction are 0.0021, 0.071, 0.27, respectively. As in the previous experiment, we also applied the traditional FLDA method on the contours of data set, as shown in Fig 4(D). Some sample points on contours seem to move perpendicularly to the contour with relatively big variation, while some remain unchanged. The direction computed by FLDA does not seem to capture visually interpretable information. In addition, as in section 3.1, we also applied the method described in [29]. The result is shown in Fig 4(E). Finally, classification accuracies for the three methods were computed as described above. The classification accuracies obtained were: 76% (traditional FLDA), 79% (PCA plus FLDA) and 81% (penalized FLDA).

We also applied the penalized FLDA method on a leaf shape data set [37] to quantify the difference in morphology between two types of leaves. The raw data consisted of gray-level images of different classes of leaves, with roughly the same size, and each class having 10 images. Some sample images for the two types of leaves are provided in Fig 5(A)(B) respectively. The contours of the leaves are provided. We followed the same procedures as described earlier to preprocess the contours. In Fig 5(C), we plot the first two discriminating modes of variations computed by the modified FLDA (with α = 200). We can see that the first discriminating mode successfully detects elongation differences as the discriminant information for this data set. The second discriminating mode is the size differences combined with the shape differences. The p-values for the t-tests on these directions were 3.09 × 10⁻⁵, 0.056 respectively. In Fig 5(D), we demonstrate the discriminating mode computed by the traditional FLDA method. In Fig 5(E), we show the discriminant variation computed by sequentially applying PCA then FLDA (as before the eigenvalues of the reconstructed vectors in the PCA portion were thresholded at 0.1% of the largest eigenvalue, to avoid ill conditioning). Because the dataset only contained 10 images in each class, we do not report classification accuracies in this case.

Figure 5.

Discriminant information computed for leaf dataset. A: Sample images for one class of leaves. B: Sample images for another class of leaves. C: First two discriminant variations computed by our modified FLDA method. D: Discriminant variation computed by directly applying the traditional FLDA method on this data. E: Discriminant variation computed by sequentially applying PCA then FLDA on this data. See text for more details.

Finally, we also applied the penalized FLDA method to a facial image data set to quantify the difference between two groups. The data is described in [31], and available online [38]. The manually annotated landmarks (obtained from the eyebrows, eyes, nose, mouth and jaw) were used in our analysis. Generalised Procrustes Analysis (GPA) was used to eliminate the translations, orientations, and scalings. Therefore, each human face I_i was decoded by a 116 dimensional vector x_i. The dataset we chose contained two classes: faces with normal expression, and faces smiling. As in the previous experiments, we compared the results from the first two modes of variations computed by the penalized FLDA method (with α = 500), traditional FLDA method, and sequentially applying PCA then FLDA (where again the threshold of 0.1% of the largest eigenvalue was used for a threshold). Figure 6 shows the corresponding results. The p-values computed from the penalized FLDA procedure were 5.88 × 10⁻⁵, 2.91 × 10⁻³. Classification accuracies were 92% (traditional FLDA), 88% (PCA plus FLDA) and 91% (penalized FLDA).

Figure 6.

Discriminant information computed for face data. A: Sample image for neutral expression. B: Sample image for smiling face. C: First two principle variations computed by the modified FLDA method. We can see that the modified FLDA method can correctly detect the different facial expression information. D: Discriminant variation computed by directly applying the traditional FLDA method on this data. E: discriminant variation computed by sequentially applying PCA then FLDA on this data.

4. Summary and discussion

Quantifying the information that is different between two groups of objects is an important problem in biology, medicine as well as general morphological analysis. We have shown that the application of the standard FLDA criterion (other discrimination methods can also suffer from similar shortfalls, see for example [17]) can lead to erroneous results in interpretation not necessarily related to ill conditioning in the data covariance matrix. We showed that the regularized version of the associated generalized eigenvalue problem is related to minimizing a modified cost function that combines both the standard FLDA term together with a least squares-type criterion. The method yields a family of solutions that varies according to the weighting (α) applied the least squares-type penalty term. At one extreme (α = 0) the solution is equal to that of the traditional FLDA method, while a the other extreme (α → ∞) the solution approaches that of the standard PCA method. We also described a method for choosing an appropriate value for weighting the penalty term. We note again that while others have also used the same regularized version of the associated generalized eigenvalue problem (see [28] for an example), geometrical explanations for this regularization are not known, to our best knowledge. We also note that the method we propose tends to select regularization values α much larger than the ones often used.

We applied the method to several discrimination tasks using both real and simulated data. We also compared the results to results generated by other methods. In most cases the traditional FLDA can be computed (ill conditioning is not an issue). Its results however, are not always visually interpretable (e.g. are far from being closed contours, etc.). Likewise, the application of PCA and FLDA serially (as in the method described in [29]) can also yield uninterpretable results, since the FLDA procedure is ultimately applied independently of the PCA method. Moreover, as shown in Fig 1(C), even if we apply PCA to discard the eigen-vectors corresponding to small eigen-values, the direction computed by the traditional FLDA is not guaranteed to be well populated by data. Results show that the penalized FLDA method we describe can help overcome these limitations.

Finally, we emphasize that although we have used contours and landmarks extracted from image data as our linear embeddings, it is possible to use the same method on other linear embeddings (for example [12]). For some such linear embeddings, however, distance measurements, projections over directions, etc., over large distances (large deformations) may not be appropriate. In such cases we believe the same modified FLDA method could be used locally, in an idea similar to that presented in [39].

• >We modify the Fisher Discriminant Analysis method to include an average distance penalty.
• >We apply the modified FDA method to problems in image-based morphometry and compare its results to other methods.
• >We build discriminant representative models to interpret differences in morphometry in two populations.

Appendix A

We note that the term defined in equation (4) contains b that multiplies the terms containing w. Since it should be minimum for all possible choices of w, b can be chosen independently of w. Therefore, we can first focus on $\underset{\mathbf{b}}{\mathit{\text{min}}}\left\{{\displaystyle {\sum }_{i=1}^N}\mathit{\text{tr }}\left[(\mathbf{b}-{\mathbf{x}}_i){(\mathbf{b}-{\mathbf{x}}_i)}^T\left(I-\frac{{\mathbf{\text{ww}}}^T}{{\mathbf{w}}^T\mathbf{w}}\right)\right]\right\}$ . It is equivalent to

$$\underset{\mathbf{b}}{\mathit{\text{min}}}\{{\displaystyle \sum _{i=1}^N}\mathit{\text{tr }}[(\mathbf{b}-{\mathbf{x}}_i){(\mathbf{b}-{\mathbf{x}}_i)}^T]\}$$ (A.1)

Differentiating with respect to b in equation (A.1) and setting it to 0 we have that ${\mathbf{b}}^{*}=\frac{{\displaystyle {\sum }_{i=1}^N}{x}_i}{N}$ . The optimal b* satisfiesn $\left\{{\displaystyle {\sum }_{i=1}^N}\mathit{\text{tr }}[({\mathbf{b}}^{*}-{\mathbf{x}}_i){({\mathbf{b}}^{*}-{\mathbf{x}}_i)}^T]\right\}\le \left\{{\displaystyle {\sum }_{i=1}^N}\mathit{\text{tr }}[(\mathbf{b}-{\mathbf{x}}_i){(\mathbf{b}-{\mathbf{x}}_i)}^T]\right\}$ .