HPAM: Hirshfeld Partitioned Atomic Multipoles

Abstract

An implementation of the Hirshfeld (HD) and Hirshfeld-Iterated (HD-I) atomic charge density partitioning schemes is described. Atomic charges and atomic multipoles are calculated from the HD and HD-I atomic charge densities for arbitrary atomic multipole rank l_max on molecules of arbitrary shape and size. The HD and HD-I atomic charges/multipoles are tested by comparing molecular multipole moments and the electrostatic potential (ESP) surrounding a molecule with their reference ab initio values. In general, the HD-I atomic charges/multipoles are found to better reproduce ab initio electrostatic properties over HD atomic charges/multipoles. A systematic increase in precision for reproducing ab initio electrostatic properties is demonstrated by increasing the atomic multipole rank from l_max = 0 (atomic charges) to l_max = 4 (atomic hexadecapoles). Both HD and HD-I atomic multipoles up to rank l_max are shown to exactly reproduce ab initio molecular multipole moments of rank L for L ≤ l_max. In addition, molecular dipole moments calculated by HD, HD-I, and ChelpG atomic charges only (l_max = 0) are compared with reference ab initio values. Significant errors in reproducing ab initio molecular dipole moments are found if only HD or HD-I atomic charges used.

Introduction

Models for partial atomic charges provide an approximate description of a molecular charge distribution, which often lead to chemically useful concepts. For example in most models, atomic charges on highly electronegative atoms, such as nitrogen or oxygen, are usually negative when bonded to less electronegative atoms, such as hydrogen and carbon, which are usually positively charged. Aside from being a useful conceptual device, partial atomic charges have also been used extensively in the development of simple models [1–7] for inter-molecular forces. Partial atomic charges are capable of providing a minimum description of electrostatic molecular properties, such as molecular dipole moment and electrostatic potential outside van der Waals radii on each atom, in which the bulk of molecular charge density is contained. In addition, the anisotropy of the electron charge density around an atom can be more accurately described by including higher order atomic multipoles [8–11]. Both atomic charges and atomic multipoles have played a crucial role in developing models for inter-molecular forces, which have been used for example, to model water [12–16].

Many different schemes for calculating partial atomic charges have been developed. One popular method for calculating atomic charges is by fitting the charges to the ab initio electrostatic potential (ESP) surrounding a molecule, as described for example, in the ChelpG procedure [1]. In a second type of method for calculating atomic charges, the molecular electron charge density ρ_mol(r) is partitioned into atomic charge densities ρ_a(r) by

$${\rho }_{\mathit{\text{mol}}}(\mathbf{r})={\displaystyle \sum _a}{\rho }_a(\mathbf{r})$$ (1)

The total atomic charge q_a on atom a is given by the difference of the positive nuclear charge Z_a and the negative integral of atomic charge density

$$q_a=Z_a-{\displaystyle \int }{d}^3\mathbf{r}{\rho }_a(\mathbf{r})$$ (2)

The two main methods for exactly partitioning ρ_mol(r) into atomic density contributions ρ_a(r) are basis set partitioning (e.g. Mulliken charges [17]) and real space partitioning (e.g. Bader’s Atom In Molecules [18] and Hirshfeld charge [19] methods).

In the Hirshfeld (HD) charge scheme, the ab initio molecular electron charge density ρ_mol(r) is partitioned into atomic density contributions ρ_a(r) by

$${\rho }_a(\mathbf{r})\equiv \left(\frac{{\rho }_a^0(\mathbf{r})}{{\displaystyle \sum _b}{\rho }_b^0(\mathbf{r})}\right){\rho }_{\mathit{\text{mol}}}(\mathbf{r})$$ (3)

where ρ_a⁰(r) is the ab initio atomic charge density of the isolated atom a in vacuum. Note that eqn. 1 is exactly satisfied and the HD atomic charges are calculated from eqn. 2. One of the major shortcomings of HD charges is that the predicted molecular dipole moments are underestimated, i.e. the charges are too small in magnitude. Davidson and Chakravorty [20] pointed out that the choice of isolated atomic charge densities ρ_a⁰(r) is arbitrary and suggested that fractional atom charge densities ${\tilde{\rho }}_a^0(\mathbf{r})$ might overcome the problems with HD atomic charges. Bultinck and co-workers [21–23] developed a Hirshfeld-Iterated (HD-I) atomic charge model, in which fractional atomic charge densities ${\tilde{\rho }}_a^0(\mathbf{r})$ replace the isolated atomic charge densities ρ_a⁰(r) in eqn. 3. The fractional atomic charge density ${\tilde{\rho }}_a^0(\mathbf{r})$ for atom a is constructed from the present atomic charge q_a and the ab initio atomic charge density of the isolated atom and its atomic ions. The fractional atom charge densities ${\tilde{\rho }}_a^0(\mathbf{r})$ lead to a new partitioning of the atomic charge density ρ_a(r) (eqn. 3), which then lead to a new set of atomic charges q_a (eqn. 2). In this way, the charges q_a are calculated iteratively until self-consistency is achieved. A more detailed description of the HD-I partitioning scheme is provided in the following section. The HD-I atomic charges are larger in magnitude and more accurately reproduce ab initio molecular dipole moments, when compared to HD atomic charges. Lillestolen and Wheatley [24] have developed a similar iterative type charge method, which does not require separate calculation of the isolated atomic charge and atomic cation/anion charge densities. In addition, atomic multipoles can be calculated from the partitioned atomic charge densities. Recently, Harrison [25] calculated atomic charges, dipoles, and quadrupoles from the partitioned HD-I atomic charge densities ρ_a(r) for linear halogenated acetylene molecules X-C≡C-H (X = H, F, Cl, Br, I).

In this work, we describe an extended implementation of the HD and HD-I atomic charge density partitioning procedure in order to calculate atomic multipoles Q_lm^a of arbitrary multipole rank l for molecules of arbitrary shape and size. The HD and HD-I atomic charges/multipoles can be calculated at the HF, DFT, MP2, or CCSD levels using ab initio Gaussian basis sets that include up to s, p, d, f, g functions for either closed shell or open shell molecules. The HD and HD-I atomic charges/multipoles are tested on a variety of small closed shell molecules by comparing molecular multipole moments and the electrostatic potential surrounding a molecule with their ab initio reference values. In addition, ChelpG atomic charges are compared with HD and HD-I atomic charges only by calculating molecular dipole moments and comparing with ab initio reference values. As most widely used force fields [26–28] employ atomic charges only, it is important to point out the properties and limitations of HD and HD-I atomic charges.

Calculating HD and HD-I atomic multipoles from the Hirshfeld partitioned charge densities offers more possibilities for exploring new models for inter-molecular forces, at least for long range electrostatic properties. In inter-molecular interactions, both atomic charges and atomic multipoles do not capture the short range penetration error [29], which is associated with the inter-molecular overlap of charge densities. However, damping functions [30–32] have been proposed as a short-ranged correction to atomic multipoles in order to overcome the penetration error. In addition, models based on charge density, such as Gaussian multipoles [33–37], have many properties similar to atomic point multipole models. Further analysis of atomic point multipole models should lead to a better understanding of current models and provide a useful guide for the development of future models.

Methods

1. Hirshfeld-Iterated (HD-I) Atomic Charge Scheme

Suppose ρ_mol(r) ≥ 0 is an ab initio molecular charge density. Let ρ_a⁽ⁿ⁾(r) be the isolated ab initio atomic charge density of atom a with n electrons, i.e. ${\displaystyle \int }{d}^3\mathbf{r}{\rho }_a^{(n)}(\mathbf{r})=n$ where n is a positive integer. If n ≠ Z_a, then ρ_a⁽ⁿ⁾(r) corresponds to an atomic ion charge density with net atomic charge Z_a − n. Suppose q_a is the present Hirshfeld-Iterated (HD-I) net atomic charge of atom a. The fractional number of electrons N_a for atom a is

$$N_a=Z_a-q_a$$ (4)

Note that N_a need not be an integer. However, N_a may be expressed as an integer contribution n_a and a real number contribution Δ_a i.e. N_a = n_a + Δ_a where 0 ≤ Δ_a ≤ 1. The fractional atomic charge density ${\tilde{\rho }}_a^0(\mathbf{r})$ of atom a corresponding to net atomic charge q_a and fractional number of electrons N_a is defined as a linear interpolation between ${\rho }_a^{(n_a)}(\mathbf{r})\text{ and }{\rho }_a^{(n_a+1)}(\mathbf{r})$ by

$${\tilde{\rho }}_a^0(\mathbf{r})\equiv {\rho }_a^{(n_a)}(\mathbf{r})+{\mathrm{\Delta }}_a[{\rho }_a^{(n_a+1)}(\mathbf{r})-{\rho }_a^{(n_a)}(\mathbf{r})]$$ (5)

Note that ${\displaystyle \int }{d}^3\mathbf{r}{\tilde{\rho }}_a^0(\mathbf{r})=N_a$.

The molecular charge density ρ_mol(r) is partitioned into HD-I atomic charge densities ρ_a(r) by

$${\rho }_a(\mathbf{r})\equiv \left(\frac{{\tilde{\rho }}_a^0(\mathbf{r})}{{\displaystyle \sum _b}{\tilde{\rho }}_b^0(\mathbf{r})}\right){\rho }_{\mathit{\text{mol}}}(\mathbf{r})$$ (6)

Given a partitioned atomic charge density ρ_a(r), a new set of atomic charges q_a′ can be calculated by

$${q_a}^{\text{'}}=Z_a-{\displaystyle \int }{d}^3\mathbf{r}{\rho }_a(\mathbf{r})$$ (7)

Starting with q_a = 0, eqns. 4 – 7 are solved iteratively for the HD-I charges until self-consistency is achieved, i.e. the new charges q_a′ are then substituted back into eqn. 4 to give a new set of fractional numbers of electrons N_a = n_a + Δ_a. The fractional numbers of electrons are then substituted into eqn. 5 to generate a new set of fractional atomic charge densities ${\tilde{\rho }}_a^0(\mathbf{r})$, which is then substituted into eqns. 6 and 7 to generate a new set partitioned atomic charge densities ρ_a(r) and a new set of atomic charges q_a. The HD atomic charges and partitioned atomic charge densities are obtained at the end of the first iteration after the q_a are initially set to 0. For each iteration, note that ρ_a(r) is an exact partition of the total molecular charge density ρ_mol(r), i.e. eqn. 1 is always satisfied.

2. Numerical Grids

The integrations over atomic and molecular charge densities are performed numerically using grids, i.e.

$${\displaystyle \int }{d}^3\mathbf{r}\rho (\mathbf{r})\cong {\displaystyle \sum _i}\rho ({\mathbf{r}}_i)w_i$$ (8)

where r_i and w_i are the grid positions and weights, respectively. The ab initio atomic and molecular charge densities ρ(r) are evaluated at the grid positions r_i (see eqn. 21 below). We have written code to generate the grids using the scheme proposed by Becke [38]. For each atom, Gauss-Chebyshev radial grids of arbitrary order and Lebedev [39–44] angular grids of orders 9, 11, 17, 23, 25, 27, 41, 47, 53, and 131 have been implemented. Multiple atomic grids have been merged together into molecular grids using Becke’s smoothing function method [38]. The number of radial points and the order of angular quadrutaure are adjustable parameters in our code.

In general, the ab initio atomic charge densities are not spherically symmetric for open shell atoms or ions. For example, this can be seen by calculating the ab initio quadrupole moment for an oxygen atom O(³P). Spherically symmetric atomic charge densities ${\rho }_a^{(n)}(r)$ are obtained by averaging over solid angle Ω

$${\rho }_a^{(n)}(r)=\frac{1}{4\pi }{\displaystyle \int }d\mathrm{\Omega }{\rho }_a^{(n)}(\mathbf{r})$$ (9)

where r = |r| is the radial distance with respect to the origin. The integrations over solid angle are calculated numerically using the Lebedev grids. If the ab initio atomic densities are not averaged over solid angle and made spherically symmetric, then the resultant HD and HD-I atomic charges may have a slight dependence on molecular orientation.

3. Multipoles

The total partitioned atomic charge density η_a(r) for atom a is defined as the sum of a positive nuclear charge contribution and the negative partitioned atomic charge density ρ_a(r) by

$${\eta }_a(\mathbf{r})\equiv Z_a\delta (\mathbf{r}-{\mathbf{R}}_a)-{\rho }_a(\mathbf{r})$$ (10)

where Z_a is the nuclear charge of atom a, R_a is the nuclear center of atom a, and δ(r − R) is a Dirac-delta function [45]. Spherical tensor atomic multipole moments Q_lm^a of the total partitioned atomic charge densities η_a(r) are calculated as [29]

$$Q_{\mathit{\text{lm}}}^a={\displaystyle \int }{d}^3\mathbf{r}{\eta }_a(\mathbf{r})C_{\mathit{\text{lm}}}(\mathbf{r}-{\mathbf{R}}_a)$$ (11)

where C_lm(r) is a solid harmonic function [46] (eqns. A.3 and A.6). Molecular multipole moments $Q_{\mathit{\text{LM}}}^{\mathit{\text{mol}}}$ are defined with respect to a molecular center R by

$$Q_{\mathit{\text{LM}}}^{\mathit{\text{mol}}}={\displaystyle \int }{d}^3\mathbf{r}{\eta }_{\mathit{\text{mol}}}(\mathbf{r})C_{\mathit{\text{LM}}}(\mathbf{r}-\mathbf{R})$$ (12)

where η_mol(r) is total molecular charge density given by

$${\eta }_{\mathit{\text{mol}}}(\mathbf{r})={\displaystyle \sum _a}{\eta }_a(\mathbf{r})={\displaystyle \sum _a}{Z}_a\delta (\mathbf{r}-{\mathbf{R}}_a)-{\rho }_a(\mathbf{r})$$ (13)

Typically, the molecular center R is taken to be the origin (R = 0) in ab initio calculations. In this work, the molecular center is the origin, which also coincides with the center of nuclear charge. The molecular multipole moments $Q_{\mathit{\text{LM}}}^{\mathit{\text{mol}}}$ can be expressed in terms of atomic multipole moments Q_lm^a by first substituting eqn. 13 into eqn. 12

$$Q_{\mathit{\text{LM}}}^{\mathit{\text{mol}}}={\displaystyle \sum _a}{\displaystyle \int }{d}^3\mathbf{r}{\eta }_a(\mathbf{r})C_{\mathit{\text{LM}}}(\mathbf{r}-\mathbf{R})$$ (14)

An addition theorem for solid harmonic functions [47] C_LM(r₁ + r₂) (eqn. A.5) with r₁ ≡ r − R_a and r₂ ≡ R_a − R is substituted into eqn. 14 to give

$$Q_{\mathit{\text{LM}}}^{\mathit{\text{mol}}}={\displaystyle \sum _a}{\displaystyle \sum _{l=0}^L}{\displaystyle \sum _{m=-l}^l}\sqrt{\left(\begin{array}{c}\hfill L+M\hfill \\ \hfill l+m\hfill \end{array}\right)\left(\begin{array}{c}\hfill L-M\hfill \\ \hfill l-m\hfill \end{array}\right)}{Q}_{\mathit{\text{lm}}}^a{C}_{L-l,M-m}({\mathbf{R}}_a-\mathbf{R})$$ (15)

In ab initio calculations, molecular multipoles are often calculated in ‘pure’ Cartesian form

$${\mathrm{\Omega }}_{l_x{l}_y{l}_z}^{(l)}\equiv {\displaystyle \int }{d}^3\mathbf{r}\rho (\mathbf{r}){(x-X)}^{l_x}{(y-Y)}^{l_y}{(z-Z)}^{l_z}$$ (16)

where (l ≡ l_x + l_y + l_z) and R ≡ (X, Y, Z). In addition, traceless Cartesian multipoles [29] with respect to the origin (R = 0) are defined by

$${\mathrm{\Theta }}_{l_x{l}_y{l}_z}^{(l)}\equiv {\displaystyle \int }{d}^3\mathbf{r}\rho (\mathbf{r}){\zeta }_{l_x{l}_y{l}_z}^{(l)}(\mathbf{r})$$ (17)

where ${\zeta }_{l_x{l}_y{l}_z}^{(l)}(\mathbf{r})$ is a traceless Cartesian multipole operator defined by

$${\widehat{\zeta }}_{l_x{l}_y{l}_z}^{(l)}(\mathbf{r})\equiv \frac{{(-1)}^l}{l!}{r}^{2l+1}{\partial }_x^{l_x}{\partial }_y^{l_y}{\partial }_z^{l_z}\frac{1}{r}$$ (18)

Expressions for converting multipole moments between ‘pure’ Cartesian, traceless Cartesian, and spherical tensor conventions have been given in previous works [48–50]. The conversion formulae follow from the polynomial properties [50] of $C_{\mathit{\text{lm}}}(\mathbf{r})\text{ and }{\zeta }_{l_x{l}_y{l}_z}^{(l)}(\mathbf{r})$ (see eqns. A.6 – A.11). The expressions needed in this work are summarized below. ‘Pure’ Cartesian multipoles can be converted to spherical tensor multipoles by

$$Q_{\mathit{\text{lm}}}={\displaystyle \sum _{k=0}^{\left[\frac{l-|m|}{2}\right]}}{\displaystyle \sum _{p=0}^{k+m_{+}}}{\displaystyle \sum _{q=0}^{k+m_{-}}}{a}_{k,p,q}^{\mathit{\text{lm}}}{\mathrm{\Omega }}_{p+q,|m|+2k-p-q,l-|m|-2k}^{(l)}$$ (19)

where $m_{\pm }\equiv (|m|\pm m)/2\text{ and }{a}_{k,p,q}^{\mathit{\text{lm}}}$ is a constant defined in eqn. A.7. Spherical tensor multipoles can be converted to traceless Cartesian multipoles by

$${\mathrm{\Theta }}_{l_x{l}_y{l}_z}^{(l)}={\displaystyle \sum _{n=0}^{l_x+l_y}}{b}_n^{l_x,l_y,l}{Q}_{l,2n-l_x-l_y}$$ (20)

where $b_n^{l_x,l_y,l}$ is a constant defined in eqn. A.10.

4. Computational Details

All ab initio calculations are performed at the B3LYP/aug-cc-pVTZ level using Gaussian 09 [51]. The molecules are initially geometry optimized at the B3LYP/aug-cc-pVTZ level. We have written code to read in the ab initio density matrix P_μν and the real atomic basis functions χ_μ(r) from ‘formatted checkpoint’ files obtained from Gaussian 09. The ab initio (molecular or atomic) charge density ρ(r) is evaluated as

$$\rho (\mathbf{r})={\displaystyle \sum _{\mu \nu }}{P}_{\mu \nu }{\chi }_{\mu }(\mathbf{r}){\chi }_{\nu }(\mathbf{r})$$ (21)

The ab initio molecular charge density is evaluated on a grid for the molecule, while the ab initio atomic and atomic ion charge densities are evaluated on atomic grids for the isolated atoms. The ab initio atomic charge densities are averaged over solid angle using eqn. 9 and stored as a tabulated function of radial distance r from the atomic center. The spherically symmetric ab initio atomic charge densities are evaluated on the molecular grid using an exponential type interpolation between neighboring radial points [r_i, r_i+1]. In this work, all calculations are done using a 100 point radial grid and a Lebedev grid of order 41 with 590 points angular points. The HD and HD-I partitioned atomic charge densities are evaluated numerically on a grid from the ab initio charge densities of the molecule and the isolated atomic charge densities using the procedure described in section 1.

The molecules studied in this work are closed shell with a spin multiplicity of 2S+1 = 1 (S = 0). However, the spin multiplicities of the isolated atoms and atomic ions are chosen which minimize the ab initio atomic energies. The spin multiplicities of the various atomic species used in this work are given in Table I. For the open shell atomic species, the atomic charge densities are obtained from unrestricted self consistent field calculations using the B3LYP density functional.

Table I.

Spin Multiplicities (2S+1) of Atoms and Atomic Cations/Anions

	X	X+	X−	X2+	X2−
H	2		1
Li	2	1		2
C	3	2	4	1	3
N	4	3	3	2	2
O	3	4	2	3	1
F	2	3	1
Na	2	1
Mg	1	2		1
Cl	2	3	1

Atomic charges and atomic multipoles are calculated from the partitioned HD and HD-I atomic charge densities using eqns. 7 and 11, respectively. The spherical tensor molecular multipole are calculated from the atomic charges/multipoles using eqn. 15 and converted to their traceless Cartesian forms using eqn. 20. The ab initio ‘pure’ Cartesian molecular multipoles are obtained from Gaussian 09 output and converted to their spherical tensor and then traceless Cartesian forms using eqns. 19 and 20, respectively. In addition, ChelpG atomic charges are calculated with Gaussian 09.

The HD and HD-I atomic charges/multipoles are further tested by calculating the ESP surrounding a molecule and comparing with ab initio reference data. The ESP calculated by atomic multipoles is given by

$$V(\mathbf{r})={\displaystyle \sum _a}{\displaystyle \sum _{l=0}^{l_{\text{max}}}}{\displaystyle \sum _{m=-l}^l}{Q}_{\mathit{\text{lm}}}^a\frac{C_{\mathit{\text{lm}}}^{*}(\mathbf{r}-{\mathbf{R}}_a)}{{|\mathbf{r}-{\mathbf{R}}_a|}^{2l+1}}$$ (19)

where r is the field point, R_a is the atomic center of atom a, and l_max is the maximum rank of the multipole expansion. The ab initio ESP is calculated with Gaussian 09. In general, a necessary condition for the multipole approximation to be valid, is that the ab initio charge density ρ(r) evaluated at the field point r should be small. The ESP is sampled on a surface surrounding a molecule where the density is small and defined by 10⁻⁴ e/ų ≥ ρ(r) ≥ 10⁻⁵ e/ų. The distance from a point on the surface to the closest atomic center is calculated and averaged over the surface. For each element, the distances are then averaged over the 24 molecules studied in this work (see Table III) and given in Table II. For comparison, the inner ChelpG radii are also given in Table II for the elements H, C, N, O. ChelpG atomic charges are fit to the ab initio ESP on a grid of points defined between inner and outer vdW radii (2.8 Å) on each atom.

Table III.

Molecular Dipole Moments (D^a) calculated by Hirshfeld, Hirshfeld-I, and ChelpG atomic charges

Molecule	Hirshfeld	Hirshfeld-I	ChelpG	QMb
Acetone	2.131	2.854	3.069	3.080
Acetylaldehyde	1.984	2.735	2.851	2.882
Ammonia	0.478	1.664	1.550	1.492
CH3CO2−	2.378	3.593	3.568	3.623c
CH3NH3+	1.913	2.184	2.163	2.158c
Chloromethane	1.211	1.290	2.027	1.986
Dichloromethane	1.032	1.395	1.842	1.678
Difluoromethane	1.313	2.034	2.017	1.975
Dimethyl Ether	0.704	1.228	1.305	1.266
Fluoromethane	1.281	1.787	1.877	1.872
Formaldehyde	1.516	2.418	2.372	2.389
Formamide	2.886	3.737	3.916	3.950
Hydrogen fluoride	0.932	2.239	1.831	1.812
LiCl	5.029	9.051	7.107	6.982
LiF	4.327	7.276	6.230	6.230
Methanol	0.789	1.928	1.609	1.656
Methyl Amine	0.332	1.230	1.216	1.287
MgF+	6.357	10.35	8.946	9.011c
MgO	4.848	9.224	7.461	7.463
NaCl	6.610	10.51	8.719	8.859
NaF	5.831	9.001	8.019	8.134
neopentane	0.000	0.000	0.003	0.000
N-methyl formamide	2.917	3.922	3.888	3.991
water	0.818	2.420	1.904	1.847
Average rmsd error	0.68	0.31	0.030

^a1 D = 0.20822678 e·Å = 3.336 ×10⁻³⁰ C·m

^bB3LYP/aug-cc-pVTZ

^cFor charged molecules, the dipole moments depends on origin R = 0, which are taken to be the center of nuclear of charge.

Table II.

Average Atomic Distance to the ESP Surface R_esp^a and Inner ChelpG Radii R_ChelpG

Element	Resp(Å)	RChelpG (Å)
H	1.69	1.5
Li	1.77
C	1.81	2.0
N	1.88	2.0
O	1.83	2.0
F	1.76
Na	1.80
Mg	1.86
Cl	1.90

^aAverage distance of the ESP surface to the closest atom R_esp. The ESP surface is defined as the volume surrounding the molecule in which the ab initio electron density ρ(r) (e/ų) satisfies 10⁻⁴ ≥ ρ(r) ≥ 10⁻⁵.

Results

1) Hirshfeld (HD) and Hirshfeld-I (HD-I) Atomic Charges

HD, HD-I, and ChelpG atomic charges are calculated for a variety of small molecules and listed in Table III. The molecular dipole moments are calculated from the atomic charges and compared to their ab initio reference values. In general, the HD atomic charges underestimate the molecular dipole moment, while the HD-I atomic charges often overestimate the molecular dipole with respect to reference ab initio results. In comparison, molecular dipole moments calculated by ChelpG atomic charges closely reproduce the ab initio molecular dipole moments. For example, the molecular dipole moments of water calculated by HD, HD-I, and ChelpG atomic charges are 0.818, 2.42, and 1.904 D, which can be compared to the reference B3LYP/aug-cc-pVTZ result of 1.847 D. The Root Mean Square Deviation (rmsd) in molecular dipole moment is calculated for each molecule and averaged over all of the molecules. For HD, HD-I, and ChelpG atomic charges, the averaged rmsd in molecular dipole moment are 0.68, 0.31, and 0.030 D, respectively.

The ChelpG atomic charges are fit to the ESP on a grid of points. Points near the nuclear centers are removed from the fit. For most small and medium sized molecules, there is sufficient ESP data to result in a numerically robust fit. However, for larger molecules with ‘buried atoms’ [4], such as that found in neopentane C-(CH₃)₄, most or all of the grid points near the central carbon have been removed, which results in a numerically less stable fit. Relatively large fluctuations are found in the ChelpG methyl carbon charges (e) of neopentane {−0.3184, −0.3073, −0.2993, −0.3120} when compared to HD-I charges {−0.39450, −0. 39450, −0.39449, −0.39449}. The fluctuations in the ChelpG charges cause a non-zero molecular dipole moment of 0.003 D, which should be zero because of symmetry. In comparison, the HD and HD-I atomic charges/multipoles are rigorously calculated through numerical integration without any fitted parameters.

2) Hirshfeld and Hirshfeld-I Atomic Multipoles

Atomic multipoles Q_lm^a are calculated from the HD and HD-I partitioned atomic charge densities ρ_a(r) using eqn. 11 for the 24 molecules listed in Table III. Traceless Cartesian molecular multipoles are calculated using eqns. 15 and 20 and compared to their ab initio reference values calculated by eqns. 19 and 20. As an example, the molecular dipole (L = 1) moment of hydrogen fluoride is given in Table IV for HD-I atomic charges (l_max = 0) and HD-I atomic charges + dipoles (l_max = 1). The molecular dipole moments of −2.2389 and −1.8124 D calculated by HD-I atomic charges only and HD-I atomic charges + dipoles, respectively, can be compared to the ab initio reference value of −1.8124 D. Note that while HD-I atomic charges predict a relatively large error of 0.3 D in the molecular dipole, HD-I atomic charges + dipoles reproduce the exact ab initio molecular dipole.

Table IV.

Molecular Dipole Moment^a (D) of hydrogen fluoride oriented along the z-axis calculated by HD-I atomic charges (l_max = 0) and HD-I atomic charges + dipoles (l_max = 1)

	Z
lmax = 0	−2.2389
lmax = 1	−1.8124
QM	−1.8124

^aB3LYP/aug-cc-pVTZ

Similar examples are given in Tables V and VI for the molecular quadrupole and octupole moments of hydrogen fluoride, respectively. Note that HD-I atomic charges + dipoles + quadrupoles (l_max = 2) exactly reproduce the ab initio molecular quadrupole, while HD-I atomic charges + dipoles + quadrupoles + octupoles (l_max = 3) exactly reproduce the ab initio molecular octupole moment (up to the numerical precision of the calculation, which is typically 10⁻⁴ DÅ^L−1). This property follows from the atomic charge densities ρ_a(r) being exact partitions of the molecular charge density ρ_mol(r) as shown in eqn. 1. In addition, atomic multipoles of rank l do not contribute to molecular multipoles of rank L for l > L, as shown in eqn. 15. For example, atomic quadrupoles (l = 2) do not contribute to the molecular dipole (L = 1).

Table V.

Molecular Quadrupole Moment^a (DÅ) of hydrogen fluoride oriented along the z-axis calculated by HD-I atomic charges (l_max = 0), HD-I atomic charges + dipoles (l_max = 1), and HD-I atomic charges + dipoles + quadrupoles (l_max = 2).

	XX	YY	ZZ	rmsd
lmax = 0	−0.8276	−0.8276	1.6552	0.238
lmax = 1	−1.0467	−1.0467	2.0934	0.019
lmax = 2	−1.0659	−1.0659	2.1319	0.000
QM	−1.0660	−1.0660	2.1319

^aB3LYP/aug-cc-pVTZ

Table VI.

Molecular Octupole Moment^a (DŲ) of hydrogen fluoride oriented along the z-axis calculated by HD-I atomic charges (l_max = 0), HD-I atomic charges + dipoles (l_max = 1), and HD-I atomic charges + dipoles + quadrupoles (l_max = 2), and HD-I atomic charges + dipoles + quadrupoles + octupoles (l_max = 3).

	XXZ	YYZ	ZZZ	rmsd
lmax = 0	0.6979	0.6979	−1.3957	0.023
lmax = 1	0.8917	0.8917	−1.7833	0.127
lmax = 2	0.8949	0.8949	−1.7899	0.129
lmax = 3	0.7279	0.7279	−1.4558	0.000
QM	0.7279	0.7279	−1.4558

^aB3LYP/aug-cc-pVTZ

The rmsd errors in molecular multipole moment calculated by HD and HD-I atomic multipoles are averaged over the 24 molecules listed in Table III and given in Table VII. The average errors in molecular multipole moment are smaller for HD-I atomic charges (l_max = 0) and HD-I atomic charges + dipoles (l_max = 1) when compared to the corresponding HD charges/multipoles. For example, the average errors in molecular quadrupole moments are 0.587 and 1.065 DÅ for HD-I and HD atomic charges, respectively. However, there is no significant difference in reproducing molecular multipole moments when comparing HD and HD-I atomic multipoles for l_max ≥ 2. For example, the average errors in molecular octupole moments calculated by HD and HD-I atomic charges + dipoles + quadrupoles (l_max = 2) are 0.362 and 0.384 DŲ, respectively. Note that the errors for molecular multipole moment of rank L are zero for atomic multipoles of rank l_max for l_max ≥ L. Consequently, the results for atomic hexadecapole (l_max = 4) are not listed in Table VII, as the errors in molecular dipole – molecular hexadecapole are zero.

Table VII.

Average rmsd errors^a in molecular dipoles (Δ_dip), molecular quadrupoles (Δ_quad), molecular octupoles (Δ_oct), and molecular hexadecapoles (Δ_hex) calculated by atomic multipoles of maximum rank l_max (HD = Hirshfeld atomic multipoles, HD-I = Hirshfeld-Iterated atomic multipoles).

	Δdip (D)	Δquad (DÅ)	Δoct (DÅ2)	Δhex (DÅ3)
HD (lmax = 0)	0.675	1.065	1.588	2.850
HD (lmax = 1)	0.0	0.582	1.314	2.875
HD (lmax = 2)	0.0	0.0	0.362	1.814
HD (lmax = 3)	0.0	0.0	0.0	0.456
HD-I (lmax = 0)	0.314	0.587	0.952	1.761
HD-I (lmax = 1)	0.0	0.348	0.762	2.267
HD-I (lmax = 2)	0.0	0.0	0.384	1.833
HD-I (lmax = 3)	0.0	0.0	0.0	0.419

^armsd error averaged over 24 molecules listed in Table III.

The electrostatic potential is calculated for both HD and HD-I atomic charges/multipoles on a surface surrounding a molecule defined from the molecular charge density ρ(r) by 10⁻⁴ e/ų ≥ ρ(r) ≥ 10⁻⁵ e/ų. The rmsd error in ESP is calculated for each molecule over the surface and averaged over the 24 molecules studied in this work and given in Table VIII. For the atomic charges models, the average rmsd errors are 1.082, 0.530, and 0.262 (10⁻² e/Å) for HD, HD-I, and ChelpG atomic charges, respectively. Van Damme et al. [23] have performed a similar analysis with HD, HD-I, and Merz-Kollman-Singh (MKS) [3] atomic charges by calculating the ESP on a grid of points and comparing with ab initio reference values. MKS atomic charges are similar to ChelpG atomic charges in that both charge models are fit to the electrostatic potential on a grid of points surrounding the molecule. The average rmsd errors reported by Van Damme et al. [23] are 1.53, 0.831, and 0.415 (10⁻² e/Å). Despite using different grids and different sets of molecules, the results reported here agree, at least qualitatively, with those reported by Van Damme et al. [23].

Table VIII.

Averaged^a Root Mean Square Deviation (rmsd) in Electrostatic Potential Surrounding^b a Molecule

Model	Averaged rmsd Error (10−2 e/Å)d	Percent Errorc (%)
ChelpG	0.262	4.89
HD (lmax = 0)	1.082	20.22
HD (lmax = 1)	0.284	5.31
HD (lmax = 2)	0.0761	1.42
HD (lmax = 3)	0.0222	0.42
HD (lmax = 4)	0.0184	0.34
HD-I (lmax = 0)	0.530	9.90
HD-I (lmax = 1)	0.167	3.12
HD-I (lmax = 2)	0.0702	1.31
HD-I (lmax = 3)	0.0170	0.32
HD-I (lmax = 4)	0.0086	0.16
	<|V|> = 5.35 (10−2 e/Å)

^aThe rmsd errors are averaged over 24 molecules listed in Table III.

^bThe surface surrounding the molecule is defined as the volume in which the ab initio electron density ρ(r) (e/ų) satisfies 10⁻⁴ ≥ ρ(r) ≥ 10⁻⁵.

^c1 e/Å = 0.5291772083 au

^dThe percent error is defined as rmsd /<|V|>.

The average rmsd errors have also been calculated for HD and HD-I atomic multipoles for l_max = 0, 1, 2, 3, 4. The average magnitude of the ESP on the grids is given by <|V|> = 5.35 10⁻² e/Å. Percent errors are defined by rmsd/<|V|>. For atomic charges, the percent errors are 20.21%, 9.90%, and 4.89% for HD, HD-I, and ChelpG atomic charges respectively. A systematic decrease in error is obtained by increasing the atomic multipole rank l_max. The percent errors in HD atomic multipoles are 20.22%, 5.31%, 1.42%, 0.42%, and 0.34% for l_max = 0, 1, 2, 3, 4, respectively. In comparison, the corresponding percent errors in HD-I atomic multipoles are 9.90%, 3.12%, 1.31%, 0.32%, and 0.16% l_max = 0, 1, 2, 3, 4, respectively. The rmsd errors in ESP for HD-I atomic multipoles are smaller than the corresponding errors in HD atomic multipoles by a factor of ~1.5x on average. A scatter plot of the ESP calculated by HD-I atomic multipoles as compared to its ab initio reference values is given in Figure 1 for l_max = 0, 1, 2, 3. As expected, a systematic increase in accuracy and precision is obtained by increasing the atomic multipole rank from l_max = 0 to l_max = 3.

Fig. 1.

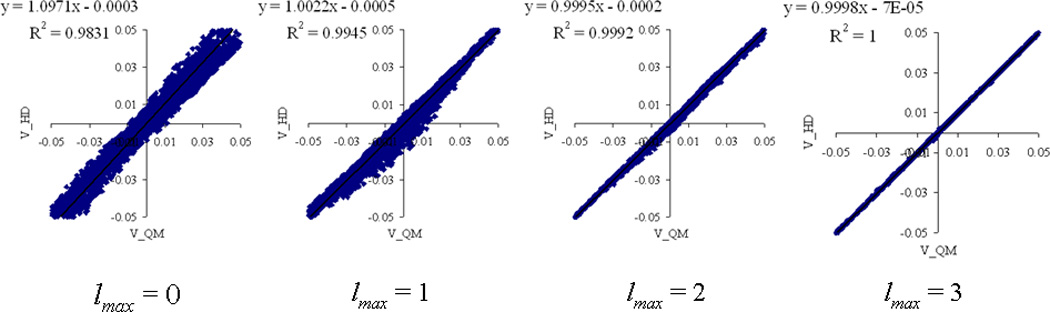
Comparison of the ESP calculated by HD-I atomic multipoles on a surface of points with ab initio reference values for the 24 molecules listed in Table III. The surfaces of points are defined by the ab initio densities ρ(r) (e/ų) by 10⁻⁴ ≥ ρ(r) ≥ 10⁻⁵.

Conclusions

A method for calculating atomic charges and multipoles from HD and HD-I partitioned atomic charge densities have been described in this work. When compared to HD atomic charges/multipoles, it is shown that HD-I atomic charges/multipoles represent an improvement in reproducing ab initio molecular multipole moments and the ESP surrounding a molecule. Since the HD and HD-I atomic charge densities are exact partitions of the molecular charge density, atomic multipoles of rank l_max exactly reproduce molecular multipoles of rank L for L ≤ l_max. For both the HD and HD-I atomic multipoles, a systematic increase in precision and accuracy in reproducing ab initio electrostatic properties is demonstrated by increasing the atomic multipole rank l_max from l_max = 0 (atomic charges) to l_max = 4 (up to atomic hexadecapoles). When compared to HD atomic charges/multipoles, HD-I atomic charges/multipoles are found to give smaller errors in electrostatic properties by a factor of 1.0 – 2.0x on average.

In addition, HD and HD-I atomic charges only (l_max = 0) are compared to ChelpG atomic charges by calculating molecular dipole moments and the ESP surrounding the molecules and comparing with their ab initio reference values. The errors in ESP for HD-I atomic charges are twice as large as the errors in ChelpG charges, while the errors in HD atomic charges are four times as large as the errors in ChelpG charges. Significant errors in molecular dipole moment are found for both HD and HD-I atomic charge only models (l_max = 0), when compared to ChelpG atomic charge models. However, ChelpG atomic charges are fit to the ESP surrounding a molecule and may suffer from numerical instabilities, if insufficient ESP data is available, as in the case of a molecule containing ‘buried atoms’. In contrast, HD and HD-I atomic charges/multipoles are rigorously calculated by integration up to the precision determined by the grids.

The hpam program and the methods for calculating HD and HD-I multipoles described in this work may be used in force field development and in the study of models for inter-molecular forces. However, we suspect the relatively large errors in reproducing ab initio molecular dipole moments for the HD and HD-I atomic charges only (l_max = 0) may limit the use of HD and HD-I atomic charges in force fields.

Appendix

A. Mathematical Background

A spherical harmonic function Y_lm(θ,ϕ) is defined on a unit sphere (θ,ϕ) in terms of Associated Legendre functions [45,46] P_lm (cos θ) by

$$Y_{\mathit{\text{lm}}}(\theta ,\varphi )\equiv {\left(-1\right)}^m\sqrt{\frac{2l+1}{4\pi }}\sqrt{\frac{(l-m)!}{(l+m)!}}{P}_{\mathit{\text{lm}}}(\text{cos }\theta )e^{\mathit{\text{im}}\varphi }$$ (A.1)

Hobson [46] has derived an especially useful polynomial expression for P_lm (cos θ) as

$$P_{\mathit{\text{lm}}}(\text{cos }\theta )=\frac{(l+m)!}{2^m}{\displaystyle \sum _{k=0}^{\left[\frac{l-m}{2}\right]}}{\left(\frac{-1}{4}\right)}^k\frac{{\text{cos}}^{l-m-2k}\theta {\text{ sin}}^{m+2k}\theta }{(l-m-2k)!(m+k)!k!}$$ (A.2)

for 0 ≤ m ≤ l. A regular solid harmonic function C_lm is defined over all space r by

$$C_{\mathit{\text{lm}}}(\mathbf{r})\equiv r^l\sqrt{\frac{4\pi }{2l+1}}{Y}_{\mathit{\text{lm}}}(\theta ,\varphi ).$$ (A.3)

An important symmetry relation for solid harmonic functions is given by

$$C_{\mathit{\text{lm}}}^{*}(\mathbf{r})={(-1)}^m{C}_{l-m}(\mathbf{r})$$ (A.4)

An important addition theorem for solid harmonic functions is given by [47]

$$C_{\mathit{\text{LM}}}({\mathbf{r}}_1+{\mathbf{r}}_2)={\displaystyle \sum _{l=0}^L}{\displaystyle \sum _{m=-l}^l}\sqrt{\left(\begin{array}{c}\hfill L+M\hfill \\ \hfill l+m\hfill \end{array}\right)\left(\begin{array}{c}\hfill L-M\hfill \\ \hfill l-m\hfill \end{array}\right)}{C}_{\mathit{\text{lm}}}({\mathbf{r}}_1)C_{L-1,M-m}({\mathbf{r}}_2)$$ (A.5)

From eqns. A.2, A.3, and A.4, a polynomial expression for C_lm(r) can be found as

$$C_{\mathit{\text{lm}}}(\mathbf{r})={\displaystyle \sum _{k=0}^{\left[\frac{l-|m|}{2}\right]}}{\displaystyle \sum _{p=0}^{k+m_{+}}}{\displaystyle \sum _{q=0}^{k+m_{-}}}{a}_{k,p,q}^{\mathit{\text{lm}}}{x}^{p+q}{y}^{|m|+2k-p-q}{z}^{l-|m|-2k}$$ (A.6)

where m_± ≡ (|m| ± m)/2 and

$$a_{k,p,q}^{\mathit{\text{lm}}}\equiv \frac{{(-1)}^{|m|+q}{A}_{\mathit{\text{lm}}}}{2^{|m|+2k}(l-|m|-2k)!p!(k+m_{+}-p)!q!(k+m_{-}-q)!}{i}^{|m|+2k-p-q}$$ (A.7)

and $A_{\mathit{\text{lm}}}\equiv \sqrt{(l+m)!(l-m)!}$. From the polynomial expressions for C_lm(r) in eqn. A.6, interconversion formulae between $C_{\mathit{\text{lm}}}(\mathbf{r})\text{ and }{\zeta }_{l_x{l}_y{l}_z}^{(l)}(\mathbf{r})$ (eqn. 18) can be derived [50] as

$${\widehat{\zeta }}_{l_x,l_y,l_z}^{(l)}(\mathbf{r})={\displaystyle \sum _{n=0}^{l_x+l_y}}{b}_n^{l_x,l_y,l}{C}_{l,2n-l_x-l_y}(\mathbf{r})$$ (A.8)

$$C_{\mathit{\text{lm}}}(\mathbf{r})={\displaystyle \sum _{k=0}^{|m|}}{c}_k^{\mathit{\text{lm}}}{\widehat{\zeta }}_{|m|-k,k,l-|m|}^{(l)}(\mathbf{r})$$ (A.9)

where $b_n^{l_x,l_y,l}\text{ and }{c}_k^{\mathit{\text{lm}}}$ are constants given by

$$b_n^{l_x,l_y,l}\equiv \frac{i^{l_y}{A}_{l,2n-l_x-l_y}}{2^{l_x+l_y}l!}{\displaystyle \sum _{q=\text{max}(0,n-l_x)}^{\text{min}(l_y,n)}}\left(\begin{array}{c}\hfill l_x\hfill \\ \hfill n-q\hfill \end{array}\right)\left(\begin{array}{c}\hfill l_y\hfill \\ \hfill q\hfill \end{array}\right){(-1)}^{n+q}$$ (A.10)

$$c_k^{\mathit{\text{lm}}}\{\begin{array}{cc}\hfill \frac{l!{(-1)}^{m_{+}}}{A_{\mathit{\text{lm}}}}\left(\begin{array}{c}\hfill |m|\hfill \\ \hfill k\hfill \end{array}\right)i^k\hfill & \hfill m\ge 0\hfill \\ \hfill \frac{l!{(-1)}^k}{A_{\mathit{\text{lm}}}}\left(\begin{array}{c}\hfill |m|\hfill \\ \hfill k\hfill \end{array}\right)i^k\hfill & \hfill m<0\hfill \end{array}$$ (A.11)