Heart Rate Variability – A Historical Perspective

Abstract

Heart rate variability (HRV), the beat-to-beat variation in either heart rate or the duration of the R–R interval – the heart period, has become a popular clinical and investigational tool. The temporal fluctuations in heart rate exhibit a marked synchrony with respiration (increasing during inspiration and decreasing during expiration – the so called respiratory sinus arrhythmia, RSA) and are widely believed to reflect changes in cardiac autonomic regulation. Although the exact contributions of the parasympathetic and the sympathetic divisions of the autonomic nervous system to this variability are controversial and remain the subject of active investigation and debate, a number of time and frequency domain techniques have been developed to provide insight into cardiac autonomic regulation in both health and disease. It is the purpose of this essay to provide an historical overview of the evolution in the concept of HRV. Briefly, pulse rate was first measured by ancient Greek physicians and scientists. However, it was not until the invention of the “Physician’s Pulse Watch” (a watch with a second hand that could be stopped) in 1707 that changes in pulse rate could be accurately assessed. The Rev. Stephen Hales (1733) was the first to note that pulse varied with respiration and in 1847 Carl Ludwig was the first to record RSA. With the measurement of the ECG (1895) and advent of digital signal processing techniques in the 1960s, investigation of HRV and its relationship to health and disease has exploded. This essay will conclude with a brief description of time domain, frequency domain, and non-linear dynamic analysis techniques (and their limitations) that are commonly used to measure HRV.

Variability is the law of life…

(William Osler, physician and educator, 1849–1919;

Olser, 1903, p. 327)

Introduction

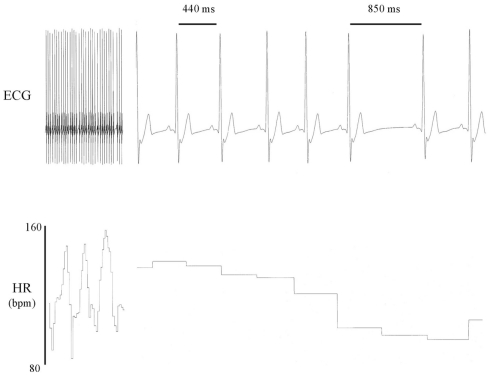
Heart rate variability (HRV), beat-to-beat variation in either heart rate or the duration of the R–R interval – the heart period (for an example see Figure 1), has become an important risk assessment tool. A reduced HRV is associated with a poorer prognosis for a wide range of clinical conditions while, conversely, robust periodic changes in R–R interval are often a hallmark of health (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Bigger, 1997; De Jong and Randall, 2005; Thayler et al., 2010). A major portion of these temporal changes in heart rate occur synchronous with respiration [heart rate increases (R–R interval shortens) during inspiration and decreases (R–R interval prolongs) during expiration] and, therefore, are referred to as the respiratory sinus arrhythmia (RSA). Although HRV and RSA are not quite the same, these terms are often used interchangeably and both are widely believed to reflect changes in cardiac autonomic regulation. The exact contributions of the parasympathetic and the sympathetic divisions of the autonomic nervous system to this variability are controversial and remain the subject of active investigation and debate (Parati et al., 2006). It is the purpose of this essay to provide a historical overview of the evolution of the concept of HRV and its application in the laboratory and in the clinic. Time and frequency domain techniques used to quantify HRV and their limitations will also be briefly discussed.

Figure 1.

Heart rate variability: representative electrocardiogram (ECG) recordings from a conscious dog that illustrate beat-to-beat variations in both R–R interval and heart rate.

Historical Overview

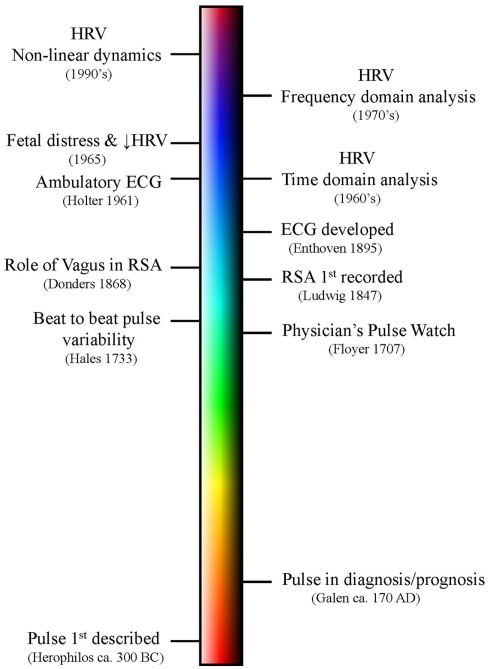
A summary of some of the major events in the evolution of the HRV concept is displayed as a timeline (not drawn to scale) in Figure 2. Undoubtedly early humans were the first to notice that the heart beat varied, increasing, for example, during physical exertion or sexual arousal. However, the first written descriptions of heart rate (measured by the pulse) are found in the fragmentary writings of the ancient Greek physician and scientist Herophilos (’HρóΦιλoς, Latinized as Herophilus, ca. 335- ca. 280 BC; Figure 3; Bedford, 1951; Bay and Bay, 2010). He was born in Chalcedon but spent the majority of his adult life in Alexandria. He was perhaps the first anatomist and published at least nine volumes of his findings, all of which have been lost (Bedford, 1951; Bay and Bay, 2010). Fortunately, his original text was extensively quoted in the works of other authors, particularly by the Greco-Roman physician Galen (Bedford, 1951; Boylan, 2007). Among his most notable findings was the demonstration that the veins carried blood, that veins and arteries were distinctly different, and that the arteries pulsed rhythmically (Bedford, 1951; Bay and Bay, 2010). These fragmentary quotations also suggest that Herophilos was the first person to measure heart rate (by timing the pulse using a water clock or clepsydra; Bedford, 1951; Bay and Bay, 2010). Galen also extensively cites and criticizes the description of the pulse made by Archigenes (’Aρχιένης, fl. first century AD, born in Syria but practiced medicine in Rome; Bedford, 1951). Archigenes apparently described eight characteristics of the pulse, including observations on its regularity and irregularity (Bedford, 1951). The first individual by whom the original texts on the pulse have survived is Rufus of Ephesus (fl second century; Bedford, 1951). He was the first to recognize that the pulse was caused by the contraction and relaxation of the heart (Bedford, 1951).

Figure 2.

A timeline of some of the major events in the discovery of heart rate variability (HRV). Please note that the timeline is not drawn to scale.

Figure 3.

Portrait of Herophilos (ca. 335–280 BC). He was the first to measure the heart beat using a water clock to time the pulse. Source: Reproduced with permission from the John P. McGovern Historical Collections and Research Center; Houston Academy of Medicine-Texas Medical Center Library; Houston, TX, USA. P-254, color photo; Artist: Joseph F. Doeve, painted in 1953.

Irrefutably, the most influential ancient physician/scientist was Galen of Pergamon (Γαληνóς, Latinized as Claudius Galenus, 131–200 AD; Figure 4). He wrote at least 18 books on the pulse including at least 8 treatises that described using pulse for the diagnosis and predicting the prognosis of disease (Bedford, 1951; Boylan, 2007). His teaching on pulse dominated medical practice for almost sixteen centuries through the Middles Ages and the Renaissance to dawn of modern era. Among his many findings, he was the first to report on the effects of exercise on pulse. For example, in “The Pulse for Beginners” he states:

Figure 4.

Portrait of Galen of Pergamon (131–200 AD). He wrote extensively about the pulse and used it for both the diagnosis and predicting the prognosis of disease. Source: National Library of Medicine (the history of medicine public domain image files). Lithograph by Pierre Roche Vigneron (Paris: Lith de Gregoire et Deneux, ca. 1865).

“Exercise to begin with – and so long as it is practiced in moderation – renders the pulse vigorous large, quick, and frequent. Large amounts of exercise, which exceed the capacity of the individual, make it small, faint, quick and extremely frequent.”

(Galen, 1997, p. 332)

It was not until the early eighteenth century that the more accurate measurement of time allowed for more quantitative evaluations of heart rate. John Floyer (1649–1734), an English physician, is credited with inventing what he called the “The Physician Pulse Watch,” a portable clock that added a second hand and push-piece that could stop the watch (Floyer, 1707, 1710). Using this device, he tabulated both pulse and respiration under a variety of conditions. He published his findings in two volumes (Floyer, 1707, 1710) and became a strong advocate of using the timing of the pulse so that “we may know the natural pulse and the excesses and defects from this in disease” (Floyer, 1707, p.13).

With the increased availability of accurate time-pieces, periodic fluctuations in the arterial pulse were soon described. In 1733, the Rev. Stephen Hales (1677–1761; Figure 5) was the first to report that the beat-to-beat interval and arterial pressure level varied during the respiratory cycle (Hales, 1733). In 1847, Carl Ludwig (1816–1895; Figure 6) using his invention, the smoked drum kymograph (a device that allowed for the measurement of mechanical activity), was the first to record periodic oscillations in the amplitude and timing of the arterial pressure waves that varied during the respiration (Ludwig, 1847). Using the dog, he noted that pulse regularly increased during inspiration and slowed during expiration, thereby providing the first documented report of what subsequently became know as the RSA (Ludwig, 1847). In the late nineteenth and early twentieth century Willem Einthoven (1860–1927), using galvanometers to measure accurately changes in electrical currents, produced the first continuous recordings of the electrical activity of the heart (Einthoven, 1895; Katz and Hellerstein, 1982; Hurst, 1998). With the development and standardization of the electrocardiogram, it became possible to evaluate beat-to-beat changes in the cardiac rhythm. In the early 1960s, ambulatory ECGs could be obtained over long periods of time (e.g., 24 h) using a small portable recorder developed by Norman “Jeff” Holter (1914–1983; Holter, 1961) which further sparked the interest in understanding the relationship between beat-to-beat variation in the heart interval and disease. With the advent of modern digital signal processing techniques (Cooley and Tukey, 1965), it became possible to quantify and to analyze subtle beat-to-beat variations in cardiovascular parameters. Beginning in the early 1970s several groups applied power spectral analysis to investigate the physiological basis for the individual frequency components that compose the periodic variations in heart rate (Hyndman et al., 1971; Sayers, 1973; Chess et al., 1975; Hyndman and Gregory, 1975; Peñáz et al., 1978; Akselrod et al., 1981; Kay and Marple, 1981; Pagani et al., 1984, 1986; Pomeranz et al., 1985; Myers et al., 1986; Malliani et al., 1991). Since these pioneering studies the field has rapidly expanded. Both time and frequency and time domain techniques have been used to quantify HRV. Recently, techniques derived from the new science of deterministic “chaos” have been used to evaluate the non-linear dynamic characteristics of HRV (Goldberger and West, 1987; Denton et al., 1990; Bigger et al., 1996; Lombardi et al., 1996; Mäkikallio et al., 1997, 1999a,b; Huikuri et al., 1998, 2000, 2003; Pikkujämsä et al., 1999). Some of these methodologies will be briefly discussed in a subsequent section of this essay.

Figure 5.

Portrait of Rev. Stephen Hales (1677–1761). He was the first to report periodic fluctuations in arterial pressure and the beat-to-beat interval that varied with respiration. These pioneering studies were performed on conscious horse. Source: Reproduced with permission from the John P. McGovern Historical Collections and Research Center; Houston Academy of Medicine-Texas Medical Center Library; Houston, TX, USA. P-261, color photo; Artist: Joseph F. Doeve, painted in 1953.

Figure 6.

Photograph of Carl Lugwig (1816–1895). He is credited with inventing the smoked drum kymograph and used it to record periodic oscillations in the amplitude and timing of arterial pressure that varied during respiration. Using the dog, he reported that the pulse rate increased during inspiration and decreased during expiration, thereby providing the first documented recordings of the respiratory sinus arrhythmia. Source: National Library of Medicine (the history of medicine public domain image files). Picture made in 1856.

The physiological basis that underlies HRV has been the subject of intensive investigation and still remains an unresolved question. In later half of nineteenth century, several investigators proposed that changes in neural activity were responsible for the periodic changes in the arterial pressure interval (Traube, 1865; Donders, 1868; Hering, 1869, 1871; Cyon, 1874; Mayer, 1876; Frédéricq, 1882). Ludwig Traube (1818–1876) proposed that “irradiation” from central neural (medullary) respiratory neurons unto the cardiovascular centers was responsible for arterial waves (Traube, 1865) while in 1871 Karl Ewald Hering (1834–1918) concluded that these periodic changes originated from the reflex activation of afferent fibers located in the lungs (Hering, 1871). Frédéricq (1851–1935) demonstrated that arterial pressure variability continued when the lung motion ceased (by opening the chest cavity) and conversely, the RSA was eliminated by the inhibition of respiratory motor activity following hyperventilation (Frédéricq, 1882). Later, Francis A. Bainbridge (1874–1921) proposed that the RSA did not involve the nervous system but rather results from mechanical distortion of the atria due to changes in thoracic pressure during the respiratory cycle (Bainbridge, 1930). The first systematic evaluation of these competing hypotheses was reported by Gleb von Anrep (1891–1955) and associates (Anrep et al., 1936a,b). They performed studies in dogs that clearly demonstrated that either central respiratory neural activity or the activation of pulmonary stretch receptors could maintain RSA when the other factor was controlled (Anrep et al., 1936b). They concluded that both central and peripheral mechanisms can contribute to these beat-to-beat changes in heart rate. It has also been subsequently suggested that cyclic activation of the arterial baroreceptor, thermoregulatory control, and the renin–angiotensin system may also contribute to oscillations in heart rate (Sayers, 1973; Hyndman, 1974; Akselrod et al., 1981; Madwell et al., 1989). Despite nearly 90 years of subsequent investigation, the relative contribution of the central and peripheral mechanisms responsible for RSA (Eckberg, 2003) and its functional significance (Hayano et al., 1996; Sin et al., 2010) remain the subject of considerable controversy and active investigation.

With regards to efferent neural contribution to periodic changes in heart rate, Franciscus C. Donders (1818–1889) suggested that the changes in heart period associated with respiration resulted from activation of the cardiac vagus nerves (Donders, 1868). This view soon gained wide-spread acceptance. By 1910, Heinrich E. Hering (1866–1948) could write that “it is known with breathing that a demonstrable lowering of heart rate … is indicative of the function of the vagi” (Hering, 1910). Hamlin et al. (1966) convincingly demonstrated that RSA in the dog resulted from activation of the vagal nerves, an observation that has been confirmed in other mammalian species (cats: Chess et al., 1975; Yongue et al., 1982; rats: McCabe et al., 1985; Cerutti et al., 1991; horse and ponies: Hamlin et al., 1972; Rugh et al., 1992), including human (Davies and Neilson, 1967; Melcher, 1976; Hirsch and Bishop, 1981; Selman et al., 1982; Eckberg, 1983). Sympathetic neural activation was also found to contribute significantly periodic arterial pressure changes (Guyton and Harris, 1951; Preiss et al., 1975). Arthur C. Guyton (1919–2003) and co-workers reported that vasomotor waves occur synchronous with increases in sympathetic nerve activity (Guyton and Harris, 1951). Similarly, a strong correlation between respiration, sympathetic nerve outflow, and changes in arterial pressure have been reported (Preiss et al., 1975). By the early 1970s several investigators began to apply modern digital processing techniques to evaluate the relationship between the autonomic neural regulation and in subtle changes in both arterial pressure waves and heart rate (Katona et al., 1970; Hyndman et al., 1971; Sayers, 1973; Chess et al., 1975; Hyndman and Gregory, 1975; Peñáz et al., 1978). For example, Katona and Jih (1975) proposed that periodic changes in heart rate that corresponded to the respiration could be used as non-invasive maker of cardiac parasympathetic regulation. A multitude of studies have been performed since these pioneering studies were competed nearly 40 years ago (for reviews see: Appel et al., 1989; Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Berntson et al., 1997; Bigger, 1997; Cohen and Taylor, 2002; Grossman and Taylor, 2007; Thayler et al., 2010). Today, it is now clear that the rhythmic changes in the heart rate at any given moment reflect the complex interactions between parasympathetic nerve fibers (activation decreases heart rate), sympathetic nerve fibers (activation increases heart rate), mechanical, and other factors on the pacemaker cells usually located in the sinoatrial node.

Heart Rate Variability Techniques

A number of techniques have now been developed to quantify this beat-to-beat variability in order to provide indices of cardiac autonomic regulation in both health and disease (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Berntson et al., 1997; Bigger, 1997; Denver et al., 2007; Grossman and Taylor, 2007; Thayler et al., 2010). There are two primary approaches for the analysis of HRV: time domain and frequency domain methods (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Berntson et al., 1997; Denver et al., 2007). The time domain measures of this variability are easier to calculate but tend to provide less detailed information than the frequency domain approaches. The time domain methods employ either statistical or geometric approaches (Table 1). Each approach shares the common feature that either heart rate at any point in time (instantaneous heart rate) or the intervals between successive normal beats are determined from a continuous ECG record. Only the normal QRS complexes are used for the calculation; that is, only beats that result from the normal electrical activation pattern (i.e., depolarization originating from the sinoatrial node) are included, any abnormal beats (atrial or ventricular arrhythmias) are excluded. Thus, the normal-to-normal (NN) interval (the interval between adjacent normal QRS complexes) or the instantaneous heart rate (heart rate calculated on a beat by beat basis) is determined and simple descriptive time domain variables such as the mean NN interval, mean heart rate, and the range (longest NN minus the shortest NN) for a given time interval can be calculated (Kleiger et al., 1987). More detailed information is provided by the statistical analysis of a continuous sequence of normal beats (NN interval) for the time period of interest. Due to the ease of calculation, the SD (i.e., the square root of the variance) of the NN interval (SDNN) is one of the most widely used time domain indices of HRV (Kleiger et al., 1987). This calculation measures the total variability that arises from both periodic and random sources (equivalent to total power as determined by frequency domain spectral analysis). Artifact recognition also can influence time domain measurements of HRV (Malik et al., 1993). As such, these approaches cannot differentiate between the various factors that contribute to the total variance. Other approaches to quantify RSA involves obtaining the difference between the peak and the valley (or trough) of heart rate that occurs during a respiratory cycle (for each inspiration and expiration; Hirsch and Bishop, 1981; Eckberg, 1983; Fouad et al., 1984) or determining the number of adjacent pairs of normal beats that differ by more than 50 ms, NN50 (Ewing et al., 1984). The peak-to-valley techniques attempt to extract periodic variability from a baseline heart rate. If the amplitude of the RSA is large relative to the baseline variance of heart rate or at slower respiratory frequencies, this technique provides a reasonable estimate of RSA that correlates well with other time domain indices (Grossman et al., 1990). However it is less accurate at higher respiratory frequencies and cannot quantify dynamic changes in the HRV on a beat by beat basis (Grossman et al., 1990). Other widely used statistical time domain calculations are listed in Table 1.

Table 1.

Conventional heart rate variability measurements.

Variable	Units	Definition
TIME DOMAIN MEASURES
a. Statistical
SDNN	ms	SD of all normal R–R intervals
SDANN	ms	SD of the average normal R–R intervals calculated over short time periods (usually 5 min) for the entire recording period (usually 24 h)
RMSSD	ms	The square root of the mean squared differences between adjacent normal R–R intervals
SDNN index	ms	Mean of the SD of the normal R–R intervals calculated over short periods time (usually 5 min) for the entire recording period (usually 24 h)
NN50		The number of pairs of adjacent normal R–R intervals that differ by more than 50 ms
pNN50	%	NN50 divided by the total number of normal R–R intervals × 100
b. Geometrical
HRV triangular index		Number of normal R–R intervals divided by the height of the histogram of all the normal R–R intervals measured on discrete scale with bins of 1/128 s (7.8125 ms)
TINN	ms	Baseline width of the minimum square difference of triangular interpolation of the highest peak of the histogram of all normal R–R intervals
FREQUENCY DOMAIN MEASURES
Total	ms2	Area under the entire power spectral curve (usually ≤0.40), variance of all normal R–R intervals
ULF	ms2	Ultra low frequency power (≤0.003 Hz)
VLF	ms2	Very low frequency power (0.003–0.0.04 Hz)
LF	ms2	Low frequency power (0.04–0.15 Hz)
HF	ms2	High Frequency power (usually 0.15–0.40 Hz*)
LFnu	nu	Normalized low frequency power (LF/LF + HF)
HFnu	nu	Normalized high frequency power (HF/LF + HF)
LF/HF		Ratio of the low-to high frequency power

Nu, normalized units; *HF is shifted to higher ranges (0.24–1.04 Hz) in infants and exercising adults.

A series of NN intervals can also be plotted to provide a geometric pattern of the variability (Mayer-Kress et al., 1988; Malik et al., 1989; Farrell et al., 1991). Measurement of the geometric pattern (the width of the distribution) or the interpolation of a mathematically defined shape such as a triangle is used to provide a measure of the HRV (Table 1). One common non-linear technique graphs the sequence of normal R–R intervals using Poincaré (return or recurrence mapping) plots, where the beat (n) is plotted against the next beat (n + 1; Woo et al., 1994; Huikuri et al., 1996; Tulppo et al., 1996). The resulting shape provides graphical display of the variability such that the greater the scatter the greater the variability.

Although time series approaches provide information about changes in the total variability, with one notable exception (see below) these techniques are less useful in identifying specific components of this variability. Beginning in the late 1960s investigators applied techniques to partition the total variability into frequency components (Hyndman et al., 1971; Sayers, 1973; Chess et al., 1975; Hyndman and Gregory, 1975; Peñáz et al., 1978; Akselrod et al., 1981; Kay and Marple, 1981; Pagani et al., 1984, 1986; Pomeranz et al., 1985; Myers et al., 1986; Malliani et al., 1991; Laude et al., 1995). Power spectral density analysis produces a decomposition of the total variance (the “power”) of a continuous series of beats into its frequency components (i.e., how the power distributes as a function of frequency; Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Berntson et al., 1997; Denver et al., 2007). The spectral power for a given frequency can then be quantified by determining the area under the curve within a specified frequency range. The two most common spectral analysis approaches are fast Fourier transform analysis (FFT) and autoregressive (AR) modeling (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Berntson et al., 1997; Denver et al., 2007). FFT is based upon the assumption that a time series is composed of only deterministic components while with AR the data are viewed as being composed of both deterministic and random components. For shorter duration recordings (2–5 min) three main peaks are often identified: very low frequency (VLF) <0.04 Hz, low frequency (LF), 0.04–0.15 Hz, and high frequency (HF) 0.15–0.4 Hz. It should be noted that in infants and in response to exercise HF is shifted to a higher frequency ranges (0.24–1.04 Hz; Berntson et al., 1997). A fourth peak, ultra low frequency (ULF) 0.003–0.04 Hz), is obtained during longer recording periods (24 h). The absolute power at a given frequency is reported as ms², but LF and HF power are often measured in normalized units (nu) obtained by dividing the frequency band of interest by total power minus VLF (in practice, since total power largely reflects the combination of VLF, LF, and HF; LF + HF is used as the divisor). Finally, the ratio of LF to HF (LF/HF, no units) has been used as an index of the sympathetic/parasympathetic balance (Pagani et al., 1984, 1986; Malliani et al., 1991). However, this concept has been challenged (Kingwell et al., 1994; Koh et al., 1994; Hopf et al., 1995; Eckberg, 1997; Houle and Billman, 1999; Billman, 2009) as there is considerable controversy concerning the relationship between these frequency components and a particular division of the autonomic nervous system (Kollai and Mizse, 1990; Randall et al., 1991; Kingwell et al., 1994; Koh et al., 1994; Hedman et al., 1995; Hopf et al., 1995; Eckberg, 1997; Houle and Billman, 1999; Taylor et al., 2001; Parati et al., 2006; Denver et al., 2007; Grossman and Taylor, 2007; Billman, 2009).

One time domain approach can also be used to partition HRV within specific frequency bands, similar to those obtained by frequency domain techniques (Porges et al., 1980; McCabe et al., 1985; Billman and Dujardin, 1990; Denver et al., 2007). This method applies a moving polynomial to the heart period (R–R interval) time series to remove slow trends from the data (Porges et al., 1980; McCabe et al., 1985; Billman and Dujardin, 1990; Denver et al., 2007). A specified bandpass filter is then applied to the detrended data to remove all variance outside of the target frequency band. The variance of the residual data set then provides an estimate of the HRV within the target frequency band (Porges et al., 1980; McCabe et al., 1985; Billman and Dujardin, 1990; Denver et al., 2007). This procedure provides a time domain equivalent of spectral analysis with two important advantages; relatively short sequences of beats are required for calculation of the variance within the bandwidth of interest and the “moving filter” allows for the extraction of the RSA from non-stationary baselines Porges et al., 1980; McCabe et al., 1985; Billman and Dujardin, 1990; Denver et al., 2007). Thus, this technique can investigate the dynamic regulation of HRV in response to physiological challenges such as exercise, its onset, and its termination (Billman and Hoskins, 1989; Halliwill et al., 1998; Houle and Billman, 1999; Smith et al., 2005; Billman, 2006a,b; Billman and Kukielka, 2007), or myocardial ischemia (Collins and Billman, 1989; Halliwill et al., 1998; Houle and Billman, 1999; Billman and Kukielka, 2006).

As was previously noted, non-linear dynamic analysis approaches as derived from Chaos Theory have also been used to evaluate HRV. It is beyond the scope of the present essay to provide a detailed history of the development of this exciting new branch of science (for an outstanding non-technical account see Gleick, 1987). However, a brief discussion of some of the central tenets of Chaos Theory is merited.

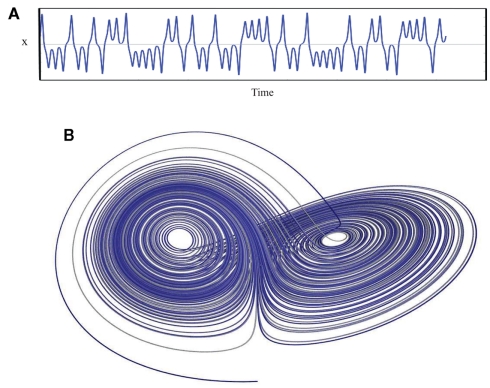
Chaos is perhaps a less than ideal word choice, as in common usage this word conveys a sense of total disorder, unpredictability, and instability. Chaos Theory describes something entirely different: an underlying order in a seemingly randomly varying sequence of events. Truly random behavior never repeats itself, it is unpredictable and disorganized while, in contrast, periodic behavior always repeats in a predictable way over some finite time interval. One might say that chaos falls somewhere between total randomness and monotonically repeating periodic behavior and has characteristics of both: an apparent randomness that emerges as a consequence of a deterministic process. There is method found in the madness. A chaotic system exhibits aperiodic behavior with a subtle but regular pattern. The behavior never quite repeats itself exactly and is constrained within a range of values. Thus, the system is stable; it does not wander off into infinity as would a random system. Deterministic chaos is non-linear, such that small changes in initial conditions lead to large changes with reiteration and also in that a single value y can be associated with more than one value of x (known mathematically as folded non-linearity; Denton et al., 1990). It is this ambiguity that gives rise to the “chaos.” In biological systems, deterministic chaos promotes the stability (variation within limits) and flexibility (more than one value of x for each y) that allows an organism to maintain an optimal internal environment as it adapts to changing external demands, a new “wisdom of the body” that updates our concept of homeostasis (West, 2010). Lorenz (1963) was the first to describe deterministic aperiodic behavior in a weather simulation model (Figure 7). He recognized that exceedingly small changes in initial conditions eventually resulted in totally different weather patterns, an observation that has become know as the butterfly effect (i.e., a butterfly flapping its wings in China produces tornados in Kansas).

Figure 7.

A plot of the Lorenz attractor. (A) represents a the time series for single variable (x) while (B) illustrates the changing relationship between all three variables. The weather model that produced this plot consists of three differential equations: (1) dx/dt = σ(y − x), (2) dy/dt = x(ρ − z) − y, (3) dz/dt = xy − βz. σ = Prandtl number, ratio of fluid viscosity to its thermal conductivity, ρ = Rayleigh number, heat transfer- the temperature difference between the top and the bottom of the gaseous system, and β = a geometric expression, the ratio of width to height of the containing holding the gaseous system. Lorenz used 10 for σ, 28 for ρ and 8/3 for β. x(t) amplitude of the convection current, y(t) temperature diffusion behavior (temperature difference between rising and falling air currents), and z(t) normal temperature deviations. Some applets that can be used to create the Lorenz attractor are found at the following websites: www.cmp.caltech.edu/~mcc/Chaos_Course/Lesson1/Demo8.html, www.geom.uiuc.edu/~worfolk/apps/Lorenz/, http://www.exploratorium.edu/complexity/java/lorenz.html.

Beginning in the 1980s, evidence began to accumulate that strongly indicated that heart rate was the not the product of a regular periodic oscillator (a sine wave generator) but rather displayed complex non-linear dynamic behavior (Guevara et al., 1981; Goldberger and West, 1987). As a consequence, simple statistical approaches to analyze heart rate time series may lack the sensitivity necessary to detect subtle non-linear changes in HRV. Therefore, analytical approaches based upon Chaos Theory and fractal mathematics have been employed to evaluate HRV (Goldberger and West, 1987; Denton et al., 1990; Bigger et al., 1996; Lombardi et al., 1996; Mäkikallio et al., 1997, 1999a,b; Huikuri et al., 1998, 2000, 2003; Pikkujämsä et al., 1999). These techniques do not measure the HRV magnitude but provide an estimate of its complexity. The most common methods evaluate fractal-like properties of the heart rate time series. For example, the heart rate frequency (f) spectrum exhibits an inverse power law relationship (1/f; Saul et al., 1987; Bigger et al., 1996; Huikuri et al., 1998, 2000; Mäkikallio et al., 1999a,b; Pikkujämsä et al., 1999) that is a defining characteristic of fractal regulatory networks (Bassingthwaighte et al., 1994). The slope of the relationship between (log) frequency and (log) spectral density (power) from 10⁻⁴ to 10⁻² Hz (an analysis of 1/f characteristics) was steeper in post-myocardial infarction and cardiac transplant patients than in healthy subjects and provided an excellent predictor of mortality following infarction (Bigger et al., 1996). These non-linear HRV measures were often better at predicting adverse cardiovascular events then were traditional markers of HRV (Bigger et al., 1996; Huikuri et al., 1998).

There are several other non-linear methods that have been used to evaluate HRV (Denton et al., 1990; Goldberger, 1990; Skinner et al., 1993; Pincus and Goldberger, 1994; Iyengar et al., 1996; Ho et al., 1997; Voss et al., 1998; Mäkikallio et al., 2001a,b; Perkiömäki et al., 2001a,b,c; Jokinen et al., 2003; Tulppo et al., 2005; Laito et al., 2006; Tuzcu et al., 2006; Perkiömäki, 2011). For example, detrended fluctuation analysis is a technique that detects the presence or the absence of fractal properties in R–R interval time series (Peng et al., 1995; Iyengar et al., 1996; Mäkikallio et al., 1999b, 2001b; Pikkujämsä et al., 1999; Perkiömäki et al., 2001a,c; Tulppo et al., 2005). Altered fractal properties have been shown to precede the onset of lethal cardiac arrhythmias; changes that traditional markers of HRV failed to detect (Mäkikallio et al., 1999b). In a similar manner, multiscale (Norris et al., 2008a,b) or approximate entropy (Pincus and Viscarello, 1992; Fleisher et al., 1993; Richman and Moorman, 2000 have been used to measure of the complexity of the system, that unlike other techniques (e.g., Lyapunov exponent, Wolf et al., 1985; Denton et al., 1990) can be applied to short data sets (Pincus and Viscarello, 1992; Richman and Moorman, 2000).

Some Limitations and Caveats

Although it is beyond the scope of the present review to analyze extensively the strengths and weaknesses of the various indices used to measure HRV, a brief discussion of some of the limitations with these techniques is merited. For a more detailed presentation the reader is encouraged to read one or more of the review articles that eloquently address the technical issues concerning the HRV and its relationship to cardiac autonomic regulation (Appel et al., 1989; Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Berntson et al., 1997; Bigger, 1997; Eckberg, 1997; Parati et al., 2006; Denver et al., 2007).

Respiratory parameters can profoundly alter heart rate and R–R interval variability independent of changes in cardiac autonomic regulation (i.e., against a constant background level of automatic regulation; Peñáz, 1957; Koepchen and Thurau, 1959; Angelone and Coulter, 1964; Davies and Neilson, 1967; Hainsworth, 1974; Melcher, 1976; Hirsch and Bishop, 1981; Brown et al., 1993). It is now well established that increases in respiratory frequency reduce the amplitude of heart rate oscillations (Peñáz, 1957; Angelone and Coulter, 1964; Melcher, 1976; Hirsch and Bishop, 1981; Brown et al., 1993) while either increases in tidal (Koepchen and Thurau, 1959; Davies and Neilson, 1967; Melcher, 1976; Hirsch and Bishop, 1981; Eckberg, 1983; Kollai and Mizse, 1990; Brown et al., 1993) or static lung volume (Hainsworth, 1974) provoke increases in the R–R interval variability. Conversely, reductions in respiratory frequency increase HRV (Peñáz, 1957; Angelone and Coulter, 1964; Melcher, 1976; Hirsch and Bishop, 1981; Brown et al., 1993) while decreases in tidal volume lead to reductions in the R–R interval variability (Koepchen and Thurau, 1959; Davies and Neilson, 1967; Melcher, 1976; Hirsch and Bishop, 1981; Eckberg, 1983; Kollai and Mizse, 1990; Brown et al., 1993). Thus, it is critical to control breathing (paced or timed breathing) in order to interpret HRV data accurately. For obvious reasons, it is much more difficult to control respiratory parameters in conscious animal than in human studies. However, these respiratory parameters frequently are not controlled even in human studies (Brown et al., 1993). Brown et al. (1993), reviewed the human literature and found that only about 51% controlled respiratory rate, and even fewer studies controlled for tidal volume (11%). They further reported that respiratory parameters not only altered HF power but also strongly influenced the LF components of the R–R interval power spectrum, a component that previously was viewed to vary independently of changes in respiration (Brown et al., 1993).

It also must be emphasized that HRV only provides an indirect assessment of cardiac autonomic activity and does not provide a direct measurement of either cardiac parasympathetic or sympathetic nerve activity. Thus, any relationship between HRV and cardiac autonomic regulation is qualitative rather than quantitative in nature. In other words, a low or high amount of HRV may reflect a decreased or increased cardiac autonomic regulation but does not provide a quantification of the actual cardiac nerve firing rate. Furthermore and as previously noted, there is considerable debate as to the exact relationship between changes in cardiac autonomic activity and a particular branch of the autonomic nervous system (Kollai and Mizse, 1990; Randall et al., 1991; Kingwell et al., 1994; Hedman et al., 1995; Hopf et al., 1995; Eckberg, 1997; Houle and Billman, 1999; Taylor et al., 2001; Parati et al., 2006; Denver et al., 2007; Grossman and Taylor, 2007; Billman, 2009). For example, frequency domain analysis of HRV usually reveals two or more peaks, a LF (<015 Hz), and a higher frequency peak (>0.15 Hz) that are often assumed to correspond to cardiac sympathetic and cardiac parasympathetic neural activity, respectively (Pagani et al., 1984, 1986; Malliani et al., 1991). However, accumulating evidence clearly demonstrates this assumption is naïve and greatly oversimplifies the complex non-linear interactions between the sympathetic and the parasympathetic divisions of the autonomic nervous system. This is particularly true with regards to the relationship between LF power and cardiac sympathetic regulation (Randall et al., 1991; Kingwell et al., 1994; Hopf et al., 1995; Eckberg, 1997; Houle and Billman, 1999; Parati et al., 2006; Billman, 2009).

Low frequency power was found to be reduced by selective parasympathectomy and also was not totally eliminated when the denervation was combined with beta-adrenoceptor blockade (Randall et al., 1991). Furthermore, interventions that would be expected to increase cardiac sympathetic activity, such as acute exercise or myocardial ischemia, not only failed to increase LF power but actually provoked significant reductions this variable (Houle and Billman, 1999). Thus, LF component of HRV reflects both sympathetic, parasympathetic and other as yet unidentified factors. Accordingly, LF power should not be used as an index of cardiac sympathetic regulation.

Although the vast majority of the clinical and the experimental studies demonstrate a strong association between HF power and cardiac parasympathetic activity (Appel et al., 1989; Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Bigger, 1997; Billman, 2009; Thayler et al., 2010), this concept has also been challenged (Kollai and Mizse, 1990; Hedman et al., 1995; Taylor et al., 2001; Parati et al., 2006). Just as parasympathetic activation exerts profound influences on the LF component of HRV, sympathetic neural activity may modulate the HF component of the R–R interval variability (Taylor et al., 2001; Cohen and Taylor, 2002). Taylor et al. (2001) found that cardioselective beta-adrenergic receptor blockade (drugs that should not indirectly alter vagal outflow via action within the central nervous system) increased RSA amplitude over a wide range of respiratory frequencies (i.e., the increases were not restricted to lower frequencies, <0.15 Hz). They concluded that “cardiac sympathetic outflow can oppose vagally mediated R-R interval oscillations and sympathetic blockade removes this effect” (Cohen and Taylor, 2002). Thus, differences in cardiac sympathetic activation during a physiological challenge (e.g., exercise or postural changes) in healthy subjects or that occur as consequence of cardiovascular disease (following myocardial infarction) could restrain vagally mediated changes HRV. These data further demonstrate that HRV is a complex phenomenon that should not be solely attributed to changes in cardiac vagal efferent nerve traffic.

In addition to autonomic influences, a portion of the HRV occurs as a consequence of the mechanical events (due to stretch of the atria that results from both changes in cardiac filling and the changing thoracic pressure that occur during respiration) as was first proposed by Bainbridge (1930). This conclusion is supported by the observation that heart transplant patients, despite the absence of cardiac nerves, still exhibit small (~2–8% of normal) change in R–R interval associated with the respiratory cycle (Bernardi et al., 1989). Taylor et al. (2001) further demonstrated that atrial stretch can exert significant influences on R–R interval in subjects with complete autonomic blockade. They found that after combined cholinergic and adrenergic receptor blockade slow deep breathing could still provoke oscillations of ~120 ms in healthy human subjects (Taylor et al., 2001). Thus, given the complex interactions between cardiac sympathetic and cardiac parasympathetic nerves that are confounded by the mechanical effects of respiration, HRV data should be interpreted with appropriate caution.

Clinical Applications

Heart rate variability has gained wide-spread acceptance as a clinical tool for the evaluation of cardiac autonomic changes in patients (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Bigger, 1997; Hohnloser et al., 1997; Billman, 2009; Thayler et al., 2010). The term “HRV” yields nearly 14,000 “hits” when placed in the pubmed search engine. A variety of cardiovascular risk factors and disease states have all been shown to reduce HRV, including diabetes (Murray et al., 1975; Ewing et al., 1985; Vinik et al., 2003; Rosengard-Barlund et al., 2009), smoking (Mancia et al., 1997; Karakaya et al., 2007), obesity (Skrapari et al., 2007), Work stress (Thayler et al., 2010), hypertension (Pagani et al., 1984; Pagani and Lucini, 2001; Maule et al., 2008), and heart failure (Saul et al., 1988; Binkley et al., 1991; Woo et al., 1994; Adamopoulos et al., 1995; Kiilavuori et al., 1995; De Jong and Randall, 2005).

Eppinger and Hess (1915) provide the first suggestion that HRV could be used to provide some insight in abnormalities in autonomic regulation in disease. They wrote “clinical facts, such as respiratory arrhythmia, habitual bradycardia, etc. have furnished the means of drawing our attention to variation in the tonus of the vagal system” (Eppinger and Hess, 1915, p. 12). They further emphasized that pharmacological manipulation of the cholinergic system might provide an avenue for treatment (Eppinger and Hess, 1915). However, the first reports of the applications of HRV in the clinic only began to appear in the mid 1960s. Hon and Lee (1965) noted that fetal stress was preceded by reduction in the inter-beat interval even before any appreciable change in average heart rate could be detected. Fetal heart rate monitoring has now become the standard of care and has contributed to reductions in morbidity associated with fetal distress. In the 1970s, Ewing and co-workers used short-term changes in R–R interval in response to simple autonomic challenges to detect autonomic neuropathy in diabetic patients (Murray et al., 1975; Ewing et al., 1985).

About the same time, Wolf was the first to demonstrate a relationship between HRV and mortality following myocardial infarction (Wolf et al., 1978). This observation has subsequently been confirmed (Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Bigger, 1997; Hohnloser et al., 1997; Thayler et al., 2010). Specifically, HRV is reduced in patients recovering from a myocardial infarction and, further, those patients with the greatest reduction in this variable also have the greatest risk for sudden death (Myers et al., 1986; Kleiger et al., 1987; Farrell et al., 1991; Bigger et al., 1992). Kleiger and co-workers (Myers et al., 1986; Kleiger et al., 1987; Bigger et al., 1992) found that in patients recovering from myocardial infarctions, those with the smallest HRV (SD of R–R interval) had the greatest risk of dying suddenly. The relative risk of mortality was 5.3 times greater in patients with R–R interval variability less than 50 ms compared to patients with variability greater than 100 ms (Kleiger et al., 1987). This finding has been subsequently confirmed by numerous more recent clinical studies; reductions in HRV following myocardial infarction now represent one of the strongest independent predictors of mortality following infraction. (La Rovere et al., 1988, 1998; Malik et al., 1989; Mazzuero et al., 1992; Huikuri et al., 1996; Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996; Bigger, 1997; Hohnloser et al., 1997; Lanza et al., 1998). To cite just one example, La Rovere et al. (1988, 1998), reporting for the ATRAMI (Autonomic Tone and Reflexes After Myocardial Infarction) group, found that post-myocardial infarction patients with either low HRV or a small heart rate response to an increase in blood pressure (i.e., baroreceptor reflex sensitivity) had a much greater risk of sudden death than those with well preserved cardiac vagal tone. The greatest risk for mortality was observed in patients with a large reduction in both markers of cardiac vagal regulation (La Rovere et al., 1998).

Similar results have also been obtained using animal model of human disease (Billman, 2006a). For example, HRV was reduced to a greater extent in animals susceptible to ventricular fibrillation as compared to animals resistant to these malignant arrhythmias (Billman and Hoskins, 1989; Collins and Billman, 1989; Halliwill et al., 1998; Houle and Billman, 1999; Smith et al., 2005; Billman, 2006a,b; Billman and Kukielka, 2006). In particular, the susceptible animals exhibited a much greater reduction (withdrawal) of cardiac vagal regulation in response to either submaximal exercise (Billman and Hoskins, 1989; Halliwill et al., 1998; Houle and Billman, 1999; Billman, 2006a,b; Billman and Kukielka, 2006) or acute myocardial ischemia (Collins and Billman, 1989; Halliwill et al., 1998; Houle and Billman, 1999; Billman, 2006a; Billman and Kukielka, 2006). Heart rate recovery and the reactivation of cardiac parasympathetic regulation following the termination of exercise were also impaired in the animals subsequently shown to prone to ventricular fibrillation (Smith et al., 2005; Billman and Kukielka, 2007); an observation that has been noted in patients. For example, post-infarction patient with the slowest heart rate recovery following an exercise stress test also exhibited the highest mortality rate during the observation period (up to 12 years; Cole et al., 1999, 2000; Nishime et al., 2000; Morshedi-Meibodi et al., 2002; Nissinen et al., 2003; Jouven et al., 2005). Thus, despite the limitations noted in a previous section, HRV has proven to be an important tool for the identification of patients at risk for adverse cardiovascular events.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.