Comparative analysis of essential collective dynamics and NMR-derived flexibility profiles in evolutionarily diverse prion proteins

Abstract

Collective motions on ns-µs time scales are known to have a major impact on protein folding, stability, binding and enzymatic efficiency. It is also believed that these motions may have an important role in the early stages of prion protein misfolding and prion disease. In an effort to accurately characterize these motions and their potential influence on the misfolding and prion disease transmissibility we have conducted a combined analysis of molecular dynamic simulations and NMR-derived flexibility measurements over a diverse range of prion proteins. Using a recently developed numerical formalism, we have analyzed the essential collective dynamics (ECD) for prion proteins from eight different species including human, cow, elk, cat, hamster, chicken, turtle and frog. We also compared the numerical results with flexibility profiles generated by the random coil index (RCI) from NMR chemical shifts. Prion protein backbone flexibility derived from experimental NMR data and from theoretical computations show strong agreement with each other, demonstrating that it is possible to predict the observed RCI profiles employing the numerical ECD formalism. Interestingly, flexibility differences in the loop between second b strand (S2) and the second a helix (HB) appear to distinguish prion proteins from species that are susceptible to prion disease and those that are resistant. Our results show that the different levels of flexibility in the S2-HB loop in various species are predictable via the ECD method, indicating that ECD may be used to identify disease resistant variants of prion proteins, as well as the influence of prion proteins mutations on disease susceptibility or misfolding propensity.

Introduction

Transmissible spongiform encephelopathies (TSEs) or prion diseases are uniformly fatal, currently incurable, infectious neurodegenerative diseases affecting both humans and animals. Creutzfeldt-Jakob disease (CJD), kuru, Gerstmann-Sträussler-Scheinker syndrome (GSS) and fatal familial insomnia (FFI) are examples of TSEs that affect humans. Chronic wasting disease (CWD), bovine spongiform encephalopathy (BSE) and scrapie are found in cervids, cattle and sheep, respectively. According to the protein-only hypothesis, the prion protein itself acts as the infectious agent behind all known TSEs.^1–4 Prion proteins are believed to become infectious as a result of the conversion of a normal cellular prion protein (PrP^C) into a misfolded and neurotoxic variant called the scrapie form (denoted as PrP^Sc). The infectious PrP^Sc is believed to catalytically convert PrP^C to PrP^Sc upon contact, thereby spreading the neurotoxic version of the protein in brain tissue.

It is clear that a thorough understanding of the molecular mechanisms and pathways involved in the PrP^C-PrP^Sc conversion will be required to eventually prevent or cure TSEs. Structures of the cellular PrP^C isoform for many species have been determined through NMR studies, indicating that the protein is mainly helical (47%) with just 3% β-sheet. In contrast, high resolution structures of the misfolded form are currently unavailable. The insolubility of the scrapie isoform makes applications of standard techniques such as X-ray crystallography and solution NMR spectroscopy difficult, while its conformational heterogeneity complicates the use of high-resolution solid-state NMR. It has been found through other structural techniques that the scrapie isoform has a relatively high β-sheet content and that it can aggregate into fibrils.^5–7 These aggregates may adopt multiple forms and variable lengths, and have been found to contain 17–30% α-helix and 43–54% extended structure.^5,8–10 Furthermore, a number of studies^11–15 indicate that it may be the smaller aggregates known as protofibrils rather than the longer, mature fibrils that are infectious and thus responsible for disease transmission. However, despite numerous experimental efforts,^5,8,16–19 the inherent insolubility and intractability of PrP^Sc has made direct experimental determination of the conversion mechanism very difficult. Consequently a number of researchers have chosen, instead, to analyze the physico-chemical properties of the more tractable cellular PrP^C isoform and identify precursor conditions that may facilitate its pathological misfolding.

The globular domain of PrP^C typically consists of 100–130 residues forming three α-helices (HA, HB and HC) and two β-strands (S1 and S2) in an anti-parallel β-sheet configuration (Fig. 1). β-strand S1 is located at the N-terminus and the largest β-helix HC is located at the C-terminus of the protein. The two larger helices, HB and HC, are connected by a disulphide bond, whereas the β-strands S1 and S2 form a β sheet in the area on the N-terminus of the globular domain. The N-terminal end of the globular domain extends to an unstructured tail of approximately 100 amino acids (not shown in Fig. 1). While a number of experiments^16–18 suggest that the helices at the C-terminus might be the part of the molecule where misfolding could be initiated, other studies based on infrared spectroscopy⁵ and circular dichroism⁸ measurements have shown that the HB-HC bundle at the C-terminus might be relatively well protected regions. Although the latest data indicate that upon conversion, the entire globular domain, rather than any of its parts appears to undergo refolding,²⁰ ongoing studies clarifying early stages and dynamical precursors of the conversion are key to understanding the conversion mechanism. In addition to experimental work, numerous computational studies^21–31 have been conducted to help provide additional molecular details about the structure and conformational tendencies in prion proteins. Among these, molecular dynamic (MD) simulations of PrP helical fragments²³ and pH induced conformational transitions^24,27 suggest that a significant degree of flexibility exists in helix HB. In contrast, other MD simulations^{21,25,26,28–31} seem to indicate that the N-terminus is the least stable part of molecule where spontaneous conformational changes may occur. Obviously, one of the limitations of any computational study of the PrP conversion process is related to the long timescales involved, which may range from hours to days.³² Today's existing computational facilities are significantly challenged by these requirements.

Figure 1.

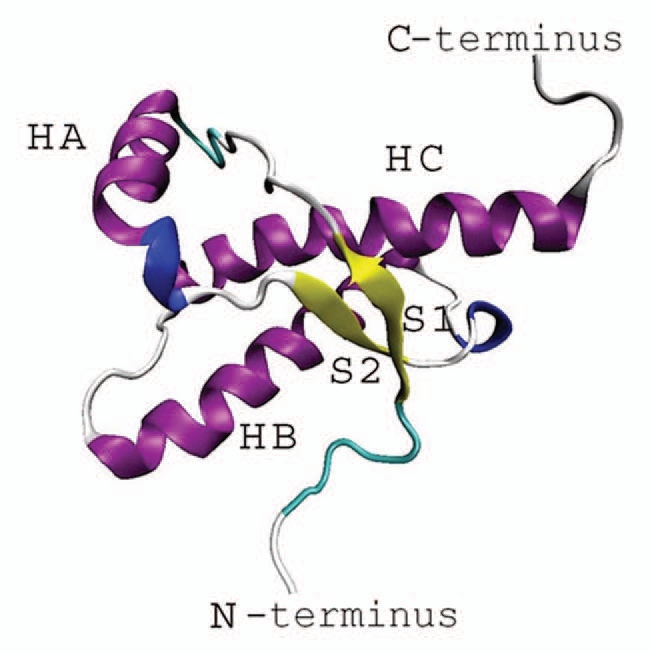
Secondary structure of the globular fold of a prion protein.

In order to fully realize the potential of computer simulations for studying the molecular mechanisms of PrP unfolding and conversion, it is imperative to provide insights relevant to the slow folding dynamics of prion proteins. A suitable method to address this problem would be a coarse-grained approach that considers just a few important collective coordinates in a protein molecule.^33,34 There are a number of examples where the dimensionality-reduction techniques such as normal mode analysis or principal component analysis (PCA) have been employed to analyze extended molecular dynamics trajectories of proteins.^36–38 Popular applications include projections of protein energy landscapes onto the collective coordinates,^39,40 as well as the use of dimensionality reduction to analyze intermolecular binding.^35,41,42 It has also been hypothesized that collective correlated motions derived from MD simulations may be employed to identify structural subunits (domains) in proteins and assess local flexibility.^43–45 However, not all the results available in the literature are straightforward to reproduce or interpret because of a broad variety of model assumptions, protocols and sampling schemes.⁴⁶ These wide variations exist, in part, because a systematic theoretical framework has been absent until recently. In particular, the identification of domains would typically require either a priori assumptions regarding the protein's domain structures, or the use of a hypothetical reference frame,⁴³ whereas the assessment of the local flexibility would typically be limited to a statistical analysis of average residue displacements.^43–45

Recently, a novel theoretical formalism has been developed in our group to analyze collective coarse-grained dynamics in proteins.⁴⁷ This approach allows one to readily identify long term collective motions in a large molecule. It also allows one to visualize them in terms of collective subunit motions (dynamic domains) and determine local conformational flexibility from a single theoretical framework.^47,48 In contrast to the conventional empirical use of principal component analysis (PCA), the present methodology relies on a robust statistical-mechanical background,^47,49 which allows for a dynamically consistent definition of protein domains, as well as a clearer description of the local bond flexibility within the same theoretical framework. Using this technique, the essential collective coordinates of a protein can be determined via PCA using small portions of standard MD trajectories thereby providing a characterization of stable structural properties that persist over a longer period (Potapov et al., submitted). This formalism—denoted here as essential collective dynamics (ECD)—has been validated in a number of ways. In particular it has been used to compare the numerical predictions for protein G⁴⁷ as well as human and chicken prion proteins⁴⁸ with NMR-derived structural data such as the model-free order parameters⁴⁷ and random coil indices.^50–52 These studies have shown excellent agreement between the computational (ECD) and the experimental (NMR) results.

In the present study, we have applied our essential collective dynamics methodology to analyze the local conformational stability in prion proteins for set of eight different species: elk, cattle, cat, hamster, human, frog, turtle and chicken. Among these animals, five species (elk, cattle, cats, hamsters and humans) are known to develop TSEs, whereas in frogs, turtles and chickens TSEs have not been observed. While recognizing that the TSE pathogenesis in a given species involves a complex interplay of many anatomical and physiological factors, it is fair to assume that TSE pathogenesis is largely determined by the structure and dynamics of prion proteins. In this paper we would like to determine whether the conformational dynamics in prion proteins of different species correlates with the known TSE susceptibility, and whether or not it is possible to distinguish the species susceptibility employing the numerical predictions.^53,54 Generally, various approaches may be employed to classify disease-prone and disease-resistant species. One approach adopts just two disease-prone and disease-resistant categories, with all species in which TSEs have been observed are identified as disease-prone.⁵⁴ Alternatively, one can consider some species to be relatively less vulnerable than others, although known to develop TSEs.^55–57 A measure of this vulnerability, however, has not been established yet. In an effort to elucidate structural trends that might distinguish TSE infectivity in diverse species, we have used both ECD and experimental NMR-derived data^50–52 to identify those regions of the prion protein exhibiting correlated motion and enhanced local backbone flexibility for all the species considered. We compared the dynamical signatures of the globular domains of the different species and identified correlations between disease susceptibility and the conformational behaviour of prion proteins.

Results

Table 1 lists the structural data that we employed for our ECD and NMR-based analysis. As outlined in the table, we have generated a series of MD trajectories spanning 4–6 ns for each vertebrate species. In this work we have limited our focus to the globular PrP domains of: elk (ePrP 121–231), bovine (bPrP 124–227), cat (cPrP 121–231), hamster (shPrP 125–228), human (hPrP 125–228), frog (xlPrP 125–226), turtle (tPrP 119–225) and chicken (chPrP 128–242). The results of our previous work in reference ⁴⁸, where we investigated the role of the various N-terminal constructs on the dynamics of human PrP, indicate that the absence of the unstructured domain has no significant effect on the conformational dynamics of the globular fold. This is also compatible with earlier experiments^66,67 suggesting that the influence of N-terminal tail on the dynamics of the C-terminal domain plays only a minor role.

Table 1.

The species considered, PDB ID numbers of structures employed for MD simulations, the corresponding residue sequences, the total number of MD trajectories analyzed, and the BMRB accession numbers of NMR chemical shifts employed to derive the RCI profiles

Species	PDB ID	Residues	Number of MD trajectories analyzed	BMRB No.	Reference
Elk	1XYW	121–231	5	6383	59
Bovine	1DWZ	124–227	4	4563	60
Cat	1XYJ	121–231	5	6377	61
Hamster	1B10	125–228	5	4307	62
Human	1QM3	125–228	2	4379	63
Frog	1XU0	125–226	5	6382	64
Turtle	1U5L	119–225	2	6282	65
Chicken	1U3M	128–242	5	6269	66

According to the methodology adopted previously in references 47 and 48, we analyzed 0.2 ns segments of the trajectories, with each segment consisting of 2,000 snapshots, and PCA was performed using K = 20 principal components for each segment. The dynamic domains were identified employing an inter-domain distance d = 0.035, (see the Methods section for more details). In the images below, we have color-coded up to six large domains considering only those domains that consist of at least two residues. Domains are colored according to their size, with the largest domain appearing in blue, and the remaining domains in red, green yellow, cyan and magenta in order of decreasing size. The off-domain portions of the protein are shown in grey. More specifically, our dynamic domains identify regions of relative rigidity in the protein, whereas off-domain regions are relatively flexible or “soft”. This is complemented by the local flexibility profiles, where high levels of the flexibility descriptor F can be interpreted as locations of high flexibility, and low levels of F as locations of low flexibility. Although our ECD methodology allows one to identify both the dynamic domains and local flexibility with atomic level precision,^47,48 in this work the calculations were performed on a per-residue basis in order to facilitate the comparison with the experimental RCI profiles shown in Figure 2. For the domain analysis, a residue was considered as belonging to a domain if its C_α atom belongs to that domain. The computed flexibility profiles have been compared with the corresponding experimental RCI dependencies. For this purpose, the flexibility descriptors F have been offset to match the RCI values in the area of the large helices HB and HC. No normalization has been applied to any of the flexibility profiles.

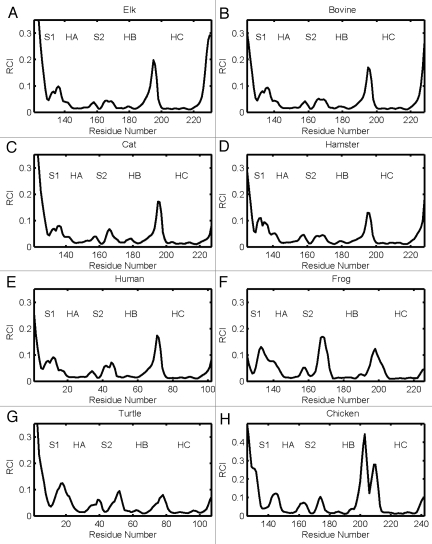
Figure 2.

RCI profiles for globular folds of elk (a), bovine (b), cat (c), hamster (d), human (e), frog (f), turtle (g) and chicken (h) prion proteins.

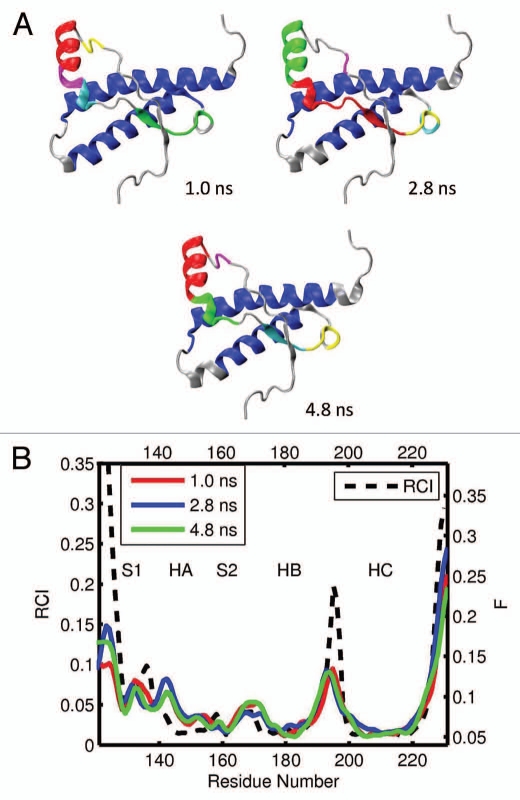
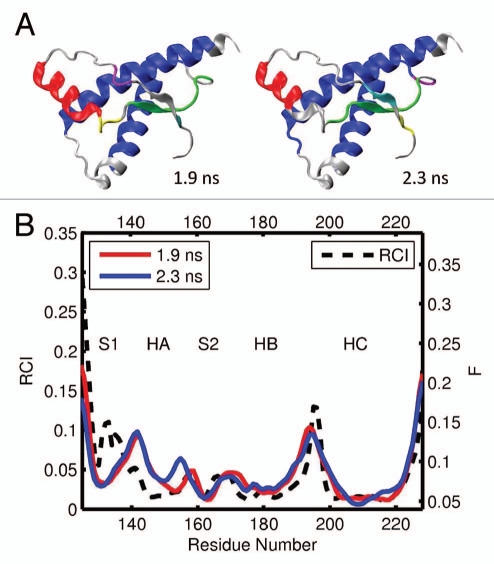
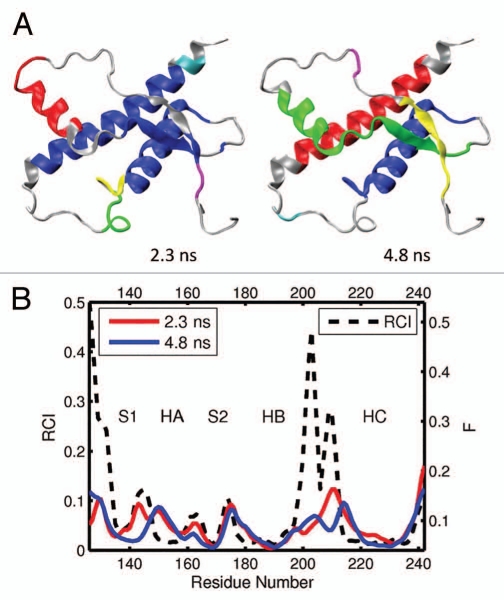
For the elk prion protein, (ePrP 121–231), we analyzed the total of 5 MD trajectories and 12 segments of 0.2 ns each (Table 1). Figures 3A and B show the results from one representative MD trajectories and 3 segments. The images in Figure 3A display 6 largest domains identified in ePrP for each segment, with the different segments described by the corresponding starting time. For example, the subscript “1.0 ns” in Figure 3A indicates that the trajectory segment starts at 1.0 ns and ends at 1.2 ns. In Figure 3B, the flexibility profiles corresponding to the different segments of the same trajectory are distinguished by different colors, and the starting times indicated in the legend have the same meaning as in Figure 3A. The black dashed curve in Figure 3B shows the experimental RCI profile for elk (Fig. 2A). The domains and flexibility profiles identified for the other 4 MD trajectories are given in the Supporting Information (Figs. S1 and S2, respectively). Note that the color scheme used to distinguish the flexibility curves for different segments is not related to that used to distinguish the domains.

Figure 3.

(A) dynamical domains for elk prion protein (ePrP) identified from a MD trajectory at times indicated by the subscripts. Six largest domains are shown with the largest domain colored blue and the smaller domains colored red, green, yellow, cyan and magenta in the order of the decreasing size. (B) flexibility profiles identified at times indicated in the legend box, over-imposed on the experimental RCI profile from 2(a) shown by black dashed curve. Further examples for elk prion protein can be found in Supporting Information, Figures S1 and S2.

As can be seen in Figures 3A and S1, helices HB and HC form the largest dynamic domain (colored blue) in ePrP. The second largest domain (colored red) is usually helix HA although in 3 out of 12 cases helix HA is identified as the third largest domain (colored green). This slight variability in the domain system appears to reflect conformational fluctuations present in the molecule. In most cases, the β-strand S2 is coupled dynamically with the HB-HC bundle, whereas the β-strand S1 is uncoupled from the rest of the molecule. The parts of the molecule colored gray do not belong to any domains and can be considered as relatively disordered and flexible. From the set of images in Figures 3 and S1 it is clear that a higher level of flexibility is consistently observed around loops HB-HC and S1-HA, not to mention the N and C termini. In contrast, the loops HA-S2 and S2-HB show a significant level of domain coverage. In other words, they are relatively well structured and rigid. In three cases, the S2-HB loop has even been identified as a part of a correlated domain consisting of the HB-HC bundle.

The predicted flexibility profiles computed for different segments and trajectories all show a similar trend, despite a slight difference in the flexibility descriptor F levels between different curves (see Figs. 3B and S2). In all cases the most rigid regions, where the values F are low, coincide with helixes HB and HC, which form a correlated dynamic domain. The β-strand S2, which has been identified as a dynamic domain with a noticeable trend to couple with the HB-HC bundle, also exhibits low flexibility levels. The highest levels of the flexibility descriptor F are observed at the loops S1-HA and HB-HC, where no major domains have been previously identified. Helix HA, which has been identified as one of largest domains, nevertheless shows relatively high levels of F. This indicates that this helix may be rigid but uncoupled dynamically from the rest of the molecule because of the high flexibility of the adjacent S1-HA loop. In contrast, the HA-S2 and S2-HB loops, which show significant domain coverage, exhibit considerably lower flexibility than the other loops. The position of maxima and minima of the predicted F profiles agrees very well with the experimental RCI profiles, except for the region 140–145, where the predicted flexibility has a maximum, whereas the RCI profile does not.

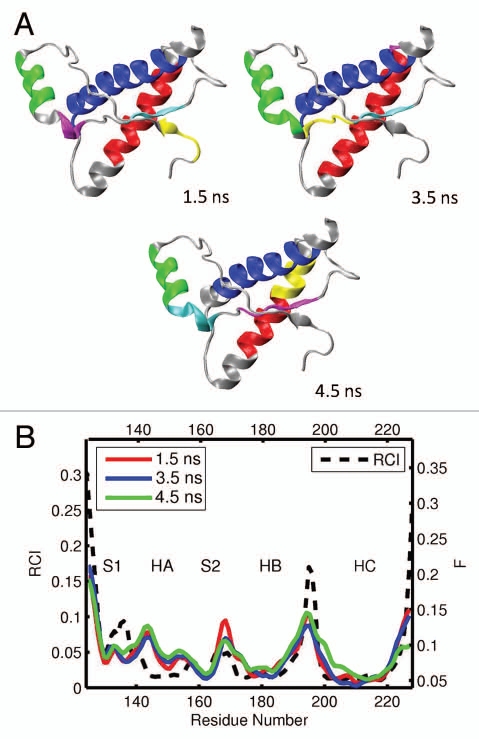
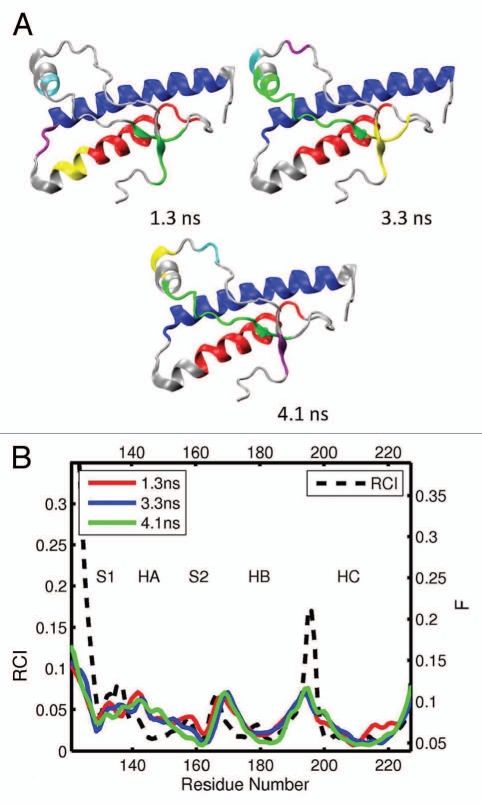
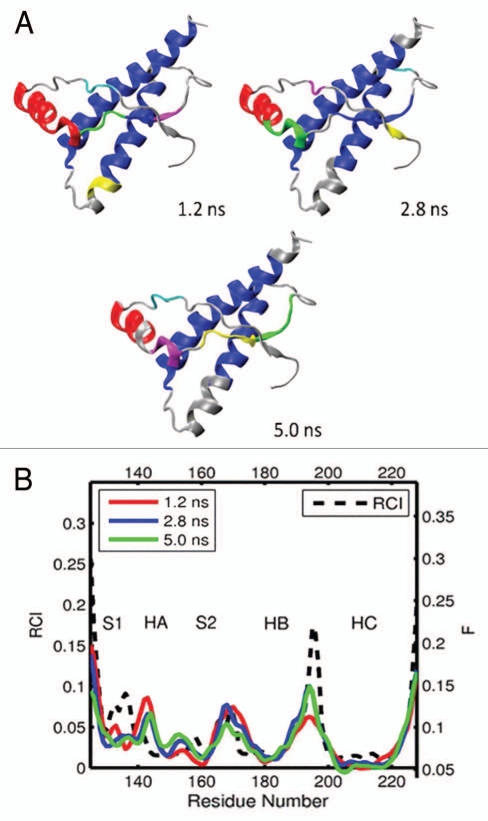
The results for bovine and cat globular domains, bPrP 124–227 and cPrP 121–231, are shown in Figures 4 and 5, respectively (see also the Supporting Information, S3–S6). For bovine PrP, we obtained 4 different MD trajectories and analyzed 11 segments. For cat PrP, 5 MD trajectories were obtained and 15 segments analyzed. The domains identified in bovine PrP are shown in Figures 4A and S3, and those in cat are given in Figures 5A and S5. In both species, helices HB and HC usually form two largest domains (colored in blue and red). These two helices, however, do not form a single correlated domain in any of the cases considered. On three occasions, for bovine and cat each, helix HB appears to consist of two different domains. Often (in 17 out of 26 cases for both species), helix HA can be identified as the third or fourth largest domain. However, in seven cases only parts of helix HA have been identified as smaller domains, whereas in two cases (both for cat) helix HA is actually identified as a component of the largest domain and coupled with the helix HC. Both the location and size of the dynamic domains in bovine and cat PrP exhibit higher levels of variability than for elk. Note that despite this variability of the domain system for bovine and cat species, the qualitative trends in the flexibility profiles from different trajectory segments are similar to those found in elk (see Figs. 4B, S4, 6B and S6). One exception appears to arise with the flexibility descriptor F adopting somewhat higher levels at the loop S2-HB [see the bovine profiles from Figs. 4B and S4(a)].

Figure 4.

(A) Dynamical domains for bovine prion protein (bPrP) identified from a MD trajectory at times indicated by the subscripts. The meaning of colors is as in Figure 3. (B) flexibility profiles identified at times indicated in the legend box, over-imposed on the experimental RCI profile from 2(b), which is shown by the dashed curve. More examples for dynamical domains and flexibility profiles in bovine prion protein are given in Figures S3 and S4, respectively.

Figure 5.

(A) Dynamical domains for cat prion protein (cPrP) identified from a MD trajectory at times indicated by the subscripts. The meaning of colors is as in Figure 3. (B) flexibility profiles at times indicated in the legend box. The dashed curve shows the experimental RCI profile from 2(c). Further results for dynamical domains and flexibility profiles in cat prion protein are given in Figures S5 and S6, respectively.

Figure 6.

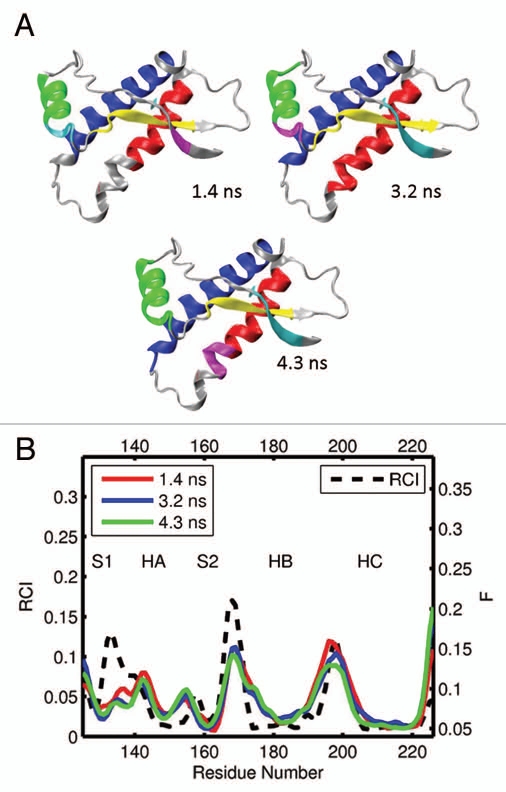
(A) Dynamical domains for hamster prion protein (shPrP) identified from a MD trajectory at times indicated by the subscripts. The meaning of colors is as in Figure 3. (B) Flexibility profiles at times indicated in the legend box. The dashed curve shows the experimental RCI profile from 2(d). Other examples for dynamical domains and flexibility profiles in hamster prion protein are given in Figures S7 and S8, respectively.

Overall, for TSE-prone species elk, cattle and cat, the HC and HB helices form the largest domains of correlated motion and also exhibit the lowest levels of flexibility—indicating they are well structured and rigid parts on the protein. In contrast, the S1-HA loop shows somewhat less dynamic correlation and exhibits a higher degree of flexibility, whereas S1 is often uncoupled dynamically from the rest of the molecule. In agreement with our earlier results,⁴⁸ this indicates that the N-terminus is likely less stable dynamically than the C-terminus. Note that a similar conclusion has recently been drawn from an experimental study of urea induced unfolding of the bovine prion protein.⁶⁸ The difference between elk PrP (ePrP) and bovine or cat PrP is that ePrP generally shows a higher level of correlated dynamics. In ePrP, the two largest helices HB and HC form a single domain of correlated motion, the β-strand S2 tends to be coupled with the HB-HC bundle, the S2-HB loop exhibits a high domain coverage, and the flexibility level F in the area of this loop is lower than in bovine and cat proteins. These results are consistent with data from a number of reported NMR experiments, which suggest that elk PrP molecules tend to exhibit a higher level of ordered structure, in the area of the S2-HB loop, compared to other species.^58,66,69 Considering that the S2-HB loop is also anticipated to play a role as a binding site for intermolecular interactions contributing to the species barrier as well as to pathological conversion induced by a hypothetical cofactor,^58,66,69,60 the comparative analysis of conformations dynamics in the area of this loop in different species is particularly interesting.

For the hamster prion protein (shPrP) spanning residues 125–228, we analyzed 11 segments out of 5 MD trajectories, see Figures 6, S7 and S8. From Figures 6A and S7 it is evident that shPrP is quite well structured and shows a high level of dynamic correlation. The two largest helices, HB and HC, form a single domain of correlated motion. Helix HA is often identified as the second or third largest domain, and in one occasion it forms a single domain with the HB-HC bundle. The S2-HB loop is covered by correlated domains almost entirely and coupled dynamically with the β-strand S2 whereas the latter is coupled with the HB-HC bundle on 5 occasions (see Fig. S7). At the same time, the β-strand S1 and the S1-HA loop are mostly domain free and/or decoupled dynamically from other parts of the molecule. The computed flexibility profiles in Figures 6B and S8 show a remarkable agreement with the NMR-derived RCI profiles, except for some discrepancies in the region of the S1-HA loop and β-strand S1. For 7 out of 11 trajectory segments, the flexibility level F in the region of the S2-HB loop is relatively low, indicating that this loop is well structured. This is also evident from the high domain coverage of this loop. The well-defined S2-HB loop has also been reported in NMR structural study of shPrP.⁷¹ What is notable is that for shPrP, both the dynamic domains and flexibility profiles show a significant degree of similarity with the corresponding results for elk. In both species, the S2-HB loop is rigid and well structured, and most of the core globule shows a significant level of dynamical correlation. The exception is the flexible and uncoupled N-terminal region, which consists of the S1-HA loop and β-strand S1.

Figures 7, S9 and S10 present the dynamic domains and flexibility profiles that we obtained for the human prion protein hPrP 125–228. In 4 out of 5 cases considered, the largest domain of correlated motion consists of both helices HB and HC, whereas HA forms the second large domain. On one occasion, the β-strand S2 has been coupled to form part of the largest domain. However, the S2-HB loop is partly domain free, as well as the loops S1-HA and HA-S2. Unlike hamster PrP, the flexibility profiles of human PrP exhibit relatively high levels of both F and RCI profiles in the area of the S2-HB loop. From published NMR structural studies it appears that hPrP indeed has relatively more flexible regions than hamster (and elk), and is more comparable in flexibility to the bovine prion protein.⁶² Our flexibility profiles F from Figure 7B as well as the observed RCI dependencies, however, demonstrate that the H2-HB loop in human PrP may be more flexible than in cattle or cat PrP.

Figure 7.

(A) Dynamical domains for human prion protein (hPrP) identified from a MD trajectory at times indicated by the subscripts. The meaning of colors is as in Figure 3. (B) Flexibility profiles at times indicated in the legend box. The dashed curve shows the experimental RCI profile from 2(e). More results for dynamical domains and flexibility profiles in human prion protein can be found in Figures S9 and S10, respectively.

Next, we analyzed 13 segments from 5 different MD trajectories of frog PrP 125–226 (xlPrP). In contrast to the species considered so far, frogs have not been observed to develop TSEs. The representative results are shown in Figure 8, and other data are given in Figures S11 and S12. It can be seen that in xlPrP, the helices HB and HC are usually identified as two largest dynamic domains, although HB may be composed of more than one domain. In comparison to other species, xlPrP has a relatively longer β sheet,⁷² which is an interesting feature for an apparently conversion resistant protein. As can be seen in Figure S11, two β-strands S1 and S2 may form a single domain of correlated motion, although both S1 and S2 are decoupled from the rest of the molecule in 11 out of 13 cases. Depending of whether or not the β-strands have formed a large domain, helix HA can be identified as either the third or fourth largest domain, although on two occasions HA and HC formed a single domain of correlated motion (see Fig. S11). Unlike the other species considered so far, most of the S2-HB loop is domain free in xlPrP. It is therefore not surprising that both the computed flexibility profiles and RCI dependencies in Figures 8B and S12 exhibit a strong flexibility increase in the region of this loop. The NMR derived RCI profile also exhibits high levels of flexibility around the S1-HA loop; however, this increase is not confirmed by our computed flexibility descriptor F.

Figure 8.

(A) Dynamical domains for frog prion protein (xlPrP) identified from a MD trajectory at times indicated by the subscripts. The meaning of colors is as in Figure 3. (B) Flexibility profiles at times indicated in the legend box. The dashed curve shows the experimental RCI profile from 2(f). See Figures S11 and S12 for further results on frog prion protein.

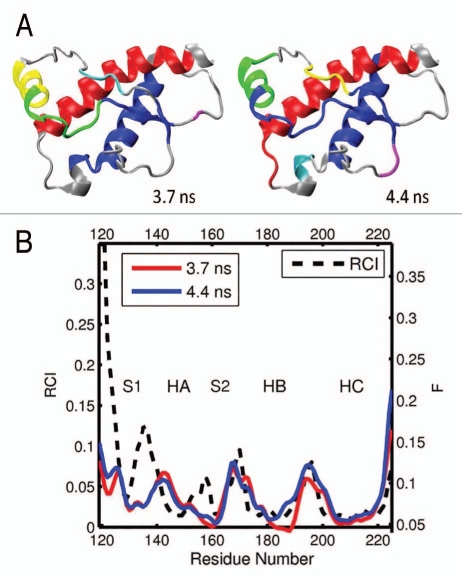
Figures 9, S13 and S14 demonstrate our numerical results from 4 segments of 2 MD trajectories for another disease resistant species, turtle (tPrP 119–125). In two out of four cases, helix HB and both β-strands represent the largest domain of correlated motion, whereas HC is identified as the second largest domain (Fig. 9A). In other two cases shown in Figure S13, HC forms the largest domain, and the second largest domain is either HB or the β sheet along with parts of the adjacent loops S1-HA and HA-S2. As in xlPrP, most of the S2-HB loop is dynamically disordered (domain free). The RCI profile as well as the computed flexibility descriptors in Figures 9B and S14 are also relatively high around the S2-HB loop. Similar to the case of frog PrP, the RCI profile has a pronounced maximum around the S1-HA loop, whereas the computed flexibility levels show a less pronounced increase.

Figure 9.

(A) Dynamical domains for turtle prion protein (tPrP) identified from a MD trajectory at times indicated by the subscripts. The meaning of colors is as in Figure 3. (B) Flexibility profiles at times indicated in the legend box. The dashed curve shows the experimental RCI profile from 2(g). More examples for dynamical domains and flexibility profiles in turtle prion protein are given in Figures S13 and S14, respectively.

We have also performed the domain and flexibility analysis for chicken chPrP 128–242, using a total of 5 trajectories and 13 segments. The representative results are shown in Figure 10, and additional data are given in Figures S15 and S16. The dynamic domains in chPrP demonstrate a bit of variability for the large helices HB and HC. In particular, it can be seen that in five cases HB and HC have formed a single domain, while in another five cases they have been identified as two different domains, and in the remaining three cases HC consists of two domains. Nevertheless, the C-terminal region always belongs to one of two largest dynamic domains in the molecule. Helix HA was also identified as a correlated domain in all cases considered. β-strand S2 tends to be coupled dynamically with the HB-HC bundle, whereas S1 is uncoupled in most cases and the S1-HA loop is largely domain free. The S2-HB loop shows considerable domain coverage in three cases and is largely unstructured in other simulations. The computed flexibility descriptor F shows a significant variability in the area of the S2-HB loop, from a pronounced increase seen in Figures 10B, S16(c) and S(d), to relatively low levels of flexibility in Figure S16(a). The RCI profile shows two prominent maxima in the area of the HB-HC loop (residues 194–213), which is longer in chicken than in any other species. Although our modeling confirms that the HB-HC loop is unstructured (does not contain large dynamic domains), the corresponding flexibility descriptor F increases only moderately in this loop. The reason for this discrepancy with RCI results still needs to be determined.

Figure 10.

(A) Dynamical domains for chicken prion protein (cPrP) identified from a MD trajectory at times indicated by the subscripts. The meaning of colors is as in Figure 3. (B) Flexibility profiles at times indicated in the legend box. The dashed curve shows the experimental RCI profile from 2(h). Further examples for chicken prion protein can be found in Figures S15 and S16.

Discussion

Overall, one can conclude that prion proteins of TSE resistant species (frog, turtle and chicken) tend to have a dynamically disordered and relatively flexible loop S2-HB. This trend is most pronounced in xlPrP, but is also evident in tPrP and in most of the chPrP cases. Also the RCI profiles of frog and turtle PrP show a strong increase in the area of the loop of S1-HA, and for chicken at the loop HB-HC. The other parts of the globular fold of frog, turtle and chicken PrP do not seem to exhibit systematic differences in comparison with the other species considered.

Our dynamic domain analysis indicates that helix HC is one of the largest and most stable domains for all species. The domain structure of helix HB shows a slightly higher level of dynamic variability in bovine, cat and frog PrPs. In these species, and also in turtle and chicken, helix HB also tends to be decoupled dynamically from helix HC. For all eight vertebrate species, the highest level of dynamic disorder and variability occurs in the area of the S1-HA loop. This is expressed in relatively low or absent domain coverage and the most significant variability in the predicted flexibility levels for different trajectory segments. Also in all species, the domain coverage of the β-strand S1 fluctuates more than in other secondary structure elements. In many cases the β-strands S1 and S2 are not identified as a single correlated domain.

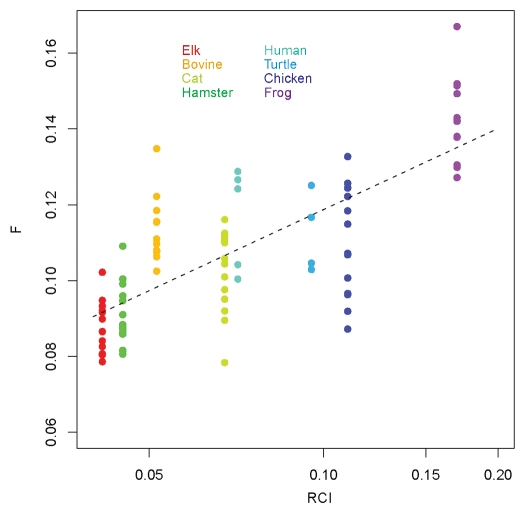
The dynamic signatures of the S2-HB loop, determined by three different methods, show the most significant systematic differences among the different vertebrate species. For this reason, in Figure 11 we have summarized the maximum flexibility values in this loop, as derived from the RCI profiles and the flexibility factor F computed over different segments. An RMS-derived dependence, which may also be interpreted as the expected average level of flexibility F for the given levels of RCI, is also shown by the dashed line. Prion proteins from elk, which are among the most TSE susceptible species, exhibit the lowest levels of flexibility in the S2-HB loop as measured via RCI or F values. The S2-HB loop flexibility measured (RCI, logarithmic scale) or calculated (F) for hamster, which is also disease susceptible, are close to those for elk. In contrast, the TSE disease resistant frog exhibits high RCI and F values. Likewise, disease resistant species such as turtle and chicken also show relatively high levels of RCI and F, although the latter varies considerably in chicken. In most cases, bovine and cat prion proteins exhibit moderate levels of flexibility (F) in this loop, whereas the human prion protein was shown to have relatively high F levels. It can be seen that some of the predicted F values for bovine, cat, chicken and frog PrP deviate to some extent from the experimentally derived RCI values. We attribute these differences to an increased dynamic variability in these species, which is also evident from the corresponding variability in the domain structure of their S2-HB loop. Notwithstanding these small differences, a pronounced correlation between experimentally determined RCI values and computationally determined flexibility (F) levels is clearly evident in Figure 11. The corresponding residual standard error of the linear-logarithmic fit is approximately 0.013, meaning that the predicted trend of the F levels is statistically significant. Furthermore, it is clear that all of the TSE disease prone species tend to have much lower RCI or F values in the S2-HB loop than disease resistant species. This difference in S2-HB loop flexibility likely originates from the differences in S2-HB loop primary structure between TSE disease prone and disease resistant species. In particular, the absence of restrictive proline residues at the N-terminal part of the loop and the larger loop length in the cases of frog and turtle PrPs are likely the major contributors (Fig. S17).

Figure 11.

Summary of the flexibilities at the loop S2-HB in various species. Shown are the maximum flexibilities in the region of the loop, as derived from the RCI profiles and the computed flexibility profiles. The points indicate the data from different segments, and the dashed line represents a root mean square fit. Note that for RCI, a logarithmic scale is employed.

In conclusion, it appears that PrP molecules of all 8 vertebrae species exhibit a considerable degree of dynamic similarity. In all cases, the α-helix HC located at the C-terminal has been identified as a part of one of the largest domains of correlated motion. Based on the theoretical framework for collective dynamics,^47,48 this can be interpreted as the helix HC being a well structured and dynamically stable part of the protein. At the same time, the N-terminal region, more specifically, the β-strand S1, and the loop S1-HA, exhibit relatively high levels of variability, dynamical disorder and local flexibility. In agreement with our earlier numerical analysis⁴⁸ and recent experiments,⁶⁸ our results indicate that the N-terminus of PrP is less stable dynamically and more flexible than the C-terminus in all species considered.

One region where the different species have shown significant and systematic differences, is the loop linking the β-strand S2 and the α-helix HB (the S2-HB loop). In elk and hamster PrP, the S2-HB loop shows significant domain coverage indicating a high degree of dynamic correlation. Also both the flexibility descriptors F and RCI are relatively low for the S2-HB loop of these species. In contrast for PrP from frog, turtle and chicken the S2-HB loop is mostly dynamically disordered (domain free), and in most cases it exhibits relatively high levels of flexibility. Most of predicted flexibility profiles for bovine and cat PrP have moderate levels of flexibility in the S2-HB loop, whereas human PrP has shown relatively high levels of the flexibility.

An interesting outcome of this study is that greater rigidity or less flexibility in the S2-HB loop of prion proteins tends to occur in species that are known to be TSE disease prone, rather than in disease resistant species. In particular, disease prone species such as elk and hamster tend to have a more rigid S2-HB loop, whereas the disease-resistant species such as frog, turtle and chicken, show a greater flexibility or dynamical variability around this loop. This may be explained by a hypothetical mechanism of pathological conversion that involves the binding of a putative conversion cofactor or the infectious PrP^Sc itself in the area of the S2-HB loop.⁷⁰ A high degree of flexibility around this loop could conceivably interfere with binding and prevent the pathological conversion—an idea which has also emerged from recent experiments.^69,73 Another possible interpretation is that the conversion of PrP^C to PrP^Sc is a collective effect comparable to a phase transition, leading to significant parts of the protein undergoing simultaneous changes. In such a scenario, a high degree of rigidity and dynamic correlation would likely facilitate the conversion, whereas a high degree of flexibility (softness) would likely prevent such a phase-state conversion. Of course, further verification of these ideas involving the analysis of a broader range of species, such as mammalian disease resistant species or mutated PrP variants, is required.

To conclude, our results show that the flexibility differences in the S2-HB loop appear to distinguish prion proteins from species that are susceptible to prion disease and those that are resistant, and that this flexibility difference is predictable by our ECD method. The remarkable correlation between the ECD simulation results and the NMR-derived RCI profiles raises an expectation that this computational approach might be used to predict what kind of dynamic responses particular sequence changes may produce in cellular prion proteins.

Methods

Molecular dynamics simulations.

MD simulations were performed with Gromacs 3.2.1,⁷⁴ using GROMOS96 43a1 force field⁷⁵ as described in reference ⁴⁸. PDB identification numbers of the cellular prion proteins employed in this study are listed in Table 1. No attempts to perform in silico glycosylation of the protein models were made because recent studies have shown little or no effect of glycosylation on the molecular dynamics of monomeric prion proteins.^76,77 The protein molecules were placed in triclinic boxes with a distance between the protein and box edges of 1.5 nm and solvated with simple point charge (SPC) water molecules. The solvent was equilibrated using 100 steps of a steepest descent gradient algorithm followed by 100 steps of the Broyden-Fletcher-Goldfarb-Shanno (BFGS),⁷⁸ minimization protocol. Positional restraints with force constant of 1 × 10⁵ kjmol⁻¹nm⁻² were applied to the protein atoms during minimization to prevent distortion of the protein structure by non-equilibrated solvent. If ions were present in original PDB models, they were also included in the models for MD simulations. Counter ions (Na⁺ or Cl⁻) were added to the system to adjust the net charge of the system to zero. After the counter ions were added, 6 cycles of short steepest descent and BFGS minimizations were performed by gradually decreasing the positional restraints on the protein atoms from 1 × 10⁵ kjmol⁻¹nm⁻² to 0. Three 5-ps equilibration MD steps were performed after this initial minimization. During the first step, positional restraints of 1 × 10⁵ kjmol⁻¹nm⁻² were applied to all protein atoms. The second and the third steps were carried out with positional restraints of the same strength on all backbone atoms and backbone atoms in secondary structure elements, respectively. The temperature of the protein and the solvent was maintained at 300 K by coupling with Berendsen thermostats.⁷⁹ The coupling time was equal to 0.1 ps. The pressure was maintained at 1 atm via isotropic pressure coupling using the Berendsen algorithm⁷⁹ with a time constant of 1 ps and compressibility of 4.5 × 10⁻⁵ bar. The MD production runs were performed for 4–6 ns. An integration step of 2 fs was used in all MD simulations. Bond lengths were restrained with the LINCS algorithm⁸⁰ using a fourth order expansion, with four iterations during minimization and two iterations during the “production” MD simulations. The radius for calculation of short-range electrostatic interactions was equal to 1.2 nm. Long-range electrostatic interactions were accounted for using a particle-mesh Ewald summation⁸¹ with maximum spacing for the FFT grid of 0.12 nm and the cubic interpolation. The neighbor list within the radius of 1.0 nm was updated every 20 fs. The cut-off radius for calculation of van der Waals interactions was 1.1 nm. Multiple (2–5) MD trajectories were obtained for each species as indicated in Table 1.

Numerical analysis of essential collective dynamics.

To analyze collective conformational dynamics in prion proteins, we employed a multiscale approach based on the ECD theory.⁴⁷ This theory combines the identification of essential collective coordinates by PCA of MD trajectories, along with the construction of the Mori projection operator with these coordinates, and the analysis of the corresponding generalized Langevin equations (GLE). Applying principal component analysis (PCA) to the MD trajectory, we obtain the normalized eigenvectors E^k = {E^k₁, E^k₂,….,E^k_3N} and eigenvalues σk of the covariance matrix, where the values E^k_n represent the direction cosines of the eigenvectors in the 3N-dimensional configuration space, N is the number of atoms, and k = 1, 2,….3N. One can consider the eigenvectors Ek as the collective dynamic coordinates in the configuration space, and the corresponding eigenvalues σk as the mean square displacements along these coordinates. Next, it is possible to rank the eigenvectors according to the corresponding eigenvalues, and consider a truncated set of collective coordinates, which correspond to the highest magnitude of displacement,

$$E^k=\{E_1^k,E_2^k,\mathrm{....},E_{3N}^k\};k=1,2,\mathrm{......},K,$$ (1)

In most cases, the dimensionality reduction to K = 10–30 captures more than 90% of the total displacement. Such a truncated set of collective coordinates is often referred to as the essential degrees of freedom.³⁷ Employing this known set of essential collective coordinates as the dynamic variables in the Mori projection operator formalism,⁴⁹ it is possible to construct the generalized Langevin equations that describe collective conformational dynamics in the system. The analysis of the resulting GLE described in reference ⁴⁷ allows to introduce a dynamical descriptor that identifies stable structural properties of macromolecules from short MD trajectories (Potapov et al., submitted). In brief, the directional cosines E^k_n from Eq. (1) are split into triplets representing x, y, z coordinates of N atoms, so that E^k = {r^k₁, r^k₂,….,r^k_N}, where r^k_i = {E^k_ix, E^k_iy, E^k_iz}, i = 1,2,…N. The theory shows that the dynamic coupling of the atoms i and j in the GLE formalism is characterized by similar sets {r¹_i, r²_i,…r^K_i} and {r¹_j, r²_j,…r^K_j}, respectively (Potapov et al., submitted).⁴⁷ The N triplets r^k_i = {E^k_ix, E^k_iy, E^k_iz} can also be seen as representing N atoms in a 3K-dimensional space of essential motions of the macromolecule. According to the theory,⁴⁷ the distance in this space represents the degree of dynamic correlation. Points that are located close to each other correspond to atoms whose motions are strongly correlated, and more distant points correspond to those atoms that are more weakly correlated.

This results in a simple methodology to identify groups of atoms moving coherently (dynamic domains). The groups of strongly correlated atoms are identified using a nearest-neighbor clustering technique.^47,82 This approach does not employ any a priori assumptions regarding the number or location of the dynamic domains. Our atomic-level identification of dynamic domains is independent of any reference configurations or postulated structural properties. It is also compatible with arbitrary atomic interaction landscapes and generally immune to vibrational or thermal noise because the domains are identified in the space of essential collective coordinates. Furthermore, this nearest-neighbor technique has the flexibility to allow different cut-offs for which a group of atoms is identified as belonging to a domain. This is achieved by varying the interdomain distance d when doing the nearest-neighbor clustering.^47,82 Varying the parameter d does not affect the correlations to be identified, but it does determine the threshold level of dynamic correlation, for the corresponding atoms to belong to the same domain.⁴⁸ All results presented in this work employ an inter-domain distance d = 0.0035, for which the maximum number of different dynamic domains can be identified in prion proteins.⁴⁸ Choosing the inter-domain distance d that maximizes the number of domains does not affect the underlying dynamic properties of the system, however, it does facilitate the analysis of the data. It should also be noted that, by the definition of the metric in the 3K-dimensional space of directional cosines of essential eigenvectors, the interdomain distance d is a dimensionless value. Further discussion of the clustering techniques used here can be found in references 47 and 48.

In addition to the identification of dynamic domains, the same theoretic framework⁴⁷ can be employed to characterize the local flexibility in the protein molecule, as described in reference ⁴⁸. In general, the theory allows one to characterize the flexibility for every atom. However, in this work we apply the theory to the main chain α-carbon atoms only in order to facilitate the comparison with experimental NMR-derived RCI profiles. The local flexibility descriptor, F, is determined as the distance in 3K dimensional space of essential collective coordinates between the point representing the C_α atom and the centroid calculated over the coordinates of all C_α atoms,

$$F_m^{C_{\alpha }}={\left({\displaystyle \sum _{l=1}^{3K}{(E_m^l-{\epsilon }^l)}^2}\right)}^{0.5},$$ (2)

where m denotes the Cα atom for which the flexibility is evaluated, FCα m is the corresponding flexibility descriptor and εk are the coordinates of the centroid,

$${\epsilon }^k=\frac{1}{N_{C_{\alpha }}}{\displaystyle \sum _{i=1}^{N_{C_{\alpha }}}{E}_i^k}.$$ (3)

Here N_Cα is the total number of C_α atoms and l = 1, 2,…3K. The set of the centroid coordinates, ε = {ε¹, ε²,…..ε^3K} represents the entire molecule, whereas the separations between C_α atoms and ε described by Eq. (2) represent the levels of correlation of motion of the individual atoms with the entire molecule. Short distances (and correspondingly, low F values) correspond to strong correlation, whereas higher distances (and large F values) correspond to a weaker correlation.

For the ECD analysis, we employed K = 20 and multiple 0.2 s long segments from each trajectory upon the convergence of the RMSD distances. The duration of 0.1–0.3 ns provides an optimum tradeoff between the robustness of the PCA averaging and the number of principal components required to sample ∼90% of the total displacement in the configuration space. Further theoretical justification of the usage of short MD trajectory segments to characterize stable dynamic properties of macromolecules has been described elsewhere in Potapov et al. (submitted).

Calculation of NMR random coil index profiles.

Experimental chemical shifts obtained from the Biological Magnetic Resonance Data Bank (BMRB)⁸³ were employed to calculate the RCI profiles for the eight species, as listed in the last column of Table 1. The corresponding NMR assignments were re-referenced through a procedure described elsewhere in reference ⁵¹. The standard random coil chemical shifts⁵² were determined based on protein primary sequences and corrected with neighboring residue correction factors for the i ± 1 and i ± 2 residues. Next, the adjusted reference chemical shifts were subtracted from the experimental chemical shifts according to previously published methods.^50,51 The resulting RCI profiles are shown in Figure 2. The RCI profiles describe the chemical shift “proximity” of the polypeptide structure and dynamics to that observed of a random coil. Generally, the chemical shifts that are used by the RCI protocol appear to be representative of conformational exchange on a time scale up to microseconds.⁵¹ This makes the RCI method capable of detecting motions over a very large range of time scales including those typical for some collective, segmental motions in proteins.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Supporting Information Available

Figures presenting dynamic domains and flexibility profiles for elk, bovine, cat, hamster, human, frog, turtle and chicken PrP, obtained from independent MD trajectories different from those considered in the main article.