Abstract
A full characterization of the thermodynamic forces underlying ligand-associated conformational changes in proteins is essential for understanding and manipulating diverse biological processes, including transport, signaling, and enzymatic activity. Recent experiments on the maltose binding protein (MBP) have provided valuable data about the different conformational states implicated in the ligand recognition process; however, a complete picture of the accessible pathways and the associated changes in free energy remains elusive. Here we describe results from advanced accelerated molecular dynamics (aMD) simulations, coupled with adaptively biased force (ABF) and thermodynamic integration (TI) free energy methods. The combination of approaches allows us to track the ligand recognition process on the microsecond time scale and provides a detailed characterization of the protein’s dynamic and the relative energy of stable states. We find that an induced-fit (IF) mechanism is most likely and that a mechanism involving both a conformational selection (CS) step and an IF step is also possible. The complete recognition process is best viewed as a “Pac Man” type action where the ligand is initially localized to one domain and naturally occurring hinge-bending vibrations in the protein are able to assist the recognition process by increasing the chances of a favorable encounter with side chains on the other domain, leading to a population shift. This interpretation is consistent with experiments and provides new insight into the complex recognition mechanism. The methods employed here are able to describe IF and CS effects and provide formally rigorous means of computing free energy changes. As such, they are superior to conventional MD and flexible docking alone and hold great promise for future development and applications to drug discovery.
Interactions between proteins and small molecules are central to life-sustaining biochemical processes and the action of many important therapeutic agents. However, the detailed mechanisms of these processes are often poorly understood and can involve a variety of motions on a wide range of time scales.1,2 For instance, many large proteins are built from multiple domains with ligand binding sites localized at the interdomain clefts. The presence of bound substrates often stabilizes a closed conformation of the cleft, while the absence of a ligand favors an open conformation. These conformational transitions play critical roles in the ligand recognition processes and are essential for diverse functions, including transport, signaling, and enzymatic activity.(3) Motions between stable protein states can expand or contract a binding site, yielding distinct chemical interactions with ligands.4−8 This inherent protein flexibility presents an important complication for computer-based approaches in drug discovery, as it is effectively harder to hit a moving target.9,10
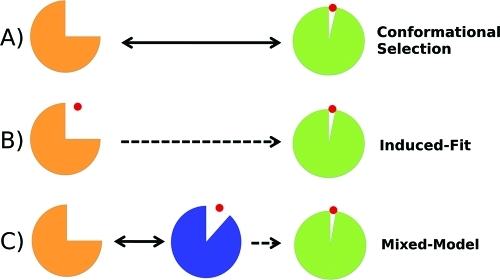
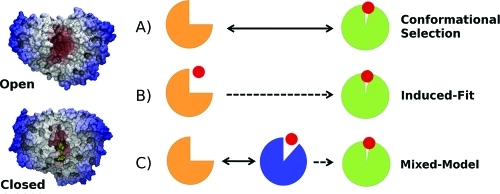
Conceptually, the realization that proteins can undergo conformational changes during or after ligand binding has led to the replacement of the traditional view of proteins as rigid objects in the so-called “lock-and-key” model(11) and to the development of the “induced-fit” (IF)(12) and “conformational selection” (CS)4,13,14 models of molecular recognition (Figure 1). Both IF and CS mechanisms incorporate the idea that proteins are free to explore energy landscapes that often display multiple stable conformational states in equilibrium.15−17 The CS model describes a scenario in which the unbound protein preexists in an ensemble of conformations. The IF model describes structural plasticity in the protein that is mainly ligand-induced. However, it is important to note that these models are not mutually exclusive. Indeed, a survey of the recent literature indicates that many recognition processes can also involve some elements of both CS and IF mechanisms.5,18−20 Improving descriptions of both IF and CS effects in computer-based drug discovery is a particularly important current challenge.6,21,22
Figure 1.
Three possible mechanisms for a protein–ligand association coupled to a conformational change. (A) The apoprotein is sufficiently flexible to exhibit open-to-closed motions, and the role of the ligand is to stabilize the closed form (CS model). (B) The unliganded protein is unable to reach the closed form, and structural plasticity is ligand-dependent (IF model). (C) A mixture of both CS and IF steps is required to reach the closed conformation.
Theoretical studies of bacterial periplasmic binding proteins (PBPs) can provide valuable information about the key roles of conformational changes occurring during ligand recognition. PBPs are expressed by Gram-negative bacteria and function to transport a variety of nutrient molecules, such as amino acids, ions, vitamins, and carbohydrates.(23) Upon ligand binding, the two domains of PBPs are able to undergo hinge-bending motions to sequester ligands inside the interdomain cleft. This action has been dubbed a “Venus-flytrap mechanism”, because of its resemblance to the traps on the carnivorous plant that close only when stimulated by prey.(24) Similar folds exist in a number of important human drug targets, including glutamate receptors.(25) In addition, modified PBPs are being researched as glucose nanosensors that could benefit more than 100 million diabetes patients worldwide.(26)
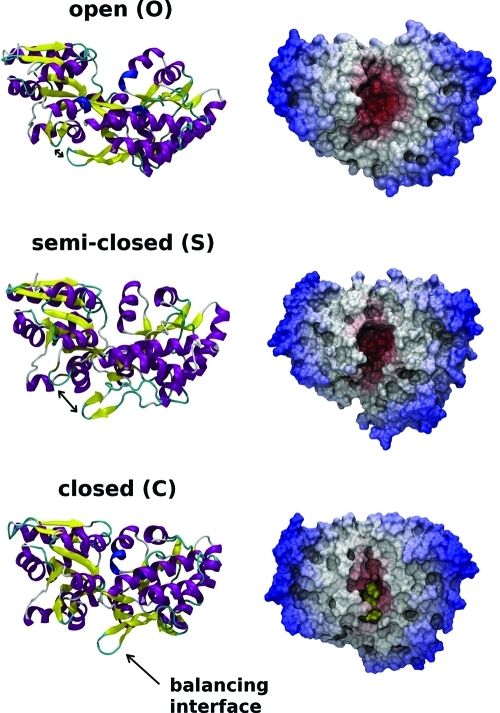
Many crystallographic structures of PBPs have been determined and provide a rich source of information about their different stable conformational states. However, static X-ray structures do not always provide information about the high-energy conformers that can be used for ligand recognition. For this reason, the detailed recognition mechanism is often unknown, and different approaches have been used to complement crystallographic studies and provide descriptions of the protein’s intrinsic flexibility, such as nuclear magnetic resonance (NMR) spectroscopy,7,27 fluorescence,(28) and molecular dynamics (MD) simulations, as reviewed in recent publications.8,29,30 Previously, we have studied the hinge-bending motion of the maltose binding protein (MBP) in atomic detail.(8) MBP is part of the maltose/maltodextrin system of Escherichia coli, which is responsible for the uptake and efficient catabolism of maltodextrins. Our simulation study of apo MBP showed the existence of two stable apo states: the open (O) and semi-closed (S) states (Figure 2). Paramagnetic relaxation enhancement rates were back-calculated from the simulations and found to be consistent with previous NMR experiments.(7) Furthermore, a similar structure for the S state was later produced by Kondo et al, using a different force field,(31) and both structures were found to be comparable to a published NMR structure [Protein Data Bank (PDB) entry 2H25],(32) with a root-mean-square deviation (rmsd) of <2 Å. In addition, the study helped uncover the existence of a motion in the balancing interface region that is coupled to the O → S transition. However, the role of the S state during the ligand recognition process remains unknown, and its study could lead to a deeper understanding of recognition processes, as several other PBPs also appear to display partially closed states, such as LAO-BP(31) and RBP.(29)
Figure 2.
Side and top views of MBP, showing the size and shape of the binding site that is modulated by the conformational state of the protein. Red indicates that the residues are close to the center of mass of the protein, where the binding site is located. The two domains (the N-terminal domain, NTD, and the C-terminal domain, CTD) are connected via a short helix and a two-stranded β-sheet that form an interdomain hinge region. X-ray structures are shown for the unliganded open state (PDB entry 1OMP)(38) and the liganded closed state (PDB entry 3MBP).(37) The semi-closed structure is taken from our previous computer simulations.(6)
In this paper, we extend our initial study of MBP to explore the ligand recognition mechanism in holo MBP and study the role of the S state during ligand recognition. In principle, conventional MD (cMD) simulations could be used to study the exchanges between conformational states in hinge-bending proteins; however, these conformational transitions typically consist of structural rearrangements on spatial scales of 10–100 Å, and the transition time for such rearrangement can be in microseconds or even milliseconds. These slow time scales render difficult the calculation of converged properties for domain motions, because current computer power often limits MD simulations to the submicrosecond time scale. Here, the accelerated MD (aMD)(33) method is used to enhance the sampling by 1–2 orders of magnitude and to allow the full characterization of the microsecond hinge-bending motions of MBP. In addition to performing cMD and aMD simulations, we computed free energy profiles with the adaptive biased force (ABF)34,35 method to determine the relative energy of different conformational states. Finally, the binding affinity for a maltotriose ligand is determined by performing thermodynamic integration (TI), using the double-decoupling method.(36) The combined results of these calculations provide an unprecedented characterization of the thermodynamic properties underlying the recognition mechanism in MBP.
Methods
The liganded and unliganded crystal structures of MBP (PDB entries 3MBP(37) and 1OMP,(38) respectively) were used as the basis of our simulation systems. The 3MBP structure corresponds to the closed conformation in the presence of maltotriose. It was determined at a resolution of 1.70 Å. Topology files have been prepared with the tleap module of the AMBER10 package,(39) and the ff03 force field,(40) with TIP3P water.(41) TI calculations were conducted with AMBER code, and ABF, aMD, and cMD simulations were conducted with the NAMD2 code.42,43 Simulations were conducted in the NVT ensemble, using a time step of 2.0 fs in combination with the SHAKE algorithm.(44) The temperature was regulated with a Langevin thermostat, using a damping coefficient of 5 ps–1. Additional simulation parameters and system details are as described in ref (8). All the simulations are summarized in Table 1.
Table 1. Summary of the Simulations Performeda.
| simulation name | type (EQ, ABF, TI, aMD) | no. and simulation time (ns) |
|---|---|---|
| open-apo-EQ | EQ | 2 × 50b |
| open-apo-aMD | aMD | 2 × 50b |
| open-holo-EQ | EQ | 10 × 40 |
| open-holo-aMD | aMD | 10 × 40 |
| open-holo-TI | TI | 10 × 6 |
| semi-apo-EQ | EQ | 2 × 50b |
| semi-holo-EQ | EQ | 10 × 40 |
| semi-holo-aMD | aMD | 10 × 40 |
| semi-holo-TI | TI | 10 × 6 |
| closed-holo-TI | TI | 10 × 6 |
| closed-holo-ABF1 | ABF | 1 × 50 |
| closed-holo-ABF2 | ABF | 20 × 20 |
| closed-apo-ABF3 | ABF | 20 × 20 |
Abbreviations: EQ, equilibrium; ABF, adaptive biased force; TI, thermodynamic integration; aMD, accelerated MD. The total simulation time was 4.1 μs.
Simulations discussed in ref (8).
To study the conformational change in holo MBP, 10 aMD and 10 cMD simulations were conducted for 40 ns each, starting from liganded O and S structures. The aMD method was able to accelerate the sampling of hinge-bending motions by facilitating variations in torsional angles. The following parameters were used: [Eb – V0, α] = [1300 kcal/mol, 260 kcal/mol]. The boost parameter, Eb, was chosen to be as high as the highest energy barriers, so that the bias potential, ΔV, is activated most of the time. The parameter α, which controls the roughness of the biased potential, was chosen so that the average ΔV remains around ∼40 kcal/mol during the simulations. At this acceleration level, it was possible to enhance significantly the hinge-bending motions, and sampling of side chain orientations, while maintaining the integrity of the protein secondary structure.
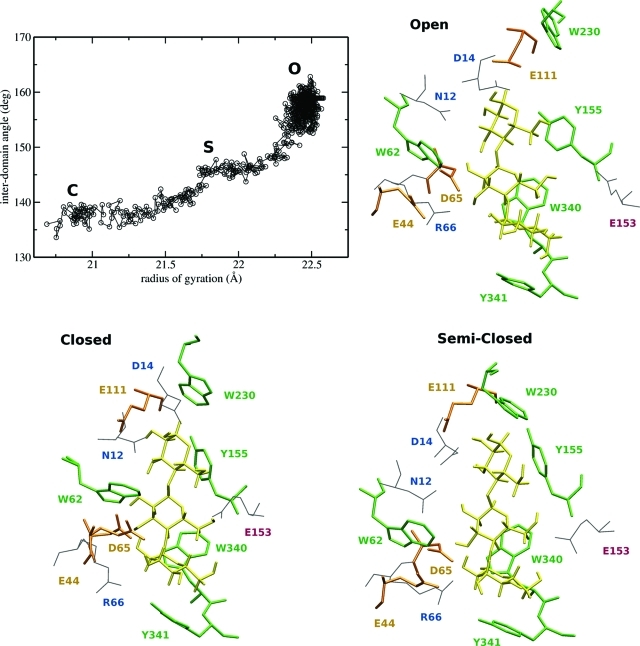
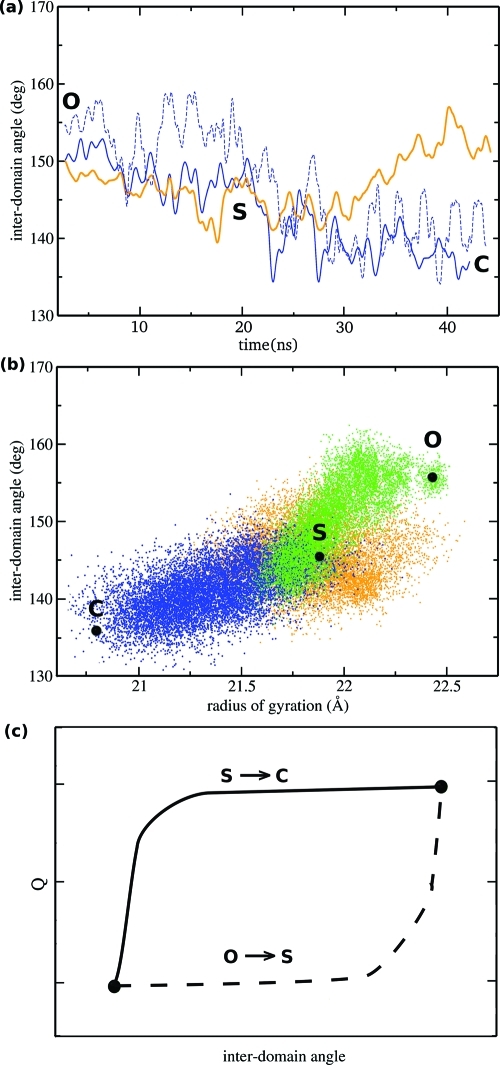
ABF simulations were performed to generate a good pose for liganded O and S structures and to compute free energy profiles for the O → C transitions in apo and holo MBP. The basic idea of the ABF method is to measure the mean force along some chosen reaction coordinate (RC) and use it to help overcome free energy barriers and provide estimates of the free energy. On the basis of our previous experience with aMD simulations of apo MBP,(8) the radius of gyration (Rg) calculated for all α-carbons was found to be a good RC for studying the conformational change. To open the liganded protein, the RC was sampled between values of 20 and 23 Å, using 500 samples prior to application of the bias force, and a bin width of 0.1 Å. A single ABF simulation of 50 ns was able to scan the three stable states of MBP (Figure 3a). To ascertain the accuracy of the liganded S and O structures, we compared unliganded structures using structural parameters such as the rmsd and the interdomain closure angle (θ). While a single ABF simulation can in principle provide a free energy estimate along the RC, the efficiency of the sampling is limited by the rate at which the system can diffuse along the RC. To accelerate the convergence of the free energy calculations, the RC was divided into overlapping windows with a width of 0.2, for values of Rg between 20.6 and 22.4 Å. Statistics were accumulated by running 20 independent ABF simulations in parallel for both apo and holo MBP, for 20 ns each, to obtain a converged profile within 0.5 kcal/mol. The resulting free energy profile is shown in Figure 4b as a function of the interdomain closure angle (θ), as it was found to increase nearly linearly with the RC.
Figure 3.
Single ABF simulation initiated from the liganded C state to generate models for the liganded O and S states. After equilibration (∼2 ns), the structures of the binding site were studied. With the exception of E153 and E111 (red), all polar residues making H-bonds with maltotriose (yellow) belong to the NTD (blue). Sugar-stacking residues (green) all belong to the CTD, except for W62.
Figure 4.
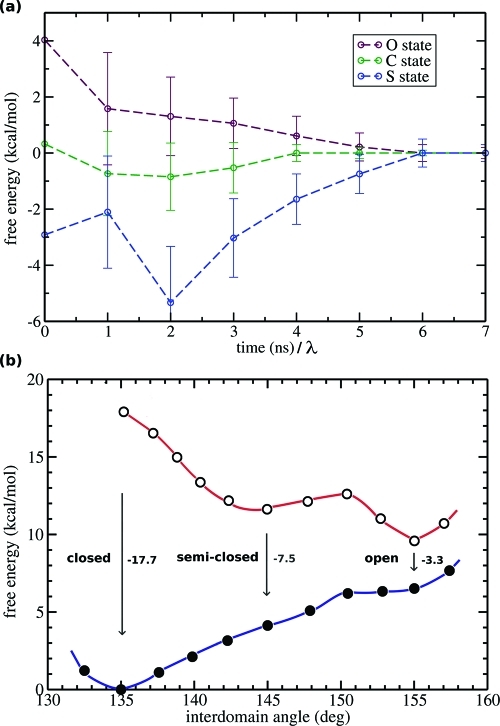
Free energy calculations. (a) Evolution of TI estimates toward a converged value [ΔGAB(t) – ΔGAB,conv], as a function of the sampling per λ point, for the binding affinity of maltotriose with MBP in the O, S, and C states. (b) Free energy profiles computed with the ABF method used to display the ΔGAB values obtained from TI calculations. Empty circles denote data for the apo form and filled circles data for the holo form. The plot shows that a “population shift” occurs in the stability of different conformations in the presence of a ligand.
TI calculations, based on the double-decoupling scheme, were performed to study the role of the S state in ligand recognition, using maltotriose as the ligand. In this scheme, the free energy simulations involve gradually turning off the electrostatic and van der Waals interaction of the ligand molecule from the rest of the system. This involves two sets of simulations: the transfer of the ligand from bulk water to the gas phase, ΔG°2, and the transfer of the ligand from the binding site pocket in the complex to the gas phase, ΔG°1. During the latter part of the simulation, the ligand is weakly coupled to the protein and would have to explore the entire simulation box for ΔG°1 to converge. A practical solution to this problem is to use a harmonic potential that can constrain the ligand position during the calculations and facilitate the proper convergence of the free energy. To choose an appropriate force constant k, an analytic formula based on the equipartition theorem is given by Gilson et al.:(36)
where ∂r2 is is the atomic fluctuation of the constrained atom or center of mass of the ligand during the course of a MD simulation with the fully unperturbed potential function, R is the molar gas constant, and T = 300 K. In this case, a harmonic potential of 1 kcal mol–1 Å–2 was chosen, and the free energy was calculated using the appropriate correction,(36) as
where C0 is the standard concentration and the volume element, VI, can be calculated as
The binding free energy of maltotriose was computed for MBP in the O, S, and C states. The ligand was decoupled from its environment in several steps characterized by a λ value between 0 and 1. The derivative of the potential energy with λ was sampled for each λ and integrated using the trapezoid rule to compute the free energy difference. The electrostatic interaction was first decoupled in 11 steps, with λ values of 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0. The van der Waals (vdW) part of the interaction energy was then decoupled in 21 steps (every 0.05), using soft-core potentials.45,46 Each point was equilibrated prior to the production run by 0.5 ns of MD simulation and run for at least 5 ns.
The convergence of the calculations was ascertained by running five independent simulations for selected λ points starting from different initial coordinates. In addition, a time series of an error estimate, σsim(t), was back-calculated at the end of the runs by comparing the current estimate of ∂H/∂λ at time t and the converged ∂H/∂λ(47) (see also Figure 4a):
where T is the total number of block averages containing uncorrelated points, [∂Ht(λ)/∂λ]λ denotes the Hamiltonian derivative, block-averaged at time t, and [∂HT(λ)/∂λ]λ is the ensemble average over the entire simulation time at a given λ. The error bars calculated in this way were found to be converged within ∼0.5 kcal/mol for sampling times longer than 5 ns per λ (Figure 4a).
In addition to thermodynamic factors, kinetic factors such as the rate of exchange between stable states can affect the recognition rate. To study the impact of conformational exchange on association kinetics, we proposed a model of the conformational dynamics between the O and S states based on the two-state model introduced by Szabo et al.(48) for studying the bimolecular association rate in the presence of stochastic gating. In this model, the biomolecular association rate, kG, is calculated as
where kUG is the steady-state ungated biomolecular association rate to the protein fixed in its most favorable conformations, k1 and k2 are the closing and opening rates, respectively, (k1 + k2)−1 is the domain gating period, and κ̃(s) is the Laplace transform of s.
For MBP, the C state is not visited in the apo form7,8,31 and kG corresponds to the rate of O ⇔ S transitions, whereas kUG corresponds to the recognition rate for a system initially fixed in the O state. Using this model, the time for the O to S exchange becomes the domain gating period, τex, and eq 5 is reduced to two limiting cases depending on the relative values of τex relative to the characteristic diffusion relaxation time, τD:(48)
Equations 6 and 7 represent substrate association in the presence of “slow” and “fast” exchange, respectively, and imply that domain motion interferes with the substrate binding kinetics only in the slow exchange limit (τex ≫ τD). In these equations, Dlig is the sum of the translational diffusion coefficients of the ligand and protein, which can be approximated as the diffusion coefficient of the ligand. The collision distance of the system, rc, can be approximated as the sum of the smallest radii of spheres that contain each molecule.
To obtain an estimate of the average time needed for a transition between O and S states, τex, we used the Smoluchowski diffusion equation, assuming a constant diffusion coefficient. The diffusion coefficient of the protein, Dprot, was estimated with the Hydropro method,(49) as the sum of the diffusion coefficient of the two domains, setting the temperature to 298.15 K, the viscosity to that of water at 298.15 K (0.890 cP), and the bead radii of the protein to 3.2 Å. For the simplest case of a flat free energy profile, the time required for the diffusion of the two domains becomes τ0 = L2/2Dprot,(50) or ∼25 ns. However, for MBP, the free energy profile is not flat and a better estimate for τex includes a penalty caused by the roughness of the profile. This stochastic diffusion process was modeled as a Markov chain, with discrete states corresponding to successive milestones on the free energy profile. Such a Markov random walk satisfies the condition of detailed balance under equilibrium conditions in the absence of net flux, and the stochastic evolution of the system obeys the Smoluchowski equation.(51) The Smoluchowski equation was discretized in space,(52) using the equation kij = k0 exp[−1/2(β/ΔGij)], where β = 1/kBT, k0 is the rate for a simple diffusion between two states i and j, and ΔGij is their free energy difference.
Results
Below we first report the results of free energy calculations exploring the binding affinity of MBP for the maltotriose ligand when the protein is in the O, S, and C states. Next, we present results on kinetic aspects of the recognition process. Finally, simulations of the conformational change that provide a complete picture of the recognition process are described.
Free Energy Calculations
Although kinetic factors can influence the yields of different molecular complexes in cellular and other nonequilibrium environments, the primary factors that are used in the analysis of molecular recognition can be described by thermodynamics.(53) To explore the initial interactions between maltotriose and MBP, we built computational models of the liganded O and S states (see Methods). After equilibration, inspection of trajectories initiated from the O, S, and C ligand-bound structures indicated that maltotriose interacts more favorably with active site residues in the C state. Details of these interactions have been described previously in detail54,55 and involve principally the hydroxyl groups of the sugar making hydrogen bonds with the NTD domain of the protein (D14, N12, and E65) and aromatic residues on the CTD (W230, Y155, W340, and Y341) that stack favorably with the sugar ring of the ligand (Figure 3).
Interestingly, in the bound O state, several favorable interactions with both NTD and CTD are lost because of the extended size of the binding site. In particular, the sugar stacking residues on the CTD (W230, Y155, W340, and Y341) are not favorably positioned. In contrast, the sugar stacking residues in the S state can interact more favorably with the ligand. Residues Y155 and W340 form interdomain H-bonds, between W340 (CTD) and D65 (NTD), and between the backbone carbonyl of E111 and Y155.(8) These H-bonds help orient the sugar-stacking side chains so that they can interact favorably with the ligand, effectively locking the protein structure in the S state.
TI calculations were used to quantify the difference in binding affinity for maltotriose in the O, S, and C states. The standard Free Energy, ΔGAB, was calculated as the energy required for removing the ligand from the binding site and moving it into the solvent. The calculations indicated that the O state displays only a weak affinity for the ligand (ΔGAB = −3.3 kcal/mol), whereas the S conformation leads to a more favorable binding energy (ΔGAB = −7.5 kcal/mol). The C state was found to display the highest affinity for maltotriose (ΔGAB = −17.7 kcal/mol). The strong binding in the C structure, when compared to that in the O and S structures, reflects the multivalent attachment of the maltotriose ligand to the receptor that includes multiple additional interactions with the NTD, such as electrostatic interactions employing the OH groups of the glucose units. When compared to the ligand in bulk, electrostatic interactions were found to play an important role in the high ligand affinity for the C state (ΔGelec values of −8.2, −1.0, and −0.2 kcal/mol for the C, S, and O states, respectively), whereas vdW interactions caused by improved sugar stacking partly explain the difference in affinity between the O and S states (ΔGvdW values of −9.5, −6.5, and −3.1 kcal/mol for the C, S, and O states, respectively). As the C state is not visited by apo MBP,7,8,31 these results suggest that the S state is the most reactive state for ligand recognition.
The binding affinities can be compared to the affinity constants determined for MBP from the association and dissociation rates (kon/koff) and measured with stopped-flow fluorescence spectroscopy.(56) In these experiments, kon is understood to be the rate of binding to the protein (which can be in the O or S state) whereas koff is much smaller and corresponds to the rate of dissociation from the C state after the conformational change. The association constant is calculated via the equation Kexp = kon/koff, and the ligand association free energy is
In our TI calculations, the time scale sampled by the simulations does not allow for the relaxation of the apoprotein from the Capo state into the more stable Oapo state. This was confirmed by computing the rmsd and the radius of gyration of the final structure. Therefore, the computed dissociation free energy for the C state corresponds only to the following transformation:
The final protein conformation (Capo) is high in energy, and the protein relaxation energy can be calculated with the ABF method or estimated via NMR spectroscopy:(57)
Combining eqs 10 and 11 and changing the sign of the free energy provide an estimate of the free energy of ligand association (eq 12), which is in good agreement with experiments (eq 9):
To provide a complete view of the free energy profiles, we used ABF simulations to determine the energy requirements for opening and closing MBP. The apo and holo curves were aligned using the value computed with TI for the maltotriose binding affinity in the C state. The two ABF curves were found to correctly reproduce the ligand binding energy of the O and S states, also computed with TI (Figure 4b and Table 2). The C apo state was found to be high in energy in the apo from, consistent with the observation that this state is not visited by apo MBP. In addition, the plot highlights the existence of a ligand-induced population shift toward the closed structure and indicates a barrier-less transition from the O form to the C form in holo MBP.
Table 2. Free Energies (kilocalories per mole) of Protein–Ligand Association for Maltotriose.
| conformation | ΔG from TI | ΔG from ABF |
|---|---|---|
| open | –3.3 ± 0.5 | –2.9 ± 0.5 |
| semi-closed | –7.5 ± 0.5 | –7.0 ± 0.5 |
| closed | –17.7 ± 0.5 | not available |
Kinetic Aspects of the Recognition Process
Although informative, the free energy profiles presented above do not tell us whether the S state is actually used by MBP during ligand recognition. In practice, the biological activity of different conformational states can be determined by several factors, in particular (I) the binding free energy, (II) the occupancy, or population, of the different states, (III) the accessibility of the binding site, (IV) the rate at which the different states can exchange, (V) the ligand concentration, and (VI) the possibility of allosteric or cooperative interactions with the ligand. Kinetic effects could be important for MBP, as the S state displays a high affinity for the ligand but has a low occupancy (∼5%(7)). If the characteristic diffusion time of the ligand is similar to the time required for the O ⇔ S transitions, then the ligand is likely to be presented to both states and hence will be able to preferably bind the most favorable state (i.e., the S state). However, if the exchange between the two states is slow compared to ligand diffusion, the extent to which the minor S state will be able to compensate for its small equilibrium probability is limited, and the rate of the recognition will be influenced by the rate of the conformational transition (eq 6).
A rough estimate of the rate of exchange between the O and S states was calculated on the basis of the computed free energy profiles, and the Smoluchowski diffusion equation (see Methods). The diffusion coefficient for the two domains of MBP was assumed to be constant at a Dprot value of ∼2 × 10–6 cm2/s (=2 × Å2/ns), which was estimated with the Hydropro method.(49) The two rigid domains have to move by a total distance L of ∼10 Å during the O → S transition, and for the simplest case of a flat free energy profile, the time required for such diffusion (τ0 = L2/2D) is 25 ns. In MBP, however, the free energy profile is not flat, and the S state is slightly higher in energy by ∼2 kcal/mol.(7) In addition, there is an energy barrier of ∼3.7 kcal/mol that was calculated by the ABF method. With this free energy profile, the time scale obtained for the O → S transitions, τex, is estimated to be ∼200 ns. Alternatively, a slightly different estimate for the free energy barrier (∼7 kcal/mol) has been obtained by Kondo et al.,(31) who used umbrella sampling. The small discrepancy between the two profiles may be due to the difference in the computational models or the fact that these authors used sampling times 40 times shorter (0.5 ns) than the sampling times per window used here (20 ns). For instance, Kondo et al did not report observing the motion of the balancing interface during O → S transitions, which suggests that the shorter sampling times may have led to a slight overestimate of the actual energy barrier. On the basis of their profile, our estimate for τex is ∼2 μs. Therefore, a conservative range of values for the time scale for the O ⇔ S transitions is between ∼200 ns and ∼2 μs. This estimate is consistent with our observation that the O → S transition in apo MBP occurs in aMD simulations(8) but is not observed in 50 ns cMD simulations. This estimate also lies within the larger bracket of possible time scale (20 ns to 20 μs) indicated by NMR experiments.(7)
The time scale of the O → S transition should be compared to the characteristic diffusion time for the ligand, which was also estimated. Dlig was calculated with the Stokes–Einstein relation as kBT/6πμr, where r is the ligand radius (∼8 Å), μ is the viscosity of water (0.001 in SI units), and rc (eq 8) is set to ∼20 Å. With these values, τD is roughly ∼16 ns. Therefore, τex is found to be at least 10 times slower than τD, which implies that the protein conformational change is in the slow exchange mode (eq 6), a result consistent with the measured first-order kinetics.(56) In summary, the evaluation of kinetic factors suggests that the S state is unlikely to compensate fully for its low relative occupancy of ∼5%. Instead, the free energy profile (Figure 4b) indicates that the O → S conformational change is fast and generally occurs within nanoseconds, but only after the ligand interacts with the O state.
Standard and Accelerated MD Simulations
To confirm the scenario outlined above, we performed direct simulations of liganded MBP. Previous MD simulations(58) have indicated that the O → C conformational change of liganded MBP occurs within ∼30 ns. This suggests that the presence of a ligand at the interdomain cleft can accelerate the transition from the O state to the S state, possibly by assisting the reorganization of relevant side chains and/or by establishing bridges linking the two domains.
To explore these questions, we conducted 10 cMD and 10 aMD simulations for 40 ns each, starting from liganded O and S states. During the aMD simulations, eight of the 10 trajectories showed the conformational transitions to the C structure (Figure 5). In the cMD runs, two conformational transitions to the C form were observed. This contrasts with our previous simulations of the apo state with cMD,(8) where no O → S transitions could be observed on a similar time scale (40 ns). Thus, simulations show that the ligand is able to accelerate significantly the rate of the conformational change. This result is consistent with the free energy profiles presented above and with our estimates for the kinetic rates.
Figure 5.
Representative trajectories. (a) Two aMD trajectories are shown that were started from the liganded O state and evolved toward the C state (blue). Instead, in standard MD simulations, only one closing event was observed, and most simulations did not reach the C state within 40 ns, as shown here for one trajectory (orange). (b) Most cMD simulations remained in their original state (orange), whereas most aMD simulations rapidly evolved toward the most stable structure. Two such transitions are shown here, O → S (green) and S → C (blue). (c) Schematic drawing of the two different conformational changes in MBP, showing the variation of the interdomain angle as a function of the number of new protein–ligand contacts in the binding site.
The ligand recognition is found to proceed in the same way in all productive trajectories, which can be described as follows. (1) The ligand is initially interacting with the sugar-stacking residues of the CTD (Y155 and W340) and with E111, which belongs to the hinge region. (2) The sugar-stacking residues of the CTD improve their positions to better stabilize the ligand, and hydrogen bonds form between Y155 and the carbonyl group of E111 and between W340 and D65, which locks the protein in the S state. During this process, the tip of the balancing interface moves into solution. (3) Favorable electrostatic interactions with negatively charged ligands of the NTD, in particular E44 and D65, exert a force pulling the NTD toward the CTD. (4) A global conformational change occurs, reducing the interdomain angle from ∼145° to ∼135° and the radius of gyration from ∼21.4 to ∼20.6 Å, to reach the closed form of MBP.
Another interesting question about the conformational change is whether local changes in the binding site occur before or after the global structural change in the protein. Simulations suggest that the O → S and S → C transitions behave differently in that respect. In the case of the O → S transition, the number of protein–ligand contacts in the binding site (Figure 3) increases only after the conformational change is completed. For example, simulations show that the O → S transition is less dependent on the presence of the ligand (Figure 5c), as it can also occur in apo MBP.(8) Moreover, the reverse S → O conformational change is also observed in simulations of holo MBP (Figure 5a) and does not appear to be prevented by the presence of the ligand. In contrast, the S → C transition is unidirectional and found to be mostly driven by the interactions of the ligand with charged side chains of the NTD (such as E44 and D65), which occur in the simulations prior to the global conformational change.
Discussion
These results indicate that an IF model best describes the ligand recognition mechanism in MBP. The rate of O to S exchange in apo MBP appears to be too far below that required for compensating fully for the small occupancy of the S state. Given that the S state has a population of only ∼5%, it is likely that initial ligand recognition involves predominantly the O state. However, we have shown that the S state displays high affinity for the ligand. This conclusion is consistent with the experiments of Telmer and Shilton, who have reported that a point mutation in the balancing interface region of MBP (Figure 2) can improve recognition by a factor of ∼200.(59) This result is explained by our observation that such mutations can induce a population shift toward the S state.(8) These forces are not electrostatic in nature but nevertheless develop into long-range (>20 Å) influences. Similarly, remote mutations in viral proteins, such as HIV-1 protease, can lead to population shifts and drug resistance without modifying the catalytic abilities of the enzyme.(60) The presence of two stable states in MBP may allow for interactions with more diverse ligands, such as, for example, sugars with one to seven glucose units. In agreement with this proposal, less promiscuous PBPs, such as GlnBP, do not appear to possess a partially closed conformation,(61) while more promiscuous PBPs, such as LAO-BP, appear to possess a semi-closed apo conformation.(31)
Interestingly, PBPs are able to create a selective binding site without displaying a molecular surface complementary to the ligand on a subangstrom level. Gerstein et al first hypothesized that in most hinge-bending proteins the open and closed states are only slightly different in energy and are in dynamic equilibrium at room temperature,(3) pointing toward a CS mechanism for most PBPs. However, recent studies have indicated that different recognition scenarios may operate within the PBP superfamily (Figure 1). For instance, a CS mechanism has been proposed for the ferric binding protein (FBP),(62) the ribose binding protein (RBP),(29) the glucose/galactose binding protein (GGBP),(63) and the choline binding protein (ChoX).(64) This mechanism has also been proposed for the l-lysine l-arginine l-ornithine binding protein (LAO-BP) transition,(65) although more recent theoretical studies point toward possible mechanisms involving both CS and IF steps.31,66 In contrast, the glutamine binding protein (GlnBP) is believed to be less flexible than other PBPs, and NMR paramagnetic relaxation experiments suggest an IF mechanism.(61) In addition to the protein intrinsic flexibility, the IF mechanism is also generally more likely to prevail over the CS mechanism when the ligand affinity is high or the ligand concentration is high.(20)
Findings from this study support a recognition mechanism for MBP that involves two possible pathways: either a pure IF mechanism or a mechanism involving both a CS step and an IF step. The IF mechanism is found to dominate, as MBP exists predominantly in the O state (95% occupancy), and the time scale of the conformational change in apo MBP is slow compared to the ligand diffusion rate (∼200 ns to 2 μs vs ∼16 ns). In fact, a similar IF mechanism may also occur in other PBPs that appear to possess minor semi-closed states, such as LAO-BP(31) and RBP,(29) as CS effects are typically slower than IF adaptations, due to the fact that they involve global transitions between protein states separated by energy barriers. Our calculations of the free energy show that the ligand induces a population shift in MBP that helps drive the system toward the closed conformation. The similarities we observe between all simulated pathways suggest that the shape of the free energy well is analogous to the funnel model used to describe protein folding pathways. The complete recognition process is best viewed as a “Pac Man” type action where the ligand is initially localized to one domain and naturally occurring hinge-bending vibrations in the protein are able to assist the recognition process by increasing the chances of a favorable encounter with side chains on the other domain, leading to a population shift. Furthermore, ligand binding to one domain also allostrerically affects the linker and interdomain interface (see also ref (67)). Indeed, the aMD simulations could uncover the detailed mechanism of the population shift and indicated that the ligand is able to create a bridge between the CTD and charged residues of the NTD.
As new methods are being developed to incorporate descriptions of CS and IF effects in computer-assisted drug discovery, there are good prospects for the rational design of inhibitors targeting flexible proteins. For instance, when comparing several popular ligand docking tools for carbohydrates, Agostino et al. found that most codes can reproduce accurately the ligand binding geometry (pose) of experimentally determined structures when using X-ray structures that were determined with the ligand bound (thereby explicitly incorporating CS and IF effects(68)). However, when using the flexible version of these docking algorithms, the poses were more unreliable as indicated by large rmsds from the known complex. In practice, ligand-bound structures are often not available, and it remains a significant challenge to model accurately IF and CS effects. As shown here for MBP, free energy calculations coupled with aMD simulations can help in the assessment of the role of CS and IF mechanisms, as well as in determining the role of high-energy states in molecular recognition. The aMD simulations were found to enhance the sampling by 1 or 2 orders of magnitude, allowing for the exploration of slow hinge-bending motions. The combination of methods provided key details about protein dynamics, and the relative free energy difference between accessible states. In this regard, these methods appear far superior to cMD and flexible docking alone. As such, they hold great promise for future development and applications to drug discovery.
Author Present Address
∥ Center for Computational Medicine and Bioinformatics, University of Michigan, Ann Arbor, MI 48109-2218.
This work was supported by the National Science Foundation, the National Institutes of Health, the Howard Hughes Medical Institute, the Center for Theoretical Biological Physics, the National Biomedical Computation Resource, and the National Science Foundation Supercomputer Centers.
Funding Statement
National Institutes of Health, United States
References
- McCammon J. A. (1984) Protein Dynamics. Rep. Prog. Phys. 47, 1–46. [Google Scholar]
- Karplus M.; McCammon J. A. (2002) Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 9, 646–652. [DOI] [PubMed] [Google Scholar]
- Gerstein M.; Lesk A. M.; Chothia C. (1994) Structural Mechanisms for Domain Movements in Proteins. Biochemistry 33, 6739–6749. [DOI] [PubMed] [Google Scholar]
- Ma B. Y.; Kumar S.; Tsai C. J.; Nussinov R. (1999) Folding funnels and binding mechanisms. Protein Eng. 12, 713–720. [DOI] [PubMed] [Google Scholar]
- Boehr D. D.; Nussinov R.; Wright P. E. (2009) The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 5, 789–796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teague S. J. (2003) Implications of protein flexibility for drug discovery. Nat. Rev. Drug Discovery 2, 527–541. [DOI] [PubMed] [Google Scholar]
- Tang C.; Schwieters C. D.; Clore G. M. (2007) Open-to-closed transition in apo maltose-binding protein observed by paramagnetic NMR. Nature 449, 1078–1082. [DOI] [PubMed] [Google Scholar]
- Bucher D.; Grant B. J.; Markwick P. R.; McCammon J. A. (2011) Accessing a hidden conformation of the maltose binding protein using accelerated molecular dynamics. PLoS Comput. Biol. 7, e1002034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson H. A. (2002) Protein flexibility and drug design: How to hit a moving target. Curr. Opin. Chem. Biol. 6, 447–452. [DOI] [PubMed] [Google Scholar]
- Ivetac A.; McCammon J. A. (2011) Molecular recognition in the case of flexible targets. Curr. Pharm. Des. 17, 1663–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer E. (1894) Ber. Dtsch. Chem. Ges. 27, 2985–2993. [Google Scholar]
- Koshland D. E. (1958) Application of a Theory of Enzyme Specificity to Protein Synthesis. Proc. Natl. Acad. Sci. U.S.A. 44, 98–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monod J.; Wyman J.; Changeux J. P. (1965) On the Nature of Allosteric Transitions: A Plausible Model. J. Mol. Biol. 12, 88–118. [DOI] [PubMed] [Google Scholar]
- Freire E. (1998) Statistical thermodynamic linkage between conformational and binding equilibria. Adv. Protein Chem. 51, 255–279. [DOI] [PubMed] [Google Scholar]
- Frauenfelder H.; Sligar S. G.; Wolynes P. G. (1991) The Energy Landscapes and Motions of Proteins. Science 254, 1598–1603. [DOI] [PubMed] [Google Scholar]
- Miller D. W.; Dill K. A. (1997) Ligand binding to proteins: The binding landscape model. Protein Sci. 6, 2166–2179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai C. J.; Kumar S.; Ma B. Y.; Nussinov R. (1999) Folding funnels, binding funnels, and protein function. Protein Sci. 8, 1181–1190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okazaki K.; Takada S. (2008) Dynamic energy landscape view of coupled binding and protein conformational change: Induced-fit versus population-shift mechanisms. Proc. Natl. Acad. Sci. U.S.A. 105, 11182–11187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant J. A.; Gorfe B. J.; McCammon A. A. (2010) Large conformational changes in proteins: Signaling and other functions. Curr. Opin. Struct. Biol. 20, 142–147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csermely P.; Palotai R.; Nussinov R. (2010) Induced fit, conformational selection and independent dynamic segments: An extended view of binding events. Trends Biochem. Sci. 35, 539–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colombo G.; Morra G.; Genoni A.; Neves M. A. C.; Merz K. M. (2010) Molecular Recognition and Drug-Lead Identification: What Can Molecular Simulations Tell Us?. Curr. Med. Chem. 17, 25–41. [DOI] [PubMed] [Google Scholar]
- Cozzini P.; Kellogg G. E.; Spyrakis F.; Abraham D. J.; Costantino G.; Emerson A.; Fanelli F.; Gohlke H.; Kuhn L. A.; Morris G. M.; Orozco M.; Pertinhez T. A.; Rizzi M.; Sotriffer C. A. (2008) Target flexibility: An emerging consideration in drug discovery and design. J. Med. Chem. 51, 6237–6255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwyer M. A.; Hellinga H. W. (2004) Periplasmic binding proteins: A versatile superfamily for protein engineering. Curr. Opin. Struct. Biol. 14, 495–504. [DOI] [PubMed] [Google Scholar]
- Mao B.; Pear M. R.; McCammon J. A.; Quiocho F. A. (1982) Hinge-Bending in l-Arabinose-Binding Protein: The Venus-Flytrap Model. J. Biol. Chem. 257, 1131–1133. [PubMed] [Google Scholar]
- Felder C. B.; Graul R. C.; Lee A. Y.; Merkle H. P.; Sadee W. (1999) The venus flytrap of periplasmic binding proteins: An ancient protein module present in multiple drug receptors. AAPS PharmSci 1, No. 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffery C. J. (2011) Engineering periplasmic ligand binding proteins as glucose nanosensors. Nano Rev. 2, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pistolesi S.; Tjandra N.; Bermejo G. A. (2011) Solution NMR studies of periplasmic binding proteins and their interaction partners. BioMolecular Concepts 2, 53–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall J. A.; Gehring K.; Nikaido H. (1997) Two modes of ligand binding in maltose-binding protein of Escherichia coli. Correlation with the structure of ligands and the structure of binding protein. J. Biol. Chem. 272, 17605–17609. [DOI] [PubMed] [Google Scholar]
- Ravindranathan K. P.; Gallicchio E.; Levy R. M. (2005) Conformational equilibria and free energy profiles for the allosteric transition of the ribose-binding protein. J. Mol. Biol. 353, 196–210. [DOI] [PubMed] [Google Scholar]
- Loeffler H. H.; Kitao A. (2009) Collective dynamics of periplasmic glutamine binding protein upon domain closure. Biophys. J. 97, 2541–2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondo H. X.; Okimoto N.; Morimoto G.; Taiji M. (2011) Free-Energy Landscapes of Protein Domain Movements upon Ligand Binding. J. Phys. Chem. B 115, 7629–7636. [DOI] [PubMed] [Google Scholar]
- Xu Y. Q.; Zheng Y.; Fan J. S.; Yang D. W. (2006) A new strategy for structure determination of large proteins in solution without deuteration. Nat. Met. 3, 931–937. [DOI] [PubMed] [Google Scholar]
- Hamelberg D.; Mongan J.; McCammon J. A. (2004) Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 120, 11919–11929. [DOI] [PubMed] [Google Scholar]
- Darve E.; Pohorille A. (2001) Calculating free energies using average force. J. Chem. Phys. 115, 9169–9183. [Google Scholar]
- Henin J.; Fiorin G.; Chipot C.; Klein M. L. (2010) Exploring Multidimensional Free Energy Landscapes Using Time-Dependent Biases on Collective Variables. J. Chem. Theory Comput. 6, 35–47. [DOI] [PubMed] [Google Scholar]
- Gilson M. K.; Given J. A.; Bush B. L.; McCammon J. A. (1997) The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys. J. 72, 1047–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiocho F. A.; Spurlino J. C.; Rodseth L. E. (1997) Extensive features of tight oligosaccharide binding revealed in high-resolution structures of the maltodextrin transport chemosensory receptor. Structure 5, 997–1015. [DOI] [PubMed] [Google Scholar]
- Sharff A. J.; Rodseth L. E.; Spurlino J. C.; Quiocho F. A. (1992) Crystallographic Evidence of a Large Ligand-Induced Hinge-Twist Motion between the 2 Domains of the Maltodextrin Binding-Protein Involved in Active-Transport and Chemotaxis. Biochemistry 31, 10657–10663. [DOI] [PubMed] [Google Scholar]
- Case D. A.; Cheatham T. E.; Darden T.; Gohlke H.; Luo R.; Merz K. M.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. (2005) The Amber biomolecular simulation programs. J. Comput. Chem. 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan Y.; Wu C.; Chowdhury S.; Lee M. C.; Xiong G. M.; Zhang W.; Yang R.; Cieplak P.; Luo R.; Lee T.; Caldwell J.; Wang J. M.; Kollman P. (2003) A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 24, 1999–2012. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. (1983) Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 79, 926–935. [Google Scholar]
- Kale L.; Skeel R.; Bhandarkar M.; Brunner R.; Gursoy A.; Krawetz N.; Phillips J.; Shinozaki A.; Varadarajan K.; Schulten K. (1999) NAMD2: Greater scalability for parallel molecular dynamics. J. Comput. Phys. 151, 283–312. [Google Scholar]
- Wang Y.; Harrison C. B.; Schulten K.; McCammon J. A. (2011) Implementation of Accelerated Molecular Dynamics in NAMD. Comput. Sci. Discovery 4, pii: 015002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciccotti G.; Ryckaert J. P. (1986) Molecular-Dynamics Simulation of Rigid Molecules. Comput. Phys. Rep. 4, 345–392. [Google Scholar]
- Beutler T. C.; Mark A. E.; Vanschaik R. C.; Gerber P. R.; Van Gunsteren W. F. (1994) Avoiding Singularities and Numerical Instabilities in Free-Energy Calculations Based on Molecular Simulations. Chem. Phys. Lett. 222, 529–539. [Google Scholar]
- Zacharias M.; Straatsma T. P.; McCammon J. A. (1994) Separation-Shifted Scaling, a New Scaling Method for Lennard-Jones Interactions in Thermodynamic Integration. J. Chem. Phys. 100, 9025–9031. [Google Scholar]
- Baron R.; Lawrenz M.; McCammon J. A. (2009) Independent-Trajectories Thermodynamic-Integration Free-Energy Changes for Biomolecular Systems: Determinants of H5N1 Avian Influenza Virus Neuraminidase Inhibition by Peramivir. J. Chem. Theory Comput. 5, 1106–1116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szabo A.; Shoup D.; Northrup S. H.; McCammon J. A. (1982) Stochastically Gated Diffusion-Influenced Reactions. J. Chem. Phys. 77, 4484–4493. [Google Scholar]
- De la Torre J. G.; Huertas M. L.; Carrasco B. (2000) Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 78, 719–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swift R. V.; McCammon J. A. (2009) Substrate Induced Population Shifts and Stochastic Gating in the PBCV-1 mRNA Capping Enzyme. J. Am. Chem. Soc. 131, 5126–5133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berneche S.; Roux B. (2003) A microscopic view of ion conduction through the K+ channel. Proc. Natl. Acad. Sci. U.S.A. 100, 8644–8648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bicout D. J.; Szabo A. (1998) Electron transfer reaction dynamics in non-Debye solvents. J. Chem. Phys. 109, 2325–2338. [Google Scholar]
- McCammon J. A. (1998) Theory of biomolecular recognition. Curr. Opin. Struct. Biol. 8, 245–249. [DOI] [PubMed] [Google Scholar]
- Quiocho F. A. (1990) Atomic Structures of Periplasmic Binding-Proteins and the High-Affinity Active-Transport Systems in Bacteria. Philos. Trans. R. Soc. London, Ser. B 326, 341–352. [DOI] [PubMed] [Google Scholar]
- Duan X. Q.; Hall J. A.; Nikaido H.; Quiocho F. A. (2001) Crystal structures of the maltodextrin/maltose-binding protein complexed with reduced oligosaccharides: Flexibility of tertiary structure and ligand binding. J. Mol. Biol. 306, 1115–1126. [DOI] [PubMed] [Google Scholar]
- Miller D. M.; Olson J. S.; Pflugrath J. W.; Quiocho F. A. (1983) Rates of Ligand-Binding to Periplasmic Proteins Involved in Bacterial Transport and Chemotaxis. J. Biol. Chem. 258, 3665–3672. [PubMed] [Google Scholar]
- Millet O.; Hudson R. P.; Kay L. E. (2003) The energetic cost of domain reorientation in maltose-binding protein as studied by NMR and fluorescence spectroscopy. Proc. Natl. Acad. Sci. U.S.A. 100, 12700–12705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stockner T.; Vogel H. J.; Tieleman D. P. (2005) A salt-bridge motif involved in ligand binding and large-scale domain motions of the maltose-binding protein. Biophys. J. 89, 3362–3371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Telmer P. G.; Shilton B. H. (2003) Insights into the conformational equilibria of maltose-binding protein by analysis of high affinity mutants. J. Biol. Chem. 278, 34555–34567. [DOI] [PubMed] [Google Scholar]
- Piana S.; Bucher D.; Carloni P.; Rothlisberger U. (2004) Reaction mechanism of HIV-1 protease by hybrid carparrinello/classical MD simulations. J. Phys. Chem. B 108, 11139–11149. [Google Scholar]
- Bermejo G. A.; Strub M. P.; Ho C.; Tjandra N. (2010) Ligand-Free Open-Closed Transitions of Periplasmic Binding Proteins: The Case of Glutamine-Binding Protein. Biochemistry 49, 1893–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atilgan C.; Atilgan A. R. (2009) Perturbation-Response Scanning Reveals Ligand Entry-Exit Mechanisms of Ferric Binding Protein. PLoS Comput. Biol., 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flocco M. M.; Mowbray S. L. (1994) The 1.9 Angstrom X-Ray Structure of a Closed Unliganded Form of the Periplasmic Glucose/Galactose Receptor from Salmonella typhimurium. J. Biol. Chem. 269, 8931–8936. [PubMed] [Google Scholar]
- Oswald C.; Smits S. H. J.; Hoing M.; Sohn-Bosser L.; Dupont L.; Le Rudulier D.; Schmitt L.; Bremer E. (2008) Crystal Structures of the Choline/Acetylcholine Substrate-binding Protein ChoX from Sinorhizobium meliloti in the Liganded and Unliganded-Closed States. J. Biol. Chem. 283, 32848–32859. [DOI] [PubMed] [Google Scholar]
- Biggin P. C.; Pang A.; Arinaminpathy Y.; Sansom M. S. P. (2005) Comparative molecular dynamics: Similar folds and similar motions?. Proteins: Struct., Funct., Bioinf. 61, 809–822. [DOI] [PubMed] [Google Scholar]
- Silva D. A.; Bowman G. R.; Sosa-Peinado A.; Huang X. H. (2011) A Role for Both Conformational Selection and Induced Fit in Ligand Binding by the LAO Protein. PLoS Comput. Biol., 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma B.; Tsai C. J.; Haliloğlu T.; Nussinov R. (2011) Dynamic Allostery: Linkers Are Not Merely Flexible. Structure 19, 907–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agostino M.; Jene C.; Boyle T.; Ramsland P. A.; Yuriev E. (2009) Molecular Docking of Carbohydrate Ligands to Antibodies: Structural Validation against Crystal Structures. J. Chem. Inf. Model. 49, 2749–2760. [DOI] [PubMed] [Google Scholar]