Abstract
We determine upper and lower bounds for the number of maximum matchings (i.e., matchings of maximum cardinality) of a tree of given order. While the trees that attain the lower bound are easily characterised, the trees with the largest number of maximum matchings show a very subtle structure. We give a complete characterisation of these trees and derive that the number of maximum matchings in a tree of order is at most (the precise constant being an algebraic number of degree 14). As a corollary, we improve on a recent result by Górska and Skupień on the number of maximal matchings (maximal with respect to set inclusion).
Keywords: Maximum matchings, Trees, Bounds, Structural characterisation
1. Introduction and statement of main results
Many problems in graph theory can be described as follows: for a certain class of graphs and a graph parameter, determine the largest and smallest possible values of the parameter, given the order of a graph (and possibly other conditions). One family that is particularly well-studied in this regard is the family of trees, not only because of their simplicity, but also in view of their many applications in various areas of science.
On the other hand, lots of natural graph parameters are defined as the number of vertex or edge subsets of a certain kind; we mention, for example, the number of independent vertex subsets [15,18], the number of matchings [7], the number of dominating or efficient dominating sets [2,3] or the number of subtrees [13,21]. Some of them play an important role in applications as well, for instance the number of matchings that is known as Hosoya index in mathematical chemistry [9,12] and is also connected to the monomer–dimer model of statistical physics [10]. The same can be said of the number of independent sets, which is studied under the name Merrifield–Simmons index in chemistry [17] and which is related to Hard Models in physics [1]. For both these parameters, the minimum and the maximum among all trees of given order are well known and are obtained for the star and the path respectively. A tremendous number of publications deal with related problems, concerning restricted classes of trees or tree-like graphs; the interested reader is referred to [22] and the references therein.
It is natural to consider variants of these graph parameters: instead of the number of matchings, one might be interested in the number of maximal matchings (maximal with respect to inclusion) or maximum matchings (matchings of largest possible cardinality). The same holds, of course, for the number of independent sets.
The number of maximal independent sets is treated in [19,23]—the maximum turns out to occur for an extended star. More recently, maximal matchings were studied by Górska and Skupień [5], who determined exponential upper and lower bounds for the maximum number of maximal matchings among all trees of given order. To the best of our knowledge, however, there are no analogous results on the number of maximum matchings, i.e., matchings of largest possible cardinality. Clearly, any maximum (cardinality) matching is also maximal with respect to inclusion, but the converse is not true. In fact, graphs for which every maximal matching is also a maximum matching are known as equimatchable [16].
In the following, we denote the number of maximum matchings in a graph by . Our goal is to characterise the trees of given order for which the maximum and the minimum of this parameter are attained. This problem also has an algebraic interpretation: it is well known that the characteristic polynomial of a tree of order coincides with the matching polynomial [16]
where is the number of matchings of cardinality in . This is a special case of a general theorem on the coefficients of the characteristic polynomial; see for instance [4]. It follows that is precisely the (absolute value of the) last nonzero coefficient of and thus the product of the absolute values of all nonzero eigenvalues. In this sense, is a multiplicative analogue of the so-called energy of a graph [8,9], which is defined as the sum of the absolute values of all eigenvalues.
The lower bound for is almost trivial, and the trees that attain it can also be characterised easily:
Theorem 1.1
For any tree of even order , with equality if and only if has a perfect matching. For a tree of odd order , with equality if and only if is obtained from a tree of order with a perfect matching by doubling one of the leaves (i.e., choosing a leaf and attaching a second leaf to ’s unique neighbour).
We note that a path of even order is an example of a tree of even order admitting a perfect matching.
The analogous problem asking for the largest possible number of maximum matchings appears to be much harder. The bound provided by Górska and Skupień for the number of maximal matchings immediately provides an upper bound for the number of maximum matchings, so that we have (the constant being a root of the algebraic equation ) by the result stated in [5]. We improve this to the following:
Theorem 1.2
For , there is a unique tree of order that maximises . For and , there are two such trees. Asymptotically,
where is the larger root of the polynomial and the constants , , are given in Table 1.
Table 1.
Constants in the asymptotics of .
| j | ||
|---|---|---|
| 0 | ≈ 0.792620574273610 | |
| 1 | ≈ 0.787947762616490 | |
| 2 | ≈ 0.783080426542439 | |
| 3 | ≈ 0.788434032505851 | |
| 4 | ≈ 0.790280714748050 | |
| 5 | ≈ 0.785510324593434 | |
| 6 | ≈ 0.784269603628599 | |
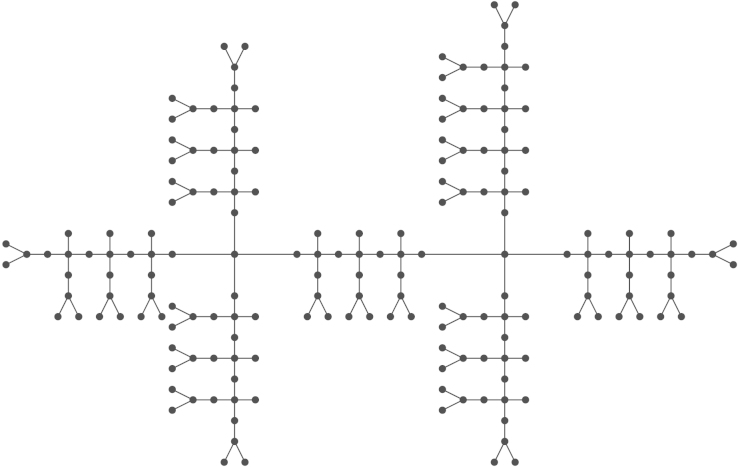
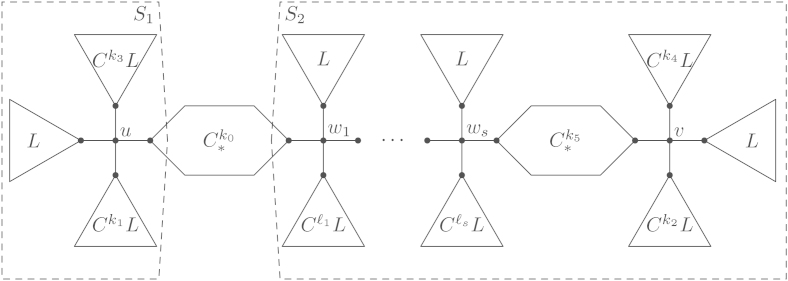
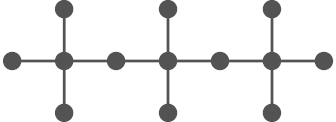
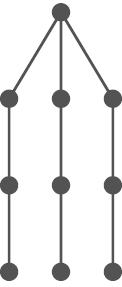
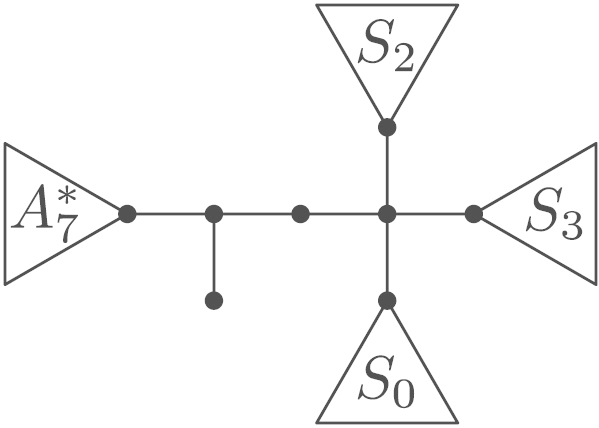
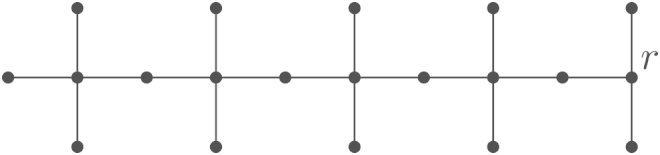
While the improvement in the constant (from 1.395337 to ) seems modest, the main part of the theorem is the characterisation of the trees , which will be stated explicitly in Section 3. Fig. 1 shows as an example. Since maximum matchings are automatically maximal matchings, the theorem also improves on the lower bound for the maximum number of maximal matchings that was given by Górska and Skupień in [5], which is (the precise constant being ).
Fig. 1.
Unique optimal tree of order 181.
The paper is organised as follows: in the following section, we deal with the simple lower bound (Theorem 1.1), the rest is devoted to the proof of Theorem 1.2. The structure of the “optimal” trees is described explicitly in Section 3, making use of the concept of an outline graph. Then, some important preliminary results (Section 4) and information about the local structure (Section 5) are gathered. The global structure is discussed in Section 6. The proof is rather long and technical—one of the reasons we consider this inevitable is the fact that seven different cases occur in the structure of the optimal trees, and that there is also a number of exceptions from the general pattern (note the case in Theorem 1.2: the precise characterisation of the structure is only valid for ). Another reason is that there are many trees that almost reach the upper bound, as can be seen from some of the estimates made on the way to our main result.
2. The lower bound
Let us start with the simple lower bound; as stated in Theorem 1.1, the minimum of is either 1 or 2, depending on the parity of the order.
Proof
In the case of even , the inequality is trivial, so that we only have to determine the cases of equality. If has a perfect matching, then this perfect matching can be reconstructed uniquely, starting from the leaves. Hence equality holds in this case. Otherwise, consider a tree of order and a maximum matching . Since it is not a perfect matching, there is a vertex that is not covered by the matching. Now choose an arbitrary neighbour of . Then must be covered by the matching , since one could otherwise add the edge to to obtain a larger matching, contradicting the choice of . Now replace the edge that covers by the edge to obtain a second matching of the same cardinality as , which shows that unless has a perfect matching.
Now let us determine which trees of odd order satisfy . Consider once again a maximum matching. Since the above argument can be carried out for any vertex that is not covered by , we can only have if there is exactly one vertex that is not covered. Furthermore, must be a leaf: otherwise, we could apply the exchange procedure for each of its neighbours to obtain at least 3 distinct maximum matchings. Let be ’s unique neighbour and assume that is covered by an edge in . Then must also be a leaf, since we could otherwise replace by and repeat the argument. This shows that equality can only hold in the described case. □
As we will see in the following sections, the analogous question for the maximum of is much harder and requires a completely different approach. Let us first give a precise description of the trees in Theorem 1.2.
3. The upper bound: description of the optimal trees
As mentioned in the introduction, we define to be the number of matchings of maximal cardinality of a tree . A tree is called an optimal tree if it maximises over all trees of the same order.
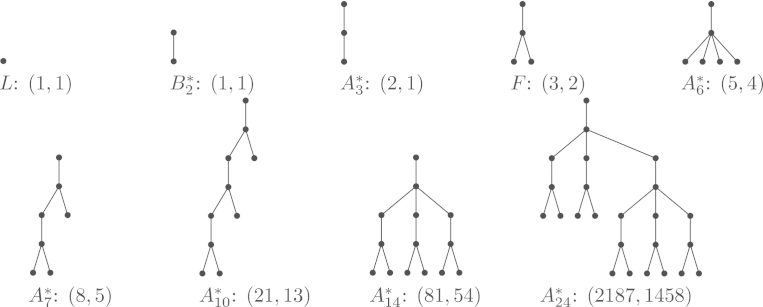
The results on the global structure are formulated in terms of leaves, forks, and chains.
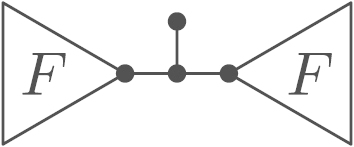
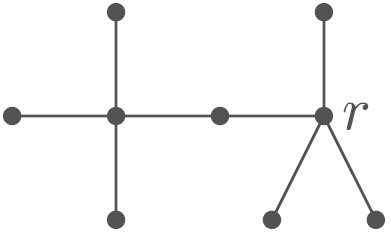
Definition 3.1
Fig. 2.
Fork and chain (Definition 3.1).
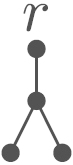
(a) .
(b) .
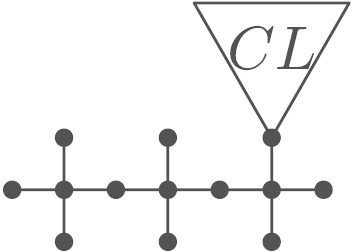
Using these definitions, we can see five copies of and one copy of as rooted subtrees of the optimal tree in Fig. 1.
Formulating as much as possible using the notations , and turns out to give compact representations for optimal trees. Let us formalise this concept:
Definition 3.2
Let be a tree. We construct the outline graph of as follows: first, all occurrences and as rooted subtrees of are replaced by special leaves “” and “”, respectively (where replacement takes place by decreasing order of the replaced rooted subtree). In a second step, we consider all occurrences of subtrees where has a unique branch . Every such subtree is replaced by the subtree , linked to the rest by a special edge “”.
As an example, the outline graph of the tree from Fig. 1 is shown in Fig. 3.
Fig. 3.
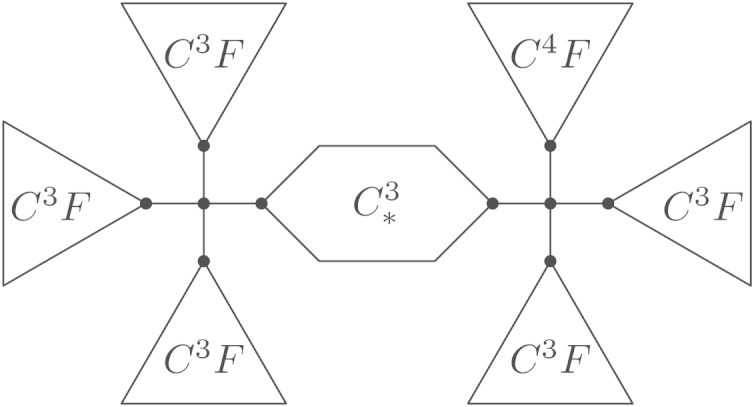
Outline of the unique optimal tree of order 181.
We are now able to state our main theorem fully describing optimal trees.
Theorem 3.3
Let and . Then there is a unique optimal tree of order .
- (1)
If , then .
- (2)
If , then is shown inFig. 4(a), wherefor .
- (3)
If , then is shown inFig. 4(b), wherefor .
- (4)
If , then .
- (5)
If , then is shown inFig. 4(c), wherefor .
- (6)
If , then is shown inFig. 4(d), wherefor .
- (7)
If , then is shown inFig. 4(e), where
If , there is also a unique optimal tree of order . For , there is only one tree of order . For , is shown in Fig. 5.
For , there are two non-isomorphic optimal trees and of order . For , (the star of order 6) and are shown in Fig. 5.
For , both and have the shape as in Fig. 4(d). We have for (this corresponds to the general case as described above) and for .
Fig. 4.
Optimal trees.
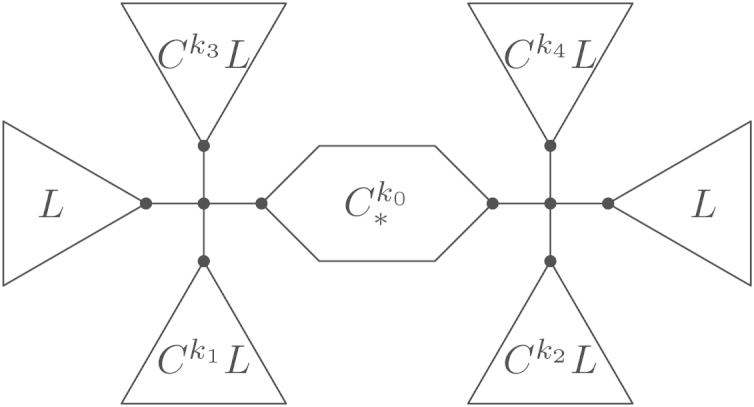
(a) for and .
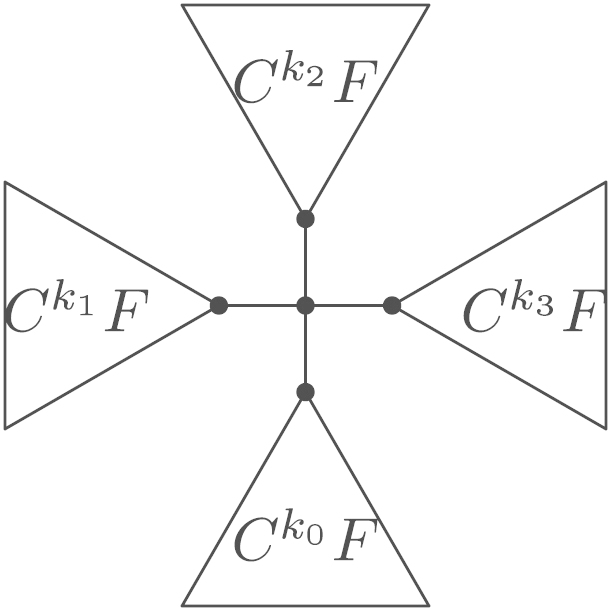
(b) for and .
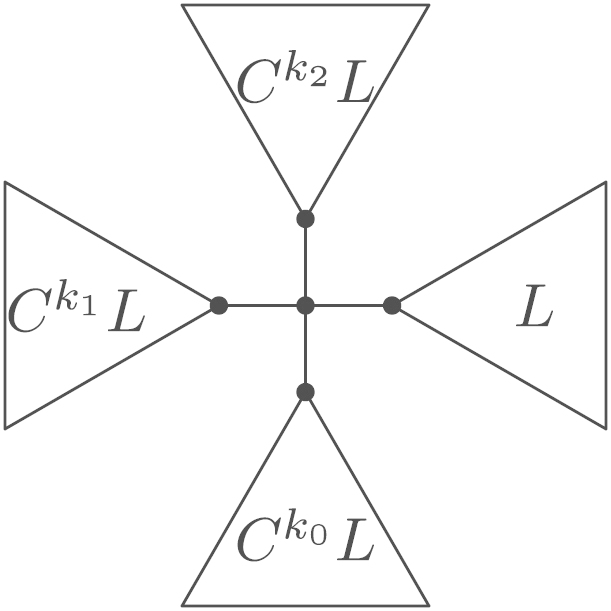
(c) for .
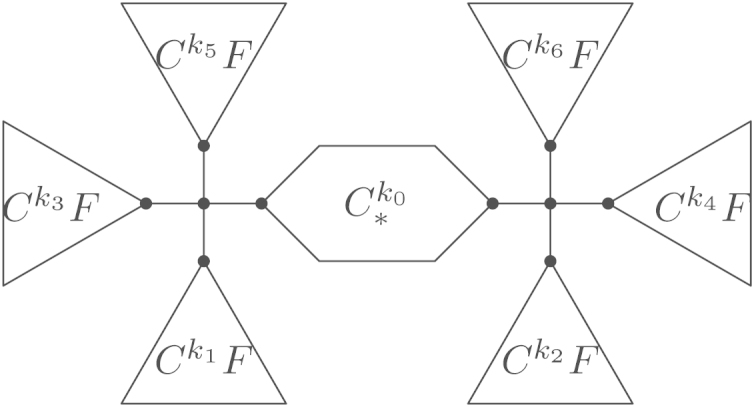
(d) for and , . For , and also have this shape.
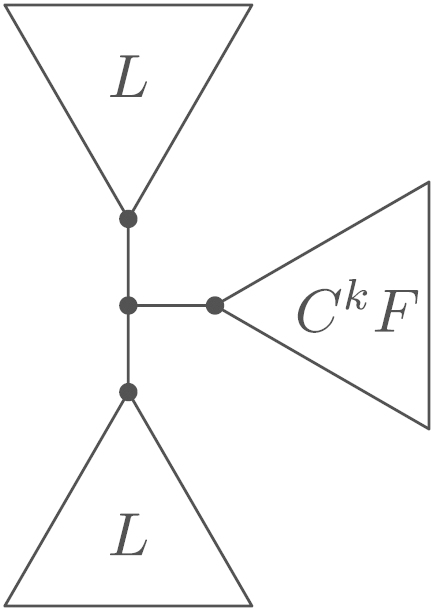
(e) for .
Fig. 5.
Optimal trees for .
(a) .
(b) .
(c) .
(d) .
(e) .
Remark 3.4
The quasi-periodicity of length 7 is somewhat reminiscent of the situation encountered for dominating sets [2,3], even though there are certain differences.
4. The upper bound: preliminaries
4.1. The bipartition condition
A tree may always be seen as a bipartite graph. In the case of an optimal tree, however, the bipartition of the vertices corresponds to a specific behaviour in terms of maximum matchings, as will be shown in this section. This will also allow us to somewhat decompose the problem.
We start with a few definitions.
Definition 4.1
Let be a forest. The matching number is the maximum cardinality of a matching of . Hence a matching of is a maximum matching if it has cardinality . Denoting the empty graph by , it is convenient to set and .
Definition 4.2
A forest is called an optimal forest if it maximises over all forests of the same order.
We now define the type of a vertex. These types will later be seen to correspond to the bipartition of the set of vertices of optimal trees.
Definition 4.3
Let be a forest. A vertex is said to be of type if admits a maximum matching that does not cover . Otherwise, is said to be of type .
A first step towards the main result on the bipartition holds for all trees: there are no edges between vertices of type :
Lemma 4.4
Let be a tree, of type , and a neighbour of in . Then is of type . Denoting the connected components of by and with and , cf. Fig. 6, we have
Fig. 6.

Decomposition of for Lemma 4.4 and Proposition 4.7.
Proof
We first note that
holds for any vertex of any tree , as any maximum matching of is a matching of and any maximum matching of minus possibly the edge covering is a matching of .
Any maximum matching of the tree either contains the edge or it does not contain the edge . In the first case, decomposes into a maximum matching of , a maximum matching of and the edge , which implies that . In the second case, decomposes into a maximum matching of and a maximum matching of , which implies that . We conclude that
(4.1) As is of type , there is a maximum matching of not covering , hence we have . In view of (4.1), this implies that , i.e., , and , i.e., .
In this case, we also have , i.e., is of type . Finally, counts the number of maximum matchings of not containing and counts the number of maximum matchings of containing , their sum is therefore . □
We now show that in almost all cases, optimal forests are trees, so we may restrict our attention to trees afterwards. Nevertheless, at one point, we will also use this result as a technical tool when considering trees.
Lemma 4.5
Let be an optimal forest of order at least 3. Then is connected, i.e., is a tree.
Proof
Let and be connected components of . For simplicity, we may assume that these are the only connected components of ; otherwise, we use the following argument inductively.
As is optimal, each of its connected components has to be optimal.
If both and are of order 1, then they both only admit the empty matching, inserting an edge between these two vertices does not alter the number of maximum cardinality matchings.
Next, we note that for , the star on vertices satisfies . Thus an optimal forest of order at least 3 does not admit a perfect matching, as perfect matchings of trees are unique (see Theorem 1.1). This implies that an optimal forest of order at least 3 has a vertex of type . As the unique vertex of a tree of order 1 is also of type , we conclude that all optimal trees except the tree of order 2 have a vertex of type .
As any neighbour of any vertex of type is of type by Lemma 4.4 and the vertices of the tree of order 2 also are of type , we conclude that every optimal tree of order at least 2 has a vertex of type .
If and are both of order 2, then there is no vertex of type , thus is not optimal.
So we may now assume that is of type and is of type . If we insert the edge , we obtain a new graph . As in Lemma 4.4, we obtain
As is of type (with respect to ) and is of type (with respect to ), we have and . This implies that , i.e., is of type with respect to and Lemma 4.4 can be applied to yield
contradiction.
Thus the only disconnected optimal forest is the forest consisting of exactly two isolated vertices. □
We can now formalise what we will call the bipartition condition.
Definition 4.6
Let be a tree. We say that fulfils the bipartition condition if the two classes in ’s unique bipartition contain precisely the vertices of type and respectively.
It turns out that indeed almost all optimal trees satisfy this condition.
Proposition 4.7
Let be an optimal tree of order at least 3. Then fulfils the bipartition condition.
Let be an edge of where is of type and is of type . The connected components of are denoted by and with and . Then and are of types and with respect to the trees and , respectively. Furthermore,
(4.2)
Proof
Assume that and are two adjacent vertices of type .
If we have , then (w.l.o.g.) and . In this case, we obtain , i.e., is of type . Contradiction.
Next, we consider the case that , i.e., the case that is not contained in any maximum matching of . Deleting the edge resulting in a forest does not alter the number of maximum matchings, i.e., . By Lemma 4.5, and therefore are not optimal, contradiction.
Finally, we consider the case , i.e., the case that is contained in every maximum matching of . Deleting all edges incident to or leads to a disconnected forest of the same order and the same number of maximum matchings. Contradiction.
Thus exactly one of and , say , is of type by Lemma 4.4 and the remaining assertions of this proposition are restatements of the results of Lemma 4.4. □
4.2. Rooted trees
For many of our arguments, we will designate a vertex of a tree as the root and recursively consider subtrees. To this end, we collect a few definitions as well as some recursive formulæ for the number of maximum matchings.
We assume that all rooted trees are non-empty. A rooted tree with underlying tree and root will be denoted by the pair ; frequently, we will simply write if the root is clear from the context. An important operation that we will frequently apply is to choose another vertex as the new root. We will usually denote the resulting rooted tree by a new symbol (and thus abbreviated to ) although the underlying unrooted trees and are identical.
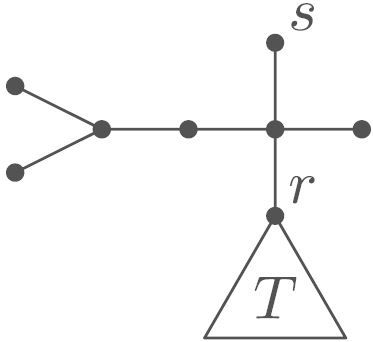
As usual, the branches of a rooted tree of the shape as Fig. 7 are the rooted trees .
Fig. 7.
Rooted tree with branches.
A rooted subtree of an unrooted tree is a connected component of for some edge of such that . Note that this definition forces to be a proper subtree of .
A rooted subtree of a rooted tree is the connected component of containing , where has to be the parent of , i.e., is the subgraph induced by all the successors of . We will also write in this case.
Let be a tree and be a vertex of with neighbours . The connected components of are denoted by such that for all . Then the rooted trees are said to be the rooted connected components of (and usually, the roots will not be mentioned).
Definition 4.8
Let be a rooted tree.
- (1)
We define to be the number of maximum matchings of covering the root .
- (2)
We define to be , the number of maximum matchings of .
- (3)
The type of is defined to be the type of the root as a vertex of the unrooted tree, i.e., is of type if and of type if . We sometimes write and , respectively.
Thus is of type if and only if it admits a maximum matching not covering the root .
We have
| (4.3) |
for the rooted tree of order 1, which implies that it is a rooted tree of type .
Definition 4.9
We define the bipartition condition for rooted trees recursively as follows: a rooted tree of order 1 (rooted at its only vertex) is said to satisfy the bipartition condition. If is a rooted tree with branches , then the rooted tree is said to fulfil the bipartition condition if all branches fulfil the bipartition condition and the type of is not equal to the type of any of the branches .
Remark 4.10
Let be an optimal tree of order at least 3 and be a rooted subtree of . Then the type of as vertex of coincides with the type of and fulfils the bipartition condition for rooted trees by Proposition 4.7.
The main goal behind the definition of the two different types is to provide a recursive method to compute . Note first that for a rooted tree , we have
We now give recursive formulæ for these quantities in terms of the branches of a rooted tree. Here, for technical reasons, we do not assume the bipartition condition for rooted trees, but a weaker version only, and derive the bipartition condition for rooted trees.
Lemma 4.11
Let be a rooted tree and its branches. We assume that are of the same type. Then is of the other type and we have
(4.4)
(4.5)
Proof
If is of order 1, then there are no branches, and the product in (4.4) and the sum in (4.5) are empty, which coincides with the values for given in (4.3). Thus we may focus on the case that the order of is at least 2.
As consists of the connected components , we clearly have and (4.4). Furthermore,
as a maximum matching either does not cover or contains the edge for some .
If all branches are of type , i.e., for all , then for all . This implies that , is of type and each of the edges can be used in a maximum matching.
If all branches are of type , i.e., for all , then for all . This implies that , is of type and again, each of the edges can be used in a maximum matching.
There are maximum matchings of containing the edge . Summing over all yields (4.5). □
If are rooted trees of type , then the rooted tree with branches is also denoted by . It is of type by Lemma 4.11.
Similarly, if are rooted trees of type , then the rooted tree with branches is also denoted by . It is of type by Lemma 4.11. If , we will omit the parentheses and simply write .
The crucial quantity in our investigation will be the following quotient:
Definition 4.12
For a rooted tree , we set .
We note that by definition, for all rooted trees .
We now reformulate the recursive formulæ for and to yield recursive formulæ for .
Lemma 4.13
Let be a rooted tree fulfilling the bipartition condition with branches . Then
Proof
This is a simple consequence of (4.4) and (4.5). □
4.3. -optimality
It turns out that a rooted subtree of an optimal tree no longer needs to be optimal. Instead, we introduce the auxiliary notion of -optimality.
Definition 4.14
Let be a non-negative real number. A rooted tree is said to be -optimal if it fulfils the bipartition condition and if
(4.6)
Note that 0-optimality is just ordinary optimality. This definition is motivated by the fact that any rooted subtree of an optimal tree is indeed -optimal for an appropriate value of :
Proposition 4.15
Let be an optimal tree, an edge of and and the connected components of , with and . Then is a -optimal tree and is a -optimal tree.
Proof
If the order of is , the statement holds trivially.
Reformulating (4.2) in terms of the function shows that
If was not -optimal, we could replace it by a -optimal tree and this would increase , contradiction. The same argument applies to . □
We note the fact that holds for all rooted trees of type by Lemma 4.13, where equality holds if and only if . Thus, by Proposition 4.15, we may restrict ourselves to the investigation of -optimal trees of type with as well as -optimal trees of type with .
A few rooted trees will be considered repeatedly in our proofs. These are shown in Fig. 8. One could indeed show that these trees are -optimal for some , but we do not need this information. On the other hand, we will later need to know that some rooted trees are not -optimal for some ranges of . We list these trees (together with a replacement ) in Table 3 in the Appendix. Similarly, we list a few non-optimal trees in Table 2, where is given in Theorem 3.3. We will simply refer to the entries of these two tables by (R1)–(R11). These tables can be verified using a Sage [20] program available in [11].
Fig. 8.
Some important rooted trees. All trees are given with the pair .
Table 3.
Replacements for rooted subtrees: , and hold for the given range of . Here, the additional abbreviation and for have been used, where, as usual, and .
| (R4) | 4 | 1 | 2 | 3 | 1 | |||
| 5 | 3 | 2 | 4 | 1 | ||||
| 7 | 4 | 4 | 7 | 4 | ||||
| 10 | 12 | 8 | 21 | 9 | ||||
| (R5) | 34 | 59049 | 39366 | 58999 | 41839 | |||
| 34 | 59049 | 39366 | 58999 | 41839 | ||||
| 44 | 1594323 | 1062882 | 1618650 | 1139139 | ||||
| 54 | 43046721 | 28697814 | 44259488 | 31126973 | ||||
| 44 | 1594323 | 1062882 | 1618650 | 1139139 | ||||
| 54 | 43046721 | 28697814 | 44259488 | 31126973 | ||||
| 64 | 1162261467 | 774840978 | 1209774005 | 850782533 | ||||
| 74 | 31381059609 | 20920706406 | 33062296902 | 23251305273 | ||||
| (R6) | 12 | 34 | 21 | 41 | 15 | |||
| (R7) | 16 | 135 | 81 | 153 | 56 | |||
| 26 | 3645 | 2187 | 4235 | 1551 | ||||
| (R8) | 25 | 2512 | 1344 | 2684 | 1551 | |||
| 28 | 6573 | 3528 | 7759 | 3696 | ||||
| 31 | 17199 | 9261 | 20967 | 9999 | ||||
| (R9) | 16 | 141 | 72 | 153 | 56 | |||
| 19 | 368 | 192 | 418 | 153 | ||||
| 22 | 960 | 512 | 989 | 571 | ||||
| (R10) | 9 | 15 | 4 | 13 | 8 | |||
| 20 | 571 | 209 | 567 | 243 | ||||
| (R11) | 27 | 5751 | 2430 | 5742 | 2457 | |||
| 37 | 155277 | 65610 | 155007 | 66420 |
Table 2.
Replacements for trees: and hold.
| (R1) | 10 | 19 | 21 | |
| 11 | 24 | 30 | ||
| (R2) | 17 | 213 | 216 | |
| (R3) | 17 | 209 | 216 |
4.4. Exchanging subtrees
In order to derive information on the structure of optimal trees, we will compare optimal trees with trees where some rooted subtrees have been exchanged. In order to estimate the effect of such exchange operations, we need an extension of our recursive formulæ (4.4) and (4.5) to finer decompositions of a tree. These extensions will be formulated in terms of continuants and continued fractions.
We therefore fix some notations and definitions in the context of continuants and continued fractions. We follow Graham, Knuth and Patashnik [6], Section 6.7.
Definition 4.16 [6, (6.127)] —
The continuant polynomial has parameters, and it is defined by the following recurrence:
(4.7) for and , .
We will omit the index in whenever it is clear from the context.
We need the following additional properties of continuants:
Lemma 4.17
We have
(4.8)
(4.9)
Proof
The symmetry relation (4.8) is [6, (6.131)], the recursion (4.9) is a consequence of the symmetry relation (4.8) and the defining recursion (4.7), cf. [6, (6.132)]. □
The following lemma shows how continuants can be used to determine . We use the Iversonian notation if is true and otherwise, cf. Knuth [14].
Lemma 4.18
Let be a tree fulfilling the bipartition condition of the shape given in Fig. 9for some , integers for , and rooted trees , , .
Then
where
Fig. 9.

Shape of for the exchange lemma.
Proof
We set
and consider as root of . We claim that
holds for . This can be shown by reverse induction on using only the recursive formulæ (4.4), (4.5) and (4.9). □
We now turn to continued fractions.
Definition 4.19
We set
As usual, for a sequence , the infinite continued fraction is defined as the limit .
The connection between continuants and continued fractions is stated in the following result.
Lemma 4.20 [6, (6.136)] —
We have
We are now able to formulate our main exchange lemma. It comes in several flavours: first, the most general version is stated, which might be cumbersome to use. Next, in a mostly symmetric case, we get a neat formulation, which will be frequently used. Finally, we give two estimates for the asymmetric case, which are not best possible, but sufficient for our purposes. For these estimates, we make some assumptions on the occurring values of which will be fulfilled in the applications later on.
Lemma 4.21
Let be an optimal tree of the shape given in Fig. 9 for some even , integers for , and rooted trees , , . We set
Let and and set
so that and . Assume that , and , .
- (1)
If , then
(4.10) - (2)
If and , then .
- (3)
If , for odd and for all even with and for fixed , thenwhere
In particular, we have
- (4)
If , for even with and for all odd and for fixed , thenwhere
In particular, we have
Proof
- (1)
Set and let be the tree arising from by exchanging against . As is even and and , the types of all are the same in and . As is an optimal tree, we haveby Lemma 4.18, (4.7), (4.9), (4.8), Lemma 4.20 and the obvious recursion formula for continued fractions. The result follows upon division by the positive quantity .
- (2)
The symmetry implies that and the result follows from (4.10).
- (3)
If , then the assertion follows from Lemma 4.21(2). So we may assume . By (4.10) we haveas decreasing the entries at even-numbered indices of a continued fraction decreases the continued fraction, and increasing entries at odd-numbered indices also decreases the continued fraction.
- (4)
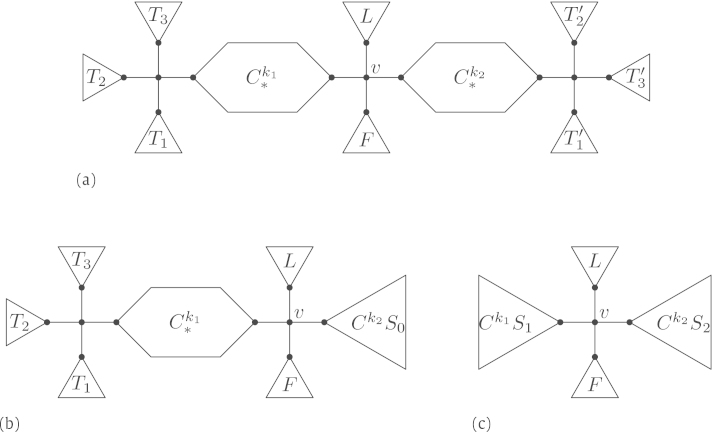
This exchange lemma will be used repeatedly in the following to deduce information about the structure of optimal trees. To simplify explanations, we will call the vertices and in Fig. 9 pivotal vertices.
5. The upper bound: local structure
We have now gathered enough auxiliary tools to start with the proof of Theorem 3.3 and thus Theorem 1.2. To abbreviate some statements, we introduce the following definitions.
Definition 5.1
Let be a tree. We say that it fulfils the local conditions (LC), if all of the following conditions are fulfilled:
- (LC1)
fulfils the bipartition condition,
- (LC2)
each vertex of type has degree 1 or 2,
- (LC3)
each vertex of type has degree at least 3,
- (LC4)
each vertex of degree 3 is adjacent to at least two leaves,
- (LC5)
each vertex has degree at most 4,
- (LC6)
no vertex is adjacent to 3 leaves.
By Proposition 4.7, an optimal tree of order fulfils LC1.
The following theorem will be shown step by step in Sections 5.1–5.3:
Theorem 5.2
Let and be an optimal tree with .
Then fulfils the local conditions LC1–LC6.
We note that it is debatable whether LC6 shall be considered to be part of the local structure as , , , fulfil LC1–LC5 and are contained in the generic cases described in Theorem 3.3. So these trees may simply be seen as degenerated cases of the generic cases even though LC6 is violated. On the other hand, and fulfil LC1–LC5, but not LC6, and these two trees are not contained in one of the generic families of Theorem 3.3. Since the overall proof is simpler when excluding the trees in at this stage, this is the route we proceed on.
5.1. Vertices of type and estimates for vertices of type
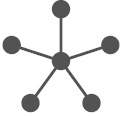
We first aim to show that almost all optimal trees fulfil LC2 and LC3. As a first step, we will show that almost all rooted subtrees of optimal trees contain a -claw for , i.e., a rooted subtree with branches all of which are single vertices, see Fig. 13(a). In a second step, the existence of -claws will provide us with bounds for for rooted subtrees of optimal trees. These bounds will be quite weak, but sufficient for using our general exchange lemma (Lemma 4.21) to give a useful technical result on decompositions of optimal trees along a path. This almost immediately yields LC2. We then characterise all optimal trees containing a or a 4-claw as a rooted subtree (there are only very few), such that from the end of this subsection, we can work exclusively with 2- and 3-claws.
Fig. 13.
-claw and tree for the proof of Lemma 5.4.
(a) -claw.
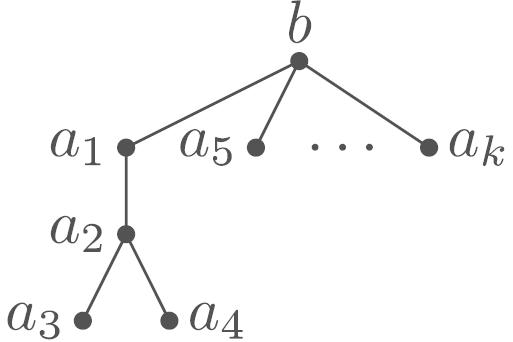
(b) .
Lemma 5.3
Let be a rooted subtree of an optimal tree . Then is isomorphic to , , or it contains a -claw for some , i.e., a rooted subtree as in Fig. 13(a).
Proof
If , then and there is nothing to show. We assume that and that does not contain a -claw for any .
Let be a leaf of of maximum height. Then is of type . If its parent (which is of type ) has other branches, they have to be leaves by the choice of and we found a -claw for , contradiction. Thus has only one branch, .
The parent of is called . It has to be of type . So all branches of are of type , thus they cannot be leaves. By construction, all branches of are isomorphic to , cf. Fig. 10(a).
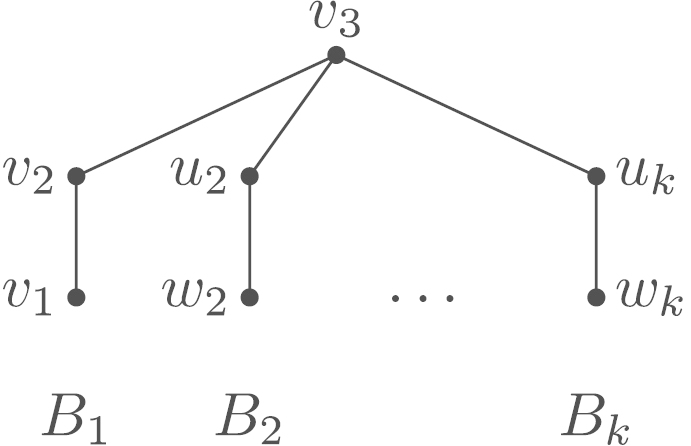
Denote the branches of the rooted tree by and assume that . Then we have and . Thus and . If we remove and add the two vertices as children of , cf. Fig. 10(b), the resulting branch has and . The modified tree has and , contradiction to Proposition 4.15. Thus has only one child.
If , then and there is nothing to show. Otherwise, the parent of is called . Then has the shape shown in Fig. 11 for some and rooted trees of type .
Each of the , is either a leaf (with ) or an with . As , Lemma 4.21(2) (with and as pivotal vertices) yields , i.e., either or and both and are isomorphic to . Thus is one of the trees in Fig. 12. The trees , , are not -optimal for any , cf. (R4), contradiction to Proposition 4.15. The tree is not -optimal for , cf. (R4), so we must have and therefore . Thus we must have , which has been excluded. □
Knowing now that almost every rooted subtree of an optimal tree contains a -claw with , we show that no -claws with occur.
Fig. 10.
Shape of and in the proof of Lemma 5.3.
(a) .
(b) .
Fig. 11.
Shape of in the proof of Lemma 5.3.
Fig. 12.
in the proof of Lemma 5.3.
(a) .

(b) .

(c) .
(d) .
Lemma 5.4
For , a -claw does not occur as rooted subtree of an optimal tree.
Proof
Let be a -claw, cf. Fig. 13(a), and be the rooted tree in Fig. 13(b) of the same order and type.
We have
For , we have and , thus cannot be -optimal for any , so it is not a subtree of an optimal tree by Proposition 4.15. □
We are now able to prove lower bounds for for rooted subtrees of optimal trees. The key idea is the following: changing the root of to another root can only alter , but remains unchanged. Changing the root of cannot increase , since this would increase , contradiction to the -optimality of . The new roots used for comparison will be leaves or roots of -claws.
We start with lower bounds for rooted subtrees of type .
Lemma 5.5
Let be a rooted subtree of type of an optimal tree . Then with equality if and only if .
Proof
Let consist of the rooted subtrees and of types and , respectively, and of the edge .
For , we have and there is nothing to show, so we assume .
By Lemmata 5.3 and 5.4, contains an -claw for some . We switch the root of to a leaf of the -claw, obtaining a new rooted tree shown in Fig. 14. The rooted tree arises from the rooted connected component of by removing the rooted subtree of type . Removing a rooted subtree of type from a rooted tree of type fulfilling the bipartition condition for rooted trees yields a rooted tree of type , so is of type .
The -optimality of together with implies that
□
Fig. 14.
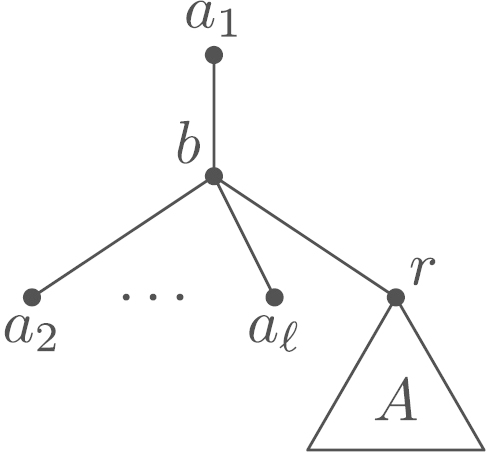
Tree in the proof of Lemma 5.5.
We are now able to prove a lower bound for for rooted subtrees of type .
Lemma 5.6
Let be a rooted subtree of type of an optimal tree with . If contains a -claw for some , then .
Proof
By Proposition 4.7, and fulfil the bipartition condition and the bipartition condition for rooted trees, respectively.
If has only one branch, say , then is of type by the bipartition condition for rooted trees and . Thus , as required. So we assume that has more than one branch.
If is the -claw, then .
Let consist of the rooted subtrees and of types and , respectively, and of the edge .
We change the root of to the root of the -claw, which results in a rooted tree with shown in Fig. 15. Here arises from a rooted subtree of of type by removing the rooted subtree . Since it was assumed that has more than one branch, we conclude that is still of type by Lemma 4.11 and that . As is -optimal by Proposition 4.15, this yields
□
Fig. 15.
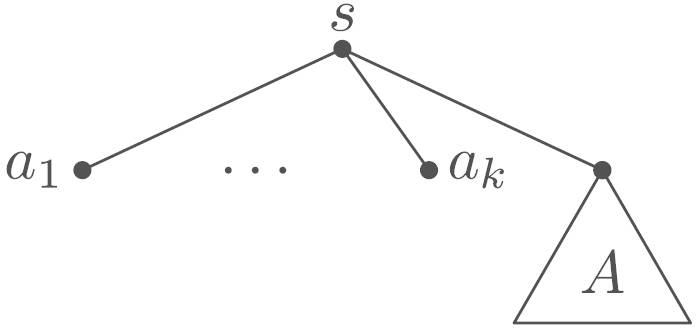
Tree in the proof of Lemma 5.6.
Next, we give a preliminary upper bound for for rooted subtrees of type :
Lemma 5.7
Let be a rooted subtree of type of an optimal tree . Then or .
Proof
Assume that . Let for suitable branches for some . By Lemmata 5.6, 5.3 and 5.4, we have , which implies
□
We have now collected the necessary (weak) bounds for for rooted subtrees of optimal trees. These suffice for the following path decomposition lemma, using the exchange lemma (Lemma 4.21) to derive bounds for along a path (as in Fig. 9) when the two ends of the path are roots of claws.
Lemma 5.8
Let be an optimal tree of the shape as in Fig. 9 for some even with , , i.e., and are the roots of an -claw and an -claw, respectively. We assume that and and set
Then is of type and for odd and for even with . In particular, we have .
Proof
By the bipartition condition and the fact that and are the roots of an -claw and an -claw, respectively, we conclude that is of type for odd and of type for even . We define the rooted trees and as two rooted versions of , so that the notations and are defined.
We prove the lemma by induction on , where we first only prove that
(5.1) i.e., we relax the upper bound for in the case of even .
We first consider the case of odd , i.e., is of type . If , we conclude that from Lemma 4.21(4) (with and as pivotal vertices). By Lemma 5.6, we have . As for , this is a contradiction. So and therefore .
Next, we consider the case of even , i.e., is of type . If , then Lemma 4.21(3) (now with and as pivotal vertices) yields , a contradiction to Lemma 5.5. Thus we have .
For the lower bound on , we assume that . Then Lemma 4.21(3) implies . As by Lemma 5.7, this is a contradiction. This concludes the proof of (5.1).
Finally, is again a consequence of Lemma 4.21(3), as .
If , then . If , then Lemma 4.21(2) and imply that , as required. □
Combining the description of rooted subtrees without any -claw with with the path decomposition lemma (Lemma 5.8) shows that is forbidden in almost all optimal trees.
Lemma 5.9
Suppose that is a rooted subtree of an optimal tree . Then .
Proof
Assume first that does not contain an -claw for any . As contains a as a rooted subtree, we have . Consider a leaf of . Then by Proposition 4.7, the rooted subtree of is of type and therefore equals by Lemma 5.3. We conclude that .
So we may now assume that contains an -claw with . Thus can be decomposed as in Lemma 5.8 with and for some . By Lemma 5.8, we have , so . If , then we have .
So we may assume that . By Lemma 5.8 again, we have , which by Lemmata 5.5 and 5.7 implies that with or with . Thus is a rooted subtree of of type and order at least 5 containing no -claw for any , contradiction to Lemma 5.3. □
Remark 5.10
Having excluded , we can also exclude the presence of as a rooted subtree in the following, which will be important in many arguments.
As a direct consequence of the path decomposition lemma (together with the information that it can always be applied as has now been excluded), we have shown LC2.
Proposition 5.11
Let be an optimal tree. Then fulfils LC1–LC2.
Proof
Let be a vertex of type in of degree at least 2. Then may be represented as in Lemma 5.8 with for some odd : choose a longest path that contains . The ends of this path are leaves, their unique neighbours are the pivotal vertices and . All but one of the neighbours of have to be leaves by the choice of the path, and there has to be more than one such neighbour in view of Lemma 5.9. The same applies to . Hence by Lemma 5.8, i.e., . □
We conclude this subsection by excluding 4-claws in almost all cases. To do so, we will use a direct substitution for those cases which are allowed by the path decomposition lemma.
Lemma 5.12
Let be an optimal tree containing a 4-claw as a rooted subtree. Then .
Proof
We denote the root of the 4-claw by . The neighbour of which is not contained in the 4-claw is denoted by . By Proposition 5.11, fulfils LC1–LC2. As is of type , is of type and . If is a leaf, then and we are done. So we assume the contrary and denote the neighbour of different from by . Then is of the shape shown in Fig. 16(a), where denote some trees of type with . If , then by Lemmata 5.4 and 5.8. Both cases do not lead to an optimal tree, cf. (R1).
So we may assume that , whence Lemma 4.21(2), with and as pivotal vertices, yields . Thus we have and or .
We consider the tree shown in Fig. 16(b) of the same order as . Using the abbreviations , and as well as the optimality of , Lemma 4.18 yields
which implies
As and (for as well as for and ) by Lemma 5.5, this is a contradiction. □
Fig. 16.
Trees considered in Lemma 5.12.
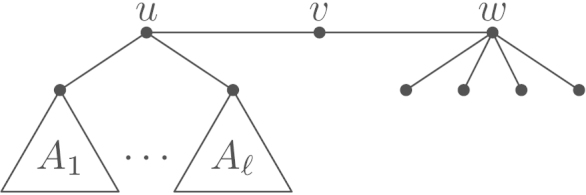
(a) .
(b) .
5.2. Lower degree bounds for vertices of type
We now want to show that almost all optimal trees fulfil LC1–LC4. In order to facilitate the discussion, we introduce the notion of a “light” vertex.
Definition 5.13
Let be a tree fulfilling the bipartition condition and a vertex of type in . Then is said to be a light vertex if it has degree and is adjacent to at most one leaf.
The sum of the -values of the rooted connected components of is quite small for a light vertex . The exchange lemma then forbids vertices whose rooted connected components have a high sum of -values.
The path decomposition lemma can be used to derive a description of light vertices:
Lemma 5.14
If is an optimal tree, then fulfils LC1–LC3. If is a light vertex of , then and is adjacent to exactly one leaf.
Proof
If has no light vertex, then fulfils LC1–LC4. So we assume that is a light vertex. Denote the rooted connected components of by with . As is a light vertex, we have . If , i.e., , we have and , which have been excluded. If , then is the root of a -claw. As is light, we have , contradiction to Lemma 5.9.
So both and contain an -claw and an -claw, respectively, for some , by Lemmata 5.3 and 5.9. By Lemma 5.8, we obtain . As by assumption, we have , thus is a leaf, as required. □
We now describe vertices of type when a light vertex is present.
Lemma 5.15
Let be an optimal tree, be a light vertex and be a vertex of type of . Then either and is not adjacent to any leaf or and is adjacent to one or two leaves.
Proof
If is light, then there is nothing to show by Lemma 5.14. Otherwise, either or and is adjacent to two leaves, as required. So we now assume that .
Denote the rooted connected components of by with and . The rooted connected component of which does not contain and is not a leaf is denoted by . By Lemma 5.5, we have (since has been excluded). Now we make use of a combination of Lemma 5.8 and Lemma 4.21(3)—the following argument will be used several times, so we only explain it in detail here: the path between and can be extended to a longest path ending in an - and an -claw, with , by Lemmata 5.9, 5.4 and 5.12. Application of Lemma 5.8 now shows that the vertices on the path between and satisfy the necessary conditions to make Lemma 4.21(3) applicable (with and as pivotal vertices), which yields
(5.2) From Lemmata 5.5 and 5.7, we obtain
which yields and . Furthermore, (5.2) together with Lemma 5.7 yields , i.e., , so is not adjacent to any leaf. □
Light vertices correspond to low values of for rooted subtrees of type . This correspondence is described in the following two lemmata.
Lemma 5.16
Let be an optimal tree and be a rooted subtree of of type that contains no light vertex of . Then
with equality for .
Proof
We prove the result by induction on the order of . If has order 1, then .
Otherwise, for suitable rooted trees of type by Proposition 5.11. As does not contain any light vertex, we have with or .
We now turn to the case . We have by the induction hypothesis and therefore
Equality holds for and . By the induction hypothesis, we conclude that , , . We have and . Next, the two trees and are not -optimal for , cf. (R5), whence they do not occur as rooted subtrees of optimal trees by Proposition 4.15 and Lemma 5.6. A further six cases have to be checked, but none of these is an -optimal tree for any , cf. again (R5). □
Lemma 5.17
Let be an optimal tree containing a light vertex and be a rooted subtree of of type . Then is a leaf or
where equality holds if and only if does not contain a light vertex.
Proof
We prove the assertion by induction on the order of . For , we have for suitable rooted trees . By Lemma 5.15, we have .
If , then where equality holds if and only if both and are leaves, i.e., does not contain a light vertex.
If , then none of , , is a leaf by Lemma 5.15, so the induction hypothesis yields with equality if and only if none of , , contains a light vertex. In both cases, we get
□
We are now ready to prove local condition LC4.
Proposition 5.18
Let be an optimal tree containing a light vertex. Then . In other words, all optimal trees except fulfil LC1–LC4.
Proof
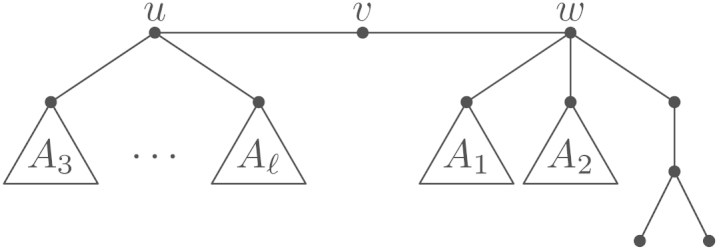
We assume that . As the tree in Fig. 17 with root is not -optimal for , cf. (R6), and any vertex of degree 3 is adjacent to at least one leaf by Lemma 5.14,
(5.3) By (R7), Lemma 5.17, Proposition 4.15 and the fact that contains a light vertex, we see that
(5.4) Let now be a rooted subtree of type of containing a vertex of degree 4 and a light vertex. We choose in such a way that its order is minimal among all rooted subtrees with these properties. We write for some (by Lemma 5.15).
We first consider the case . By Lemma 5.15, we have . As contains a vertex of degree 4, so does . By minimality of , does not contain a light vertex. By Lemmata 5.16 and 5.17, we have and therefore , contradiction to (5.4).
Thus we are left with the case . By the minimality of , each of the either contains a light vertex and does not contain a vertex of degree 4, whence by (5.3), or does not contain a light vertex, whence by Lemmata 5.16 and 5.17.
We first consider the case that one of , , , say , is an . Then can be decomposed as in Fig. 18(a) for some rooted tree of type . As , Lemma 4.21(2) yields . Analogously, we get . Thus we have . By (R8), is not -optimal, contradiction to Proposition 4.15.
So we are left with the case that . As contains a light vertex, we may assume that . If , we note that switching and the of yields the tree shown in Fig. 18(b) with by Lemma 4.18. But is not optimal by (5.4). We conclude that . By (R9), Lemma 5.17 and Proposition 4.15, the only remaining case is . This case is ruled out by (R2).
So there is no rooted subtree of type containing both a light vertex and a vertex of degree 4. By Lemmata 5.15 and 5.3, contains a 2-claw. Removing this 2-claw from yields a rooted tree of type of containing a light vertex. We conclude that does not contain a vertex of degree 4, thus by (5.3). The case yields , the case is impossible in view of (R6) (cf. Fig. 17). □
Fig. 17.

Subtree of in Proposition 5.18.
Fig. 18.
Decomposition of and in Proposition 5.18.
(a) .
(b) .
5.3. Upper degree bounds for vertices of type
We now conclude the proof which shows that almost all optimal trees fulfil LC1–LC6.
If an optimal tree contains a 2-claw, the upper degree bound LC5 for degrees of type is a consequence of the exchange lemma together with the improved lower bound for for rooted subtrees of type obtained by the exclusion of light vertices.
Lemma 5.19
Let be an optimal tree. If contains a 2-claw as a rooted subtree, then fulfils LC1–LC5.
Proof
Assume that there is a vertex of type of degree . We denote the rooted connected components of by , where a 2-claw is contained in . Now we combine Lemma 5.8 and Lemma 4.21(3) as before: since (where is one of the leaves of the 2-claw contained in ), we have
As contains no light vertex by Proposition 5.18, Lemma 5.16 yields
We conclude that , as required. □
We are now left with optimal trees containing 3-claws. The arguments are somewhat similar as in the case of light vertices, except that we now have to deal with “heavy” vertices.
Lemma 5.20
Let be an optimal tree containing a 3-claw and containing a vertex of degree 4 which is adjacent to at most 2 leaves.
Then is adjacent to exactly 2 leaves. Furthermore, each vertex of degree is adjacent to at most 2 leaves.
Proof
Denote the rooted connected components of by , where we assume that contains a 3-claw and is not a leaf. By Lemma 5.8, we have , i.e., and are indeed leaves.
We have therefore shown that every vertex of degree 4 is adjacent to 2 or 3 leaves.
Assume that is a vertex of degree in . Still denoting the rooted connected components of by , , , , we may now assume that is contained in ( also contains a 3-claw, since otherwise Lemma 5.19 would apply, so we can interchange the roles of and if necessary). The rooted connected components of are denoted by with the assumption that is contained in and . Combining Lemmata 5.8 and 4.21(3) again (with and as pivotal vertices and ), we get
which implies that and therefore is adjacent to at most 2 leaves. □
The lower bound in the following lemma is the same as in Lemma 5.16; but instead of considering a rooted subtree of an optimal tree, we only assume LC1–LC4.
Lemma 5.21
Let be a tree fulfilling LC1–LC4 and be a rooted subtree of type . Then
Proof
Analogous to Lemma 5.16. □
We will exclude the occurrence of three or more 3-claws in an optimal tree by substituting two 3-claws by 2-claws and use the additional vertices in order to create a light vertex. To make this work, we have to analyse the effects of these substitutions. As the intermediate steps do not necessarily lead to optimal trees, we can only use the above bound.
Lemma 5.22
Let be a tree fulfilling LC1–LC4.
- (1)
If one 3-claw in is replaced by a 2-claw, we have and for the resulting tree . Furthermore fulfils LC1–LC4.
- (2)
If one 3-claw in is replaced by a , we have and for the resulting tree .
Proof
Let consist of a 3-claw, a rooted tree of type and the edge connecting the root of the 3-claw and the root of . We have by Lemma 5.21.
- (1)
By Lemma 4.4, we have
- (2)
Analogous. □
We now deal with optimal trees containing a 3-claw. The restrictions are now so strict that we can discuss all cases.
Proposition 5.23
Let be an optimal tree which contains a 3-claw. Then .
Proof
Assume that contains 3 rooted subtrees isomorphic to a 3-claw. Replacing two of them by a 2-claw and the third by a yields a tree with and
by Lemma 5.22, contradiction.
We conclude that contains at most 2 rooted subtrees isomorphic to a 3-claw.
We now assume that has a vertex of degree . By Lemma 5.19, does not contain a 2-claw and thus no vertices of degree 3 by Proposition 5.18. Thus every rooted subtree of either contains a 3-claw or is a leaf by Lemmata 5.3, 5.4, 5.9 and 5.12. As there are at most 2 subtrees isomorphic to a 3-claw in , there are at least leaves. By Lemmata 5.4 and 5.12, we conclude that is adjacent to exactly leaves. Denote the rooted connected components of by . By Lemma 5.8, we have
i.e., . By Lemma 5.20, we conclude that all vertices of degree 4 in are adjacent to 3 leaves, i.e., they are the root of a 3-claw.
Thus is of the shape given in Fig. 19(a) for some (as there is no vertex of degree for ). As the tree in Fig. 19(b) with root is not -optimal for , cf. (R10), we conclude from Proposition 4.15, Lemmata 5.5 and 5.9 that this tree does not occur as a subtree of an optimal tree. Thus has no vertex of degree , i.e., fulfils LC1–LC5.
So by Lemma 5.20, every vertex of of type is adjacent to 2 or 3 leaves and has degree 3 or 4. We conclude that or it is a caterpillar tree of the shape given in Fig. 20 for some and some . We note that the tree in Fig. 21 with root is not -optimal for , cf. (R10), thus this tree does not occur as a rooted subtree of an optimal tree by Proposition 4.15 and Lemma 5.5. This implies that or . For , the resulting tree is not optimal, cf. (R3). The remaining cases correspond to . □
Fig. 19.
Shape of in Proposition 5.23.

(a).
(b).
Fig. 20.
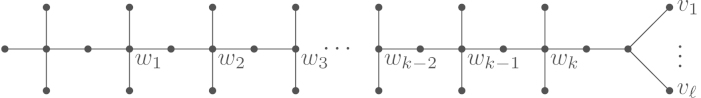
Shape of in Proposition 5.23.
Fig. 21.
Subtree of in Proposition 5.23.
We are now able to prove Theorem 5.2.
Proof of Theorem 5.2
As , has no light vertex by Proposition 5.18 and fulfils LC1–LC4. By Proposition 5.23, contains no 3-claw as a rooted subtree, so fulfils LC1–LC4 and LC6. By Lemmata 5.3, 5.4, 5.9, 5.12 and LC6, contains a 2-claw and fulfils LC5 by Lemma 5.19. □
We conclude this section with refined bounds on for subtrees of type of optimal trees. The bounds only depend on the LC.
Lemma 5.24
Let be a tree fulfilling the LC and let be a rooted subtree of of order >1 and type . Then
If no branch of the unique branch of is a leaf, then
Proof
We prove the result by induction on the order of . By the LC, we have for some and rooted trees . If , then both and are leaves by the LC and with .
We now consider the case . By the LC, there are at most two leaves among , , . Thus by the induction hypothesis. We obtain
If none of , , is a leaf, we use the upper bound to obtain
□
If there is a vertex of type and degree 4 which is adjacent to two leaves (e.g., in a ) in an optimal tree, this has consequences to every vertex of type , as the following lemma shows.
Lemma 5.25
Let be an optimal tree. If there is a vertex of degree 4 of which is adjacent to two leaves, then every vertex of of type is adjacent to at least one leaf.
Proof
We assume the contrary and denote the rooted connected components of by , , , where is contained in and the rooted connected components of by , , , with contained in . As , Lemmata 5.8 and 4.21(3) yield
a contradiction. □
6. The upper bound: global structure
6.1. Outline graph
Now we start with the discussion of the global structure of optimal trees. Let us first collect a few results on the outline graph of an optimal tree.
Lemma 6.1
Let be an optimal tree of order and its outline graph as defined in Definition 3.2. Then has the following properties.
- (1)
The leaves of correspond to rooted subtrees of type of , the non-leaves of correspond to vertices of type of .
- (2)
If there is a vertex of degree 3 in , then , has the shape as given inFig. 4(e) and
- (3)
There is no vertex in which is adjacent to an and an .
- (4)
If is of order 1, then and or and .
Proof
- (1)
By construction, all special leaves of correspond to rooted subtrees of type of . A leaf in is either contained in some larger special leaf or is eventually seen as an in . All non-leaves of of type are either contained in some larger special edge or special leaf or they are transformed into a . Thus all non-leaves of have to correspond to vertices of type of .
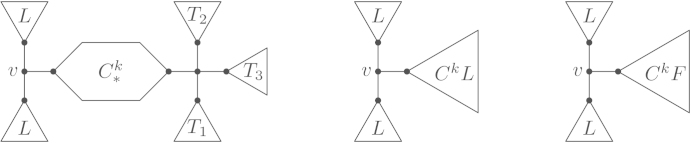
- (2)
We denote the vertex of degree 3 by . By Theorem 5.2, two of the neighbours of are leaves. Thus we have one of the situations in Fig. 22 for appropriate and rooted trees , , . The first case is a contradiction to the construction of the outline, as a subtree would have been contracted earlier than the . The second case is also not a correct outline, as this graph is isomorphic to a (use the in the present as the new root).
So we are left with the third case. In this case, we have , which immediately implies and . And this is exactly the situation in Fig. 4(e).
- (3)
We assume that there is a vertex in which is adjacent to an and an . This could mean one of the situations in Fig. 23, where for .
- (a)
In the situation in Fig. 23(a), a would have been used in the outline of instead of , , , and .- (b)
In the situation in Fig. 23(b), a would have been used in the outline of instead of , , , and .- (c)
We consider the situation in Fig. 23(c).If , the graph is isomorphic to the graph in Fig. 4(e), i.e., a would have been combined with a vertex of degree 3 and two leaves in the outline of .If , the graph is isomorphic to , and this would have been taken in the outline of .- (4)
If is of order 1, then the unique vertex of must be a or a for a suitable . In the first case, we have , in the second . □
Fig. 22.
Possible cases in Lemma 6.1.
Fig. 23.
Possible cases in Lemma 6.1.
6.2. Chains
In the global structure of optimal trees, chains as introduced in Definition 3.1 occur prominently. This subsection is devoted to the computation of the relevant parameters and to some further necessary optimality criteria in relation to chains. Recall that the growth constant in Theorem 1.2 is defined as the larger root of the polynomial . In the following, the other root of this polynomial is denoted by .
Lemma 6.2
- (1)
Let be a rooted tree of type . Thenwith
- (2)
We have
- (3)
Let and . If , then the sequence is strictly increasing, if , then the sequence is strictly decreasing. In both cases, .
In particular, is strictly increasing and is strictly decreasing.
Proof
- (1)
This is a straightforward consequence of the recursive formulæ (4.4) and (4.5) for , and .
- (2)
The eigenvalues of are and . Thus the sequences , , , for are elements of the linear space spanned by and . Another basis of this linear space is given by and . It therefore suffices to check the formulæ for and .
- (3)
It is easily checked that is the unique positive fixed point of . The assertions on are easy consequences of the definition of . Finally, the assertions on and follow from and . □
Next we show that an and a never occur as neighbours of the same vertex in the outline of an optimal tree.
Lemma 6.3
Let be an optimal tree, a vertex of degree 4 and , , , the rooted connected components of . We assume that and for some . Then . In particular, is not in the outline of .
Proof
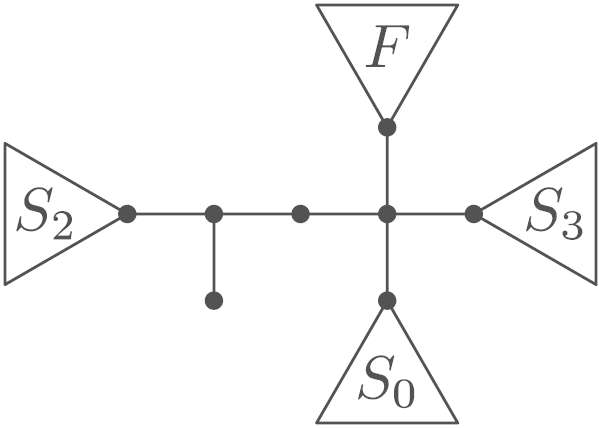
We assume . Without loss of generality, we also assume that . The tree has the shape shown in Fig. 24(a). If , we have by Lemma 4.21(2), which implies that and by Lemma 5.24, contradiction.
Therefore, we have , thus by Lemma 5.16. In the case , Lemma 6.1 yields the result. Thus we are left with .
We consider the tree where and have been exchanged, cf. Fig. 24(b). From Lemma 4.18 we conclude that , i.e., is also an optimal tree. We rewrite as in Fig. 24(c). For , the rooted tree is not -optimal for any , cf. (R11). As by Lemma 5.24, this is a contradiction to Proposition 4.15 and the optimality of . □
Fig. 24.
Trees and considered in Lemma 6.3.
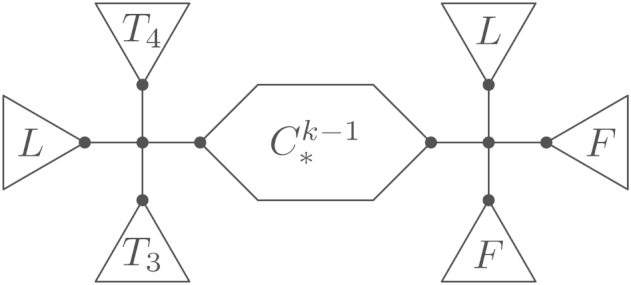
(a) .
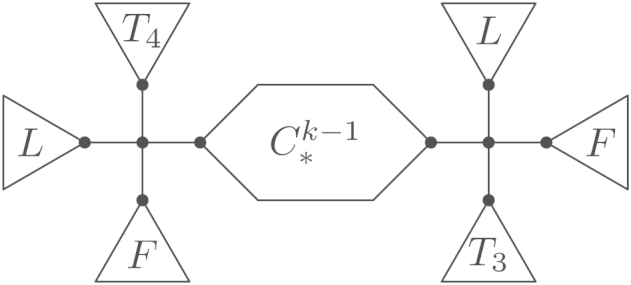
(b) .
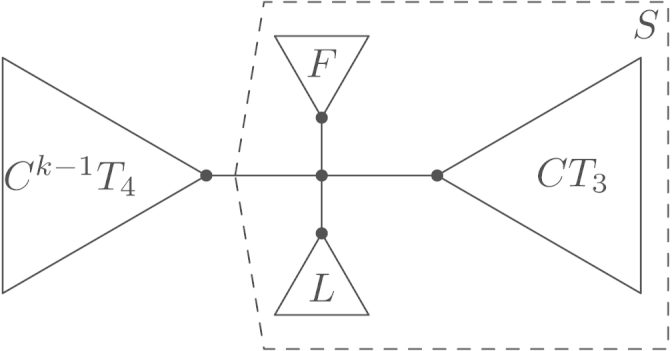
(c) .
We now prove a necessary optimality condition involving one chain element.
Lemma 6.4
Let be an optimal tree, a vertex of type and degree 4 of and , , , the rooted connected components of for some rooted trees , , , .
- (1)
If neither nor is a leaf, then
- (2)
If is a leaf and , then
Proof
If , then by Lemma 4.21(2), i.e., or is a leaf by Lemma 5.24.
If , then by Lemma 4.21(2), i.e., either both and are non-leaves or , say, is a leaf and .
The contrapositions are the statements of the lemma. □
The following lemma lists some consequences of this result.
Lemma 6.5
Let be an optimal tree, a vertex of degree 4 and , , , the rooted connected components of .
- (1)
Let and let for some and some rooted tree with for . Further assume that is not a leaf for and that .
Then and, if for some , then .
- (2)
If , , with , , with for and finally , then we have .
Furthermore, if , then .
Proof
- (1)
Assume that . Thenby the monotonicity of , Lemmata 5.24, 6.4 and the fact that . We conclude that , i.e., , contradiction. Thus .
which yields in view of the monotonicity of .
- (2)
Assume that . By Lemma 6.4, we havewhich yields by Lemma 6.2 and therefore . If , then the same inequality holds trivially as has been assumed to be at most 1.
by Lemma 6.4, which yields , i.e., , as required. For , there is nothing to show. □
6.3. Switching forks and leaves
So far, we mainly compared optimal trees to trees where some subtrees have been switched between two positions. It turns out that more invasive operations are needed in order to obtain information on the global structure of optimal trees.
The basic idea is the following: if 7 forks are replaced by 7 leaves, the order of the tree is reduced by 7⋅3=21. As a chain element requires 7 vertices, these 21 “free” vertices can be used to introduce 3 chain elements. If all this is done at the “right” positions, then increases. In some circumstances, however, the inverse operation may be beneficial.
Before we state the main lemma regarding such exchange operations, we collect two technical details concerning the floor function in the following lemma.
Lemma 6.6
- (1)
For real and positive integers , the identityholds.
- (2)
Let and be integers withThen
for .
Proof
- (1)
Cf. Graham, Knuth and Patashnik [6, (3.26)].
- (2)
Choose such that . Then andfor . □
Now we are able to provide the required exchange operations. Their consequences will be exploited afterwards. The proof relies on similar ideas as the proof of Lemma 5.22.
Lemma 6.7
Let be a tree fulfilling the LC and let be a tree that is obtained from by replacing one rooted subtree by , where and will be specified below.
- (1)
If with for some and , then and .
- (2)
If with for some and , then and .
- (3)
If with for some and , then and .
- (4)
Ifand for some , , , then and .
- (5)
If and for some , then and .
- (6)
If and for some , then and . If , then .
- (7)
If and for some , , , then and .
- (8)
Ifand for some and , then and .
- (9)
If and for some and , then and .
Proof
- (1)
Let consist of some rooted subtree , and the edge between the roots of and . Then from Lemma 4.4 we obtainwhere
cf. Lemma 6.2 and Lemma 5.24 have been used. From Lemmata 6.2 and 6.6, we get
with , where we replaced the explicit formulæ obtained from Lemma 6.2 by asymptotic expansions for ease of presentation; the actual computations leading to the given constant have been performed exactly—in this particular case, it even turned out that the whole expression was strictly decreasing in . The explicit branch of has been taken into account exactly instead of using Lemma 6.2.
We have and by Lemma 6.6.
- (2)
Analogous.
- (3)
Analogous.
- (4)
Analogous.
- (5)
Analogous, but the lower bound (Lemma 5.24) has to be used, as .
- (6)
Analogous.
- (7)
Analogous.
- (8)
Analogous, but simpler, as this is a finite case and no limits have to be considered.
- (9)
Analogous. □
Remark 6.8
The precise proof of Lemma 6.7 has been carried out using Sage [20]. The program is available in [11].
6.4. -free optimal trees
Throughout this subsection, we assume that is an optimal tree which is -free, i.e., it does not contain a as a rooted subtree. Obviously, such a tree does not contain any as rooted subtree for . We will describe all optimal trees with this property.
Lemma 6.9
Let be a -free optimal tree and be a vertex of degree 4 in the outline graph of which is adjacent to at least three “special leaves” , , with . Then there is a such that with for .
Proof
As is -free, for any and . So for every we have or for some . As is optimal, the case is excluded by LC6. The cases , and , , are excluded by Lemma 6.3. Thus for some for all . As is in the outline of , it is not adjacent to a leaf by Lemma 6.3. Thus Lemma 6.5(1) (with ) and Lemma 6.6 prove the assertion. □
Lemma 6.10
Let be a -free optimal tree. Then there are no three distinct vertices in the outline of such that each of them is adjacent to three “special leaves”.
Proof
Assume that there are three distinct vertices , , in the outline of such that is adjacent to , , with for some and . By Lemma 6.9 this is the only case to consider.
Replacing the rooted subtree with root and branches , , by a rooted subtree with root and branches , , , cf. Lemma 6.7(1), yields a tree which is not necessarily optimal, but fulfils the LC.
Replacing the rooted subtree with root and branches , , in by a rooted subtree with root and branches , , , cf. Lemma 6.7(2), yields a tree , which still fulfils the LC.
Replacing the rooted subtree with root and branches , , in by a rooted subtree with root and branches , , , cf. Lemma 6.7(3), yields a tree .
Lemma 6.7(1, 2 and 3) yields and
thus , contradiction to the optimality of . □
Lemma 6.11
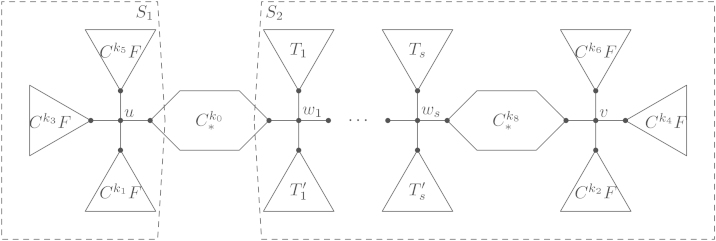
Let be a -free optimal tree of order and , two distinct vertices of degree 4 in the outline graph of which are adjacent to three special leaves.
Then and is of the shape given in Fig. 4(d) where
for or .
Proof
By Lemma 6.1, the outline of does not contain a vertex of degree 3. By Lemma 6.10, the outline graph of is a caterpillar tree. By Lemma 6.9, it must be of the shape shown in Fig. 25 for some , some non-negative integers and some special leaves , for . As is -free, is a leaf or a and is a leaf or a for suitable , and .
Assume that . By Lemma 5.25, it is impossible that both and , as is not adjacent to a leaf. By Lemma 6.3 we conclude that and for some , . Lemma 5.24 implies that and .
W.l.o.g. we assume . We claim that
(6.1) If or , this follows from Lemma 6.5(1). So we consider the case that and . By Lemma 5.16 and the shape of as shown in Fig. 25, this implies that . In particular, we have , i.e., . As , we have and by Lemma 6.5(1). Thus we have by Lemma 5.16 and . Then which is not optimal by (R5). This concludes the proof of (6.1).
W.l.o.g we assume . If , then and , thus also by (6.1). Thus in this case by Lemma 6.5(1). If , we get the same estimate from Lemma 6.5(1).
Replacing in by as in Lemma 6.7(4) yields a tree fulfilling the LC.
Replacing in as in Lemma 6.7(2) yields a tree .
By Lemma 6.7(2 and 4), we have and
contradiction to the optimality of .
Thus we have shown that , i.e., is of the shape given in Fig. 4(d). We set and have and in particular .
We set and . Without loss of generality we assume . By Lemmata 6.5(1) and 6.6, we have
(6.2) If , we obtain , thus , and Lemmata 4.21(2) and 6.2 yield
a contradiction. We conclude that . From (6.2) we immediately conclude that holds in both cases.
From Lemmata 6.5(1) and 5.24 we see that and .
If , we therefore obtain
where we have in the first case and in the second case.
If , then and thus by Lemma 6.5(1). Thus we have
and therefore for by Lemma 6.6. We have , the case corresponds to . Indeed, . □
Fig. 25.
Decomposition of for Lemma 6.11.
Proposition 6.12
Let be a -free optimal tree of order . Then , or and has the shape described in Theorem 3.3 for these congruence classes.
Proof
Let be the outline of . If has a vertex of degree 3, Lemma 6.1 yields the required result.
If has at least two vertices of degree 4, then there are at least two vertices of degree 4 which are adjacent to at least 3 special leaves. In this case, Lemma 6.11 yields the required result.
We now consider the case that has exactly one vertex of degree 4. Its neighbours are special leaves , , , , where each is either an or a for . We assume that . The case corresponds to . Then by Lemma 6.3, we cannot have a leaf, so for . From Lemmata 6.5(1) and 6.6, we obtain that for and . We have
We conclude that and obtain
and of course, has the shape given in Fig. 4(b).
Finally we consider the case that has order 1. This case is covered by Lemma 6.1. Both graphs mentioned in this lemma ( and ) contain a except for . □
6.5. Optimal trees containing
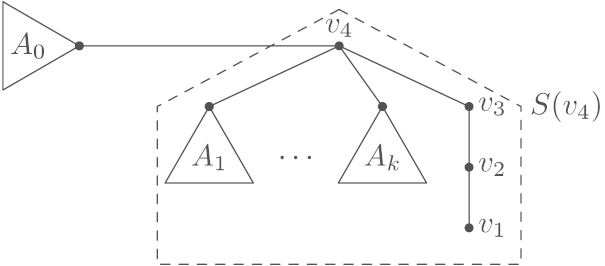
This final subsection is devoted to optimal trees containing a as a rooted subtree. By Lemma 5.25, every vertex of type of such a tree is adjacent to a leaf. By Lemma 6.3, does not contain any rooted subtree of the shape for .
Lemma 6.13
Let be an optimal tree containing as a rooted subtree and a vertex of degree 4 in the outline of which is adjacent to 3 special leaves , , with . Then there is a such that for .
Proof
Let , , , denote the rooted connected components of . None of them is a for by Lemmata 6.3 and 5.25. Thus and for suitable , . As and cannot be rooted subtrees of by Lemma 5.25, we have by Lemma 5.16. Thus Lemma 6.5(2) can be used to see that . With , Lemma 6.6 and LC6, the desired result follows. □
Lemma 6.14
Let be an optimal tree containing as a rooted subtree. Then there are no three distinct vertices in the outline of such that each of them is adjacent to three special leaves.
Proof
Assume that there are three distinct vertices , , in the outline of such that is adjacent to , , with for some and . By Lemma 6.13 this is the only case to consider.
Replacing the rooted subtree with root and branches , , by a rooted subtree with root and branches , , , cf. Lemma 6.7(5), yields a tree , which does not have to be optimal, but fulfils the LC.
Replacing the rooted subtree with root and branches , , in by a rooted subtree with root and branches , , , cf. Lemma 6.7(5), yields a tree , which still fulfils the LC.
Replacing the rooted subtree with root and branches , , in by a rooted subtree with root and branches , cf. Lemma 6.7(6), yields a tree .
Lemma 6.7(5 and 6) yields and
thus , contradiction to the optimality of . □
Next we need better bounds on the -values of subtrees of type which are visible in the outline of an optimal tree.
Lemma 6.15
Let be an optimal tree containing a , be a vertex of degree 4 in the outline of and , , , be the rooted connected components of . We assume that and set . We further set .
Then
Proof
We prove the lemma by induction on the order of .
By Lemma 5.24 and LC6, we have .
We write for suitable trees and maximal for . As the outline of does not contain a by Lemmata 6.3 and 5.25, we conclude that either is a leaf or we have by the induction hypothesis. By Lemma 6.2, we have in both cases.
We obtain
□
Lemma 6.16
Let be an optimal tree of order containing a whose outline contains at least two vertices of degree 4. Then and is of the shape given in Fig. 4(a) with
for .
Proof
By Lemma 6.1, the outline of has no vertex of degree 3. By Lemma 6.14, the outline graph of is a caterpillar tree. By Lemmata 5.25, 6.13 and 6.3, it must be of the shape shown in Fig. 26 with , . By LC6, we have and .
We claim that ; let us assume, to the contrary, that . Then by Lemma 6.15, we have
As and , Lemmata 6.5(2) and 6.13 imply
(6.3) (the last statement following from the two inequalities for ) and the analogous inequalities
(6.4) Without loss of generality, we may assume .
We consider 3 cases:
- (1)
We replace as in Lemma 6.7(7) and obtain a tree fulfilling the LC.
Replacing in as in Lemma 6.7(6), we obtain a tree . We havea contradiction.
- (2)
We assume that and . By (6.4), this implies and .
We assume first that and replace in as in Lemma 6.7(7) and obtain a tree fulfilling the LC.
We now replace in as in Lemma 6.7(9) and obtain a tree .
We conclude thata contradiction.
from Lemmata 6.2 and 4.21(3). This is a contradiction.
- (3)
We assume that . By (6.3) this implies and . Consequently, we have , thus , and by (6.4).
We assume first that and replace in as in Lemma 6.7(8) and obtain a tree .
We now replace in as in Lemma 6.7(9) and obtain a tree . We conclude thata contradiction.
Thus we have . It follows that . In each of the possible cases remaining, it turns out that for the tree given in Fig. 4(d) (or for ), contradiction.
So we have shown that and that therefore has the shape as in Fig. 4(a). We set and obtain and in particular.
We set and and assume that . From Lemmata 6.5(2) and 6.6, we see that
If , we have and therefore by Lemmata 4.21(2) and 6.2, a contradiction. Thus and in both cases.
By Lemmata 6.15 and 6.5(2), we have (in analogy to (6.3) and (6.4))
(6.5) If , we have and by (6.5) and , i.e., for by Lemma 6.6.
If , we have and (6.5) yields
and therefore for by Lemma 6.6. □
Fig. 26.
Decomposition of for Lemma 6.16.
Proposition 6.17
Let be an optimal tree of order containing a as a rooted subtree. Then , , or and has the shape described in Theorem 3.3 for these congruence classes.
Proof
Let be the outline of . If has a vertex of degree 3, Lemma 6.1 shows that does not contain a as a rooted subtree.
If has at least two vertices of degree 4, then there are at least two vertices of degree 4 which are adjacent to at least 3 special leaves. In this case, Lemma 6.16 yields the required result.
We now consider the case that has exactly one vertex of degree 4. Its neighbours are special leaves , , , . By Lemma 5.25, we have after suitable reordering. As is in the outline of , we have . By Lemma 6.3, we must have for some for . Thus is of the shape given in Fig. 4(c). This yields ; in particular .
Without loss of generality, we may assume that . By Lemma 6.5(2), we have
From Lemma 6.6, we conclude that
for , as required.
Finally we consider the case that has order 1. This case has been considered in Lemma 6.1. □
Proof of Theorem 3.3
Let be an optimal tree of order . If , then there are two possibilities: can be -free or it can contain a as a rooted subtree. Then Propositions 6.12 and 6.17 respectively show that has the shape given in Theorem 3.3 with the parameters as given by the theorem. For , the trees in the exceptional set still have this shape. For or , however, it is not possible for a tree of order to have the shape shown in Fig. 4 (since is too small). In these cases, the optimal tree has to be an element of the exceptional set , which gives us a unique optimal tree for and two optimal trees for . Finally, let us remark that the asymptotic formulæ given in Theorem 1.2 follow easily from the structure of the trees by means of Lemma 6.2. □
Acknowledgements
C. Heuberger is supported by the Austrian Science Fund (FWF): S09606, that is part of the Austrian National Research Network “Analytic Combinatorics and Probabilistic Number Theory.” This paper was partly written while C. Heuberger was a visitor at Stellenbosch University.
This material is based upon work supported financially by the National Research Foundation of South Africa under grant number 70560.
Contributor Information
Clemens Heuberger, Email: clemens.heuberger@tugraz.at.
Stephan Wagner, Email: swagner@sun.ac.za.
Appendix. Tables of replacements
See Tables 2 and 3.
References
- 1.Baxter R.J., Enting I.G., Tsang S.K. Hard-square lattice gas. J. Statist. Phys. 1980;22(4):465–489. [Google Scholar]
- 2.Bród D., Skupień Z. Trees with extremal numbers of dominating sets. Australas. J. Combin. 2006;35:273–290. [Google Scholar]
- 3.Bród D., Skupień Z. Recurrence among trees with most numerous efficient dominating sets. Discrete Math. Theor. Comput. Sci. 2008;10(1):43–55. [Google Scholar]
- 4.Cvetković D.M., Doob M., Sachs H. third ed. Johann Ambrosius Barth; Heidelberg: 1995. Spectra of Graphs. [Google Scholar]
- 5.Górska J., Skupień Z. Trees with maximum number of maximal matchings. Discrete Math. 2007;307(11–12):1367–1377. [Google Scholar]
- 6.Graham R.L., Knuth D.E., Patashnik O. second ed. Addison-Wesley; 1994. Concrete Mathematics. A Foundation for Computer Science. [Google Scholar]
- 7.Gutman I. Graphs with greatest number of matchings. Publ. Inst. Math. (Beograd) (N.S.) 1980;27(41):67–76. [Google Scholar]
- 8.Gutman I. The energy of a graph: old and new results. (Gößweinstein, 1999); Berlin: Springer; 2001. pp. 196–211. [Google Scholar]
- 9.Gutman I., Polansky O.E. Springer-Verlag; Berlin: 1986. Mathematical Concepts in Organic Chemistry. [Google Scholar]
- 10.Heilmann O.J., Lieb E.H. Theory of monomer–dimer systems. Comm. Math. Phys. 1972;25:190–232. [Google Scholar]
- 11.C. Heuberger, S.G. Wagner, The number of maximum matchings in a tree—online ressources, http://www.math.tugraz.at/~cheub/publications/max-card-matching/. [DOI] [PMC free article] [PubMed]
- 12.Hosoya H. Topological index as a common tool for quantum chemistry, statistical mechanics, and graph theory. Mathematical and Computational Concepts in Chemistry; (Dubrovnik, 1985); Chichester: Horwood; 1986. pp. 110–123. [Google Scholar]
- 13.Kirk R., Wang H. Largest number of subtrees of trees with a given maximum degree. SIAM J. Discrete Math. 2008;22(3):985–995. [Google Scholar]
- 14.Knuth D.E. Two notes on notation. Amer. Math. Monthly. 1992;99(5):403–422. [Google Scholar]
- 15.Lin S.B., Lin C. Trees and forests with large and small independent indices. Chinese J. Math. 1995;23(3):199–210. [Google Scholar]
- 16.Lovász L., Plummer M.D. Vol. 121. North-Holland Publishing Co; Amsterdam: 1986. Matching theory. (North-Holland Mathematics Studies). [Google Scholar]
- 17.Merrifield R.E., Simmons H.E. Wiley; New York: 1989. Topological Methods in Chemistry. [Google Scholar]
- 18.Prodinger H., Tichy R.F. Fibonacci numbers of graphs. Fibonacci Quart. 1982;20(1):16–21. [Google Scholar]
- 19.Sagan B.E. A note on independent sets in trees. SIAM J. Discrete Math. 1988;1(1):105–108. [Google Scholar]
- 20.W.A. Stein, et al. Sage Mathematics Software (Version 4.6), The Sage Development Team, (2010), http://www.sagemath.org.
- 21.Székely L.A., Wang H. Binary trees with the largest number of subtrees. Discrete Appl. Math. 2007;155(3):374–385. [Google Scholar]
- 22.Wagner S., Gutman I. Maxima and minima of the Hosoya index and the Merrifield–Simmons index: a survey of results and techniques. Acta Appl. Math. 2010;112(3):323–346. [Google Scholar]
- 23.Wilf H.S. The number of maximal independent sets in a tree. SIAM J. Algebraic Discrete Methods. 1986;7(1):125–130. [Google Scholar]