Compartmental Modeling of ¹¹C-HOMADAM Binding to the Serotonin Transporter in the Healthy Human Brain

Abstract

The novel PET radioligand ¹¹C-N,N-dimethyl-2-(2′-amino-4′-hydroxymethylphenylthio)benzylamine (¹¹C-HOMADAM) binds with high affinity and selectively to the serotonin transporter (SERT). The purpose of this study was to develop a reliable kinetic model to describe the uptake of ¹¹C-HOMADAM in the healthy human brain.

Methods

Eight volunteers participated in the study; 5 of them were fitted with arterial catheters for blood sampling and all were scanned on a high-resolution research tomograph after the injection of ¹¹C-HOMADAM. Regional distribution volumes and binding potentials were calculated with 2- and 4-parameter arterial-input compartment models, a 3-parameter reference tissue compartment model, and the Logan graphic approach.

Results

The 2-parameter arterial-input compartment model was statistically superior to the 4-parameter model and described all brain regions. Calculated binding potentials agreed well between the arterial-input model and the reference tissue model when the cerebellum was used as the reference tissue. The Logan graphic approach was not able to estimate the higher concentration of SERT in the dorsal raphe than in the midbrain.

Conclusion

¹¹C-HOMADAM is a highly promising radioligand with high ratios of specific binding to nonspecific binding in known SERT-rich structures, such as the raphe nuclei. The 3-parameter reference tissue model approach permits a simplified quantitatively accurate method for estimating SERT binding potentials.

Alterations in the neurotransmitter serotonin have been implicated in several neurologic disorders, including depression, schizophrenia, Alzheimer’s disease, and Parkinson’s disease (1–3). Serotonin receptors and transporters are concentrated primarily in the raphe nucleus bodies of the brain stem and populate areas such as the thalamus, striatum, cingulate cortex, and cerebral cortex (4,5). Very high-density serotonin transporter (SERT) expression is observed in the thalamus, midbrain, and striatum; moderate-density expression is seen in the amygdalae and cingulated cortex; and lower-density expression is seen in the neocortical regions, including the cerebellum. The SERT concentration in cell bodies of the presynaptic serotoninergic neurons is an indicator of terminal viability and integrity (6–8). Therefore, SERT represents a specific marker of serotoninergic neuron density permitting quantitative mapping in vivo by PET with highly specific radiotracers. These highly specific radioligands have the potential to reveal regional brain distributions of SERT in various states of mood, disease, and treated and untreated conditions.

Several high-affinity ligands have been developed and introduced into humans to map SERT distributions in the central nervous system (9–11). Of these, ¹¹C-3-amino-4-(2-dimethylaminomethyl-phenylsulfanyl)-benzonitrile (¹¹C-DASB) and trans-1,2,3,5,6,10-ß-hexahydro-6-[4-(methylthio)phenyl]pyrrolo-[2,1-a]-isoquinoline (¹¹C-McN 5652) have been extensively studied and have been found to accumulate in SERT-rich regions of the brain stem, midbrain, and striatum. Compared with the more recently developed ¹¹C-N,N-dimethyl-2-(2-amino-4-methylphenylthio)benzylamine (¹¹C-MADAM) (10), both of these tracers exhibit moderately high free uptake and nonspecific binding (12–14), as indicated by the high total distribution volume (V_T) in the cerebellum. The presence of nonspecific uptake may present difficulties in the delineation of small structures, such as the raphe nuclei, or in comparisons of cortical regions with low SERT densities. The low nonspecific binding of ¹¹C-MADAM is potentially advantageous for these reasons, but equilibrium occurs late, with peak radioactivity levels occurring between 30 and 60 min after injection. ¹¹C-5-bromo-2-[2-(dimethylaminomethylphenylsulfanyl)]phenylamine (¹¹C-DAPA) and ¹¹C-2-[2-(dimethylaminomethyl)phenylthio]-5-fluoromethylphenylamine (¹¹C-AFM) are 2 other recently synthesized SERT ligands; compared with ¹¹C-DASB and ¹¹C-McN-5652, they have higher ratios of specific binding to nonspecific binding. However, to date, studies with these 2 ligands have been conducted only with primate models (15).

Jarkas et al. reported on the labeling of N,N-dimethyl-2-(2′-amino-4′-hydroxymethylphenylthio)benzylamine (HO-MADAM) with ¹¹C, a highly specific SERT imaging agent (16). Preliminary studies characterizing the tracer kinetics in vivo in a male rhesus monkey revealed rapid binding kinetics, high uptake in the midbrain and thalamus, moderate uptake in the brain stem and pons, and low uptake in the cerebellum. High ratios of specific binding to nonspecific binding were reported, with thalamic-to-cerebellum, midbrain-to-cerebellum, and cortical-to-cerebellum ratios being higher than those of ¹¹C-DASB (15,16). In addition, the time to peak radioactivity levels in SERT-rich regions was shorter with this tracer than with ¹¹C-DASB and ¹¹C-AFM. Quasi-equilibrium was subsequently reached at 22–45 min in regions of the thalamus and midbrain; the corresponding values for ¹¹C-DASB and ¹¹C-AFM were 65 and 85 min, respectively. The higher concentration of ¹¹C-HOMADAM in the subcortical regions of the brain than in the cerebellum and its rapid kinetics are attractive characteristics and are the reasons for further investigation.

The aim of this work was to use ¹¹C-HOMADAM uptake data from 8 healthy human subjects to evaluate whether SERT density can be reliably measured. We present quantitative modeling with measured arterial plasma radioactivity in 2- and 4-parameter compartment models and with a reversible-binding graphic method. In addition, a simplified compartment model and the graphic method were evaluated with reference tissue as the input.

MATERIALS AND METHODS

Human Subjects

This study was conducted under the auspices of the Emory University Internal Review Board and within the Emory University Hospital. Five female and 3 male volunteers (20.0 ± 1.1 y [mean ± SD]) participated in the study after giving informed consent. All subjects were judged to be healthy on the basis of the absence of any medical history of neurologic or psychiatric disorders (including substance abuse) and a physical examination including blood and urine analyses. Each participant underwent an MRI scan of the brain before a single PET scan with ¹¹C-HOMADAM. The MRI scan served as an anatomic reference for registering PET data when defining regions of interest (ROIs).

Radiochemistry

¹¹C-HOMADAM was obtained by methylation of N-methyl-2-(2′-amino-4′-hydroxymethylphenylthio)benzylamine with ¹¹C-CH₃I as previously described (16). The injected activity ranged from 186 to 913 MBq delivered intravenously, with an average specific activity of 89 ± 63 GBq/μmol, equating to an injected mass ranging from 0.64 to 4.8 μg.

PET Protocol

All scans were performed with a Siemens high-resolution research tomograph (HRRT), a dedicated 3-dimensional brain scanner with depth-of-interaction discrimination and an intrinsic isotropic in-plane resolution of 2.2 mm at full width at half maximum (FWHm) (17). Subjects were placed in the supine position with head movement constrained by a rigid head holder and strap restraints. Before the emission scan, 6 min of ¹³⁷Cs transmission data were acquired for attenuation correction and to judge proper subject placement. An arterial catheter inserted into the radial artery under local anesthesia provided access for blood sampling, and a venous catheter placed in a vein in the opposite forearm was used for injection of the radiopharmaceutical. Of the 8 volunteers, 5 (2 female and 3 male) underwent arterial sampling. A 145-min emission scan was started simultaneously with a 5-min constant infusion of ¹¹C-HOMADAM through a syringe pump. The slow infusion was preferable to a rapid bolus injection with regard to the timing of the manual blood sampling through the arterial catheter. The HRRT collected emission data in the list mode format; the data were later binned into 23 frames (6 × 30 s, 4 × 180 s, and 13 × 600 s).

Arterial samples were collected manually in 2-mL aliquots every 30 s for the first 5 min; every minute up to 10 min; and at 15, 20, 30, 60, 90, and 120 min after injection of the radiopharmaceutical. Samples were chilled to slow metabolic degradation and were centrifuged at high gravity for 6 min, separating the plasma fraction from the red blood cells and proteins. Counts in samples (200 μL) of the plasma-rich supernatant were determined in duplicate with an NaI Packard Cobra well γ-counter (Perkin-Elmer) and decay corrected to the injection time.

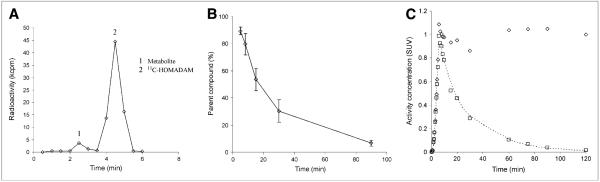
Six additional larger samples (5 mL) were collected at 5, 8, 15, 30, and 90 min after injection in ethylenediaminetetraacetic acid; mixed; and chilled on ice to determine the ratio of the parent compound to its metabolic derivatives. These samples were deproteinized by the addition of 0.7 mL of acetonitrile, vortexed for 1 min, and centrifuged as described earlier to recover the protein-free plasma supernatant. The protein-free plasma was then filtered and injected into a reverse-phase Waters Xterra RP 18 high-performance liquid chromatography (HPLC) column (mobile phase of methanol:water:triethylamine, 70%:30%:0.1%) (Waters Corp.) coupled to a radiometric detector (BioScan). All mass peaks were recorded with Waters millennium software, integrated, and reported as a percentage of the parent peak. Input functions were calculated from the total parent fraction in the plasma counts and were linearly interpolated to the 21 arterial blood sampling time points over the imaging course (Fig. 1). Parent compound radioactivity concentrations in blood were converted to standardized uptake values and fitted to a sum of 2 gaussians and 3 exponentials by minimizing the residual squared sum. The fit provided an analytic form of the input function suitable for model optimization routines.

FIGURE 1.

(A) Chromatogram of ¹¹C-HOMADAM and metabolite in plasma 5 min after injection. (B) measured fraction of ¹¹C-HOMADAM (parent) in plasma. (C) Representative arterial plasma time–activity curve from female volunteer (weight, 60.5 kg) injected with 718 MBq of ¹¹C-HOMADAM. □ = ¹¹C-HOMADAM; ◇ = total; broken line represents fit. Standardized uptake value (SUV) of 1 in this plot corresponded to plasma radioactivity concentration of 12 kBq/mL.

Image Analysis

Images were reconstructed with an ordinary Poisson ordered-subset expectation maximization (OP-OSEm) algorithm (6 iterations, 16 subsets) at a resolution of 2.2 mm and postsmoothed with a 4-mm FWHm gaussian filter. The quantitative accuracy of HRRT data reconstructed with OP-OSEm was shown to be within 10%–15% of that of clinical HR+ scanners (Siemens) for brain phantom measurements at frame durations of greater than 30 s (18). In a comparison study in which HRRT and HR+ scanners were used to evaluate dopamine transporter binding with ¹¹C-PE2I in age- and sex-matched controls, it was revealed that comparable binding potentials and intersubject variabilities could be achieved by smoothing the HRRT images with a 5.5-mm FWHm gaussian filter to match the resolution of the HR+ images (19). In the absence of smoothing (native HRRT resolution), dopamine transporter binding potentials obtained with the HRRT scanner were greater than those obtained with the HR+ scanner by as much as 30%–92%. There is still very little published literature available to fully appreciate the high-resolution benefit of the HRRT system. Therefore, to minimize the effects of low-count statistics and differences in resolution between the HRRT and clinical scanners, frame durations were limited to ≥30 s, and images were postsmoothed with a 4-mm gaussian filter after reconstruction.

After reconstruction, intraframe alignment was performed with a mutual information metric (20). Data were summed from 10 to 45 min and coregistered with each subject’s mRI for ROI drawing. ROIs were drawn manually on MR images in 4 consecutive planes by following anatomic boundaries provided by a brain atlas (21). The raphe nuclei in the brain stem cannot be separated from one another on MR images and therefore were delineated on fused PET/MR images by use of a circular ROI with a 6-mm diameter. The tectum of the midbrain and the dorsal raphe nucleus were distinguished from one another on late summed PET images (45–95 min), on which these regions showed individual focal uptake centers. A total of 14 regions were transferred to PET images, and regional radioactivity concentrations were calculated for each frame, corrected for decay, and plotted over time. Data from bilateral regions were pooled.

The time dependence of the regional distribution volumes calculated from the estimated model parameters was investigated with datasets containing 15–145 min of scan data in 10-min successively decreasing increments. V_T values derived from the arterial-input compartment model were normalized to V_T values calculated from all 145 min of data and expressed as a percentage. The variability in the percentage was calculated from the SDs of the normalized values and plotted. V_T was considered to be time independent when the normalized V_T was within 10% of that derived at 145 min.

Quantitative Analysis

The general 4-parameter (K₁, k₂, k₃, and k₄) compartment model assumes that the compartments with free uptake and nonspecific binding equilibrate rapidly, resulting in 2 tissue compartments. K₁ (mL/min/g) and k₂ (1/min) represent the unidirectional fractional rate constants, corresponding to the influx and efflux of radioligand across the blood–brain barrier, respectively. k₃ (1/min) represents the product of the radioligand association rate and the number of available binding sites, and k₄ (1/min) represents the rate of disassociation between the brain and (specifically bound) receptor compartments. These parameters were determined with an iterative nonlinear least-squares fit by use of the Powell method implemented in the Interactive Data Language (ITT Visual Solutions Inc.) as previously described (22). Measured data were weighted by individual frame durations in the χ² model.

The 4-parameter compartment model with arterial radioactivity concentration as the input function did not provide a unique solution for all subjects or brain regions. The ratios of the kinetic parameters were also not stable and were underidentified. The failure of the 4-parameter model to provide stable rate constants was also reported in the modeling of ¹¹C-DASB and ¹¹C-McN-5652 (12,13,15). A potential explanation is that the binding and release of ¹¹C-HOMADAM are rapid compared with the transport of the radioligand across the blood–brain barrier. Reducing the number of floating parameters in the model to 2 resulted in more stable kinetic rate constants. This parameter reduction required the efflux rate (k₂) to be redefined as

$$k_2^{\prime }=k_2∕[1+(k_3∕k_4\left)\right].$$ Eq. 1

The rapid binding and disassociation of ¹¹C-HOMADAM indicate that it is reversibly bound and therefore may lend itself to a quantitative graphic approach as described by Logan et al. (23).

In brief, the linear relationship

$${\int }_0^T\mathrm{Aroi}\left(\text{t}\right)\mathrm{dt}∕\mathrm{Aroi}\left(\text{T}\right)={\mathrm{V}}_{\mathrm{T}}\times {\int }_0^{\mathrm{T}}{\mathrm{C}}_{\mathrm{p}}\left(\text{t}\right)\mathrm{dt}∕\mathrm{Aroi}\left(\text{T}\right)+b$$

, where Aroi(t) is the regional time–activity curve and C_p(t) is the plasma input, is plotted. After an effective equilibration time, the slope of the linear portion is equal to V_T with intercept b (23).

A simplified modeling approach was explored with reference tissue as the input. The 5-parameter (R, k₂, k_2a, k₃, and k₄) reference tissue model described by Lammertsma et al. (24) was reduced to 3 parameters (R, k₂, and k_2a), where k_2a is the rate of efflux from the compartment with specific uptake to the plasma compartment in the reference tissue, analogous to k₂’ in the 2-parameter compartment model. This parameter reduction also assumes that free, nonspecific, and specific uptake is rapid compared with transport. A least-squares minimization was performed by use of the Powell method, simultaneously fitting all 3 parameters (R, k₂, and k_2a).

Similarly, the graphic approach described by Logan et al. (23) was applied with reference tissue as the input. The result of substituting a reference region into the previously described linear relationship is a slope equal to the ratio of the distribution volumes of the target region and the reference region. Given that the distribution volume cannot be calculated directly with reference tissue, the distribution volume ratios were calculated for all of the models, and the binding potentials were compared.

Distribution volumes can be used to estimate receptor densities by comparing the target region with a reference region that exhibits negligibly low specific uptake, such as that found in the cerebellum (25). Furthermore, the binding potential (BP_ND) can be defined as the distribution volume ratio corrected for nondisplaceable uptake (26), as follows:

$${\mathrm{BP}}_{\mathrm{ND}}={\mathrm{f}}_{\mathrm{ND}}{\mathrm{B}}_{\mathrm{avail}}∕{\mathrm{K}}_{\mathrm{d}}=({\mathrm{V}}_{\mathrm{T}}∕{\mathrm{V}}_{\text{T}-\mathrm{Ref}})-1,$$ Eq. 2

where f_ND represents the free fraction of radioligand in the nondisplaceable tissue region, B_avail (mol/L) is the number of available binding sites, K_d is the equilibrium dissociation constant, and V_Tref is the reference tissue distribution volume. V_T values derived from the 2-parameter model and the arterial-input graphic approach can be substituted into Equation 2. Calculation of this binding potential depends strongly on the assumption that uptake in the reference region is nondisplaceable and does not vary significantly between subject groups.

In the reference tissue model, the ROI influx rate, K₁, and the reference region influx rate, K₁’, enter the equations as a ratio, R, and were allowed to vary with respect to k₂/k_2a. Therefore, the parameters fitted in the reference tissue model can be rearranged to define the ratio of the target distribution volume to the reference distribution volume, R × (k_2a/k₂). A binding potential analogous to that calculated in Equation 2 can then be computed with the reference tissue model (BP_ND-Ref), as follows:

$${\mathrm{BP}}_{\mathrm{ND}-\mathrm{Ref}}=[\mathrm{R}\times (k_{2\mathrm{a}}∕k_2\left)\right]-1.$$ Eq. 3

Likewise, the binding potential computed with the Logan graphic approach with reference tissue as the input (BP_ND-Logan) is equal to

$${\mathrm{BP}}_{\mathrm{ND}-\mathrm{Logan}}=\mathrm{DVR}-1,$$ Eq. 4

where DVR is distribution volume ratio.

Statistics

Data are presented as mean ± SD. Given the small sample size, group comparisons were analyzed with the Kruskal–Wallis one-way ANOVA. Paired comparisons were performed with a Wilcoxon signed rank test, the nonparametric analog of the matched-pairs Student t test. A Bonferroni correction was applied to accommodate multiple comparisons, and the type I error for each paired test is reported with the P value. Correlations between the arterial-input compartment models and each of the reference methods were calculated with Spearman rank analysis. Comparisons of the 2- and 4-parameter arterial-input compartment models were performed by calculating the Akaike information criterion (AIC) (27) and the Schwarz criterion (SC) (28). Small AIC and SC values indicated a more statistically preferable fit to the data for a given number of parameters.

RESULTS

Three of the 8 healthy volunteers did not undergo arterial sampling because of difficulties occurring with the catheter placement and therefore were not included in the arterial-input compartment models or the graphic analysis. One primary polar metabolite appeared rapidly in the HPLC analysis of arterial blood; it had a retention time shorter than that of the parent compound (Fig. 1A). The radiometric detector coupled to the HPLC output was not sensitive enough to accurately determine the parent and metabolite peaks for aliquots drawn after 30 min. Therefore, the radiometric measurements were duplicated on the NaI Packard Cobra well γ-counter by determining counts in 30-s fractions from the HPLC. This method was adopted as a modification of previously described methods for determining the fraction of the parent compound at all blood sample times. The fraction of ¹¹C-HOMADAM radioactivity in plasma decreased rapidly over time, from an average of 89% at 5 min after injection to 7% at 90 min after injection (Fig. 1B). The total plasma radioactivity curves were corrected for the presence of the ¹¹C-HOMADAM metabolite and plotted over time (Fig. 1C).

Summed images acquired from 10 to 45 min in one female subject showed rapid accumulation of ¹¹C-HOMADAM in SERT-rich regions of the raphe nuclei, midbrain, hypothalamus, and striatum (Fig. 2). Radioactivity concentrations peaked in these SERT-rich regions at 30 min and in the dorsal raphe slightly later, at 40 min. Radioactivity concentrations in the cortical regions, including the cerebellum, reached a peak earlier, at 20 min. The lowest tracer concentration at all time points was observed in the cerebellum. The rank order of ¹¹C-HOMADAM uptake in the brain at 30 min was as follows: midbrain > hypothalamus > pulvinar thalamus > striatum > cingulate cortex > cerebellum.

FIGURE 2.

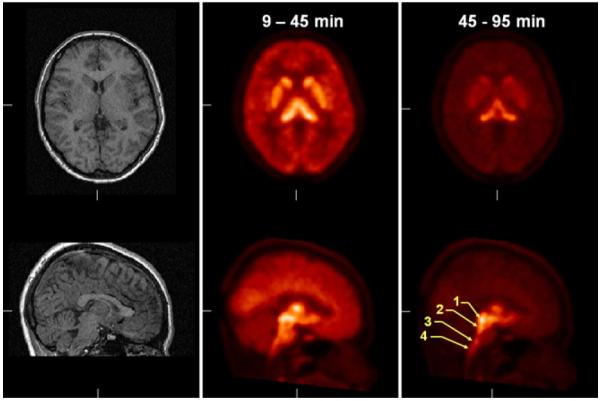
Coregistered MR images (left) and summed PET images (middle and right) showing regional radioactivity uptake of ¹¹C-HOMADAM. 1 = midbrain; 2 = dorsal raphe; 3 = magnus raphe; 4 = pallidus raphe.

The 4- and 2-parameter compartment models converged in all 14 regions for all subjects who underwent arterial sampling. The 2- and 4-parameter fits described the time–activity curves well but were indistinguishable from one another. The 4-parameter compartment model did not provide stable ratios for the kinetic parameters k₃/k₄ or (K₁/k₂) × [1 + (k₃/k₄)], and the ratios were underidentified for the analyzed time–activity information. The 2-parameter compartment model was statistically superior to the 4-parameter model in describing the time–activity curves in all brain regions. A comparison of the goodness-of-fit metrics AIC and SC in the midbrain is provided in Table 1.

TABLE 1.

Statistical Comparison of 2- and 4-Parameter Arterial-Input Models in Midbrain

Subject	No. of parameters in model	K1	k2	k3	k4	VT	RSS	AIC	SC
1	2	0.72	0.02			33.0	4.18	3	9
	4	0.66	0.22	1.26	0.12	33.0	4.20	7	15
2	2	0.81	0.02			44.3	0.87	4	12
	4	0.70	0.03	0.08	0.03	90.3	0.82	8	19
3	2	0.48	0.02			25.6	0.68	4	13
	4	0.39	0.02	0.03	0.15	25.6	0.69	8	19
4	2	0.68	0.03			26.3	3.94	3	9
	4	0.59	0.04	0.26	0.50	24.9	3.94	7	16
5	2	0.39	0.02			17.8	1.55	4	11
	4	0.32	0.03	0.26	0.29	17.8	1.54	8	17

DV = distribution volume; RSS = residual sum of squares.

The 2-parameter compartment model yielded a good fit to the regional time–activity curves and identified all rate constants in the ROIs (Fig. 3). Regional distribution volumes indicated the presence of high radioligand accumulation in the midbrain and low radioligand accumulation in the cerebellum (Table 2). Significant differences were observed in distribution volumes in regions of the midbrain, striatum, and cerebellum within each model (P < 0.01; α = 0.02). The distribution volumes calculated from the arterial-input graphic analysis were, on average, lower than those calculated from the 2-parameter compartment model (P < 0.02; α = 0.05), but the methods were highly correlated (ρ = 0.99; confidence interval = 0.989–0.999; P < 0.001).

FIGURE 3.

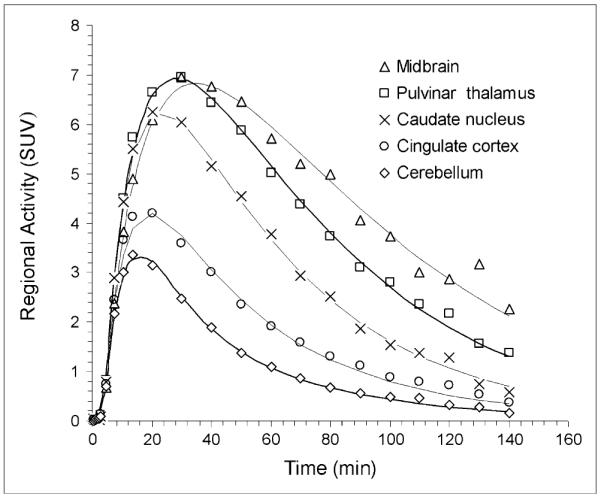
Time–activity curves of ¹¹C-HOMADAM concentrations in midbrain, pulvinar thalamus, caudated nucleus, cingulate cortex, and cerebellum. Solid lines represent 2-parameter compartment model fits. SUV = standardized uptake value.

TABLE 2.

Rate Constants and Calculated V_T for 2-Parameter Compartment Model and Logan Graphic Analysis

Region	Mean ± SD				Minimum scan duration (min)
	K1 (mL/min/g)	k2 (1/min)	VT (mL/g)	VT (graphic)
Cerebellum	0.77 ± 0.46	0.12 ± 0.07	6.3 ± 1.6	4.5 ± 1.7	25
Cingulate cortex	0.65 ± 0.2	0.06 ± 0.02	10.6 ± 2.8	6.9 ± 1.6	35
Dorsal raphe	0.58 ± 0.17	0.02 ± 0.01	31.2 ± 11.9	17.7 ± 6.7	35
Amygdalae	0.48 ± 0.17	0.03 ± 0.01	15.3 ± 4.6	9.3 ± 2.2	65
Caudate nucleus	0.84 ± 0.29	0.05 ± 0.02	17.7 ± 4.8	11.2 ± 2.7	35
Frontal cortex	0.77 ± 0.42	0.09 ± 0.05	9.1 ± 3.0	5.9 ± 1.5	35
Occipital cortex	0.65 ± 0.32	0.07 ± 0.03	9.0 ± 3.0	5.9 ± 1.9	45
Pulvinar thalamus	0.73 ± 0.22	0.03 ± 0.01	23.3 ± 6.2	14.4 ± 3.9	35
Putamen	0.89 ± 0.33	0.05 ± 0.02	19.0 ± 5.1	12.0 ± 2.5	35
Magnus raphe	0.55 ± 0.19	0.03 ± 0.01	17.6 ± 5.7	10.7 ± 3.3	35
Hypothalamus	0.65 ± 0.21	0.02 ± 0.01	28.4 ± 8.9	17.8 ± 6.8	45
Midbrain	0.61 ± 0.17	0.02 ± 0.00	29.4 ± 9.9	17.2 ± 5.5	45
Pons	0.56 ± 0.24	0.06 ± 0.02	9.6 ± 3.3	6.1 ± 2.2	35
Pallidus raphe	0.52 ± 0.16	0.03 ± 0.01	17.1 ± 6.3	10.5 ± 4.1	45

Binding potentials calculated from Equations 2–4 agreed well for the modeling methods (Table 3). On average, binding potentials were highest with the 2-parameter model, followed by the reference tissue model, the Logan model with reference tissue as the input, and the arterial-input Logan model. A statistically significant difference was not found for the binding potentials calculated with the 4 modeling approaches (Kruskal–Wallis test value = 1.44; P = 0.69; α = 0.05). The rank order from SERT-rich regions to SERT-poor regions was consistent across methods and matched that observed in postmortem studies (29–31). Cortes et al. (30) reported a higher concentration of serotonin in the dorsal raphe than in the midbrain, a finding that is consistent with those of the 2-parameter compartment model and reference model approaches. The graphic approach was not able to estimate the higher concentration of serotonin in the dorsal raphe than in the midbrain.

TABLE 3.

SERT Binding Parameters for 2-Parameter Compartment Model, Reference Tissue Model, and Logan Graphic Method

	Mean ± SD
	Arterial-input model (n = 5)		Reference-input model (n = 8)
Region	BPND	BPND-Logan	BPND-Ref	BPND-Logan
Dorsal raphe	3.84 ± 0.74	2.91 ± 0.34	3.58 ± 0.59	3.10 ± 0.53
Midbrain	3.60 ± 0.38	2.92 ± 0.19	3.57 ± 0.40	3.30 ± 0.40
Hypothalamus	3.46 ± 0.43	2.84 ± 0.45	3.31 ± 0.39	3.11 ± 0.35
Pulvinar thalamus	2.72 ± 0.35	2.27 ± 0.34	2.59 ± 0.28	2.51 ± 0.22
Putamen	2.06 ± 0.52	1.77 ± 0.5	1.83 ± 0.34	1.81 ± 0.31
Caudate nucleus	1.83 ± 0.32	1.55 ± 0.33	1.66 ± 0.20	1.57 ± 0.23
Magnus raphe	1.78 ± 0.37	1.41 ± 0.22	1.59 ± 0.21	1.48 ± 0.20
Pallidus raphe	1.65 ± 0.36	1.31 ± 0.18	1.63 ± 0.30	1.47 ± 0.26
Amygdalae	1.43 ± 0.36	1.12 ± 0.31	1.28 ± 0.18	1.22 ± 0.14
Cingulate cortex	0.68 ± 0.14	0.58 ± 0.21	0.61 ± 0.13	0.60 ± 0.13
Pons	0.50 ± 0.15	0.36 ± 0.04	0.54 ± 0.20	0.45 ± 0.13
Frontal cortex	0.44 ± 0.24	0.36 ± 0.24	0.57 ± 0.57	0.34 ± 0.19
Occipital cortex	0.41 ± 0.15	0.32 ± 0.15	0.44 ± 0.15	0.45 ± 0.16

Values are listed in descending order.

The stability of the distribution volumes for decreasing scan durations relative to the complete 145-min dataset is shown in Table 2. The mean ± SD regional scan duration for a time-independent measure of V_T was 39 ± 9 min. The plot of V_T over time in the midbrain is shown in Figure 4 and is similar to that in the other regions. Stable measurements of V_T in the midbrain were achieved with 40 min of scan data. In addition, the effective equilibration time for the graphic approach was calculated from the minimum time point resulting in a slope change of less than 5% and was found to occur at 23 ± 13 min into the scan. A representative plot obtained with the Logan graphic approach with reference tissue as the input is shown in Figure 5.

FIGURE 4.

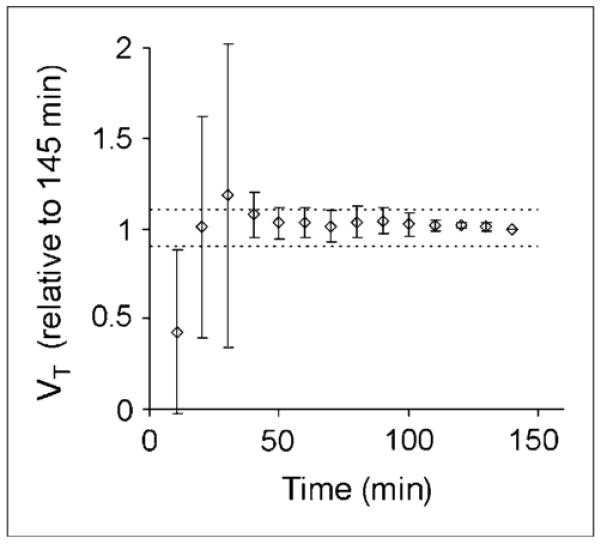
Effect of study duration on stability of V_T calculated from 2-parameter arterial-input compartment model for durations of 10–145 min. V_T is plotted relative to that calculated from 145 min of scan data (n = 5).

FIGURE 5.

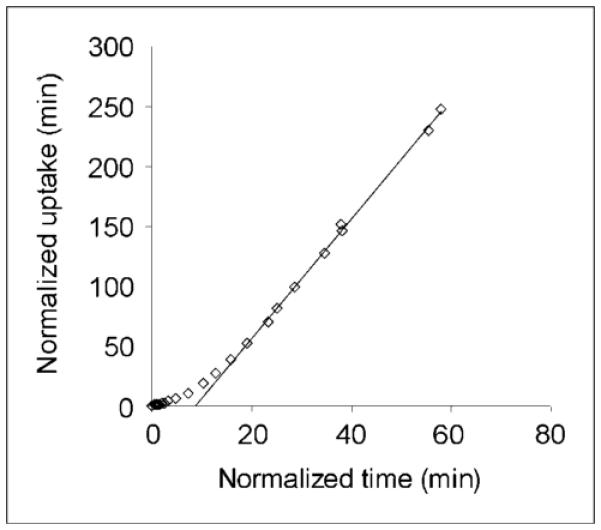
Logan plot of ¹¹C-HOMADAM uptake in midbrain with cerebellum as reference input. Mean ± SD effective equilibration for all regions was estimated to occur at 23 ± 13 min of scanning.

DISCUSSION

The objective of this study was to evaluate kinetic modeling approaches for estimating SERT densities with ¹¹C-HOMADAM in the human brain. In the application of a 2-parameter compartment model with arterial input, the minimization routine converged in all cases, and the model had a statistically more appropriate number of parameters than the 4-parameter model. The 2-parameter model in this analysis was consistent with the 1-compartment model chosen for the SERT imaging agents ¹¹C-McN-5652 (11,14,32) and ¹¹C-DASB (12,13).

The ratio of the number of prompt events recorded in the last two 10-min frames across the subjects ranged from 2.2 to 6.8 (125–135 min) and 1.9 to 4.8 (135–145 min) times the prompt event total generated by the detector crystal’s intrinsic radioactivity, ¹⁷⁶Lu (2.6%; half-life = 3.7 × 10¹⁰ y), present in lutetium oxyorthosilicate crystals. The intrinsic prompt event rate was estimated from a 10-min acquisition of a 20-cm right cylinder phantom (no radioactivity). The decreased image statistics in these last few frames posed concerns about the accuracy of estimating the random and scatter contributions. van Velden et al. (18) reported that reconstructed radioactivity concentrations can deviate by as much as 20% and 50% in regions of gray matter and white matter, respectively. The influence of low-count reconstructions in the present study appeared to be minimal on the basis of the time stability data presented in Figure 4, which showed that the midbrain distribution volume varied by less than 4% for 90 or 145 min of scan data.

The values for the kinetic parameter representing tracer influx across the blood–brain barrier, K₁, were high, ranging from 48 ± 17 mL/min/100 g in the amygdalae to 89 ± 33 mL/min/100 g in the putamen. Brain blood flow studies in healthy human subjects have reported values ranging from 40 to 100 mL/min/100 g (33,34), suggesting that ¹¹C-HOMADAM readily crosses the blood–brain barrier and that it is highly extracted from the plasma compartment. Although it has been acknowledged that individual rate constant estimations are less reliable than estimations for grouped parameters (e.g., V_T) (35), the high influx rate estimates may also have been attributable to ¹¹C-HOMADAM that was bound to protein and that was available for binding to SERT. It is also possible that additional binding took place in the blood samples between the time of collection and the time of analysis. Measurements of the rates of dissociation from proteins in plasma were not obtained to prove this hypothesis; therefore, this factor represented an added source of variability in the binding potential calculation relative to the preferable binding potential parameter, BP_F, the ratio of specifically bound to free radioligand in tissue at equilibrium (26).

The distribution volumes of ¹¹C-HOMADAM in SERT-rich regions were comparable to those reported for ¹¹C-DASB (12,13), ¹¹C-McN-5652 (14), and ¹¹C-MADAM (10); the distribution volume of ¹¹C-HOMADAM in the cerebellum reference region was lower than that of ¹¹C-DASB and ¹¹C-McN-5652 but was similar to that of ¹¹C-MADAM (10). The density of SERT in the cerebellum is not zero (29–31). The choice of the cerebellum as a reference region was based on a previous ¹¹C-HOMADAM primate chase study in which R,S-citalopram was administered 40 min into the uptake study, resulting in significant displacement of ¹¹C-HOMADAM radioactivity from SERT-rich sites to levels of the cerebellum (16). No observable radioactivity concentration changes were observed in the cerebellum after the chase, indicating that the SERT concentration in this region of the primate brain was negligible. On the basis of these primate model results and good agreement in binding potentials between the 2-parameter arterial-input compartment model and the reference tissue model, the cerebellum was considered to be an appropriate reference tissue for evaluating SERT density with ¹¹C-HOMADAM in humans.

Binding potentials were comparable across methods; the 2-parameter compartment model and the reference tissue model values were nearly identical and estimated the same SERT density rank orders in the brain. On average, the graphic approach consistently underestimated binding potentials by 20% compared with the 2-parameter compartment model (Table 3); this tendency of the graphic approach was shown to be caused by increasing statistical noise in the image data (36,37). The estimation of kinetic parameters from the compartment models was not affected by the same systematic bias as that from the graphic approach, but several authors have described methods to account for underestimation of the distribution volume ratio from Logan analysis (37–40). Furthermore, the graphic approach did not estimate the same SERT density rank order as the compartment models. Therefore, the graphic method originally described by Logan et al. (41) is not recommended.

Calculated binding potentials were 1.4, 1.5, and 2 times higher for ¹¹C-HOMADAM in SERT-rich subcortical regions of the striatum, midbrain, and thalamus, respectively, than for ¹¹C-DASB (12,13); similarly, binding potentials in the same regions were 2.1, 2.5, and 4.2 times higher than those for ¹¹C-McN-5652 (13), indicating higher image contrast and specifically bound to reference tissue signal. The comparable distribution volumes of ¹¹C-DASB, ¹¹C-McN-5652, and ¹¹C-HOMADAM in SERT-rich regions suggested that the estimated model parameters were not markedly biased by resolution effects, as discussed by Leroy et al. (19). The most apparent difference among these tracers was the distribution volume in the cerebellum, which was calculated to be 6.3 ± 1.6 mL/g for ¹¹C-HOMADAM; in comparison, the distribution volumes were 10.1 ± 2.0 mL/g for ¹¹C-DASB and 20.8 ± 3.6 mL/g for ¹¹C-McN-5652 (13). HRRT scanning of age-matched controls with ¹¹C-McN-5652, ¹¹C-DASB, and ¹¹C-HOMADAM would provide a more definitive comparison of binding potential data, given that HRRT quantitation can vary by up to 10%–15% from that of lower-resolution scanners, as discussed earlier.

CONCLUSION

Arterial-input and reference tissue methods provided appropriate kinetic models for the characterization of ¹¹C-HOMADAM in SERT-rich areas of the raphe nuclei, midbrain, and striatum. The use of the cerebellum as the reference region provided a reliable estimation of the model parameters that agreed with the postmortem SERT distribution. The high correlation between the 2-parameter compartment model and the reference tissue model suggested that a reference tissue model without a third compartment offers a sufficient number of parameters to describe the binding of ¹¹C-HOMADAM to SERT. This method offers reduced variability because of the absence of arterial sampling, less sensitivity to changes in regional blood flow, and straight-forward application for routine use in future studies.