Optimal Weights for Multi-Atlas Label Fusion

Abstract

Multi-atlas based segmentation has been applied widely in medical image analysis. For label fusion, previous studies show that image similarity-based local weighting techniques produce the most accurate results. However, these methods ignore the correlations between results produced by different atlases. Furthermore, they rely on preselected weighting models and ad hoc methods to choose model parameters. We propose a novel label fusion method to address these limitations. Our formulation directly aims at reducing the expectation of the combined error and can be efficiently solved in a closed form. In our hippocampus segmentation experiment, our method significantly outperforms similarity-based local weighting. Using 20 atlases, we produce results with 0.898 ± 0.019 Dice overlap to manual labelings for controls.

1 Introduction

Atlas-based segmentation is motivated by the observation that segmentation strongly correlates with image appearance. A target image can be segmented by referring to labeled images that have similar image appearance. After warping an atlas’s reference image to the target image via deformable registration, one can directly transfer labels from the atlas to the target image. As an extension, multi-atlas based segmentation makes use of more than one atlas to compensate for potential errors imposed by using any single atlas.

Errors produced by atlas-based segmentation can be attributed to dissimilarity in anatomy and/or appearance between the atlas and the target image. Recent research has been focusing on addressing this problem. For instance, research has been done on optimally constructing a single atlas from training data that is the most representative of a population [8]. Constructing multiple representative atlases from training data has been considered as well, and usually works better than single-atlas based approaches. Multi-atlas construction can be done either by constructing one representative atlas for each mode obtained from clustering training images [1] or by simply selecting the most relevant atlases for the target image on the fly [13]. Either way, one needs to combine the segmentation results obtained by referring to different atlases to produce the final solution. In this regard, image similarity-based local weighting has been shown to be the most accurate label fusion strategy [2, 14].

For label fusion, similarity-based local weighting techniques assign higher weights to atlases that have more similar appearance to the target image. These methods require a pre-selected weighting model to transfer local appearance similarity into non-negative weights. The optimal parameter of the weighting model usually needs to be determined in an ad hoc fashion through experimental validation. More important, the correlations between the results produced by different atlases are completely ignored. As a result, these methods cannot produce optimal solutions when the results are correlated, e.g. instead of producing random errors, different atlases tend to select the same wrong label.

In this paper, we propose a novel label fusion approach to automatically determine the optimal weights. Our key idea is that to minimize errors in the combined result, assigning weights to atlases should explicitly consider the correlations between results produced by different atlases with respect to the target image. Under this formulation, the optimal label fusion weights can be efficiently computed from the covariance matrix in a closed form. To estimate the correlations between atlases, we follow the basic assumption behind atlas-based segmentation and estimate label correlations from local appearance correlations between the atlases. We apply our method to segment the hippocampus from MRI and show significant improvements over similarity-based label fusion with local weighting.

2 Label fusion based multi-atlas segmentation

In this section, we briefly review previous label fusion methods. Let T_F be a target image and $A^1=\left(A_F^1,A_S^1\right),\dots ,A^n=\left(A_F^n,A_S^n\right)$ be n registered atlases. $A_F^i\text{ and }{A}_S^i$ denote the i_th warped atlas image and the corresponding warped manual segmentation. Each $A_S^i$ is a candidate segmentation for the target image. Label fusion is the process combining these candidate segmentations to produce the final segmentation. For example, the majority voting method [6, 9] simply counts the votes for each label from all registered atlases and chooses the label receiving the most votes. The final segmentation T̂_S is produced by:

$${\widehat{T}}_S(x)={\text{argmax}}_{l\in \{1\dots L\}}{p}_x(l)$$ (1)

where l indexes through labels and L is the number of labels. x indexes through image voxels. p_x(l) is the votes for label l at x, given by:

$$p_x(l)={\displaystyle \sum _{i=1}^n}\frac{1}{n}p(l|A^i,x)$$ (2)

where p(l|Aⁱ, x) is the posterior probability that Aⁱ votes for label l at x, with ∑_{l∈{1,…,L}} p(l|Aⁱ, x) = 1. Typically, for deterministic atlases that have one unique label for every location, p(l|Aⁱ, x) is 1 if $l=A_S^i(x)$ and 0 otherwise. Continuous label posterior probabilities can be used as well especially when probabilistic atlases are involved. Even for deterministic atlases, continuous label posterior probabilities still can be derived, see [14] for some examples.

Majority voting makes a strong assumption that different atlases produce equally accurate segmentations for the target image. Since atlas-based segmentation uses example-based knowledge representations, the segmentation accuracy produced by an atlas depends on the appearance similarity between the warped atlas image and the target image. To improve label fusion accuracy, recent work focuses on developing segmentation quality estimations based on local appearance similarity. For instance, the votes received by label l can be estimated by:

$$p_x\left(l\right)={\displaystyle \sum _{i=1}^n}{w}^i\left(x\right)p\left(l|A^i,x\right)$$ (3)

wⁱ(x) is a local weight assigned to the i_th atlas, with ${\displaystyle {\sum }_{i=1}^n}{w}^i(x)=1$. The weights are determined based on the quality of segmentation produced by each atlas such that more accurate segmentations play more important roles in the final decision. One way to estimate the weight is based on local image similarity under the assumption that images with similar appearance are more likely to have similar segmentations. When the summed squared distance (SSD) and a Gaussian weighting model are used [14], the weights can be estimated by:

$$w^i(x)=\frac{1}{Z(x)}\mathit{\text{exp}}(-{\displaystyle \sum _{y\in 𝒩(x)}}{[A_F^i(y)-T_F(y)]}^2/\sigma )$$ (4)

where 𝒩(x) defines a neighborhood around x and $Z(x)={\displaystyle {\sum }_{i=1}^n}{w}^i(x)$ is a normalization constant. In our experiment, we use a (2r + 1) × (2r + 1) × (2r + 1) cube-shaped neighborhood specified by the radius r. Since segmentation quality usually is nonuniform over the entire image, the estimation is applied based on local appearance dissimilarity. The inverse distance weighting has been applied as well [2]:

$$w^i(x)=\frac{1}{Z(x)}{\left[{\displaystyle \sum _{y\in 𝒩(x)}}{(A_F^i(y)-T_F(y))}^2\right]}^{-\beta }$$ (5)

where σ and β are model parameters controlling the weight distribution. Experimental validations usually are required to choose the optimal parameters. Furthermore, the correlations between atlases are not considered in the weight estimation. Next, we introduce a method that does not have these limitations.

3 Estimating optimal weights through covariance matrix

The vote produced by any single atlas for a label l can be modeled as the true label distribution, p(l|T_F, x), plus some random errors, i.e.:

$$p(l|A^i,x)=p(l|T_F,x)+\epsilon (A^i,x)$$ (6)

Averaging over all segmentations produced by the same error distribution, the error produced by Aⁱ at x can be quantified by:

$$E\left[{(p(l|A^i,x)-p(l|T_F,x))}^2\right]=E\left[\epsilon {(A^i,x)}^2\right]$$ (7)

After combining results from multiple atlases, the error can be quantified by:

$$E\left[{(p_x(l)-p(l|T_F,x))}^2\right]={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{w}^i(x)w^j(x)M_x(i,j)$$ (8)

where p_x(l) is given by (3) and M_x is the covariance matrix with:

$$M_x(i,j)=E[(p(l|A^i,x)-p(l|T_F,x))(p(l|A^j,x)-p(l|T_F,x))]$$ (9)

M_x(i, i) quantifies the errors produced by i_th atlas and M_x(i, j) estimates the correlation between two atlases w.r.t. the target image when i ≠ j. Positive correlations indicate that the corresponding atlases tend to make similar errors, e.g., they tend to vote for the same wrong label. Negative correlations indicate that the corresponding atlases tend to make opposite errors. To facilitate our analysis, we rewrite (8) in matrix format as follows:

$$E\left[{(p_x(l)-p(l|T_F,x))}^2\right]=W_x^t{M}_x{W}_x$$ (10)

where W_x = [w¹(x); …;wⁿ(x)] and t stands for transpose. For optimal label fusion, the weights should be selected s.t. the combined error is minimized, i.e.,

$$\begin{array}{ccc}{W}_x^{*}=\underset{W_x}{\text{argmin}}{W}_x^t{M}_x{W}_x\hfill & \text{subject to}\hfill & \hfill {\displaystyle \sum _{i=1}^n{W}_x(i)=1}\hfill \end{array}$$ (11)

The optimal weights can be solved via applying Lagrange multipliers, provided the covariance matrix M_x. The solution is:

$$W_x=\frac{M_x^{-1}{1}_n}{1_n^t{M}_x^{-1}{1}_n}$$ (12)

where 1_n = [1; 1; …; 1] is a vector of size n. When M_x is not full rank, the weights can be reliably estimated using quadratic programming optimization [11].

In fact, previous segmentation quality-based local weighting approaches can be derived from (12) by ignoring the correlations between atlases, i.e., setting M_x(i, j) = 0 for i ≠ j. The main difference is that the weights computed by our method can be either positive or negative, while the weights used by segmentation quality-based weighting are non-negative. When the segmentations produced by different atlases are positively correlated, applying negative weights to some of the atlases allows to cancel out the common errors shared by these negatively weighted atlases and other positively weighted atlases, which may result in smaller combined errors (see (8)).

3.1 Estimating correlations between atlases

Since the true label distribution p(l|T_F, x) is unknown, we seek approximations to estimate the pairwise error correlations between atlases with respect to the target image. To simplify the estimation problem, we consider binary label posterior probabilities for the target image, i.e. p(l|T_F, x) = 0 or 1. Under this constraint, error correlation between atlases are non-negative because:

$$[p(l|A^i,x)-p(l|T_F,x)][p(l|A^j,x)-p(l|T_F,x)]\ge 0\text{ for }1\le i,j\le n$$ (13)

Hence, we only need to consider the absolute label errors. Following the common assumption that image segmentation strongly correlates with image intensities, we estimate label errors by local image dissimilarities as follows:

$$|p(l|A^i,x)-p(l|T_F,x)|~|A_F^i(x)-T_F(x)|$$ (14)

Note that we use a linear function to model the relationship between segmentation labels and image intensities. Typically, the real appearance-label relationship is more complicated than linear correlations. However, as we show below, using such a simple linear model already produces excellent label fusion results. Furthermore, using intensity-based covariance estimation allows more straight-forward comparison between our method and previous label fusion methods.

Recall that the segmentation quality produced at x by an atlas is characterized by an error distribution. The estimated error (14) can be interpreted as an estimation for one random sample from this distribution. Since the registration quality produced using one atlas usually varies smoothly over spatial locations, the errors estimated at voxels near x can be considered as approximately sampled from the same error distribution as well. Hence, the error expectation produced at x can be estimated by averaging the estimated errors from its neighborhood:

$$E[|p(l|A^i,x)-p(l|T_F,x)|]~\frac{1}{|𝒩(x)|}{\displaystyle \sum _{y\in 𝒩(x)}}|A_F^i(y)-T_F(y)|$$ (15)

Similarly,

$$M_x(i,j)~\frac{1}{|𝒩(x)|}{\displaystyle \sum _{y\in 𝒩(x)}}|A_F^i(y)-T_F(y)||A_F^j(y)-T_F(y)|$$ (16)

Note that when i = j, the label error produced by any single atlas is estimated by the commonly used summed squared distance over local image intensities as $E\left[{(p(l|A^i,x)-p(l|T_F,x))}^2\right]~{\displaystyle {\sum }_{y\in 𝒩(x)}}|A_F^i(y)-T_F(y){|}^2$.

The image similarity-based estimation captures the atlas correlations produced by the actual registrations. However, local image similarity is not always a reliable estimator for registration errors, therefore may not always be reliable for estimating error correlations. To address this problem, one may also incorporate empirical covariances estimated from training data to complement the similarity-based estimation.

3.2 Toy examples

In this section, we demonstrate the usage of our method with two toy examples. In the first example, suppose that for a target image, atlases A¹ and A² produce segmentations with similar qualities at location x, but their results are uncorrelated, with the covariance matrix $M_x=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right]$ The optimal weights computed by (12) are $W_x^{*}=[0.5;0.5]$, which are the same as the solution produced by segmentation quality-based weighting. Now suppose that another atlas A³, which is identical to A¹, is added to the atlas library. Obviously, A¹ and A³ are strongly correlated because they produce identical label errors. Ignoring such correlations, quality-based weighting assigns equal weights to each of the three atlases. Hence, the final result is biased by the atlas that is repeatedly applied. However, given M_x(1, 3)=1 and M_x(2, 3)=0, our method assigns the weights, $W_x^{*}=[0.25;0.5;0.25]$. The bias caused by using A¹ twice is corrected.

Fig. 1 shows applying our method to another toy example. In this binary segmentation problem, we have five atlases. The pairwise correlations between the results produced by the atlases are all positive. Note that A¹ and A⁴ have the largest combined inter-atlas correlations, indicating that they contain the most common errors produced by all atlases. As a result, majority voting produces a result biased towards atlas A¹ and A⁴. Due to the strong correlations, similarity-based label fusion with Gaussian weighting (LWGau) reduces to single-atlas segmentation, i.e. only the most similar atlas, A³, has a non-zero weight. To compensate the overall bias towards A⁴, only A⁴ receives a negative weight by our method to cancel out the consistent errors among all atlases.

Fig. 1.

Illustration of label fusion on a toy example. The target segmentation, T, is shown on the top left corner, followed by five warped atlases, A¹ to A⁵. For simplicity, each atlas produces binary votes and we assume that the images have the same appearance patterns as the segmentations. The voting errors produced by each atlas are shown in the matrix underneath it. For similarity-based label fusion with Gaussian weighting (LWGau) and our method, the atlas weights computed for the center pixel are also used for other pixels in this example.

3.3 Remedying registration errors by local searching

As recently shown in [5], the performance of atlas-based segmentation can be moderately improved by applying a local searching technique. This method also uses local image similarity as an indicator of registration accuracy and remedies registration errors by searching for the correspondence, that gives the most similar appearance matching, within a small neighborhood around the registered correspondence in each warped atlas.

Note that the goal of image-based registration is to correspond the most similar image patches between the registered images. However, the correspondence obtained from registration may not give the maximal similarity between all corresponding regions. For instance, deformable image registration algorithms usually need to balance the image matching constraint and the regularization prior on deformation fields. A global regularization constraint on the deformation fields is necessary to clarify the ambiguous appearance-label relationship arising from employing small image patches for matching. However, enforcing a global regularization constraint on the deformation fields may compromise the local image matching constraint. In such cases, the correspondence that maximizes the appearance similarity between the warped atlas and the target image may be within a small neighborhood of the registered correspondence.

Motivated by this observation, instead of using the original registered correspondence, we remedy registration errors by searching for the correspondence, that gives the most similar appearance matching, within a small neighborhood centered around the registered correspondence in each atlas. The locally searched optimal correspondence is:

$$x^i={\text{argmin}}_{x\prime \in 𝒩\prime (x)}{[A_F^i(𝒩(x\prime ))-T_F(𝒩(x))]}^2$$ (17)

xⁱ is the location from i_th atlas with the best image matching for location x in the target image within the local neighborhood 𝒩′(x). Again, we use a cubic neighborhood definition, specified by a radius r_s. Note that 𝒩′ and 𝒩 may represent different neighborhoods and they are the only free parameters in our method. Instead of the registered corresponding patch Aⁱ(𝒩(x)), we apply the searched patch Aⁱ(𝒩(xⁱ)) to produce the fused label at x for the target image, i.e. (3) becomes $p_x(l)={\displaystyle {\sum }_{i=1}^n}{w}^i(x^i)p(l|A^i,x^i)$.

To search for the most similar image patches, larger searching windows are more desirable. However, using larger searching windows more severely compromises the regularization constraint on the deformation fields, which complicates the appearance-label relationship on local patches. As a result, the linear appearance-label function (14) becomes less accurate. It is reasonable to expect an optimal searching range that balances these two factors.

4 Experiments

In this section, we apply our method to segment the hippocampus using T1-weighted magnetic resonance imaging (MRI). The hippocampus plays an important role in memory function. Macroscopic changes in brain anatomy, detected and quantified by MRI, consistently have been shown to be highly predictive of AD pathology and highly sensitive to AD progression [15]. Accordingly, automatic hippocampus segmentation from MRI has been widely studied.

We use the data in the Alzheimer’s Disease Neuroimaging Initiative (ADNI, www.loni.ucla.edu/ADNI). Our study is conducted using 3 T MRI and only includes data from mild cognitive impairment (MCI) patients and controls. Overall, the data set contains 139 images (57 controls and 82 MCI patients). The images are acquired sagitally, with 1 × 1 mm in-plane resolution and 1.2 mm slice thickness. To obtain reference segmentation, we first apply a landmark-guided atlas-based segmentation method [12] to produce the initial segmentation for each image. Each fully-labeled hippocampus is manually edited by a trained human rater following a previously validated protocol [7].

For cross-validation evaluation, we randomly select 20 images to be the atlases and another 20 images for testing. Image guided registration is performed by the Symmetric Normalization (SyN) algorithm implemented by ANTS [3] between each pair of the atlas reference image and the test image. The cross-validation experiment is repeated 10 times. In each cross-validation experiment, a different set of atlases and testing images are randomly selected from the ADNI dataset. The results reported are averaged over the 10 experiments.

We focus on comparing with similarity-based local weighting methods, which are shown to be the most accurate label fusion methods in recent experimental studies, e.g. [2, 14]. We use majority voting (MV) and the STAPLE algorithm [16] to define the baseline performance. For each method, we use binary label posteriors obtained from the deterministic atlases. For similarity-based label fusion, we apply Gaussian weighting (4) (LWGau) and inverse distance weighting (5) (LWInv).

Our method has two parameters, r for the local appearance window used in similarity-based covariance estimation, r_s for the local searching window used in remedying registration errors. For each cross-validation experiment, the parameters are optimized by evaluating a range of values (r ∈ {1, 2, 3}; r_s ∈ {0, 1, 2, 3}) using the atlases in a leave-one-out cross-validation strategy. We measure the average overlap between the automatic segmentation of each atlas obtained via the remaining atlases and the reference segmentation of that atlas, and find the optimal parameters that maximize this average overlap. Similarly, The optimal local searching window and local appearance window are determined for LWGau and LWInv as well. In addition, the optimal model parameters are also determined for LWGau and LWInv, with the searching range σ ∈ [0.05, 0.1, …, 1] and β ∈ [0.5, 1, …, 10], respectively.

For robust image matching, instead of using the raw image intensities, we normalize the intensity vector obtained from each local image intensity patch s.t. the normalized vector has zero mean and unit variance. To reduce the noise effect, we spatially smooth the weights computed by each method for each atlas. We use mean filter smoothing with the smoothing window 𝒩, the same neighborhood used for local appearance patches.

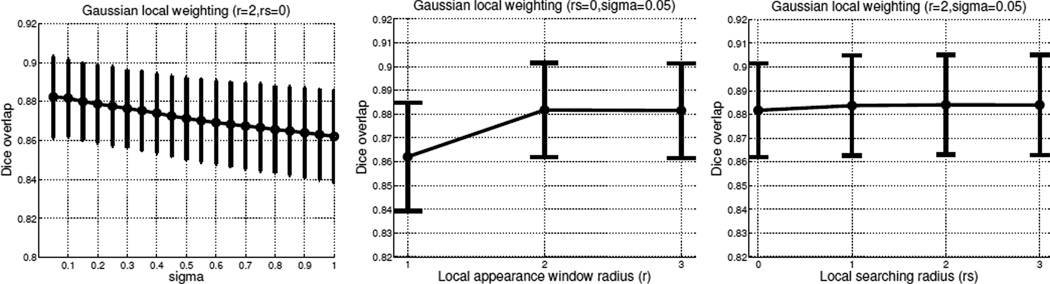
Fig. 2 shows some parameter selection experiments for LWGau in the first cross-validation experiment. The results are quantified in terms of Dice overlaps between automatic and manual segmentations of the atlases. The Dice overlap between two regions, A and B, measures the volume consistency as $\frac{2|A\cap B|}{|A|+|B|}$. For this cross-validation experiment, the selected parameters for LWGau are σ = 0.05, r=2, r_s = 2. Note that local searching only slightly improves the performance for LWGau. Similar results are observed for LWInv as well.

Fig. 2.

Visualizing some of the parameter selection experiments for LWGau using leave-one-out on the atlases for the first cross-validation experiment. The figures show the performance of LWGau with respect to the Gaussian weighting function (left), local appearance window (middle) and local searching window (right), respectively when the other two parameters are fixed (the fixed parameters are shown in the figure’s title).

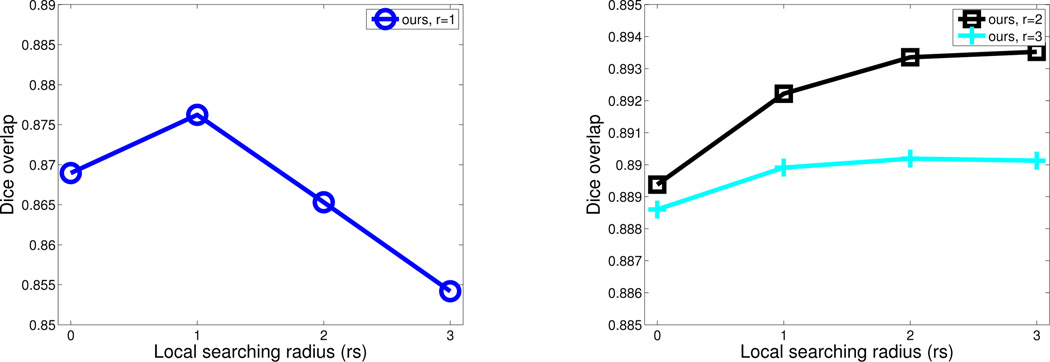
For our method, when the covariance matrix M_x is not full rank, we use the quadratic programming optimization tool quadprog in MATLAB (version R2009b) to estimate the weights. Fig. 3 shows the performance of our method when applied on the atlases in a leave-one-out fashion in the first cross-validation experiment. Without using local searching, our method already outperforms LWGau as shown in Fig. 2. Comparing to LWGau, local searching yields more improvement for our method. Overall, our method produces ~ 1% Dice improvement over LWGau and LWInv in this cross-validation experiment.

Fig. 3.

Leave-one-out performance by our method on the atlases for the first cross-validation experiment when different appearance and searching windows are used. Since the results produced using appearance window with r = 1 are significantly worse than using larger appearance windows, for better visualization, we separately plot the results using r = 1 on the left. Note that the best results produced by our method is about 1% better than those produced by LWGau in Fig. 2.

Using the appearance window with r = 1, our method performs significantly worse than using larger appearance windows. This indicates that the estimated error covariance using too small appearance windows are not reliable enough. When small appearance window with r = 1 is applied, our method performs comparably to the competing methods, but when larger appearance windows are used, our method significantly outperforms the competing methods. Note that applying larger appearance windows yields smoother local appearance similarity variations, therefore results in smoother local weights for label fusion. When large appearance windows with r > 2 are applied, the performance drops as r increases for all three methods. Hence, over-smoothing the local weights reduces the label fusion accuracy.

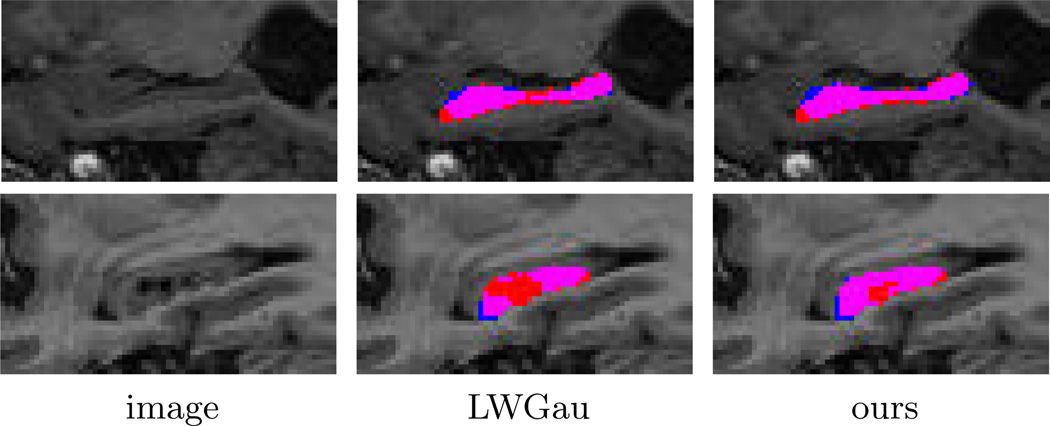
In terms of average number mislabeled voxels, LWGau and LWInv produce 369 and 372 mislabeled voxels for each hippocampus, respectively. By contrast, our method produces 352 mislabeled voxels. Table 1 shows the results in terms of Dice overlap produced by each method. Overall, LWGau and LWInv produce similar results. Both significantly outperform majority voting and the STAPLE algorithm. Our method outperforms similarity-based local weighting approaches by ~1% of Dice overlap. Since the average intra-rater segmentation overlap is 0.90, our method reduces the performance gap between MALF segmentation and intra-rater segmentation from ~2% Dice overlap to ~1% Dice overlap, a 50% improvement. Our improvement is statistically significant, with p<0.00001 on the paired Student’s t-test for each cross-validation experiment. Fig. 4 shows some results produced by LWGau and our method.

Table 1.

The performance in terms of Dice overlap produced by each method.

method	left	right
MV	0.836±0.084	0.829±0.069
STAPLE	0.846±0.086	0.841±0.086
LWGau	0.886±0.027	0.875±0.030
LWInv	0.885±0.027	0.873±0.030
ours	0.894±0.024	0.885±0.026

Fig. 4.

Sagittal views of segmentations produced by LWGau and our method. Red: manual; Blue: automatic; Pink: overlap between manual and automatic segmentation.

Comparing to the state of the art in hippocampus segmentation

As pointed out in [4], direct comparisons of quantitative segmentation results across publications are difficult and not always fair due to the inconsistency in the underlying segmentation protocol, the imaging protocol, and the patient population. However, the comparisons carried out below indicate the highly competitive performance achieved by our label fusion technique.

[4, 5, 10] present the highest published hippocampus segmentation results produced by MALF. All these methods are based on label fusion with similarity-based local weighting. The experiments in [4, 5] are conducted in a leave-one-out strategy on a data set containing 80 control subjects. They report average Dice overlaps of 0.887 and 0.884, respectively. For controls, we produce Dice overlap of 0.898 ± 0.019, more than 1% Dice overlap improvement. [10] uses a template library of 55 atlases. However, for each atlas, both the original atlas and its flipped mirror image are used. Hence, [10] effectively uses 110 atlases for label fusion. [10] reports results in Jaccard index $(\mathit{\text{JI}}(A,B)=\frac{|A\cap B|}{|A\cup B|})$ for the left side hippocampus of 10 controls, 0.80±0.03, and 10 MCI patients, 0.81±0.04. Our results for the left side hippocampus are 0.823±0.031 for controls and 0.798±0.041 for MCI patients. Overall, our results for controls are better than the state of the art and our results for MCI patients are slightly worse, but we use significantly fewer atlases than [4, 5, 10].

5 Conclusions

We proposed a novel method to derive optimal weights for label fusion. Unlike previous label fusion techniques, our method automatically computes weights by explicitly considering the error correlations between atlases. To estimate the correlations between atlases, we use a linear appearance-label model. In our experiment, our method significantly outperformed the state of the art label fusion technique, the similarity-based local weighting methods. Our hippocampus segmentation results also compare favorably to the state of the art in published work, even though we used significantly fewer atlases.