Fast and Accurate Approximation to Significance Tests in Genome-Wide Association Studies

Abstract

Genome-wide association studies commonly involve simultaneous tests of millions of single nucleotide polymorphisms (SNP) for disease association. The SNPs in nearby genomic regions, however, are often highly correlated due to linkage disequilibrium (LD, a genetic term for correlation). Simple Bonferonni correction for multiple comparisons is therefore too conservative. Permutation tests, which are often employed in practice, are both computationally expensive for genome-wide studies and limited in their scopes. We present an accurate and computationally efficient method, based on Poisson de-clumping heuristics, for approximating genome-wide significance of SNP associations. Compared with permutation tests and other multiple comparison adjustment approaches, our method computes the most accurate and robust p-value adjustments for millions of correlated comparisons within seconds. We demonstrate analytically that the accuracy and the efficiency of our method are nearly independent of the sample size, the number of SNPs, and the scale of p-values to be adjusted. In addition, our method can be easily adopted to estimate false discovery rate. When applied to genome-wide SNP datasets, we observed highly variable p-value adjustment results evaluated from different genomic regions. The variation in adjustments along the genome, however, are well conserved between the European and the African populations. The p-value adjustments are significantly correlated with LD among SNPs, recombination rates, and SNP densities. Given the large variability of sequence features in the genome, we further discuss a novel approach of using SNP-specific (local) thresholds to detect genome-wide significant associations. This article has supplementary material online.

1. INTRODUCTION

Genome-wide association studies (GWAS) of inheritable diseases routinely test hundreds of thousands to millions of single nucleotide polymorphisms (SNPs) for significant disease-SNP association. Each SNP consists of two alternative alleles (denoted as A or a, say), yielding three possible genotypes (AA, Aa, aa) per individual. In a typical GWAS, the genotypes of all SNPs are collected from two groups of individuals called cases (affected) and controls (unaffected). A common strategy to detect disease-SNP association is to test if, for a candidate SNP, the genotype distribution among the cases and that among the controls are signifiantly different. The test is performed for every genotyped SNP, resulting in many thousands of test scores in a typial GWAS. The adjustment of genome-wide significance of SNP tests in GWAS is thus a multiple testing problem. It is well known that the Bonferroni correction method is overly conservative for GWAS (e.g., see Figure 1), because SNPs in nearby genomic regions are often in linkage disequilibrium (LD) (i.e., correlated). The conservativeness of the Bonferroni correction will inevitably reduce the power of association mapping. A statistical method that can more accurately evaluate the genome-wide significance of SNP tests is therefore needed. In addition to LD, the sample size of a case control study also influences the genome-wide significance of SNP associations. When the sample size is relatively small for a SNP with very imbalanced allele frequencies, the test statistics often cannot be approximated well by their asymptotic distributions, which further complicates the multiple testing adjustment problem.

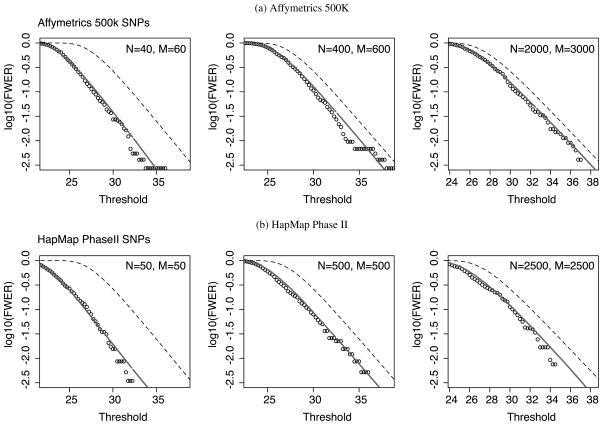
Figure 1.

Accuracy of the approximated family-wise Type I error rate for (a) WTCCC SNPs and (b) HapMap Phase II SNPs. Permutation p-values adjusted for 1,000,000 SNPs are shown in circles at different thresholds. Adjusted p-values by our method are shown in solid lines. Bonferroni corrected p-values are shown in dashed lines. N and M denote the case and control sample sizes, respectively.

Many methods have been proposed in the past decades to evaluate genome-wide significance of SNP tests in GWAS in consideration of SNP LD. Other than the Bonferroni correction, permutation tests often serve as a reliable approach. In a permutation test, the disease status or trait labels of the sampled individuals are randomly shuffled, so that the empirical rate of false positive associations can be computed from the permuted datasets. Despite its simplicity, the permutation test is computationally intensive for genome-wide studies. Many algorithms are therefore proposed to alleviate the computational burden of permutation tests and simultaneously aim to achieve accurate p-value adjustment. Nyholt (2004) proposed a simple correction method that estimates an effective number of independent tests genome-wide. Dudbridge and Koeleman (2004) proposed to fit an extreme value distribution to the sum of the largest association statistics, where the fitting is done based on a small number of permutations of the case control sample. Lin (2005) proposed a simulation-based procedure that saves a significant amount of computation by repeatedly using the same covariance matrices of SNPs in all permuted datasets. Kimmel and Shamir (2006) proposed an importance sampling method that saves computation time by permuting samples in a specific way such that at least one SNP in the permuted dataset demonstrates significant associations with the disease. Conneely and Boehnke (2007) proposed a numerical integration approach to calculate the minimum p-value of all SNPs from a multivariate normal distribution. Han, Kang, and Eskin (2009) proposed a fast simulation procedure to generate association scores of all SNPs from a multivariate normal distribution, assuming local dependence of SNPs.

In this article, we propose a new method, the Genome-wide Poisson Approximation to Statistical Significance (GPASS), to accurately and efficiently compute the genome-wide significance of SNP associations in GWAS. The method can calculate both the genome-wide significance of SNPs of interest and thresholds corresponding to user specified significance levels. Our approach is based on the Poisson heuristic (Aldous 1989) and a novel declumping procedure. The key idea is to use a Poisson distribution to approximate the genome-wide significance of SNPs after compensating for the LD among SNPs. In our method, the total number of tests is just a scalar in the family-wise Type I error rate formulation, and we develop an efficient importance sampling algorithm to compute nominal p-values of arbitrarily large statistics. As a result, our method accurately adjusts p-values much more efficiently than existing methods based on permutation, resampling, and other simulation-based methods. Our method can calculate the significance of one or multiple SNPs adjusting for millions of correlated comparisons within seconds, and keep the computation time almost constant for any sample size, SNP size, and thresholds. By deriving explicit bounds for the error of Poisson approximation and the variance of our importance sampling procedure, we also theoretically guarantee the accuracy of our method.

The method proposed in this article is closely related to a previous method we developed for genomic studies (Zhang 2008). The problem addressed in this article is different and more complex in several aspects. First, the SNP correlation in GWAS is nowhere homogeneous in the human population, as opposed to the homogeneous correlation structure we assumed in the genomic study. Thus, we estimate local covariance matrices from different genomic locations to account for the variability in SNP correlation. Second, the SNP data in GWAS takes discrete and finite values, as opposed to the continuous normal data we assumed in the genomic study. The distribution of genotype counts may be well approximated by normal distributions only if the sample size is sufficiently large, which unfortunately does not hold for studies with smaller samples or rare SNPs. We develop in this article truncation techniques to adjust for the sample size effects. Third, the SNP test in GWAS is a multivariate joint test in quadratic forms, as opposed to a one-sided Z-test used in genomic studies. We therefore need to develop a new importance sampling procedure and prove its efficiency analytically.

The performance of our method is evaluated using simulated datasets from real genome-wide studies obtained from The Wellcome Trust Case Control Consortium (2007) (WTCCC) and The International HapMap Project (2007). We demonstrate that our method produces the most accurate and computationally efficient genome-wide p-values compared with existing methods. We further evaluate the consistency, variability, and sequence effects of SNP significance using European and African samples, and data from 10 resequenced ENCODE regions (The ENCODE Project Consortium 2007). Our analysis shows that p-value adjustments of SNP signifiances are strongly dependent on recombination rate, SNP density, and sample size, whereas the the adjustment variability evaluated from different chromosomes and ENCODE regions is well conserved between European and African samples.

This article is organized as follows. In Section 2, we introduce the declumping idea and the Poisson approximation to p-value adjustment. In Section 3, we describe an efficient importance sampling method to estimate the parameters in the Poisson approximation. In Section 4, we evaluate the accuracy of our method via simulation, and we compare our method with some existing methods in Section 5. We further apply our method to real genome-wide datasets to evaluate the impacts of sequence features on p-value adjustment results in Section 6. Distinct from existing simulation-based approaches and other approximation methods, our method can be easily generalized to approximate genome-wide significance of context-dependent SNP tests. We show in Section 7 that our method can detect significant associations using SNP-specific thresholds, while maintaining an overall valid family-wise Type I error rate. In addition, our method can be straightforwardly adapted to estimate false discovery rate (FDR) (Benjamini and Hochberg 1995).

2. DECLUMPING AND POISSON APPROXIMATION FOR GWAS

Let S denote all SNPs tested in a GWAS, and let L = |S| denote the size of S. The SNPs in S can be partitioned into two disjoint sets: S = S₀ ∪ S₁, where S₀ contains the SNPs that are not associated with the disease, and S₁ contains the associated SNPs. We further let L₀ = |S₀| and L₁ = |S₁| denote the sizes of S₀ and S₁, respectively. If we use an indicator I_i = 1 to denote the rejection of the test on SNP i, and I_i = 0 otherwise, we have W = Σ_i∈S0 I_i equal to the total number of false rejections. Suppose that the Type I error per SNP test is controlled at level α, which in a typical GWAS is very small, and that L₀ is large (e.g., tens of thousands to milions). If the SNPs are mutually independent, then the distribution of W can be approximated well by a Poisson distribution, that is, W ~ Poisson(λ) approximately, and the family-wise significance level can be approximated by P(W > 0) = 1 − e^−λ. In reality, however, the SNPs are often in high LD, which makes the Poisson approximation fail. We outline below a declumping procedure to compensate for correlations among SNPs.

2.1 Declumping

We define a clump i to be all SNPs genotyped in a neighborhood of SNP i, where we call SNP i the central SNP of clump i. LD among SNPs mostly extends to a finite distance in the human genome. Clump i therefore contains most SNPs in strong LD with the central SNP i. There are L clumps corresponding to the L SNPs genome-wide. Let {i − k_i, …, i, …, i + l_i} denote the indices of SNPs in clump i, where k_i (< i) and l_i (< L − i) are nonnegative integers specific to clump i. We use T_i−ki, …, T_i, …, T_i+li to denote the corresponding disease-association test statistics. Here, we assume testing of individual SNPs, but the same notations and methods can be applied straightforwardly to test haplotypes or other models.

The SNP test statistics within one clump are positively correlated due to LD. We compensate for their positive correlation by testing on the unit of a clump using the following statistic:

$$R_i=I_{T_i\ge t}\prod _{j=i-k_i}^{i-1}{I}_{T_j<T_i}\prod _{j=i+1}^{i+l_i}{I}_{T_j\le T_i}.$$ (1)

Here, t denotes a large threshold, beyond which SNP i will be rejected with significant disease association, and I_e is the indicator for event e. Clearly, R_i is a binary variable such that R_i = 1 if and only if SNP i is the peak in its neighborhood with T_i ≥ t. Association mapping can then be performed by calculating R_i for all SNPs i = 1, …, L and reporting those SNPs with R_i = 1 at threshold t. In definition (1), if there are multiple identical peaks (SNPs) in a clump, only the left-most peak (SNP) will be reported. Note that this tiebreaker is arbitrary and can be easily modified. The new tests based on {R_i}_i=1,…,L have local negative correlations. If SNP i and SNP j are closely located in the genome, at most one of R_i and R_j can be 1.

2.2 Significance Approximation

Let W_r = Σ_i∈S0 Ri. If none of the SNPs are associated with the disease, we have W_r = 0 if and only if the original test statistics T of all SNPs are smaller than t. Hence, P(W_r > 0) is equal to the genome-wide false positive rate with respect to T at threshold t. On the other hand, if the data contain some disease SNPs, we may have W_r = 0 but T > t for some unassociated SNPs (i.e., those in S₀) that are close to a disease SNP (∈ S₁). In this case, P(W_r > 0) may not equal to the genome-wide false positive rate with respect to T. In a typical GWAS, we have L₁ ≪ L₀ (typically L₀ is many thousands times L₀). Thus, the proportion of SNPs in S₀ that are close to SNPs in S₁ is very small. As a consequence, P(W_r > 0) approximates the genome-wide false positive rate of the association test T very accurately.

At large t values, the event {R_i = 1} is rare. We thus may approximate the distribution of W_r by a Poisson distribution with mean λ_r = E(W_r), and P(W_r > 0 ≃ 1 − e^−λ_r. An error bound of this Poisson approximation can be obtained by the Chen–Stein method (Stein 1972; Chen 1975a, 1975b). Let B(i) denote the set of indices of clumps that are dependent with clump i (and are under the null hypothesis of no disease association). We note that B(i) contains two sets of indices, B(i) = B₁(i)∪B₂(i), where B₁(i) contains the indices of clumps whose central SNP is within clump i, and B₂(i) contains the indices of clumps whose central SNP is outside of clump i but some of its SNPs are dependent on one or more SNPs in clump i. Let c denote the average size of B₁(i), which is just the average clump size. If we assume that that all SNPs in LD with SNP i are included in clump i, for all clumps defined at SNPs in S₀, then the average size of B₂(i) is 2(c − 1), and hence the average size of B(i) is about 3c. According to theorem 1 in Arratia, Goldstein, and Gordon (1990), we have

$$\left|P(W_r=w)-e^{-{\lambda }_r}\frac{{\lambda }_r^w}{w!}\right|\le 2\left((b_1+b_2)\frac{1-e^{-{\lambda }_r}}{{\lambda }_r}+b_{3}min(1,1.4{\lambda }_r^{-1/2})\right),$$

where

$$\begin{array}{l}{b}_1=\sum _{i\in {\mathbf{S}}_0}\sum _{j\in \mathbf{B}(i)}Pr(R_i=1)Pr(R_j=1),\\ b_2=\sum _{i\in {\mathbf{S}}_0}\sum _{j\ne i,j\in \mathbf{B}(i)}Pr(R_i=1,R_j=1),\text{and}\\ b_3=0\text{under}\text{the}\text{local}\text{LD}\text{assumption}.\end{array}$$

It is easy to check that $b_1\simeq {\lambda }_r\frac{3c{\lambda }_r}{L_0}$. Based on definition (1), for any j ∈ B₁(i), at most one of R_i and R_j can be 1. We thus can rewrite b₂ as

$$\begin{array}{l}{b}_2=\sum _{i\in {\mathbf{S}}_0}\sum _{j\in {\mathbf{B}}_2(i)}Pr(R_i=1,R_j=1)\\ \le \sum _{i\in {\mathbf{S}}_0}\sum _{j\in {\mathbf{B}}_2(i)}Pr(R_i=1,T_j\ge t).\end{array}$$

We prove in Theorem A.1 in the Appendix that Pr(R_i = 1, T_j ≥ t) ≤ Pr(R_i = 1)P(T_j ≥ t) for all i ∈ S₀, j ∈ B₂(i). Let p_t = Pr(T ≥ t), that is, the nominal significance of threshold t. Thus, we obtain an upper bound for b₂ as: b₂ ≤ 2cλ_rp_t.

As a result, we have

$$\left|P(W_r=w)-e^{-{\lambda }_r}\frac{{\lambda }_r^w}{w!}\right|\le \frac{6c{\lambda }_r}{L_0}+4{cp}_t.$$ (2)

If c ≪ L₀, as is true in a typical GWAS, and the threshold t is large (such that 4cp_t ≪ 1), then our Poisson approximation is accurate.

The Poisson heuristic and the declumping procedure reduce the problem to computing

$$\begin{array}{l}{\lambda }_r=E(W_r)=\sum _{i\in {\mathbf{S}}_0}E(R_i)=\sum _{i\in {\mathbf{S}}_0}P(R_i=1)\\ =\sum _{i\in {\mathbf{S}}_0}P(T_i\ge t)P\left(\underset{j=i-k_i}{\overset{i-1}{\cup }}\{T_j<T_i\},\underset{j=i+1}{\overset{i+l_i}{\cup }}\{T_j\le T_i\}|T_i\ge t\right)\\ \equiv L_0\overline{P}(T\ge t)\overline{P}(T\text{is}\text{peak}\mid T\ge t).\end{array}$$ (3)

The term L₀P̄(T ≥ t) corresponds to the standard Bonferroni correction of nominal p-values. The last term is a conditional probability taking values in [0, 1]. If SNPs are independent, the conditional probability will be close to 1 at large thresholds t. If SNPs are correlated, however, the conditional probability can be much smaller than 1, particularly at small thresholds t, which explains the conservativeness of the Bonferroni correction. Formula (3) also indicates that the “effective number of independent tests” is dependent on the threshold t for declaring significance. It is thus insufficient to adjust p-values using a common effective number of independent tests at different threshold values.

3. THE IMPORTANCE SAMPLING ALGORITHM

We describe here an importance sampling algorithm (see Liu 2001 for more references) to estimate λ_r. Compared with permutation and bootstrapping methods, importance sampling is particularly advantageous when the threshold t is large. The pipeline of approximating λ_r is as follows: (1) randomly select a clump i in the genome; (2) estimate a covariance matrix of all SNPs in clump i; (3) estimate P(R_i = 1) using importance sampling (since the number of true disease SNPs in a typical GWAS is much smaller than the number of SNPs tested, we assume in this computation that all SNPs in the clump are not associated with the disease); (4) repeat steps (1)–(3) to obtain an average estimate P̄(R = 1) over clumps randomly sampled from different genomic locations (to account for LD heterogeneity); and (5) multiply P̄(R = 1) by L to obtain an estimate of λ_r [we in fact should multiply P̄(R = 1) by L₀, which is unknown; however, L = L₀ + L₁ is very close to L₀ because L₁ ≪ L₀]. Finally, we approximate the genome-wide significance of threshold t by 1 − e^−λ_r. Following this pipeline, our approach can easily accommodate other association test statistics, either continuous or discrete, either model-based or distribution-free. We can also replace steps (4) and (5) in the above procedure by exhaustively scanning through all SNP markers in consideration and summing up the estimated probabilities, which is a bit computationally expensive, but quite feasible, especially with the help of parallel computing infrastructures.

3.1 The Proposal Distribution

Let d denote the number of distinct genotypes per SNP, {n_i1, …, n_id} and {m_i1, …, m_id} denote the genotype counts at SNP i in cases and controls, respectively, and $N={\sum }_{j=1}^d{n}_{ij}$ and $M={\sum }_{j=1}^d{m}_{ij}$ denote the case and control sample sizes, respectively. Let ${\mathbf{X}}_i=(\frac{n_{i1}}{N}-\frac{m_{i1}}{M},\dots ,\frac{n_{i,d-1}}{N}-\frac{m_{i,d-1}}{M})$ denote a row vector of the first d − 1 genotype frequency contrasts between cases and controls. If N and M are not too small, X_i follows approximately a multivariate normal distribution. Disease association test statistics, such as a chi-square test, are often in the form or can be approximated by $T_i={\mathbf{X}}_i{\mathbf{\sum }}_i^{-1}{\mathbf{X}}_i^{\prime }$, where Σ_i denotes the covariance matrix of the variables in X_i. When Σ_i is unknown, as is the case in our problem, we estimate Σ_i by its maximum likelihood estimator (MLE) Σ̂_i under the multivariate normality assumption of X_i. We then compute T_i by $T_i={\mathbf{X}}_i{\widehat{\mathbf{\sum }}}_i^{-1}{\mathbf{X}}_i^{\prime }$, which follows approximately a chi-square distribution with large samples. Using estimated covariance matrices will increase estimation uncertainty. If the sample size is small, the test statistics may also deviate from chi-square distributions. Our simulation studies shown in Section 4, however, suggest that using estimated covariance matrices works quite well in practice.

For testing purposes, it suffices to consider the genotype frequency contrasts X_i at each SNP. Let X = (X_i−ki, …, X_i+li) denote a concatenated row vector of genotype contrasts of all SNPs in clump i. Under the null hypothesis of no associations, the vector X asymptotically follows a multivariate normal distribution N(0, Σ), where the covariance Σ_j of SNP j is a sub-matrix on the diagonal of Σ. Again, if Σ is unknown, we estimate Σ by its MLE Σ̂ from the data. Given a clump at SNP i, a generic importance sampling procedure for approximating P(R_i = 1) works as follows: (1) generate a realization x of the genotype contrast vector X at all SNPs in the clump from a trial distribution G with probability density function g(·); (2) compute a test statistic $t_j={\mathbf{x}}_j{\widehat{\mathbf{\sum }}}_j^{-1}{\mathbf{x}}_j^{\prime }$ for every SNP j in the clump from x; (3) compute a clump statistic r_i and an associated weight w_i, where w_i = h(x)/g(x), and h(·) denotes the probability density function of N(0, Σ̂); (4) repeat steps (1)–(3) many times to obtain n pairs of clump statistics and weights, denoted as (r_i1, w_i1), …, (r_in, w_in), and estimate P(R_i = 1) by $\widehat{P}(R_i=1)=\frac{1}{n}{\sum }_{j=1}^n{r}_{ij}{w}_{ij}$.

The efficiency of our importance sampling relies on the choice of the trial distribution G. We choose G such that the probability of R_i = 1 under G is much larger than that under the null hypothesis of no disease association. In particular, we generate data that contain a strong association signal at SNP i. We first rearrange the SNP orders such that SNP i is placed first in the vector X, that is, X* = (X_i, X_i−ki, …, X_i−1, X_i+1, …, X_i+li) The columns and rows of Σ̂ are also rear-ranged accordingly and the rearranged covariance matrix is denoted by Σ̂*. We simulate realizations of X* using Cholesky decomposition. Let A denote a lower triangular matrix such that Σ̂* = AA′. We first simulate a vector Z of independent standard normal random variables, and then let X* = ZA′, which follows the desired distribution.

Let Z₁ denote the first (d − 1) elements in Z. By the above procedure, Z₁ and only Z₁ contributes to the realization of SNP i in the rearranged vector X*. To add a strong association signal to SNP i, therefore, we replace Z₁ in Z by ${\mathbf{Z}}_1^{\ast }={\mathbf{Z}}_1\sqrt{1+r^2/{\left|\right|{\mathbf{Z}}_1\left|\right|}^2}$, and we denote the new vector by Z*. Here, r² is a chosen positive constant and ||Z₁||² denotes the sum of squares of all elements in Z₁. We generate X* = Z*A′ as the new genotype frequency contrasts of all SNPs in the clump. It then follows that the association test statistic at SNP i becomes

$$T_i={\mathbf{X}}_1^{\ast }{\widehat{\mathbf{\sum }}}_1^{\ast -1}{\mathbf{X}}_1^{\prime \ast }={\mathbf{Z}}_1^{\ast }{\mathbf{Z}}_1^{\prime \ast }={\left|\right|{\mathbf{Z}}_1\left|\right|}^2+r^2,$$

which is a shifted chi-square statistic at SNP i with shifting parameter r². Due to LD and the characteristics of Cholesky decomposition, the chi-square statistics of neighboring SNPs will also be elevated. We can show that the importance sampling weight is w_i = f_(d−1)(||Z₁||² + r²)/f_(d−1)(||Z₁||²) where f_(d−1)(·) denotes the density function of a chi-square distribution of (d − 1) degrees of freedom (online Supplementary Materials). We choose constant r² so as to generate data from a desired range of significance thresholds. For example, we can let $r^2={\chi }_{{10}^{-5}}^2(d-1)$ to sample a test statistic with nominal p-value smaller than 10⁻⁵.

3.2 Sample Size Effect, Computational Complexity, and Error Bounds

When the case–control sample size is relatively small, particularly for rare alleles, the discreteness of genotype frequency contrasts makes the normal approximation to their distributions inappropriate. To accurately approximate p-values in this case, we use a truncated normal distribution to model the distribution of genotype frequency contrasts.

Let o_j = n_j + m_j denote the total number of genotype j at a given SNP in cases and controls. With o_j fixed, we have n_j bounded between [b₁, b₂] = [max(0, o_j − M), min(N, o_j)]. The truncation bounds for the genotype frequency contrasts are therefore [ $(\frac{1}{N}+\frac{1}{M})b_1-\frac{o_j}{M},(\frac{1}{N}+\frac{1}{M})b_2-\frac{o_j}{M}$]. In our sampling procedure, whenever a simulated genotype contrast is beyond the bounds, we let the sampling weight w_i = 0. We further need to compute the normalizing constant for the truncated multivariate normal distribution, because the support of our trial distribution G does not cover the support of the target distribution (because the test statistic of the data simulated from G is always ≥r²). We use a separate Monte Carlo simulation to determine the normalizing constant. Unlike p-values, the normalizing constant is typically easy and fast to compute.

Our method consists of three main steps: (a) randomly sample K clumps across the genome (in our experience, a few hundreds of clumps is sufficient) and estimate the covariance matrix of SNPs in each clump; (b) simulate data in each clump and compute the clump statistic; and (c) approximate the genome-wide significance from a Poisson distribution. Let t_a and t_b denote the time complexity of steps (a) and (b), respectively. The time complexity of our method can be written as K(t_a + t_b) [step (c) essentially costs no time]. In particular, K is chosen by the user and should be proportional to the heterogeneity (variability) of LD across the genome, t_a is ~O(c³), where c denotes the clump size that is proportional to the distance of LD decay, and t_b is ~O(c²). Neither the total number of SNPs nor the case–control sample size have a major influence on the time complexity. The former is relieved by the Poisson heuristic and declumping, while the latter is due to the use of SNP covariance matrices in simulation (as opposed to permutation).

The error in our p-value approximation comes from several sources. First, the Poisson heuristic may introduce bias, which, however, is bounded by the Chen–Stein bound in (2), and is typically small for large-scale studies. Second, the computation of the Poisson mean depends on which set of clumps are selected from the genome and the accuracy of the estimated covariance matrices of SNPs. With a random sample of clumps and unbiased covariance estimates, the computed Poisson mean is unbiased, with variance converging to 0 at a linear rate with respect to the number of the sampled clumps K. By default, we let K = 500. Third, importance sampling may introduce additional variance to the results, but the variance again converges to 0 at a linear rate with respect to the number of Monte Carlo samples. With a proper choice of the shifting parameter r², the standard deviation of each importance sampling iteration can be controlled in the same scale as the nominal p-value being approximated (online Supplementary Materials). As a result, a few hundred of Monte Carlo samples are sufficient to reduce the standard deviation of importance sampling to a lower magnitude than the nominal p-value.

4. ACCURACY OF POISSON APPROXIMATION FOR GWAS

We evaluate the accuracy of our method using two sources of GWAS data. The first sets of data were obtained from the Wellcome Trust Case Control Consortium (2007). The data consist of 2000 patients of type 1 diabetes and 3000 control individuals. The individuals were genotyped by 500-K Affymetrix chips, providing an average genotyping density of 6 kb per SNP. We imputed missing genotypes from the maximum genotyping scores, and we filtered out nonpolymorphic SNPs. The second sets of data were simulated from the HapMap Phase II (2007) individuals of European ancestry (CEU). There were 60 unrelated CEU individuals genotyped at 2.55 million SNPs. The genotyping density is about five times greater than that of the WTCCC data. We used HAPGEN program to simulate data of desired sizes from the CEU individuals.

4.1 Evaluation of the Poisson Fit

We first checked if the number of significant clumps based on our definition follows a Poisson distribution. Results are affirmative (online Supplementary Materials). We next used permutation p-values to benchmark the accuracy of our approximation method. For both WTCCC data and HapMap data, we randomly picked 1,000,000 consecutive SNPs, which is of the typical size of GWAS. We also computed Bonferroni adjusted p-values to demonstrate its conservativeness (we replaced the Bonferroni correction by the Sidak correction for large p-values). We further randomly sampled subsets of individuals to evaluate the sample size effect. In particular, we compared the permutation p-values and the approximated p-values using 40 cases and 60 controls, 400 cases and 600 controls, and 2000 cases and 3000 controls, respectively.

As shown in Figure 1, our method tracks the permutation p-values accurately for all the samples sizes we tested, for a wide range of thresholds, and for both WTCCC data and HapMap Phase II data. The Bonferroni correction, on the other hand, are overly conservative in all cases. Interestingly, we observed a significant decrease of Type I error rate at the same thresholds when the sample size (cases plus controls) decreases from 5000 to 100, which is due to the fact that the asymptotic chi-square distribution of the test statistics does not hold for small sample sizes. We are, however, able to correct this sample size effect and approximate the Type I errors accurately using our truncation technique.

Comparing between WTCCC and HapMap results, we observed smaller Type I error rate from the HapMap SNPs than that from the WTCCC SNPs, evaluated at the same thresholds. For example, when the sample size is 5000, the estimated Type I error rate at the Bonferroni predicted 0.05-level is 0.014 for the HapMap data and 0.025 for the WTCCC data. This indicates that stronger LD leads to reduced Type I error rates. When the sample size is 100, we again observed a strong sample size effect, where our estimated Type I error rate at the Bonferroni 0.05 level is 0.002 for the HapMap data and 0.01 for the WTCCC data. We further note that the accuracy of our method does not rely much on the number of individuals used for the p-value approximation. Our method can approximate p-values for different case–control sample sizes from a common input, because the method only uses the summary information of SNPs. For instance, all p-values approximated in Figure 1 were calculated from 100 randomly selected individuals.

In terms of computation time, it took about 20 seconds and 3 minutes on a 3.0 GHz CPU to approximate p-values for each WTCCC and HapMap Phase II plot in Figure 1, respectively. The greater amount of time spent on the HapMap Phase II data was due to its higher SNP density and hence larger clump sizes. For all cases, our method calculated family-wise Type I error rates between [10⁻⁴, 1] (i.e., nominal Type I error rates between [10⁻¹⁰, 10⁻⁶]) in a single run. We only showed the family-wise error rates between [10^−2.5, 1] because the permutation test was too slow (in days) to estimate smaller p-values for 1,000,000 SNPs in 5000 individuals.

4.2 Choice of the Clump Size

The accuracy of our method relies on the clump definition. We define a clump to include all SNPs within a neighborhood of the center SNP. The choice of the neighborhood size depends on the LD decay, which varies in different populations and across different genomic regions. The LD in the European population, for example, may extend to 173 kb as measured by the span of haplotype blocks (defined in Gabriel et al. 2002), and the maximum block span is only 94 kb in the African population (Gabriel et al. 2002). Most blocks, however, span in much shorter distance, with an average of 22 kb in the European population and 11 kb in the African population (Gabriel et al. 2002). Prior knowledge of recombinations further showed that the LD around telomeres tends to be lower than the LD around centromeres, and is strongly related with sequence features such as GC contents, gene density, and the presence of short interspersed repeats (Fullerton, Carvalho, and Clark 2001; Yu et al. 2001; Kong et al. 2002; Dawson et al. 2002; Smith et al. 2005).

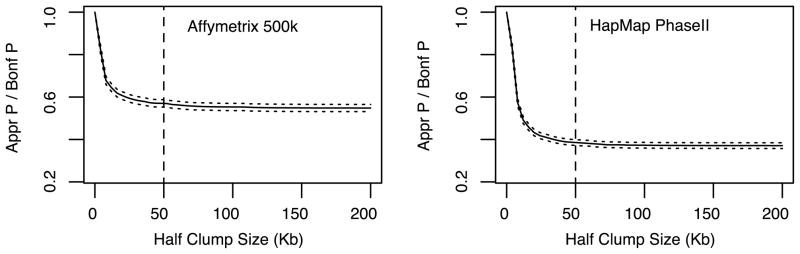
Using both WTCCC and HapMap Phase data, we checked the effect of clump size on the accuracy of approximated p-values. In Figure 2, we show the ratio between our Poisson-approximated p-value and the Bonferroni adjusted p-value (at the nomial 0.05 level) as a function of half clump sizes (number of SNPs included in the clump on one side of the center SNP). We observed that our approximated p-values decreased quickly as more distant SNPs are included in a clump, indicating the effect of LD on p-values, but the decreasing trend stabilized quickly after 10~20 kb. This is consistent with previous reports (Gabriel et al. 2002) that most SNPs in strong LD are physically close. The results in Figure 2 were calculated at the significance level of 0.05 adjusting for 1,000,000 comparisons. Based on the observed curves, we define a clump to include all SNPs within 50 Kb on each side of the center SNP by default. This definition may not include all SNPs in LD with the center SNP, but will capture most strongly correlated SNPs. Increasing the clump size may improve the approximation accuracy slightly, but at the same time incurs more computation.

Figure 2.

Impact of clump sizes on p-value approximations. Using the WTCCC1 dataset (5004 individuals) and the simulated HapMap Phase II dataset (5000 individuals), we calculated the ratio between our approximated p-values and the Bonferroni p-values adjusting for 1,000,000 tests. The family-wise significance level was controlled at 0.05.

5. COMPARISON WITH EXISTING METHODS

We compare our method (GPASS) with three recent methods adjusting p-values for correlated multiple comparisons: RAT by Kimmel and Shamir (2006), which uses an importance sampling based permutation algorithm to adjust p-values; pACT by Conneely and Boehnke (2007), which adjusts p-values by numerically integrating up to 1000 normal random variables; and SLIDE by Han, Kang, and Eskin (2009), which directly simulates association statistics assuming local dependence. We used the HAPGEN program to randomly generate case control datasets from the HapMap Phase II CEU sample. Each dataset contained 1000 SNPs with one disease SNP of varying risks. A total of six datasets were generated, where three datasets contained 250 cases and 250 controls, and three datasets contained 2500 cases and 2500 controls. The most significant (unadjusted) p-value observed in each dataset is reported in Column 2 of Table 1. We performed 50,000 permutations to serve as the ground truth of the adjusted p-values (Column 3 of Table 1), and compared the results from GPASS, RAT, pACT, and SLIDE with that of the permutation method. Since RAT only calculates 1-df chi-square statistics on alleles (assuming Hardy–Weinberg Equilibrium, HWE), all methods were used to adjust the significance of allele associations under HWE, but not genotype associations.

Table 1.

Comparison of adjusted p-values for 1000 correlated comparisons

Na	p	PERMb	GPASSc	pACT	RAT	SLIDE
500	3.15e–4	1.22e–1	1.32e–1 (1.08)	1.12e–1 (0.92)	1.40e–1 (1.15)	1.35e–1 (1.11)
	3.20e–5	1.53e–2	1.52e–2 (0.99)	1.32e–2 (0.86)	1.13e–2 (0.74)	1.49e–2 (0.97)
	4.85e–6	2.28e–3	2.37e–3 (1.04)	1.94e–3 (0.85)	1.82e–3 (0.80)	2.81e–3 (1.23)
5000	5.45e–4	2.31e–1	2.51e–1 (1.09)	1.93e–1 (0.84)	3.69e–2 (0.16)	2.18e–1 (0.94)
	1.80e–5	1.03e–2	1.10e–2 (1.07)	1.26e–2 (1.22)	1.90e–3 (0.18)	1.00e–2 (0.97)
	1.00e–6	6.30e–4*	5.75e–4 (0.91)	4.74e–4 (0.75)	7.99e–5 (0.13)	5.70e–4 (0.90)

^aTotal number of individuals, including equal number of cases and controls.

^bPermutation p-values based on 50,000 independent permutations (*100,000 permutations).

^cRatio between adjusted and permutation p-values are shown in parenthesis.

As shown in Table 1, when the case–control sample size was 500, all the four methods produced similar adjusted p-values, which were all close to the empirical family-wise Type I error rates obtained by permutations (as seen from the ratio between the adjusted p-value by each method and the permutation p-value). When the case–control sample size was increased to 5000, however, RAT significantly underestimated the family-wise Type I error rate by a factor of 5 or 10 in all three cases. For example, when the permutation p-value was 0.231, the RAT adjusted p-value was 0.0369 with a reported standard error of 0.00875, which would be falsely regarded as significant at family-wise 0.05 level. In contrast, all other three methods produced reasonably accurate results. Overall, GPASS and SLIDE produced the best p-value adjustments.

In terms of computation time, both RAT and GPASS took one minute or less to adjust the smallest p-value in each dataset. The computation time of pACT and SLIDE was also within the one-minute range when the p-value was large (e.g., when the adjusted p-value > 0.01), but the computation time increased drastically to adjust each of the two smallest p-values in Table 1. It is easily checked that the time complexity of both SLIDE and pACT is O(p⁻¹) in order to maintain a lower magnitude of estimation error relative to the p-value, which highlights the distinction between importance sampling methods (such as GPASS and RAT) and direct simulation procedures (such as pACT and SLIDE). In addition, pACT cannot adjust p-values for more than 1000 SNPs. SLIDE takes a linear time with respect to the number of SNPs tested. For example, SLIDE takes 0.6 hour to adjust p-values for 500,000 SNPs (Han, Kang, and Eskin 2009), and thus it may take hours to adjust p-values for a GWAS of millions of SNPs. RAT has an option that adjusts p-values using local SNP information, which is similar to our approach. The current version of RAT, however, adjusts one p-value at a time. The computation of RAT also depends on the sample size, where more permutations are needed for larger samples in order to obtain a desired accuracy of p-value. GPASS, in comparison, has a time complexity unrelated to both the number of SNPs and the sample size. GPASS can approximate family-wise significance of both large (close to 1) and small (approaching 0) p-values.

6. UNDERSTANDING SEQUENCE EFFECT ON p-VALUE ADJUSTMENT

If we conduct L independent tests and observe the most significant p-value as p₀, the Bonferroni adjustment gives us Lp₀ as a good approximation as its real significance. If the L tests are dependent as in GWAS and the adjusted p-value is p_a, then we can think of L_E = p_a/p₀ as the effective number of independent tests, and we define D = L_E/L as the deflation rate of the independent tests. Although we have demonstrated that L_E varies as we changes the significance threshold, it can still be used to measure the size of multiple comparisons at a fixed threshold. In particular, we use the deflation rate D to evaluate the variability and consistency of sequence impacts on p-value adjustments.

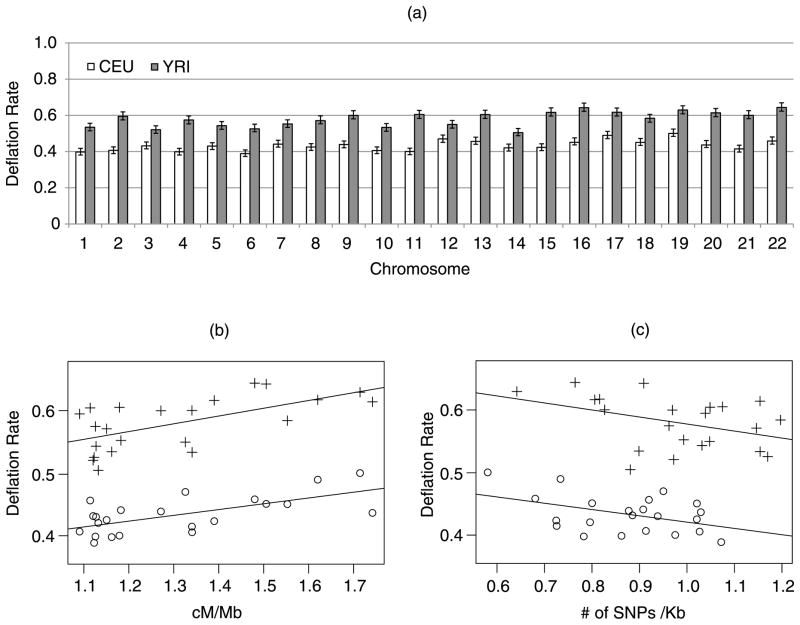
We downloaded the HapMap Phase II individuals with European (CEU) and African ancestry (YRI), respectively. We used their SNPs on each of the 22 automosomal chromosomes to compute deflation rates (D_i, i = 1, …, 22) at t = 35.8, which yields a Bonferroni adjusted significance of 0.05 for 3,000,000 SNPs. As shown in Figure 3(a), the deflation rates calculated from the CEU sample are significantly smaller than the corresponding ones calculated from the YRI sample for each of the 22 chromosomes, resulting in a mean L_E of 1.29 million for CEU and 1.77 million for YRI, respectively. This is due to the difference in LD between the two populations (Gabriel et al. 2002).

Figure 3.

Deflation rates (D_i, i = 1, …, 22) estimated from HapMap Phase II SNPs on each automosomal chromosome, assuming 3 million SNPs tested genome-wide at a Bonferroni adjusted significance of 0.05. (a) Bar-plots of D_i calculated from CEU and YRI individuals, respectively, with 95% confidence intervals. (b) Scatter plot of D_i plotted against chromosome-wise average recombination rate (+: YRI; ○: CEU). (c) Scatter plot of D_i plotted against chromosome-wise SNP density (+: YRI; ○: CEU). The correlations are −0.44 and −0.40 with corresponding p-values 0.065 and 0.038 for the two populations.

The D_i calculated from individual chromosomes varied considerably. Shorter chromosomes tend to yield larger numbers, which may be attributable to their increasing recombination rates (Kong et al. 2002). The fluctuation of deflation rates over different chromosomes, however, are consistent between the European and the African populations, with correlation 0.47 (p-value 0.0255). This result suggests that the impact of sequence on p-value adjustments is reasonably conserved across populations. In particular, Figure 3(b) shows that deflation rate is significantly correlated with the chromosome-wise recombination rates (cM/Mb), with correlation 0.65 (p-value 0.001) for the Eropean population and 0.62 (p-value 0.002) for the African population. It is known that LD variation and recombination hotspots are conserved across populations (Smith et al. 2005), which can explain the consistent patterns observed in Figure 3. We also observed weakly significant negative correlations (with p-values 0.065 and 0.038 for the two populations, respectively) between deflation rate and SNP density across chromosomes.

We further performed a similar analysis on 10 resequenced ENCODE regions (The ENCODE Project Consortium 2007). The ENCODE data capture almost the complete set of common SNPs in the human genome. After filtering out nonpolymorphic SNPs, the average SNP density in ENCODE regions is 2.0 SNPs per kb for CEU and 2.5 SNPs per kb for YRI, which is two to three times denser than HapMap Phase II SNPs, 10–15 times denser than WTCCC SNPs, and roughly accounts for 6 million SNPs genome-wide. From our analysis (online Supplementary Materials), we again observed large variability of the deflation rates D calculated from 10 ENCODE regions, yet the variability is conserved between CEU and YRI samples (correlation 0.925, p-value 0.0001). We also observed a significant correlation between D and recombination rates (0.90 for CEU with p-value 0.0008; 0.87 for YRI with p-value 0.002). A previous report (Pe’er et al. 2008) has also used the same ENCODE regions to evaluate the sequence impacts on p-value adjustment. They also observed a large variability of D across ENCODE regions. They, however, failed to explain the variability of the deflation rate by either recombination rate or SNP density, which could be due to the large uncertainty in their calculation.

7. CONDITIONAL HYPOTHESIS TESTING

Given the large variability in LD and SNP allele frequencies, the effect of nearby sequence composition on the actual significance of a SNP may vary considerably in the context of multiple comparisons. Rather than using a constant threshold to test significant associations at all SNPs, alternatively we can test individual SNPs at a SNP-specific threshold determined by the SNP’s local information. For example, we may want to require each tested SNP to have a SNP-specific threshold so that the Type I error rate per SNP is constant throughout the genome. In other words, it requires SNP-dependent thresholds so that the deflation rate d at each SNP remains constant. Intuitively, SNPs in regions with fewer recombination events may be tested at lower thresholds, because the effective numbers of independent SNPs in those regions are smaller than the numbers in regions with more recombination events. Theoretically, when conditioning on the neighborhood structure, the same value of test statistics obtained from different regions have different adjusted p-values (family-wise significance). This issue is related to the conditional test in statistics literature (Cox and Hinkley 1974), which addresses the question regarding the strength of the evidence against the null hypothesis conditional on ancillary statistics (environment). Note that it is infeasible to use permutation test and most existing methods to derive such varying thresholds for declaring significance.

Our approximation method can be directly used to compute any kind of SNP-specific thresholds. To calculate a threshold for SNP i, we first calculate the significance of the corresponding clump i over a range of thresholds. We then use linear local interpolation to compute a threshold t_i that yields a desired significance level α_i at SNP i. We can further obtain smoothness between local thresholds of neighboring SNPs, by calculating an average significance level of a window of clumps around SNP i over a range of thresholds, and then we use linear interpolation to compute t_i for SNP i. To use the SNP-specific thresholds, we report significant association at SNP i if and only if its test statistic is ≥T_i and is the largest compared to the statistics of its neighboring SNPs. By default, we let α_i = 0.05/L for each of the L SNPs, such that the genome-wide significance level is maintained at 0.05.

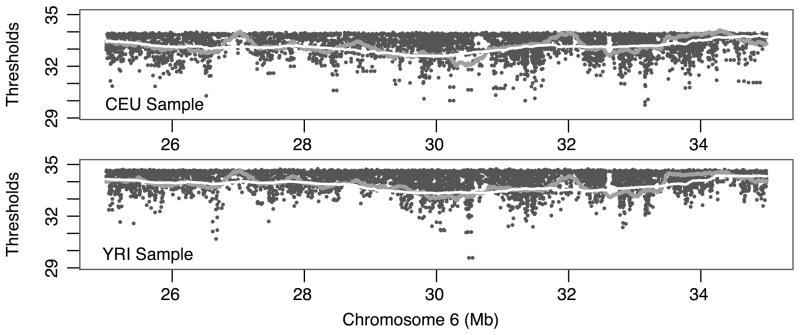
We calculated individual thresholds at all HapMap Phase II SNPs assuming a genome-wide significance level of 0.05, for both CEU and YRI samples. The thresholds for individual SNPs (without smoothing) vary considerably. For the CEU population, the thresholds vary between 27.33 and 34.06 for 2.55 million SNPs, with median 33.46 and standard deviation 0.57. For the YRI population, the thresholds vary between 28.01 and 34.81 for 2.74 million SNPs, with median 34.37 and standard deviation 0.47. We show in Figure 4 an example of the thresholds calculated for SNPs within a 10-Mb region (25–35 Mb) on chromosome 6. The region contains the well-known major histocompatibility complex (MHC) gene cluster. We observed a very similar physical distribution of thresholds over CEU SNPs and YRI SNPs, particularly for smoothed thresholds calculated by the method described above. Interestingly, lower thresholds occur more often at SNPs of larger minor allele frequencies and at locations with higher SNPs densities. Most current genome-wide association studies are using common SNPs in the human population, and regions of potential interest are often genotyped with high SNP coverage. Using varying thresholds can therefore potentially improve the power of GWAS than traditional methods using a common threshold, particularly if the disease association is captured by common alleles or if the disease loci have high SNP coverage.

Figure 4.

Illustration of varying thresholds estimated for the MHC region (25–35 Mb) on chromosome 6. Three types of thresholds are shown: snp-specific (black dots), 500-Kb-window average (dark grey), and 2-Mb-window average (light grey). The genome-wide significance is controlled at 0.05 for HapMap Phase II SNPs in CEU and YRI populations, respectively.

8. DISCUSSION

We introduced a fast and accurate method for approximating the genome-wide significance of disease associations. The key idea is to compensate for the correlations among the multiple comparisons by a simple declumping technique. A Poisson distribution on the number of declumped significant associations is then used to approximate genome-wide significance. The accuracy of our method weakly depends on the choice of clump sizes, which should be chosen as proportional to the decay of LD among neighboring SNPs. In theory, the p-value estimates are insensitive to the larger-than-necessary clump sizes used, and will become more conservative (which is good) when smaller-than-necessary clump sizes are employed. In practice, larger clumps demand more computation. We demonstrated that clumps including SNPs in a 100-Kb window are sufficient to produce accurate approximation to p-values for both Affymetrics 500-K and HapMap Phase II SNPs. Assuming that a clump includes all SNPs in LD with the center SNP, we further derived an explicit error bound for our p-value approximation, which is typically very small in GWAS.

By analyzing various real datasets from different human populations, we observed a considerable amount of sequence variability that strongly affects the genome-wide significance of SNP associations. Traditional methods that detect significant associations using a common threshold for all SNPs may not be ideal, as we have available to us approximately ancillary information regarding the covariance structure among the test statistics of nearby SNPs. An alternative approach is to use conditional testing by employing SNP-specific thresholds, where the threshold for each SNP is calculated from its local information only. The varying threshold approach can be further generalized to incorporate any prior knowledge about the spatial distribution of disease loci. For example, lower thresholds may be used at genes that are potentially related with the disease, and higher thresholds may be used in other regions so to balance out the total Type I error rate. Many sources of information can be used to construct such a prior distribution, including previously identified susceptible loci of the same or related diseases, initial scans of the genome from small sets of individuals in a two-stage design, and gene regulation data related with the disease. We have applied similar ideas to a genomic study for detecting transcription factor binding (Chen and Zhang 2010), which is a simpler problem than GWAS, and we obtained very promising results.

In addition to case–control designs, our method can be applied straightforwardly to data with continuous traits and environmental factors, which typically involves score statistics or likelihood ratio tests under certain statistical models. If such test statistics can also be written as functions of multivariate normal random variables, when the sample size is large, we can design a Monte Carlo strategy similar to the one described here to evaluate the genome-wide significance of associations. Furthermore, given that our method estimates the expected number of false positive associations, the method can be adapted to estimate FDR as well.

We assume in the article that the case–control individuals are homogeneous and independent. In practice, affected individuals may be more related than normal individuals due to their sharing of a common disease ancestry. The population sample is also prone to stratification. Both the relatedness and population stratification among individuals are well known to potentially create spurious disease associations, making the genome-wide significance control invalid. A simple solution is to first apply existing methods to remove the population structure from the sample and then use our method to detect significant associations. It is desirable to further generalize our method to account for sample structures simultaneously when approximating the genome-wide significance. Since our method only uses local information, it is also possible to account for admixture effects.

APPENDIX: A THEOREM FOR THE ERROR BOUND OF POISSON APPROXIMATION

In this section, we prove a theorem (Theorem A.1) that provides a tight error bound for our Poisson approximation presented in the main text. By default, all vectors used in our proof are row vectors.

Lemma A.1

Let X denote a row vector of random variables following a k-dim multivariate normal distribution with mean 0 and covariance Σ, that is, X ~ N(0, Σ). Let c denote a k-dim unitary vector and let β ≥ 0 denote a scalar. We define S(βc) as a convex set in the k-dim space that is symmetric with respect to βc [i.e., if v ∈ S(βc), then 2βc − v ∈ S(βc)]. Then, P(X ∈ S(βc)) is a nonincreasing function with respect to β ≥ 0.

Proof

Let f (·) denote the density function of X,

$$\begin{array}{l}\frac{d}{d\beta }{\oint }_{\mathbf{S}(\beta \mathbf{c})}f(\mathbf{x})d\mathbf{x}=\frac{d}{d\beta }{\oint }_{\mathbf{S}(\beta \mathbf{c})}\frac{1}{{(2\pi )}^{k/2}{\mid \mathbf{\sum }\mid }^{1/2}}{e}^{-(1/2)\mathbf{x}{\mathrm{\sum }}^{-1}{\mathbf{x}}^{\prime }}d\mathbf{x}\\ =\frac{d}{d\beta }{\oint }_{\mathbf{S}(0)}\frac{1}{{(2\pi )}^{k/2}{\mid \mathbf{\sum }\mid }^{1/2}}{e}^{-(1/2)(\mathbf{t}+\beta \mathbf{c}){\mathrm{\sum }}^{-1}{(\mathbf{t}+\beta \mathbf{c})}^{\prime }}d\mathbf{t}\\ =-\frac{1}{{(2\pi )}^{k/2}{\mid \mathbf{\sum }\mid }^{1/2}}\times {\oint }_{\mathbf{S}(0)}{e}^{-(1/2)(\mathbf{t}+\beta \mathbf{c}){\mathbf{\sum }}^{-1}(\mathbf{t}+\beta {\mathbf{c}}^{\prime })}[\mathbf{c}{\mathrm{\sum }}^{-1}(\mathbf{t}+\beta {\mathbf{c}}^{\prime })]d\mathbf{t}\\ =-\frac{1}{{(2\pi )}^{k/2}{\mid \mathbf{\sum }\mid }^{1/2}}{\oint }_{\mathbf{S}(\beta \mathbf{c})}{e}^{-(1/2)\mathbf{x}{\mathrm{\sum }}^{-1}{\mathbf{x}}^{\prime }}\mathbf{c}{\mathrm{\sum }}^{-1}{\mathbf{x}}^{\prime }d\mathbf{x}.\end{array}$$

Write Σ⁻¹ = AA′ and let Z = XA′. Then we have Z ~ N(0, I). Further, let c₁ = cA′, and S₁(βc₁) = S(βc)A′ denote the transformed set. The derivative of the integral can be written as

$$\begin{array}{l}\frac{d}{d\beta }{\oint }_{\mathbf{S}(\beta \mathbf{c})}f(\mathbf{x})d\mathbf{x}=-\frac{1}{{(2\pi )}^{k/2}}{\oint }_{{\mathbf{S}}_1(\beta {\mathbf{c}}_1)}{e}^{-(1/2){\mathbf{zz}}^{\prime }}{\mathbf{c}}_1{z}^{\prime }d\mathbf{z}\\ =-{\mathbf{c}}_{1}E{(\mathbf{Z}\mid {\mathbf{S}}_1(\beta {\mathbf{c}}_1))}^{\prime }\end{array}$$

which is the negative inner product between c₁ and the expectation of Z constrained within S₁(βc₁). We want to show that the inner product is nonnegative when β > 0, and thus the derivative is nonpositive, which implies the nonincreasing property of the integral with respect to β ≥ 0.

Let R denote a rotation matrix, such that c₂ = c₁R is a vector that has 0s in all but the 1st element, that is, c₂ = (c₂, 0, …, 0). Correspondingly, let S₂(βc₂) = S₁(βc₁)R. Note that any rotation matrix is unitary, and hence the rotation of Z is still a independent standard normal random vector. As a result,

$$\frac{d}{d\beta }{\oint }_{\mathbf{S}(\beta \mathbf{c})}f(\mathbf{x})d\mathbf{x}=-c_{2}E(Z_1\mid {\mathbf{S}}_2(\beta {\mathbf{c}}_2)),$$ (A.1)

where Z₁ denotes the first element in Z.

To show that the derivative in (A.1) is nonpositive, we need to show that the conditional expectation E(Z₁|S₂(βc₂)) has the same sign with c₂. Imagine a 1-dim line l(βc₂) cutting through the point βc₂, and let ${\mathbf{Z}}_0^{\ast }$ denote the projection of the origin 0 onto l(βc₂). We denote the intersection of l(βc₂) and S₂(βc₂) by I_S(βc₂). Since linear transformations and rotations preserve the convexity and symmetry property of S(βc) and l(βc₂), we have both S₂(βc₂) and I_S(βc₂) convex and symmetric with respect to βc₂. The conditional distribution of Z given l(βc₂) is 1-dim normal with mean at ${\mathbf{Z}}_0^{\ast }$. Due to linear projection, the conditional distribution of Z₁ (the first element of Z) given l(βc₂) is also a 1-dim normal distribution with mean $Z_0^{\ast }$ (the first element of ${\mathbf{Z}}_0^{\ast }$). Clearly $E(Z_1\mid \mathbf{l}(\beta {\mathbf{c}}_2))=Z_0^{\ast }$ has the same sign with βc₂, and I_S(βc₂) is a segment symmetric with respect to βc₂. It thus holds true that E(Z₁|I_S(βc₂)) is between $Z_0^{\ast }$ and βc₂, and thus has the same sign with βc₂. As a result, E(Z₁|S₂(βc₂)) = E(E(Z₁|I_S(βc₂)|S₂(βc₂)) has the same sign with βc₂. Consequently, when β ≥ 0, the derivative in (A.1) is nonpositive. The conclusion of Lemma A.1 is proved.

Lemma A.2

Given k + 1 (k ≥ 1) random variables X, Y₁, …, Y_k. If their joint distribution is multivariate normal with mean 0 and an arbitrary covariance matrix, then P(|X| ≤ x, {|Y_i| ≤ y_i}_i=1,…,k) ≥ P(|X| ≤ x)P({|Y_i| ≤ y_i}_i=1,…,k) for any positive values of x, y₁, …, y_k.

Proof

Without loss of generality, we assume that the variance of the k + 1 variables equals to 1. Let ρXY_i denote the correlation between X and Y_i for i = 1, …, k, then $Y_i={\rho }_{{XY}_i}X+\sqrt{1-{\rho }_{{XY}_i}^2}{Z}_i$, where Z_i ⊥ X denotes a standard normal random variable. We only need to consider ρXY_i ∈ (−1, 1), because otherwise Y_i is redundant.

Let h(x, {y_i}) = P(|X| ≤ x, {|Y_i| ≤ y_i}_i=1,…,k) − P(|X| ≤ x) × P({|Y_i| ≤ y_i}_i=1,…,k). We want to show that h(x, {y_i}) ≥ 0 for all positive x and {y_i}. Our strategy of proof is as follows: (1) it suffices to show that, for any fixed $\{y_i\}=\{y_i^{\ast }\}$, the function $h(x,\{y_i^{\ast }\})$, which is a function with respect to x, is nonnegative for all x ≥ 0; (2) to prove (1), given that $h(0,\{y_i^{\ast }\})=h(\infty ,\{y_i^{\ast }\})=0$, it suffices to show that all the modes of $h(x,\{y_i^{\ast }\})\ge 0$.

Taking derivative with respect to x,

$$\begin{array}{l}\frac{\partial h(x,\{y_i\})}{\partial x}=P(\{\mid Y_i\mid \le y_i\}\mid X=x)f(x)+P(\{\mid Y_i\mid \le y_i\}\mid X=-x)f(-x)-P(\{\mid Y_i\mid \le y_i\})f(x)-P(\{\mid Y_i\mid \le y_i\})f(-x)\\ =P\left(\left\{\frac{-y_i-{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\le Z_i\le \frac{y_i+{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\right\}\right)f(x)+P\left(\left\{\frac{-y_i+{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\le Z_i\le \frac{y_i+{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\right\}\right)f(-x)-P(\{-y_i\le Y_i\le y_i\})f(x)-P(\{-y_i\le Y_i\le y_i\})f(-x)\\ =2\left[P\left(\left\{\frac{-y_i-{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\le Z_i\le \frac{y_i-{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\right\}\right)-P(\{-y_i\le Y_i\le y_i\})\right]f(x),\end{array}$$

where f (·) denotes the standard normal density function. The last equality is due to the symmetry property of multivariate normal distributions with respect to the mean (in our case the mean is 0).

Let the derivative equal to 0, we obtain

$$P\left(\left\{\frac{-y_i-{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\le Z_i\le \frac{y_i-{\rho }_{{XY}_i}x}{\sqrt{1-{\rho }_{{XY}_i}^2}}\right\}\right)=P(\{-y_i\le Y_i\le y_i\}).$$ (A.2)

That is, for any fixed $\{y_i\}=\{y_i^{\ast }\},h(x,\{y_i^{\ast }\})$ is at a mode if x = x* that satisfies (A.2). The interval of interest for {Z_i} on the left-hand side of (A.2) is centered at { $\frac{-{\rho }_{{XY}_i}}{\sqrt{1-{\rho }_{{XY}_i}^2}}{x}^{\ast }$} with fixed widths { $\frac{2y_i^{\ast }}{\sqrt{1-{\rho }_{{XY}_i}^2}}$}, for i = 1, …, k. Due to Lemma A.1, we have for any t ∈ [0, x*],

$$P\left(\left\{\frac{-y_i-{\rho }_{{XY}_i}t}{\sqrt{1-{\rho }_{{XY}_i}^2}}\le Z_i\le \frac{y_i-{\rho }_{{XY}_i}t}{\sqrt{1-{\rho }_{{XY}_i}^2}}\right\}\right)\ge P(\{-y_i\le Y_i\le y_i\}).$$ (A.3)

This is because the left-hand side of (A.3) is an integral of normal random variables over an symmetric convex interval with fixed sizes, but its center is a linear function of t. By Lemma A.1, the integral is a nonincreasing function with respect to t ≥ 0, and thus for 0 ≤ t ≤ x*, we have (A.3) holds true.

Given the partial derivative $\frac{\partial h(x,\{y_i^{\ast }\})}{\partial x}{\mid }_t\ge 0$ for t ∈ [0, x*], and $h(0,\{y_i^{\ast }\})=0$, we have

$$h(x^{\ast },\{y_i^{\ast }\})=h(0,\{y_i^{\ast }\})+{\int }_0^{x^{\ast }}{\frac{\partial h(x,\{y_i^{\ast }\})}{\partial x}|}_{t}dt\ge 0.$$

That is, the mode of $h(x,\{y_i^{\ast }\})$ is nonnegative. Further due to the boundary conditions $h(0,\{y_i^{\ast }\})=h(\infty ,\{y_i^{\ast }\})=0$, it implies $h(x,\{y_i^{\ast }\})\ge 0$ for all x > 0, and thus h(x, {y_i}) ≥ 0 for all positive x and {y_i}.

Lemma A.3

Let X = (X₁, …, X_k) denote a concatenated row vector of random variables consisting of k subvectors. If X follows a multivariate normal distribution with mean 0 and covariance matrix Σ. Let $T_i={\mathbf{X}}_i{\mathbf{\sum }}_i^{-1}{\mathbf{X}}_i^{\prime }$ denote a chi-square statistic computed from the subvector X_i, for i = 1, …, k, then P({T_i ≤ t_i}_i=1,…,k) ≥ P(T₁ ≤ t₁)P({|T_i| ≤ t_i}_i=2,…,k) for any positive values of t₁, …, t_k.

Proof

This is a more general version of Lemma A.2. The proof can be obtained by using the same arguments in Lemma A.2, except that the sets constrained by the chi-square inequalities are ellipsoids, but not 1-dim intervals as in Lemma A.2. Ellipsoids are convex and symmetric with respect to their centers, and thus the result from Lemma A.1 applies.

Theorem A.1

Let X, Y, Z denote three row vectors of random variables, where Y = (Y₁, …, Y_k) consists of k subvectors. Suppose the joint distribution of (X, Y, Z) is multivariate normal with mean 0 and covariance matrix Σ. Let T_X, {T_Yi}, and T_Z denote the corresponding chi-square statistics obtained from X, Y, Z, respectively. If X ⊥ Z, then for any t_x ≥ 0 and t_z ≥ 0,

$$\begin{array}{l}P(T_X\ge t_x,T_Z\ge t_z,{\{T_{Y_i}\le T_X\}}_{i=1,\dots ,k})\\ \le P(T_X\ge t_x,{\{T_{Y_i}\le T_X\}}_{i=1,\dots ,k})P(T_Z\ge t_z).\end{array}$$

Proof

By Lemma A.3, we have

$$\begin{array}{l}P(T_Z\ge t_z,\{T_{Y_i}\le t_{y_i}\})=P(\{T_{Y_i}\le t_{y_i}\})-P(T_Z\le t_z,\{t_{Y_i}\le t_{y_i}\})\\ \le P(\{T_{Y_i}\le t_{y_i}\})-P(T_Z\le t_z)P(\{T_{Y_i}\le t_{y_i}\})\\ =P(T_Z\ge t_z)P(\{T_{Y_i}\le t_{y_i}\})\end{array}$$

which implies

$$P(T_Z\ge t_z\mid \{T_{Y_i}\le t_{y_i}\})\le P(T_Z\ge t_z).$$

Therefore,

$$\begin{array}{l}P(T_X\ge t_x,T_Z\ge t_z\{T_{Y_i}\le T_X\})={\int }_{t_x}^{\infty }P(T_Z\ge t,\{T_{Y_i}\le s\})f(T_X=s\mid T_Z\ge t_z,\{T_{Y_i}\le s\})ds\\ \le {\int }_{t_x}^{\infty }P(T_Z\ge t_z)P(\{T_{Y_i}\le s\})f(T_X=s\mid \{T_{Y_i}\le s\})ds\\ =P(T_Z\ge t_z)P(T_X\ge t_x,\{T_{Y_i}\le T_X\}),\end{array}$$

where f (·|·) denotes the conditional density function of T_X, and T_Z ≥ t_z is removed from the condition due to X ⊥ Z.