Sampling Development

Abstract

Research in developmental psychology requires sampling at different time points. Accurate depictions of developmental change provide a foundation for further empirical studies and theories about developmental mechanisms. However, overreliance on widely spaced sampling intervals in cross-sectional and longitudinal designs threatens the validity of the enterprise. This article discusses how to sample development in order to accurately discern the shape of developmental change. The ideal solution is daunting: to summarize behavior over 24-hour intervals and collect daily samples over the critical periods of change. We discuss the magnitude of errors due to undersampling, and the risks associated with oversampling. When daily sampling is not feasible, we offer suggestions for sampling methods that can provide preliminary reference points and provisional sketches of the general shape of a developmental trajectory. Denser sampling then can be applied strategically during periods of enhanced variability, inflections in the rate of developmental change, or in relation to key events or processes that may affect the course of change. Despite the challenges of dense repeated sampling, researchers must take seriously the problem of sampling on a developmental time scale if we are to know the true shape of developmental change.

Our Current Toolbox

As developmental psychologists, we should be ashamed of ourselves. Our appellation “developmental” implies a focus on change processes; most developmental researchers endorse the aim of characterizing developmental change; and most researchers agree that accurate depictions of the path of change are foundational to building and testing theories about change mechanisms. But most of us (present authors included) expend alarmingly little effort on selecting appropriate methods for sampling development in our daily work. Instead we rely on convenience, tradition, or intuition. Generally, we sample development at widely spaced time intervals—cross-sectional snapshots of children’s behavior in multiple age groups, lo-and-behold demonstrations of infants’ earliest manifestations of a skill, and broad-sweeping longitudinal observations at distant time points—without considering the potential cost of infrequent sampling. This global ignorance about the timing of observations in development is analogous to a science of astronomy that does not have accepted practices for charting the movements of celestial bodies.

The potential cost of inadequate sampling is that we misrepresent the path of change and as a consequence build developmental theories on shaky or fictional foundations. With overly large sampling intervals, we may fail to detect relationships between developmental events (Boker & Nesselroade, 2002; Collins, 2006), overlook brief but significant periods of development (Collins & Graham, 2002), underestimate variability and reversions in development (Siegler, 2006), reify developmental milestones that are mere blips in the trajectory, and reduce our ability to fit appropriate functions to patterns of change (Burchinal & Appelbaum, 1991). Moreover, without adequate sampling intervals, we cannot distinguish among alternative trajectories—linear with smooth monotonic improvements, nonlinear with accelerating or decelerating rates of change, step-like or episodic with abrupt discontinuities, vacillating and variable, U- or N-shaped, and so on (Adolph, Robinson, Young, & Gill-Alvarez, 2008). Given the paucity of developmental data obtained from dense sampling, a likely conclusion is that we have no real idea of the shape of developmental change for most of the behaviors that we study. Subsequently, our theories about underlying change mechanisms may be unconstrained, or worse, simply wrong, and we have no way of knowing the difference.

Astronomy provides a telling illustration: Tycho Brahe’s greater precision in measuring the trajectories of the planets revealed new orbital anomalies, set the stage for Kepler’s three laws of planetary motion, and laid the groundwork for Newton’s discovery of celestial dynamics and theory of gravitation (Koestler, 1959). Closer to home is the case of physical growth. The standard growth charts in developmental textbooks and pediatricians’ offices erroneously depict growth as a continuous process with accelerations during infancy and adolescence (U.S. Department of Health and Human Services). The misrepresentation is a direct consequence of sampling at quarterly intervals and fitting idealized curves through cross-sectional data. Daily measurements reveal that growth is actually episodic, with dramatic spurts occurring in a single day separated by static plateaus of days or weeks when little or no growth occurs (Caino, Kelmansky, Adamo, & Lejarraga, 2010; Hermanussen, 1998; Lampl, Veldhuis, & Johnson, 1992).

This article is intended as a wake up call. We need a new set of tools for sampling development. Unfortunately, like others who have argued for improved sampling methods (Burchinal & Appelbaum, 1991; Collins, 2006; Hertzog & Nesselroade, 2003; McArdle & Epstein, 1987; Siegler & Crowley, 1991), we cannot provide the necessary tools to specify the appropriate time intervals between observations, total number of required observations, and adequate distribution of observations across periods of stability and periods of developmental change. We cannot apply formal rules such as the Nyquist (1928/2002) sampling theorem because developmental data are not strictly periodic waveforms. We cannot use formal theoretical models to dictate the number of required observations points and their temporal spacing because we do not have a priori descriptions of the shape of the underlying developmental function. We cannot offer the equivalent of a power analysis for determining adequate sampling intervals in developmental studies because we do not yet know enough about the rate of change or patterns of variability in the underlying process.

We can, however, offer several suggestions for improving the situation. Our suggestions are more like the chalk outlines of missing tools on the pegboard in the garage than a fully stocked toolbox. Given our own areas of expertise, our examples are drawn from cognitive and motor development in infancy and childhood. However, our concerns about sampling intervals and suggestions for improvement are germane to all areas of development across the lifespan and apply to developmental loss (e.g., abandoning inefficient or faulty cognitive strategies, cessation of crawling after walking onset) as well as gains (acquisition of new ways of thinking, learning to crawl).

The Trace of the Tools

Vygotsky (1930/1978) and other historical notables cautioned that widely spaced sampling intervals can only reveal stable endpoints or reference points along the developmental path. In fact, the search for stable markers of change is a primary reason why researchers sample development at wide intervals. But stable markers are, in Vygotsky’s words, already fossilized indices of change (p. 68). Only dense longitudinal sampling can reveal change as it is occurring. Piaget’s (1952) detailed observations of his children’s cognitive development provide a well-known example of dense longitudinal sampling. More recently, proponents of microgenetic (Siegler, 2006; Siegler & Crowley, 1991) and dynamic systems approaches (Thelen & Ulrich, 1991) have advocated for dense sampling intervals relative to the rate of change of the phenomenon. But without knowing the shape of the underlying trajectory or the rate of change in the phenomenon of interest, how can we know how small of a time interval is small enough? We’re left with a chicken-and-egg problem: We need the sampled data to inform us how to sample the data.

Sample small!

We recently demonstrated that widening the sampling interval one day at a time causes a surprisingly rapid and dramatic loss of precision in the ability to determine the shape of developmental change (Adolph, Robinson, et al., 2008). We collected daily summaries of 32 motor skills (rolling, sitting, walking, etc.) from 11 infants from birth to 17 months. Over the course of each day, parents reported whether their infant performed each skill to criterion. Then we simulated the effects of sampling at increasingly larger time intervals (every other day, every third day, every fourth day, and so on). Even our largest simulated sampling interval, once per month, would be considered a heroic, detailed, microgenetic study by most developmental researchers.

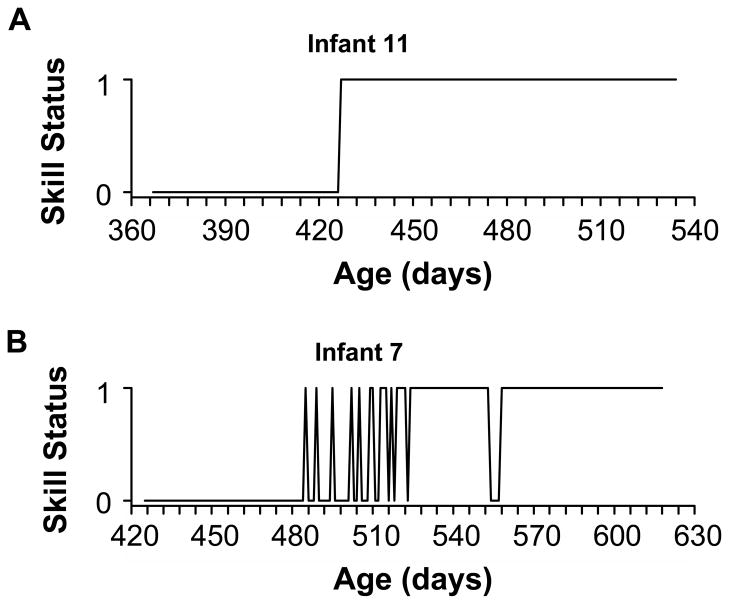
At the daily rate, only 16% of the original time series showed abrupt, step-like trajectories, where infants never performed the skill before a certain date and always performed the skill thereafter (Figure 1A). Most (84%) of the original time series showed variable trajectories, where skills stuttered in and out of infants’ repertoires: Infants displayed the skill to criterion on one day, but not on the next (Figure 1B). The number of vacillations between “pass and fail” ranged from 3 to 72 for the time series with variable trajectories. However, our ability to detect these long and variable transition periods dropped precipitously with each day that we widened the sampling interval. The loss of sensitivity to detect more than one transition was best described by an inverse power function, meaning that the rate of loss of sensitivity was greatest at the smallest sampling intervals and declined as intervals grew larger. Increasing the sampling interval from one to two days caused sensitivity to drop from 100% to 57%. At a weekly sampling rate, 51% of the variable time series erroneously showed step-like trajectories, and at a monthly sampling rate, 91% appeared to involve a single, abrupt transition. By the time we simulated biweekly sampling, Infant 7 pictured in Figure 1B with 21 pass/fail transitions in the acquisition of standing was indistinguishable from Infant 11 with a single step-like transition.

Figure 1.

Examples of developmental trajectories in two infants derived from daily data for standing, where the criterion for success was balancing upright for ≥ 3s without holding a support. (a) Trajectory from Infant #11 that exhibits an abrupt step-function from failure to success from one day to the next. (b) Variable trajectory from Infant #7, where the skill vacillated 21 times between failure and success over the course of several weeks.

The findings suggest that even when developmental researchers sample behavior at seemingly high rates—weekly or monthly intervals—they are likely to miss critical details in the underlying path of developmental change. In the case of motor skill acquisition, small increases in sampling intervals drastically reduce our ability to distinguish between variable and step-like trajectories, with the erroneous and long-held implication that motor skill acquisition follows a step-like trajectory, as if like turning on a faucet, at first infants cannot walk and then thereafter they can. Similarly, in other domains such as dynamic systems (Thelen & Smith, 1994), learning theory (Siegler, 2006), language acquisition (Fenson, et al., 2000; van Geert & van Dijk, 2002), cognitive development (Alibali & Goldin-Meadow, 1993; Siegler, 2007), neural development (Purves, White, & Riddle, 1996), and Darwinian models of developmental change (Sporns & Edelman, 1993), researchers have found that variability in the form and temporal expression of behavior can play a crucial role in the process of development.

So how small is small enough? Perhaps the default sampling rate in most cases should be daily summaries over each 24-hour period. With days representing the ticks on the x-axis, researchers maximize the likelihood of identifying periods of stability and the trajectory of change between them. Why daily summaries? Circadian rhythms exert a powerful influence on activity levels such that most behaviors do not occur at continuous rates over the course of the day (Waterhouse, Redfern, & Minors, 2003). Infants walk in short bouts of activity (Adolph, Komati, Garciaguirre, Badaly, & Sotsky, 2011) and they cannot exhibit walking while they are sleeping or napping; bone growth in the legs occurs in small increments primarily during sleeping and napping while infants are laying down and the legs are unloaded (Noonan, et al., 2004). Thus, daily summaries are preferable to point samples because the latter will be confounded with the effects of circadian rhythms, behavioral context, environmental stimuli, mood and motivation, and so on (Fagen & Young, 1978). For daily summaries of binary data (pass/fail to criterion), researchers could note the absence or presence of the skill over the course of the day; for ordinal data (e.g., skills with ordered levels), record the average or highest level attained over the course of the day or a measure of variability such as the number of reversals or levels straddled; and for interval or ratio data, collect a summary score such as the mean, accumulated sum, maximum value, or measure of variability over the course of the day.

Of course, important developmental changes can occur within the course of a day, say in learning to ride a bike or in instruction-based learning. Moreover, underlying psychological and physiological mechanisms may operate at extremely short time scales—minutes to milliseconds. But sampling at intervals smaller than daily summaries is warranted only when the state of our knowledge about the underlying process points to faster rates of change. Training studies when pre- and post-test occur within the same day are a case in point where smaller sampling intervals are necessary to reveal the change mechanisms (Alibali & Golden-Meadow, 1993; Johnson, Amso, & Slemner, 2003).

Are there risks of sampling too small? Dense longitudinal sampling undoubtedly requires more effort and concomitant expense for data collection. Dense sampling also yields more data, creating greater challenges for data management and analyses. In particular, dense samples may require re-sampling at reduced rates before meaningful patterns are revealed. In fact, oversampling and filtering or smoothing the data is de rigueur in physiology, psychophysics, and neuroscience. But these practical concerns do not constitute risks of misinterpretation or inaccurately representing the pattern of developmental change.

Can sample-to-sample fluctuations in behavioral measures simply represent noise? Possibly, but only with sufficiently dense sampling can noise be distinguished from meaningful variation. For example, spontaneously emitted behaviors have different base rates of occurrence: frequently, occasionally, or rarely. Behaviors with high base rates, such as walking or talking, are likely to occur on a daily basis after reaching a mature, stable level of performance. But behaviors with lower base rates, such as climbing a ladder or singing, may be absent for days or weeks after reaching mature, stable levels. Is true variability indistinguishable from noise when base rates are low? Although counterintuitive, dense sampling is necessary to characterize variability regardless of base rate. For behaviors with high base rates, absence on a given day of development may be regarded as an accurate measure of variable, intermittent performance. But for behaviors with low base rates, developmental changes in the amount or pattern of occurrence over a series of days will still allow periods of enhanced variability to be distinguished from stable patterns of mature expression (Adolph, Robinson, et al., 2008).

Finally, repeated sampling may induce artifacts that bias interpretations of the data. Spontaneously emitted behaviors such as motor skills, physical growth, imaginary play, and language are likely immune. But experimentally-elicited behaviors such as certain cognitive abilities (e.g., theory of mind, A-not-B errors) or social skills (e.g., attachment) may be adversely affected by repeated testing (learning the correct response, becoming bored by the testing situation, etc.). Depending on the outcome measure, such considerations may limit the minimum practical sampling rate. Measures such as pass/fail and proportion of correct responses may be especially reactive to repeated sampling.

Preliminaries

Given the expense of dense longitudinal sampling, what might researchers do to ensure that the cost is warranted and to maximize the bang for the buck? Many of the sampling strategies that are already widely in use—single age demonstrations, cross-sectional comparisons of multiple age groups, and widely spaced longitudinal observations—can serve as preliminary groundwork prior to committing resources to dense sampling. Such sampling regimens can help to establish reference points along the developmental trajectory and to narrow the focus toward identifying periods of stability and change. Researchers must recognize, however, that these popular sampling regimens cannot provide definitive evidence about the path of development; they are merely preliminaries for deciding where to concentrate denser sampling. A useful rule of thumb is to collect additional samples between stable periods, thereby cutting the sampling interval into smaller and smaller chunks.

Cross-sectional age comparisons deserve a special caveat: Comparisons of multiple age groups cannot ultimately characterize the path of change because individual differences among children are rampant. With cross-sectional designs, the path, rate, cause, and outcome of developmental changes must be inferred across children rather than observed directly within individual children. The 6-month-old in the current sample will become 7 months old, but will not necessarily get to the same outcome by the same path at the same rate for the same reasons as the 7-month-old did in the current sample.

Another useful preliminary is a rough sketch of the shape of change. The easiest method is cross-sectional sampling with age treated as a continuous variable: Sample broadly across the entire age-range of interest and fit an appropriate function through the resulting data points (e.g., Curran, Obeidat, & Losardo, 2010). Noise due to individual differences is inevitable, but with a sufficiently large N, most of the daily age intervals can be covered. A more labor-intensive method is to sketch the shape of the trajectory with longitudinal observations. For example, cross-sectional observations of improvements in infants’ walking skill yielded negatively accelerated performance curves, and longitudinal samples collected at 3-week intervals yielded similar functions, suggesting that the most rapid changes in the development of walking occur in the first few months after walking onset (Adolph, Vereijken, & Shrout, 2003). Rough sketches, however, can turn out to be erroneous, as illustrated in the case of physical growth, where both cross-sectional and longitudinal sampling missed the fits-and-starts that characterize episodic growth.

Methods designed to reveal developmental mechanisms can also serve as preliminaries for describing developmental trajectories. For example, an “age-matched control” design jettisons age from the abscissa by sampling within a tight age-window (e.g., 12-month-olds ± 1 week). This design differs from a single-age demonstration proof because children are divided along some measure of interest (i.e., whether infants crawl or walk, have produced N words or not, etc.) or the measure of interest is treated as a continuous predictor variable (days of crawling/walking experience, number of words in the productive vocabulary). Age-matched control studies can test hypotheses about underlying developmental mechanisms, while simultaneously providing clues about where dense longitudinal sampling may be most revealing of developmental change. For example, 12-month-old crawlers perceive the limits of their abilities to descend slopes and cliffs, but 12-month-old walkers plunge recklessly over the edge of impossibly steep slopes and high cliffs (Adolph, Tamis-LeMonda, Ishak, Karasik, & Lobo, 2008; Kretch & Adolph, 2011). More crawling and walking experience predicts more adaptive responses. Thus, dense longitudinal sampling would be most revealing of the underlying developmental process over the transition from experienced crawler to novice walker.

Training studies provide similar pay-offs. For example, 4-month-olds do not make anticipatory eye movements to an object moving back and forth behind an occluder, but 6-month-olds do (Johnson, et al, 2003). When given a brief period of exposure to objects moving along an unoccluded trajectory, 4-month-olds subsequently increase their anticipatory eye movements while viewing the occluded trajectory, suggesting that everyday experiences viewing objects moving in and out of occlusion contribute to the formation of object representations. Six-month-olds reap no additional benefits from training; apparently, they’ve already got robust object representations during occlusion conditions. In this case, dense longitudinal sampling would be most revealing between 4 and 6 months of age.

Training studies can also yield information about periods of enhanced variability that can pinpoint periods when dense sampling is especially informative (Siegler, 2006). Periods of rapid developmental change, instability, or sensitivity to learning often are marked by increased variability, and it is during these periods where smaller sampling intervals are necessary to reveal the path of change. At an earlier time point, for example, children do not understand mathematical equivalence. At a later time point, they do. Between these two time points, there is a fleeting period during which representations are in a transitional state, and children are most likely to benefit from instruction (Alibali & Goldin-Meadow, 1993). The evidence for a transitional knowledge state comes from discordant spoken and gestured responses during a single trial: Children state an incorrect answer in speech, while simultaneously giving the correct answer in their manual gestures. Such findings suggest that dense sampling during the transitional knowledge state is especially revealing about the time course and path of developmental change.

Many of the sampling strategies commonly used by developmental psychologists thus can establish stable reference points, create a provisional sketch of the path of developmental change, and/or narrow in on periods of important developmental change. Dense longitudinal sampling—optimally, daily summaries of the target behavior—then can be applied strategically to enhance resolution at key periods along the trajectory. At this point, various curve fitting algorithms would be most meaningful for advancing developmental theory.

Conclusions: Why Bother?

Understanding development necessitates understanding the process of change. Although the fact of change can be documented with before-and-after snapshots or occasional dips into the behavioral stream, understanding process requires a detailed and precise characterization of the rate and pattern of change. Only dense longitudinal sampling can reveal an accurate picture of developmental trajectories. But after considering the substantial cost of obtaining dense repeated samples, many researchers may ask, “Why bother?”

The argument proffered here is not a straw man. Developmental psychologists have been fascinated with the shape of developmental change since the pioneering work of Vygotsky, Werner, and Piaget. But we are conducting our research in a pre-Kepler universe. Developmental trajectories with abrupt, step-like transitions figure prominently in our history, and have fostered numerous stage theories of development. Trajectories with unusual shapes (U, N, W, and so on) are of particular interest to developmental theorists—witness the recent collection of 15 articles published in this journal debating the theoretical implications of U-shaped developmental curves (Zelazo, 2004) and a subsequent target article focusing on U- and N-shaped development (Rakison & Yermolayeva, in press). Our point is not to question or support any theoretical perspective, but simply to ask whether such theories are built upon a firm empirical foundation (Adolph, Robinson, et al., 2008; Vouloumanos, in press). If the path of change has not been sampled with sufficient resolution, then what evidence do we really have that the developmental transition is step-like, U-shaped, or any other shape? Researchers appear satisfied to draw a line through two points or a curve through three (Curran, et al., 2010), but how can we be confident that development actually traces a linear or U -shaped path? How can we know the true shape of developmental change if we don’t take sampling on a developmental time scale seriously?