Distinctive Features Hold a Privileged Status in the Computation of Word Meaning: Implications for Theories of Semantic Memory

Abstract

The authors present data from 2 feature verification experiments designed to determine whether distinctive features have a privileged status in the computation of word meaning. They use an attractor-based connectionist model of semantic memory to derive predictions for the experiments. Contrary to central predictions of the conceptual structure account, but consistent with their own model, the authors present empirical evidence that distinctive features of both living and nonliving things do indeed have a privileged role in the computation of word meaning. The authors explain the mechanism through which these effects are produced in their model by presenting an analysis of the weight structure developed in the network during training.

The issue of how word meaning is stored in the mind, and computed rapidly when needed, is central both to theories of language comprehension and production and to understanding knowledge deficits in patients with neural impairments. Although we are far from a complete understanding, significant progress has been made since Tulving (1972) first introduced the term “semantic memory.” Much of this progress can be attributed to the implementation and development of semantic memory models and the advancement of tools (e.g., semantic feature production norms and word co-occurrence statistics) that enable the rigorous testing of predictions generated from these models.

The first models of semantic memory were hierarchical network theory (Collins & Quillian, 1969) and spreading activation theory (Collins & Loftus, 1975). Although both have been extremely influential and have provided predictions for numerous behavioral studies, both have lost favor owing to a number of well-understood and documented flaws (see Rogers & McClelland, 2004, for a recent review). A number of theories of semantic structure have been proposed as alternatives, including the sensory/functional theory (Warrington & McCarthy, 1987), the conceptual structure account (Tyler & Moss, 2001), and the domain-specific hypothesis (Caramazza & Shelton, 1998). Theories of semantic processing have also been proposed, often framed in terms of connectionist networks, and include the work of Plaut and Shallice (1993), Rumelhart and Todd (1993), Rogers and McClelland (2004), and McRae, de Sa, and Seidenberg (1997). Current research focuses on discriminating among these models, integrating the structural and processing components, and developing them to account for behavioral data.

One way in which these models are being tested concerns whether concept–feature and feature–feature statistical relations are embedded in the semantic system and to what extent they influence processing. It has been demonstrated that language users implicitly encode various types of statistical regularities, such as those that exist in text (Landauer & Dumais, 1997; Lund & Burgess, 1996) and speech (Saffran, 2003), and the co-occurrence of features of objects and entities to which words refer (Rosch & Mervis, 1975). One fruitful approach to the study of semantic computation that explores how statistical regularities are encoded has been the pairing of feature-based theories of semantic representation with the computational properties of attractor-based connectionist networks (see McRae, 2004, for a synthesis of examples of this approach). For example, McRae et al. (1997) demonstrated that measures of feature correlations derived from empirically generated semantic feature production norms predict priming and feature verification effects in both humans and connectionist simulations. More recently, attention has turned to feature distinctiveness, which can be thought of as the opposite end of the spectrum from feature intercorrelation.

Distinctive features are those that occur in only one or a very few concepts and thus allow people to discriminate among similar concepts. For example, whereas some features, such as 〈moos〉, occur in only one basic-level concept and are thus distinctive, others, such as 〈has a lid〉, occur in a moderately large number of concepts, and still others, such as 〈made of metal〉, occur in a huge number of concepts. Thus, a truly distinctive feature is a perfect cue to the identity of the corresponding concept (cow, in this case) in that it distinguishes it from all other basic-level concepts. Distinctive features can also be viewed in relation to a specific semantic space or a relatively narrow contrast set. That is, if it is already established that the concept in question is horselike, 〈has stripes〉 is a strong cue that it is a zebra. In this article, we focus on the former definition (i.e., relative to all basic-level concepts). This dimension has been measured in various ways and given several names over the years, including cue validity (Bourne & Restle, 1959), distinguishingness (Cree & McRae, 2003), distinctiveness (Garrard, Lambon Ralph, Hodges, & Patterson, 2001), and informativeness (Devlin, Gonnerman, Andersen, & Seidenberg, 1998). To date, distinctive features have been especially useful in accounting for performance in concepts and categorization tasks, and in explaining the patterns of deficits observed in patients with category-specific semantic deficits. Little attention has been given to how distinctive semantic information is computed when a word is read or heard.

The goal of the present research is to adjudicate among two current models of semantic memory, the conceptual structure account and feature-based connectionist attractor networks, by examining the contrasting predictions generated from each with regard to the time course of the computation of distinctive features. We focus on these two theories because they have both been implemented as computational models, allowing us to derive firm predictions, and they both make clear claims about the special status of distinctive features. Throughout the article, we contrast the predictions of these two models with the alternative predictions generated from more traditional models of semantic memory.

Distinctive Features

Distinctiveness can be viewed as a continuum in which truly distinctive features lie at one end and highly shared features at the other. The oldest measure that captures this continuum is cue validity, which was introduced by Bourne and Restle (1959) and then reintroduced to the literature by Rosch and Mervis (1975). Cue validity is the conditional probability of a concept given a feature, which is measured as the probability of a feature appearing in a concept divided by the probability of that feature appearing in all relevant concepts. Because a distinctive feature appears in at most a few things, the cue validity of a distinctive feature is high. In the extreme case, if a feature is truly distinctive, as 〈moos〉 is for cow, it will have the maximum cue validity of 1.0. In contrast, if a feature is shared by many concepts, its cue validity is extremely low (e.g., 〈eats〉). Distinctiveness and cue validity are related to feature salience, which refers to the prominence of a feature, or how easily it “pops up” when thinking of a concept (Smith & Medin, 1981; e.g., “redness” of fire engine). All of these measures are related to the probability of occurrence of the feature in instances of a concept (Smith & Osherson, 1984). Note, however, that distinctive features are not identical to salient features. For example, 〈has seven stomachs〉 is a distinctive feature of cow, but it is not highly noticeable, is infrequently listed in feature-norming tasks, and presumably does not play a prominent role in the representation of cow.

Why Might Distinctive Features Have a Privileged Status?

Distinctive features have played a central role in explaining patterns of impairment in cases of category-specific semantic deficits. The explanations are related to computations of semantic similarity, as first highlighted by Tversky (1977). According to Tversky’s contrast rule, distinctive features play a critical role in judged similarity between two objects, and the presence of distinctive features in an object makes it less similar to other objects. Many of the tasks used to demonstrate category-specific semantic deficits require patients to discriminate a specific concept from among similar ones. For example, in a word–picture matching task, participants may be asked to select the picture to which a word refers (e.g., zebra) from among a set of distractors that are similar on numerous dimensions (e.g., a horse, a cow, and a deer). In such a task, it is beneficial to the participant to be able to recall or recognize a visual feature that is unique to the item to which the target word refers (e.g., a zebra’s stripes). Furthermore, Cree and McRae (2003) found that the proportion of distinguishing features in a category predicted several major trends in the patterns of impairment observed in category-specific semantic deficits patients.

Given the importance of distinctive features in explaining patient performance, they have a privileged status in many theories of semantic organization. For example, the sensory/functional theory (Warrington & McCarthy, 1987) is based on the idea that sensory and functional information is particularly distinctive for living and nonliving things, respectively, and that category-specific impairments arise, therefore, from damage to either the sensory or functional knowledge processing pathways. Gonnerman, Andersen, Devlin, Kempler, and Seidenberg (1997) used a con-nectionist attractor network to demonstrate how correlated and distinctive features might be lost at different rates during the progression of degenerative dementia, giving rise to different patterns of impairment at different times. The conceptual structure account builds on these claims (see Tyler & Moss, 2001, for a review).

Distinctive features have an especially important status in the conceptual structure account of semantic organization. Tyler and Moss (2001) argued that there are key differences in how correlated and distinctive features are related in living and nonliving things. They argued that there are few correlations among the distinctive properties of living things. In contrast, nonliving things have distinctive forms that are highly correlated with the specific functions for which the items were created. Given that correlated features appear to be relatively robust to damage, the distinctive features of living things should be particularly susceptible to impairment, because they do not receive reinforcement from other features. Moss, Tyler, and colleagues have reported patient data supporting these claims (Moss, Tyler, & Devlin, 2002; Moss, Tyler, Durrant-Peatfield, & Bunn, 1998). This has motivated researchers to test whether the influence of these privileged connections can be seen in semantic tasks in normal participants.

Speed of Computation of Distinctive Features in Normal Adults

Randall, Moss, Rodd, Greer, and Tyler (2004) conducted an experiment to test “the central prediction of the conceptual structure account—that there will be a consistent disadvantage in processing the distinctive properties of living things relative to other kinds of features” (p. 394). They used a speeded feature verification task in which participants were asked to indicate as quickly and accurately as possible whether features were true of concepts. They reported data supporting these predictions, finding that the distinctive features of living things were verified consistently more slowly than those of nonliving things.

There are, however, several reasons why Randall et al.’s (2004) data should be interpreted with caution. First, several variables that are known to influence feature verification latency were not sufficiently controlled. Randall et al. stated, “It was not possible to match on all variables because of the limited set of potential items. Also, some variability is simply inherent to particular feature types” (Randall et al., 2004, p. 396). Although we agree that matching distinctive and shared features is an extremely difficult task, it is still necessary. Perhaps most important, the living-thing distinctive features were substantially lower in production frequency as measured by Randall et al.’s norms (an average of 9 of 45 participants listed the distinctive feature for the relevant living thing concepts) than the nonliving-thing distinctive features (22 of 45), with the living and nonliving shared features falling in the middle (13 and 16, respectively). Ashcraft (1978) and McRae et al. (1997) found that production frequency is a strong predictor of feature verification latency. In the Randall et al. data, the pattern of production frequency mirrored the pattern found in the verification latencies. Simply put, the living-thing distinctive features are less likely to come to mind when people read the concept name than are the nonliving-thing distinctive features. This is reflected in the fact that the living-thing distinctive features were lower than the nonliving-thing distinctive features in association strength as measured by the Birkbeck association norms. Note also that the error rate on the living-thing distinctive features was extremely high, 33%. In addition, perhaps contributing to Randall et al.’s data pattern was the fact that the living-thing distinctive feature names were longer, and occur less frequently in the CELEX lexical database, when compared with the features in the other three conditions.

Most problematic, however, is that the accuracy of Randall et al.’s (2004) distinctiveness manipulation is questionable. The distinctiveness measure was computed across only 93 concepts. This is a small sample, and it is possible therefore that some features that were distinctive in their norms may actually occur in many more concepts in the world. Therefore, these features may not have been distinctive to participants.

Randall et al.’s (2004) Computational Model

Randall et al. (2004) reported simulations intended to illustrate “whether an interaction between domain and distinctiveness can emerge from differences in the correlational structure of living and nonliving things” (p. 401). They trained a feed-forward three-layer back-propagation network to map from word forms to semantic features. They used the network to simulate a feature verification experiment by looking at whether the distinctive and shared features of the concepts used in their behavioral experiment were activated above (correct) or below (error) a specific activation threshold. They reported a main effect of distinctiveness, with higher error rates for distinctive than for shared features. They also reported an interaction between distinctiveness and domain, with higher error rates for living- than for nonliving-thing distinctive features but no difference between domains for shared features. They reported similar results with a cascaded activation version of their simulations in which they measured the time it took distinctive and shared features to reach an activation threshold. They found the same interaction as reported when the dependent variable was percentage of errors.

Most relevant to the present discussion, Randall et al. (2004) argued that “although there is a main effect of distinctiveness in the model, this is a very similar pattern to the one in the speeded feature verification task” (p. 402). This is a curious claim, given that in the speeded feature verification task, Randall et al. reported a main effect of domain (feature verification latencies to living things were slower than for nonliving things) and no main effect of distinctiveness. Furthermore, distinctiveness interacted with domain, with participants’ verification latencies to the living-thing distinctive items being longer than for the other three conditions. Their results are similar in that the living-thing distinctive items show the worst performance in both the experiments and the simulations, and the shared properties of both living and nonliving things are almost identical in both. However, the experiments demonstrate an advantage for nonliving-thing distinctive items, whereas the simulations lead one to believe that there should be a disadvantage for those items relative to shared features.

Alternative Predictions

Randall et al.’s (2004) findings are inconsistent with predictions generated from both hierarchical network theory and spreading activation theory, the two most commonly used frameworks for discussing semantic phenomena. In hierarchical network theory (Collins & Quillian, 1969), distinctive features are stored at the lowest concept node in the hierarchy to which the feature applies. Thus, 〈moos〉 would be stored at the cow node, whereas 〈eats〉 would be stored at a higher level, such as the animal node. One would therefore predict that distinctive features should be accessed more rapidly than shared features when a concept name is encountered. Furthermore, there is no apparent basis for predicting a difference between living and nonliving things.

Spreading activation theory (Anderson, 1983; Collins & Loftus, 1975; Quillian, 1962, 1967) provides a different set of predictions. In such models, semantic memory consists of a network of nodes representing concepts (canary, bird) that are connected through labeled links. Concepts are linked to feature nodes (e.g., 〈wings〉) via a relational link (e.g., has). Spreading activation is determined by the number of connections from the activated node and the strength, or length, of the relational link. That is, the greater is the number of links originating from a node, the weaker is the activation spreading out from it to any specific node. Collins and Loftus (1975) further assume that the strength of a link between any two nodes is determined by the frequency of its usage, and that the strength of a link between a concept node and a feature node is determined by criteriality that corresponds to the definingness, or the necessity of a feature to the concept, as in Smith, Shoben, and Rips’s (1974) feature comparison model. If items are chosen appropriately, so that distinctive and shared features are equated for criteriality, then there should be no difference in the length of time it takes to activate the two types of features.

We were motivated by these contrasting predictions to test whether a model of semantic memory we have used to simulate other behavioral effects (Cree & McRae, 2001; Cree, McRae, & McNorgan, 1999; McRae, Cree, Westmacott, & de Sa, 1999) would provide results consistent with Randall et al.’s (2004) behavioral data. We then tested the predictions of the models in two behavioral experiments of our own. Before conducting the simulations and experiments, we conducted a norming study to develop a set of tightly controlled items that we then used in both our simulations and our experiments.

Concept Generation Norms

The goal of this study was to derive a set of living and nonliving things, each paired with a distinctive and a matched shared feature. The items were chosen from McRae, Cree, Seidenberg, and McNorgan’s (2005) feature production norms for 541 concepts. Participants were given features from McRae et al.’s norms and were asked to generate names of concepts that possess that feature. Although the feature norms include a large set of concepts, they obviously do not exhaust the realm of possibilities. Determining the degree to which a feature is distinctive requires taking into account all possible concepts; that is, a feature might be highly distinctive for a concept when only the 541 concepts from the norms are taken into account but may not be so with respect to all of the concepts that a person knows. In the concept generation norms, participants were free to generate any concept that they believed possessed a specific feature, with the result being a more refined measure of distinctiveness.

Method

Participants

Forty University of Western Ontario undergraduates participated for course credit, 20 per list.

Materials

Because a number of variables influence feature verification latencies, and it is difficult to equate distinctive and shared features on them, two rounds of norming were necessary. The stimuli for the first round consisted of 89 concepts paired with a distinctive and a shared feature (30 living and 59 nonliving things) selected from McRae et al.’s (2005) norms. The distinctive and shared features were matched roughly on the variables that influence verification latency. However, after using the first round of concept generation to select concepts and their distinctive features, we found that it was not possible to match them perfectly to shared features that had been included. Therefore, a new set of 36 concepts paired with two features was normed, and those results are presented here (see Appendix A for the items).

Appendix A.

Concept–Feature Pairs Used in Experiments 1 and 2

Concept	Distinctive feature	Shared feature
Living things
ant	lives in a colony	lives in ground
apple	used for cider	used in pies
banana	has a peel	has a skin
beaver	builds dams	swims
butterfly	has a cocoon	has antennae
cat	purrs	eats
chicken	clucks	pecks
coconut	grows on palm trees	grows in warm climates
corn	has husks	has stalks
cow	has an udder	has 4 legs
dog	barks	has legs
duck	quacks	lays eggs
garlic	comes in cloves	comes in bulbs
lion	roars	is ferocious
owl	hoots	flies
pig	oinks	squeals
porcupine	shoots quills	is dangerous
sheep	used for wool	used for meat
Nonliving things
ashtray	used for cigarette butts	made of plastic
ball	used by bouncing	used for sports
balloon	bursts	floats
belt	has a buckle	has holes
bike	has pedals	has brakes
bottle	has a cork	has a lid
bow	used for archery	used for hunting
clock	ticks	is electrical
cupboard	used for storing dishes	used for storing food
jeans	made of denim	has pockets
key	used for locks	made of metal
napkin	used for wiping mouth	used for wiping hands
pencil	has an eraser	made of wood
submarine	has a periscope	has propellers
telephone	has a receiver	has buttons
toilet	used by flushing	holds water
train	has a caboose	has an engine
umbrella	used when raining	used for protection

Two lists were constructed, each containing nine living- and nine nonliving-things distinctive features and nine living- and nine nonliving-things shared features. Only feature names were presented. No participant was presented with any feature name twice.

Procedure

Participants were tested individually and were randomly presented with one of the two lists. For each feature name, they were asked to list up to three concepts that they believed included that feature. They were also instructed to check a box marked “more” if they believed there were other concepts that included that feature. It took about 20 min to complete the task. A typical line in the concept generation form appeared as follows:

purrs _____ _____ _____ ___ MORE

Results and Discussion

Table 1 shows that the groups vary on a number of variables that are related to distinctiveness. Statistics were calculated separately for living and nonliving things. From the concept generation norms, there were two measures of the availability of the target concept given a feature. Target concept first is the number of participants who listed the target concept in the first slot given a specific feature (maximum = 20). Target concept total is the number of participants who listed the target concept in any of the three slots (maximum = 20). For both variables, target concepts for distinctive features were produced more often than for shared features. Results for the next two variables show that concepts other than the target concept were produced more often for shared than for distinctive features. Other concepts (type) is the number of unique concept names listed that were not the target concept (maximum = 60 if all participants provided 3 unique nontarget concepts). Other concepts (token) is the total number of concept names (token frequency) listed other than the target concept (maximum = 60 if the target concept was never listed). Cue validity was measured as target concept total divided by the sum of target concept total and other concepts (token). Distinctive features have a higher cue validity than do shared features. Also presented in Table 1 are distinctiveness measures derived from McRae et al.’s (2005) norms. Concepts per feature (number of concepts in which a feature was included in the norms) is lower for distinctive features. Distinctiveness (inverse of concepts per feature) is higher for distinctive features. Paired t tests revealed that the distinctive and shared features differ on all of these distinctiveness measures, for both living and nonliving things.

Table 1.

Measures of Feature Distinctiveness for Distinctive Versus Shared Features

Factor	Distinctive		Shared		t(17)	p <
	M	SE	M	SE
Living
From concept generation norms
Target concept first	14.9	1.2	2.9	0.9	9.21	.001
Target concept total	16.5	0.9	6.1	1.3	7.46	.001
Other concepts (type)	8.2	0.9	16.8	1.3	−5.21	.001
Other concepts (token)	16.2	2.4	47.4	2.8	−9.39	.001
Cue validity	0.5	0.1	0.1	0.0	9.18	.001
From feature production norms
Concepts per feature	1.4	0.3	17.6	4.4	−3.57	.01
Distinctiveness	0.9	0.1	0.3	0.1	6.48	.001
Cue validity	0.9	0.1	0.3	0.1	6.36	.001
Nonliving
From concept generation norms
Target concept first	15.1	0.9	1.2	0.5	15.74	.001
Target concept total	16.8	0.8	4.2	1.3	9.08	.001
Other concepts (type)	10.6	1.3	21.1	1.9	−5.60	.001
Other concepts (token)	25.7	2.8	52.1	1.4	−9.10	.001
Cue validity	0.4	0.1	0.1	0.0	8.27	.001
From feature production norms
Concepts per feature	1.3	0.2	20.3	8.1	−2.33	.05
Distinctiveness	0.9	0.1	0.3	0.1	5.52	.001
Cue validity	0.9	0.1	0.3	0.1	5.85	.001

Table 2 presents variables that were equated between groups because they may influence feature verification latency. Production frequency, the number of participants who listed the feature for the concept in McRae et al.’s (2005) norms, was equated because Ashcraft (1978) and McRae et al. (1997) found that it influences feature verification latency. Production frequency reflects the ease of accessibility of a feature given a concept. This measure is also considered an index of salience, as defined as the probability of the feature occurring in instances of the concept (Smith & Osherson, 1984; Smith, Osherson, Rips, & Keane, 1988). Ranked production frequency is the rank of each feature within a concept when a concept’s features are ordered in terms of production frequency. This variable was equated because it also has been found to predict feature verification latency (McRae et al., 1997), although it is highly correlated with production frequency. Because features differed between groups, variables associated with feature-name reading time had to be equated, or at least matched, so that they favored the shared features. These included the mean frequency of the words in the feature names (ln[freq] from the British National Corpus) and the length of the features in terms of both number of words and number of letters. Finally, feature types based on Wu and Barsalou (2005) were closely matched because they may influence semantic processing (e.g., external components may be accessed faster than functional features).¹

Table 2.

Means and Paired t Values for Equated Variables for Distinctive Versus Shared Features

Factor	Distinctive		Shared		t(17)	p
	M	SE	M	SE
Living
Production frequency	11.2	1.2	11.1	1.1	0.22	> .80
Rank production frequency	7.4	1.0	7.1	1.0	0.32	> .70
ln(BNC) feature frequency	5.1	0.6	7.1	0.5	−4.51	< .01
Feature length in words	2.2	0.3	2.2	0.2	0.00
Feature length in letters	9.6	1.0	9.8	1.0	−0.26	> .70
Nonliving
Production frequency	12.5	1.4	13.0	1.1	−0.36	> .70
Rank production frequency	5.7	0.8	4.6	0.6	1.38	> .10
ln(BNC) feature frequency	6.6	0.6	8.0	0.4	−2.37	< .05
Feature length in words	2.9	0.2	2.6	0.2	2.05	> .05
Feature length in letters	13.8	1.2	12.9	0.9	1.23	> .20

Note. BNC = British National Corpus.

Additional tests were conducted to see whether the selected living- and nonliving-thing concepts were matched on four variables known to influence feature verification latency: concept word frequency (ln(freq) from the British National Corpus), concept length in letters, the number of features generated to a concept in the feature production norms (features per concept; Ashcraft, 1978), and concept familiarity (McRae et al., 1999). The latter two variables were derived from McRae et al.’s (2005) norms, whereas familiarity ratings were acquired from participants by asking them to rate how familiar they are with the concept, on a 9-point scale on which 9 indicates extremely familiar. Living and nonliving things were well matched on frequency, t(34) = 1.14, p > .20 (M = 7.3, SE = 0.3, for living; M = 7.7, SE = 0.3, for nonliving) and concept length in letters, t(34) = 1.28, p = .20 (M = 5.0, SE = 0.5, for living; M = 5.8, SE = 0.4, for nonliving). However, the living things possessed a greater number of features than did the nonliving things, t(34) = 2.36 (M = 15.2, SE = 0.8, for living; M = 12.7, SE = 0.6, for nonliving).² The living things were also rated as less familiar, t(34) = 2.11 (M = 6.1, SE = 0.4, for living; M = 7.4, SE = 0.4, for nonliving).

In summary, the concept generation norming study confirmed that the selected set of distinctive and shared features were in fact significantly different in terms of multiple measures of distinctiveness and were well matched on variables that have been shown to influence feature verification latency (or, if a difference existed, it favored the shared features).

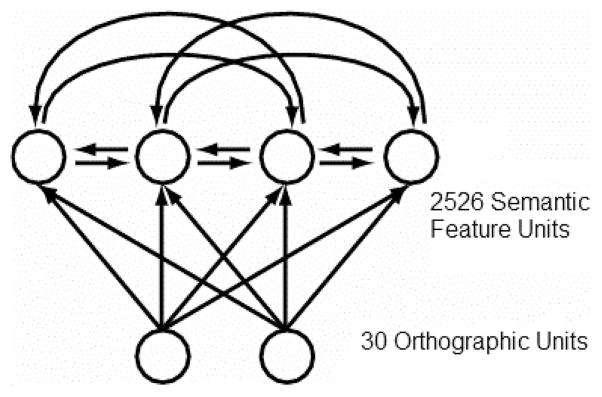
Simulations

A connectionist attractor network was trained to map from the names of 541 concepts to feature-based semantic representations. Connectionist attractor networks are a class of models that have been used to account for numerous behavioral phenomena involving the mapping from word form to meaning (Devlin et al., 1998; Harm & Seidenberg, 1999, 2004; Hinton & Shallice, 1991; Joanisse & Seidenberg, 1999; Plaut & Shallice, 1993). We have used attractor networks to simulate semantic similarity priming effects (Cree et al., 1999; McRae et al., 1997), the effects of correlations among features on feature verification latencies (McRae et al., 1997, 1999), and typicality effects (Cree & McRae, 2001).

One of our overarching research goals is to develop a single computational model that can account for both established and new experimental results in the area of semantic memory. We focus on developing a single model, rather than a unique model for each behavioral phenomenon. Note that the present model differs in minor ways from our earlier implementations simply because we now possess a larger set of training patterns. An important aspect of our incremental model development is that a consistent set of underlying theoretical principles are instantiated in the models. In the present case, the theoretical principles are identical to our previously published models (cited in the previous paragraph). We believe that as a body of empirical observations accumulates that can be insightfully understood using these principles, the position from which we can argue for our theory strengthens. Thus, the simulations described herein should be considered within the broader context of the expanding set of simulations of related empirical phenomena that we and others have reported.

Our goals with respect to the specific simulations reported herein are twofold. First, we use the model to provide predictions for Experiments 1 and 2. It is important to note that the predictions both differ from those of Randall et al. (2004), and, to foreshadow our results, fit with the strongest behavioral evidence regarding the time course of computation of distinctive semantic features available to date. Second, we analyze the internal weight structure of the model to provide insight into one plausible mechanism through which the human data can be interpreted. Of course, as with almost all modeling endeavors, we are open to the possibility that alternative explanations of the human data are possible, and we describe and evaluate some of those possibilities herein.

Simulation 1

Simulation 1 tested whether distinctive features are activated more quickly and/or strongly than shared features when a concept name has been presented. On the basis of analyses of a similar network (Cree, 1998) trained with fewer concepts, we predicted that there would be a distinctiveness effect for both living and nonliving things. In contrast, proponents of the conceptual structure account would predict a disadvantage in processing the distinctive features of living things relative to other features. Details of the network architecture and training can be found in Appendix B.

Method

Items

Thirteen living- and 12 nonliving-thing items from the concept generation norming study were used. It was inappropriate to use all of the items, because some features that appear in several concepts in the world are distinctive in the norms, and thus also in the network. This is because the norms, although large, do not sample the entire space of concepts.

Procedure

Each feature verification trial was simulated as follows. First, the initial activations of all feature units were set to a random value between 0.0 and 0.1, but they were free to vary throughout the remaining ticks of the trial (as in training). Next, the concept’s word form representation was activated (activation = 1.0) for each of 60 ticks, and the activations of the distinctive and shared features were logged. Thus, activations of target units were a function of the net input from the word form units and the other feature units.

As in McRae et al. (1997, 1999), we assumed that verification latency is monotonically related to the activation of the distinctive or shared feature. Note that it is not obvious how to simulate the decision component of the feature verification task. Indeed, there exists no explicit theory regarding how people perform a feature verification task. Our model is intended to simulate speeded conceptual computations but not the entire decision-making process. A more complex model would be required to make predictions that include the decision-making process (see, e.g., Joordens, Piercey, & Azerbehi, 2003, for ideas about how a random-walk decision-making process could be added to a connectionist model of word meaning computation).

Results and Discussion

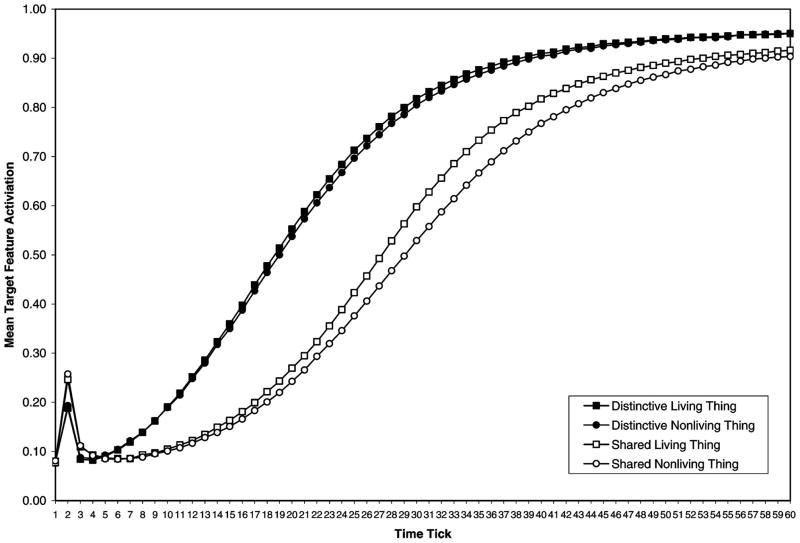
The results of Simulation 1 are presented in Figure 1. An analysis of variance (ANOVA) was conducted on the target feature activations with domain (living vs. nonliving) as a between-items independent variable and distinctiveness (distinctive vs. shared) and tick (1 to 60) as within-item variables.

Figure 1.

Simulation 1: Activation of target features when preceded by a concept name (as in Experiment 1).

Distinctive features were more active than shared features, F(1, 23) = 56.53. Planned comparisons revealed a significant difference between distinctive and shared features for Ticks 8–60 (p < .01 for Ticks 10–45, p < .01 for Ticks 9 and 46–52, p < .05 for Ticks 8 and 53–60), suggesting that once the network was given sufficient time to process a concept name, the effect of distinctiveness emerged and remained. When considering just the living things, the distinctiveness effect was significant for Ticks 9–48 (p < .05 at Ticks 9 and 44–48, p < .01 for Ticks 10–11 and 39–43, and p < .01 for Ticks 12–38). For the nonliving things, the effect was significant for Ticks 9–54 (p < .05 for Ticks 9 and 49–54, p < .01 for Ticks 10–11 and 44–48, and p < .01 for Ticks 12–43). Distinctiveness interacted with tick because distinctiveness effects were largest at Ticks 10–45, F(59, 1357) = 50.67. Target features became more active as the network settled to a stable state, F(59, 1357) = 1,241.72. No other main effects or interactions were significant.

Consistent with the predictions of hierarchical network theory but contrary to the conceptual structure account, distinctive features were activated more quickly and/or strongly than shared features for both living and nonliving things. It is difficult to imagine how spreading activation would account for these results. The production frequency data from McRae et al.’s (2005) norms support the assumption that the criterialities between the distinctive and shared features were equated in our stimuli. Furthermore, given that the same concept was used in both groups, the number of links emitting from a concept is equated. Note also that unlike hierarchical network theory, there is no hierarchy in our network, yet we still obtain results similar to those predicted from hierarchical network theory. It is therefore imperative that we analyze the network to understand why this effect is occurring.

Why do we see the distinctiveness effect in our network? Distinctive features are useful for discriminating among similar concepts. Thus, in a multidimensional semantic space in which each feature is a dimension, distinctive features are key dimensions along which similar patterns can be separated. During training, the network’s task is to divide the multidimensional space into regions that correspond to each concept. Given the dynamics of processing, once the system enters one of these regions, it will settle to a stable state within that region. These stable states are called attractors, and the regions are referred to as attractor basins. Many factors interact to influence how the weights are shaped during learning and form the attractor basins that influence the time course of feature unit activation during settling. A feature’s distinctiveness influences the degree to which it helps the network enter the correct attractor basin. One solution to the learning task is to activate distinctive features first and then complete the remainder of the concept through activation flowing from distinctive features to the other relevant features. Distinctive features could also inhibit activation of features from other concepts that share features with a target concept, thus preventing a snowball effect of shared features activating features of other concepts.

Analyses of the weights suggest that these two possible roles of distinctive features are part of the picture. The weights from the concept word form units to that concept’s distinctive feature units (M = 1.4, range = 0.68 to 2.35) are significantly higher than the weights to the corresponding shared feature units (M = 0.5, range = −1.85 to 2.63), t(74) = 9.15, p < .01. That is, the network tends to develop stronger weights between word form units and distinctive features. Furthermore, on average, the weights leaving the distinctive features are significantly higher (M = 0.8, range = 0.03 to 2.05) than those leaving the shared features (M = 0.4, range = −2.14 to 3.98), t(353) = 9.95, p < .01. In both cases, the weights leaving distinctive features are always positive because these features are a good cue to the other features in the concept, whereas the weights leaving shared units are often negative because these features do not discriminate among concepts to as great a degree.

In short, the distinctive features effect is due to at least two factors: pressure in an attractor network to settle to a stable state as quickly as possible and the manner in which learning causes the structure of the environment to be reflected in the weights.

Experiment 1

Concept names were presented prior to feature names to allow us to investigate predictions generated from Simulation 1 and contrast them with the conceptual structure account. We investigated potential time course changes by manipulating the stimulus onset asynchrony (SOA) between the presentation of the concept name and the target feature. Simulation 1 showed distinctiveness effects of similar magnitudes for both living and nonliving things, a prediction that directly contrasts with the conceptual structure account. It also suggested that although there should be significant distinctiveness effects at all SOAs, they may be somewhat muted at longer SOAs.

Method

Participants

Eighty-six University of Western Ontario undergraduates were paid $5 for their participation. All were native speakers of English and had either normal or corrected-to-normal visual acuity. The data from 6 participants were discarded because their error rate exceeded 25% across experimental trials (filler and target trials). This left 20 participants per list.

Materials

The 36 concepts (and their features) selected using the concept generation norms were converted into 72 feature–concept pairs. The stimuli were divided into two lists, such that if a distinctive feature occurred with the corresponding concept name in List 1 (owl 〈hoots〉), then its control shared feature occurred with the same concept in List 2 (owl 〈flies〉), and vise versa. Each list contained 18 distinctive features (for each of 9 living and 9 nonliving things) and 18 shared features (9 living and 9 nonliving). Thirty-six filler concept–feature pairs were included in each list so that there were equal numbers of “yes” and “no” responses. To avoid cuing the decision, we matched feature type (e.g., perceptual, function, characteristic behavior) as closely as possible between targets and fillers such that, for example, for each target external component that required a “yes” response (〈has a buckle〉), there was a filler feature of the same type requiring a “no” response (〈has a blade〉). The filler items used 18 living and 18 nonliving things so that when combined with the targets, there were an equal number of living and nonliving concepts that required a “yes” or a “no.” The same fillers appeared in both lists. Forty feature–concept pairs, 20 “yes” and 20 “no” items, were constructed for practice trials, roughly equating the proportion of feature types relative to the experimental trials and the number of living and nonliving thing items (20 living- and 20 nonliving-thing pairs). Across the practice, filler, and experimental items, no participant encountered a concept or feature name more than once.

Procedure

Participants were tested individually using PsyScope (Cohen, MacWhinney, Flatt, & Provost, 1993) on a Macintosh G3 computer equipped with a 17-in. color Sony Trinitron monitor. Verification latencies were recorded with millisecond accuracy using a CMU button box (New Micros, Dallas, Texas) that measured the time between the onset of the target concept and the onset of the button press. Participants used the index finger of their dominant hand for a “yes” response and the other hand for a “no” response. Participants were randomly assigned to one of the eight conditions formed by crossing the four SOAs (300, 750, 1,200, or 1,650 ms) by two lists.

Each trial in the 300-ms SOA condition proceeded as follows: A fixation point (+) appeared in the center of the screen for 500 ms; a blank screen for 100 ms; a concept name in the center of the screen for 300 ms; and then a feature name one line below the concept name. Both the feature and concept names remained on screen until the participant responded. Trials were presented in random order. The intertrial interval was 1,500 ms. The 750-, 1,200-, and 1,650-ms SOA conditions were identical except that the concept name was presented for 750 ms, 1,200 ms, or 1,650 ms before the onset of the feature name.

Participants were instructed to read both the concept and feature names silently and then to indicate, as quickly and accurately as possible, whether the feature was reasonably true of the concept. They completed the 40 practice trials and then the 72 experimental trials. Following the practice trials, they were encouraged to ask any questions they might have about the task. The experiment took approximately 25 min.

Design

The independent variables were distinctiveness (distinctive vs. shared), SOA (300, 750, 1,200, 1,650 ms), and concept domain (living vs. nonliving thing). List and item rotation group were included for participants and items analyses, respectively, as dummy variables to help stabilize variance due to the rotation of participants and items across lists (Pollatsek & Well, 1995). Distinctiveness was within participant (F₁) and within item (F₂), domain was within participant but between items, and SOA was between participants but within item. The dependent measures were verification latency and the square of the number of errors (Myers, 1979). Planned comparisons were conducted to investigate the difference between distinctive and shared features at each SOA for living and nonliving things.

Results and Discussion

The verification latency data are presented in Table 3, and the error data in Table 4. In Experiments 1 and 2, analyses of verification latencies included only correct responses. Verification latencies greater than three standard deviations above the grand mean were replaced by the cutoff value, which affected 2% of the data.

Table 3.

Feature Verification Latencies (ms) by SOA and Concept Domain for Distinctive Versus Shared Features in Experiment 1 (Concept Name Presented First)

Condition and SOA (ms)	Shared		Distinctive		Difference
	M	SE	M	SE
Living
300	840	41	693	33	147**
750	941	35	856	32	85**
1,200	892	30	744	22	148**
1,650	1,045	49	887	45	158**
Nonliving
300	785	32	716	34	69*
750	927	32	818	31	109**
1,200	871	37	725	29	146**
1,650	992	48	926	45	66*

Note. SOA = stimulus onset asyncrony.

^*p < .05 by participants only.

^**p < .05 by participants and items.

Table 4.

Percentage of Feature Verification Errors by SOA and Concept Domain for Distinctive Versus Shared Features in Experiment 1 (Concept Name Presented First)

Condition and SOA (ms)	Shared		Distinctive		Difference
	M	SE	M	SE
Living
300	12.2	2.4	8.9	2.5	3.3
750	8.3	2.1	7.8	2.6	0.5
1,200	11.7	3.1	5.6	2.1	6.1
1,650	10.0	2.5	8.9	2.7	1.1
Nonliving
300	9.4	1.9	2.8	1.4	6.6*
750	10.6	1.9	5.6	1.9	5.0
1,200	12.8	2.2	2.2	1.0	10.6**
1,650	9.4	2.6	5.0	2.3	4.4

Note. SOA = stimulus onset asynchrony.

^*p < .05 by participants only.

^**p < .05 by participants and items.

Verification latency

Collapsed across SOA and domain, verification latencies were 116 ms shorter for distinctive (M = 796 ms, SE = 14 ms) than for shared features (M = 912 ms, SE = 15 ms), F₁(1, 72) = 132.94, F₂(1, 32) = 30.73. The three-way interaction among distinctiveness, SOA, and domain was significant by participants, F₁(3, 72) = 3.16, and marginal by items, F₁(3, 96) = 2.56, p < .06. Planned comparisons showed that for nonliving things, distinctive features were verified more quickly than shared features at the 750-ms SOA, F₁(1, 137) = 18.01, F₂(1, 67) = 8.26, and at the 1,200-ms SOA, F₁(1, 137) = 32.32, F₂(1, 67) = 15.65. Furthermore, the effect was significant by participants and marginal by items at the 300-ms SOA, F₁(1, 137) = 7.22, F₂(1, 67) = 3.71, p > .05, and at the 1,650-ms SOA, F₁(1, 137) = 6.60, F₂(1, 67) = 3.61, p > .05. The influence of distinctiveness was stronger for living things in that distinctive features were verified more quickly than shared features at all SOAs: for 300 ms, F₁(1, 137) = 32.76, F₂(1, 67) = 14.62; for 750 ms, F₁(1, 137) = 10.95, F₂(1, 67) = 5.14; for 1,200 ms, F₁(1, 137) = 33.21, F₂(1, 67) = 17.14; and for 1,650 ms, F₁(1, 137) = 37.85, F₂(1, 67) = 21.06.

Collapsed across SOA, the Distinctiveness × Domain interaction was significant by participants, F₁(1, 72) = 3.14, but not by items (F₂ < 1). For living things, participants responded 134 ms faster to distinctive features, whereas the effect was 98 ms for nonliving things.

SOA did not interact with distinctiveness, F₁(3, 72) = 1.19, p > .30; F₂(3, 96) = 1.84, p > .10. Crucially, collapsed across domain, verification latencies for distinctive features were shorter at every SOA. When the SOA was 300 ms, distinctive features were verified 108 ms faster (distinctive: M = 704 ms, SE = 24 ms; shared: M = 812 ms, SE = 26 ms), F₁(1, 72) = 28.89, F₂(1, 96) = 36.22. When the SOA was 750 ms, the distinctiveness advantage was 97 ms (distinctive: M = 837 ms, SE = 22 ms; shared: M = 934 ms, SE = 23 ms), F₁(1, 72) = 23.31, F₂(1, 96) = 29.40. When the SOA was 1,200 ms, the advantage was 148 ms (distinctive: M = 734 ms, SE = 18 ms; shared: M = 882 ms, SE = 23 ms), F₁(1, 72) = 54.26, F₂(1, 96) = 73.04. Finally, the distinctiveness effect was 111 ms at a 1,650-ms SOA (distinctive: M = 907 ms, SE = 32 ms; shared: M = 1,018 ms, SE = 34 ms), F₁(1, 72) = 30.52, F₂(1, 96) = 46.12.

Finally, there was a main effect of SOA, F₁(3, 72) = 7.33, F₂(3, 96) = 60.39. The mean latencies were 758 ms (SE = 18 ms) at the 300-ms SOA, 886 ms (SE = 17 ms) at the 750-ms SOA, 808 ms (SE = 17 ms) at the 1,200-ms SOA, and 963 ms (SE = 24 ms) at the 1,650-ms SOA. Verification latencies did not differ for living (M = 862 ms, SE = 15 ms) versus nonliving things (M = 845 ms, SE = 15 ms), F₁(1, 72) = 3.14, p > .05; F₂ < 1. Domain did not interact with SOA (F₁ < 1, F₂ < 1).

Errors

Collapsed across SOA and domain, participants made 4.8% fewer errors to distinctive (M = 5.8%, SE = 0.8%) than shared features (M = 10.6%, SE = 0.8%), F₁(1, 72) = 29.70, F₂(1, 32) = 7.84, suggesting distinctive features are more tightly tied to a concept than shared features.

Distinctiveness, domain, and SOA did not interact (F₁ < 1, F₂ < 1). Planned comparisons showed that nonliving-thing error rates were significantly lower for distinctive features at the 1,200-ms SOA, F₁(1, 139) = 10.53, F₂(1, 76) = 9.32, and there was a marginal difference at the 300-ms SOA, F₁(1, 139) = 5.00, F₂(1, 76) = 3.58, p > .05. There was a nonsignificant difference at the 750-ms SOA, F₁(1, 139) = 3.39, p > .05; F₂(1, 76) = 2.53, p > .05, and at the 1,650-ms SOA, F₁(1, 139) = 1.62, p > .05; F₂ < 1. For living things, error rates did not differ significantly at any SOA; at the 300-ms SOA, F₁ < 1, F₂ < 1; at the 750-ms SOA, F₁ < 1, F₂ < 1; at the 1,200-ms SOA, F₁(1, 139) = 2.09, p > .05, F₂(1, 76) = 2.40, p > .05; and at the 1,650-ms SOA, F₁ < 1, F₂ < 1.

Distinctiveness interacted with domain by participants, F₁(1, 72) = 8.52, but not by items, F₂(1, 32) = 1.12, p > .05. Participants made 6.7% fewer errors to nonliving-thing distinctive (M = 3.9%, SE = 1.0%) than to shared features (M = 10.6%, SE = 1.0%), F₁(1, 139) = 36.77, F₂(1, 32) = 7.43. There were nonsignificantly fewer errors to living-thing distinctive (M = 7.8%, SE = 1.3%) than to shared features (M = 10.6%, SE = 1.3%), F₁(1, 139) = 5.60, F₂(1, 32) = 1.51, p > .05.

The main effect of SOA was significant by items, F₂(3, 96) = 3.85, but not participants, F₁(3, 72) = 1.81, p > .10. The error rates for each SOA were as follows: for 300 ms: M = 8.3%, SE = 1.1%; for 750 ms: M = 8.1%, SE = 1.1%; for 1,200 ms: M = 8.1%, SE = 1.2%; and for 1,650 ms: M = 8.3%, SE = 1.3%. SOA did not interact with distinctiveness, F₁(3, 72) = 1.38, p > .20; F₂(3, 96) = 2.11, p > .10. Finally, participants made nonsignificantly more errors on living-thing items (M = 9.2%, SE = 0.9%) than on nonliving-thing items (M = 7.2%, SE = 0.7%), F₁(1, 72) = 2.13, p > .10; F₂(1, 32) = 2.10, p > .10. Domain did not interact with SOA, F₁(3, 72) = 1.31, p > .20; F₂(3, 96) = 1.01, p > .30.

In summary, when items were chosen to maximize differences in distinctiveness while equating for other variables as closely as possible, distinctiveness effects were strong. Collapsed across living and nonliving things, the effect was significant at all SOAs. The distinctiveness advantage for living things was significant at all SOAs, and for nonliving things, it was significant either by both participants and items (750 and 1,200 ms) or by participants only (300 and 1,650 ms). The results match Simulation 1 in that distinctive effects were clear for both living and nonliving things across SOAs. Furthermore, they did not differ significantly for living versus nonliving things (there was no Distinctiveness × Domain interaction). However, the network’s SOA predictions were not borne out; distinctiveness effects did not decrease at the longer SOAs.

Experiment 1 failed to match critical aspects of Randall et al.’s (2004) simulations and human results. Although they reported a distinctiveness advantage for nonliving things, as we found in Experiment 1, they also predicted and reported a distinctiveness disadvantage for living things. In contrast, we found a large distinctiveness advantage for living things at all four SOAs.

Researchers often invoke the notion of explicit expectancy generation to account for performance when long SOAs are used (Neely & Keefe, 1989). However, it seems unlikely to account for the present results. Because each pair of distinctive and shared features was derived from the same concept, the total number of features that participants might have generated was equated. Furthermore, feature production frequency is a measure of the likelihood that a feature is generated given a concept name, and both production frequency and ranked production frequency were equated for distinctive versus shared features. Therefore, if participants were generating expected upcoming features, it seems that they would be as likely to generate the shared as they would the distinctive features, producing null distinctiveness effects. This suggests that the influence of distinctiveness resides in the computation of word meaning, as in Simulation 1.

Simulation 2

Simulation 2 was analogous to a feature verification task in which the feature name was presented before the concept name. It tested whether activation from a distinctive feature better evokes the representation of the target concept than does activation from a shared feature. If the distinctive features effect observed in Experiment 1 is due to the patterns of weights we argue are developed during training (described in Simulation 1), then we would expect to see a robust distinctive features effect for both living and nonliving things when the feature is presented before the concept. Randall et al. (2004) did not make specific predictions concerning this presentation order. It seems reasonable to suggest, however, that they would predict a disadvantage for the distinctive features of living things, because according to the conceptual structure account, they are not strongly correlated with other features, unlike shared features of living things and both distinctive and shared properties of nonliving things.

Method

Items

The items were the same as in Simulation 1.

Procedure

Each feature–concept verification trial was simulated as follows. First, all word form and semantic units were set to activation values of 0. A single feature unit, corresponding to either a distinctive or a shared feature, was clamped at a high value (15.0) for 20 ticks. Because each feature was represented as a single unit, activation greater than 1.0 was necessary for one of 2,526 feature units to significantly affect the dynamics of the system. The activation values for all other semantic units were free to vary. On each trial, over 20 ticks, we recorded the activation of each of the semantic features that are part of the target concept’s representation. The number of ticks in Simulation 2 is less than that used in Simulation 1. In Simulation 1, the concept’s word form was the input, and then semantic computations began from that point. In Simulation 2, however, we began by directly activating semantics (i.e., a feature node), so fewer ticks were required to represent the relevant temporal properties of the analogous human task.

For interpreting the simulations, we adopted assumptions from McRae et al.’s (1999) feature verification simulations. The activation levels of the other semantic features possessed by the target concept were measured at each iteration to assess how the distinctive or shared feature influences the ensuing computation of a concept containing it and how this influence changes over time. We assumed that feature–concept verification latency is determined partly by the amount of time required for the semantic system to move from the state resulting from activating a single feature to the state representing the concept. We therefore assumed that verification latency in Experiment 2 is monotonically related to the mean activation of the target concept’s features that are preactivated by the distinctive or shared feature.

Results and Discussion

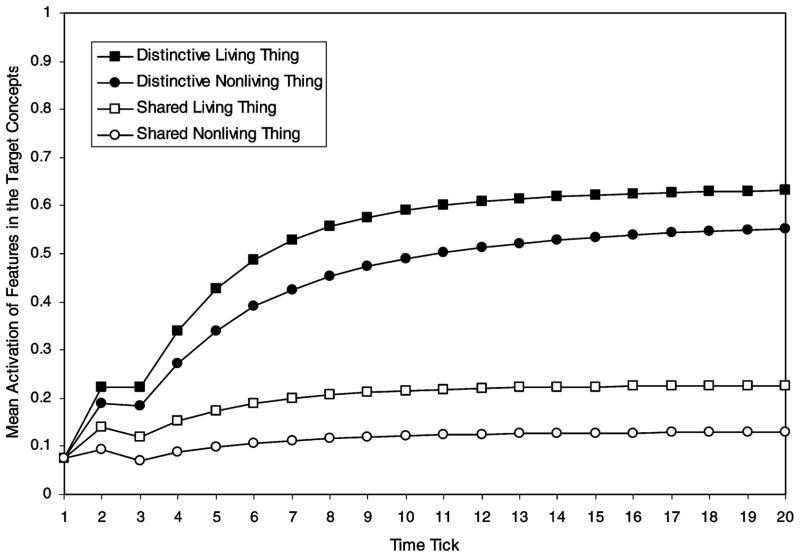
Figure 2 shows that the average activation of the features in the target concepts was higher for distinctive than for shared features, for both living and nonliving things. An ANOVA was conducted with the mean activation of the target concepts’ features as the dependent variable, domain (living vs. nonliving) as a between-items independent variable, and distinctiveness (distinctive vs. shared) and tick (1 to 20) as within-item independent variables.

Figure 2.

Simulation 2: Average activation of the target concept’s features when preceded by a feature (as in Experiment 2).

Distinctive features more strongly activated the target concepts than did shared features, F(1, 23) = 61.94. Of note, collapsed across domains, planned comparisons revealed significant differences between distinctive and shared items at all but the first tick. Planned comparisons revealed that this contrast was significant for both living and nonliving things, when considered separately, for Ticks 3–20 in both cases (p < .05 at Tick 3, p < .01 at Tick 4, and p < .01 at Ticks 5–20). Distinctiveness and tick interacted because the influence of distinctiveness was more pronounced at later time ticks, F(19, 437) = 75.71. Overall, living-thing features were more strongly activated than those of nonliving things, F(1, 23) = 5.01. Domain and tick interacted because the overall living–nonliving difference increased over the 20 ticks, F(19, 437) = 3.60. The three-way interaction was not significant (F < 1). Finally, target concepts’ features became more active at later ticks, F(19, 437) = 195.49.

In summary, Simulation 2 provides three main predictions. First, there should be distinctiveness effects for living and nonliving things across a range of SOAs. Second, these effects should not differ substantially for living versus nonliving things. Third, the simulation predicts that distinctiveness will interact with SOA in that distinctiveness effects should increase as the SOA becomes longer.

Experiment 2

We used a feature verification task to test whether a distinctive feature activates a relevant concept more strongly than does a shared feature. This method is congruent with tests of cue validity because both index the availability of a concept given a feature. The influence of distinctive versus shared features was investigated using the same SOAs as in Experiment 1.

Method

Participants

Eighty University of Western Ontario undergraduates were paid $5 for their participation. All were native English speakers and had either normal or corrected-to-normal visual acuity.

Materials

The target, filler, and practice stimuli were identical to those in Experiment 1.

Procedure

The procedure was identical to that of Experiment 1 except that the feature name was presented prior to the concept name for the length of the SOA. The experiment took approximately 25 min.

Design

The design was identical to that of Experiment 1.

Results and Discussion

The verification latency data are presented in Table 5, and the error data in Table 6.

Table 5.

Feature Verification Latencies (ms) by SOA and Concept Domain for Distinctive Versus Shared Features in Experiment 2 (Feature Name Presented First)

Condition and SOA (ms)	Shared		Distinctive		Difference
	M	SE	M	SE
Living
300	1,114	65	961	43	153**
750	914	49	730	41	184**
1,200	858	55	640	56	218**
1,650	951	54	715	58	236**
Nonliving
300	1,066	54	1,001	56	65*
750	880	42	767	49	113**
1,200	827	45	710	52	117**
1,650	940	48	767	53	173**

Note. SOA = stimulus onset asynchrony.

^*p < .05 by participants only.

^**p < .05 by participants and items.

Table 6.

Percentage of Feature Verification Errors by SOA and Concept Domain for Distinctive Versus Shared Features in Experiment 2 (Feature Name Presented First)

Condition and SOA (ms)	Shared		Distinctive		Difference
	M	SE	M	SE
Living
300	12.8	2.9	3.9	1.2	8.9**
750	10.0	3.4	5.0	1.5	5.0
1,200	12.8	2.9	5.6	1.5	7.2**
1,650	7.9	2.2	1.8	0.9	6.1*
Nonliving
300	9.4	1.9	2.2	1.3	7.2**
750	13.9	2.5	2.2	1.0	11.7**
1,200	10.0	2.1	3.3	1.2	6.7*
1,650	8.3	2.1	1.7	0.9	6.6*

Note. SOA = stimulus onset asynchrony.

^*p < .05 by participants only.

^**p < .05 by participants and items.

Verification latency

Collapsed across SOA and concept domain, verification latencies were 158 ms shorter for distinctive (M = 786, SE = 19) than for shared features (M = 944, SE = 19), F₁(1, 72) = 213.25, F₂(1, 32) = 34.67. The three-way interaction among distinctiveness, SOA, and domain was not significant (F₁ < 1, F₂ < 1). Planned comparisons revealed that for nonliving things, distinctive features were verified more quickly than shared features at the three longest SOAs: for 750 ms, F₁(1, 141) = 11.81, F₂(1, 71) = 7.96; for 1,200 ms, F1(1, 141) = 12.66, F₂(1, 71) = 6.69; and for 1,650 ms, F₁(1, 141) = 27.67, F₂(1, 71) = 14.43. When the SOA was 300 ms, the effect of distinctiveness was marginal, F₁(1, 141) = 3.91, p < .06; F₂(1, 71) = 2.15, p > .10. For living things, the advantage for distinctive features was reliable at all SOAs: for 300 ms, F₁(1, 141) = 21.64, F₂(1, 71) = 9.12; for 750 ms, F₁(1, 141) = 31.30, F₂(1, 71) = 14.43; for 1,200 ms, F₁(1, 141) = 43.94, F₂(1, 71) = 19.32; and for 1,650 ms, F₁(1, 141) = 51.50, F₂(1, 71) = 22.46.

Collapsing across SOA, the Distinctiveness × Domain interaction was significant by participants, F₁(1, 72) = 10.62, but not by items, F₂(1, 32) = 1.37, p > .10. This reflects the fact that for living things, verification latencies were 197 ms shorter for distinctive features, (distinctive: M = 762 ms, SE = 26 ms; shared: M = 959 ms, SE = 30 ms), whereas the effect was 117 ms in nonliving things (distinctive: M = 811 ms, SE = 29 ms; shared: M = 928 ms, SE = 25 ms).

The distinctiveness advantage approximately doubled across the SOAs, F₁(3, 72) = 3.36, F₂(3, 96) = 2.85. Crucially, however, simple main effects analyses show that, collapsed across concept domain, verification latencies for distinctive features were shorter at every SOA. When the SOA was 300 ms, distinctive features were verified 110 ms faster (distinctive: M = 981 ms, SE = 35 ms; shared: M = 1,090 ms, SE = 42 ms), F₁(1, 72) = 25.73, F₂(1, 96) = 21.07. When the SOA was 750 ms, the distinctiveness advantage was 149 ms (distinctive: M = 748 ms, SE = 32 ms; shared: M = 897 ms, SE = 32 ms), F₁(1, 72) = 47.57, F₂(1, 96) = 45.44. When the SOA was 1,200 ms, the advantage was 167 ms (distinctive: M = 675 ms, SE = 33 ms; shared: M = 842 ms, SE = 35 ms), F₁(1, 72) = 60.25, F₂(1, 96) = 50.53. Finally, the distinctiveness effect was 204 ms at a 1,650-ms SOA (distinctive: M = 741 ms, SE = 38 ms; shared: M = 945 ms, SE = 36 ms), F₁(1, 72) = 89.80, F₂(1, 96) = 75.51.

There was a main effect of SOA, F₁(3, 72) = 6.83, F₂(3, 96) = 36.69. This effect is due largely to long verification latencies at the 300-ms SOA (for 300-ms SOA: M = 1,035 ms, SE = 28 ms; for 750-ms SOA: M = 823 ms, SE = 24 ms; for 1,200-ms SOA: M = 759 ms, SE = 26 ms; for 1,650-ms SOA: M = 843 ms, SE = 28 ms).

Finally, verification latencies for nonliving things (M = 870 ms, SE = 20 ms) did not differ overall from living things (M = 860 ms, SE = 21 ms; F₁ < 1, F₂ < 1). In addition, concept domain did not interact with SOA (F₁ < 1, F₂ < 1).

Errors

The numbers of errors were square-root transformed for the ANOVAs (Myers, 1979). Overall, participants made 7.4% fewer errors to distinctive features (M = 3.2%, SE = 0.4%) than to shared features (M = 10.6%, SE = 0.9%), F₁(1, 72) = 58.07, F₂(1, 32) = 13.27, providing further evidence that distinctive features are more tightly tied to a concept than are shared features.

The three-way interaction among distinctiveness, domain, and SOA was not significant (F₁ < 1, F₂ < 1). Planned comparisons showed that for nonliving things, participants made fewer errors on distinctive features at the 300-ms SOA, F₁(1, 141) = 13.32, F₂(1, 77) = 6.01, and at the 750-ms SOA, F₁(1, 141) = 20.53, F₂(1, 77) = 8.44. The difference was marginal at the 1,200-ms SOA, F₁(1, 141) = 6.99, F₂(1, 77) = 2.52, p > .05, and at the 1,650-ms SOA, F₁(1, 141) = 8.02, F₂(1, 77) = 2.52, p > .05. For living things, participants also made fewer errors on distinctive features at the 300-ms SOA, F₁(1, 141) = 8.02, F₂(1, 77) = 7.17, and at the 1,200-ms SOA, F₁(1, 141) = 5.42, F₂(1, 77) = 4.36. However, the difference was marginal at the 1,650-ms SOA, F₁(1, 141) = 7.32, F₂(1, 77) = 1.98, p > .05, and nonsignificant at the 750-ms SOA, F₁(1, 141) = 2.28, p > .05; F₂(1, 77) = 1.98, p > .05.

Distinctiveness did not interact with domain, F₁(3, 72) = 2.76, p > .10, F₂ < 1, or with SOA (F₁ < 1, F₂ < 1). The main effect of SOA was significant by items, F₂(3, 96) = 3.85, but not by participants, F₁(3, 72) = 1.81, p > .10. This marginal effect was due to fewer errors occurring at the longest SOA (for 300 ms, M = 7.1%, SE = 1.1%; for 750 ms, M = 7.8%, SE = 1.2%; for 1,200 ms, M = 7.9%, SE = 1.1%; and for 1,650 ms, M = 4.9%, SE = 0.9%). Finally, participants made approximately the same number of errors for living (M = 7.4%, SE = 0.8%) and nonliving things (M = 6.4%, SE = 0.7%; F₁ < 1, F₂ < 1).

With items chosen to maximize differences in distinctiveness while equating for other variables as closely as possible, distinctiveness effects were strong. Thus, Experiment 2 supports the hypothesis that a distinctive feature evokes a concept’s representation more strongly than does a shared feature and therefore is a better cue for a corresponding concept than is a shared feature. Collapsed across living and nonliving things, the distinctiveness effect was significant at all SOAs. For living things, distinctiveness influenced verification latency at all SOAs, and for nonliving things, the effect was significant at all SOAs except 300 ms, where it was significant by participants but not by items. These results provide evidence for the influence of cue validity on the online computation of semantic knowledge.

One marginal planned comparison was found for nonliving things. It seems that an SOA of 300 ms may not have been long enough for participants to finish reading many of the nonliving-thing feature names prior to the presentation of the concept name. This presumably was more pronounced for nonliving things because, as Table 2 shows, the feature names paired with nonliving things were substantially longer on average than those paired with living things. The pattern of verification latencies over SOAs supports this interpretation (i.e., they are substantially longer at the 300-ms SOA). Thus, the difference between living and nonliving things at the 300-ms SOA may not reflect interesting differences between these domains but rather may simply reflect feature length in our items. To test this possibility, we correlated feature length in letters and words with verification latency at each SOA. Both variables were significantly correlated with verification latency at the 300-ms SOA (.48 for letters, .44 for words). For length in words, the largest correlation over the remaining three SOAs was .14. For length in letters, the correlation dropped to .25 at 750 ms, then .09 at 1,200 ms, and .22 at 1,650 ms. Only at the 300-ms SOA did feature length influence verification latency, thus supporting the idea that 300 ms was not sufficient time to read the feature names.

In contrast to the conceptual structure account, Simulation 2 predicted distinctiveness effects for both living and nonliving things, and these effects were obtained in Experiment 2. In addition, increased distinctiveness effects were predicted across SOAs, and this was also obtained in the human data. This SOA × Distinctiveness interaction is consistent with analogous effects in semantic priming experiments. Priming effects are often larger at longer SOAs, and these results have often been interpreted as suggesting that long SOAs involve a more substantial strategic processing component (prospective expectancy generation; Becker, 1980; Neely & Keefe, 1989). At long SOAs in Experiment 2, participants may have generated explicit expectancies, whereas the shorter SOAs may have prohibited this. That is, at long SOAs, participants may have generated a set of concepts after reading each feature name, expecting that one of them would be presented. Because distinctive features are included in fewer concepts than are shared features, the expectancy set for the former would be smaller than for the latter and would be more likely to include the target concept (as suggested by the concept generation study). Of interest, however, Simulation 2 predicted the SOA × Distinctiveness interaction without recourse to explicit expectancy generation, suggesting that the interaction may be a natural consequence of the semantic computations being simulated.

There were, however, two inconsistencies between the results of Simulation 2 and Experiment 2. First, there was no overall verification latency advantage for living things in Experiment 2, whereas one was predicted by Simulation 2. Second, unlike Experiment 2, the distinctiveness effects were similar in Simulation 2 for living and nonliving things. Although the difference in distinctiveness effects between domains at the 300-ms SOA in Experiment 2 was due at least in part to the length of feature names, which does not influence the network’s predictions, the differences at the other SOAs were also substantial. On the other hand, the Distinctiveness × Domain interaction was only marginal in Experiment 2, so perhaps this is not a critical issue.

Finally, the results differed substantially from predictions of the conceptual structure account. Rather than a distinctiveness disadvantage for living things, large distinctiveness advantages were obtained. An advantage for nonliving-thing distinctive features was found, which is consistent with this account. In contrast, spreading activation models, which were unable to account for the findings of Experiment 1, naturally account for the results of Experiment 2. Shorter verification latencies for distinctive features when a feature name is presented first would be predicted because fewer connections originate from a distinctive than from a shared feature.

General Discussion

Two experiments investigated whether distinctive features are activated more quickly and/or strongly than shared features during semantic computations. Predictions for the experiments were generated from a connectionist attractor network that has been used previously to account for semantic phenomena. In Experiment 1, in which the concept name was presented prior to the feature name, verification latency was shorter to distinctive than to shared features for both living and nonliving things, as was predicted by the network. This suggests that distinctive features are activated more quickly and/or strongly in the time course of the computation of word meaning. In Experiment 2, distinctive features activated a concept more strongly than did shared features for both living and nonliving things, again as predicted by the network, suggesting that they are better cues for a concept. The results provide further evidence that distinctive features hold a privileged status in the organization of semantic memory and in the computation of word meaning.

Contrary to the conceptual structure account of semantic memory, we found no evidence for a shared feature advantage for living things. In both experiments, participants were consistently faster to verify distinctive than shared features, regardless of whether a feature was paired with a living or a nonliving thing.

Note that we are not arguing that no differences exist between living and nonliving things with respect to distinctive and shared features. The stimuli in our experiments were chosen to maximize the probability of showing distinctiveness effects. These findings do not negate the fact that, on average, nonliving things have a greater number of distinctive features than do living things (Cree & McRae, 2003). Instead, the present experiments emphasize the importance of distinctive features in semantic memory, thus bolstering the argument that the difference in the number of distinctive features for living versus nonliving things has important implications for understanding neurological impairments.

Distinctive and Correlated Features

The distinctive feature advantage may at first glance appear to contradict McRae et al.’s (1999) results showing an advantage for strongly intercorrelated features over matched weakly intercorrelated ones. Statistically based knowledge of feature correlations is highlighted in statistical learning approaches, such as the attractor networks used herein, that naturally encode how features co-occur. Correlation is a matter of degree; some pairs of features are much more strongly correlated than others. The network’s knowledge of feature correlations that is encoded in, for example, feature–feature weights influences its settling dynamics and is a strong determinant of its semantically based pattern-completion abilities (McRae et al., 1997, 1999).

McRae et al. (1999) computed statistical correlations among a large set of features from feature production norms. They then computed a measure called intercorrelational strength, which is the sum of the proportions of shared variance between a specific feature and the other features of a specific concept. Attractor network simulations predicted that features that are strongly inter-correlated with the other features of a concept should be verified more quickly than matched features that are weakly intercorrelated (distinctiveness was equated in these experiments). This prediction was borne out by the human experiments.

It is therefore important to situate the shared features from the present experiments in terms of their degree of intercorrelational strength with respect to the items used in McRae et al. (1999). We computed intercorrelational strength for all of the shared features used in Experiments 1 and 2 (distinctive features have an intercorrelational strength of 0 because they do not appear in a sufficient number of concepts to be able to derive valid correlations). Mean intercorrelational strength was 43 for the nonliving shared features and 25 for the living shared features. The corresponding mean intercorrelational strengths for McRae et al.’s strongly intercorrelated features were 161 (their Experiment 1) and 225 (their Experiment 2), whereas for their weakly intercorrelated items, they were 32 and 26, respectively. Thus, the shared features in the present experiments resembled the weakly intercorrelated items of McRae et al.

To understand the relation between distinctive and correlated features, it may be useful to think of a two-dimensional space (a square or a rectangle), with one dimension being distinctiveness and the other being intercorrelational strength. Truly distinctive features such as 〈moos〉 would reside in one corner of the space (they occur in only one concept and do not participate in correlations). Highly shared features that are strongly correlated with other features of a concept would reside in the opposite corner. The shared features used as controls in the present Experiments 1 and 2 and in McRae et al. (1999) would occupy the middle portions of the space. Therefore, the present experiments, combined with those of McRae et al., suggest that the degree to which a feature activates a concept, as well as the degree to which a concept activates a feature, is highest in the truly distinctive and highly intercorrelated extremes of this two-dimensional space, all else being equal.

Association Between the Concept and Feature Names

We have focused on comparing predictions between two connectionist models of semantic memory, discussing alternative models along the way. One final possible alternative account of the present results is that the distinctive feature names are simply more associated with the concept names than are the shared feature names. Production frequency ratings from McRae et al.’s (2005) norms suggest that this is not the case. A semantic feature production task can be viewed as a type of controlled word-association task wherein responses are restricted to features. The distinctive and shared features of Experiments 1 and 2 were matched on both production frequency and ranked production frequency. Therefore, under the assumption that one factor underlying performance on the feature production norms is the strength of association from a concept to a feature name, an association view seems unlikely to account for the results of Experiment 1, in which the concept name was presented first.

The story is somewhat different for Experiment 2, in which the feature name was presented first. In this case, the relevant norms are the concept generation norms. If it is assumed that one factor underlying performance on these norms is the association strength from a feature name to a concept name, then it could be argued that the results of Experiment 2 are due to a stronger associative link from the distinctive features to the target concepts. On the other hand, the concept generation and word-association norms differ on the factors that restrict possible responses. It is precisely the point that the set of concept names that could be generated to a distinctive feature is more restricted than the set of possibilities for a shared feature, so that it is difficult to imagine obtaining equivalent results for the two feature types.

Conclusion

The present research provides the clearest empirical evidence to date for the privileged status of highly distinctive features in semantic memory using an online task that directly taps the computation of word meaning. Using a feature verification task, we demonstrated that distinctive features activate a corresponding concept more strongly than do shared features, and that they are activated more strongly when that concept is computed from verbal input. The key results were predicted by attractor network simulations, providing further evidence that connectionist attractor networks provide an appropriate framework for modeling semantic memory.

Appendix B. Description of Model Used for Simulations 1 and 2

Network Architecture

The network’s architecture is presented in Figure B1. The network mapped directly from 30 input units, representing word form, to 2,526 semantic feature units, representing word meaning. All semantic units were directly interconnected, with no self-connections, and had a standard trainable bias weight.

Figure B1.

Network architecture.

Training Patterns

Input to the network was an abstract word form representation that can be interpreted as either spelling or sound. Each word’s form was represented by activating a unique set of 3 of the 30 units to a value of 1 and the rest of the units to 0. Of the 91,390 possible input patterns, 541 were assigned randomly (without replacement) to the concept names. These word form representations were designed to capture the facts that word form representations are highly overlapping and that the mapping from word form to semantics is relatively arbitrary for monomorphemic English words.

Semantic representations were taken from the McRae et al. (2005) semantic feature production norms. In those norms, there are 2,526 unique features listed for 541 concepts. Thus, the network contained 2,526 semantic feature units. Word meaning was represented as patterns of activity distributed across those units (1 if a feature was present, 0 if it was not).

Computing the Meaning of a Word

To compute a word’s meaning, its word form was presented at the input layer and activation was allowed to propagate to the semantic layer for 20 ticks of time. The pattern of activation produced at the semantic layer was interpreted as the meaning of the word. Before a word form was presented, semantic unit activations were set to a randomly selected value between .00 and .10, to put the network into a random activation state.

Training

The network was trained using the continuous recurrent back-propagation through time training algorithm (Pearlmutter, 1995), using time-averaged inputs and online learning. The training and simulation software was written in the C programming language using Mikenet Version 8.02 libraries and was run on a dual 1-GHz processor AMD computer running Redhat Linux 7.2. At the beginning of training, weights were initialized to random values between ±.05. Each training epoch iterated through the entire training set of 541 concepts in random order. For each training trial, the input pattern was clamped for 20 units of time (ticks), and the error was injected for the last 10 ticks. Consistent with our previous models, we used the cross-entropy error measure. Training was stopped when at least 95% of the units that were intended to be active (calculated across all patterns) surpassed an activation threshold of .70 (the same threshold used by Cree et al., 1999). This threshold represents an average of .60 units incorrectly below threshold per item. Thirty-eight training epochs were required to reach this criterion. The learning rate was set to .01. Momentum of .90 was added after the first 10 epochs of training.

In summary, there were two main differences between this model and that of Cree et al. (1999). First, this model was trained with 541 concepts instead of 181. Second, it included weights that directly connected the semantic features units, whereas Cree et al. connected semantic units through a layer of hidden units. Direct connections allow for a more explicit and interpretable encoding of the degree to which specific features activate other features, but they were not feasible in our previous models owing to computational constraints.