A multi-layer evaluation approach for protein structure prediction and model quality assessment

Abstract

Protein tertiary structures are essential for studying functions of proteins at molecular level. An indispensable approach for protein structure solution is computational prediction. Most protein structure prediction methods generate candidate models first and select the best candidates by model quality assessment (QA). In many cases, good models can be produced but the QA tools fail to select the best ones from the candidate model pool. Because of incomplete understanding of protein folding, each QA method only reflects partial facets of a structure model, and thus, has limited discerning power with no one consistently outperforming others. In this paper, we developed a set of new QA methods, including two QA methods for target/template alignments, a molecular dynamics (MD) based QA method, and three consensus QA methods with selected references to reveal new facets of protein structures complementary to the existing methods. Moreover, the underlying relationship among different QA methods were analyzed and then integrated into a multi-layer evaluation approach to guide the model generation and model selection in prediction. All methods are integrated and implemented into an innovative and improved prediction system hereafter referred to as MUFOLD. In CASP8 and CASP9 MUFOLD has demonstrated the proof of the principles in terms of both QA discerning power and structure prediction accuracy.

INTRODUCTION

Predicting protein three-dimensional structure is an important approach for understanding its functions. Compared to the traditional experimental methods (e.g., X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy), protein structure prediction, i.e., inferring tertiary structure from protein sequence has become an indispensable tool (1) to study protein’s structure and function in a cost-effective and high-throughput way due to the significant progress made over the past two decades(1–6). The demand for protein structure prediction has been dramatically increasing given the large amounts of protein sequences identified from next-generation genomic sequencing.

The traditional paradigm of protein structure prediction generally consists of two phases: 1) candidate model generation and 2) model selection. For many existing prediction tools, good models could be generated but the best or near-native models from the candidate pool cannot be easily selected which has become a key bottleneck in structure prediction. To address this issue, quality assessment (QA), i.e., evaluating the quality of predicted structural models has become a critical approach in structure prediction (7). Existing QA methods can be roughly classified into two categories: 1) global QA which assesses the overall structural quality; and 2) local QA which predicts the structural quality of individual residues in a model. In this study, we focus on the global QA.

The global QA methods can be further classified into single-model QA and consensus QA. Single-model QA methods utilize physical-based potentials, knowledge-based potentials, and/or machine learning-based scores to evaluate an individual model without requiring any other auxiliary information. Physical-based potential methods, calculating energy of a model as well as its interaction with the solvent according to some physical laws, are often time-consuming and too sensitive to small atomic displacement (8, 9), which is usually impractical in evaluating and ranking models. Knowledge-based potentials methods based on the statistical distribution of atoms or residues in known native structures are widely used in protein structure prediction with some success (10–14). However, they only reflect the statistical (or average) properties of known protein structures and have limited discerning power. Machine-learning methods, evaluating models according to some trained “machines” (15) (e.g., Support Vector Machine (SVM) or Artificial Neural Networks (ANN) from a set of training dataset can address some issues in knowledge-based potentials methods by training on both native and incorrect conformations, but they may not reflect the properties of the model dataset across different protein targets.

The consensus QA approaches evaluate a model according to its relationship to the others in the same pool, which could be clustering-based or similarity-based. Clustering-based methods cluster similar models into groups and pick the representative one from the largest group as the best one (16–18). Similarity-based methods first calculate the average similarity of each model against all the others (19–21) or models in a subset called the reference set (22) in the same pool, and then rank the models according to the corresponding average similarity scores. Consensus methods perform very well if most of the models in the pool are close to the native structure. However, if poor models dominate the model pool, consensus methods may perform worse than single-model QA approaches. Consensus QA methods consistently outperform single-model QA in CASPs (23, 24), but they are not widely applied in individual protein structure prediction tools.

Currently, QA methods have limited discerning power and no one method can outperform other methods consistently. The main reasons for this limitation are that current understanding of protein folding is incomplete and each QA method only reflects partial facets of a structure model. In this paper, we will present some new QA methods to reveal complementary facets to existing methods. The goal of this research is not to develop a single QA method that can be applied universally; instead, a multi-layer evaluation approach is used to integrate various QA methods and thereby guide the model generation more efficiently which ultimately improves the overall accuracy of predicted models.

Specifically, a set of novel QA methods are first developed to perform evaluation at different levels. Then, the underlying relationships among different QA methods and among various models for the same protein target are investigated and integrated to improve the QA discerning power. Finally, the hybridized QA methods are used to guide the model generation process. All the methods are then integrated and implemented into the MUFOLD prediction system (25). We believe that the multi-layer approach can best utilize the combined discerning power from multiple facets of protein structure properties. In CASP8 (23) and CASP9 (24), MUFOLD has demonstrated the proof of the principles in terms of QA discerning power and structure prediction accuracy.

MATERIALS AND METHODS

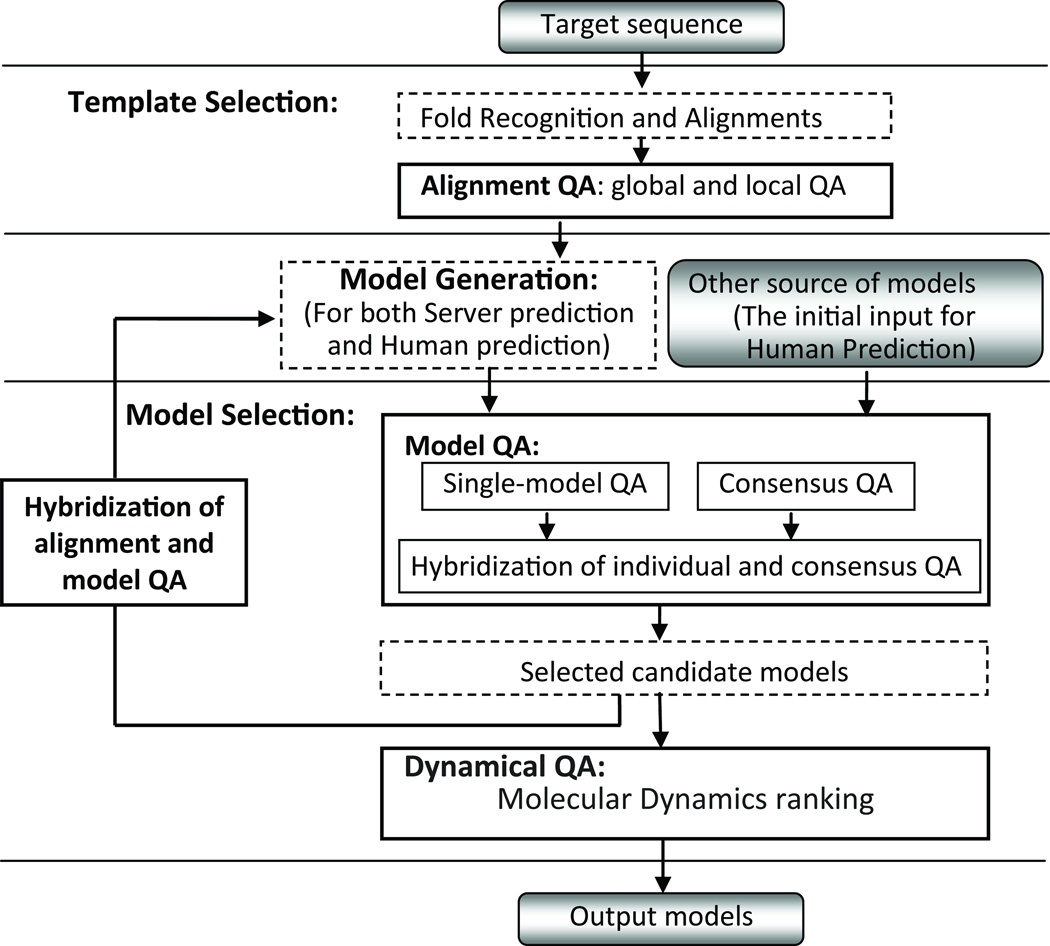
In MUFOLD, a multi-layer evaluation approach is implemented for QA and model generation as shown in Figure 1. The system includes three phases: Template Selection, Model Generation and Model Selection. The last two phases are executed interactively and iteratively. It is noted that the MUFOLD human (or manual) prediction in CASP9 followed a similar approach to the server prediction except that restraints between residues from server models rather than from PDB templates are used.

Figure 1. Framework of the multi-layer evaluation in MUFOLD.

The MUFOLD system includes three phases: Template Selection, Model Generation, and Model Selection, which are separated by solid lines. The bold solid line boxes illustrate different levels of quality evaluation modules and the broken line boxes illustrate other modules in MUFOLD.

In this framework, different evaluation methods are developed and deployed in various phases. In the Template Selection phase, evaluation methods are developed to distinguish top alignments and detect both the high quality and low quality regions in each alignment. In the Model Selection phase, both single-model QA and consensus QA methods are developed to evaluate the quality of models. Most importantly, the alignment QA and model QA methods are hybridized to guide the model generation and improve the model quality iteratively.

Evaluation of alignments

Choosing the best template structure(s) and assuring quality of alignment(s) are critical for structure prediction (26). The MUFOLD system has two levels of alignment evaluation: 1) top alignment selection which removes low-quality alignments (based on the likelihood of yielding poor structural model from the aligned region) and selects the high-quality ones for further model generation; and 2) detection of conserved and non-conserved region, which indicates the confidence of alignment regions for guiding the further conformation search.

Top alignments selection

In MUFOLD, three programs-- PSIBLAST (27), HHSearch (28), and our in-house threading tool PROSPECT (29)--are applied to obtain a number (typically around 200–500) of alignment hits. With these alignment hits, a QA method is developed to evaluate their quality and select top ones for further model generation. The main idea of the QA method is to calculate the fitness of the aligned sub-structure from the templates to the target sequence and select good ones according to the distribution of the fitness of all alignments. The detailed algorithm is given as follows:

1. Fitness calculation of each aligned template structure to the target sequence. The fitness scores include sequence similarity, the matches between the templates’ SS (secondary structure), SA (solvent accessibility) and the predicted SS, SA of the target sequence, respectively. Fitness scores are also determined by environment fitness (29) of the target sequence to the template structures (Note, the environment fitness is the sum of the preferences for aligning the residues of the target sequence to the corresponding template positions with structural environment defined by secondary structure and solvent accessibility) and the structural consensus measured by pair-wise GDT_TS (30) of one template structure to all the other template structures, etc.

2. Normalization of the fitness of each alignment j to a Z-score (Zscore_Ali). This process is based on the following equation:

   $$\mathit{\text{Zscore}}\_{\mathit{\text{Ali}}}_j={\displaystyle {\sum }_i}{W_i}^{*}\{(x_{\mathit{\text{ji}}}-{\overline{X}}_i)/\mathit{\text{dev}}(X_i)\},$$ (1)

   where x_ji is the i-th fitness score for the j-th alignment; X_i is the i-th fitness score for all alignments; W_i is the weight of the i-th fitness score and determined by the correlation between different fitness scores and the impact of the fitness score to the quality of the alignment; X̅_i and dev(X_i) are the average and standard deviation of the score, respectively. Then alignments are sorted according to the Zscore_Ali.

3. Selection of top-k alignments according to the distribution of Zscore_Ali. Here, k is determined by the distribution.

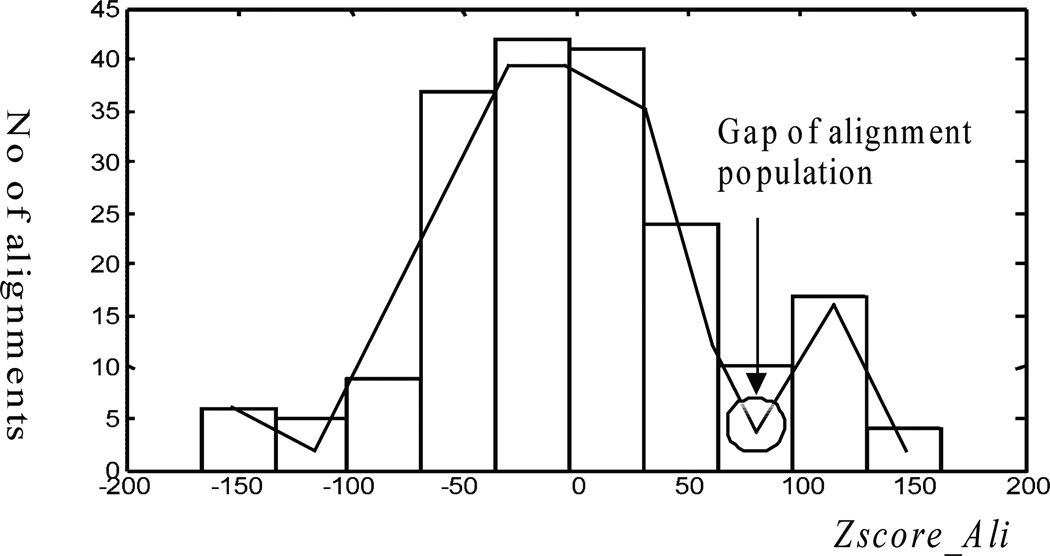
Figure 2 shows an example of Zscore_Ali distribution of 324 alignments. As we can see, a gap in a bimodal distribution exists between good Zscore_Ali scores and poor ones. The gap can serve as a natural boundary for alignment selection and we removed all the alignments with Zscore_Ali scores below the gap. With this selection, top k = 21 alignments were kept. In fact, It turned out that the best alignment in the whole set was included during the final analysis. Copying the template structure to the target protein using this alignment would yield a GDT_TS of 74.28. The population of selected alignments was relatively homogeneous, as the worst one among the 21 alignments had GDT_TS of 69.94. All 21 alignments provided some high-quality aligned regions, i.e., copying the template structure using the alignments of these regions to the target protein would lead to a partial model with small RMSD (root mean square deviation) to native structure. Hence, these alignments were useful for the model generation in the following steps.

Figure 2. One example of Zscore_Ali distribution of 324 alignments.

A gap exists between alignments with high and low Zscore_Ali scores, and it can be used to select the top-k (here, k = 21) alignments.

We found that the above gap separating the alignment population is common to most prediction cases. This is likely due to the fact that alignments are clustered into groups. It is known that E_value (31) of alignments provides good assessment for the quality of the alignments. For those targets where we can find significant alignments (i.e., with E_value lower than 1e-3), there is typically a clear boundary between the significant and non-significant alignments according to the criterion of E_value. Similarly, there is generally a gap separating the alignment population according to the criterion of Zscore_Ali. For free modeling targets, there are no significant alignments. Therefore, there may not be any obvious gap. In these cases, we select as many as 20 top alignments according to Zscore_Ali. Based on this QA method, reliable spatial restraints are likely to be retrieved from the top alignments for further model generation.

Graph-based global conserved region detection

Before evaluating the specific regions of each alignment, the selected top alignments are clustered into different groups by comparing the pair-wise RMSD of the commonly aligned regions. Since gaps in the alignments generally exist, many residues in the target protein are not covered by any template structure. In MUFOLD, some short alignments (i.e., fragments) that are consistent with the top alignments are also selected to cover the gaps. Consequently, the alignments in each group can cover as many as possible target residues, share highly similar substructures (i.e., conserved regions), and keep diversities (i.e., non-conserved regions) simultaneously. After this evaluation, a QA method is developed to detect the conserved and non-conserved regions in alignments.

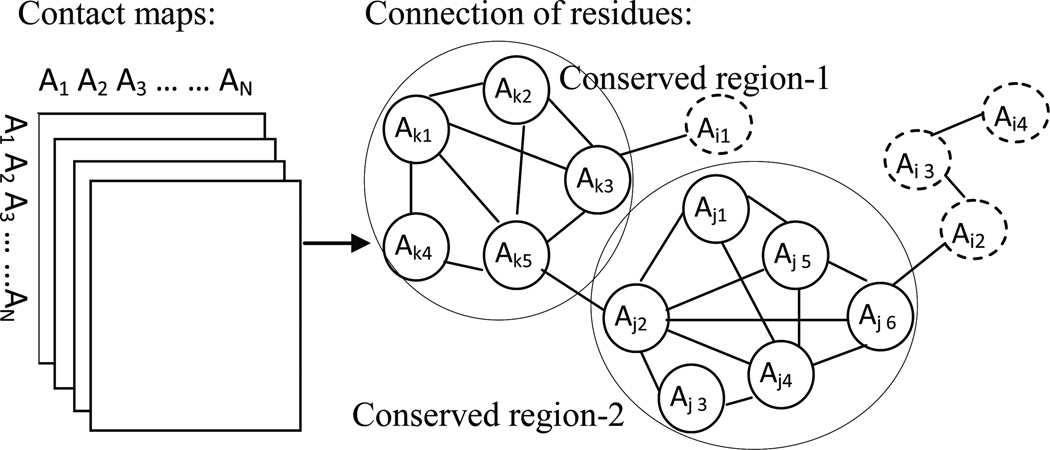
Considering two residue positions in the target sequence, if the corresponding spatial distances evaluated by the alignments in a group are consistent, the two residue positions can be treated as potential conserved positions supported by the group of alignments. A subset of positions in which any two positions are potentially conserved will represent the conserved region of the target (supported by the group of alignments). Thus, we can draw a connection network (graph) of the residue positions from the spatial distance information provided by the alignments in a group, and search the interested sub-graphs such that each pair (or most pairs) of residue positions in the sub-graph is (or are) conserved. Consequently, the sub-graphs will represent the conserved regions. In this way, the MUFOLD researchers developed a graph-based method to detect the conserved regions of the target sequence. The detailed algorithm is delineated as follows:

1. Contact map calculation. For each alignment, the pair-wise distance of C-alpha atoms of aligned residues in the alignment are calculated to construct the contact map. Thus, k contact maps are generated from a group with k alignments.

2. Graph construction. A graph, G = (V, E) for a group is constructed, where V is the set of residues of the target sequence and E is the set of edges. Consider the k contact maps, for each pair of residues A_i and A_j, if more than m (m ≤ k, a preset threshold depending on k) distances d(A_i, A_j) exist and these distances are very similar (e.g., the standard deviation is smaller than a threshold), an edge will be added to connect the two vertices in G. If A_i and A_j can be linked by an edge, it means that most of the alignments in the group support a consistent distance for A_i and A_j; thus the distance between the two residues can be considered as conserved.

3. Conserved region detection. In the above graph G, some subsets can be detected in which the nodes tend to create tightly knit groups. The nodes (or residues) in these subsets represent conserved segments. In the graph theory, a clustering coefficient (CC) (32, 33) is a measure of degree to which nodes in a graph tend to cluster together.

   $$\mathit{\text{CC}}=\frac{3\times \text{number of triangles}}{\text{number of connected triples of vertices}}=\frac{\text{number of closed triplets}}{\text{number of connected triples of vertices}}.$$ (2)

   Therefore, we calculate quasi-cliques in the graph such that the CC value of each quasi-clique is larger than a threshold.

Figure 3 illustrates the graph-based algorithm. The conserved and diverse restraints from the corresponding template sub-structures can be retrieved after the conserved regions are detected. According to the above algorithm, the parameter CC can be used to measure the density of each quasi-clique and set the weight (or confidence) for the corresponding restraints; therefore, the larger the CC, the higher the confidence. Generally, the conserved restraints with higher weight have higher priority to be satisfied while diverse restraints lead to a wide and deep search space for further model sampling.

Figure 3. Graph-based method to detect the conserved regions.

The connection of residues of the target sequence is generated from the contact maps of the selected alignments. An edge between two residues indicates that the distances between the two residues derived from all alignments have small variations. A big circle in which the residues connect with each other tightly indicates a cluster. The residues shown by small solid line circles in each cluster are considered to represent the conserved regions among alignments. The residues with sparse connection to the others (shown in small dashed circles) represent the non-conserved region.

The conserved regions represent the structure topology (or skeleton) of the target sequence. In the further model generation phase, the spatial constraints from the globally conserved regions should be satisfied with small changes to keep the topology undistorted. As the graph is derived from contact maps, the above algorithm can be applied to models or a mixture of alignments and models, which makes the hybridization of the QAs for alignments and models applicable. In the following section, we will describe such hybridization in detail.

Evaluation for models

Model-level QA is very important for structure prediction as a model can provide more detailed information in 3D than sequence alignment. In MUFOLD, in addition to applying the existing state-of-the-art QA tools, two kinds of QA methods, including single-model QA and consensus QA, are developed to reveal new and complementary facets of protein structures and achieve better evaluation results.

Single-model molecular dynamics ranking (MDR)

Different from the existing single-model QA methods that use static scoring functions and ignore the dynamics properties of the protein, our new MDR is a dynamics-based method that uses full-atom MD simulations to evaluate and rank structure models according to their stabilities against external perturbations. The MDR method is based on the theory that because the native configuration of a protein corresponds to the global minimum of its free energy, the so called thermodynamic hypothesis of protein folding (34), the closer a predicted model to the corresponding native structure, the more stable the model against temperature-induced unfolding. In many cases, the behavior of the model during MD-simulated heating can provide a better structural quality assessment than conventional methods based on static scoring functions. Hence, MDR is a useful complementary approach to static QA methods.

MDR consists of the following steps involving all candidate models: 1) structure optimization through energy minimization (our MD simulations were performed with NAMD2 using the CHARMM (35) all-atom force field); 2) gradual heating (with a rate of 1 K/ps) through MD simulation for 100ps during which the temperature is increased from 40K to 140K; (3) stability test by monitoring the change in cRMSD (C-alpha RMSD with respect to the initial model) during the simulated heating process; (4) ranking of the models according to a MDR score (e.g., the mean cRMSD against the initial model during the simulated heating process).

Consensus QA methods

Different from the single-model QA, the consensus methods focus on seeking the goodness of a model by detecting its similarity (or common characteristics) to the others. As demonstrated in the previous CASPs, the consensus-based QA methods outperformed the single-model QA methods by a large margin.

The existing consensus methods are based on the calculation of the average similarity (measured by pair-wise GDT_TS) of one model to all the others, which is called total consensus. Let S be a set of models. The QA of a model s_i, s_i∈S, is calculated by $\mathit{\text{QA}}(s_i)=\frac{1}{|S|}{\displaystyle \sum _{s_j\in S}}\mathit{\text{GDT}}\_\mathit{\text{TS}}(s_i,s_j)$. However, the performance of consensus QA heavily depends on the distribution of the models. This means one should consider how close the models with respect to the native structure and how many good models there are in the pool. Unfortunately, the selection of near-native models is not a trivial task without the knowledge of native structures. Based on a thorough systematic analysis of the different reference set selection strategies, we chose two approaches as possible ways to improve the performance of consensus QA: 1) using different reference sets for different model pools and 2) weighting different reference models differently; in particular, avoiding use of redundant models or outliers (completely different from the other models) in the reference set. Consequently, three new consensus methods, MUFOLD-QA, MUFOLD-WQA, and MUFOLD human QA are developed for the reference selection.

MUFOLD-QA

One intuitive way to select the reference set is to pre-evaluate the individual models using some single-model QA methods. We have conducted a series of experiments to select reference set R from S with widely used scoring functions, such as OPUS-CA (11), OPUS-PSP (12), DDFire (13) and Cheng Score (15). The experimental results show that the performance is even inferior to the total consensus, i.e., the one using all models as references. During the experiments, disturbing results proved that the redundant models and the outliers in the set of S could adversely affect the QA performance dramatically. Hence, rather than applying single-model QA, we removed the redundancy and outliers of the model dataset to obtain better references.

Specifically, a threshold Z is first determined to recognize redundancy based on the average similarity among the models in a model pool (22). If the pair-wise GDT_TS between each pair of models s_i and s_j is greater than Z, either s_i or s_j is regarded as redundant and one of them is randomly removed from being a reference. It should be noted that none of the existing selection approaches, neither single-model QA methods nor consensus approaches, is effective in choosing a better one from a pair of models. Hence, redundant structures were discarded randomly. In addition, if one model had a very low similarity (less than a pre-defined threshold) to all the others, its status was changed to outlier.

After checking each pair of models and discarding the redundant ones and outliers, a reference set R is constructed. Then, MUFOLD-QA evaluates each model by comparing it against the selected reference models. The similarity measurement can be any commonly used metric, such as GDT_TS, TM-score (36), or Q-score (37). We tested these metrics on CASP8 dataset and found that GDT_TS generates slightly better result for QA. The QA score of a model s_i, s_i∈S, is calculated by:

$$\mathit{\text{QA}}(s_i)=\frac{1}{|R|}{\displaystyle \sum _{s_j\in R}}\mathit{\text{GDT}}\_\mathit{\text{TS}}(s_i,s_j),$$ (3)

where |R| is the number of members in R. In addition to calculating the QA score for each model, the MUFOLD-QA method can also perform the best model selection based on the generated QA score.

MUFOLD-WQA

In reality, many high-quality models share similar conformations and removing these kinds of redundant models will reduce the sensitivity of the references. One solution is to set lower weight for those redundant models rather than to discard them totally. A weighted QA method, MUFOLD-WQA, was developed to assign different weight to different models. One weight function is the sigmoid function, $\mathit{\text{sig}}(x)=\frac{1}{1+e^{c(x-\alpha )}}$, where x is the similarity of the candidate model to another model in the pool and in the range [0, 1]; c and α are constants. When c is large, the function becomes a simple step selection function: step(x) = 0 if x ≥ α; step(x) = 1 if x < α, where 0<α<1. Generalizing the step function, we have the band selection function: band(x) = 1 if a<x<b; 0, otherwise.

Parameters of these functions were determined empirically using CASP8 dataset. For template-based targets, most of the predicted models share similar conformations, while for template-free targets, predicted models are different because they are derived from various fold topologies. Therefore, the best parameters for different targets should be different. We split targets into three classes, easy, medium, and hard, based on some indicators of the average pair-wise GDT_TS of all server models (cited as cgdt for convenience). Based on the CASP8 dataset, the best parameters were determined for targets in the three classes and applied to the CASP9 data. Although the sigmoid function is flexible, the step function with good parameters can achieve similar performance as the sigmoid function. Thus, band function is implemented in our MUFOLD-WQA.

In particular, given a model set S, MUFOLD-WQA assesses the quality of s_i, s_i∈S by summing a weighted similarity score,

$$\mathit{\text{QA}}(s_i)=\frac{{\displaystyle \sum _{s_j\in S-\{s_i\}}}{w}_{\mathit{\text{ij}}}\mathit{\text{GDT}}\_\mathit{\text{TS}}(s_i,s_j)}{{\displaystyle \sum _{s_j\in S-\{s_i\}}}{w}_{\mathit{\text{ij}}}},$$ (4)

where w_ij is a weight in the range of 0 to 1,which is generated by a Band Weight Function defined as: Band(x) = 1 if a<x<b; and 0 otherwise. The weight is 1 when the similarity of a pair of models is between a and b, and 0 otherwise.

MUFOLD human QA

MUFOLD human QA server took advantage of the availability of QA server predictions. To assess the quality of CASP9 model, all QA server predictions were first downloaded, and then MUFOLD-QA was applied to select a set of QA servers as references. Finally, the predicted scores of the models by these selected structure prediction servers were averaged to generate a consensus prediction,

$$\mathit{\text{QA}}=\frac{{\displaystyle \sum _i}{w}_i{X}_i}{{\displaystyle \sum _i}{w}_i},$$ (5)

where X_i is the QA scores by the selected server i, w_i is the weight of the server i, which was calculated by the average Pearson correlation coefficient of server i to all the other selected servers.

Hybridization of single-model and consensus QA for model evaluation

In the Model Selection phase, two methods are used to hybridize single-model and consensus QA: 1) the hybridization of different single-model QAs, and 2) the hybridization of single-model and consensus QA.

Before hybridizing single-model QA methods, we investigated the correlation between three QA methods: OPUS-CA, DDFire and Cheng Score, and set a weight value for each QA score. After a large number of models were generated during the Model Generation phase, three QA tools were applied to evaluate the quality of individual model j by a normalized score, which is given as follows:

$${\mathit{\text{Score}}}_j={\displaystyle {\sum }_{1\le i\le 3}}{W_i}^{*}{\mathit{\text{Zscore}}}_{\mathit{\text{ji}}}={\displaystyle {\sum }_{1\le i\le 3}}{W_i}^{*}\{(x_{\mathit{\text{ji}}}-{\overline{X}}_i)/\mathit{\text{dev}}(X_i)\},$$ (6)

where Score_j is the score of model j, Zscore_ji is the i-th normalized QA score of model j, and W_i is the weight of the i-th QA score.

The single-model and consensus QA are combined in two ways: 1) the normalized single-model QA score is used to filter out poor models and just keep a small model set for further consensus QA; 2) a normalized single-model and consensus QA is calculated and used to evaluate models. Here, Equation (6) is used to calculate the normalized score, where consensus QA score is added as one additional QA score.

Hybridization of alignment and model QA for model generation

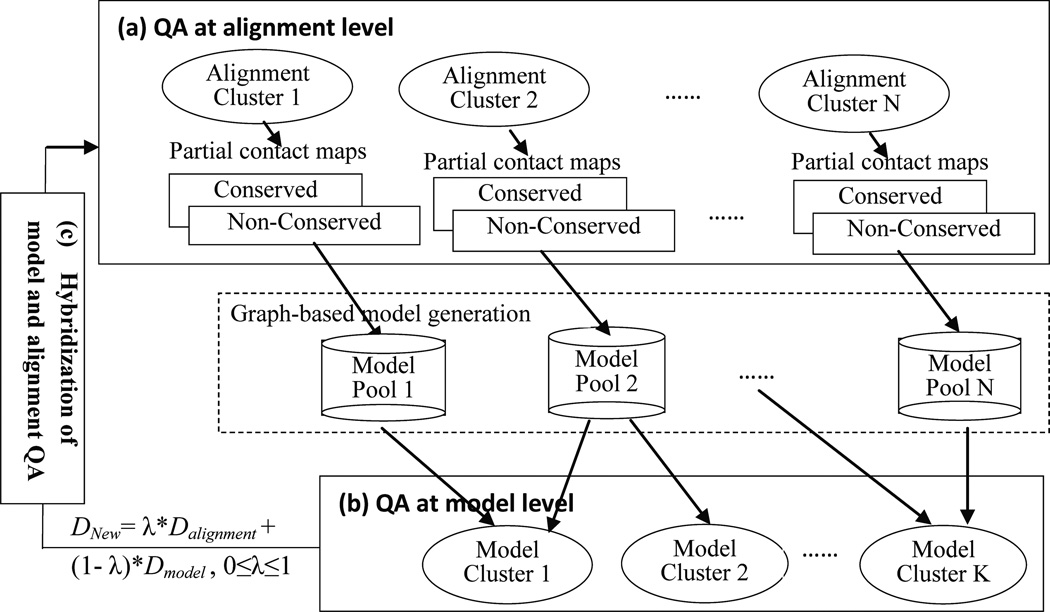
In this section, we introduce the method for hybridizing different levels of QA methods to improve the model quality iteratively. Figure 4 shows the framework of hybridizing different levels of QA methods.

Figure 4. Integration of QA methods at different levels.

(a) the QA at alignment level including top alignments selection, top alignments clustering, and the conserved/non-conserved regions detection; (b) the QA at model level, including model evaluating and filtering by single-model QA methods, model ranking by consensus QA methods, and model clustering; (c) the hybridization of model and alignment QA. Note the broken line contour illustrates the model generation module.

First, the global quality of alignments is evaluated and some top alignments and the corresponding clusters are obtained. Simultaneously, a graph-based QA method is used to detect the conserved regions and the corresponding spatial restraints from each alignment cluster are retrieved. Second, single-model QA methods are applied to filter out poor models, rank and cluster the remaining models by the consensus QA method. Thus, some top clusters of models are generated. Finally, the graph-based QA method is utilized again to detect the conserved regions and the corresponding spatial restraints for each model cluster as well as for the mixture of the top alignments and top model cluster.

After a large number of restraints are produced from the alignments and models, the restraints are filtered and iteratively refined by combining the original restraints derived from the alignments (Dalignment) and the measured distances from the generated models (Dmodel) as follows:

$$\mathit{\text{Drefine}}={\lambda }^{*}\mathit{\text{Dalignment}}+{(1-\lambda )}^{*}\mathit{\text{Dmodel}},0\le \lambda \le 1,$$ (7)

where, value of λ is decided by the graph-based QA method. By performing this iterative generation, the quality of models often becomes better and better, while many deficiencies in the models are fixed over iterations.

RESULTS

The proposed QA methods have been integrated into the MUFOLD system and gave successful performance in both CASP8 and CASP9. For example, MUFOLD-MD was one of the top servers in the Free Modeling (FM) category in CASP8 and CASP9; all MUFOLD QA applications--MUFOLD-QA, MUFOLD-WQA and MUFOLD human QA--were ranked as top performers in the Quality Assessment category in CASP9 in terms of Pearson correlation values (between the predicted and the real GDT_TS of the server models) and model selection; MUFOLD was ranked as No. 1 in Human prediction in CASP9 in terms of sum and average Z score of GDT_TS. The performance of MUFOLD-Server in CASP9 has been substantially improved compared to that of CASP8 showing a consistent progress of the MUFOLD system.

What went right?

(1) MDR helps select near-native structures for Free Modeling targets

We tested MDR on models generated by MUFOLD and various decoy sets. Extensive testing of the MDR method shows that statistically the best ranking indicator for the predicted structures is their mean cRMSD during heating from 40K to 140K. Besides energy minimization, this requires only 100ps long MD simulations. The performance of MDR varies for different cases while it is most efficient when the pool of decoys contains some high-resolution structures (cRMSD < 3 Å) besides the low-resolution ones. Table 1 lists the ranking of MDR on a testing set of 22 proteins randomly selected from the 200 benchmark sequences (25), by selecting three sets, i.e., high-quality (cRMSD~3Å), medium-quality (cRMSD~4.5Å) and poor-quality (cRMSD~6Å) structures for each protein. As shown in Table 1, the MDR method had an 80% success rate in identifying the best structure with cRMSD < 3Å (8 cases out of 10), and 77% success rate in selecting the best structure regardless of its cRMSD.

Table 1.

MDR ranking for the testing set of 22 proteins. For each protein, the values indicate the cRMSD with respect to the native structure and expressed in Å, with the best models shown in bold font.

Protein	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22
Rank	1BIA	1FFT	1T4G	1NO8	1P7H	1FUP	1NPS	1G7O	1JIF	1T56	1MLA	1OLZ	1T1H	1U5T	1DGN	1ROA	1E32	1UA7	1LFD	1OKS	1ZFJ	1NVM
1	2.68	1.94	2.63	2.76	2.52	2.52	2.87	2.06	6.00	4.53	3.62	3.58	3.81	3.24	3.04	3.66	3.71	3.03	3.94	4.50	6.02	4.50
2	4.50	4.77	4.51	4.50	6.01	6.01	6.00	6.00	2.59	1.70	4.50	4.51	4.60	4.50	6.00	4.67	6.43	5.23	4.86	6.00	3.54	3.49
3	6.00	6.07	6.00	6.00	4.51	4.50	4.50	4.50	4.50	6.01	6.00	6.09	6.00	6.01	4.52	7.29	5.12	6.36	7.53	3.88	4.52	6.00

The MDR method also has been implemented into the MUFOLD-MD server and tested in both CASP8 and CASP9. In CASP8, MUFOLD-MD was ranked No. 1 among 81 competing servers in the Free Modeling (FM) category (38). In CASP9, MUFOLD-MD was ranked No. 4 among prediction teams on 30 FM domains. MUFOLD-MD also performed better than the MUFOLD-Server that applied static scores for quality assessment. These results clearly demonstrate the effectiveness of the MDR methods in probing the dynamical properties of protein models for their quality assessment.

(2) Our modified consensus approach is effective in evaluating models

In CASP8, we developed a single-model QA method for a fully automatic server to predict global quality of models and select the best model. At that time, like all other single-model QA methods, our QA performance was not good. While in CASP9, based on our new consensus approach, MUFOLD-QA, MUFOLD-WQA, and MUFOLD human QA, led to the development of three fully automatic servers MUFOLD-QA, MUFOLD-WQA and Mufold, respectively, thereby obtaining much better performance.

According to the problem formulation in the subsection of “MUFOLD-QA”, it is important to determine the threshold Z to recognize redundancy based on the average similarity among the models in a model pool. In practice, we calculated the corresponding threshold Z in such a way that approximately 25% of most redundant models were removed for each target. For MUFOLD-WQA, different parameters of a and b in the Band Weight Function will have an impact on the performance of the quality assessment. We divided the targets into three categories (Easy, Midium and Hard) according to the average pair-wise GDT-TS values (cgdt) of the predicted models and set different parameters for these three categories. For example, if the cgdt is within the range of (50, 100], then we treat the target as an easy case, and the parameters a and b are set as 0 and 0.7, respectively. Similarly, the target will be treated as a medium (or hard) case if the corresponding cgdt is within the range of (30,50] (or (0, 30]), and the corresponding parameters of a and b are set as 0.2, 0.5 (or 0.2, 0.4), respectively. We also used these parameters for the QA prediction in CASP9.

We compared the performance of top-1 model selection by MUFOLD-QA and MUFOLD-WQA with some single-model QA methods such as, OPUS-PSP (12). DDFIRE (13), Model Evaluator (15), DOPE (39), RAPDF (40), and the naïve consensus method using all of the models as references on 122 CASP8 targets and 117 CASP9 targets, and the result is listed in Table 2. In the second column we also list the GDT_TS of the best-predicted model. The results show that both MUFOLD-QA and MUFOLD-WQA are significantly better than all of the single-model QA methods. For CASP8 targets, both MUFOLD-QA and MUFOLD-WQA are better than the naïve consensus method while for CASP9 targets, the MUFOLD-QA is slightly worse than the naïve consensus method. If we consider the correlation of predicted and observed model quality scores (MQAS vs. GDT_TS) on the per-target basis (measured by the average Pearson correlation), MUFOLD-QA (with Pearson correlation of 0.936), MUFOLD-WQA (0.936) and Mufold (0.930) all outperformed the naïve consensus method (0.9284).

Table 2.

GDT_TS of the top-1 selected models of MUFOLD-QA, MUFOLD-WQA and other single-model QA methods and the naïve consensus method on CASP targets.

Targets	Best model	OPUS- PSP	DDFIRE	Model Evaluator	DOPE	RAPDF	Naïve consensus	MUFOLD- QA	MUFOLD- WQA
CASP8 (122)	67.99	52.39	53.31	56.13	51.96	58.56	62.67	63.15	62.92
CASP9 (117)	64.02	54.18	50.8	45.78	51.49	45.52	58.22	57.88	58.55

Pearson correlation of MQAS and GDT_TS reflects how consistently a QA method can assess models with different quality (good and poor), while the top-1 model selection reflects how good a QA method can select near-native (good) models. Most of the QA methods only achieve one of these two different goals (http://predictioncenter.org/casp9/doc/presentations/CASP9_QA.pdf). For example, QMEANclust (41) achieves the same Pearson correlation values as MUFOLD-WQA and MUFOLD-QA; however, it is not among the best 10 servers for top-1 model selection. MUFOLD-WQA has overall the best performance as it was ranked as top 1 and top 2 in terms of the above two criteria, respectively.

(3) The integrated QA methods helped both server and human predictions

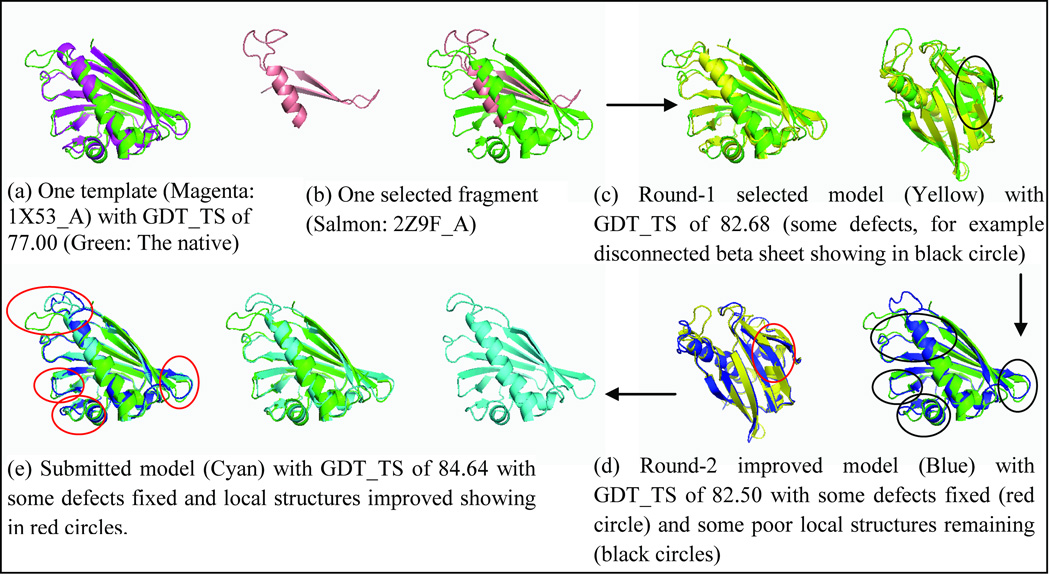
We developed/integrated the QA methods into the MUFOLD-Server, including top alignments selection, graph-based globally conserved region detection, and hybridization of alignment QA and model QA to guide model generation and refinement. According to the official CASP9 evaluation (http://predictioncenter.org/casp9/doc/presentations/CASP9_TBM.pdf), MUFOLD-Server was ranked as top-10 server in the TBM (Template Based Modeling) category of server prediction, which showed a substantial improvement compared to that of CASP8. An example from CASP9 target T0594 (140 residues) is shown in Figure 5, which illustrates the model generation and refinement guided by different QA methods.

Figure 5. An example shows how different QA methods guide the model generation and refinement for CASP9 target T0594 (140 residues).

In the first step, some good templates and fragments are selected by the “top alignments selection” QA. In Figure 5 (a), chain A of protein 1X53 was selected as one of the best templates, and the GDT_TS of the alignment turns out to be 77.00 after the native structure became known, meaning that we can get a model with 77.00 GDT_TS to the native structure by simply copying the C-alpha coordinates from the aligned template residues. However, some gaps exist in the target/template alignment; thus, another fragment from chain A of 2Z9F was selected as shown in Figure 5 (b). From the figure, we can see that the secondary structures of the fragment are consistent with the templates, and their loop region can cover the missed residues in target/template alignment. In fact, the conformation of the loop region of the selected fragment is also close to the native structure.

After the first round of model generation, some models were selected by QA methods. In Figure 5 (c), one model with GDT_TS of 82.68 was selected which is much better than the 77.00 of the target/template alignment. However, the model includes a disconnected beta sheet, which is inconsistent with the target/template alignment. By applying the “hybridization of alignment QA and model QA for model generation,” the models generated in the second round were greatly improved as shown in Figure 5 (d) and the defects of disconnected beta sheets were corrected. In this step, some of the local structures were less than ideal which prompted more iterations to improve the overall quality of models. Finally, a model with GDT_TS of 84.64 was achieved and submitted which had 7.64 points improvement in GDT_TS compared to 77.00 generated by the original alignment. More importantly, local structures in the submitted model were improved, and disconnected beta sheets no longer existed.

MUFOLD human (manual) prediction follows a similar framework as that of the MUFOLD server prediction, except that the original restraints between residues are from the selected CASP server models rather than from PDB templates. In CASP9, 57 targets with 78 domains in total were released for Human prediction and we submitted predictions for 56 targets with 77 domains. According to the official evaluation of CASP9, MUFOLD models achieved the highest sum of Z-Score (78.012) of GDT_TS, with the highest average Z-Score per target (1.013) and the highest average GDT_TS per target (56.561) among all CASP9 predictors.

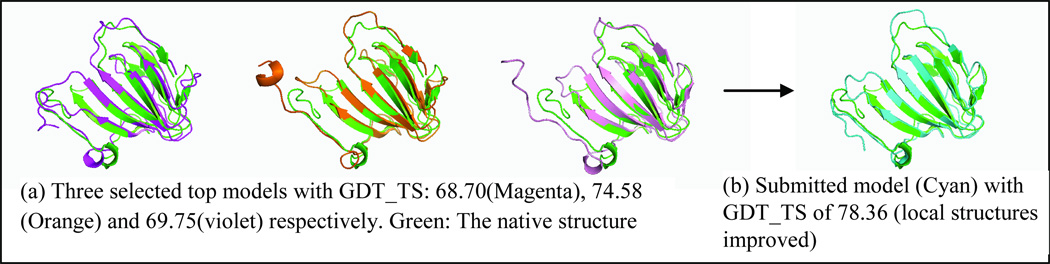
It is noted that the best models could not be selected from the server model pool by the MUFOLD QA methods. We analyzed the data of 51 targets (all human/server targets except for T0517, T0529, T0540, T0543, T0556, T0581, T0614, T0631, and T0633) from http://zhanglab.ccmb.med.umich.edu/casp9/ for convenience. Among the 51 targets, the average GDT_TS of the best model in the pool was 55.43 while the average GDT_TS of our selected top-1 model is only 50.37, although our QA for top-1 model selection was one of the best performers according to the official CASP9 evaluation. The 5.06-point gap means that the top-1 selected models were not sufficient to obtain better prediction. However, using our multi-level QA evaluations and the QA guided model generation, we further improved the quality of top-1 selected models by a large margin. Specifically, our manual prediction was performed as follows: 1) selecting a cluster of models including top models ranked by the QA method, 2) applying the QA-guided model generation in MUFOLD to generate and evaluate new models, and 3) submitting the final improved models based on QA. For most of the cases, the submitted model was better than our selected top-1 model. One example of the prediction for T0582 Domain 1 is shown in Figure 6. We started from a cluster of models including top-3 models with GDT_TS of 68.70, 74.58 and 69.75, and finally submitted a significantly improved model with GDT_TS of 78.36. The average GDT_TS of our submitted models for the 51 targets was 52.39, gaining 2.02 points compared to 50.37 of the selected top-1 models from the server predictions.

Figure 6. An example of MUFOLD human prediction for target T0582-Domain-1 (123 residues).

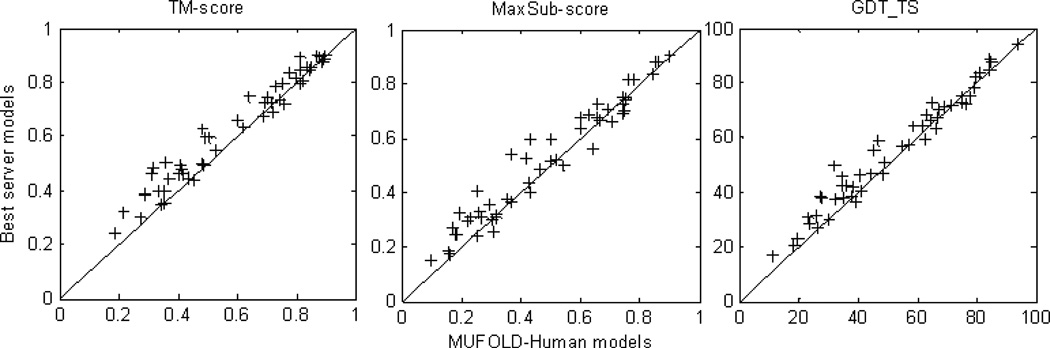
Since we began the human prediction utilizing the CASP9 server predicted models, we also compared the MUFOLD human predictions with the best CASP server models for the 51 targets. The average TM-score, MaxSub-score (42) and GDT_TS of MUFOLD human models are 0.5895, 0.4812, and 52.39 while the corresponding values for the best server predicted models are 0.6291, 0.5117 and 55.43, respectively. Detailed comparison of the 51 targets is shown in Figure 7 and clearly demonstrates that compared to the criteria of TM-score and GDT_TS, the MUFOLD human models are better than the best server predicted models in terms of MaxSub-score for many targets. For example, for 15 of the 51 targets, MUFOLD human models are significantly better, i.e., gaining more than 1 point than the best server predicted models in terms of MaxSub-score; and for three targets, MUFOLD human models are marginally better. In contrast, for 12 targets, MUFOLD models are better than the best server predicted models in both TM-score and GDT_TS. This proves that MUFOLD may not always improve the whole structure, but it improves some sub-structures locally. The most important finding is that by using our strategy, we have a good chance to generate and select new models to outperform the best model in the initial pool even though we cannot select the best model from that pool to start with the improvement.

Figure 7. The comparison between MUFOLD human predicted models and the best CASP server models in TM-score, MaxSub-score and GDT_TS for 51 server/human prediction targets.

All of the scores were calculated by using the TM-score package(17).

What went wrong?

The biggest issue of the current MUFOLD system is alignment, which led to unsatisfactory performance of MUFOLD-Server for some targets. The performance of MUFOLD depends on the selected top templates and alignments. When the top templates and alignments closely reflect the native structure, even if the best template or alignment is not selected, the chance of getting high-quality models using MUFOLD is still high; otherwise, there is little chance for MUFOLD to make major adjustment for structure quality improvement. Currently, we are applying PSIBLAST and HHSearch as the alignment tools for easy and medium targets and the threading tool PROSPECT for hard targets. For medium targets, although we usually identified the correct fold, the average accuracy of the alignments has not been high enough to guide high accurate modeling. For hard targets, recognizing the correct fold became difficult in many cases.

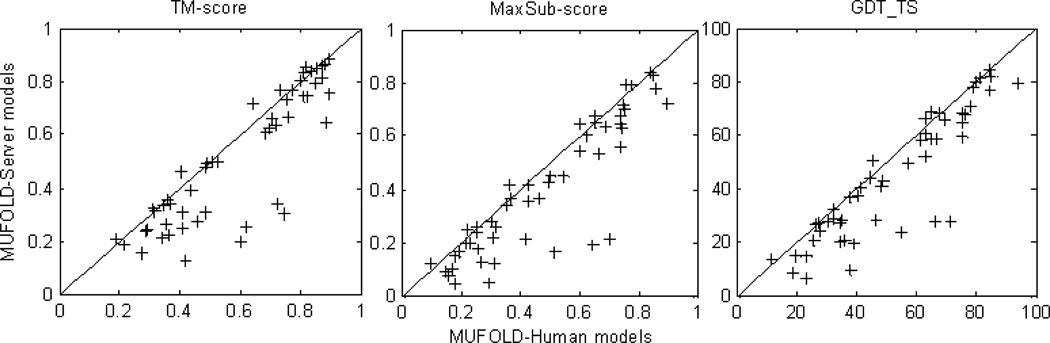
As mentioned above, MUFOLD human prediction in CASP9 followed a similar approach to the MUFOLD-Server except that restraints between residues from server models were used. Figure 8 is a head-to-head comparison of MUFOLD-Server and MUFOLD Human predictions in terms of TM-score, MaxSub-score and GDT_TS for the first models of 51 human prediction targets. When the TM-score (or GDT_TS) of MUFOLD-Server models is less than 0.6 (or 60), the difference of the server and human predictions is significant. It shows that our alignments obtained in MUFOLD-Server for medium and hard targets were not sufficient. Consequently, we are developing new alignment methods to improve alignment accuracy.

Figure 8. Comparison between MUFOLD human and MUFOLD-Server models in TMscore, MaxSub-score and GDT_TS for 51 server/human prediction targets.

All of the scores were calculated by using the TM-score package (17).

The second issue is model-level QA. In many cases we generated good models but could not select them correctly. The gap between the selected top-1 model and the best-generated model is often larger than 8 points in terms of GDT_TS. In MUFOLD, we integrated single-model QA and consensus QA methods and determined to select good models for iterative refinement. However, in some cases, the QA methods failed to select the top models in the newly generated refinement model pool, and hence, the refinement process did not improve the quality of initial models. Figure 9 shows a comparison of GDT_TS of the top-1 selected models and the final submitted first model of MUFOLD-Human prediction. The former was selected from CASP server models by our consensus QA method and used as the initial model for the iterative improvement process in the MUFOLD-Human prediction. We can observe that for most cases the MUFOLD-Human models were better than the initially selected top-1 models. However, nine cases of the MUFOLD-Human models lost more than 1 point of GDT_TS and five cases lost more than 2 points of GDT_TS over the selected top-1 models, showing the failure of the QA methods during the refinement process. We are developing new QA methods to improve the discerning power to pick up top models.

Figure 9. Comparison of the top-1 selected models from CASP server models by our consensus QA method and the submitted model 1 of MUFOLD-Human prediction in terms of GDT_TS.

The targets are sorted by the GDT_TS of MUFOLD-Human model 1.

The third issue is side-chain generation using template information. Currently we produce coarse-grain models (with C-alpha or backbone atoms) first and then generate full-atom models using pulchar (43) or modeler (2). Side-chain restraints from the alignments are lost during the coarse-grain models generation. Therefore, MUFOLD does not pack some sides-chains well and loses some hydrogen bonds. We are working on extending the MDS method to include some side-chain atoms to help resolve this issue.

Discussion

QA for target/template alignments and predicted structural models is critical for the computational structure prediction. There have been numerous studies to develop different QA methods for evaluating structural models. Because of incomplete understanding of protein folding, each QA method only reflects partial facets of a structure model and has limited discerning power. A significant gap exists between the top-1 selected models by any QA method and the best model in a pool. Considering the complexity of protein, more QA methods are needed to evaluate structure models from different aspects or properties of models. More importantly, the discerning power from multiple facets of protein structure properties should be combined to obtain better evaluation.

In this paper, we present a set of new QA methods, including QA methods for target/template alignments, MD-based single-model QA and references selection guided consensus QA. These QA methods can help reveal new and complementary facets of protein structures to existing methods for better evaluation. This paper also covers research on the relationships among different QA methods, the usage of model distribution in a pool for QA, and the way to hybridize the multi-layer QA methods for guiding a better model generation and selection. The evaluation results from the blind tests in both CASP8 and CASP9 show that these strategies are successful in terms of both QA discerning power and structure prediction accuracy. The most exciting observation is that under this multi-layer QA framework, we have a good chance to generate and select new models that outperform the best model in the initial pool even though we cannot select the best one from the pool in the beginning.

As a new framework, the method and the MUFOLD tool will be fine tuned, especially for more consistent prediction performance in an automated fashion. Many possible improvements can be done to enhance the overall QA discerning power and the accuracy of structure prediction. For example, we can improve the MDR by applying different force fields, including solvent in the simulation and considering a longer heating interval, etc. In addition to the reference selection, the individual model can be better assessed by combining its own features (evaluated by various single-model QAs) and its relationships with the other models in terms of structural similarity and feature similarity to these models. Thus, a network-based QA analysis can be implemented in which each model will interact with others and evaluated by its own features as well as the relationship with its neighbors and information retrieved from the whole network.

Finally, we are planning to extend the QA framework for more applications. We will try more strategies to integrate the alignment and model QA methods to systemically guide a more specific, efficient and accurate model generation or model refinement process in MUFOLD without using a starting model pool. In addition, we plan to provide a standalone and publicly available QA package for general usage, which will enable users to apply this package to evaluate and refine structure models generated from their software tools or from their own initial models.