Aggrecan, an Unusual Polyelectrolyte: Review of Solution Behavior and Physiological Implications

Abstract

Aggrecan is a high molecular weight, bottlebrush-shaped, negative-charged biopolymer that forms supermolecular complexes with hyaluronic acid. In the extracellular matrix of cartilage, aggrecan-hyaluronic acid complexes are interspersed in the collagen matrix and provide the osmotic properties required to resist deswelling under compressive load. In this review we compile aggrecan solution behavior from different experimental techniques, and discuss them in the context of concentration regimes that were identified in osmotic pressure experiments. At low concentration, aggrecan exhibits microgel-like behavior. With increasing concentration, the bottlebrushes self assemble into large complexes. In the physiological concentration range (2 < c_aggrecan < 8 % w/w), the physical properties of the solution are dominated by repulsive electrostatic interactions between aggrecan complexes. We discuss the consequences of the bottlebrush architecture on the polyelectrolyte characteristics of the aggrecan molecule, and its implications for cartilage properties and function.

1. Introduction

Aggrecan, a negatively charged proteoglycan, is a major macromolecular component of cartilage extracellular matrix. Like many biological macromolecules, the structure of aggrecan is uniquely tailored for its physiological function: it has a bottlebrush architecture and a semi-rigid character [1–3]. The bottlebrushes are enmeshed within the collagen network of cartilage, and exert a high osmotic swelling pressure that resists compressive loads [4, 5].

The goal of this review is to compare aggrecan solution behavior reported in different publications. Recent osmotic studies have shown that aggrecan solutions display at least four distinguishable concentration regimes with sharply differing solution behavior [6, 7]. However, aggrecan solution data from literature, which span a wide range of concentrations, and have not been compared or interpreted in the context of these regimes. Furthermore, aggrecan molecules show polyelectrolyte behavior that is unlike typical linear polyelectrolytes in solution [6, 7] and on surface [8]. For instance, the conformation of aggrecan is practically unaffected by the salt concentration of the solution, whereas many polyelectrolytes (poly[acrylic acid], DNA, etc.) show strong sensitivity to changes in the ionic environment. Understanding the unusual polyelectrolyte behavior of aggrecan is important for designing aggrecan-like polymers for cartilage tissue engineering [9]. Efforts in the field have mainly focused on hydrogels and double networks of linear hydrophilic polymers [10–12].

In this review we compile the aggrecan solution behavior from static (osmotic pressure measurements) and dynamic (diffusion, light scattering and rheology) experiments, and discuss the physical properties in the framework of the concentration regimes identified by osmotic pressure measurements. An attempt is made to understand the physiological implications of the bottlebrush architecture, and highlight similarities and differences between the behavior of aggrecan and linear polyelectrolytes. We also briefly describe recent surface studies and modeling endeavors on aggrecan molecules and assemblies.

1.1 Structure

Fig. 1a shows schematically the structure of a single aggrecan bottlebrush. It consists of a linear protein core (300 kDa) with glycosaminoglycan (GAG) side chains extending from glycosylated serine residues [2]. The core protein has 3 globular domains: GD1, GD2 and GD3. The GAG chains are located between GD2 and GD3. GAGs are polymer repeats of disaccharides composed of glucuronic acid and a glycosamine. The predominant GAG in aggrecan is Chondroitin Sulfate (CS), which consists of repeating units of glucuronic acid and 4/6-sulphated N-Acetyl Galactosamine. Up to 100 CS chains are found per aggrecan molecule, with 40–50 disaccharide repeats per chain [2, 3]. The GAG chain Keratan Sulfate (KS) is also present in aggrecan in smaller amounts, about 30 chains per monomer. The KS chains are shorter, composed of 20–25 repeating units of Galactose and N-Acetyl Glucosamine. Interspersed among the GAG chains are 8–10 short N- and O- linked oligosaccharides. The aggrecan bottlebrushes isolated from tissues are polydisperse (molecular weights MW range from 1–3 MDa), due to the variations in the number and length of the attached GAGs [13].

Fig. 1. The aggrecan monomer.

(a) 2D schematic representation of the structure of aggrecan monomer, along with the length/radius dimensions of the components [1, 3, 37, 79]. (b) AFM imaging of aggrecan monomer on APTES-coated mica.

1.2 Charged and semi-rigid character

The disaccharide building block of GAGs contains carboxylate and sulfate groups, which are negatively charged at physiological pH 7.4 (carboxylate pKa ~3–5, sulfate pKa ~1.5 –2) [14–17]. Each disaccharide has 2 negative charges spaced 1–1.5 nm apart. With ≈30 disaccharides per GAG and ≈100 GAGs per bottlebrush [2], the aggrecan monomer is a highly negatively charged polyelectrolyte. The length of each GAG in the bottlebrush is comparable with its persistence length (14 – 21nm [1]). As a result, the GAG chains are semi-rigid and assume an extended conformation in solution. The charged and semi-rigid side-chains make aggrecan a stiff polyelectrolyte with a persistence length of about 90 nm [1]. By comparison the persistence length of linear polyelectrolytes such as dsDNA and polyacrylic acid are about 42 nm [18] and 1.4 nm [19], respectively.

1.3 Aggregate/Hyaluronic acid aggregate

In cartilage extra-cellular matrix aggrecan is bound to hyaluronic acid (HA) via the G1 domain of the core protein. HA is a GAG chain like CS, but does not contain sulfate groups [3] and has many more disaccharide repeat units (contour length ~ 1 – 7 μm) [20]. The aggrecan/HA aggregate exhibits a secondary bottlebrush structure with about 100 aggrecan monomers attached along the linear HA chain at about 12 nm apart [21]. The length of the aggregate varies between 500 – 4000 nm [22], and its apparent persistence length is about 100 nm [23, 24] The aggregation with HA greatly improves the compressive properties of the aggrecan solutions [25]. We note that we use the term ‘Aggrecan/HA aggregate’ in the present review when referring to aggrecan bound to HA, and the term ‘assembly’ when referring to aggrecan assemblies formed in the absence of HA.

1.4 Physiological function

In cartilage, extracellular matrix aggrecan is confined within the collagen network and occupies a much smaller volume than in free solution. Also because of the high negative-charge density, it attracts counter-ions. Consequently, a large osmotic swelling pressure is generated, which is responsible for the hydration and load-bearing capacity of cartilage [5, 26, 27]. The bottlebrush conformation allows aggrecan to serve as a space-filling molecule, and exert a large frictional drag which is responsible for the decreased hydraulic permeability and damping properties of cartilage [5, 28]. Cartilaginous tissue also plays the role of precursor scaffold for bone formation; shielding loads and maintaining the expanded volume necessary for chondrocytes to proliferate during bone development [3].

The importance of aggrecan’s physiological function is evident from the number of pathological conditions that accompany impairments in its structure or synthesis. Aggrecan degeneration in intervertebral discs is a leading cause of lower back pain [29]. Certain genetic diseases where aggrecan is missing (due to truncation of the core protein) result in shortened and malformed bones, spinal disorders and respiratory difficulties from collapse of the tracheal cartilage [30]. In genetic diseases where aggrecan is under-sulfated, the symptoms may range from bone deformities at birth and dwarfism to being still-born or dead within minutes of birth, depending on the degree of under-sulfation [31, 32]. Since cartilage is a precursor scaffold for bone, a reduction in aggrecan charge density leads to decreased tissue hydration, and therefore, a decrease in the tissue volume that is replaced by bone. This results in shortened bones [3]. Aggrecan is particularly susceptible to proteases, especially at the IGD region, due to the extended nature of its core protein [3]. The production of proteases is closely regulated by chondrocytes. However, the regulation is disturbed in degenerative diseases like osteoarthritis (OA) and rheumatoid arthritis (RA) [3, 33]. In both cases, degradation of aggrecan is accompanied by loss of collagen, diminished load-bearing capacity, joint pain, and reduced motion, as cartilage degenerates and exposes the subchondral bone.

2. Solution behavior of aggrecan molecules

In this section, we compile data on aggrecan solution behavior from different experimental techniques, and examine them in the different concentration regimes identified by osmotic pressure measurements. Each solution technique is discussed separately. Unless otherwise stated, most of the compiled data involves aggrecan dissolved in NaCl solutions (0.1 < c < 0.15 M and pH 6.5 < pH < 7.4). Table 1 lists the buffer conditions for the solutions.

Table 1.

Aggrecan solution conditions from published sources

Study	NaCl	Buffer	Temp (°C)	Aggrecan source
Osmotic Pressure
Horkay et al. [7]	0.100 M	pH 7	25	Bovine articular cartilage (Sigma Inc.)
Meyer et al. [80]	0.200 M	0.01M NaHCO3	5	Bovine intervertebral disc
Urban et al. [35]	0.150 M	pH 8.3	37	Disc, hip and bovine nasal cartilage
Werner et al. [34]	0.154 M	pH 7.4		Pig articular cartilage
Williams et al. [36]	0.140 M	0.01M PBS, pH 7.5	20	Swarm rat chondrosarcoma tumor
Hydrodynamic
Gribbon et al. [55]	0.138 M	0.01M PBS	25	Porcine laryngeal cartilage
Harper et al. [81]	0.15–2 M	0.01 M MES	20	Bovine nasal cartilage
Scattering
Horkay et al. [7]	0.100 M	pH 7	25	Bovine articular cartilage (Sigma Inc.)
Reihanian et al. [45]	0.150 M	0.01M Mes, pH 7	25	Bovine nasal septum
Soby et al.	0.150 M	0.01M Mes, pH 6.8	25	Bovine articular cartilage
Rheology
Mow et al. [59]	0.150 M	0.01 Mes, pH 7	20	Bovine nasal cartilage
Hardingham et al. [64]	0.140 M	0.01M PBS, pH 7.2	20	Porcine laryngeal cartilage
Nishimura et al.[25]	0.150 M	PBS	37	Calf rib cartilage
Papagiannopolos et al. [24, 63]		EDTA buffer, pH 7.4		Porcine laryngeal cartilage

2.1 Osmotic Studies

This technique provides insight into the thermodynamics properties and interactions of the aggrecan molecules over an extended concentration range.

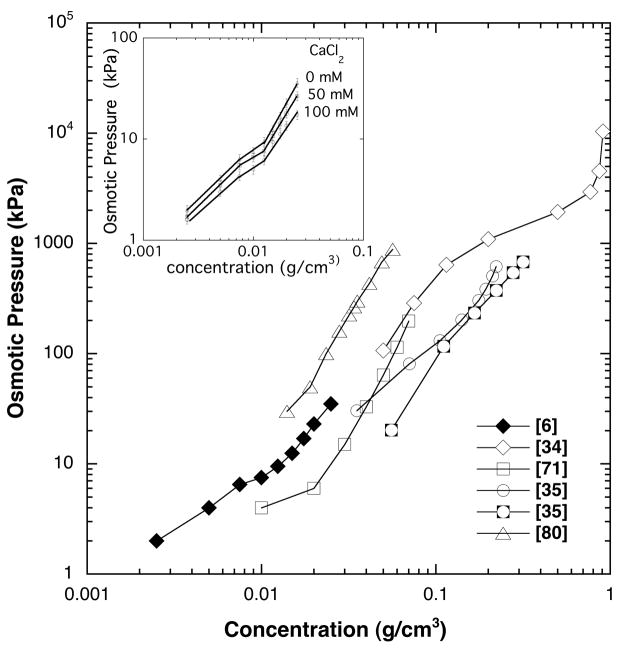
Figure 2 shows the concentration dependence of osmotic pressure (π) for aggrecan solutions culled from the literature [6, 34–36]. The inset in Figure 2 shows data measured in the aggrecan concentration range 0.001 < c < 0.1 g/cm³ at three different CaCl₂ concentrations in 100 mM NaCl [6]. There are shifts between the data sets from different publications, which can be attributed to differences in the salt concentration (see Table 1), the charge density and the aggrecan source [35]. However, one can clearly distinguish four regimes in which the concentration dependence of π is different. We refer to these regimes as the ‘dilute’, ‘assembly’, ‘physiological’, and ‘concentrated’ regimes (see Figure 3). Note that these labels are solely for the purpose of this review. To give an idea of the average distance between the aggrecan molecules in the different concentration regimes, we estimated the separation distance between the centers of “cigar-shaped” aggrecan protein cores, assuming aggrecan MW of 3 MDa and idealized cylindrical shape of 400 nm length.

Fig. 2.

Osmotic Pressure vs. aggrecan monomer concentration compiled from different publications. Data from Horkay et al. [6] (inset) in the concentration range of 0.001 – 0.1 g/cm³, shows three osmotic distinct regimes which are not affected by the Ca⁺⁺ concentration.

Fig. 3.

Osmotic pressure vs. concentration of aggrecan solutions with representative data from Horkay et al. [6] (black filled squares) and Werner et al. [34] (black unfilled squares). Four concentration regimes are distinguishable, where the osmotic pressure shows different power-law dependence on concentration. Shown alongside in grey squares, is the estimated separation distance between aggrecan protein cores. The separation distances were estimated assuming average aggrecan MW of 3 KDa, and an idealized cylinder shape of length 400 nm.

2.1.1 ‘Dilute’ Region

In this regime (< 0.0075 g/cm³) the aggrecan concentration is much lower than that in the cartilage matrix (0.02–0.08 g/cm³). The average separation between protein cores (61–35 nm) is comparable to the diameter of an aggrecan molecule with extended side chains (40–80 nm). Phillips et al. [37] estimated that for average GAG lengths of 40 nm, the side-chains start to overlap at about 0.0023 g/cm³. In this region π exhibits a linear dependence on the concentration (Fig. 3). A linear dependence on concentration is typically shown by dilute solutions of non-interacting components. Linear dependence is also expected for semi-dilute solutions of linear polyelectrolytes, when their charge density is much greater than the salt concentration of the solution [38]. The addition of salt (NaCl, CaCl₂) does not change the linear concentration dependence, but reduces π proportionally throughout the regime [6]. The addition of Hyaluronic acid (HA), however, reduces π as well as changes the concentration dependence [7].

2.1.2 ‘Assembly’ Region

The aggrecan concentration in this regime (0.0075–0.01 g/cm³) is still below the physiological concentration in cartilage. The average separation between protein cores is less than the overlap distance for fully extended side chains. In this regime the concentration dependence of π is weak (the power law exponent is less than one). Such dependence indicates that the addition of extra solute only weakly alters the water activity of the solution. Osmotic flattening is typical of associating solutions [39]; and is observed in surfactant solutions around the critical micelle concentration where the molecules self-assemble into micelles [40, 41].

2.1.3 ‘Physiological’ Region

The aggrecan concentration in this regime (0.01– 0.1 g/cm³) is similar to that in cartilage. The separation distance between the protein cores (25 – 9 nm) is much smaller than the diameter of the extended aggrecan cylinders, and similar to the separation distance between protein cores in HA/aggregates [42]. π shows a quadratic power-law dependence on the concentration, which is expected for polyelectrolyte solutions when excluded volume and charge interactions dominate [35, 43]. In the ‘physiological’ region π is governed primarily by the fixed charge density of the GAG chains [35] and is only weakly affected by their attached state to aggrecan or HA-aggregates [7, 35].

2.1.4 ‘Concentrated’ Region

The calculated separation distance between the protein cores in the ‘concentrated’ regime (0.1–0.7 g/cm³) ranges from 3 – 9 nm, and π shows a weaker dependence on the concentration. At high concentrations (m_water/m_total ≈ 10%) π diverges, which can be attributed to partial dehydration [34]. Due to the paucity of data in this regime, and because it is well beyond concentrations of physiological interest, we do not consider it in the rest of the paper.

2.1.5 Osmotic Modulus of Aggrecan Solutions

The load bearing ability of cartilage is governed by the osmotic modulus, K_os (=c∂π/∂c), which is obtained from the concentration dependence of π. A high osmotic modulus is of critical importance for structural polymers in order to maintain compressive resistance under external load. Horkay et al. [7] reported that (a) in near physiological solutions (0.07 g/cm³ aggrecan, 100 mM NaCl) K_os = 520 kPa; and (b) in solutions of aggrecan/HA aggregates K_os increases by approximately 10% (K_os = 575 kPa at c = 0.07 g/cm³), close to the value reported for cartilage [44].

2.2 Scattering Studies

2.2.1 Static Scattering

In a scattering experiment, the arrangement of the scattering elements is probed at length scales of 2π/q, where q is the scattering vector

$$q=\frac{4\pi n_0}{\lambda }sin\frac{\theta }{2}$$ (1)

In equation 1, n_o is the refractive index of the scattering medium, λ is the wavelength of the radiation, and θ is the detection angle. By varying λ and θ, a wide range of wave vectors can be used to probe the sample at different spatial resolutions.

A range of scattering techniques (Small Angle Neutron Scattering, Small Angle X-ray Scattering, Light Scattering) has been used to investigate aggrecan solutions from 5 nm to 1500 nm resolution [6, 7]. In Table 2 we summarized the power-law dependences of the scattering intensity I(q). The data indicate that aggrecan assemblies behave like microgel particles with an extended branched structure composed of semirigid chains.

Table 2.

The power-law exponents of scattered intensity at different length scales

Structural resolution	Structural moiety	Power-law	Solution behavior
50nm < 2π/q < 1.5um	single/multiple aggrecan molecules	I(q)∝ q−2	large fractal clusters or micro gels
5nm < 2π/q < 50nm	multiple GAG chains	I(q) ∝ q−2.7	branched clusters
5nm < 2π/q	single GAG chain	I(q) ∝ q−1	locally rod-like structures

Interestingly, increasing the concentration from the ‘dilute’ to the ‘assembly’ regime did not affect the scattering response at length scales below 50 nm. Both the power-law dependence and the scattering intensity remain unchanged, implying that the structural characteristics of single and multiple GAG chains are unaffected by the concentration increase. A weak concentration effect was observed at length scales > 50 nm. The power-law exponent changed from −2 at 0.0002 g/ml to −2.2 at 0.01 g/ml, which can be attributed to densification of the microgel-like aggrecan assemblies at these length scales.

2.2.2 Dynamic Light Scattering

Dynamic Light Scattering (DLS) probes the correlation of the scattered light intensity over time, due to fluctuations in the polymer concentration. When the concentration fluctuations are due to Brownian motion, the relaxation rate (Γ) of the intensity autocorrelation exhibits a q² dependence, and is related to the diffusion coefficient by

$$\mathrm{\Gamma }={Dq}^2$$ (2)

Assuming that the diffusion is governed by the Stokes-Einstein law, the equation

$$\mathrm{\Gamma }=\frac{k_B{Tq}^2}{6\pi \eta \xi }$$ (3)

can be used to estimate the hydrodynamic radius of the diffusing entity. In Eq. 3 k_B is the Boltzmann constant, T is the absolute temperature, η is the solvent viscosity, and ξ is the hydrodynamic correlation length.

Several studies have been made on dilute aggrecan solutions by DLS. Reihanian et al.[45] fitted the correlation function with a single relaxation rate; and Papagiannopoulos et al.[24] used two relaxation rates: one corresponding to the internal motions within the aggrecan molecule and the other corresponding to the translational motion of the aggrecan itself. The resulting diffusion coefficients (Eq. 2) are shown in Fig. 4. The apparent diffusion coefficient is practically independent of the concentration up to about 0.002 g/ml in the dilute regime and then decreases with increasing concentration. Henceforth, we refer to this region within the dilute regime where there is a concentration dependence of the diffusion coefficient, as the ‘dilute transition’ regime. Below the ‘dilute transition’ regime, the diffusion of the scattering unit appears unaffected by inter-particle effects and can be described by Stokesian hydrodynamics (Eq. 3). The hydrodynamic radii estimated from Eq. 3 were 73 nm [45] for the aggrecan bottlebrush, and 44 nm and 202 nm for the internal and translational relaxation modes, respectively [24].

Fig. 4.

The diffusion coefficient of aggrecan monomers as determined from Dynamic Light Scattering, by assuming a single relaxing entity [45] (black unfilled) and two relaxing entities [24] (black filled). Also shown (dashed lines) is the concentration range where the aggrecan monomers in solution are assembled into fractal clusters [6, 7].

Horkay et al.[6, 7] analyzed the autocorrelation function in terms of several relaxation rates, and determined the weight-averaged relaxation rate [46]. The measurements were performed at two concentrations in the ‘dilute’ regime (0.0002 g/ml, 0.0014 g/ml). The average relaxation rate was found proportional to q³. Probing the dynamics of aggrecan solutions by DLS and neutron spin-echo, the q³ dependence was observed over a wide range of wave-vectors, and hence over a wide range of characteristic lengths (from about 1.3 nm to 1.5 μm). A q³ dependence can be rationalized from Eq. 3, if the hydrodynamic radius were proportional to the structural length probed by each wave-vector; i.e. ξ ~ q⁻¹. Such dependence is typically found in microgels where the intrinsic size of the fluctuating volume is much larger than the length scale probed by the scattering vectors. [6, 7]. Finally, at the resolutions probed in these dynamic scattering measurements, complexation of aggrecan with HA did not significantly affect the dynamic response of aggrecan solutions in the ‘dilute’ regime [7]. Also, increasing the NaCl or CaCl₂ well beyond the physiological salt concentration range did not influence the scattering response, which is unlike most linear polyelectrolytes [6, 7, 45]. Recent results show that aggrecan solutions exhibit exceptional insensitivity to changes in the CaCl₂ concentration over the range 0–200 mM [6].

2.3 Hydrodynamic Studies

Hydrodynamic studies allow us to estimate the hydrodynamic friction exerted by molecules, which is a measure of the drag resisting motion relative to the solvent. At the macroscale, hydrodynamic friction can be estimated from hydraulic permeability experiments, i.e., from the velocity of solvent permeation through a macromolecular solution under a pressure gradient. A low hydraulic permeability indicates large hydrodynamic friction. At the microscale, hydrodynamic friction can be determined from molecular diffusion measurements, i.e., from the drag resistance to Brownian forces. The hydrodynamic measurements give information on the conformation of aggrecan (in general, an extended state gives higher hydrodynamic friction due to the increased area exposed to flow), its water-structuring properties (which also affects the hydrodynamic radius), and its interaction with neighboring aggrecan molecules. The hydrodynamic friction of aggrecan influences the time-dependent response of cartilage to loading [47].

2.3.1 Hydraulic Permeability

Proteoglycans have been found to exhibit some of the highest resistance to fluid flow per unit mass, among a wide range of polymers [28, 48]. The measurements of hydraulic permeability were found to correlate with structural features of the CS chains, but did not depend on whether the CS chains were part of the aggrecan bottlebrushes or the aggrecan/HA aggregates [28, 48]. It also appears that GAGs like CS, KS and HA have a significantly higher hydrodynamic friction than most polysaccharides mainly due to the nature of the glycosidic bonds between their sugar residues, and not because of the charge on the residues [49]. For instance, changing the charge of the CS chains by varying pH (3.2 – 8.7), removing sulphate/carboxyl groups, or changing the ionic strength, did not significantly alter the hydraulic permeability of the corresponding solution [50]. On the other hand, the hydraulic permeability is significantly increased by periodate oxidation of CS [50], which disrupts hydrogen bonds along the CS backbone by reducing the number of –OH groups [53]. Also, in a separate study it was found that the arrangement of sugar linkages in GAGs tends to promote hydrogen bonding and restrict inter-sugar rotation along the backbone [49]. Therefore, the hydraulic permeability of aggrecan is likely governed by the intrinsic stiffness of the CS chains due to the extensive hydrogen bonding between the sugar residues along its backbone. The role of hydrogen bonding in increasing the apparent stiffness of the GAG backbone was also reported by Gribbon et al. [54]. Large-scale hydrogen bonding between CS molecules does not significantly contribute to the hydraulic permeability, since disruption of the hydrogen bonds by Guanidine Hydrochloride (GdHCl) and NaF did not appreciably increase it [50]. Unlike GAGs or aggrecan in solution, the hydraulic permeabilities of GAG chains immobilized on gels and of aggrecan embedded in cartilage are affected by changes in charge and ionic strength, which can be attributed to the electrokinetic coupling that occurs in porous/fibrous charged media [51, 52].

Hydrodynamic permeability experiments also indicate inter-aggrecan interaction and molecular association occurring at higher concentrations. At aggrecan concentrations of 0.002 g/ml (‘dilute’ regime), the hydrodynamic radius is about 80 nm [48], which is in the range expected for a single aggrecan bottlebrush [45]. At aggrecan concentrations of 0.010 g/ml (‘assembly’ regime), however, the apparent hydrodynamic radius is about 600 nm [48], suggesting that the diffusing unit involves interacting bottlebrushes. Correspondingly, increasing aggrecan concentration from 0.00047 g/ml (‘dilute’ regime) to 0.0124 g/ml (‘physiological’ regime) was found to decrease aggrecan transport across a membrane (nominal pore size = 400 nm) to less than 10% indicating the formation of larger assemblies at the higher concentration [48].

2.3.2 Self Diffusion

Self diffusion describes the diffusion of a macromolecule within a solution of itself, in the absence of concentration gradients. It is quantified by the self-diffusion coefficient (D_self), which depends upon the intrinsic Brownian dynamics of the particle as well as inter-particle steric and interaction effects. Figure 5 shows the self-diffusion coefficient of aggrecan as a function of concentration from the works of Comper et al.[48] and Gribbon et al. [55]. In the former, D_self of aggrecan was deduced from sedimentation kinetics measurements [48]. In the latter, D_self of fluorescent-labeled aggrecan molecules (labeled at the protein core) was estimated from confocal FRAP (Flourescence Recovery after Photobleaching) [55], and the results were in reasonable agreement with the sedimentation measurements. In figure 5, D_self is nearly constant at low concentrations in the ‘dilute’ regime (< 0.002 g/ml) indicating the absence of significant inter-particle interactions. However, above 0.002 g/ml, D_self exhibits an increasingly negative power-law dependence on the concentration. The concentration dependence of D_self in the ‘dilute-transition’ regime (0.002 g/ml – 0.007 g/ml) which indicates the presence of inter-particle interactions in this regime, is consistent with light scattering observations (Fig. 4)

Fig. 5.

The self-diffusion coefficient of aggrecan monomers reproduced from Gribbon et al. [55] (black filled) and Comper et al.[48] (black unfilled). The self-diffusion coefficient shows different power-law dependence in the different concentration regimes.

2.3.3 Solute Diffusion

The diffusion coefficient of tritiated water (HTO) in 0.041 g/ml aggrecan solution (‘physiological’ regime) is about 96% of that measured in the aggrecan-free solvent indicating the absence of significant water structuring [48]. Glucose (MW = 180, Stokes radius = 0.37 nm) diffusion in cartilage does not change significantly when the aggrecan is digested away, suggesting that small uncharged solutes can penetrate into the aggrecan bottlebrush at physiological concentrations [56]. However, in cartilage the diffusion of larger uncharged molecules is hindered. For instance, Inulin (Stokes radius 3.4 nm) and dextran (Stokes radius 5.8 nm) show a 100 fold increase in diffusion when the cartilage proteoglycans are removed [56].

In summary, hydrodynamic studies suggest that aggrecan molecules exert a large frictional drag due to the intrinsic rigidity and extended conformation of the GAG chains. The stiffness of the GAG molecules is primarily enhanced by hydrogen bonding, while the charge repulsion between them plays a limited role. Inter-aggrecan interactions were observed in the ‘dilute-transition’ regime and beyond (concentrations above 0.002 g/ml). At the ‘assembly concentration’, the size of the diffusing unit gradually exceeds that of the single aggrecan bottlebrush. While aggrecan exerts a large hydrodynamic drag, its internal volume is unstructured and accessible to small diffusing solutes even in the ‘physiological’ concentration range.

2.4 Rheology Studies

Oscillatory shear experiments probe the spectrum of relaxation times. The force response of a polymer to an oscillatory shear strain can be decomposed into an in-phase component and an out-of-phase component. The former is an estimate of the polymer’s elastic or solid-like character, and is governed by the storage modulus G′(ω). The latter is an estimate of the polymer’s viscous or fluid-like character, and is governed by the loss modulus G″(ω). The evolution of the storage and loss moduli as a function of the shear frequency (ω) gives information on the relaxation dynamics of the polymer.

2.4.1 Storage and Loss modulus

Figure 6 shows the storage (G′) and loss moduli (G″) of aggrecan solutions with increasing sinusoidal frequencies for two concentrations: 0.007 g/ml (‘dilute-transition’ regime) and 0.0321 g/ml (‘physiological’ regime), respectively [24, 57]. The dynamic response in the ‘dilute-transition’ range was determined from particle tracking micro-rheology experiments, and the loss modulus was expressed as G″- η_oω where η_o is the solvent viscosity [24]. The rheological properties in the ‘physiological’ regime were determined from oscillatory shear experiments at 5% strain, 25°C [57, 58].

Fig. 6.

Rheology of aggrecan monomers in two concentration regimes compiled from Papagiannopoulos et al. [24] and Soby et al.[57]. The light grey plots shows data for 0.007 g/ml aggrecan concentration (‘dilute-transition’ regime) [24]. The dark grey plots show data for 0.032 mg/ml aggrecan concentration (‘physiological’ regime) [57] The storage modulus (G′) and the loss modulus (G″) are in units of kPa. η is the viscosity in kPa sec.

At both concentrations, aggrecan dynamics is similar to that of other polymers below the entanglement regime, i.e., the solutions exhibit primarily viscous behavior with G″ > G′. The storage modulus G′ increases with frequency without plateau-ing indicating that the internal deformations relax at the time-scale of these frequencies. In the 0.007 g/ml aggrecan solution, a cross-over can be seen at higher frequencies, which is usually associated with the onset of topological constraints. However, it is interesting that crossover is seen only at frequencies beyond 10³ rad/sec indicating that aggrecan molecules relax from the constraints rather rapidly. From the available rheological data, it is not clear how the relaxation behavior changes from the ‘dilute-transition’ to ‘physiological’ regime because of self-assembly [57, 58]. A continuum of relaxation times is observed in both regimes, which is consistent with the DLS observation [7]. Figure 7 shows the variation of the high-frequency storage modulus (measured at 10⁵ rad/sec) as a function of concentration [24]. A large increase in the storage modulus is observed beyond the ‘assembly’ region.

Fig. 7.

The reduced viscosity of aggrecan monomers at different concentrations, culled from Papagiannopoulos et al. [24] (black filled circles), Hardingham et al. [64] (black filled squares) and Mow et al.[59] (black unfilled squares). The storage modulus at 10⁵ rad/s (black cross) is also shown [63]. The units for reduced viscosity and storage modulus are (mg/ml)⁻¹ and Pa, respectively.

2.4.2 Viscosity

The viscosity (η) is related to the loss modulus by η = G″ω, and is a measure of the total hydrodynamic drag contribution of the aggrecan molecules. Aggrecan solutions in both dilute transition and physiological regimes show only a small decrease in viscosity (shear thinning) for over two decades of strain frequencies (Fig. 6) [24, 57, 59]. This finding suggests that no major flow-induced reordering occurs at the time-scale of these frequencies. The aggrecan sample in the ‘dilute-transition’ regime exhibits moderate shear thinning around about 100 rad/s and more pronounced shear thinning around about 1000 rad/s, while in the ‘physiological’ regime a moderate shear thinning can be observed around 10 rad/sec [57–59].

There are two possible mechanisms causing shear thinning: (a) hydrodynamic rearrangements driven by the imposed shear, that reduces the drag on each molecule [60], and (b) the breakage of inter-molecule interactions [61]. The former occurs at shear frequencies in the neighborhood of the Peclet number (Pe) = 1. Peclet number is the ratio of the time-scale of imposed deformation to the time-scale of the Brownian diffusion randomizing the deformation,

$$Pe=\frac{R_h^2\omega }{D}=\frac{6\pi {\eta }_o{R}_h^2\omega }{k_{B}T}$$ (4)

where R_h, ω, and D are the hydrodynamic radius, imposed shear frequency and diffusion coefficient, respectively.

The hydrodynamic radius of aggrecan in the ‘dilute-transition’ (0.007 mg/ml) and ‘physiological’ (0.0321 g/ml) regions are 400 nm, and >1000 nm, respectively [48]; which corresponds to frequencies 3 rad/s, and 0.01 rad/s, at Pe = 1 (Eq. 4). Since shear thinning does not occur at these frequencies, it is likely that the shear thinning is caused by disruption of inter-monomer interactions. [62]

Figure 7 shows the reduced viscosity (η/cη_o; c is aggrecan concentration, η_o is solvent viscosity) of the aggrecan solution as a function of concentration, from the dilute to physiological regime. The data are compiled from Papagiannopoulos et al. [63], Hardingham et al. [64], and the zero shear viscosity data of Mow et al.[59]. The reduced viscosity shows different concentration dependencies in the different regimes. In the ‘dilute’ regime it decreases with increasing concentration (η/cη_o∝ c^−.5). Such behavior is typically seen in semi-dilute solutions of linear polyelectrolytes when the polyelectrolyte chains start to overlap [38].

In summary, aggrecan solution displays a predominantly viscous character at all concentrations. The ‘dilute-transition’ solution shows topological constraints at high frequencies. Peclet number calculations suggest that shear thinning in the ‘dilute-transition’ and ‘physiological’ regimes is due to disruption of inter-monomer interactions. The reduced viscosity data in the ‘dilute’ regime suggest similarities with semi-dilute solutions of linear polyelectrolytes.

3. Surface Behavior of Aggrecan Molecules

Recent studies of adsorbed and end-grafted aggrecan molecules made by Atomic Force Microscopy (AFM) have revealed some interesting similarities and differences between the behavior of aggrecan molecules on surfaces and in solution. The surface studies of end-grafted aggrecan aimed to measure the interaction between GAG chains and aggrecan molecules in configurations expected to occur in the cartilage.

The topographical image of adsorbed aggrecan molecules generated by AFM reflects both the variations in tip-polymer interactions and the changes in height along the macromolecules. Aggrecan molecules in 0.1 M NaCl adsorb on a positively charged, hydrophobic surface (mica surface coated with APTES (3- amino propyltriethoxysilane) [1] or APS (1-[3-Aminopropyl] Silatrane) [8]) with visible and mostly extended GAG chains. On APTES-mica the molecules assume a semi-flexible conformation of persistence length 80–110 nm, estimated from the worm-like chain model [65]. Also, with increasing aggrecan concentration, at least three distinct patterns of aggrecan arrangement can be identified [8]. At low concentrations the adsorbed aggrecan molecules (in 0.1M NaCl) form a dispersed and non-interacting pattern. At intermediate concentrations, the aggrecan adsorbs in clusters of conforming bottlebrushes. At high concentrations a densely-packed monolayer is formed with adjacent molecules conforming along the bottlebrush lengths [1, 8]. No significant interpenetration of the GAG side chains has been observed.

AFM was also used to probe the effect of changes in the ionic environment on aggrecan conformation and interactions in the surface-adsorbed and end-grafted state. In the former case, the addition of CaCl₂ does not significantly change the average extension of the GAG chains and the adsorption patterns, which is similar to that observed in solution [8]. In the latter case, the bottlebrushes were end-grafted via the globular domain to functionalized mica surfaces or AFM tips, mimicking its arrangement in aggrecan/HA aggregates [66–70]. In this state, the concentration of Na⁺ and Ca⁺⁺ was found to affect the monolayer height and interaction forces [66–70]. Increasing salt concentration decreases monolayer height. This effect can be attributed to the decrease in electrostatic repulsion between the bottlebrushes from increased charge screening. Increasing salt concentration also increases the monolayer resistance to deformation, which indicates strong steric repulsions between the molecules [68, 69]. Increasing Ca⁺⁺ concentration beyond 2 mM has no effect on the monolayer height and shear resistance [69]. The largest resistance to compression was obtained when bottlebrushes were packed at near physiological density in the monolayer.

4. Modeling Studies of Aggrecan Molecules

Several aggrecan models have been proposed with different degrees of sophistication. Donnan-like models assume that the charges within the proteoglycan assemblies are distributed uniformly [71]. These models consider only the contribution of the charges to the osmotic pressure, and do not capture the concentration dependence of the osmotic pressure at physiological proteoglycan concentrations [71].

More advanced, Poisson Boltzmann-type models capture the charge localization on the GAG chains of the bottlebrush by modeling the aggrecan molecule as a series of charged rigid rods or plates [71]. These models consider the electrostatic repulsion between the GAGs as well as the counterion entropy, but neglect the conformational entropy of the GAG chains and the protein core. Basser et al. [72] showed that the simple Donnan model can be recovered by a first-order homogenization and approximation of the charged-plate model. The structural sophistication of the charged-rod model was found sufficient to predict the concentration dependence of proteoglycan osmotic pressure in the ‘self-assembly’ and ‘physiological’ regimes [71].

The charged-rod model was extended to capture the interaction between aggrecan bottlebrushes by treating each bottlebrush as a set of rigid charged cylinders attached to a planar surface [66]. The charged rods, mimicking GAG chains, were assumed to interdigitate at aggrecan separation distances less than twice the GAG height. The model predicts the interaction forces observed in surface experiments between monolayers of end-grafted GAG chains, but only up to the distances where the GAG chains start to overlap [66]. Also, since the conformational entropy of the GAG chains was not accounted for, this model is unable to reproduce the height response of the end-grafted monolayers to changes in pH and salt concentration [67].

Nap et al. [73] introduced a higher level of structural sophistication. The aggrecan bottlebrush was modeled as a rigid cylinder, with flexible and charged polymer chains attached to it. The model accounts for the conformational entropy of the GAG chains, the counter-ion entropy, and the electrostatic interaction between the counter-ions, solvent ions and polymer charges. However, it does not account for the semi-flexible nature of the GAG chains and for the flexible nature of the protein core. The model predicts the changes in height and interaction forces observed experimentally for end-grafted GAG chains with changes in pH and ionic strength [67, 68, 74]. Notably it shows that the repulsive interactions between the GAG chains are smaller for polymers tethered to a cylindrical surface than to a planar surface, due to the larger volume fraction and the ability of the polyelectrolytes to move out of plane [73]. Consequently, interdigitation occurs less frequently for GAG chains attached to a cylindrical surface than to a planar surface [73]. While the model is able to capture the behavior of end-grafted GAG and aggrecan monolayers, it is not clear how well it describes the behavior of aggrecan assemblies in solution, for instance their insensitivity to changes in the ionic environment.

5. Discussion of Aggrecan Solution Behavior

In this section, we highlight some aspects of aggrecan solution behavior, particularly those which differ from typical linear polyelectrolytes, and we comment on some of the physiological consequences of these differences.

5.1 Aggrecan Molecules in the ‘Dilute’ Regime

Remarkably, aggrecan molecules in the ‘dilute’ regime possess properties similar to linear polyelectrolytes in the semi-dilute regime. For instance both ‘dilute’ aggrecan and semi-dilute polyelectrolyte solutions exhibit the relations η/cη_o ∝ c^−.5, G′ ∝ c, and D_self ∝ c⁰ [38, 75]. In simple polyelectrolyte models, the chains overlap in the semi-dilute concentration regime. The dynamics of the polyelectrolyte solution is governed by the intra-chain charge repulsion which favors chain extension, and inter-chain steric repulsion which promotes chain bending [75]. In the semi-dilute regime the polyelectrolyte chain bends increasingly with concentration, which causes the hydrodynamic drag per chain or reduced viscosity (η/cη_o) to decrease with concentration [75].

The similarity between the rheological properties of dilute aggrecan and semi-dilute polyelectrolyte solutions suggests that the aggrecan protein-cores start to overlap in the ‘dilute’ regime. Assuming protein-core length l_p = 400 nm, and volume occupied by free aggrecan bottlebrush = (4/3)πl_p³, the overlap of the core-proteins starts at ~0.00002 g/ml. In other words, aggrecan solutions exhibit anomalous viscosity (the reduced viscosity decreases with concentration) at concentrations < 1 mg/ml, whereas linear polyelectrolytes exhibit it at much higher concentrations of about 10 – 100mg/ml [76] depending on the molecular weight. This difference is physiologically important because load bearing is not effective in the anomalous viscosity region, but the physiological aggrecan concentration is well beyond this region.

5.2 Aggrecan Clusters and Self-Assembly

Light scattering data show that aggrecan molecules form microgel-like clusters even in ‘dilute’ solutions. Osmotic pressure measurements indicate that the bottlebrushes undergo self-assembly in the ‘assembly’ regime [41]. However, the organization of the aggrecan molecules in the clusters is not fully understood. Light scattering measurements [6, 7] and rheological data [57, 59, 63, 64] do not indicate significant changes in the structure of the interacting molecules when the concentration increases from the ‘dilute’ to the ‘assembly’ regime. The increase in concentration is accompanied by increased aggrecan packing, but with no appreciable change in the interpenetration of the GAG side chains [7]. Only the relaxation time for aggrecan deformations increases, which can be attributed to the increased packing density. This implies that the structure of the aggrecan clusters in the ‘dilute’ regime is similar to that of the self-assembled aggrecan subunits in the ‘assembly’ regime. The self-assembly characteristics of aggrecan may play a role in its cooperative clustered binding on HA [21].

5.3 Physiological Implications of Aggrecan Bottlebrush Structure

One of the most important consequences of the bottlebrush architecture is that highly charged GAG chains are densely packed and their GAG lengths are on the order of the persistence length. As a result of the mutual repulsion and intrinsic stiffness, the GAG chains maintain an extended conformation, allowing it to serve effectively as a space-filling molecule. It prevents the infiltration of vascular and neuronal cells in the nucleosus pulposa [29]. It also exerts a large hydrodynamic drag while remaining highly hydrated. The large hydrodynamic drag is critical for sustaining dynamic loads in the cartilage while the large water content is necessary for the free diffusion of solute nutrients. The latter is particularly critical in cartilage since there are no blood vessels to supply the chondrocytes. Also, the extended conformation allows aggrecan solution to exhibit semi-dilute polyelectrolyte behavior at relatively low concentrations, which favor load bearing. Importantly, since the semi-rigidity of GAG chains is imparted by hydrogen bonding along the chain, the extended conformation of the bottlebrushes is not as sensitive to pH and Ca⁺⁺ ion fluctuation as other polyelectrolytes like DNA and polyacrylic acid [6]. Finally, the bottlebrush architecture and microgel properties limit the interpenetration of the GAG chains and aggrecan rheology does not exhibit entanglements up to large frequencies, which is important for its lubrication effects [77, 78].

6. Conclusions

Aggrecan is a bottlebrush molecule that is responsible for the load bearing and swelling properties of cartilage matrix. We compile aggrecan solution data from different experimental techniques, and examine them in the context of concentration regimes identified in osmotic experiments. We show that the bottlebrush architecture confers aggrecan with unique polyelectrolyte properties, which have important physiological consequences. Aggrecan molecules self-assemble and exhibit micro-gel like properties even at dilute concentrations. The bottlebrush architecture enables aggrecan to function as a space-filling molecule, bearing compressive loads at much lower concentrations than regular polymers. Its large swelling pressure arises from a combination of several factors: the high negative charge density, the hydrodynamic drag of the elongated conformation, and the semi-rigidity of the component GAG chains. Aggrecan is a biomolecule with superior lubrication and swelling properties, and its unusual polyelectrolyte properties need to be considered by researchers seeking to design novel biomolecules that can replace aggrecan function in damaged or engineered cartilage.