Abstract
Desensitization of ligand-gated ion channels plays a critical role for the information transfer between neurons. The current view on γ-aminobutyric acid (GABA)A and glycine receptors includes significant rapid components of desensitization as well as cross-desensitization between the two receptor types. Here, we analyze the mechanism of apparent cross-desensitization between native GABAA and glycine receptors in rat central neurons and quantify to what extent the current decay in the presence of ligand is a result of desensitization versus changes in intracellular Cl− concentration ([Cl−]i). We show that apparent cross-desensitization of currents evoked by GABA and by glycine is caused by changes in [Cl−]i. We also show that changes in [Cl−]i are critical for the decay of current in the presence of either GABA or glycine, whereas changes in conductance often play a minor role only. Thus, the currents decayed significantly quicker than the conductances, which decayed with time constants of several seconds and in some cells did not decay below the value at peak current during 20-s agonist application. By taking the cytosolic volume into account and numerically computing the membrane currents and expected changes in [Cl−]i, we provide a theoretical framework for the observed effects. Modeling diffusional exchange of Cl− between cytosol and patch pipettes, we also show that considerable changes in [Cl−]i may be expected and cause rapidly decaying current components in conventional whole cell or outside-out patch recordings. The findings imply that a reevaluation of the desensitization properties of GABAA and glycine receptors is needed.
INTRODUCTION
γ-Aminobutyric acid (GABA)A and glycine receptors, which mediate the majority of fast inhibitory transmission in the central nervous system, desensitize upon prolonged agonist exposure. Fast desensitization, which may take place during short (1–10-ms) GABA applications, is considered critical in shaping inhibitory synaptic currents (Jones and Westbrook, 1995), and slow components of desensitization (decay time constants of ∼1 s or longer) may decrease synaptic efficacy during prolonged exposure to agonist or during repetitive activation (Overstreet et al., 2000; Bianchi and Macdonald, 2002). Slow desensitization may also play a role during tonic, extrasynaptic GABAA receptor activation (Mtchedlishvili and Kapur, 2006; Lagrange et al., 2007). The physiological importance of desensitization is reflected by the modulatory influence of endogenous substances (Zhu and Vicini, 1997; Haage et al., 2005) and clinically important drugs (Orser et al., 1998). In addition, cross-desensitization between GABAA and glycine receptors may provide an important means for interactions between the two transmitters (Barker and McBurney, 1979; Baev et al., 1992; Grassi, 1992; Lewis and Faber, 1993; Trombley et al., 1999; Li and Xu, 2002; Wu et al., 2002; Li et al., 2003; Breustedt et al., 2004). Several aspects of desensitization are, however, poorly understood. This applies to mechanisms underlying cross-desensitization, the marked variation in desensitization often reported, e.g., between different patches with the same receptor type (e.g., see Pitt et al., 2008), and the correlation between desensitization and current amplitude that is seen in a variety of conditions (see below).
This study addresses the mechanisms underlying the current decay at GABAA and glycine receptor activation, with the aim of explaining apparent cross-desensitization as well as the large variability in reported desensitization and its correlation with current amplitude. Current knowledge on GABAA and glycine receptor desensitization is largely based on recording the current decay under voltage-clamp conditions. Although it is known that changes in intracellular Cl− concentration ([Cl−]i) may contribute to the current decay, such changes are usually ignored or assumed to be of minor importance in studies of desensitization. Knowledge about possible changes in [Cl−]i that may occur during GABAA and glycine receptor activation is, however, crucial for understanding how quickly and to what degree these receptors do desensitize. Such knowledge is also important because of the recent insight that changes in [Cl−]i may contribute to or accompany several pathological conditions, including epilepsy and chronic pain (Vale and Sanes, 2000; Schwartz-Bloom and Sah, 2001; Coull et al., 2003; Khalilov et al., 2003).
In this study, we quantify the changes in [Cl−]i during activation of native GABAA and glycine receptors, mostly in neurons of the rat medial preoptic nucleus (MPN) but also in cortical and hippocampal neurons. The analysis shows dramatic changes in [Cl−]i during GABAA and glycine receptor activation. We find that the altered [Cl−]i accounts for the cross-desensitization between GABA and glycine. We also find that the changing [Cl−]i is the main determinant of current decay in the presence of agonist, whereas the decay in conductance (“true desensitization”) plays a minor role only. By providing a theoretical framework that enables modeling of expected changes in [Cl−]i, we show that the results are theoretically consistent and that large changes in [Cl−]i may be expected under a variety of recording conditions. Although GABAA and glycine receptors of some subtypes or in some conditions may desensitize rapidly, our findings imply that in many cases, a reevaluation of GABAA and glycine receptor desensitization may be necessary.
MATERIALS AND METHODS
Ethical approval
Ethical approval of the procedures described was given by the regional ethics committees for animal research (“Stockholms södra djuförsöksetiska nämnd,” approval no. S201/04, and “Umeå djurförsöksetiska nämnd,” approval nos. A17-05 and A13-08).
Slice preparation
In total, 82 male Sprague-Dawley rats, aged from 3 to 5 wk, were used for the experiments described. They were housed at 20 ± 0.5°C with a 12-h light/dark cycle and free access to food and water. For preparation of brain tissue and isolated cells, rats were lightly anesthetized with 5% isoflurane and decapitated, or alternatively, decapitated without anesthetics. (No systematic difference in recorded parameters was observed for the two groups.) The brain was rapidly removed and placed in pre-oxygenated ice-cold (4°C) incubation solution, which was used throughout the entire slicing procedure and contained (in mM): 150 NaCl, 5 KCl, 2 CaCl2, 1.2 MgCl2, 10 HEPES, 10 glucose, and 4.93 Tris-base, pH 7.4 (95% O2, 5% CO2). A block of tissue containing the area of interest (anterior hypothalamus, motor cortex, or hippocampus) was used to cut 200–300-µm-thick coronal slices using a vibratome (Vibratome 1000plus; Ted Pella, Inc., or Vibroslicer 752 M; Campden Instruments). After cutting, slices were allowed to recover for at least 1 h in incubation solution at 21–23°C.
Acute dissociation of neurons
The procedure for dissociation of MPN neurons followed the details described previously (Karlsson et al., 1997b). Neurons from the motor cortex, layer V, and from the hippocampus, area CA1–CA2, were prepared in a similar way.
Recording solutions
Recordings were made using either the amphotericin B–perforated patch technique (Rae et al., 1991) or the gramicidin-perforated patch technique (Abe et al., 1994; Kyrozis and Reichling, 1995). Amphotericin B, which forms pores that are permeable to small cations but also to Cl−, was used in the first series of experiments to enable control of [Cl−]i while simultaneously preventing washout of possible critical intracellular factors. Gramicidin, which forms pores that are permeable to small cations but not to Cl−, was used in a second series of experiments when avoiding equilibration of [Cl−]i with pipette Cl− was required for quantification of changes in [Cl−]i. The extracellular solution contained (in mM): 137 NaCl, 5.0 KCl, 1.0 CaCl2, 1.2 MgCl2, 10 HEPES, and 10 glucose, pH 7.4 (NaOH). GABA, glycine, strychnine, gabazine (SR-95531), or bicuculline methiodide was added to the extracellular solution, as indicated in Results. In some experiments, 3.0 µM gabazine was used in the extracellular solution throughout the experiment to block spontaneous inhibitory postsynaptic currents (sIPSCs; see Results).
The standard solution used for filling the recording (patch) pipettes for amphotericin B–perforated patch recording contained (in mM): 140 Cs-gluconate, 3.0 NaCl, 1.2 MgCl2, 10 HEPES, and 1.0 EGTA, pH 7.2 (CsOH). For the control experiments with symmetrical chloride concentrations, the pipette-filling solution contained (in mM): 140 KCl, 3.0 NaCl, 1.2 MgCl2, 10 HEPES, and 1.0 EGTA, pH 7.2 (KOH). Amphotericin B (Sigma-Aldrich) was prepared from a stock solution (6 mg/100 µl DMSO) and added to a final concentration of 120 µg/ml of pipette-filling solution. For gramicidin-perforated patch recordings, as well as for conventional whole cell recordings, the pipette-filling solution contained (in mM): 140 K-gluconate, 3.0 NaCl, 1.2 MgCl2, 10 HEPES, and 1.0 EGTA, pH 7.2 (KOH). Gramicidin (Sigma-Aldrich) was prepared from a stock solution (120 mg/1.0 ml DMSO) to a final concentration of 600 µg/ml of pipette-filling solution.
GABAA receptors as well as glycine receptors are mainly permeable to Cl− but show a significant permeability also to HCO3− (∼20–40% of the permeability to Cl−; Farrant and Kaila, 2007). HCO3− is, via carbonic anhydrase, in equilibrium with CO2 that may easily cross the cell membrane. To avoid confounding factors caused by the sometimes complex dynamics of HCO3− and CO2 flux at GABAA receptor activation (Staley et al., 1995), and to enable studies of the receptor channel properties per se, we did not include HCO3− (or supplement with CO2) in the extracellular solution nor in the pipette-filling solution.
Electrophysiological recordings
The majority of recordings were made in the perforated patch configuration (see above), with neurons placed in a chamber of volume of 400 µl. The chamber was positioned on the stage of an inverted microscope (Diaphot 200; Nikon, or Axiovert 25; Carl Zeiss) and continuously superfused with extracellular solution at 21–23°C. Some recordings were made using an upright microscope (BX51WI; Olympus) supplied with a water-immersion objective (×40) for detection of possible changes in cell shape. Recording electrodes were pulled from borosilicate glass (GC150; Harvard Apparatus) and had a resistance of 3–4 MΩ when filled with gluconate-containing solutions. Signals were recorded using an Axopatch 200A amplifier, a Digidata 1200 interface, and pClamp software (versions 8 and 9; all from Axon Instruments). The signals were sampled at 2–5 kHz after low-pass filtering at 1–2 kHz (−3 dB). For the gluconate-containing pipette-filling solutions, a liquid-junction potential of −14 mV was corrected for.
The membrane potential (Vm) was clamped at a steady level, changed between two different levels in between pre- and test applications of agonists, or changed continuously by application of voltage ramps (sequences of three ramps: from −14 to −94 to +26 to −14 mV; ramp rate of ±1.6 V s−1), often giving two different estimates of the reversal potential (Vrev).
During perforated patch recordings, uncompensated series resistance (Rs) was in the range of 13–31 MΩ for cells used for quantitative evaluation of current amplitude and time course. A variable degree of Rs compensation, up to 90%, was used, and the remaining Rs was in the range of 2.0–6.6 MΩ (mean of 4.4 ± 0.4 MΩ; n = 10). For some of the experiments, effects of remaining Rs were expected to be critical to the interpretation. Therefore, we derived equations to quantify the effects of Rs (see below).
To provide a measure of conductance that was not significantly influenced by the effect of Rs on Vm, a series of experiments with two gramicidin-containing patch pipettes attached to the same cell was performed. In these cases, one pipette was used for voltage clamp, with application of voltage ramps and current recording, as described above. The second pipette was used to directly record the Vm under current-clamp conditions (at zero current). In this way, the effect of Rs on the estimate of Vm was bypassed, and an additional estimate of Rs was obtained (from Eq. 5 below).
Drugs and drug application
Tested compounds were applied using either a DAD-12 superfusion system (ALA Scientific Instruments) or a home-built gravity-fed fast perfusion system controlled by solenoid valves via a computer. The solution exchange time constant, which was estimated from the current change measured from an open patch pipette in alternating extracellular solution and 140 mM KCl, was ∼30 ms for the majority of experiments used for quantitative evaluation. The corresponding solution exchange time constant measured in the whole cell (perforated patch) mode was 53 ± 5 ms for 11 cells when resting on the bottom of the recording chamber, as the majority of cells in this study.
Control experiments with faster solution exchange (time constant of <1.0 ms; open pipette), made using a high-speed solution exchange system with two outlets (HSSE-2; ALA Scientific Instruments), did not reveal more rapidly desensitizing current components in response to 1.0 mM GABA when tested in five MPN cells. (One of the cells was lifted from the bottom of the recording chamber. This further increased the speed of solution exchange, as judged from the onset of GABA-evoked current, but did not reveal additional, more rapid components of desensitization.) Strychnine, bicuculline methiodide, picrotoxin (from Sigma-Aldrich), and gabazine (SR-95531 hydrobromide; Tocris Bioscience) were dissolved in DMSO at a concentration of 10–50 mM and thereafter diluted in extracellular solution to the final concentration.
Data analysis
The whole cell currents were analyzed offline using pClamp (see above). Baselines were subtracted from current responses measured during steady voltages and currents during voltage ramps in control solution were subtracted from those obtained in the presence of agonists to eliminate possible contribution of leak and voltage-gated currents. For recordings with two patch pipettes attached to the same cell, when Vm was directly measured, we used a leak current subtraction procedure where differences between Vm during control ramps without ligand application and Vm during test ramps with ligand application were taken into consideration. The I-V relation in the absence of ligand was found to be well described by the exponential relation:
| (1) |
The constants A, B, and C, obtained by fitting the equation to the current responses in the absence of ligand (i.e., the “leak” current), were later used to calculate the expected leak current during Vm measured when voltage ramps were applied in the presence of ligand. The obtained leak current was subsequently subtracted from the current recorded in the presence of agonist.
Capacitive currents during the voltage ramps were too small to significantly affect the estimates of conductance as well as of Vrev and were therefore ignored. (For a typical cell, a steady capacitive current of ±4.5 pA would be expected if Rs were zero, and a smaller current as a consequence of the attenuating effect of Rs on the rate of voltage change. The total current during the voltage ramps typically changed several nanoamperes.)
Peak values were used for current amplitudes, unless stated otherwise. Concentration–response curves (Fig. 2 A, bottom) were obtained by fitting the logistic (Hill) equation:
| (2) |
to the experimental data, where I is current with subscript “max” denoting maximum current, C is agonist concentration, EC50 is the concentration producing the half-maximal current, and n is the “Hill slope.” An equivalent equation with ln(C) as x axis was used to obtain the SEM of ln(EC50). The conductance was calculated from the Vrev and the current at 0 mV, as recorded during the rising phase of the ramp.
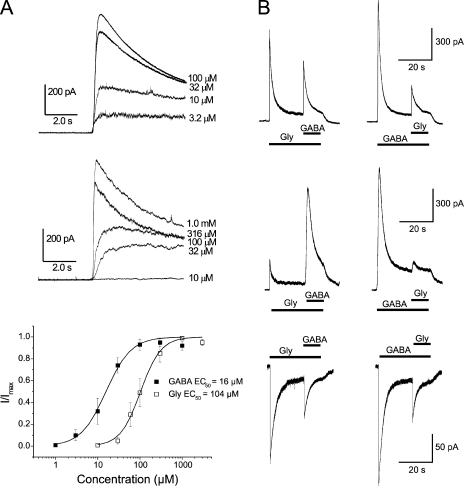
Figure 2.
Currents evoked by GABA and glycine. (A) Currents evoked by GABA (top) and by glycine (middle) in concentrations as indicated, at a Vm of −8 mV. (Different cells used for top and middle). (Bottom) Concentration–response curves for currents evoked by GABA and glycine. Symbols show peak currents (mean ± SEM; n = 4–6) recorded at −8 or 0 mV and normalized to the maximal response in each neuron. Smooth lines are described by Eq. 2 fitted to the experimental data. The Hill slopes were 1.5 and 1.8 for GABA and glycine (Gly), respectively, and SEM of ln(EC50) were 0.090 and 0.054. (B) Apparent cross-desensitization of GABA- and glycine-evoked currents, recorded when GABA or glycine was added 20 s after the start of perfusion with the other agonist. Left and right panels are from the same cell. Note that the responses to the second (within each pair) application are reduced compared with the responses to the same agonist applied first. Note also that apparent cross-desensitization was observed with standard solutions (see Materials and methods) when GABA- and glycine-evoked currents were of roughly similar magnitude (top, Vm of −8 mV) as well as when glycine-evoked currents were considerably smaller than GABA-evoked currents (middle, Vm of 0 mV), and that apparent cross-desensitization was also observed with nearly symmetrical Cl− concentrations (see Materials and methods) resulting in inward currents at −40 mV (bottom). Interval between pairs (left and right columns) was 140 s (top), 120 s (middle), and 84 s (bottom). (For some cells, recordings at −8 mV were preferred over those at 0 mV because of substantially lower background noise.) Amphotericin-perforated patch mode (A and B).
Chloride equilibrium potential (VCl) was calculated from the Nernst equation:
| (3) |
[Cl−]i was also derived from Eq. 3, assuming the Vrev = VCl. R, T, and F have their usual meanings. When estimating changes of [Cl−]i, the initial “resting” [Cl−]i was either calculated from the Vrev measured for sIPSCs or set artificially by applying agonist at the required Vm, as described in Results.
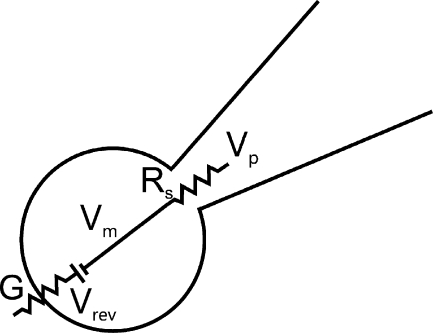
When analyzing the additivity of currents evoked by GABA and glycine, the effect of Rs on the recorded current was considered by taking the parameters shown in the simplified diagram of Fig. 1 into account. Seal resistance and membrane resistance (not depicted) beside the agonist-activated conductance were assumed to be high, and currents through these pathways neglected. The recorded current (I) depends on the conductance (G), Vm, and Vrev according to:
| (4) |
and
| (5) |
where Vp is pipette (command) potential.
Figure 1.
Simplified part of recording circuit containing a patch pipette and cell membrane. The diagram shows the relevant parameters at peak current or at steady state, when dV/dt = 0, and when current through the relatively high membrane resistance and seal resistance (not depicted) may be neglected. The conductance (G) is that activated by GABA or glycine.
Thus, we may calculate the current
| (6) |
or conductance
| (7) |
It may be noted that with increasing G, I approaches the asymptote:
| (8) |
It is thus clear that currents caused by the opening of different conductance pathways are not expected to add linearly. To estimate the expected current at coapplication of GABA and glycine for separate and independent conductances, we calculated the conductance causing the current at application of each agonist separately, from the Rs (remaining after compensation) according to Eq. 7. Using the sum of obtained conductances, we subsequently calculated the expected current at coapplication of GABA and glycine from Eq. 6.
It is clear from Eq. 6 that the recorded current, I, will vary in proportion to (Vp − Vrev) according to the proportionality factor (G−1 + Rs)−1, which we for convenience call the “apparent conductance” (G′). Thus, we may calculate the “true conductance” (G) from the recorded G′ and Rs:
| (9) |
For the analysis of responses to 1.0 mM GABA, cells where 3.0 µM gabazine was used to block sIPSCs were pooled with cells without gabazine, because at this low concentration, gabazine had negligible effects on the currents induced by 1.0 mM GABA (see supplemental text, section I). All data are given as mean ± SEM. Statistical significance was evaluated by using the Wilcoxon matched-pairs signed-ranks test or Wilcoxon two-sample test, as appropriate, with P < 0.05 chosen to imply significance.
Computation of [Cl−]i and its contribution to current decay
Changes in [Cl−]i and their contribution to current decay in the absence of conductance decay were computed numerically, taking the equivalent cytosolic volume (vequ) into account, as described in Results. GABA binding/unbinding and activation/deactivation were assumed to follow the simplified model described previously for synaptic GABA-mediated currents in MPN neurons (Haage et al., 2005), but the desensitized state was omitted. Thus, a linear three-state model with “unbound” (closed), “bound” (closed), and open states was used. The rate constants for GABA were: binding, 3.0 µM−1 s−1; unbinding, 723 s−1; activation (transition from bound to open state), 2,500 s−1; and deactivation (transition from open to bound state), 142 s−1. The details of activation kinetics were, however, not critical because activation was considerably faster than the changes in [Cl−]i. From the fraction of channel population in the open state (O), described by the above rate constants, the conductance (G), current (I), and [Cl−]i as a function of time (t) were computed numerically by (forward) Euler integration, according to the following (for clarity written as five separate) equations:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
The integration time step, Δt, was 0.2 ms unless indicated otherwise. For all types of responses computed, the stability of numerical computation was verified by similar responses upon reduction of Δt to one tenth of the values given in the text. The computations were made using Turbo Basic software (Borland). Unless specified otherwise in the figure legends, [Cl−]o was assumed to be constant (146.4 mM), [Cl−]i initially was 9.0 mM, and VCl was computed according to Eq. 3. The maximum conductance (Gmax) was set to 54 nS to match the experimentally observed maximum conductance evoked by 1.0 mM GABA (54 ± 7 nS; n = 15). The vequ was set to 50% of the total cell volume (see Results) in a spherical cell of radius 6.2 µm. Alternatively, initial [Cl−]i, Gmax, and cell radius were set to match a particular neuron studied experimentally. Glycine-activated conductance was assumed to follow similar kinetics as GABA-activated conductance, except rate constant for glycine binding = 0.46 µM−1 s−1 to account for the different EC50 values. Extensions of the model, to take into account outward Cl− transport and Cl− exchange between cytosol and recording pipette as a consequence of diffusion and electric current during conventional whole cell or outside-out patch recording, are described in the supplemental text (sections VI and VIII).
Online supplemental material
The online supplemental material includes, in respective sections: (I) a pharmacological analysis of responses to GABA and glycine in MPN neurons; (II) detailed results from tests of “apparent” versus “true” cross-desensitization; (III) detailed data on GABA- and glycine-evoked currents measured with gramicidin-perforated patches in MPN neurons; (IV) control experiments showing that estimated [Cl−]i changes do not depend on leak or voltage-gated currents; (V) data examples from cells with minimal conductance decay during 20 s in GABA and glycine; and (VI) a model of currents and [Cl−]i that includes outward Cl− transport, (VII) an evaluation of effects of solution–exchange speed on desensitizing current components, (VIII) a description of modeling changes in [Cl−]i during conventional whole cell and outside-out patch recording, and (IX) experimental data from conventional whole cell recordings. The supplemental text and Figs. S1–S7 are available at http://www.jgp.org/cgi/content/full/jgp.201110674/DC1.
RESULTS
Currents evoked by GABA and glycine
A first series of experiments was performed with amphotericin B as the perforating substance. In agreement with our previous report (Karlsson et al., 1997a), all MPN neurons tested (n = 114) responded to application of GABA as well as to glycine (Fig. 2 A). The concentration–response curves show apparent EC50 values of 16 and 104 µM, respectively (Fig. 2 A, bottom). To evoke maximal currents, 1.0 mM GABA and 1.0–3.0 mM glycine were used for the remainder of the experiments. The outward current evoked by 3.0 mM glycine at 0 mV (and with 5.4 mM Cl− in the patch pipette) reached a peak of 577 ± 127 pA and subsequently decayed with a time constant of 1,671 ± 182 ms (n = 10). The current evoked by 1.0 mM GABA under similar conditions reached a peak of 2,227 ± 393 pA and decayed with a time constant of 1,153 ± 147 ms (n = 10). A pharmacological analysis with application of common GABAA and glycine receptor blockers showed differential effects on the responses evoked by GABA and by glycine, supporting the idea that the two agonists act at separate receptors (see supplemental text, section I).
Cross-inhibition of GABA-evoked currents by pre-application of glycine and vice versa
Apparent cross-talk was demonstrated as a clear reduction in the current response to GABA by 20-s pre-application of glycine and vice versa (Fig. 2 B). This apparent “cross-desensitization” was thus qualitatively symmetric. In neurons where the currents induced by GABA and by glycine were of the same order of magnitude, the apparent cross-desensitization was also quantitatively roughly symmetric (Fig. 2 B, top). In neurons where currents induced by glycine were significantly smaller than those induced by GABA, pre-application of glycine had a smaller effect on the responses to GABA (Fig. 2 B, middle). The average reduction of the GABA-evoked current by glycine pre-application was to 42 ± 10% of the control amplitude (n = 7). In the same set of neurons, the average reduction of the glycine-evoked current by GABA pre-application was to 25 ± 3% of the control amplitude (n = 7).
A roughly similar apparent cross-desensitization was also observed when nearly symmetrical intracellular (pipette) and extracellular Cl− concentrations (145 and 144 mM, respectively) were used and inward currents were recorded at −40 mV (Fig. 2 B, bottom). Under these conditions, the average reduction of the GABA-evoked current by glycine pre-application was to 38 ± 9% of control amplitude, and the average reduction of the glycine-evoked current by GABA pre-application was to 35 ± 3% of control amplitude (n = 3). Although this suggests that neither the Cl− concentration of the patch pipette nor the Vm at which the currents are studied is critical for the occurrence of the apparent cross-desensitization, it does not rule out a contribution of changes in Cl− concentration as a cause of this phenomenon (see below).
Alternative hypotheses explaining interactive effects of GABA and glycine
Apparent interactive effects between GABA receptors and glycine receptors as described above may possibly take place because (a) of ion concentration changes caused by the current flux (hypothesis of concentration changes; Grassi, 1992); (b) these agonists bind to a common ligand-gated ion channel (hypothesis of common conductance or dual agonist sensitivity; Barker and McBurney, 1979; Baev et al., 1992; Lewis and Faber, 1993; Trombley et al., 1999; Amakhin and Veselkin, 2010); or, as several studies during later years suggest, (c) two different types of receptor channels interact (hypothesis of receptor cross-talk; receptor here meaning the whole ligand-gated channel with binding sites for either GABA or glycine; Li and Xu, 2002; Wu et al., 2002; Li et al., 2003; Breustedt et al., 2004).
Additivity of currents and conductances evoked by GABA and glycine
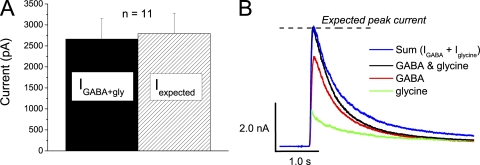
A commonly presented argument for cross-talk between currents evoked by GABA and by glycine, as well as for a conductance with dual agonist sensitivity (i.e., hypotheses (b) and (c) above), is that such currents are found to be non-additive, that is, the current evoked by coapplication of GABA and glycine is smaller than the sum of currents evoked by each agonist alone. Usually, however, the effect of pipette Rs is neglected during such comparisons, although a consequence of Rs is that the current will not increase linearly with conductance (see Materials and methods: Eqs. 6 and 8). We therefore calculated the conductances from the currents recorded at application of each agonist separately according to Eq. 7, and then the expected current at coapplication from the sum of conductances and Eq. 6, as described in Materials and methods. The peak current recorded at coapplication of 1.0 mM GABA and 3.0 mM glycine at 0 mV with standard solutions (2.7 ± 0.5 nA; n = 11) did not differ significantly (P = 0.32; Wilcoxon matched-pairs signed-ranks test) from the calculated expected current for the same neurons (2.8 ± 0.5 nA; n = 11; Fig. 3, A and B). Thus, the peak conductances activated by GABA and glycine appeared to be additive.
Figure 3.
Additivity of conductances evoked by GABA and glycine. (A) The peak current evoked by coapplication of 1.0 mM GABA and 3.0 mM glycine at 0 mV (IGABA + gly; shaded bar) does not differ significantly from the expected peak current (Iexpected; hatched bar) calculated from the sum of GABA- and glycine-evoked conductances, as described in Results. Error bars denote SEM (n = 11). (B) Example current traces evoked by 1.0 mM GABA (red) and 3.0 mM glycine (green), and coapplication of 1.0 mM GABA and 3.0 mM glycine (black), in a cell with a remaining uncompensated Rs of 2.0 MΩ. The blue curve shows the sum of currents evoked by GABA and glycine separately, and the dashed line indicates the calculated expected peak current. Note that at peak, the current at coapplication matches the sum of responses to each agonist as well as the calculated expected peak current. In cells with higher remaining uncompensated Rs, the current at coapplication may differ from the sum of responses to each agonist, but may still match the expected peak current. Note also that at some time after peak, the current at coapplication (black) is smaller than the sum of responses to each agonist (blue). The latter feature is explained by the model presented in Fig. 8. Currents were recorded in amphotericin-perforated patch mode.
“Apparent” versus “true” cross-desensitization
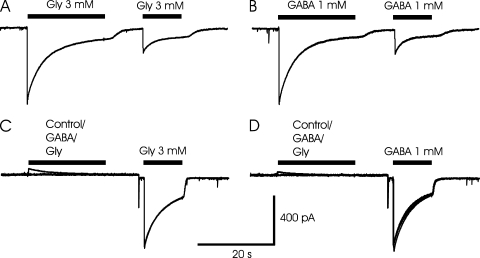
We next examined whether the apparent cross-desensitization between currents evoked by GABA and glycine reflected a “true” desensitization in the sense that the conductance of the receptor channels was less sensitive to the agonist or if the apparent cross-desensitization alternatively was a result of an altered “driving force” as a consequence of changes in Cl− concentration in the vicinity of the channels (Grassi, 1992). To clarify whether there is cross-desensitization independent of current flux and concentration changes, we tested whether any cross-desensitization could be observed when the desensitizing pre-application of ligand was made with the voltage close to the Vrev (i.e., with a negligible or no current, as found in the range of −10 to 0 mV with nearly symmetrical Cl− concentrations). Test application was made after 4–10-s washout of the pre-applied ligand and at a Vm of −40 mV. The results showed that there is little, if any, true cross-desensitization at application of GABA and glycine (Fig. 4 and supplemental text, section II, for details).
Figure 4.
Lack of true cross-desensitization between GABA and glycine-evoked currents. (A and B) Repetitive application of either glycine (A) or GABA (B) at −40 mV reveals a substantial apparent desensitization. However, when either agonist is pre-applied at −10 mV, close to the Vrev, neither true cross-desensitization nor true self-desensitization was observed in the same cell (C and D). (Note that some true self-desensitization was observed in a majority of cells.) Recordings with nearly symmetrical Cl− concentration (see Materials and methods) and pre-application at −10 mV, and test applications at −40 mV. (C and D) Test application of 3.0 mM glycine (C) and 1.0 mM GABA (D) after pre-application of control solution, 1.0 mM GABA, or 3.0 mM glycine. The three curves are superimposed. Note that the currents during the test applications are nearly identical and therefore difficult to separate by eye. (A–D) From the same neuron with currents recorded in amphotericin-perforated patch mode.
Currents measured with gramicidin-perforated patches
The results above suggested that the Cl− current during GABA or glycine application causes changes in [Cl−]i that may account for a large part or all of the apparent desensitization seen at repetitive or sequential application of these agonists. If such changes occur, they should also contribute to the time course of current (apparent desensitization) during single agonist applications. It should be noted that the above results were obtained with amphotericin B–perforated patch recordings, where [Cl−]i is expected to equilibrate with Cl− from the recording pipette. If substantial changes in [Cl−]i occur under these conditions, even larger changes may be expected when [Cl−]i is unaffected by the pipette content. To estimate the changes in [Cl−]i under such conditions, we made perforated patch recordings with gramicidin, which forms pores that are not significantly permeable to Cl− (Abe et al., 1994; Kyrozis and Reichling, 1995). Unless stated otherwise, all experiments described below were made with gramicidin as a perforating substance. To simplify quantification of cell volume and because [Cl−]i may differ in neurites and cell body, and because voltage-clamp control may be impaired in neurites, and also to simplify interpretation, cells without neurites (a majority of cells) or with neurites shorter than about one cell diameter were chosen.
The general properties of GABA- and glycine-evoked currents recorded with gramicidin as perforating substance were similar to those recorded with amphotericin B (supplemental text, section III). However, a marked difference from the recordings with amphotericin B was that, with gramicidin, recovery from the apparent desensitization was not reached within several minutes (see below).
[Cl−]i decays faster than conductance
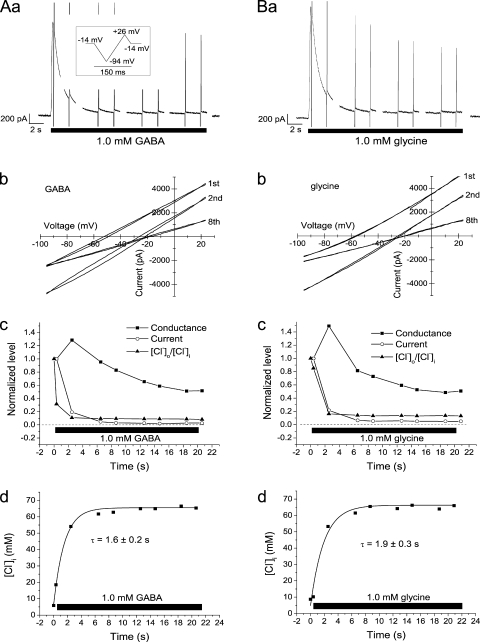
To estimate the time course of changes in [Cl−]i and their contribution to the current time course during single agonist applications, we used high-rate voltage ramps (see Materials and methods). From the current responses to these, we obtained measurements of the Vrev, giving [Cl−]i as well as the conductance (see Materials and methods). It was clear from these experiments that there were dramatic changes in [Cl−]i. Example results obtained from one cell are shown in Fig. 5. Here, [Cl−]i changed from ∼5 to ∼65 mM during the 20-s application of either 1.0 mM GABA (Fig. 5 A) or 1.0 mM glycine (Fig. 5 B). The change followed a roughly exponential time course, with a time constant of only 1.6 s for GABA (Fig. 5 A, d) and 1.9 s for glycine (Fig. 5 B, d). This change was much faster than the decay in conductance (i.e., true desensitization; Fig. 5, A, c, and B, c). At the time of the second ramp sequence (after 2.5 s in GABA), when the GABA-evoked current had declined ∼80%, [Cl−]i had increased to 900% of the resting value, from 6 to 54 mM, but the conductance reached its maximum. A slow or late increase in conductance as frequently observed here may possibly be explained by the parallel increase in [Cl−]i (see Discussion).
Figure 5.
Rapid changes in [Cl−]i during GABA and glycine application. (A and B) Currents, conductances, and [Cl−]i during application of either 1.0 mM GABA (A) or 1.0 mM glycine (B) to the same neuron. Raw currents shown in A (a) and B (a). (Gaps are a result of limitations of the sampling protocol used.) Vm = −14 mV, except during the voltage ramps. Inset shows voltage protocol during each ramp sequence. (A, b, and B, b) I-V relation for the currents recorded during the first, second, and eighth ramp sequences, as indicated. Note the large shift in Vrev and the slight increase in slope from the first to the second ramp sequence. (A, c, and B, c) Comparison of the time course for current, conductance, and the ratio [Cl−]o/[Cl−]i. (The ratio was used to plot a decaying function of time to simplify comparison.) [Cl−]o/[Cl−]i normalized to that before agonist application, current, and conductance to the values at the first ramp sequence, close to peak current. (A, d, and B, d) Time course of [Cl−]i, computed as described in Results. Smooth curves are fitted exponentials with time constants of 1.6 s (A, d) and 1.9 s (B, d). Currents were recorded in gramicidin-perforated patch mode (A and B).
The change in estimated [Cl−]i was not associated with any change in leak current or voltage-gated current (supplemental text, section IV). There was also no detectable change in cell shape. It was thus clear that the increase in [Cl−]i, and not the decay of conductance, was the main determinant of the current decay. Similar results as for GABA were obtained for glycine. Similar results were also obtained in several cells, although the relative importance of the change in [Cl−]i and the change in conductance varied between cells. Thus, on average, the current evoked by 20-s application of 1.0 mM GABA to 13 neurons decayed by 95 ± 1% with a time constant of 1.4 ± 0.1 s, whereas [Cl−]i increased from 8.8 ± 0.4 mM to 64 ± 3 mM with a time constant of 2.1 ± 0.3 s, and the conductance decayed by 73 ± 5% with a time constant of 6.4 ± 0.7 s. (Here, and in the next description, the exponential fit of the conductance time course included only the peak value and the subsequent decay. Thus, the rising phase was excluded. The given mean time constant underestimates the time required for decay because in a few cells, the decay was too slow to be fitted by an exponential function.)
The current evoked by 1.0 mM glycine in seven neurons decayed by 95 ± 1% with a time constant of 1.9 ± 0.2 s, whereas [Cl−]i increased from 8.7 ± 0.1 mM to 65 ± 2 mM with a time constant of 3.1 ± 0.5 s, and the conductance decayed by 55 ± 6% with a time constant of 6.4 ± 1.0 s. Notably, there were cells where the GABA- or glycine-evoked conductance did not decay significantly, not even below the level at the time of peak current, during the 20-s agonist application (supplemental text, section V).
A series of control experiments of the type described above was performed with the GABAB receptor antagonist saclofen (100 µM) added to the external solution to exclude possible contribution of GABAB receptors to the current responses to GABA. The analyzed parameters, peak current and decay time constants for current, conductance, and [Cl−]o/[Cl−]i, did not differ significantly from recordings without saclofen in five neurons studied. Similarly, the same parameters analyzed from another series of control experiments with Ca2+-free external solution (Co2+ substituted for Ca2+ and 2.3 mM EGTA added) to minimize spontaneous release of transmitter from remaining nerve terminals on the isolated cells did not differ significantly from the results with standard extracellular solution (seven neurons studied with 1.0 mM GABA; five neurons with 1.0 mM glycine).
Estimates of conductance and [Cl−]i obtained from “double patch” recordings
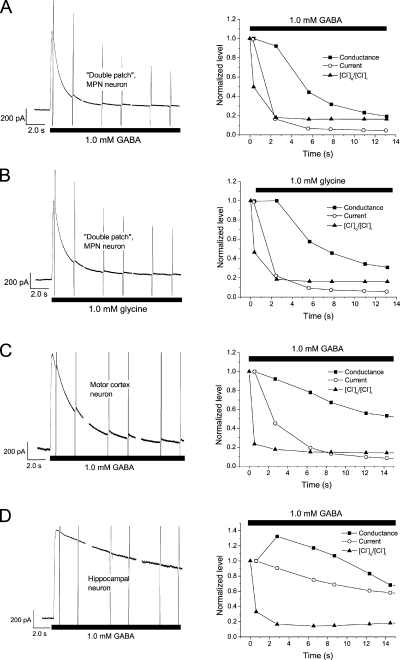
The conductance calculated from the currents recorded during the voltage ramps described above depends to some extent on the estimate of Rs and its effect on Vm. To provide an estimate of membrane conductance that does not depend on the accuracy of the estimated Rs value, we performed a few control experiments with two gramicidin-containing patch pipettes attached to the same neuron. While the first pipette was used for applying voltage ramps and current recording as described above, the second pipette was used to directly record the membrane voltage (see Materials and methods). These “double patch” recordings thus enabled estimates of conductance from the recorded current and the recorded voltage with the effect of Rs on voltage being bypassed. The method also provided an independent estimate of Rs obtained from command (pipette) potential, recorded Vm, and membrane current (Eq. 5). Because the method was technically challenging (sealing the second pipette usually destroyed the seal between the cell membrane and the first pipette), we only recorded four cells, which were exposed to glycine as well as to GABA. Although the mean time constants describing the decay of current and conductance for these four cells differed somewhat from the corresponding values obtained from the cells studied with a single patch pipette above, this was likely a result of the small sample: The values obtained with double patch recording were within the range for those obtained with a single pipette, and a statistically significant difference could not be proven. Importantly, there was a clear mismatch between current decay (time constant 1.3 ± 0.2 s for glycine and 1.5 ± 0.5 s for GABA) and conductance decay (5.6 ± 0.5 s for glycine and 3.8 ± 0.6 s for GABA; Fig. 6, A and B). Further, [Cl−]i increased dramatically from 10 ± 5 mM to 64 ± 4 mM at glycine application and from 13 ± 2 mM to 60 ± 2 mM at GABA application (during 20-s exposure to 1.0 mM of the agonist).
Figure 6.
Changes in [Cl−]i and mismatch between current and conductance, seen with double patch recording from MPN neurons and with “single patch” recording from cortical and hippocampal neurons. (A and B) Current, conductance, and ratio [Cl−]o/[Cl−]i from an MPN neuron recorded with two patch pipettes for direct measurement of Vm as well as current, during application of either 1.0 mM GABA (A) or 1.0 mM glycine (B). (C and D) Parameters as in A and B recorded (with a single patch pipette) upon application of 1.0 mM GABA to a pyramidal-shaped neuron from motor cortex, layer V (C), and a neuron from hippocampal area CA1–CA2 (D). Note the dramatic changes in [Cl−]o/[Cl−]i and the mismatch between current and conductance in A–D. Voltage ramp protocol and normalization as in Fig. 5. Gramicidin-perforated patch mode used in A–D.
[Cl−]i changes and mismatch between current and conductance in neurons from the motor cortex and from the hippocampus
To clarify whether the observed [Cl−]i changes and the mismatch between recorded current and conductance were phenomena specific to the MPN neurons studied, we performed additional recordings with gramicidin as perforating substance and with the voltage ramp protocol described in the previous section, but applied to pyramidal-shaped neurons from layer V of the motor cortex and to neurons from hippocampal area CA1–CA2. The cells were dissociated from rat brain slice preparations as described for the MPN neurons. These neurons were considerably larger than the MPN neurons, with a membrane capacitance of 14 ± 3 pF (n = 4) and 9.9 ± 0.9 pF (n = 5), respectively. Thus, their membrane area was likely ∼4.8 times and ∼3.5 times larger than the mean area of MPN neurons, and their volumes presumably ∼11 times and ∼7 times that of MPN neurons.
Substantial changes in [Cl−]i and a considerable mismatch between current and conductance in response to 1.0 mM GABA were observed in all studied neurons from the motor cortex and from the hippocampus. In neurons from the motor cortex, [Cl−]i increased with a time constant of 1.0 ± 0.2 s to 43 ± 9 mM, and the current decayed with a time constant of 2.7 ± 0.4 s, but the conductance (peak, 143 ± 11 nS) decayed with a time constant of 6.2 ± 2.5 s (n = 4; Fig. 6 C). Similar observations (conductance decay time constant of 5.9 ± 1.4 s; [Cl−]i rise with time constant of 1.7 ± 0.6 s to 54 ± 8 mM) were made in the hippocampal neurons (n = 5), although the peak conductance (62 ± 27 nS) was smaller and the current decay slower (τ = 3.8 ± 0.9 s; Fig. 6 D). It should be emphasized that the time constant for the conductance decay was obtained from the best mono-exponential fit of the decay phase and underestimates the time needed for decay. This is because of a nonexponential time course and sometimes even a slow increase, during several seconds, before the decay (e.g., see Fig. 6 D, right). The findings show that the large changes in [Cl−]i and the mismatch between current and conductance are not unique for MPN neurons but may be found in other, considerably larger neuron types. Thus, the observed phenomena may reflect properties that are relatively common among central neurons from different brain regions.
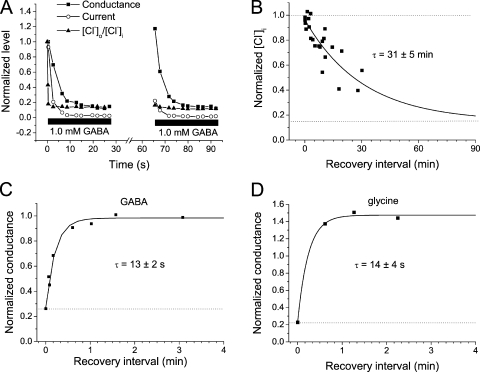
Recovery of current, conductance, and [Cl−]i in MPN neurons
After the decay of current evoked by GABA or glycine, full recovery was usually obtained when amphotericin B–perforated patch recordings were used and there was a washout interval of ∼1 min before a second agonist application. This was in contrast to the recordings with gramicidin as perforating substance, where full recovery was not, in general, obtained within 10 min: In only one of five MPN neurons tested did the current recover within ∼10 min after a preceding 20-s application of 1.0 mM GABA. On average, the recovery in these cells was to 62 ± 14% of the peak amplitude at the first GABA application (measured after 9–11 min). The recovery of conductance as measured from voltage ramps, however, was much quicker, with a time constant of only 13 ± 2 s (n = 8) for GABA and 14 ± 4 s (n = 3) for glycine (Fig. 7). However, recovery of [Cl−]i was very slow. The fitted exponential curve had a time constant of 31 ± 5 min (n = 8; data combined for 1.0 mM GABA and 1.0 mM glycine; Fig. 7 B). Thus, it is clear that under these conditions, the slow recovery of [Cl−]i, which in gramicidin recordings should reflect the cellular capacity for outward Cl− transport, is limiting the degree of current recovery.
Figure 7.
Conductance recovers quicker than [Cl−]i and current. (A) Conductance, current, and [Cl−]o/[Cl−]i during two sequences of GABA application, separated by a recovery interval of 38 s, from one neuron. [Cl−]i normalized to that before agonist application, current, and conductance to the values at the first ramp sequence, close to peak current during the first application. Note that conductance recovered fully during the 38-s interval, whereas there was only slight recovery of current and very little of [Cl−]i. Vm = −14 mV; GABA concentration, 1.0 mM. (B) [Cl−]i, normalized to that after 20 s in 1.0 mM GABA or 1.0 mM glycine, plotted versus the recovery interval without agonist. Lower dashed line corresponds to the [Cl−]i (∼9 mM) before agonist application. The smooth curve is a fitted exponential with a time constant of 31 min. Data are from 10 neurons. (C and D) Conductance at a second application of 1.0 mM GABA (C) or 1.0 mM glycine (D), normalized to that at peak current during a first 20-s agonist application and plotted versus the recovery interval. Smooth curves are fitted exponentials with time constants of 13 s (C) and 14 s (D). Data are from eight (C) and three (D) neurons. Gramicidin-perforated patch mode used in A–D.
For experimental purposes, however, the rapid changes in [Cl−]i during agonist application could be used to quickly alter [Cl−]i. After choosing the right voltage from Eq. 3, application of GABA or glycine for a few seconds quickly altered [Cl−]i to the desired value. When the recovery processes were not analyzed, this method was generally used to set [Cl−]i at ∼9 mM before applying agonist to neurons studied with gramicidin as the perforating substance. This concentration was chosen because [Cl−]i obtained from Eq. 3 and the Vrev of sIPSCs in four cells was 9.1 ± 1.6 mM.
Theory: Equivalent space
The above results clearly show that rapid changes in [Cl−]i occur during application of GABA and glycine, and that these changes largely determine the time course of currents. Are such changes quantitatively consistent with the movement of Cl− during the currents recorded and with the volumes that may be affected by these ions? To answer this question, we first estimated the “equivalent space,” i.e., a theoretical homogenous cytosolic volume that may account for the observed current decay, if it is caused by changes in [Cl−]i only. For this, we analyzed the GABA-evoked currents in two cells that did not show any true desensitization (no reduction in peak current when agonist was pre-applied close to VCl), and therefore all current decay was likely a consequence of changes in [Cl−]i. The type of experiment was as in Fig. 4 (with amphotericin B–perforated patches and 145 mM Cl− in the pipette). First, VCl was estimated from the Vrev of currents without and with pre-application of 1.0 mM GABA. From this, [Cl−]i before and after GABA application was calculated (from Eq. 3), and values of the change in [Cl−]i (Δ[Cl−]i) of −50 and −44 mM, respectively, for the two cells were obtained. The charge transfer (Q) during pre-application was subsequently measured (by integrating the current over time), and the equivalent space (vequ) where this charge transfer would cause the estimated changes in concentration was calculated from
| (15) |
The result was vequ = 798 and 992 µm3, respectively, for the two cells. For the first of these cells, the procedure was repeated for currents evoked by 3.0 mM glycine, giving vequ = 895 µm3. These values correspond to 45% (51% for glycine-evoked currents) and 56% of the total cell volume (in both cells above calculated from an estimated average radius of 7.5 µm and a spherical shape). These results thus suggest that if the change in [Cl−]i caused by the recorded currents is evenly distributed in roughly 50% of the cell volume, this would account for the observed changes in Vrev and reduction in current after pre-application of agonist. The cytosol has been estimated to occupy roughly 50% of the total cell volume (Alberts et al., 2008), and thus concentration changes evenly spread throughout the entire cytosol may account for the observed effects of pre-application on current amplitudes at subsequent agonist applications.
Theory: Model
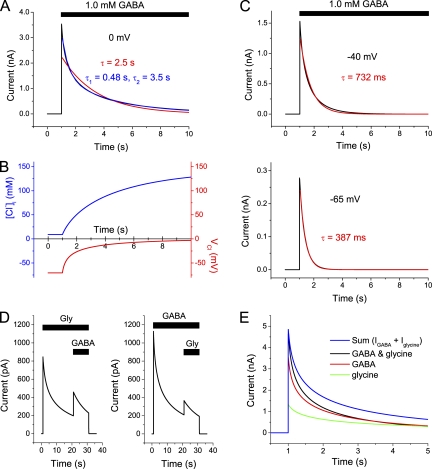
Although several previous studies have shown that changes in [Cl−]i to some degree may contribute to the decay of GABA-evoked currents or potentials (Huguenard and Alger, 1986; Akaike et al., 1987; Thompson and Gähwiler, 1989a,b; Grassi, 1992; Le Foll et al., 2000), a quantitative theoretical framework on the expected contribution of altered [Cl−]i is missing. The above calculations of an equivalent space that corresponds roughly to the expected cytosolic volume show that the magnitude of charge transfer during GABA- or glycine-activated currents is consistent with very large changes in [Cl−]i, which may explain the reduction in current at repeated agonist application. To examine whether the observed time course of current decline (“apparent desensitization”) in the presence of agonist was also consistent with this idea, and to be able to predict the time course of current under various conditions, we constructed a simplified computational model that takes changes in [Cl−]i into account. The basic idea was to use a conductance without true desensitization and, taking the cytosolic equivalent space into account, numerically compute the expected changes in [Cl−]i, “driving force” (Vm − VCl), and current according to Eqs. 10–14 (see Materials and methods). (The equivalent space was assumed to be 50% of the cell volume.) It was obvious that the computed GABA-evoked currents decayed with approximately the same time course as observed experimentally, although there was no decay in conductance incorporated in the equations used (Fig. 8). A notable finding was that at more negative voltages, the decay was faster although the currents were smaller (Fig. 8, A and C). At −65 mV, it was roughly exponential with a time constant of only 387 ms. This implies that if the cells are exposed to millimolar concentrations of GABA or glycine for a few hundred of milliseconds, changes in [Cl−]i may be of importance for the time course of currents also near physiological resting potentials.
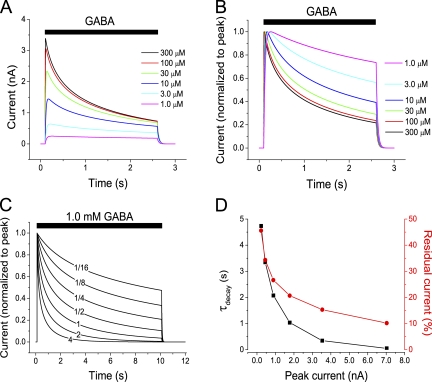
Figure 8.
Computed currents decay rapidly in the absence of true desensitization. (A) Computed current evoked by 1.0 mM GABA in the absence of decay in conductance. Vm = 0 mV. Time constants for fitted mono-exponential (red) and bi-exponential (blue), as shown. (B) Computed change in [Cl−]i (blue) and VCl (red) during the current in A. (C) Computed currents, with superimposed fitted mono-exponentials. As in A, except voltage = −40 mV (top) and −65 mV (bottom). Note the faster decay at more negative voltages. (D) Apparent cross-desensitization between GABA- and glycine-evoked currents, expected from changes in [Cl−]i, under conditions corresponding to those used experimentally for the records in Fig. 2 B (top). Maximum conductances were set to match those observed without pre-applied agonist, and the cell was approximated by a sphere of radius of 9.0 µm. (E) Computed currents evoked by 1.0 mM GABA (red), 3.0 mM glycine (green), and coapplication of GABA and glycine (black) at 0 mV, without true desensitization. Maximum conductances for GABA and glycine were set to match the experimental responses to each agonist illustrated in Fig. 3 B. No adjustment of kinetics was made. Note that after peak current, there is a deviation of current at coapplication (black) from the sum of responses to each agonist (blue), as experimentally observed in Fig. 3 B. Cell approximated by a sphere of radius of 5.5 µm.
Modeling the expected apparent cross-desensitization as a result of changes in [Cl−]i under conditions as experimentally observed and shown in Fig. 2 B (top) was made by introducing a simplified conductance to glycine (see Materials and methods). Although the model in many respects is very crude, it clearly shows that in the absence of any decrease in conductance, we should expect a marked cross-dependence (apparent cross-desensitization) as a consequence of the Cl− flux and the expected cytosolic volume (Fig. 8 D). Remarkably, the model also explained the time course of current at coapplication of GABA and glycine, where the current matched the sum of responses to each agonist at the time of peak but thereafter was smaller than this sum (Fig. 3 B). This is exactly what is to be expected from the change in [Cl−]i, as shown by the computed currents in Fig. 8 E.
Expected [Cl−]i changes explain correlations between peak current and the rate and extent of decay
In many experimental situations, a positive correlation between peak current amplitude and the rate and extent of desensitization has been reported: This is the case for (a) the increased peak currents at higher agonist concentration (Oh and Dichter, 1992), as well as for (b) currents of variable amplitude at constant agonist concentration (Legendre et al., 2002), even for well-defined receptor types (heterologously expressed α1β glycine receptors; Pitt et al., 2008). This correlation between peak current amplitude and current decay properties also seems to be present (c) when receptors of different subunit composition are compared. Thus, GABAA receptors thought to contribute to “tonic” conductances (receptors with α4 or α6 subunits in combination with δ subunits, or receptors containing α5 subunits) show less or slower desensitization than other GABAA receptors but also, in most comparative studies, appear to give rise to smaller currents than other GABAA receptors (Saxena and Macdonald, 1996; Haas and Macdonald, 1999; Bianchi and Macdonald, 2002; Bianchi et al., 2002; Brown et al., 2002; Wohlfarth et al., 2002; Caraiscos et al., 2004). Finally, (d) the increased magnitude of GABA-evoked current, when subject to modulation by steroids, is also accompanied by faster desensitization (Bianchi et al., 2002; Wohlfarth et al., 2002). The present finding that changes in [Cl−]i do contribute substantially to the current decay suggests that changes in [Cl−]i may contribute to or completely account for the observed correlation between peak current amplitude and current decay properties, for comparisons of the types (a–d) described above. This is because larger currents imply larger changes in [Cl−]i. We verified that our model without true desensitization reproduced the faster current decay that is seen experimentally (compare Fig. 2 A, top and middle) when agonist concentration is raised (Fig. 9, A and B) as well as when the conductance is raised at constant agonist concentration (Fig. 9 C), giving rise to a correlation between the peak current and the rate and extent of current decay (Fig. 9 D). Thus, a correlation between peak current amplitude and the apparent desensitization, as observed under a wide range of experimental conditions, should be expected if the apparent desensitization is an artifact because of [Cl−]i changes.
Figure 9.
The rate and extent of current decay is correlated to conductance and current amplitude. (A) Computed currents, as for Fig. 8 A, but with the indicated concentrations of GABA applied for 2.5 s. (B) Currents as in A, but normalized to peak current to facilitate comparison of decay rate. Note the faster decay at higher GABA concentration. (C) Currents as in B, but with 1.0 mM GABA applied for 10 s, and with a variable maximum conductance. The maximum conductance for each trace is given relative to the mean conductance (54 nS) experimentally observed at 1.0 mM GABA. (D) Relation between decay time constant, residual current after 10 s in GABA, and the peak (absolute) current for computations similar to those used for C. No true desensitization included in the model (A–C).
Including outward Cl− transport in the model
As implicated by the slow recovery of [Cl−]i (Fig. 7 B), the outward transport of Cl− after the influx during GABAA or glycine receptor activation was slow. Thus, incorporating outward Cl− transport in our computational model did not significantly change the time course of current or of [Cl−]i during the 20-s agonist applications modeled (supplemental text, section VI).
Do changes in [Cl−]i contribute to the current decay in conventional whole cell and outside-out patch recordings?
Our findings above show that the recorded current during GABAA and glycine receptor activation is expected to decay rapidly also when the conductance does not decay. This raised the question of the extent to which the apparently rapid desensitization seen in other studies is an artifact. Computations that included the time course of solution exchange showed that, in the present work, it is not likely that rapid components of desensitization remained undetected because of insufficient speed of solution exchange (supplemental text, section VII). Because most previous studies of desensitization were made with conventional whole cell or outside-out patch recording techniques, we also considered the effects of diffusional Cl− exchange between the cytosol and recording pipette under such conditions. This was made by including in the model the equations derived by Pusch and Neher (1988) and by Mathias et al. (1990) to describe the diffusional exchange between small cells and patch pipettes (supplemental text, section VIII). In addition, but in contrast to when the gramicidin-perforated patch technique is used, a significant fraction of the current across the cytosol–pipette intersection may be carried by Cl− moving into or out from the pipette. This was also taken into account in the model by using the expected transference number for Cl− (supplemental text, section VIII). Fig. 10 shows that changes in [Cl−]i are expected to affect the currents dramatically, even in whole cell or outside-out patch recordings: A decay of current that may be mistaken for desensitization is caused by the change in [Cl−]i. It should be noted that this decay will be more rapid when the radius of the cell/patch is smaller (Fig. 10 B), thus potentially explaining the more rapid desensitization seen with outside-out patches compared with whole cells (e.g., see Bianchi and Macdonald, 2002). Considerable changes in [Cl−]i and a mismatch between current and conductance during conventional whole cell recording were also observed experimentally (supplemental text, section IX).
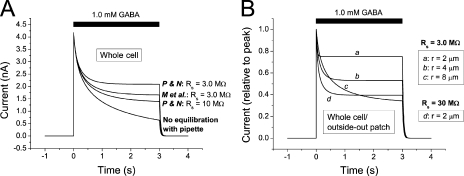
Figure 10.
Computed currents in whole cell and outside-out patch mode. (A) Computed current responses to 1.0 mM GABA in the absence of desensitization, with diffusional exchange between [Cl−]i and [Cl−] in pipette according to equations by Pusch and Neher (1988; marked P and N), Mathias et al. (1990; marked M et al.), and without any diffusional exchange (bottom curve). Cell radius, 6.2 µm. Rs between pipette and cell, as indicated. (B) Computed responses to 1.0 mM GABA with equilibration according to Mathias et al. (1990) for cell radii, r, as indicated. Note the faster decay but higher relative steady current (normalized to peak current) at smaller radius. Maximum conductance per unit area constant for all simulations. Rs as indicated. For all computations of diffusional exchange (A and B), Cl− movement between cytosol and pipette as a consequence of the electric current was also included. (See supplemental text, section VIII, for equations.) Initial [Cl−]i was as in the pipette solution, 5.4 mM.
DISCUSSION
Here, we show that activation of GABAA or glycine receptors in central neurons may be accompanied by dramatic changes in [Cl−]i, and that such concentration changes may significantly influence the current through the receptor channels. We provide experimental as well as theoretical evidence that such changes in [Cl−]i cause the apparent cross-desensitization between responses to GABA and glycine. In addition, we show that the decay of current in the presence of either glycine or GABA is largely determined by changes in [Cl−]i and that a true desensitization, meaning a decay of conductance, plays a minor role only. Using a computational model, we show that rapid changes of [Cl−]i are to be expected under a variety of recording conditions when the Cl− flux and cytosolic volume are taken into account. We also show experimentally that similar changes occur in several types of neuron. The findings imply that a reevaluation of the desensitization properties of GABAA and glycine receptors may be needed: True desensitization may be considerably slower than previously thought and in some cases possibly absent.
It may be expected that ion concentration changes of a similar nature should take place also when other types of large conductances are activated for long durations and the affected volumes are small. Indeed, it was reported at an early stage, by Frankenhaeuser and Hodgkin (1956), that a decline in voltage-gated K+ current was likely a consequence of K+ accumulation outside the axonal membrane.
Cross-talk
Earlier mechanistic explanations for cross-talk between glycine receptors and GABA receptors are diverse. Although one of the early reports suggested changes in [Cl−]i as an underlying cause (Grassi, 1992), other explanations have been dominating. Thus, several authors suggest that the two agonists may activate a common conductance (Barker and McBurney, 1979; Baev et al., 1992; Lewis and Faber, 1993; Trombley et al., 1999; Amakhin and Veselkin, 2010). A majority of later papers, however, propose some communication, other than that mediated by Cl− flux, between two different receptor types (Li and Xu, 2002; Wu et al., 2002; Li et al., 2003; Breustedt et al., 2004). However, the arguments against changes in [Cl−]i are not convincing because in none of the above studies was [Cl−]i properly estimated at different times during GABA/glycine application and with contribution of nonspecific conductances subtracted.
An argument for cross-talk that is often presented and may first seem inconsistent with changes in [Cl−]i is the non-additivity of current responses to GABA and to glycine (Trombley et al., 1999; Li and Xu, 2002; Wu et al., 2002; Li et al., 2003; Breustedt et al., 2004; Amakhin and Veselkin, 2010). Our model predicts that at saturating agonist concentrations, the currents should be additive at the time of peak current. Why then are non-additive peak currents often observed? A likely explanation is that the Rs of the recording pipette introduces an error that will cause non-additivity of currents through independent conductances (see Eqs. 4–8). Even after Rs compensation, the remaining Rs will affect the recorded currents, especially when the conductance is large.
This study does not only demonstrate that dramatic changes in [Cl−]i and Vrev do indeed occur. The theoretical considerations show that, taking the current amplitudes and cytosolic volumes into account, dramatic changes in [Cl−]i must occur, unless some compensatory mechanism counteracts such changes very rapidly. The transfer rate of ion transport mediated by the ion channels of GABAA and glycine receptors is several orders of magnitude higher than for carrier proteins (Hille, 2001). Thus, the carriers would have to outnumber the ion channels by at least two orders of magnitude to account for such rapid compensation.
Determinants of current decay in the presence of agonist
Desensitization is a hallmark of most well-studied ligand-gated channels and essential for many features of synaptic transmission. Several early studies (Huguenard and Alger, 1986; Akaike et al., 1987; Thompson and Gähwiler, 1989b; Grassi, 1992; see also Le Foll et al., 2000) showed that changes in [Cl−]i may contribute to current decay at GABAA or glycine receptor activation. Nevertheless, in a majority of studies, current decay in the presence of agonist is taken to represent desensitization, and changes in [Cl−]i are not considered and the conductance is not directly measured. Although we do not exclude the possible presence of rapid desensitization of other receptor subtypes or in other conditions, this work shows that desensitization of GABA and glycine receptors in several types of central neurons is much slower than the decay of current. To our surprise, we found that for several cells, there was no or very little decay of conductance during 20 s of agonist application. Remarkably, this was true for GABA as well as for glycine. Thus, it is clear that there are GABAA and glycine receptors that allow for a strong, long-lasting action on neuronal signaling.
It may be noted that we frequently observed a rise in conductance during a time interval between several hundred milliseconds and a few seconds after the start of ligand application (see Figs. 5, A, c, and B, c, and 6 B, right). This rise is likely to, at least partly, be a result of the parallel rise in [Cl−]i: For a constant Cl− permeability, the constant field equation (Goldman, 1943; Hodgkin and Katz, 1949) predicts that the conductance should rise with [Cl−]i (e.g., to 152% when [Cl−]i changes between ∼18 and 54 mM, as between the two first conductance estimates in Fig. 5 A, c, and when conductance is measured as described in Materials and methods).
Importantly, the computations made on the basis of the theoretical framework presented showed that similar changes in [Cl−]i are to be expected from the Cl− flux and cytosolic volume under a variety of recording conditions, including conventional whole cell and outside-out patch recording. It should be noted that in the latter conditions, the pipette and cytosolic volumes cannot be expected to be in equilibrium when Cl− currents are evoked by GABA or glycine. This is because equilibration, even with a low-resistance patch pipette, according to available empirical evidence and theory, is slow compared with the kinetics of GABA- and glycine-evoked currents. This raises the possibility that the fast desensitization observed in the majority of studies where [Cl−]i and conductances were not directly measured may to some extent be an artifact. If this is the case, the rate and extent of current decay (apparent desensitization) should be correlated to the current magnitude also in isolated membrane patches. Further, desensitization should be considerably smaller or absent when kinetics is obtained from single-channel dwell times rather than from current amplitudes. Remarkably, both these predictions were fulfilled in a recent analysis of heterologously expressed α1β glycine receptors: Currents in “macropatches” showed a variable but prominent desensitization that was correlated to peak current amplitude, but “single-channel recordings were well described by a scheme that did not include any desensitization” (Pitt et al., 2008). Although not recognized by Pitt et al. (2008), it is striking that this is exactly what should be expected if current decay is a result of changes in Cl− concentration and not to true desensitization. Thus, it seems likely that, in many cases, earlier interpretations of channel kinetics, including drug effects on kinetics, may be mistaken.
From the reasoning above, it seems likely that very slowly desensitizing or nondesensitizing glycine receptors as well as GABAA receptors may be more common than so far recognized. Such slowly desensitizing receptors may be especially important for tonic inhibition (compare Mtchedlishvili and Kapur, 2006; Lagrange et al., 2007). For MPN neurons, where all fast inhibitory postsynaptic currents are blocked by GABAA receptor blockers (Hoffman et al., 1994; Haage et al., 1998; Malinina et al., 2005; this study), the possibility that glycine, taurine, or β-alanine is released nonsynaptically from glial cells (Mori et al., 2002; Dopico et al., 2006) and act at extrasynaptic receptors may suggest a functional role for glycine receptors in these cells.
Similar changes in [Cl−]i that occur in the continued presence of agonist, although likely smaller, may also be expected during repetitive synaptic activation. Indeed, even with sharp microelectrodes or conventional whole cell recording techniques, which are expected to disturb the cytosolic ion composition considerably, reduction in GABA-mediated synaptic responses as a result of altered VCl during repetitive synaptic activation has been recorded (Thompson and Gähwiler, 1989a; Ling and Benardo, 1995; Chub and O’Donovan, 2001). Possibly, such changes may be larger when the cytosol is less affected by the recording techniques.
Slow restoration of [Cl−]i provides a basis for interactive effects
This study showed that the recovery of conductance after desensitization occurs with a time constant of ∼10 s (13 s for GABA and 14 s for glycine). This is in good agreement with earlier reports (Jones and Westbrook, 1995; Le Foll et al., 2000). On the contrary, in this study, restoration of the altered [Cl−]i necessary for current recovery was extremely slow when equilibration with pipette Cl− was prevented by gramicidin-perforated patch recordings, with a time constant of ∼1/2 h. Thus, the effects of intense GABAergic or glycinergic stimulation may be expected to induce dramatic and long-lasting changes in the response properties of the cell. These effects provide the basis for “cross-talk” between all signaling systems that depend on [Cl−]i, e.g., between responses of GABAA receptors and glycine receptors (apparent cross-desensitization). These effects thus differ from true desensitization in that (a) they may be much more long-lasting, and (b) they will not be limited to responses mediated by the same receptors that were recently activated, but will be “sensed” by all receptors in contact with the cytosolic space where Cl− equilibrates.
GABA/glycine receptor activation to alter [Cl−]i
A previously unrecognized possibility, implied by the present findings, is that prolonged GABAA or glycine receptor activation may be used if rapid changes of [Cl−]i are advantageous for neuronal signaling. When the Vm is determined mainly by other conductances, GABAA or glycine receptor activation for a few seconds will adjust [Cl−]i roughly in accordance with a VCl corresponding to that potential. Thus, we may speculate that the same method as experimentally used to set [Cl−]i may possibly be used by the nervous system.
Changes in [Cl−]i occurring at a completely different time scale, during individual development, are known consequences of altered expression of Cl− transporters and are thought to play crucial roles for signaling in the central nervous system, determining, e.g., whether GABAA receptor activation will cause excitation or inhibition (Rivera et al., 1999; Ben-Ari, 2002). There is also evidence that more rapid changes in [Cl−]i, albeit slower and smaller than those reported here, may contribute to disease. Intriguingly, activity-induced elevation of [Cl−]i may be a crucial step in the induction of epileptic activity (Khalilov et al., 2003) as well as of neuropathic pain (Coull et al., 2003). Elevated [Cl−]i may also accompany deafferentation (Vale and Sanes, 2000) and ischemia (Schwartz-Bloom and Sah, 2001). The maintenance of such conditions has been attributed to changes in Cl− transporter activity (e.g., see Huberfeld et al., 2007). Although down-regulation of the K-Cl cotransporter KCC2 may take place at a surprising rate, the time constant is still ∼10 min or longer (Rivera et al., 2004). The present findings lead us to the speculation that direct influx of Cl− through slowly or nondesensitizing GABAA receptors, or possibly glycine receptors, may contribute to the induction or maintenance of such pathological conditions by altering [Cl−]i in a time scale of seconds or shorter.
Conclusions
In conclusion, this work shows that cross-talk, in the form of apparent cross-desensitization, between GABAA receptors and glycine receptors in MPN neurons from rat depends on the changes in [Cl−]i that follow upon receptor activation. We also show that such changes, in several types of central neurons, are larger and quicker than previously recognized, are to be expected if current amplitude and cytosolic volumes are considered, and are the main determinants of current decay at prolonged activation of either GABAA receptors or glycine receptors. Thus, true desensitization, meaning a decay of conductance, plays a minor role only, and may in some cases be virtually absent even during 20-s application of either GABA or glycine. The changes in [Cl−]i, which may be explored by using the simple theoretical framework presented, are likely to be important for neuronal information processing.
Acknowledgments
This work was supported by the Swedish Research Council (project no. 21401), Gunvor och Josef Anérs stiftelse, the Royal Swedish Academy of Sciences, and Umeå University.
Angus C. Nairn served as editor.
Footnotes
Abbreviations used in this paper:
- [Cl−]i
- intracellular Cl− concentration
- GABA
- γ-aminobutyric acid
- MPN
- medial preoptic nucleus
- Rs
- series resistance
- sIPSC
- spontaneous inhibitory postsynaptic current
- VCl
- chloride equilibrium potential
- vequ
- equivalent cytosolic volume
- Vm
- membrane potential
- Vrev
- reversal potential
References
- Abe Y., Furukawa K., Itoyama Y., Akaike N. 1994. Glycine response in acutely dissociated ventromedial hypothalamic neuron of the rat: new approach with gramicidin perforated patch-clamp technique. J. Neurophysiol. 72:1530–1537 [DOI] [PubMed] [Google Scholar]
- Akaike N., Inomata N., Tokutomi N. 1987. Contribution of chloride shifts to the fade of γ-aminobutyric acid-gated currents in frog dorsal root ganglion cells. J. Physiol. 391:219–234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberts B., Johnson A., Lewis J., Raff M., Roberts K., Walter P. 2008. Molecular Biology of the Cell. Fifth edition Garland Science, New York: 1268 pp [Google Scholar]
- Amakhin D.V., Veselkin N.P. 2010. Characteristics and interaction of GABAergic and glycinergic processes in frog spinal cord neurons. Neurosci. Behav. Physiol. 40:557–564 10.1007/s11055-010-9297-1 [DOI] [PubMed] [Google Scholar]
- Baev K.V., Rusin K.I., Safronov B.V. 1992. Primary receptor for inhibitory transmitters in lamprey spinal cord neurons. Neuroscience. 46:931–941 10.1016/0306-4522(92)90195-8 [DOI] [PubMed] [Google Scholar]
- Barker J.L., McBurney R.N. 1979. GABA and glycine may share the same conductance channel on cultured mammalian neurones. Nature. 277:234–236 10.1038/277234a0 [DOI] [PubMed] [Google Scholar]
- Ben-Ari Y. 2002. Excitatory actions of gaba during development: the nature of the nurture. Nat. Rev. Neurosci. 3:728–739 10.1038/nrn920 [DOI] [PubMed] [Google Scholar]
- Bianchi M.T., Macdonald R.L. 2002. Slow phases of GABA(A) receptor desensitization: structural determinants and possible relevance for synaptic function. J. Physiol. 544:3–18 10.1113/jphysiol.2002.020255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianchi M.T., Haas K.F., Macdonald R.L. 2002. α1 and α6 subunits specify distinct desensitization, deactivation and neurosteroid modulation of GABAA receptors containing the δ subunit. Neuropharmacology. 43:492–502 10.1016/S0028-3908(02)00163-6 [DOI] [PubMed] [Google Scholar]
- Breustedt J., Schmitz D., Heinemann U., Schmieden V. 2004. Characterization of the inhibitory glycine receptor on entorhinal cortex neurons. Eur. J. Neurosci. 19:1987–1991 10.1111/j.1460-9568.2004.03266.x [DOI] [PubMed] [Google Scholar]
- Brown N., Kerby J., Bonnert T.P., Whiting P.J., Wafford K.A. 2002. Pharmacological characterization of a novel cell line expressing human α4β3δ GABAA receptors. Br. J. Pharmacol. 136:965–974 10.1038/sj.bjp.0704795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caraiscos V.B., Elliott E.M., You-Ten K.E., Cheng V.Y., Belelli D., Newell J.G., Jackson M.F., Lambert J.J., Rosahl T.W., Wafford K.A., et al. 2004. Tonic inhibition in mouse hippocampal CA1 pyramidal neurons is mediated by α5 subunit-containing γ-aminobutyric acid type A receptors. Proc. Natl. Acad. Sci. USA. 101:3662–3667 10.1073/pnas.0307231101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chub N., O’Donovan M.J. 2001. Post-episode depression of GABAergic transmission in spinal neurons of the chick embryo. J. Neurophysiol. 85:2166–2176 [DOI] [PubMed] [Google Scholar]
- Coull J.A.M., Boudreau D., Bachand K., Prescott S.A., Nault F., Sík A., De Koninck P., De Koninck Y. 2003. Trans-synaptic shift in anion gradient in spinal lamina I neurons as a mechanism of neuropathic pain. Nature. 424:938–942 10.1038/nature01868 [DOI] [PubMed] [Google Scholar]
- Dopico J.G., González-Hernández T., Pérez I.M., García I.G., Abril A.M., Inchausti J.O., Rodríguez Díaz M. 2006. Glycine release in the substantia nigra: interaction with glutamate and GABA. Neuropharmacology. 50:548–557 10.1016/j.neuropharm.2005.10.014 [DOI] [PubMed] [Google Scholar]
- Farrant M., Kaila K. 2007. The cellular, molecular and ionic basis of GABAA receptor signalling. Prog. Brain Res. 160:59–87 10.1016/S0079-6123(06)60005-8 [DOI] [PubMed] [Google Scholar]
- Frankenhaeuser B., Hodgkin A.L. 1956. The after-effects of impulses in the giant nerve fibres of Loligo. J. Physiol. 131:341–376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman D.E. 1943. Potential, impedance, and rectification in membranes. J. Gen. Physiol. 27:37–60 10.1085/jgp.27.1.37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grassi F. 1992. Cl−-mediated interaction between GABA and glycine currents in cultured rat hippocampal neurons. Brain Res. 594:115–123 10.1016/0006-8993(92)91035-D [DOI] [PubMed] [Google Scholar]
- Haage D., Karlsson U., Johansson S. 1998. Heterogeneous presynaptic Ca2+ channel types triggering GABA release onto medial preoptic neurons from rat. J. Physiol. 507:77–91 10.1111/j.1469-7793.1998.077bu.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haage D., Bäckström T., Johansson S. 2005. Interaction between allopregnanolone and pregnenolone sulfate in modulating GABA-mediated synaptic currents in neurons from the rat medial preoptic nucleus. Brain Res. 1033:58–67 10.1016/j.brainres.2004.11.020 [DOI] [PubMed] [Google Scholar]
- Haas K.F., Macdonald R.L. 1999. GABAA receptor subunit γ2 and δ subtypes confer unique kinetic properties on recombinant GABAA receptor currents in mouse fibroblasts. J. Physiol. 514:27–45 10.1111/j.1469-7793.1999.027af.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. 2001. Ion Channels of Excitable Membranes. Third edition Sinauer Associates, Inc., Sunderland, MA: 814 pp [Google Scholar]
- Hodgkin A.L., Katz B. 1949. The effect of sodium ions on the electrical activity of giant axon of the squid. J. Physiol. 108:37–77 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman N.W., Wuarin J.P., Dudek F.E. 1994. Whole-cell recordings of spontaneous synaptic currents in medial preoptic neurons from rat hypothalamic slices: mediation by amino acid neurotransmitters. Brain Res. 660:349–352 10.1016/0006-8993(94)91312-9 [DOI] [PubMed] [Google Scholar]
- Huberfeld G., Wittner L., Clemenceau S., Baulac M., Kaila K., Miles R., Rivera C. 2007. Perturbed chloride homeostasis and GABAergic signaling in human temporal lobe epilepsy. J. Neurosci. 27:9866–9873 10.1523/JNEUROSCI.2761-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huguenard J.R., Alger B.E. 1986. Whole-cell voltage-clamp study of the fading of GABA-activated currents in acutely dissociated hippocampal neurons. J. Neurophysiol. 56:1–18 [DOI] [PubMed] [Google Scholar]
- Jones M.V., Westbrook G.L. 1995. Desensitized states prolong GABAA channel responses to brief agonist pulses. Neuron. 15:181–191 10.1016/0896-6273(95)90075-6 [DOI] [PubMed] [Google Scholar]
- Karlsson U., Haage D., Johansson S. 1997a. Currents evoked by GABA and glycine in acutely dissociated neurons from the rat medial preoptic nucleus. Brain Res. 770:256–260 10.1016/S0006-8993(97)00857-3 [DOI] [PubMed] [Google Scholar]
- Karlsson U., Sundgren A.K., Näsström J., Johansson S. 1997b. Glutamate-evoked currents in acutely dissociated neurons from the rat medial preoptic nucleus. Brain Res. 759:270–276 10.1016/S0006-8993(97)00262-X [DOI] [PubMed] [Google Scholar]
- Khalilov I., Holmes G.L., Ben-Ari Y. 2003. In vitro formation of a secondary epileptogenic mirror focus by interhippocampal propagation of seizures. Nat. Neurosci. 6:1079–1085 10.1038/nn1125 [DOI] [PubMed] [Google Scholar]
- Kyrozis A., Reichling D.B. 1995. Perforated-patch recording with gramicidin avoids artifactual changes in intracellular chloride concentration. J. Neurosci. Methods. 57:27–35 10.1016/0165-0270(94)00116-X [DOI] [PubMed] [Google Scholar]
- Lagrange A.H., Botzolakis E.J., Macdonald R.L. 2007. Enhanced macroscopic desensitization shapes the response of α4 subtype-containing GABAA receptors to synaptic and extrasynaptic GABA. J. Physiol. 578:655–676 10.1113/jphysiol.2006.122135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Foll F., Soriani O., Vaudry H., Cazin L. 2000. Contribution of changes in the chloride driving force to the fading of IGABA in frog melanotrophs. Am. J. Physiol. Endocrinol. Metab. 278:E430–E443 [DOI] [PubMed] [Google Scholar]
- Legendre P., Muller E., Badiu C.I., Meier J., Vannier C., Triller A. 2002. Desensitization of homomeric α1 glycine receptor increases with receptor density. Mol. Pharmacol. 62:817–827 10.1124/mol.62.4.817 [DOI] [PubMed] [Google Scholar]
- Lewis C.A., Faber D.S. 1993. GABA responses and their partial occlusion by glycine in cultured rat medullary neurons. Neuroscience. 52:83–96 10.1016/0306-4522(93)90184-H [DOI] [PubMed] [Google Scholar]
- Li Y., Xu T.L. 2002. State-dependent cross-inhibition between anionic GABAA and glycine ionotropic receptors in rat hippocampal CA1 neurons. Neuroreport. 13:223–226 10.1097/00001756-200202110-00010 [DOI] [PubMed] [Google Scholar]
- Li Y., Wu L.-J., Legendre P., Xu T.-L. 2003. Asymmetric cross-inhibition between GABAA and glycine receptors in rat spinal dorsal horn neurons. J. Biol. Chem. 278:38637–38645 10.1074/jbc.M303735200 [DOI] [PubMed] [Google Scholar]
- Ling D.S.F., Benardo L.S. 1995. Activity-dependent depression of monosynaptic fast IPSCs in hippocampus: contributions from reductions in chloride driving force and conductance. Brain Res. 670:142–146 10.1016/0006-8993(94)01298-V [DOI] [PubMed] [Google Scholar]
- Malinina E., Druzin M., Johansson S. 2005. Fast neurotransmission in the rat medial preoptic nucleus. Brain Res. 1040:157–168 10.1016/j.brainres.2005.01.094 [DOI] [PubMed] [Google Scholar]
- Mathias R.T., Cohen I.S., Oliva C. 1990. Limitations of the whole cell patch clamp technique in the control of intracellular concentrations. Biophys. J. 58:759–770 10.1016/S0006-3495(90)82418-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori M., Gähwiler B.H., Gerber U. 2002. β-alanine and taurine as endogenous agonists at glycine receptors in rat hippocampus in vitro. J. Physiol. 539:191–200 10.1113/jphysiol.2001.013147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mtchedlishvili Z., Kapur J. 2006. High-affinity, slowly desensitizing GABAA receptors mediate tonic inhibition in hippocampal dentate granule cells. Mol. Pharmacol. 69:564–575 10.1124/mol.105.016683 [DOI] [PubMed] [Google Scholar]
- Oh D.J., Dichter M.A. 1992. Desensitization of GABA-induced currents in cultured rat hippocampal neurons. Neuroscience. 49:571–576 10.1016/0306-4522(92)90227-S [DOI] [PubMed] [Google Scholar]
- Orser B.A., McAdam L.C., Roder S., MacDonald J.F. 1998. General anaesthetics and their effects on GABAA receptor desensitization. Toxicol. Lett. 100–101:217–224 10.1016/S0378-4274(98)00188-X [DOI] [PubMed] [Google Scholar]
- Overstreet L.S., Jones M.V., Westbrook G.L. 2000. Slow desensitization regulates the availability of synaptic GABAA receptors. J. Neurosci. 20:7914–7921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitt S.J., Sivilotti L.G., Beato M. 2008. High intracellular chloride slows the decay of glycinergic currents. J. Neurosci. 28:11454–11467 10.1523/JNEUROSCI.3890-08.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pusch M., Neher E. 1988. Rates of diffusional exchange between small cells and a measuring patch pipette. Pflugers Arch. 411:204–211 10.1007/BF00582316 [DOI] [PubMed] [Google Scholar]
- Rae J., Cooper K., Gates P., Watsky M. 1991. Low access resistance perforated patch recordings using amphotericin B. J. Neurosci. Methods. 37:15–26 10.1016/0165-0270(91)90017-T [DOI] [PubMed] [Google Scholar]
- Rivera C., Voipio J., Payne J.A., Ruusuvuori E., Lahtinen H., Lamsa K., Pirvola U., Saarma M., Kaila K. 1999. The K+/Cl− co-transporter KCC2 renders GABA hyperpolarizing during neuronal maturation. Nature. 397:251–255 10.1038/16697 [DOI] [PubMed] [Google Scholar]
- Rivera C., Voipio J., Thomas-Crusells J., Li H., Emri Z., Sipilä S., Payne J.A., Minichiello L., Saarma M., Kaila K. 2004. Mechanism of activity-dependent downregulation of the neuron-specific K-Cl cotransporter KCC2. J. Neurosci. 24:4683–4691 10.1523/JNEUROSCI.5265-03.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saxena N.C., Macdonald R.L. 1996. Properties of putative cerebellar γ-aminobutyric acid A receptor isoforms. Mol. Pharmacol. 49:567–579 [PubMed] [Google Scholar]
- Schwartz-Bloom R.D., Sah R. 2001. γ-Aminobutyric acidA neurotransmission and cerebral ischemia. J. Neurochem. 77:353–371 10.1046/j.1471-4159.2001.00274.x [DOI] [PubMed] [Google Scholar]
- Staley K.J., Soldo B.L., Proctor W.R. 1995. Ionic mechanisms of neuronal excitation by inhibitory GABAA receptors. Science. 269:977–981 10.1126/science.7638623 [DOI] [PubMed] [Google Scholar]
- Thompson S.M., Gähwiler B.H. 1989a. Activity-dependent disinhibition. I. Repetitive stimulation reduces IPSP driving force and conductance in the hippocampus in vitro. J. Neurophysiol. 61:501–511 [DOI] [PubMed] [Google Scholar]
- Thompson S.M., Gähwiler B.H. 1989b. Activity-dependent disinhibition. II. Effects of extracellular potassium, furosemide, and membrane potential on ECl- in hippocampal CA3 neurons. J. Neurophysiol. 61:512–523 [DOI] [PubMed] [Google Scholar]
- Trombley P.Q., Hill B.J., Horning M.S. 1999. Interactions between GABA and glycine at inhibitory amino acid receptors on rat olfactory bulb neurons. J. Neurophysiol. 82:3417–3422 [DOI] [PubMed] [Google Scholar]
- Vale C., Sanes D.H. 2000. Afferent regulation of inhibitory synaptic transmission in the developing auditory midbrain. J. Neurosci. 20:1912–1921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wohlfarth K.M., Bianchi M.T., Macdonald R.L. 2002. Enhanced neurosteroid potentiation of ternary GABAA receptors containing the δ subunit. J. Neurosci. 22:1541–1549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu L.J., Li Y., Xu T.L. 2002. Co-release and interaction of two inhibitory co-transmitters in rat sacral dorsal commissural neurons. Neuroreport. 13:977–981 10.1097/00001756-200205240-00016 [DOI] [PubMed] [Google Scholar]
- Zhu W.J., Vicini S. 1997. Neurosteroid prolongs GABAA channel deactivation by altering kinetics of desensitized states. J. Neurosci. 17:4022–4031 [DOI] [PMC free article] [PubMed] [Google Scholar]