Loss of trabeculae by mechano-biological means may explain rapid bone loss in osteoporosis

Abstract

Osteoporosis is characterized by rapid and irreversible loss of trabecular bone tissue leading to increased bone fragility. In this study, we hypothesize two causes for rapid loss of bone trabeculae; firstly, the perforation of trabeculae is caused by osteoclasts resorbing a cavity so deep that it cannot be refilled and, secondly, the increases in bone tissue elastic modulus lead to increased propensity for trabecular perforation. These hypotheses were tested using an algorithm that was based on two premises: (i) bone remodelling is a turnover process that repairs damaged bone tissue by resorbing and returning it to a homeostatic strain level and (ii) osteoblast attachment is under biochemical control. It was found that a mechano-biological algorithm based on these premises can simulate the remodelling cycle in a trabecular strut where damaged bone is resorbed to form a pit that is subsequently refilled with new bone. Furthermore, the simulation predicts that there is a depth of resorption cavity deeper than which refilling of the resorption pits is impossible and perforation inevitably occurs. However, perforation does not occur by a single fracture event but by continual removal of microdamage after it forms beneath the resorption pit. The simulation also predicts that perforations would occur more easily in trabeculae that are more highly mineralized (stiffer). Since both increased osteoclast activation rates and increased mineralization have been measured in osteoporotic bone, either or both may contribute to the rapid loss of trabecular bone mass observed in osteoporotic patients.

1. Introduction

Osteoporosis is a skeletal disease in which bone mass is lost, leading to a deterioration in bone architecture and increased risk of bone fracture. Femoral neck fractures and vertebral microfractures commonly occur and have serious health and social implications for sufferers. It has been estimated that one in three women and one in five men over the age of 50 will experience an osteoporotic fracture (Melton et al. 1992, 1998). Indeed, the lifetime risk of sustaining an osteoporotic fracture is greater than developing breast cancer in white females (Cummings et al. 1989). Osteoporosis is generally an ageing affliction and because recent advances in healthcare have increased life expectancy worldwide, the number of bone fractures is set to increase; for example, hip fractures are projected to increase by 240% in women and 310% in men by 2050 (Gullberg et al. 1997). Therefore, osteoporosis is a serious health concern for many millions of people across the world and it is imperative to use all research approaches, including computational modelling, to try and understand the pathology of the disease.

Ongoing in bone is a continuous remodelling process carried out by the coupled action of osteoclast (bone resorbing) and osteoblast (bone forming) cells. These cells function together as a basic multicellular unit (BMU; Frost 1964). Osteoporosis is generally attributed to an imbalance in the coupled action of the cells whereby osteoclastic bone resorption occurs without matching osteoblastic bone formation. One factor that may give rise to this imbalance is oestrogen deficiency, as occurs in postmenopausal women. Oestrogen deficiency has been shown to affect the behaviour of osteoclasts (Oursler et al. 1991); when oestrogen levels drop the activation frequency of osteoclasts is increased while their apoptosis rate decreases (Hughes et al. 1996; Recker et al. 2004); both of these may increase the depth of resorption pits (Eriksen et al. 1985) and lead to excess bone removal. However, this slow loss of bone tissue due to an osteoclast/osteoblast imbalance does not fully explain the rapid and complete loss of individual bone struts, which occurs during osteoporosis (Parfitt et al. 1983; Waarsing et al. 2006). Are there other mechanisms that could cause the loss of trabeculae as shown in figure 1?

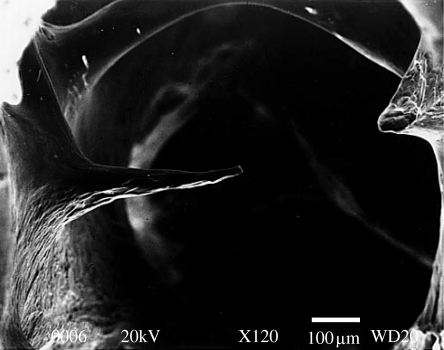
Figure 1.

Scanning electron microscopy image of trabecular bone showing the osteoclastic perforation of a thin horizontal strut. Reproduced with permission from Mosekilde (2000). Copyright © Springer Science and Business Media.

Material properties of the bone tissue itself are also altered during osteoporosis. Mechanical testing of individual trabecular struts taken from normal and ovariectomized rats has shown a higher elastic modulus for osteoporotic trabeculae compared with trabeculae in healthy bone (McNamara et al. 2006a). Such increases in the elastic modulus may result from increases in the mineral content that occurs in osteoporotic trabecular tissue (Boyde et al. 1998; Ciarelli et al. 2003; McNamara et al. 2006a). Currey investigated the effect of changes in the mineral content on the mechanical properties of normal cortical bone and found that increases in the mineralization lead to reduced toughness and impact strength thereby allowing cracks to propagate more easily through the tissue (Currey 1984; Currey et al. 1996). Given that bone cell activity is believed to be influenced by mechanical stimuli (Lanyon 1993), and in particular by strain and/or microdamage, then it is possible that such changes in the elastic properties could affect the stimuli getting through to bone cells and alter the remodelling process.

Experimental evidence implicates both strain and microdamage as bone remodelling stimuli (Lanyon et al. 1982; Burr et al. 1985; Frost 1996). Various mechanisms by which these strain and damage stimuli may be sensed within the bone have been put forward. For example, it has been postulated that strain-derived fluid flow within canaliculi (Klein-Nulend et al. 1995) or physical deformation of the osteocytes (You et al. 2001) may stimulate biochemical signals from osteocytes. A mechanism for damage sensation may be the severance of osteocyte processes (Frost 1960; Taylor et al. 2003) or local strain field changes due to unloading of damaged tissue (Prendergast & Huiskes 1996). It has also been suggested that osteocyte apoptosis due to microdamage may either directly or indirectly signal damage removal (Noble 2003). An average crack length, consistent between sites, was found to exist in bone lending further support to the idea of damage as a stimulus for bone remodelling (Lee et al. 2002). Previous theoretical and computational studies have been mainly concerned with how strain regulates bone remodelling (Cowin & Hegedus 1976; Huiskes et al. 1987; Weinans et al. 1992). However, bone cells may be responsive to microdamage as well (Frost 1996), and a remodelling algorithm that incorporates both the strain and damage stimuli was proposed by McNamara & Prendergast (2007). They examined a number of different algorithms and found that the one which provided the most realistic prediction of BMU behaviour was a combined strain and microdamage stimulus where damage-stimulated resorption only occurs once a critical damage level is exceeded.

Others have used computational simulations of bone turnover to examine some of the mechano-biological causes behind the adaptation of bone during osteoporosis. Van der Linden et al. (2004) investigated the effect that the increases in bone tissue elastic modulus may have on the architecture of blocks of trabecular bone and found that a more anisotropic architecture is produced together with a reduction in bone mass. From computational simulations on a lattice of trabecular bone, Ruimerman et al. (2005) found that by modelling oestrogen deficiency as an increase in the recruitment of osteoclasts, a thinning of a structure similar to that found in osteoporotic patients resulted. However, neither van der Linden et al. (2004) nor Ruimerman et al. (2005) considered the mechanism of trabecular perforation.

In any computational simulation of a complex biological process, such as bone remodelling, rules may be added to simulate the numerous biochemical signalling pathways that become active (Shefelbine et al. 2005). In particular to bone remodelling, it has been proposed that osteoclastic enzymes remaining on the newly resorbed surface may provide signals that determine the preferred location of osteoblastic attachment (Sheu et al. 2002). Indeed, it has been found that pre-osteoblasts are generally observed at the bottom of resorption cavities (Eriksen et al. 1984a) and that osteoblasts form bone in layers out from the centre of the trabecula resulting in the lamellar structure of trabecular bone.

In this study, a finite-element analysis, together with a mechano-regulation algorithm that includes control of osteoblast attachment, is used to analyse the possible effect of the depth of resorption cavity or increase in elastic modulus on trabecular perforation and loss during osteoporosis. Firstly, we hypothesize that, for a given trabecular thickness, a critical cavity depth exists for which resorption pits of greater depths cannot be refilled by the repair process and instead perforation occurs. Secondly, we hypothesize that even with bone cells behaving normally, altered tissue stiffness will cause the loss of trabeculae and drive the detrimental changes in bone architecture that are observed during osteoporosis.

2. Methods

2.1 Mechano-regulation algorithm

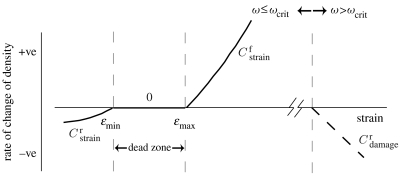
The algorithm implemented in this study regulates remodelling according to strain energy density if damage is below some critical level, denoted ω_crit; if ω_crit is exceeded then removal of the damaged tissue by resorption is initiated irrespective of the strain signal (figure 2). It is assumed that the strain and damage stimuli are perceived by the mechano-sensors (cells which sense changes in mechanical stimuli) within the trabecula. As trabecular bone remodelling is a surface phenomenon, these signals are then transmitted to the surface of the trabecula.

Figure 2.

Combined strain-adaptive remodelling (solid line) and damage-simulated resorption (dashed line) algorithm. The rates of remodelling are indicated beside their corresponding curve.

Resorption is simulated by changing the bone tissue's actual density, ρ, and is calculated each iteration as follows:

$$\begin{array}{l}\text{if}\omega >{\omega }_{\text{crit}}\text{then}\frac{\partial \rho }{\partial t}=C_{\text{damage}}^{\text{r}}{S}_{\text{damage}},\hfill \\ \text{else}\text{if}ϵ<{ϵ}_{\text{min}}\text{then}\frac{\partial \rho }{\partial t}=C_{\text{strain}}^{\text{r}}{S}_{\text{strain}},\hfill \\ \text{else}\text{if}ϵ>{ϵ}_{\text{max}}\text{then}\frac{\partial \rho }{\partial t}=C_{\text{strain}}^{\text{f}}{S}_{\text{strain}},\hfill \\ \text{else}\frac{\partial \rho }{\partial t}=0,\hfill \end{array}\}$$ (2.1)

where ω is the damage level and ϵ is the strain at the mechano-sensor; ϵ_min and ϵ_max are the lower and upper strain limits, respectively; S_strain is the strain signal; S_damage is the damage signal at the mechano-sensor; $C_{\text{strain}}^{\text{r}}$ and $C_{\text{damage}}^{\text{r}}$ are the rates of bone resorption; and $C_{\text{strain}}^{\text{f}}$ represents the bone formation rate. The new density is then approximated each iteration using the Euler forward method. As the new density can be a combination of bone and resorbed bone, the apparent density of the tissue is calculated using the exponentially determined relationship between the elastic modulus and density of bone of Morgan et al. (2003), i.e.

$$E=K{\rho }^n,$$ (2.2)

where K and n are empirical constants (table 1).

Table 1.

Constants used in bone remodelling algorithm.

	magnitude
resorption/formation rates
$C_{\text{strain}}^{\text{r}}$ (g2 N−1 cm−4 d−1)	20.0
$C_{\text{strain}}^{\text{f}}$ (g2 N−1 cm−4 d−1)	24.5
$C_{\text{damage}}^{\text{r}}$ (g cm−3 d−1)	1.05×1012
strain parameters
ϵ min	1000 μϵ
ϵ max	2000 μϵ
damage parameters
T (°C)	37; Carter et al. (1976)
H	−7.789; Carter et al. (1976)
J	−0.0206; Carter et al. (1976)
K	2.364; Carter et al. (1976)
M	15.470; Carter et al. (1976)
constants
K (kN cm2 g−2)	65; Morgan et al. (2003)
n	2; Morgan et al. (2003)

2.1.1 Microdamage-stimulated resorption

The damage levels are determined throughout the bone tissue in the model and are allowed to accumulate in each iteration, thus providing the loading history of the trabecular strut. Newly formed bone is assigned zero damage levels. Damage is calculated using the remaining life approach: if damage is assumed to grow linearly to a maximum value of 1 (total failure) with the number of cycles to failure denoted N_f, then the damage accumulation rate, denoted $\dot{\omega }$, equals 1/N_f (Prendergast & Taylor 1994); in this study, N_f is calculated from the S–N curve determined by Carter et al. (1976) as follows:

$${\text{log}}_{\text{10}}{N}_{\text{f}}=H{\text{log}}_{\text{10}}\sigma +JT+K\rho +M,$$ (2.3)

where T is the temperature of the bone (°C); ρ is the density of the bone (g cm⁻³); and H, J, K and M are all empirical constants (table 1). This equation was determined experimentally for cortical bone; however, it is comparable with the relationship determined by Choi & Goldstein (1992) from fatigue testing of single trabecular struts within the stress range experienced in this simulation. By summing the damage over the time period, a value for the level of accumulated damage, ω, is then calculated as follows:

$$\omega ={\int }_0^t\dot{\omega }\text{d}t.$$ (2.4)

According to the algorithm, when damage accumulates such that ω is greater than ω_crit the damaged region is resorbed. The critical level of damage, ω_crit, at which this repair process is initiated is taken here to be the damage caused by a single loading cycle at 3500 μϵ (numerically this value is 1.3×10⁻¹²). If the level of damage is greater than ω_crit then the damage signal, S_damage, is the difference between the actual damage at the mechano-sensor minus the critical damage and the bone tissue is resorbed, otherwise damage levels are acceptable and S_damage=0, with damage being accumulated forward to the next iteration, i.e.

$$\begin{array}{l}\text{if}\omega >{\omega }_{\text{crit}}\text{then}{S}_{\text{damage}}=\omega -{\omega }_{\text{crit}},\hfill \\ \text{else}{S}_{\text{damage}}=0\text{and}\omega =\omega +\dot{\omega }\text{d}t.\hfill \end{array}$$ (2.5)

2.1.2 Strain-adaptive remodelling

The strain-adaptive remodelling stimulus is based on the strain energy density per unit mass (Fyhrie & Carter 1990; Weinans et al. 1992), denoted U, and is calculated as follows:

$$U=\frac{E{ϵ}^2}{2\rho },$$ (2.6)

where E is the elastic modulus of the material at the mechano-sensor (GPa); ϵ is the strain tensor; and ρ is the density of the material (g cm⁻³). The strain signal, S_strain, is given as follows:

$$S_{\text{strain}}=U-U_{\text{ref}},$$ (2.7)

where U_ref is the reference strain energy density. Following Carter (1984), a zone of equilibrium strains (the so-called ‘dead zone’) was incorporated into the model, between ϵ_min and ϵ_max (figure 2; table 1), within which no change in material properties and therefore no change in bone architecture occurs. For strains below the lower limit, ϵ_min, bone resorption occurs and for strains greater than the upper limit, ϵ_max, bone formation is initiated to strengthen the strut and reduce strain levels to homeostatic values. To account for the dead zone, the value for U_ref and therefore the magnitude of S_strain is dependant on the strain at that particular mechano-sensor.

$$\begin{array}{l}\text{If}ϵ<{ϵ}_{\text{min}}\text{then}{U}_{\text{ref}}=\frac{E{ϵ}_{\text{min}}^2}{2\rho }\text{and}{S}_{\text{strain}}=U-U_{\text{ref}},\hfill \\ \text{else}\text{if}ϵ>{ϵ}_{\text{max}}\text{then}{U}_{\text{ref}}=\frac{E{ϵ}_{\text{max}}^2}{2\rho }\text{and}{S}_{\text{strain}}=U-U_{\text{ref}},\text{else}{S}_{\text{strain}}=0.\hfill \end{array}$$ (2.8)

2.1.3 Inclusion of a ‘rule’ governing the location of osteoblast attachment

To take account of signalling molecules released during the remodelling process and which may affect bone cell behaviour, a rule restricting osteoblast attachment to regions overlying bone tissue surfaces was included. Such regions were determined by firstly finding the neighbouring region of the potential osteoblast attachment site, which was nearest the centre of the strut and then determining whether its elastic modulus was equal to that of bone. If so then it is a suitable site for bone deposition. This rule ensures that bone formation preferentially occurs where osteoclastic enzymes are still present on the surface (Sheu et al. 2002) because, in this case, the most recently resorbed surface is the bottom of the resorption cavity. With this rule, bone forms towards the surface one layer at a time resulting in the lamellar structure generally associated with trabecular bone.

2.2 Computational implementation

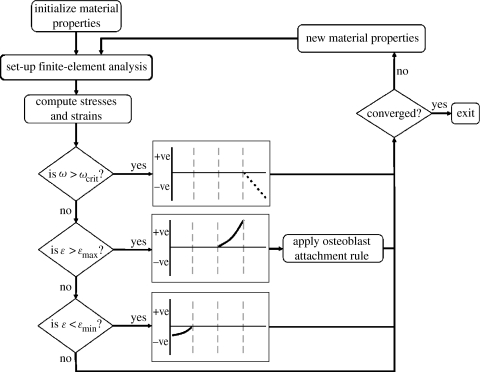
Linear-elastic, 8-nodal hexahedral elements of size 10×10×10 μm were used to model the trabecula as a strut of length 800 μm and diameter 90 μm (figure 3). The values for the elastic moduli of the bone tissue were obtained from mechanical testing of individual trabeculae (McNamara et al. 2006a). Normal bone tissue was assigned an elastic modulus (E) of 2.6 GPa and osteoporotic tissue 4.0 GPa. Both bone tissues were assumed to have a density (ρ) of 2.0 g cm⁻³ (Morgan et al. 2003) and a Poisson's ratio (ν) of 0.3. These elastic moduli served as upper thresholds for the newly calculated elastic moduli whereas an elastic modulus of 0.002 GPa, representing completely resorbed bone, served as the lower limit. This low value was chosen so that these resorbed elements did not contribute to the mechanical stiffness of the strut. Two loading conditions were investigated: a prescribed displacement of 1.2 μm and an applied force of 0.017 μN; both of these resulted in a strain of 1500 μm along the strut with no resorption pit. The boundary conditions were as shown in figure 3. The mechano-sensors in the model were assumed to be the bone-lining cells (Miller et al. 1989). These mechano-sensors were modelled as surface integration points, that is, integration points having an elastic modulus greater than resorbed bone, 0.002 GPa, but which have at least one resorbed bone integration point as a nearest neighbour. A finite-element analysis was performed and, at each of these sensor locations, the finite element results were used to calculate the strain and microdamage stimuli. Material properties were changed depending on the magnitude of these signals according to the mechano-regulation algorithm (equation (2.1)). These new material properties were then inputted back into the model and the simulation was iterated until convergence was reached (figure 4). As trabecular bone remodelling occurs along the surface of a strut, changes in material properties were restricted to surface integration points.

Figure 3.

Cylindrical trabecular strut showing the dimensions and the applied boundary conditions.

Figure 4.

Flow chart of the combined strain and damage remodelling algorithm.

Eriksen et al. (1984b) calculated a rate of bone resorption of 1.4 μm d⁻¹ for normal bone. In this study, it is assumed that this rate occurs at a strain of 900 μϵ for strain-adaptive resorption and at a strain of 3600 μϵ for damage-adaptive resorption, arbitrarily chosen as 100 μϵ above and below the thresholds. The values for $C_{\text{strain}}^{\text{r}}$ and $C_{\text{damage}}^{\text{r}}$ were then calculated as the constants required to achieve this level of resorption based on the signals received under these strains. For example, under a constant strain of 900 μϵ, $C_{\text{strain}}^{\text{r}}$ is calculated such that the change in density would equate to a 10 μϵ depth of bone tissue being resorbed in 8 days. As the magnitude of the signal increases, the rate at which bone is resorbed also increases. Similarly, bone formation has been shown to occur at a rate of 0.43 μm d⁻¹ (Eriksen et al. 1984a). This rate was assumed to be experienced under a strain of 2100 μϵ for the strain-adaptive formation and the corresponding constant for resorption, $C_{\text{strain}}^{\text{f}}$ was calculated (table 1).

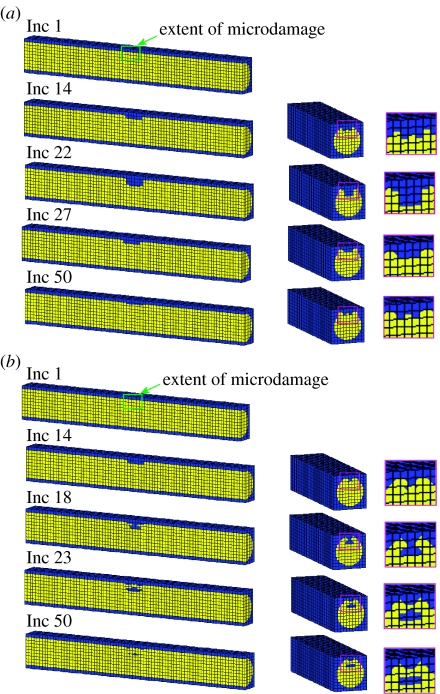
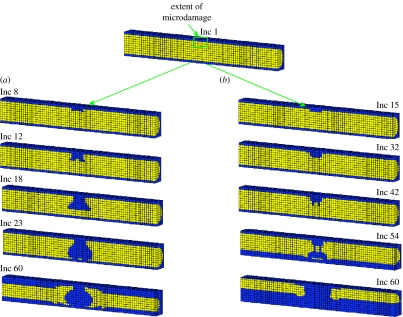
To initiate the remodelling process, a region of bone was defined to have a pre-existing damage level equivalent to one loading cycle under a strain of 3600 μϵ (resulting in a damage level greater than ω_crit). The damaged bone consisted of a cuboid portion (of depth 25 μm and length 60 μm) of bone located on the surface, halfway along the strut (figure 5).

Figure 5.

Progression of a BMU in longitudinal and transverse cross section of a strut with the normal elastic modulus (E=2.6 GPa) under displacement control loading condition (a) including osteoblast attachment rule and (b) without rule. Yellow elements represent bone and blue resorbed bone. Inc represents the number of simulation increments, with 1 increment being the equivalent of 1 day.

Using this computational model in conjunction with the mechano-regulation algorithm, the effect of including a rule which takes account of osteoblast attachment during bone remodelling simulations was first investigated. The algorithm was firstly applied to the trabecular strut with the normal elastic modulus (E=2.6 GPa) without the osteoblast attachment rule—this was done to determine the influence of such a rule. The simulation was then rerun including a rule governing osteoblast attachment as described in §2.1.3.

2.3 Testing of hypotheses

The effect of increases in elastic moduli (ranging from 2.0 to 6.0 GPa) on BMU progression was investigated firstly to test the hypothesis that perforation occurs more readily if the elastic modulus increases. Secondly, to test the hypothesis that there is a cavity depth above which remodelling activity cannot refill, the range of depths, from 10 to 80 μm, was studied, using normal bone material properties, and their outcome on BMU behaviour was computed.

3. Results

3.1 Normal bone remodelling

Using the mechano-regulation algorithm shown in figure 4, complete resorption of the damage region was followed by refilling of the cavity by strain-adaptive remodelling in a similar manner as is observed histologically. The predicted pattern of the BMU progression under the displacement control loading condition is shown in figure 5a. There was no appreciable difference between displacement and force controls.

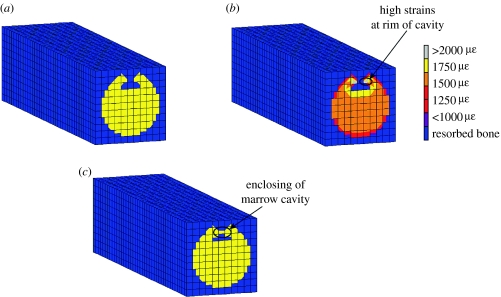
With no preferred sites for osteoblast attachment, it was found that damage initiated the remodelling process and complete resorption of the damaged bone occurred, but the strain-stimulated deposition to refill it gave unusual behaviour. Matrix was initially deposited at the rim of the forming cavity, enclosing a void within the bone strut. Bone formation then followed along behind the resorbing damaged bone (figure 5b). This unexpected cellular activity occurred owing to elevated strains at the rim of the forming cavity. These strain levels were sufficiently high to form bone but not high enough to create damage above the critical level (figure 6).

Figure 6.

(a) Longitudinal cross section of trabecula under the combined strain and damage algorithm. (b) High strains at rim of cavity causing (c) bone formation at rim.

3.2 Change in elastic modulus

When the elastic modulus was changed to that of osteoporotic bone (E=4.0 GPa), with all other parameters remaining identical to those in §3.1, perforation occurred. The reason for this is that the increased elastic modulus caused higher stress levels that further damaged the trabecular tissue at the base of the resorption pit. As BMUs target damage, this newly damaged tissue was then resorbed creating successive damage removal. In this way, resorption propagated until the trabecula was perforated. Figure 7a shows such a perforation under displacement control.

Figure 7.

Trabecular perforation in longitudinal cross section with osteoporotic elastic modulus (E=4.0 GPa) under (a) displacement control loading condition and (b) force control loading condition. Inc represents the number of simulation increments, with 1 increment being the equivalent of 1 day.

A similar situation occurred under force control; however, the manner in which the strut perforated differed somewhat from the displacement control (figure 7b). The difference occurred because the increased elastic modulus caused the strains along the strut to fall below ϵ_min resulting in an initial slight thinning of the whole strut. Although the same volume of damaged bone was resorbed, the stresses at the base of the cavity were elevated due the smaller cross-sectional area underneath. The mechanisms then followed that of displacement control with damage accumulating until it reached the critical level, leading to resorption, increasing stresses and creating further damage and subsequent bone resorption.

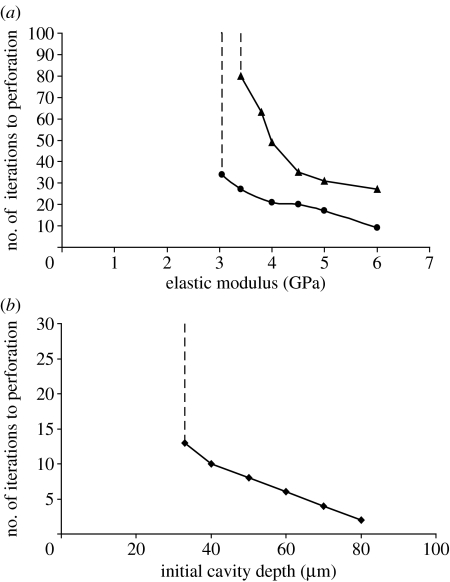
It was found that the resorption cavity would refill when the elastic modulus of the bone was 3.0 GPa or less for displacement and 3.3 GPa for the force control. However, if the elastic modulus was greater than these critical values, the perforation of the strut always resulted. It was also found that the higher the elastic modulus the more rapidly the trabeculae perforated (figure 8a). This was true for both displacement and force control, although more rapid perforation occurred under displacement control.

Figure 8.

(a) Plot of the elastic modulus against number of iterations to perforation in a strut of 90 μm diameter with a damage region of 25 μm in depth. Perforation occurs for moduli greater than 3.0 GPa (circles, displacement control) and 3.3 GPa (triangles, force control). (b) Plot of the depth of cavity against number of iterations to perforation with normal material properties (E=2.6 GPa). If the cavity resorbed by osteoclasts is greater than 32 μm then perforation is inevitable.

3.3 Change in resorption cavity depth

It was found that cavities of 32 μm or less were capable of being refilled in a 90 μm diameter strut. However, cavities of greater depth than this resulted in perforation of the strut (figure 8b). This is due to the notching effect produced by the deeper cavity—the higher stresses damaged the bone tissue to levels above that of the critical damage value. As BMUs are regulated by damage, this damaged tissue was removed forming an even deeper notch that leads to yet further damage and removal until perforation.

4. Discussion

In this paper, it was established that a bone remodelling algorithm based on a combined strain/damage stimulus (with damage-stimulated bone resorption occurring above a critical amount of accumulated damage), in conjunction with a rule governing osteoblastic attachment could successfully predict the remodelling cycle in trabecular bone, as described, for example, by Parfitt (1984). As the remodelling algorithm relies on the strain and damage levels, the model was examined under both displacement and force control. However, the loading mode was not found to affect the results very much. In the algorithm, bone remodelling targets damaged regions by resorbing damaged tissue. In that respect, it is similar to the algorithm employed by Huiskes et al. (2000) and Ruimerman et al. (2005), where osteoclasts are directed to damaged zones. Of course, our simulations do not prove that bone turnover is mechano-regulated, but they do support the concept that bone remodelling is a process of removing microdamage to form a pit that refills until strains reach homeostatic values. Without the osteoblast attachment rule, successful mechano-biological control of remodelling could not be predicted—this was unexpected and runs counter to other theoretical bone remodelling studies (Huiskes et al. 2000; Ruimerman et al. 2005; McNamara & Prendergast 2007).

The main result of this study is that, if osteoporosis causes an increase in the actual tissue modulus, as some experiments on trabecular tissue have shown (McNamara et al. 2006a), then the perforation of struts during osteoporosis may result from normal bone remodelling of pathologically stiffer tissue. Furthermore, if oestrogen deficiency causes the depth of bone tissue resorbed by an osteoclast to increase, as shown by the experiments of Eriksen et al. (1985), a cavity may be created, which is incapable of being refilled by remodelling, leading to the perforation of the trabecula. Therefore, the two hypotheses posed in §1 are corroborated. Furthermore, the results lend support to the idea that the thinning of trabeculae by osteoclast/osteoblast ‘imbalance’ is not the only mode of trabecular perforation in osteoporosis—trabeculae may also be lost by mechano-biological means.

Several assumptions and simplifications were made in this model. Firstly, a cylinder with isotropic, homogeneous, linear elastic material properties was used to model a trabecular strut. In reality, trabeculae are often irregular in shape consisting of a lamellar structure with anisotropic and heterogeneous material properties. We believe that due to the idealized architecture and material properties of the model a pit is resorbed rather than a groove as is generally observed histologically. Secondly, there are numerous non-mechanical factors that affect bone cell behaviour during remodelling; however, only one of these factors—regarding the attachment of osteoblasts—was included directly in our model. However, from this study, it would seem that there is no need to account for complex coupling mechanisms between osteoclasts and osteoblasts, as the mechano-regulatory algorithm alone is sufficient to initialize and direct the formation process. Remodelling rates included in the model were based on the average values from experimental data (Eriksen et al. 1984a,b). In reality, these rates will differ between individuals. Susceptibility to bone loss may be patient specific and influenced by these rates. As both bone-lining cells and osteocytes have been proposed as possible mechano-sensors (Mullender et al. 1994), a simulation was performed (results not shown) using osteocytes as mechano-sensors but it was found that successful resorption and formation of a cavity could not be achieved as the density of osteocytes was not sufficient. A more complex model incorporating osteocyte processes, similar to the method employed by Adachi et al. (2007), would be necessary to pick up local strain stimuli.

The values for the elastic moduli used in the simulation were experimentally measured by McNamara et al. (2006a). These values would appear to be at the lower end of the scale for measured material properties of bone; however, the magnitude of the elastic modulus was found not to affect the perforation phenomenon because it is the relative increase in the elastic modulus from the normal that determines whether a strut will perforate. To examine their effect on the remodelling process and on the results obtained, a parametric study was also carried out on each parameter used. Variations in the resorption (from 1.0 to 2.0 μm d⁻¹) and formation (from 0.09 to 0.6 μm d⁻¹) rates were shown to influence the time sequence of the remodelling stages but did not alter the critical elastic modulus or resorption cavity depth. Also, decreasing the width of the dead zone to 0 did not affect these results. However, by increasing the width of the dead zone above 1400 μϵ, the elastic modulus below which perforation occurs was reduced significantly. Therefore, if mechano-sensitivity reduces by increasing the width of the dead zone—as it may do with age—then perforation by mechano-biological mechanisms will become easier in older people. Examining the effect the critical damage level may have on the results, it was found that decreasing the value to below 3300 μϵ also decreased the critical elastic modulus, whereas increasing ω_crit to values greater than 3800 μϵ increased the critical elastic modulus. However, the results still showed a critical elastic modulus above which perforation of a strut occurs but below which normal BMU behaviour is simulated.

Several investigations have been made into the mineral content of osteoporotic bone with conflicting results. Some have found no change or a decrease to occur in the disease (Li & Aspden 1997; Roschger et al. 2001); whereas increases have also been reported (Boyde et al. 1998; Ciarelli et al. 2003; McNamara et al. 2006a). In this study, the possible effect of an increase in the mineral content on BMU behaviour was investigated. If the mineral content, and therefore elastic modulus, is found to increase, it is not known whether this change would cause osteoporosis, or be an ontogenetic adaptation to it. In other words, whether these changes in the tissue properties are a consequence of adaptation to an already weakened architecture or whether these alterations drive the loss of trabecular struts is an open question. Although oestrogen deficiency increases bone turnover, it is possible that the mineralization process may also be altered leading to a more mineralized tissue. What we have shown is that, if bone remodelling is in fact regulated by a combination of strain and microdamage and an increase in the elastic modulus does occur, it will predispose osteoporotic bone to trabecular perforation. A critical value of elastic modulus was found to exist below which refilling of the resorption cavity is possible but above which, for a particular diameter of strut and depth of cavity, perforation is inevitable. The increase in the elastic modulus from the healthy value of 2.6 GPa to the pathological value of 3.0 GPa is only 0.4 GPa. Therefore, this study would suggest that the increased stiffness of bone tissue that may occur in osteoporosis leads to easier and more rapid perforation of trabecular struts.

Parfitt (1987) proposed that the mechanism behind rapid loss of trabeculae in osteoporosis is the increase in the depth of osteoclastic resorption cavities leading to localized perforation of thin struts. However, we suggest an additional mechanism to the final part of Parfitt's proposal which is that perforation finally occurs from continued osteoclast resorption due to microscopic damage from elevated stresses at the base of the resorption pit. In our model, a critical depth of 32 μm was found for a strut of diameter 90 μm; below 32 μm depth, the pit will be refilled whereas greater than this perforation of the strut will ensue.

Although both results are possible mechanisms for the accelerated bone loss experienced in osteoporotic patients, they differ in the trabecular struts that they target for resorption. If osteoporosis is driven by increased osteoclast activity then the thinnest struts would be more prone to resorption, leaving the thicker ones behind. On the other hand, as changes in tissue properties occur over time and to varying degrees in each trabecula, perforation due to increases in the elastic modulus would not necessarily be restricted to the thinnest struts. Whether thin struts or the more highly mineralized struts are targeted is not known, but further research using a combination of backscattered electron imaging and micro-computed tomography to examine the change in mineral content with time may be able to lend further support to these proposed mechanisms.

The importance of developing algorithms that include rules to take account of biological factors during bone remodelling simulations was demonstrated. Without a rule governing osteoblast attachment, abnormal BMU activity occurred with bone forming at the rim of the cavity enclosing a void. The cause of this unphysiological behaviour was due to the high strains experienced along the top edge of the cavity. This elevated strain distribution was found not to be a consequence of the architecture used in the model as has been noted in other studies; around the rim of an idealized (Smit & Burger 2000) and an in vivo resorption cavity (McNamara et al. 2006b). This result would suggest that further developments of computer simulations of bone remodelling should incorporate appropriate rules alongside the purely mechanical aspects. Indeed, the mechano-biological algorithms proposed by Claes & Heigele (1999) and Shefelbine et al. (2005) in their work on fracture healing found it essential to implement rules to take account of purely biological control of preferred bone formation locations.

5. Conclusion

Osteoporosis has now become one of the most prevalent human diseases. The number of sufferers is set to increase even further in our ageing society. It is, therefore, imperative that both experimental and computational studies interface with each other for complete understanding behind the pathology of this disease. Although bone remodelling is carried out by cells, the disease causes biomechanical failure of the load-bearing skeleton. Therefore, investigations into both the cellular behaviour and the mechanical conditions are necessary if a thorough analysis is to be achieved. In this study, a computational approach is taken which includes parameters and observations of cellular behaviour obtained from experiments. Using this model, two different mechanisms, which may contribute to the rapid bone loss observed during osteoporosis, were examined. Firstly, it was found that the increases in the resorption cavity depths lead to bone loss—and not bone loss due to fracturing of a weakened strut but bone loss by continued resorption of damaged tissue. Secondly, it was predicted that relatively small increases in the elastic modulus of bone tissue caused perforation of a single strut to occur, even under normal BMU activity. As osteoporotic drugs generally target bone cell activity and in particular osteoclasts, it is interesting to speculate that the bone tissue and in particular control of its mineral content might be an alternative therapeutic target.