Assemblathon 1: A competitive assessment of de novo short read assembly methods

Abstract

Low-cost short read sequencing technology has revolutionized genomics, though it is only just becoming practical for the high-quality de novo assembly of a novel large genome. We describe the Assemblathon 1 competition, which aimed to comprehensively assess the state of the art in de novo assembly methods when applied to current sequencing technologies. In a collaborative effort, teams were asked to assemble a simulated Illumina HiSeq data set of an unknown, simulated diploid genome. A total of 41 assemblies from 17 different groups were received. Novel haplotype aware assessments of coverage, contiguity, structure, base calling, and copy number were made. We establish that within this benchmark: (1) It is possible to assemble the genome to a high level of coverage and accuracy, and that (2) large differences exist between the assemblies, suggesting room for further improvements in current methods. The simulated benchmark, including the correct answer, the assemblies, and the code that was used to evaluate the assemblies is now public and freely available from http://www.assemblathon.org/.

Sequence assembly is the problem of merging and ordering shorter fragments, termed “reads,” sampled from a set of larger sequences in order to reconstruct the larger sequences. The output of an assembly is typically a set of “contigs,” which are contiguous sequence fragments, ordered and oriented into “scaffold” sequences, with gaps between contigs within scaffolds representing regions of uncertainty.

There are numerous subclasses of assembly problems that can be distinguished by, among other things, the nature of (1) the reads, (2) the types of sequences being assembled, and (3) the availability of homologous (related) and previously assembled sequences, such as a reference genome or the genome of a closely related species (Pop and Salzberg 2008; Chaisson et al. 2009; Trapnell and Salzberg 2009). In this work we focus on the evaluation of methods for de novo genome assembly using low-cost “short read” technology, where the reads are comparatively short in length but large in number, the sequences being assembled represent a novel diploid genome and the nearest homologous genome to that being assembled is significantly diverged.

In bioinformatics, the reads used in an assembly are derived from an underlying sequencing technology. For a recent review of sequencing technologies, see Metzker (2010). For the assembly problem there are a number of key considerations, notably (1) the length of the reads, (2) the error characteristics of the reads, (3) whether and how the reads are “paired,” i.e., where reads are produced in pairs separated by an approximately fixed length spacer sequence, and finally (4) the number of reads produced for a given cost.

Sanger sequencing (Sanger et al. 1977) produces relatively long reads, typically between 300 and 1000 bp in length, with a low error rate, but which are comparatively expensive to produce. After relying primarily on Sanger sequencing for decades, the field of sequencing has recently witnessed a diversification of competing technologies (Margulies et al. 2005; Bentley 2006; Pourmand et al. 2006; Pandey et al. 2008; Eid et al. 2009) and a rapid rate of overall change. One direction of this development has been a move toward shorter reads, often ≤150 bp, but at a much lower cost for a given volume of reads (Bentley 2006; Pourmand et al. 2006; Pandey et al. 2008).

As the field of sequencing has changed so has the field of sequence assembly; for a recent review, see Miller et al. (2010). In brief, using Sanger sequencing, contigs were initially built using overlap or string graphs (Myers 2005) (or data structures closely related to them) in tools such as phrap (http://www.phrap.org/), GigAssembler (Kent and Haussler 2000), Celera (Myers et al. 2000; Venter et al. 2001), ARACHNE (Batzoglou et al. 2002), and Phusion (Mullikin and Ning 2003), which were used for numerous high-quality assemblies such as human (Lander et al. 2001) and mouse (Waterston et al. 2002). However, these programs were not generally efficient enough to handle the volume of sequences produced by the next-generation of sequencing technologies, spurring the development of a new generation of assembly software.

While some maintained the overlap graph approach, e.g., Edena (Hernandez et al. 2008) and Newbler (http://www.my454.com/), others used word look-up tables to greedily extend reads, e.g., SSAKE (Warren et al. 2007), SHARCGS (Dohm et al. 2007), VCAKE (Jeck et al. 2007), and OligoZip (http://linux1.softberry.com/berry.phtml?topic=OligoZip). These word look-up tables were then extended into de Bruijn graphs to allow for global analyses (Pevzner et al. 2001), e.g., Euler (Chaisson and Pevzner 2008), AllPaths (Butler et al. 2008), and Velvet (Zerbino and Birney 2008). As projects grew in scale, further engineering was required to fit large whole-genome data sets into memory (ABySS) (Simpson et al. 2009), Chapman et al. (2011) (SOAPdenovo) (Li et al. 2010a), Cortex (in prep.). Now, as improvements in sequencer technology are extending the length of “short reads,” the overlap graph approach is being revisited, albeit with optimized programming techniques, e.g., SGA (Simpson and Durbin 2010), as are greedy contig extension algorithms, e.g., PRICE (http://derisilab.ucsf.edu/software/price/index.html), Monument (http://www.irisa.fr/symbiose/people/rchikhi/monument.html).

In general, most sequence assembly programs are multistage pipelines, dealing with correcting measurement errors within the reads, constructing contigs, resolving repeats (i.e., disambiguating false-positive alignments between reads), and scaffolding contigs in separate phases. Since a number of solutions are available for each task, several projects have been initiated to explore the parameter space of the assembly problem, in particular in the context of short read sequencing (Phillippy et al. 2008; Alkan et al. 2011; Hubisz et al. 2011; Lin et al. 2011; Narzisi and Mishra 2011; Zhang et al. 2011). In this work we are concerned with evaluating assembly programs as a whole, with the aim of comprehensively evaluating different aspects of assemblies.

It is generally the case that the right answer to an assembly problem is unknown. Understandably therefore, a common method for assessing assembly quality has been the calculation of length summary statistics on the produced scaffold and contig sequences. Such metrics include various weighted median statistics, such as the N50 defined below, as well as the total sequence lengths and total numbers of sequences produced (Lindblad-Toh et al. 2005; Ming et al. 2008; Church et al. 2009; Liu et al. 2009; Li et al. 2010a; Colbourne et al. 2011; Locke et al. 2011).

Other methods have been proposed for evaluating the internal consistency of an assembly; for example, by analyzing the consistency of paired reads, as in the clone-middle plot (Huson et al. 2001), by looking for variations in the depths of read coverage supporting a constructed assembly (Phillippy et al. 2008), and looking at haplotype inconsistency (Lindblad-Toh et al. 2005).

To assess accuracy, assemblies may be compared with finished sequences derived from independent sequencing experiments or to sequences held out of the assembly process. For the dog genome, nine bacterial artificial chromosomes (BACs) were sequenced to finishing standards and held out of the assembly (Lindblad-Toh et al. 2005), for the panda genome, which was primarily an Illumina assembly, extra Sanger sequencing of BACs was performed (Li et al. 2010a). Additionally, if genetic mapping data is available, such information can also be used to assess scaffold quality (e.g., Church et al. 2009), which used a combination of linkage, radiation hybrid, and optical maps. Church et al. (2009) also demonstrate that transcriptome (the set of RNA molecules for a given cell type) information, if available, can also be used to assess the validity of a genomic assembly by checking the extent to which the assembly recapitulates the transcriptome.

When a reference genome or sequence is available, a comparison between the assembly and reference can be performed. This has previously been accomplished by studies using several different genome alignment methods, including BLAST (e.g., Zhang et al. 2011), LASTZ (e.g., Hubisz et al. 2011), and Exonerate (Hernandez et al. 2008; Zerbino and Birney 2008). Given such an alignment, most simply, the proportion of a reference's coverage can be reported (Li et al. 2010b; Zhang et al. 2011). Notably, Gnerre et al. (2011) compared novel short-read assemblies with the human and mouse reference genomes and performed a comprehensive set of analyses that encompassed coverage, contig accuracy, and the long-range contiguity of scaffolds. Related to the work described here, Butler et al. (2008) described a graph-based pattern analysis using an assembly to reference alignment.

Comparison can also be made to a well-sequenced, related species. This can be done using the complete genomic sequence of an outgroup; for example, Meader et al. (2010) presented an assessment method based on patterns of insertions and deletions (indels) in closely related interspecies genome alignments. Alternatively, specific genomic features can be studied; for example, Parra et al. (2009) examined the fraction of “core genes,” those present in all genomes, which could be identified in draft genome assemblies.

Simulation has been a mainstay of genome assembly evaluation since assembly methodology was first developed and with few exceptions (e.g., MacCallum et al. 2009; Gnerre et al. 2011) is de rigueur when introducing new de novo assembly software (e.g., (Myers et al. 2000; Lander et al. 2001; Venter et al. 2001; Batzoglou et al. 2002; Dohm et al. 2007; Jeck et al. 2007; Warren et al. 2007; Butler et al. 2008; Chaisson and Pevzner 2008; Zerbino and Birney 2008, etc.). In this work we have also chosen to use simulations, utilizing the new Evolver genome evolution simulation tool (http://www.drive5.com/evolver/) to produce a simulated diploid genome with parameters that approximate that of a vertebrate genome, though at ∼1/10^th of the scale.

From this novel genome we simulate reads, modeling an Illumina sequencing run, using a newly developed read simulator. Assembly teams were asked to assemble this novel genome blind, and we present an analysis of the resulting assemblies. By using simulation, we know a priori the haplotype relationships; by a process of multiple sequence alignment (MSA) we assess the relationships between the assemblies and the original haplotypes of our simulation. This novel process allows us evaluate haplotype-specific contributions to the assemblies. Additionally, as a positive control for our results, we assess the generated assemblies using more traditional BLAST (Hubisz et al. 2011; Zhang et al. 2011) methods, and support our assessments by making all of the code and data from our assessments public and freely available (http://compbio.soe.ucsc.edu/assemblathon1/, http://www.assemblathon.org/).

Results

We start by giving an overview of the Assemblathon 1 data set and its generation. We then describe the assemblies before giving the results of different evaluations.

Genome simulation

Rather than use an existing reference genome for assessment, we opted to simulate a novel genome. We did this primarily for three reasons. First, it gave us a genome that had no reasonable homology with anything other than out-group genomes that we generated and provided to assemblers. This allowed for a fair, blind test in which none of the assembly contributors had access to the underlying genomes during the competition. Second, we were able to precisely tailor the proportions of the simulated genome to those desired for this experimental analysis, i.e., to limit the size of the genome to less than that of a full mammalian genome, and thus allow the maximum number of participants, while still maintaining a size that posed a reasonable challenge. Third, we could simulate a diploid genome; we know of no existing diploid data set (simulated or real) in which the contributions of the two haplotypes are precisely and fully known. This allowed us to assess a heretofore-unexplored dimension of assembly assessment.

To simulate the genome we used the Evolver suite of genome evolution tools. Evolver simulates the forward evolution of multichromosome haploid genomes and includes models for evolutionary constraint, protein codons, genes, and mobile elements.

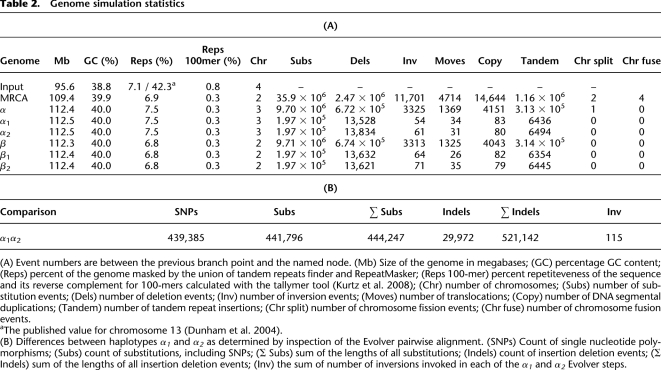
The input genome for the simulation, termed the root genome, was constructed by downloading the DNA sequence and annotations (see Methods) for human chromosome 13 (hg18/NCBI36, 95.6 non-N megabases [Mb]) from the UCSC Table Browser (Fujita et al. 2011) and dividing it into four chromosomes of approximately equal length. Figure 1 shows the phylogeny used to generate the simulated genomes, with branch lengths to scale. We first evolved the root genome for ∼200 million years (my) to generate the most recent common ancestor (MRCA) of the final leaf genomes. We performed this long burn-in on the genome in order to reshuffle the sequence and annotations present, thereby preventing simple discovery of the source of the root genome. The simulation then proceeded along two independent lineages, generating both α and β, each ∼50 my diverged from the MRCA. Finally, in both lineages we split the evolved genome into two sublineages, termed haplotypes, and evolved these sublineages for a further ∼1 my, to produce a pair of diploid genomes, α_1,2 and β_1,2, each with a degree of polymorphism. The α_1,2 genome's haplotypes, α₁ and α₂, each had three chromosomes, and both haplotypes were 112.5 Mb in total length with chromosome lengths of 76.3, 18.5, and 17.7 Mb.

Figure 1.

The phylogeny of the simulated haploid genomes. The root genome derives from human chromosome 13. The α₁ and α₂ haplotypes form the diploid genome from which we generated reads. The β₁ and β₂ haplotypes form a diploid out-group genome that was made available to the assemblers.

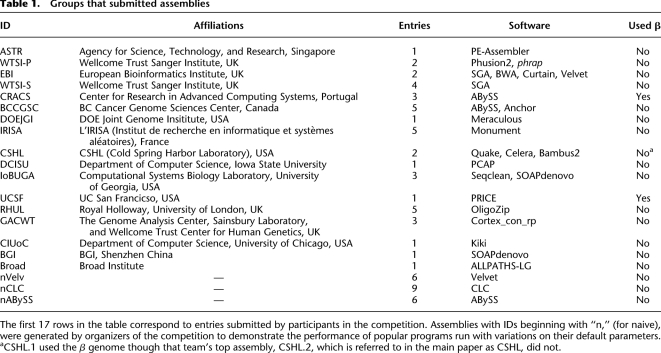
The diploid α_1,2 genome was used as the target genome for the assembly. The β_1,2 genome's haplotypes, their common ancestor, β, and their annotations, were provided to the assemblers as an out-group. Relatively few assemblers (see Table 1) reported using these sequences to assist in the assembly process.

Table 1.

Groups that submitted assemblies

Table 2A provides a count of some of the events that took place along particular branches in the phylogenetic tree during the course of the simulation. Table 2B provides a summary of the pairwise differences between the α₁ and α₂ haplotypes and Supplemental Figure 1 shows a dot-plot of their alignment. Supplemental Figures 2 and 3 show the length distribution of annotations for the root, MRCA, internal node, and leaf genomes, demonstrating that these annotations remained approximately static over the course of the simulation. We examined repeat content of the simulated genomes (see legend to Table 2) and found a comparable portion of annotated repeats to that in the original human chromosome 13, but a reduction of slightly more than half in the proportion of repetitive 100-mers (Supplemental Fig. 4). The simple substitution model used by Evolver, which fails to capture some of the higher order dependencies in substitution patterns that made the original human DNA sequence more repetitive, likely explains this latter observation.

Table 2.

Genome simulation statistics

Read simulation

As mentioned, there are many competing technologies now available for sequencing, giving us many possible options in designing the data sets for the first Assemblathon. However, we opted to simulate just one combined short read data set, with multiple read libraries, for the Illumina Hi-seq platform (http://www.illumina.com/systems/hiseq_2000.ilmn), which is the current market leader for low-cost de novo sequencing on this scale. The advantage of this was chiefly (1) the avoidance of fragmentation in the entries to the Assemblathon, thereby preventing categories with few or just one entry, and (2) the ability to assess all of the submitted assemblies with common sets of evaluations.

We needed a program that would generate short reads and model sources of error that the Illumina protocols introduce. As we knew of no existing software that was capable of this (see Methods for a discussion of existing read simulators), we wrote our own short read simulator, called SimSeq (https://github.com/jstjohn/SimSeq).

Abstractly, reads were sampled from the genome using one of two types of Illumina-paired read strategy, so called “paired-end” and “mate-pair” strategies, after which an error profile was applied to each read in its proper orientation. In addition to generating reads from the target α_1,2 genome, three copies of an Escherichia coli sequence (gi 312944605) were added to the two haplotype sequences to yield a ∼5% bacterial contamination rate. Bacterial sequence was included as an attempt to model the sort of contamination occasionally present in data from sequencing centers, though the specific choice of E. coli and the 5% level were arbitrary. Participants in the contest were notified that some bacterial contamination was present in the data, though they were not told about its precise nature nor explicitly told to remove it.

Multiple libraries were generated for both the paired-end and mate-pair strategies. Paired-end libraries with 200- and 300-bp inserts contributed 80×, mate-pair libraries with separations of 3 and 10 kb contributed a further 40×, giving a total coverage of 120× for the sample. Removing contamination reads gave an overall coverage of ∼55× per haplotype.

A detailed description of the simulation method, the types of errors simulated, and the simulator's limitations are given in the Methods section. Importantly, due to human error, the error model was mistakenly reversed along the reads. This resulted in bases with a slightly higher error rate tending to appear toward the beginning of the reads rather than toward the end of reads (see Supplemental Fig. 5). This issue only manifests itself if the reads are treated asymmetrically; we surveyed participants on this matter and only one group, L'IRISA, indicated that their methodology was possibly harmed more than other methods due to the mistake.

Assemblies

The competition started in January 2011 and teams were given just over 1 mo to submit their assemblies. Teams were allowed to submit up to five separate assemblies for consideration. Additionally, assemblies were created by the organizers with popular assembly programs, using default parameters, as a way of comparing naively generated assemblies with those that were contributed by independent groups. Table 1 lists the evaluated assemblies, the main program used to generate them, and the groups that contributed them (see Supplemental section 8.2 for detailed information on submissions). In total there were 59 assemblies, with 41 independently contributed by 17 different groups using 15 different assembly programs and 18 generated by the organizers using three popular programs.

Evaluations

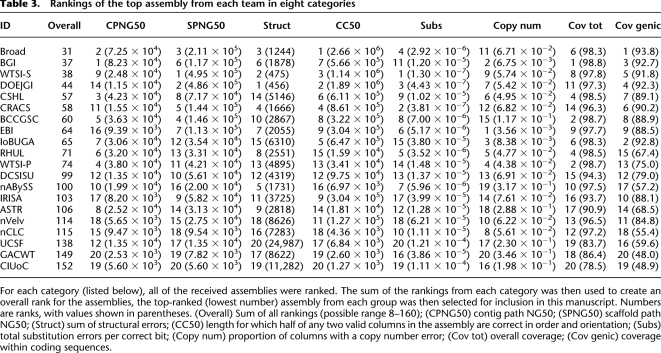
We assessed all of the contributed assemblies, full results for which can be found in the Supplemental material. However, to make the presentation succinct we choose to present only the “top” assembly from each group in the following evaluations. To enable this we created a ranking of the assemblies (see Table 3; Supplemental Table 1), using the evaluations described below, and selected the assembly from each group with the top overall ranking for inclusion. Full results for each evaluation on every assembly in the main text can be found in the Supplemental material.

Table 3.

Rankings of the top assembly from each team in eight categories

N50 and NG50

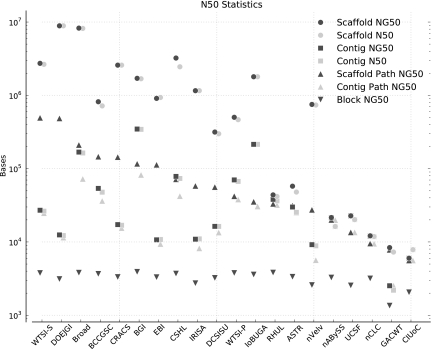
A commonly used metric to assess assemblies is the N50 statistic. The N50 of an assembly is a weighted median of the lengths of the sequences it contains, equal to the length of the longest sequence s, such that the sum of the lengths of sequences greater than or equal in length to s is greater than or equal to half the length of the genome being assembled. As the length of the genome being assembled is generally unknown, the normal approximation is to use the total length of all of the sequences in an assembly as a proxy for the denominator. We follow this convention for calculating N50, but additionally we define the NG50 (G for genome). The NG50 is identical to N50, except that we estimate the length of the genome being assembled as being equal to the average of the length of the two haplotypes, α₁ and α₂. Contig N50s and NG50s, where the sequences are the set of assembly contigs, and scaffold N50s and NG50s, where the sequences are the set of assembly scaffolds, are shown in Figure 2, Supplemental Figure 6, and Supplemental Table 2.

Figure 2.

N50 statistics. Assemblies are sorted left to right in descending order by scaffold path NG50. Data points for each assembly are slightly offset along the x-axis in order to show overlaps.

The total span of most of the submitted assemblies was slightly larger than the haploid genome size, primarily because of the degree of polymorphism of the two haplotypes. Thus, the assembly-specific N50s are in general smaller than the NG50s, with the median absolute difference between contig NG50 and contig N50 being 599 bp (7.7%), and the median absolute difference between scaffold NG50 and scaffold N50 being 1942 bp (3.6%). These differences are quite small, though not negligible in every case; for example, the CSHL assembly has a scaffold NG50 ∼800 kb (31.6%) longer than scaffold N50.

Multiple sequence alignment

While N50 statistics give a sense of the scale and potential contiguity of an assembly, they say nothing necessarily about the underlying coverage or accuracy of an assembly. To compare each assembly with the simulated genome and bacterial contamination we constructed a multiple sequence alignment (MSA). The sequence inputs to the MSA were the two haplotypes, the bacterial contamination, and the scaffolds of the assembly. To generate the MSA we used an adapted version (see Methods) of the newly developed Cactus alignment program (Paten et al. 2011b), a new MSA program able to handle rearrangements, copy-number changes (duplications), and missing data. The result of this alignment process was, for each assembly, a high-specificity map of the alignment of the assembly to the two haplotypes and the bacterial contamination.

As we aligned both the bacterial contamination and the two haplotypes together, we used the hypothetical existence of any alignments between the haplotypes and the bacterial contamination as a negative control for nonspecific alignment. We did not observe any such alignments. As an additional control we replicated a similar, confirmatory analysis using a simple BLAST (Altschul et al. 1990) strategy, details of which can be found in Supplemental section 7.1, and references to which are made below.

Coverage

An MSA can be divided up into columns, each of which represents a set of individual base-pair positions in the input sequences that are considered homologous. We call columns that contain positions within the haplotypes haplotype columns. We define the overall coverage of an MSA as the proportion of haplotype columns that contain positions from the assembly. Similarly, we can define the coverage of X, where X is a specific haplotype or the bacterial contamination, as the proportion of columns containing positions in X that also contain positions from the assembly.

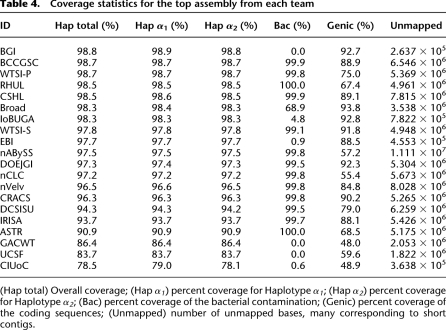
Table 4 shows the overall, haplotype-specific, and bacterial contamination-specific coverage. There is very little difference between the specific haplotype's coverage and the overall coverage and, indeed, little difference between many of the assemblies. The highest overall coverage was the BGI assembly with 98.8%, but nearly all assemblies performed well in this metric with even the assembly with 14^th highest coverage, the CRACS assembly, providing 96.3% coverage. However, there were huge differences in the coverage of the bacterial contamination (Supplemental Figs. 7, 8), with many groups opting successfully to completely filter it out. For example, the BGI assembly had no coverage of the bacterial sequence, while the ASTR assembly had 100.0% coverage of the bacterial sequence.

Table 4.

Coverage statistics for the top assembly from each team

Blocks and contig paths

Within an MSA a block is a maximal gapless alignment of a set of sequences and is therefore composed of a series of contiguous columns. The length of a block is equal to the number of columns that it contains. We can use the block structure to define the block NG50, which is exactly like the NG50, except that we use the distribution of block lengths rather than sequence lengths. Supplemental Figures 9 and 10 show block coverage across the haplotypes. Alignment of sequences that are very closely related are likely to contain fewer blocks with a greater base-pair length than sequences that are significantly diverged from one another. Unfortunately, the two simulated haplotypes are sufficiently polymorphic with respect to one another, which the block NG50 of an alignment of just the two haplotypes is ∼4 kb. As this length is much less than the length of many sequences in the assemblies, assessing an assembly requires methods that do not penalize the reconstruction of haplotype-specific polymorphisms. This is evident by looking at Figure 2, which shows that block NG50 is poorly discriminative. See Supplemental section 7.1.1 and Supplemental Figure 11 for supporting BLAST based analysis.

To extend our analysis we use a graph theoretic model of the alignments, which we now describe in overview. An MSA can be described as a graph, and we call the simplest such graph an adjacency graph. A formal description of the adjacency graph used here can be found in Paten et al. (2011a), it is closely related to the similarly named graph introduced in Bergeron et al. (2006a), but also to a directed bigraph representation of a de Bruijn graph used in assembly (Medvedev and Brudno 2009) and the multiple breakpoint graph used in the study of genome rearrangements (Alekseyev and Pevzner 2009).

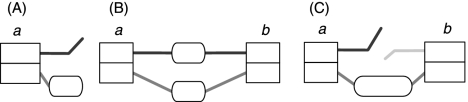
An adjacency graph G contains two kinds of edges, block edges, which represent the gapless blocks of the alignment, and adjacency edges, which represent collections of connections between the ends of segments of DNA. The nodes in the graph represent the ends of blocks of aligned sequences. Figure 3 illustrates an example.

Figure 3.

An adjacency graph example demonstrating threads, contig paths, and scaffold paths. Each stack of boxes represents a block edge. The nodes of the graph are represented by the left and right ends of the stacked boxes. The adjacency edges are groups of lines that connect the ends of the stacked boxes. Threads are represented (inset) within the graph as alternating connected boxes and colored lines. There are three threads shown: (top to bottom) black, gray, and light gray. The black and gray threads represent two haplotypes; there are many alternative haplotype threads that result from a mixture of these haplotype segments, which are equally plausible given no additional information to deconvolve them. The light-gray thread represents an assembly sequence. For the assembly thread, consistent adjacencies are shown in solid light gray. The dashed light gray line between the right end of block g and the left end of block i represents a structural error (deletion). The dashed light-gray line between the right end of block k and the left end of block m represents a scaffold gap, because the segment of the assembly in block n contains wild-card characters. The example, therefore, contains three contig paths: (from left to right) blocks a…g ACTGAAATCGGGACCCC; blocks i, j, k GGAAC; and block m CC. However, the example contains only two scaffold paths because the latter two contig paths are concatenated to form one scaffold path.

Each edge in G is labeled with the subsequences it represents, called segments; thus, it is possible to discern whether the edge represents segments in the haplotypes, the assembly, the bacterial contamination or some combination. As previously stated, no edges are contained in G that represent segments in both the haplotypes and the bacterial contamination.

Within G, a sequence is represented as a path of alternating adjacency and block edges, termed a thread. We can assess the accuracy of assembly sequences by analyzing their thread representation in the adjacency graph. Let P be the thread representing an assembled sequence in G. Any edge e in P is consistent if that edge is also labeled with segments from either or both of the haplotypes. For any P, a contig path is a maximal subpath of P in which all the edges are consistent. Thus, P can be divided up into a series of contig paths, possibly interspersed with edges in P that are not contained in a contig path, see Figure 3 for an example. The base-pair length of a contig path is equal to the sum of the base-pair lengths of the block edges it contains. Contig paths represent maximal portions of the assembled sequence that are consistent with one or both of the haplotypes and contain no assembly gaps, they can be thought of as portions of an assemblies' contigs that perfectly follow a path through the graph of haplotype polymorphism.

Figure 2 shows contig path NG50s, defined analogously to block NG50; Supplemental Figures 12 and 13 show contig path coverage across the haplotypes, while Supplemental Figures 14 and 15 show, in contrast, the same plots, but instead use raw contig lengths. The contig path NG50s are substantially larger than block NG50s; for example, the BGI assembly has a contig path NG50 1.5 orders of magnitude bigger than its block NG50. The difference between the largest and smallest block NG50 is 2556 bp (GACWT 1351 bp to BGI 3907 bp); the difference between the largest and smallest contig path NG50 is 79,731 bp (GACWT 2533 bp to BGI 82,264 bp). Thus, the contig path NG50 results demonstrate that assemblies are able to reconstruct substantial regions perfectly, and contig path NG50 appears to be a more discriminative statistic than block NG50, as it indicates large differences between the assemblies.

Scaffold paths

To account for gaps within scaffolds, which we henceforth call scaffold breaks, we define scaffold paths. Scaffold paths can be thought of as portions of the assemblies' scaffolds that perfectly follow a path through the graph of haplotype polymorphism, but which are allowed to jump unassembled sequences at scaffold gaps. Scaffold gaps are scaffold breaks (denoted as contiguous runs of wild-card characters in an assembly) whose surrounding contig ends are bridged by a path of haplotypes representing edges within the adjacency graph; see Figure 3 for an example and the Methods section for a formal definition.

Notably, our definition of a scaffold gap within the graph is permissive in that it allows (1) any sequence of Ns to define a scaffold break, and (2) the sequence of Ns that define the scaffold break to be aligned within the ends of the block that sandwich the gap in the assembly. This definition was sought because there is currently a wide variation in the syntax used to define such gaps within different assemblers, and to be tolerant of alignment errors caused by the phenomena of edge wander (Holmes and Durbin 1998) caused when the alignment of positions around a gap has more than one equally probable scenario. As a scaffold path is a concatenation of contig paths, its base-pair length is just the sum of the base-pair lengths of the contig paths that it contains.

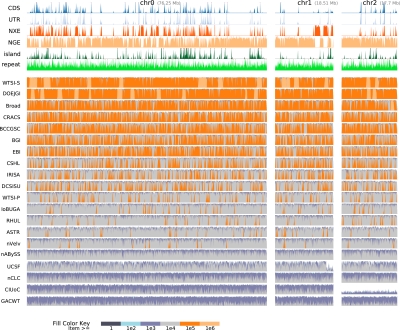
Figure 2 shows the scaffold path NG50, defined analogously to the block and contig path NG50s, sorted with respect the scaffold NG50. In many cases the scaffold path NG50 is substantially larger than the contig path NG50. Figure 4 shows a stack fill plot of the coverage of scaffold paths along the three chromosomes of haplotype α₁ (see also Supplemental Figs. 16–19). It demonstrates the substantial differences between the assemblies and shows that large, megabase regions of the haplotype can be reconstructed with assembly gaps, but without apparent error.

Figure 4.

Assembly coverage along haplotype α₁ stratified by scaffold path length weighted overall coverage. The top six rows show density plots of annotations. (CDS) Coding sequence; (UTR) untranslated region; (NXE) nonexonic conserved regions within genes; (NGE) nongenic conserved regions; (island) CpG islands; (repeats) repetitive elements. The remaining rows show the top-ranked assembly from each group, sorted by scaffold path length weighted overall coverage. Each such row is a density plot of the coverage, with colored stack fills used to show the length of scaffold paths mapped to a given location in the haplotype. For example, the left-most light-orange block of the WTSI-S assembly row represents a region of haplotype α₁ that is almost completely covered by a scaffold path from the WTSI-S assembly greater than one megabase in length.

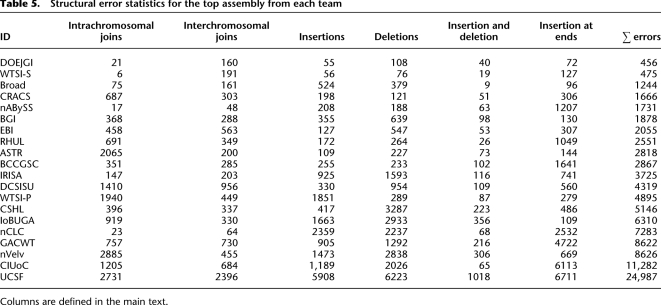
Structural errors

Despite the long lengths of many scaffold paths, for most assemblies the scaffold NG50 is substantially larger than the scaffold path NG50, indicating that there were apparent errors that broke scaffolds into smaller sets of scaffold paths. To analyze these errors we continued our graph analysis, defining a number of subgraph types to represent them, which we formally define in the Methods section. These subgraph definitions include erroneous intra- and interchromosomal joins, insertions, deletions, simultaneous insertion and deletions, and insertions at the ends of assembled sequences. Table 5 (and Supplemental Table 3) shows the numbers of structural errors for each assembly; Supplemental Figures 20 and 21 show structural errors across the haplotypes. Many assemblies do not have categories of error to which they are particularly prone, but a few do. In these cases there may be a systematic bias in the operation of the programs that generated them or in the way that we interpreted them.

Table 5.

Structural error statistics for the top assembly from each team

Insertion and deletion (indel) structural errors involve, respectively, the addition and removal of a contiguous run of bases. In Supplemental Figures 22 and 23 we investigate the size distribution of such errors, using both the described MSA and supporting alignments from the progressiveMauve program (Darling et al. 2010). We find that in almost all cases, the size distribution of the segments of inserted and deleted bases follows an approximately geometrically decreasing distribution.

We also searched for subgraphs in which the assembly created a haplotype to contamination chimera, but did not find any such subgraphs. To investigate this surprising result we searched for such chimeras using BLAST with relaxed parameters (Supplemental section 7.1.3; Supplemental Fig. 24). Using this approach we found 56 assemblies with no such chimeras, seven assemblies with 1 chimera, one assembly with two chimeras, and one outlier assembly with 26 chimeras. In each case we verified that these chimeras were missed in the graph approach due to the stringent MSA parameters.

Long-range contiguity

The MSA graph theoretic analysis we have described is local in nature and quite strict, in that it has no notion of large-scale contiguity and refuses to stitch together paths that would be joined, but for a small error. We thus sought a method to analyze the larger scale contiguity between pairs of separated points in the genome. Formally, for two positions x_i and x_j in a haplotype chromosome x, such that i < j, if there exists two positions y_k, y_l in an assembly scaffold y such that (1) y_k is in the same column as x_i, (2) y_l is in the same column as x_j, and (3) k < l, we say y_k and y_l are correctly contiguous. Pairs may be correctly contiguous but not necessarily covered by the same contig path or scaffold path, and indeed there may be arbitrary numbers of assembly errors between two correctly contiguous positions.

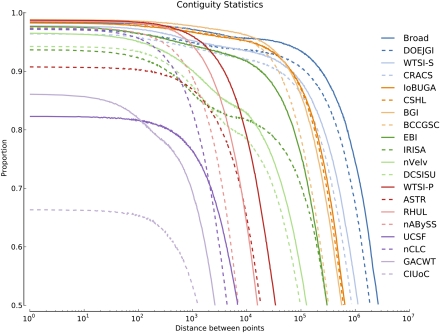
Figure 5 shows the proportion of correctly contiguous pairs as a function of the pairs' separation distance for each assembly. Taken at a high level, in all of the assemblies the proportion of correctly linked pairs monotonically decreases with separation distance. Therefore, we take the separation distance at the 50^th percentile, termed the correct contiguity 50 (CC50) as an essentially sufficient statistic. See Supplemental section 7.1.2 and Supplemental Figures 25 and 26 for supporting BLAST-based analysis.

Figure 5.

The proportion of correctly contiguous pairs as a function of their separation distance. Each line represents the top assembly from each team. Correctly contiguous 50 (CC50) values are the lowest point of each line. The legend is ordered top to bottom in descending order of CC50. Proportions were calculated by taking 100,000,000 random samples and binning them into 2000 bins, equally spaced along a log₁₀ scale, so that an approximately equal number of samples fell in each bin.

Annotation analysis

Evolver maintains annotations for a number of classes of simulated sequence, including genes, which Evolver models as having exons, introns, and untranslated regions (UTRs), and conserved noncoding elements. Additionally, while Evolver does not track the history of individual repeat elements following their insertion, it maintains a library of mobile elements, and thus, using RepeatMasker (v1.25 http://www.repeatmasker.org) and tandem repeats finder (v4.0, http://tandem.bu.edu/trf/trf.html) with this library, we identified a subset of repetitive sequence within the haplotypes.

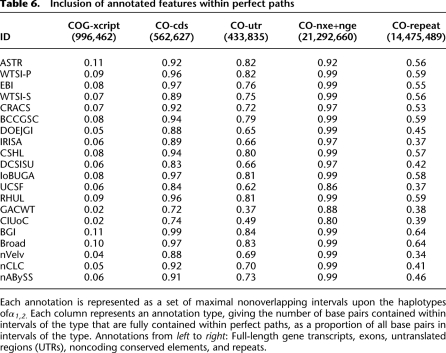
Continuing the previous MSA analysis, we define a perfect path as a maximal subpath of a haplotype thread that is isomorphic to a subpath of an assembly thread. For a given assembly, the corresponding set of perfect paths reflects the regions of the haplotypes that are perfectly reconstructed. Unlike contig and scaffold paths, perfect paths are intolerant of haplotype polymorphism, but give a well-defined set of intervals within α_1,2 for comparison with a set of annotations. Table 6 shows for each assembly the proportion of each annotation type contained within perfect paths.

Table 6.

Inclusion of annotated features within perfect paths

Both haplotypes of the α_1,2 genome contain 176 protein-coding genes, Supplemental Figure 27 show the distribution of their lengths; we find that only a small proportion (max 11% of base pairs, min 2% of base pairs) of these full-length transcripts are perfectly reconstructed by the assemblies. Conversely, we find that in the best assemblies almost all exons and a high proportion of UTRs are perfectly reconstructed, for example, 99% of base pairs in exons and 84% of base pairs in UTRs of the BGI assembly. We also find that most perfectly reconstructed genes are intronless (data not shown); the assemblies therefore fail mostly to reconstruct introns perfectly. To further characterize this failure we used tBLASTN (Altschul et al. 1990; see Supplemental section 7.1.4) to align the spliced transcripts of α₁ (without introns and UTRs) to the scaffolds of the assemblies, counting a match if it included 95% of the given transcript; see last column of Table 4, labeled genic correctness, and Supplemental Table 1. This more tolerant analysis reveals that in the best assemblies the majority of exon chains are reconstructed contiguously (in the correct order and orientation) within single scaffolds, e.g., the Broad assembly has 107 spliced transcripts (93.8% of base pairs) reconstructed by this metric.

As expected, repeats were the least well-reconstructed annotation types, with the best assembly, BGI, reconstructing only 64% of repeats perfectly (see last column of Table 6). As these regions are naturally difficult to align correctly within an MSA, we also performed BLAST-based fragment analysis, see Supplemental section 7.1.5, with similar results.

Finally, we also looked at conserved noncoding regulatory elements, which Evolver both models and tracks. As these elements are short and relatively nonrepetitive, the majority (88%–99% of base pairs) were perfectly reconstructed by the assemblies.

Substitution errors

We have so far described assessments of structural correctness and contiguity, both overall and for functional genic elements. We now turn to the assessment of somewhat orthogonal issues, first by looking at base calling and then finally by analyzing copy number errors.

Although we do not allow structural rearrangements within MSA blocks, blocks are tolerant of substitutions. Let a (haplotype) column of aligned bases within a block that (1) contains a single position from both haplotypes, and (2) a single position from an assembly sequence, be called valid. We use these criteria because such columns unambiguously map a single assembled sequence to a single position in the alignment of both haplotypes while avoiding the issues of paralogous alignment and multiple counting. We distinguish two types of valid columns: (1) homozygous columns: those containing the same base pair from both haplotypes, and (2) heterozygous columns: those containing distinct base pairs from each haplotype. We also initially considered columns that contain one but not both haplotypes, but found that the numbers of such columns that we could consider reliably aligned was not sufficient for us to confidently compute statistics.

Assemblers are free to use IUPAC ambiguity characters to call bases. To allow for this we use a bit-score to score correct but ambiguous matches within valid columns (see Methods). We say there has been a substitution error if the position in the assembly sequence has an IUPAC character that does not represent either of the haplotypes' base pair(s).

Some of the substitution errors that we observe are likely due to misalignments. These can occur due to edge wander (Holmes and Durbin 1998) or the larger scale misalignment of an assembled sequence to a paralog of its true ortholog. The sum of substitution errors over all valid columns is therefore an upper bound on the substitution errors within valid columns. To obtain a higher confidence set of substitution errors we select a subset of valid columns that meet the following requirements: (1) are part of blocks of at least 1 kb in length, avoiding errors within short indels, (2) are not within five positions of the start and end of the block, avoiding edge wander, and (3) are within blocks with 98% or higher sequence identity, ensuring that the alignments are unlikely to be paralogous. The sum of substitution errors within these high-confidence valid columns represents a reasonable lower bound of the number of substitution errors within valid columns.

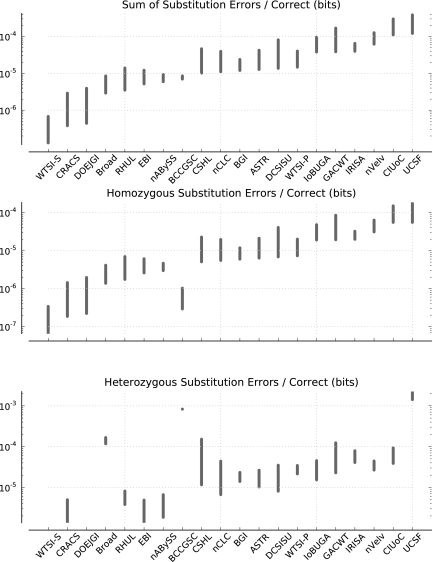
Figure 6 (also Supplemental Fig. 29; Supplemental Tables 4, 5) show, as might be expected, that there are, in general, proportionally more errors made in heterozygous columns than homozygous columns, though there are naturally much fewer overall heterozygous positions; for example, the WTSI-S and CRACS assemblies made no heterozygous errors. We find a strong correlation between error rates in heterozygous and homozygous columns, with the exceptions of the Broad and BCCGSC assemblies, which have proportionally higher rates of heterozygous errors. The Broad result is explained by the large number of N ambiguity characters called at heterozygous sites, which makes the number of errors per bit correspondingly higher, while the BCCGSC result was due to a programmatic error in the assembler's pipeline that has since been identified and resolved as a result of this analysis. Interestingly, we find considerable variation between the programs in overall error rates. The strongest assembly, WTSI-S, makes one error for every 15.3 × 10⁶–2.94 × 10⁶ correct bits, or approximately one every 7.7 × 10⁶–1.49 × 10⁶ bases, while the weakest assembly, UCSF, makes an error for every 6.7 × 10³–1.81 × 10⁴ correct bits, or approximately one in every 3.3 × 10³–9.0 × 10³ bases.

Figure 6.

Substitution (base) errors for the top assembly from each team. (Top) Substitution errors per correct bit within all valid columns; (middle) substitution errors per correct bit within homozygous columns only; (bottom) substitution errors per correct bit within heterozygous columns only. Assemblies are sorted from left to right in ascending order by the sum of substitutions per correct bit. In each faceted plot, each assembly is shown as an interval, giving the upper and lower bounds on the numbers of substitution errors (see main text).

Copy-number errors

Within any haplotype column of the MSA, the copy number of the simulated diploid genome can be described by an interval (min, max), where min is the minimum number of bases either of the two haplotypes contributes and max is the maximum number of bases either of the two haplotype contributes. To establish whether assemblies were producing too many or too few copies of the homologous positions within the two haplotypes, we looked for haplotype columns where the copy number of the assembly lay outside of this copy-number interval. There are two possibilities, either the number of copies in the assembly is less than min, in which case there is a deficiency in the copy number, or the number of copies in the assembly is greater than max, in which case there is an excess in the copy number.

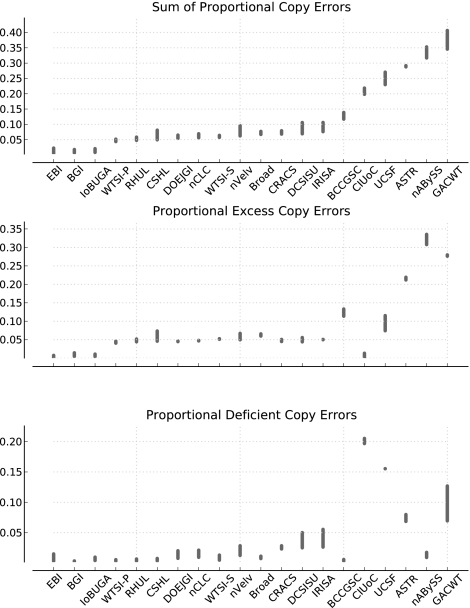
Figure 7 (also Supplemental Fig. 30) shows the proportions of haplotype columns with copy-number excesses and deficiencies. Again, to address contributions made by alignment errors we choose to produce an upper and lower bound on these proportions. The lower bound is taken over all haplotype columns in the alignments, while the upper bound is computed over only haplotype columns that are part of blocks of at least 1 kb in length.

Figure 7.

Copy-number errors for the top assembly from each team. (Top) Proportion of haplotype containing columns with a copy-number error; (middle) proportion of haplotype containing columns with an excess copy-number error; (bottom) proportion of haplotype containing columns with an excess copy-number error. Assemblies are sorted from left to right in ascending order according to the proportion of haplotype containing columns with a copy-number error. In each faceted plot, each assembly is shown as an interval, giving the upper and lower bounds on the numbers of copy-number errors (see main text).

The deficiencies are dominated by cases in which the assembly is not present; therefore, copy-number deficiency is closely correlated with coverage. Unfortunately, there are not a sufficient number of cases where the assembly is present but the copy number is deficient so that we may make reliable inferences about this interesting category. This appears to be a consequence of the genome simulation lacking sufficient numbers of recent duplications, and may be an indication that the genome simulation is somewhat unrealistic, as other investigators (Worley and Gibbs 2010; Alkan et al. 2011) have discussed that recent segmental duplications cause substantial problems for assemblies generated with short reads.

We find that there are substantial numbers of copy-number excesses, such that generally the number of excesses was larger than the number of deficiencies. We find that excesses do not correlate particularly well with deficiencies, particularly for programs with extremes of deficiency or excess. We do find, however, that excesses correlate well with input assembly size (data not shown). The best assembly, EBI, has excesses between 0.0521% and 0.752% of haplotype columns, while the least assembly, nABySS, has excesses between 30.8% and 33.5% of haplotype columns.

Discussion

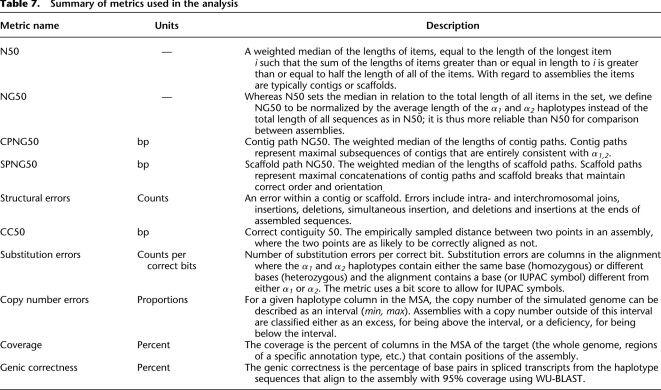
We have used simulation to create a novel benchmark data set for de novo assembly. We have evaluated a previously unprecedented 41 different assemblies from 17 different groups, making it the largest short read de novo assembly evaluation to date. In summary, we have assessed coverage, the lengths of consistent contig and scaffold paths, structural errors, long-range contiguity, the assembly of specific annotated regions, including genes and repeats, base calling errors, and copy number errors; Table 7 conveniently summarizes these evaluation metrics. This benchmark data set is freely available online at http://www.assemblathon.org/ and is supplemented by a code that can take new assemblies and amalgamate the new result into the analysis we present here. It is our hope that this standard will assist the assembly community when introducing new methods by providing a large set of metrics and methods with which to compare.

Table 7.

Summary of metrics used in the analysis

Given the degree of polymorphism within the α_1,2 genome, the haplotype aware evaluations proved critical to the assessment. For example, the haplotype aware path analysis demonstrates that methods are able to reconstruct multiple megabases, with scaffold breaks, essentially perfectly. We chose to treat switches between the haplotypes of α_1,2 permissively, because the assemblers were not asked to reconstruct the two haplotypes, but rather to produce a consensus reference of the two. It is an open question whether, with this data set or one like it, an assembly could produce phased variants of each scaffold. In section 7.3 of the Supplemental material we tested whether there was any evidence of teams phasing single nucleotide polymorphisms (SNPs) or structural variants by preferentially choosing one haplotype, but we did not find convincing evidence for either, apart from that inadvertently caused by a bias in the simulated reads (see Methods: problems with the error model used in Assemblathon 1).

Table 3 shows the rankings of each of the featured assemblies for each of the described assessments; additionally, in Supplemental Figures 31 and 32 we assess correlations between the logs of different metrics. Intuitively, one might expect the path analysis metrics and the contiguity assessments to be correlated to one another and inversely correlated with structural errors. Indeed, this intuition proves partially correct. Contiguity (CC50) and scaffold path NG50 are strongly correlated (R² = 0.77, P < 0.001), while structural errors are inversely correlated with scaffold path NG50s, with one explaining about half the variance of the other (R² = 0.48, P < 0.001). However, contig path NG50 is only weakly correlated with scaffold path NG50 (CPNG50–SPNG50 R² = 0.38, P < 0.001) and contiguity (CPNG50–CC50 R² = 0.31, P < 0.01), suggesting that the scaffolding process is more important in producing accurate long scaffolds than the prior contigging process.

Given the popularity and simplicity of N50 statistics, it is perhaps reassuring how well these metrics correlate with the path and contiguity metrics (SN50–CC50 R² = 0.98, P < 0.001; SN50–SPNG50 R² = 0.74, P < 0.001; CN50–CPNG50 R² = 0.64, P < 0.001), suggesting that one may usefully compare N50 measurements between assemblies, and not just between assemblies by the same program. Interestingly, the genic correctness measure also correlates with all of the N50 measures, and most strongly with the correct contiguity 50 (R² = 0.98, P < 0.001) and scaffold N50 measures (R² = 0.98, P < 0.001).

We do not find that substitution errors and copy-number errors correlate substantially with anything else, except for a correlation between substitution errors and structural errors (R² = 0.45, P < 0.001). This is perhaps unsurprising, given the orthogonal basis of these metrics to each other and the other evaluations. Perhaps, surprisingly, coverage does not correlate strongly with other measures, and in particular, not with contig or scaffold N50 statistics, suggesting such naive measures are not good proxies for coverage.

Table 3 highlights that while the best assemblies are stronger in most categories than the weakest assemblies, all of the assemblies have areas in which they can improve relative to their peers, if at a trade-off cost in other categories. For example, the BGI assembly, while having the largest contig path NG50, has only the sixth largest scaffold path NG50, which is more than four times smaller than the strongest method in this category (WTSI-S), suggesting that its scaffolding could be improved. Conversely, the WTSI-S and DOEJGI assemblies had large contiguity (CC50) and scaffold path (SPNG50) measures and low numbers of structural errors, but relatively short contig paths (CPNG50), suggesting that their contigging could be made more aggressive, though possibly with a corresponding increase in structural errors.

We have demonstrated in simulation that the best current sequence assemblers can reconstruct at high coverage and with good accuracy large sequences of a substantial de novo genome. This is concordant with other recent work that suggests that short read sequencing is becoming competitive with capillary sequencing (MacCallum et al. 2009; Gnerre et al. 2011). MacCallum et al. (2009) looked at five microbial genomes with sizes ranging from 2.8 Mb (Staphylococcus aureus) to 39.2 Mb (Neurospora crassa) and determined that with data from two paired libraries, the ALLPATHS 2 program was able to produce assemblies with qualities that exceeded draft assemblies using Sanger methods. Gnerre et al. (2011) sequenced two genomes: a human cell line (GM12878) and a mouse strain (C57BL/6J female) and assembled them using the ALLPATHS-LG program. The investigators found that with Illumina reads of 100× coverage in four library types their assemblies neared capillary sequencing quality in completeness, long-range connectivity, contiguity, and accuracy.

There are a number of important limitations with the current work. First, the use of simulation makes it hard to know how applicable these results are to any other data set; though this is arguably true of any data set, the simulation's limitations, in particular the noted issues with the read simulation and with the low repeat content of the genome likely influence the results. Second, the limited size of the simulated genome means that some of the strategies used here may not work as effectively, or at all, on larger vertebrate scale genome data sets. Finally, as our results derive from a single data set in which no attempt was made to measure the variance of our various metrics, it is questionable how reliable our measurements are. To address these issues, a second competitive evaluation, Assemblathon 2, is now underway.

Given the scale of challenges in making assessments and to avoid fragmentation, we suggest that Assemblathon 2 continue to focus on the assessment of complete pipelines, rather than attempting to assess individual pipeline components. We also suggest that it continue to rely on the individual assembly teams to compute their own assemblies, despite this making it difficult to compare the computational requirements of the pipelines, given the self-reported nature of such data and the heterogeneous equipment upon which the assemblies are computed.

However, we conclude by making three distinguishing suggestions for Assemblathon 2 that would sufficiently expand its scope from this initial competition. First, it should feature at least one mammalian genome scale data set to test the scaling of the assembly pipelines. Second, it should feature real data to compare with the simulation results presented in this competition; this may necessitate the use of a different set of evaluation metrics, where the “correct” answer is unknown. Third, it should be expanded to include other sequencing technologies so that a better comparative, unbiased understanding of available sequencing technologies can be made.

Methods

Genome simulation

The Evolver simulation was managed by a set of scripts (https://github.com/dentearl/evolverSimControl/), which control the execution of Evolver and allow a general phylogeny to be simulated.

As well as a starting sequence, Evolver also requires a set of annotations that are used to assign sequences to element types that undergo differential evolution simulation. The following annotations were used: UCSC Genes, UCSC Old Genes, CpG Islands, Ensembl Genes, and MGC Genes from the UCSC table browser (Fujita et al. 2011). The root genome was then coupled with parameters and a mobile element library (A Sidwo, pers. comm.) to form the Evolver in-file set for the simulation.

Evolver proceeds iteratively by a series of discrete steps. We used an Evolver step length of 0.01 substitutions per site, meaning the initial branch length of 0.4 substitutions per site (∼200 my) (Hedges et al. 2006; Fujita et al. 2011) from the root node to the most recent common ancestor (MRCA) of the final leaf genomes node consisted of 40 separate Evolver cycles. The lineages leading from the MRCA to α and β descend for a distance of 0.1 (∼50 my) substitutions per site in 10 Evolver cycles. The final splits into the lineages leading to the leaf genomes were each performed in one Evolver cycle of 0.002 substitutions per site (∼1 my), with parameters scaled appropriately. An alignment between the α₁ and α₂ haplotypes is available on the project website (http://compbio.soe.ucsc.edu/assemblathon1/).

Read simulation

Prior to writing our own read simulator we considered several pre-existing tools. We first considered wgsim (Li et al. 2009). Unfortunately, this program does not model mate-pair llumina reads, and it models error rates uniformly across the sequence. We note that this error rate limitation is removed in dwgsim (http://sourceforge.net/apps/mediawiki/dnaa/). However, dwgsim does not model chimeric mate-pair reads or paired-end contamination, which we wished to model. We contacted Illumina and requested their in-house programs for simulating reads. The Illumina software package was capable of modeling chimeric mate-pair reads, and it modeled error rates by copying quality strings from a user supplied file of Illumina reads. Unfortunately, this method did not allow us to model different error rates conditioned on different underlying bases, which we felt was important. We also considered several other software packages for modeling Illumina style reads, including metasim (Richter et al. 2008), PEMer (Korbel et al. 2009), ReSeqSim (Du et al. 2009), SimNext (http://evolution.sysu.edu.cn/english/software/simnext.htm), Flux Simulator (http://flux.sammeth.net/index.html), and Mason (part of the SeqAn package) (Döring et al. 2008), all of which lack one or more of the criteria we desired.

Given these findings, we wrote our own simulator, which combined the capabilities of the Illumina supplied software to model chimeric mate-pair reads, as well as standard paired-end reads, with our own position and reference-base-specific empirical error model trained on Illumina data.

Read sampling strategy

For read sampling we used two separate methods, one for mate-pair libraries and the other for paired-end libraries. Reads were first sampled uniformly across each sequence. Coverage depth was kept approximately uniform by weighting the number of reads sampled from each sequence by its length. Read fragments were sampled from either strand with equal probability. Duplicates were produced with some probability before the error was applied to the reads. See Supplemental Figure 33 for a density map of read depth across the haplotypes.

Paired-end sampling

Illumina paired-end sampling was the most straightforward strategy to simulate. It involved randomly selecting fragments in the 150–500-bp range uniformly across the genome until the desired coverage was met (specific sizes below). Fragment size was sampled from a normal distribution with a specified mean and variance. The reads were oriented facing each other and were sampled from either strand with equal probability. The following paired-end libraries were generated:

• 200 bp insert ±20 SD

  • 2× 100 bp

  • 22,499,731 read pairs (∼40× coverage of the diploid sequence)

  • 0.01 probability of being a duplicate

• 300 bp insert ±30 SD

  • 2× 100 bp

  • 22,499,731 read pairs (∼40× coverage)

  • 0.01 probability of being a duplicate

Mate-pair sampling

Illumina mate-pair library construction differs from paired-end library construction in that it introduces several unique types of error into the reads. In reality, these libraries are constructed by attaching a chemical tag onto the ends of a long sequence fragment, typically in the range of from 2 to 10 kb, after which the fragment is circularized. The circularized product is then further fragmented into sizes typically within the 200–500-bp range, which is the upper limit on fragment lengths for Illumina sequencing. Finally, the resulting mixture is purified for fragments that contain the chemical tag, so that DNA from near the ends of the original 2–10-kb loop are what ideally get sequenced.

There are three common types of error introduced in the mate-pair library preparation process, and we modeled two of them. First, when the fragments are circularized, there is a chance that a loop will be formed between two nonrelated long fragments, resulting in chimeric reads between two unrelated parts of the genome. We did not model this type of error. Assuming that the fragment is properly circularized, the second type of error is produced when a fragment that does not contain the chemical tag is mistakenly sampled. When this happens, the loop join is not part of the fragment, and a paired-end style read with a short insert is mixed in with the rest of the library. We did model this type of error, and varied the probability of its occurrence with each mate-pair library. The final major source of error is created during the random fragmentation process and results in the loop join position occurring in the middle of a read rather than between the two reads. We modeled this by assuming a uniform distribution of loop join sites across a sampled loop fragment, which resulted in chimeric reads as a function of the size of the fragmented loop piece, and the length of the reads. For example, shorter reads and longer loop fragmentation pieces were less likely to result in a chimeric read. The following mate-pair libraries were generated:

• 3 kb loop length ±300 SD

  • 2× 100 bp

  • 500 bp loop fragmentation size ±50 bp

  • 0.2 probability of sampling a PE fragment rather than an MP fragment

  • 11,249,866 read pairs (∼20× coverage)

  • 0.05 probability of being a duplicate

• 10 kb loop length ±1 kb SD

  • 2 × 100 bp

  • 500 bp loop fragmentation size ±50 bp

  • 0.3 probability of sampling a PE fragment rather than an MP fragment

  • 11,249,866 read pairs (∼20× coverage)

  • 0.08 probability of being a duplicate

Base-level error model

We utilized an error model that is dependent on the position within the read and the underlying reference base. To generate this model we assembled a human mitochondrial genome using reads from an Illumina HiSeq run (http://www.illumina.com/systems/hiseq_2000.ilmn) with the reference-guided assembler MIA (Green et al. 2010). We then took that assembly and mapped all reads back to it using BWA with default settings to do a paired-end mapping to the sequence. We kept all alignments with a mapq quality score over 10. We then iterated through the alignment and built an empirical distribution of phred (Ewing et al. 1998) scores and the probabilities of observing one of A, C, G, T, or N given the reference base, the position in the read, and the reported phred quality score. The error model was therefore conditioned on the phred score, position, and reference base, and did not assume that the phred scores were an accurate representation of the underlying error rates.

Problems with the error model used in Assemblathon 1

The error model used was appealingly simple but has limitations that should be understood. First, in generating the error model we omitted many reads that had an error rate that was too high to confidently map to the assembled mitochondria. In the future this could partially be overcome by using the PhiX control lane (http://www.illumina.com/products/multiplexing_sequencing_primers_and_phix_control_kit.ilmn), where one can confidently force the vast majority of the reads to map back to the PhiX 174 genome (NCBI accession no. NC_001422.1) and do not have to be as sensitive to false-positive alignments.

Second, since we used a flat naive prior on the distribution of phred scores; when training our empirical model there was, due to noise, a mixture of good and poor quality bases at the ends of the reads. Since each position was treated independently, the distribution of phred scores was therefore likely not typical, resulting in the likely relative failure of assembler heuristics used to trim strings of bad phred scores at the ends of reads.

Third, since we wrote the simulator following the general algorithmic flow of the wgsim read simulator (Li et al. 2009), reads were randomized within haplotype chromosomes, but not between haplotype chromosomes, resulting in reads from each haplotype and chromosome being clustered together separately in the data. Thankfully, an investigation of phasing bias in Supplementary section 7.3 shows that only a few assemblies showed evidence of any bias that could likely be attributable to this.

Cactus alignment assessment

Alignment generation

The Cactus program starts by using the Lastz pairwise alignment program (http://www.bx.psu.edu/∼rsharris/lastz/) to generate a set of pairwise alignments between all of the input sequences, including intrasequence alignments that arise from recent duplications. In the adapted version of Cactus used for the Assemblathon, which we henceforth call Cactus-A, we used the following parameters to Lastz, after discussion with the program's author:–step=10–seed=match12–notransition–mismatch=2,100–match=1,5–ambiguous=iupac–nogapped–identity=98. This ensured that the resulting pairwise alignments were ungapped (without indels), of minimum length of 100 bp, and with an identity (sequence similarity) of 98% or greater, in concordance with the evolutionary distance between the haplotypes. Cactus-A uses these alignments to build a “sparse map'” of the homologies between a set of input sequences. Once this sparse map is constructed, in the form of a Cactus graph (Paten et al. 2011a), a novel algorithm is used to align together sequences that were initially unaligned in the sparse map. To prevent sequences that are not homologous from being aligned in this process we set the alignment rejection parameter, called γ, to 0.2, to filter positions from being aligned that are not likely to have very recently been diverged. The results of Cactus-A are stored as MAF files (Blanchette et al. 2004), one for each assembly; these are available in the Supplemental material.

Scaffold gaps, error subgraphs, and scaffold paths

Let P be a sequence of block edges [(x₁, x₂), (x₃, x₄) … (x_n-1, x_n)] in a thread [thus ignoring the alternating adjacency edges (x₂, x₃), (x₄, x₅), etc.] representing an assembled sequence in the adjacency graph. The ambiguity of a sequence is equal to the number of wild-card characters that it contains (denoted as Ns). Similarly, the ambiguity of a subsequence of P is equal to the ambiguity of the subsequence of the assembly sequence it represents. The prefix ambiguity of (x_i, x_j) is equal to the number of wild-card characters in the first five bases of the assembly sequence that (x_i, x_j) represents, orienting the sequence from x_i to x_j. The approximate ambiguity of a subsequence Q = [(x_i, x_i+1), (x_i+2, x_i+3) … (x_i+j-1, x_i+j)] is equal to the ambiguity of Q plus the prefix ambiguity of (x_i-1, x_i-2) and (x_i+j+1, x_i+j+2), if these edges exist. By using approximate ambiguity rather than just ambiguity we allow for wobble in the alignment caused by edge wander (Holmes and Durbin 1998) when denoting a scaffold gap.

We say a thread is empty if it represents a sequence of zero length, or else we say it is nonempty.

Let a maximal thread of inconsistent adjacency edges and block edges that do not contain haplotypes or bacterial contamination segments be called a joining thread. A joining thread represents an unaligned portion of an assembly sequence. A scaffold gap or error subgraph is defined by a joining thread incident at one or both ends with blocks that contain haplotype segments. We classify such joining threads as follows:

• (A) If the joining thread is not attached to anything at one end (i.e., it terminates) (Fig. 8A):

  • If it has approximate ambiguity, then we classify it as a scaffold gap.

  • Else we classify it as a hanging insert error.

• (B) If the joining thread is attached at each ends to blocks, a and b, containing haplotype segments:

  • If a and b are connected by a thread containing haplotype segments (Fig. 8B):

    • i. If the joining thread has approximate ambiguity, then it is a scaffold gap.

    • ii. Else it is an indel (insertion/deletion) error:

      1. If the joining thread is empty, then it is a deletion error; by definition all haplotype paths between a and b must be nonempty.

      2. Else if all haplotype threads are empty then it is an insertion error; by definition the assembly thread must be nonempty.

      3. Else, all the haplotype threads and the assembly thread are nonempty, and it is an insertion and deletion error.

  • Else a and b are not attached by a thread of haplotype containing edges:

    • i. If a and b both contain positions from one or more common haplotype sequences, then it is an intrahaplotype joining error (Fig. 8C).

    • ii. Else it is an interhaplotype joining error (Fig. 8C).

• (C) Else, the joining thread is attached at one end to a bacterial contamination containing block (Fig. 8B), and we classify it as a haplotype to contamination joining error (Fig. 8C).

Figure 8.

Scaffold gap and error subgraphs. Diagrams follow the format of Figure 3. The rounded boxes represent extensions to the surrounding threads. Line ends not incident with the edge of boxes represent the continuation of a thread unseen. In each diagram the right end of block a and the left end of block b (if present) represent the ends of contig paths, and the enclosed gray thread represents the joining thread. The black thread represents a haplotype thread. The gray thread represents either a haplotype or bacterial contamination thread. (A) (Hanging) scaffold gaps and hanging insert errors. (B) Scaffold gaps and indel errors. (C) Intra- and interchromosomal joining errors and haplotype to contamination joining errors.

For any thread P representing an assembly sequence, a scaffold path is a maximal subpath of P, in which all of the edges are consistent and/or part of a scaffold gap subgraph.

Substitution errors

We use a bit-score to score correct, but ambiguous matches within valid columns. We assign to each valid column the bit score –m*log₂(n/4), where n is the number of different bases the IUPAC character in the assembly represents and m is the number of distinct base pairs in the two haplotypes that matches or is represented (amongst others) by the assembly IUPAC character. Thus, in homozygous columns the score is at most 2, in heterozygous columns the score is 2, if, and only if, the assembly correctly predicts one of the two base pairs, or if it predicts an ambiguity character that represents both and only those two base pairs.