Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2007 Sep 4;274(1627):2857–2864. doi: 10.1098/rspb.2007.0954

The role of gap phase processes in the biomass dynamics of tropical forests

Kenneth J Feeley 1,*, Stuart J Davies 2, Peter S Ashton 1, Sarayudh Bunyavejchewin 3, MN Nur Supardi 4, Abd Rahman Kassim 4, Sylvester Tan 5, Jérôme Chave 6
PMCID: PMC3227128  PMID: 17785266

Abstract

The responses of tropical forests to global anthropogenic disturbances remain poorly understood. Above-ground woody biomass in some tropical forest plots has increased over the past several decades, potentially reflecting a widespread response to increased resource availability, for example, due to elevated atmospheric CO2 and/or nutrient deposition. However, previous studies of biomass dynamics have not accounted for natural patterns of disturbance and gap phase regeneration, making it difficult to quantify the importance of environmental changes. Using spatially explicit census data from large (50 ha) inventory plots, we investigated the influence of gap phase processes on the biomass dynamics of four ‘old-growth’ tropical forests (Barro Colorado Island (BCI), Panama; Pasoh and Lambir, Malaysia; and Huai Kha Khaeng (HKK), Thailand). We show that biomass increases were gradual and concentrated in earlier-phase forest patches, while biomass losses were generally of greater magnitude but concentrated in rarer later-phase patches. We then estimate the rate of biomass change at each site independent of gap phase dynamics using reduced major axis regressions and ANCOVA tests. Above-ground woody biomass increased significantly at Pasoh (+0.72% yr−1) and decreased at HKK (−0.56% yr−1) independent of changes in gap phase but remained stable at both BCI and Lambir. We conclude that gap phase processes play an important role in the biomass dynamics of tropical forests, and that quantifying the role of gap phase processes will help improve our understanding of the factors driving changes in forest biomass as well as their place in the global carbon budget.

Keywords: carbon cycling, carbon dioxide, disturbance, global change, succession, tree-fall gaps

1. Introduction

Deforestation and land-use change is one of the largest sources for carbon dioxide emissions, especially from developing tropical nations (DeFries et al. 2002; Achard et al. 2004). Despite high rates of land-use change and carbon emissions, some atmospheric inversion models show the terrestrial tropics to be carbon neutral or even slight carbon sinks (Gurney et al. 2002; Stephens et al. 2007; reviewed by Denman et al. 2007). One possible explanation is that the carbon emissions from land-use change are largely offset by augmented biomass and increased carbon sequestration in the remaining intact forests (Schimel et al. 2001). Consistent with this hypothesis, studies based on repeated tree diameter measurements from a network of Amazonian inventory plots have indicated that the above-ground woody biomass in these forests has increased over the past several decades (Phillips et al. 1998; Baker et al. 2004). However, the generality and the cause(s) of these increases remain heavily debated (e.g. Laurance et al. 2005; Nelson 2005; Wright 2005, 2006; Lewis 2006; Lewis et al. 2006).

It has been proposed that the observed changes in biomass reflect a widespread concerted response to increased resource availability, possibly due to continent-wide increases in incoming solar radiation, increased rates of nutrient mineralization and/or CO2 fertilization. This hypothesis is supported by the associated shifts in demography (e.g. simultaneous increases in tree growth, recruitment, mortality and above-ground biomass within the same plots; Phillips 1996; Lewis et al. 2004a,b) and species composition (Phillips et al. 2002a,b; Laurance et al. 2004), and is also in accord with theoretical models (Melillo et al. 1993; Cramer et al. 2001; summarized by Denman et al. 2007) and with findings from CO2 addition experiments conducted in growth chambers (Curtis & Wang 1998) and in some temperate forests (Norby et al. 2005; but see Körner et al. 2005).

Alternatively, the observed changes in tropical forest biomass (either increases or decreases) may simply reflect ‘natural’ processes, such as recovery from past large-scale disturbances or internal gap phase dynamics (here defined as localized disturbances and subsequent regrowth; Brokaw 1985), and be largely or entirely independent of external drivers such as elevated CO2 and/or other global change phenomena (Körner 2003; Saleska et al. 2003; Vieira et al. 2004). Even in undisturbed forests under steady-state dynamics (i.e. no long-term change in total biomass at the landscape scale), the majority of area is expected to be gradually accumulating biomass most of the time due to the recovery from past gap-forming events. In contrast, offsetting biomass decreases are mostly attributable to the death of individual large trees and are therefore of high magnitude but rarer in space and/or time (Watt 1947; Bormann & Likens 1979; Fearnside 2000; Moorcroft et al. 2001; Körner 2003; Saleska et al. 2003). Consequently, it may be difficult to accurately capture the frequency of these rare disturbance events and adequately account for them in estimates of biomass change based on the repeated measurements of inventory plots.

If inventory plots miss disturbance events, they will overestimate the rates of biomass increase. This potential for ‘immature forest bias’ will be amplified if site selection disproportionably favours early successional forests (e.g. in flood plains or human-impacted forests), and/or if plots experiencing disturbance events are subsequently abandoned (Saleska et al. 2003; Clark 2004; Phillips et al. 2002a). Conversely, plots may potentially overrepresent disturbance events, especially if placement is biased towards mature forests (i.e. ‘majestic forest bias’; Phillips et al. 2002a). In order to accurately monitor changes in tropical forest biomass, dynamics should ideally be measured over very large spatio-temporal scales (Körner 2004). Unfortunately, this may not be feasible given the relative scarcity of long-term tree plot data from much of the tropics and especially from outside the New World. Here we explore an alternative approach, which is to explicitly account for the contribution of gap phase processes when quantifying rates of biomass change.

To investigate gap phase processes and biomass dynamics of tropical forests, we use repeat tree census data from four forest dynamics plots (FDPs) located at Barro Colorado Island (BCI, Panama), Pasoh (Peninsular Malaysia), Lambir (Sarawak, Malaysia) and Huai Kha Khaeng (HKK, Thailand). All these FDPs represent ‘old-growth’ forests but vary greatly in geography, climate, topography, diversity and history (Losos & Leigh 2004; table 1). Each FDP encompasses an area of at least 50 ha, which helps to minimize placement bias and ensures that all gap phases from recent disturbances to mature patches are as accurately represented as possible. Using the spatially explicit stem size data recorded at each of the FDPs over the past 5–20 years, we examine the role of gap phase processes in driving tropical forest biomass dynamics. We then estimate the rate of biomass change at each site accounting for the contribution of gap phase processes.

Table 1.

Characteristics of forest dynamic plots (FDPs).

FDP location (latitude, longitude) mean annual precipitation (mm) no. of months with <100 mm precipitation elevation (m) census years no. of stems no. of species
BCI 9°09′ N, 79°51′ W 2551 3–4 (Jan–Apr) 120–160 1985, 1990, 1995, 2000, 2005 213 802 301
Pasoh 2°58′ N, 102°18′ E 1788 0–1 (Jan) 80–104 1986, 1990, 1995, 2001 305 942 817
Lambir 4°10′ N, 114°01′ E 2664 0 104–244 1991, 1997, 2002 359 603 1180
HKK 15°37′ N, 99°12′ E 1476 6 (Nov–Apr) 549–638 1994, 1999 72 509 251
Open in a new tab

2. Material and methods

(a) Plot inventories

At each of the four FDPs, all trees above or equal to 10 mm diameter at breast height (dbh) were identified to species, mapped, tagged and measured for dbh (to the nearest millimetre) at approximately 5-year intervals over the past 5–20 years (Losos & Leigh 2004; table 1). To minimize errors due to irregular dbh measurements, we applied several statistical filters. Growth measurements of above or equal to 45 mm yr−1 or up to −5 mm yr−1 were assumed erroneous. For these trees, we used the mean growth rate of all other individuals in the same diameter class (breakpoints between diameter classes were set to: 10, 15, 20, 25, 30, 40, 50, 100, 200, 300, 400, 500, 600, 700, 10 000 mm). We also applied this correction to any recruits with anomalously large diameters and to trees for which the point of measurement changed between censuses.

The Lambir FDP covers an area of 52 ha. However, to facilitate cross-plot comparisons, we used only the data from the westernmost portion of 50 ha for all analyses presented here. We repeated all analyses for only the easternmost portion of the plot but results did not differ significantly.

(b) Gap phase

We estimated the relative gap phase (GP) for small areas within each FDP based on the logged ratio of basal area in large versus small stems,

GP=ln(BA300+1)−ln(BA100+1), (2.1)

where BA300 is the total basal area of all trees with dbh≥300 mm and BA100 is the total basal area of all stems with dbh≥10 and ≤100 mm. The choice of size cut-offs was chosen to make a clear distinction between canopy and understorey stems. However, GP is robust to choice of size categories (table S1 in the electronic supplementary material).

Within each FDP, GP was calculated for 20×20 m subplots (n=1250 per FDP). In order to facilitate cross-plot comparisons and correct for inherent differences in mature forest structure between sites, we standardized GP based on the maximum value recorded at each FDP, such that it is on a scale of 0–1 (with 1 representing the most mature phase patches). At HKK, one of the subplots was found to have an exceptionally high GP value due to the presence of single extremely large strangler fig (Ficus spp.). Owing to their atypical growth form, strangler figs may be poorly represented by allometric equations; therefore, we deemed this subplot as an outlier and excluded it from all subsequent analyses.

To test the performance of GP as a measure of gap phase, we compared the calculated values with several other measures of forest maturity where appropriate data were available. Other measures included maximum canopy height per subplot (BCI, Hubbell et al. (1999) and Lambir, T. Ohkubo 2006, personal communication), relative abundance of pioneers (Lambir; Russo et al. 2005), total basal area (all sites) and density of stems (all sites). In accord with predictions, GP was positively correlated with canopy height and basal area and negatively correlated with the abundance of pioneers and density of stems (i.e. stem thinning; Brokaw 1985; table S2 in the electronic supplementary material). Importantly, GP also performed as predicted under the expectations of gap phase dynamics (Watt 1947; Bormann & Likens 1979; Brokaw 1985): for individual subplots, GP tended to increase through time, the probability of a decrease (i.e. disturbance) increased at high GP, and decreases in GP were generally of greater magnitude than increases. Based on these diagnostics, we believe that gap phase is a valid measure of the relative GP and suitable for investigating forest dynamics; however, we acknowledge that GP is also potentially influenced by many other factors (e.g. species composition, natural variability in forest structure, predominance of emergents), which we did not explicitly account for here.

The distribution of GP within a forest will be influenced by the scale of gap formation versus the scale at which GP is calculated. Most gaps are smaller than the 400 m2 subplots used here (e.g. 99% at BCI; Hubbell et al. 1999); therefore, it is possible that when GP is calculated at this scale, it will average over patches at different phases of regeneration, resulting in a spurious increase in the frequency of intermediate GP values (i.e. intermediate GP values could be caused by both sampling an area composed entirely of mid-phase forest or including mixes of mature- and early-phase patches). To test this, we calculated the variation in total basal area of large trees (above or equal to 300 mm dbh) per 10×10 m quadrat. At all sites, the relationship between GP and variation in large tree basal area was log-linear (figure S2 in the electronic supplementary material), indicating that variation in forest structure does not increase at intermediate values and supporting our choice of sampling scale.

(c) Changes in distribution of GP

We used the Wilcoxon rank-sum test with continuity correction to determine whether the distribution of GPs changed through time.

(d) Estimates of above-ground woody biomass

In addition to GP, we estimated above-ground woody biomass in each of the 20×20 m subplots at each census using established allometric relationships between dbh, wood specific gravity and above-ground woody biomass (Chave et al. 2001). Two equations were used to account for the difference in tree allometry between dry (HKK) and moist forests (BCI, Pasoh and Lambir), which are as follows:

dryforests:AGB=WSG×exp(−0.667+1.784ln(D)+0.207(ln(D))2−0.0281(ln(D))3), (2.2)
moistforests:AGB=WSG×exp(−1.499+2.148ln(D)+0.207(ln(D))2−0.0281(ln(D))3), (2.3)

where AGB is the estimated above-ground woody biomass (in Mg); D is the dbh (in cm); and WSG is the wood specific gravity (Chave et al. 2005). WSG is the oven-dry mass of a sample of wood divided by the mass of the water displaced by that sample and is unitless. When available, species-specific WSG values were used; for those species for which these data were not available, WSG was designated as the mean value of all congeneric species occurring in the respective plot (Chave et al. 2005). For trees with multiple stems, AGB was calculated for each stem and then summed to generate tree-level estimates of above-ground biomass.

Using the spatially explicit census data, we calculated the total above-ground woody biomass for each subplot at each census. The annual rate of relative biomass change (ΔAGB) was then calculated for each subplot as

ΔAGB=ln(TAGB2)−ln(TAGB1)t, (2.4)

where TAGB is the total above-ground biomass in the subplot estimated at times 1 and 2 and t is the number of years between the censuses (measured in days).

(e) Change in biomass versus GP

We calculated the relationship between the relative change in above-ground biomass (ΔAGB) and the initial GP by binning subplots into five discrete categories of GP (breakpoints set to: 0.0, 0.2, 0.4, 0.6, 0.8, 1.0) and calculating the mean ΔAGB (between the initial and final censuses) within each category. Estimates of 95% CIs were based on 5000 bootstrapped resamples.

(f) Changes in biomass accounting for gap phase dynamics

We used two separate tests to analyse the changes in biomass independent of gap phase dynamics. First, we conducted a reduced major axis (RMA, type II) regression of change in biomass (ΔAGB) versus change in GP (between the initial and final censuses) with CIs estimated through bootstrapping (5000 resamples). If biomass is changing independent of the changes in GP, then the intercept of the relationship is predicted to differ significantly from zero. Second, we conducted analyses of covariance (ANCOVA; TAGB coded as the response variable, census as the effect and GP as the covariate) and tested for significant differences in the intercept and the slope between all censuses and between only the initial and final censuses.

All analyses were conducted in R v. 2.2.1 (http://www.R-project.org/) using modified functions from the CTFS R package (http://cran.us.r-project.org/src/contrib/PACKAGES.html).

3. Results

Within each of the FDPs, the distribution of GP was approximately normally distributed but skewed slightly towards an increased abundance of plots in the earlier phases of gap regeneration (i.e. at all FDPs, median GP<0.50; figure 1). The distribution of GP did not change significantly between the initial and final censuses at BCI, Lambir or HKK. In contrast, there were significant decreases in the mean and median GP values at Pasoh (Wilcoxon rank-sum test: W=826 292, p=0.013; table 2; figure S1 in the electronic supplementary material).

Figure 1.

Figure 1

Open in a new tab

Distribution of change in estimated above-ground biomass and GP in the four FDPs. (a) The annual relative change in above-ground biomass (% yr−1) between the initial and final censuses for 20×20 m subplots versus initial GP (binned at intervals of 0.20) within each plot (mean±95% CIs based on 5000 bootstrapped resamples). (b) The initial distribution of GP at each plot. Vertical bars in (b) indicate the median initial GP at each site. Circles, BCI; squares, Pasoh; triangles, Lambir; diamonds, HKK.

Table 2.

GP and above-ground woody biomass (Mg) per hectare at the forest dynamic plots (FDPs).

FDP median gap phase (GP) total biomass (Mg ha−1)
census 1 census 2 census 3 census 4 census 5 census 1 census 2 census 3 census 4 census 5
BCI 0.40 0.39 0.39 0.40 0.40 300.51 303.75 302.38 303.25 301.27
Pasoh 0.40 0.39 0.38 0.38 n.a. 326.36 337.54 346.26 339.50 n.a.
Lambir 0.49 0.48 0.49 n.a. n.a. 490.05 501.01 496.89 n.a. n.a.
HKK 0.40 0.41 n.a. n.a. n.a. 211.12 210.29 n.a. n.a. n.a.
Open in a new tab

Forest patches with low initial GP consistently increased in biomass over time at all forests. With increasing GP, the rate of biomass increase declined such that the mean change in biomass of subplots, where GP>0.40, was always negative or not significantly different from zero (figure 1). The variance in biomass change also increased with increasing GP, reflecting both the high stochasticity of disturbance events and the decrease in sample size at high GP.

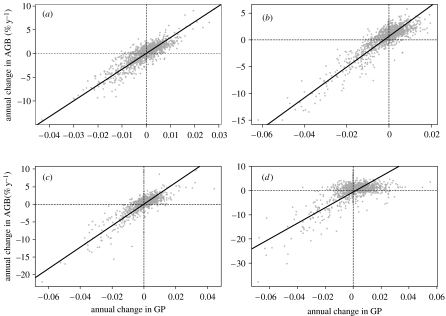
At Pasoh, the intercept of the RMA regression between the change in GP and ΔAGB was significantly positive, indicating that there was an increase in biomass beyond what could be attributed to changes in GP (figure 2). This ‘extra’ biomass increase was at the rate of 0.72% yr−1 (95% CI=0.65–0.78% yr−1), which is significantly faster than the observed plot-wide increase of 0.30% yr−1. In contrast, at HKK, the intercept of the RMA regression was significantly negative, indicating a 0.56% annual decrease in above-ground biomass independent of GP changes (95% CI=−0.74 to −0.37% yr−1). This is significantly more rapid than the observed decrease of 0.07% yr−1. At BCI and Lambir, there was no significant change in biomass after accounting for the concurrent changes in GP (BCI: 95% CI=−0.02–0.10% yr−1; Lambir: 95% CI=−0.00 to 0.20% yr−1).

Figure 2.

Figure 2

Open in a new tab

Change in above-ground forest biomass accounting for gap phase dynamics at (a) BCI, (b) Pasoh, (c) Lambir and (d) HKK. These depict the relationship between the annual relative change in estimated above-ground woody biomass (% yr−1) and the annual change in GP per 20×20 m subplot. Dashed lines indicate zero change. The intercept differs significantly from zero at two of the sites, indicating that biomass is increasing at Pasoh and decreasing at HKK independent of changes in GP.

These results are largely supported by the ANCOVA tests, which indicated a significant increase in biomass at Pasoh between the initial and final censuses independent of changes in GP (p<0.0001). There were no significant changes in above-ground biomass at BCI, Lambir or HKK after accounting for GP (table 3). At Lambir, there were significant changes in biomass between the censuses but the direction of change was not consistent (increased then decreased), such that there was no net change between the initial and final censuses (table S3 in the electronic supplementary material).

Table 3.

Results of ANCOVA comparing the relationships between TAGB and GP between the initial and final censuses at each forest. (Italics typeface indicates significant effects.)

degrees of freedom sum of squares mean square F-value p
BCI
census period 1 0.03 0.03 0.4446 5.05×10−1
gap phase (GP) 1 772.59 772.59 11 899.0198 2.20×10−16
census×GP interaction 1 0.002174 0.002174 0.0335 8.55×10−1
residuals 2496 162.06 0.06
Pasoh
census period 1 1.19 1.19 27.52 1.68×10−7
gap phase (GP) 1 695.67 695.67 16 065.67 2.20×10−16
census×GP interaction 1 0.00 0.00 0.07 7.94×10−1
residuals 2496 108.08 0.04
Lambir
census period 1 0.24 0.24 2.78 9.58×10−2
gap phase (GP) 1 955.00 955.00 11 098.42 2.00×10−16
census×GP interaction 1 0.01 0.01 0.06 8.03×10−1
residuals 2496 214.78 0.09
HKK
census period 1 0.02 0.02 0.20 6.54×10−1
gap phase (GP) 1 728.10 728.10 6245.31 2.20×10−16
census×GP interaction 1 0.10 0.10 0.83 3.64×10−1
residuals 2494 290.76 0.12
Open in a new tab

4. Discussion

Concentrations of atmospheric CO2 have increased steadily over the past several decades. The impacts of this and other global anthropogenic changes on tropical forest ecosystems are still poorly understood and heavily debated (Laurance et al. 2005; Nelson 2005; Wright 2005; Lewis et al. 2006; Clark 2007). Understanding the effects of global change on tropical forests has extremely important implications, especially, given their role in global change and the potential for feedback cycles (Clark 2007).

Previous studies investigating changes in tropical forest dynamics and structure have reported significant increases in above-ground biomass through time (Phillips et al. 1998; Baker et al. 2004). Based on concurrent changes in tree demographic rates and composition, the observed increases in biomass were attributed to elevated nutrient availability and/or carbon fertilization (Laurance et al. 2004; Lewis et al. 2004a). However, an important limitation is that while these previous studies acknowledged the potentially confounding effects of gap phase dynamics (Phillips et al. 2005), they did not explicitly control for it in their estimates of biomass change, making it difficult to distinguish the influence of environmental factors from natural successional processes.

Using spatially referenced census data from four 50 ha plots in old-growth lowland tropical forests representing both the neo- and palaeotropics, we calculated the rates of change in biomass while accounting for the contribution of gap phase dynamics. Two of the sites experienced significant changes in above-ground biomass independent of concurrent changes in GP; at Pasoh, above-ground biomass increased significantly and at HKK biomass decreased. In fact, the corrected rates of biomass change at both of these sites were significantly faster than the observed rates of overall change. This is because GP decreased at Pasoh, which in the absence of other factors is expected to lead to reduced standing biomass; at HKK, the distribution of GP remained stable through time and thus no change in biomass was expected.

The reason(s) for the changes in biomass at Pasoh and HKK remains undetermined. Atmospheric concentrations of CO2 and rates of nutrient deposition have increased globally, but these widespread increases in resource availability explain neither the loss of biomass at HKK nor the apparent stability of biomass at BCI and Lambir. Furthermore, we have shown elsewhere that the growth of trees at both Pasoh and BCI has decelerated over the study period (Feeley et al. 2007). This is in direct contradiction to the fertilization hypothesis and suggests that there must be compensatory changes in the turnover, structure or composition of these forests to account for the observed patterns. However, none of the forests exhibited significant increases in the relative dominance of fast-growing or canopy tree species as predicted under elevated resource availability (Chave et al., submitted). It thus appears probable that at these sites, idiosyncratic or regional factors (changes in temperature, cloudiness, precipitation, anthropogenic disturbances, etc.) are taking primacy over the global increase in resource availability. For example, Central American and Southeast Asian forests (where our study sites were located) have experienced large temperature increases over the past half-century (Malhi & Wright 2004), which may be decreasing productivity and counteracting any fertilization effect (Feeley et al. 2007). In contrast, temperature increases have been less severe through much of the Amazon and thus those forests may be responding more to changes in resource availability. Additional research will be required to reveal the identity and relative importance of the various environmental changes operating within different forests.

An important caveat is that this study examined only the changes in estimates of above-ground course woody biomass (Chave et al. 2005). While woody production in forests accounts for as much as 45% of above-ground biomass and 30% of above-ground net primary productivity (Chambers et al. 2001), external drivers may also affect forest biomass through non-structural carbohydrates or other forest components that were excluded from our estimates, such as twigs, foliage, reproductive organs (flowers, fruits and seeds), lianas, roots, course woody debris or even fauna (Nascimento & Laurance 2002; Würth et al. 2005). For example, the production of flowers by trees at BCI increased significantly over the study period (Wright & Calderon 2006). Likewise, the relative abundance of lianas, or woody climbing vines, has increased dramatically throughout much of the neotropics (Phillips et al. 2002a,b) including at BCI (Wright et al. 2004). Greater liana abundances may result in short-term increases in forest biomass, but through time this will probably cause increased tree mortality due to overshading, leading to eventual declines in total forest biomass and carbon sequestration (Granados & Körner 2002; Körner 2004).

Another potential limitation is that the methods employed here may fail to accurately distinguish between the role of gap phase dynamics and external drivers (e.g. increased CO2 or nutrient deposition) if these drivers indirectly impact biomass dynamics by influencing the rates of disturbance and/or subsequent recovery, as suggested by a purported increase in tropical forest turnover (Phillips & Gentry 1994). Furthermore, if environmental changes disproportionately impact certain size classes of stems (e.g. elevated concentrations of CO2 are predicted to decrease the light compensation point of photosynthesis and thereby lead to greater relative increases in the biomass growth of shaded understorey plants; Würth et al. 1998), it could mimic the changes in forest structure associated with gap phase processes and confound the analyses. At all the forests studied here, the distribution of GP remained significantly stable or decreased through time (figure S1 in the electronic supplementary material), contradicting the predictions of accelerated gap recovery. Furthermore, changes in growth rates were consistent across all size classes of stems at BCI and Pasoh (Feeley et al. 2007), suggesting that the observed relationships are probably not due to differential size-related growth responses.

In conclusion, natural gap phase processes clearly play an important role in the biomass dynamics of tropical forests. As such, it is critical that we explicitly account for gap phase processes if we hope to understand how the structure and dynamics of these forests may be responding to regional and global environmental changes. Of the four tropical forests studied here, only two exhibited significant changes in biomass independent of changes in GP; however, even between these two forests, the direction of change was not consistent (one increased and another decreased). These findings, while preliminary, support the prevailing influence of regional versus global environmental changes on tropical forest structure and dynamics (Phillips et al. 1998; Feeley et al. 2007). The remaining uncertainties regarding how and why some tropical forests are changing through time, as well as their contribution to global change, clearly highlight the need for additional large-scale, long-term research (Clark 2007).

Acknowledgments

We thank P. Hall and R. Condit for their assistance in developing methods to estimate biomass. M. Potts, J. Wright, H. Muller-Landau, S. Russo, J. Baltzer and two anonymous reviewers provided their insightful comments. We also thank the many workers and researchers who have contributed to the CTFS plot network. Financial support was provided by the Harvard University Arnold Arboretum, NSF grant DEB-9806828 to the CTFS, the Andrew W. Mellon Foundation, the Smithsonian Tropical Research Institute, the Forest Research Institute of Malaysia, the Thai Royal Forest Department, the National Institute of Environmental Studies (Japan) and the John D. and Catherine T. McArthur Foundation.

Supplementary Material

Supplementary tables and figures

Table S1. Pearson correlation (R) coefficients between the indexes of gap phase (GP) as calculated using various stem size criteria in each FDP. Table S2. Pearson correlation coefficients (R) between GP and various measures of forest maturity at the FDP. Table S3. Results of ANCOVA including all census intervals. Figure S1. Distribution of GP at the initial (filled symbols, solid line) and final census (open symbols, dashed line) at (a) BCI, (b) Pasoh, (c) Lambir and (d) HKK. Vertical lines indicate the median values in each census (nearly indistinguishable in a and c). GP decreased significantly at Pasoh (W=826 292, P=0.013). Figure S2. Variation in total basal area of trees ≥300 mm dbh per 10×10 m subplot versus GP (calculated per 20×20 m subplot) at (a) BCI, (b) Pasoh, (c) Lambir and (d) HKK. There is no evidence of increased variation at intermediate GP values

rspb20070954s12.doc (210KB, doc)

References

  1. Achard F, Eva H.D, Mayaux P, Stibig H.-J, Belward A. Improved estimates of net carbon emissions from land cover change in the tropics for the 1990s. Global Biogeochem. Cycles. 2004;18:GB2008. doi:10.1029/2003GB002142 [Google Scholar]
  2. Baker T.R, et al. Increasing biomass in Amazonian forest plots. Phil. Trans. R. Soc. B. 2004;359:353–365. doi: 10.1098/rstb.2003.1422. doi:10.1098/rstb.2003.1422 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bormann F.H, Likens G.E. Springer; New York, NY: 1979. Pattern and process in a forested ecosystem. [Google Scholar]
  4. Brokaw N.V.L. Gap-phase regeneration in a tropical forest. Ecology. 1985;66:682–687. doi:10.2307/1940529 [Google Scholar]
  5. Chambers J.Q, Higuchi N, Tribuzy E.S, Trumbore S.E. Carbon sink for a century. Nature. 2001;410:429. doi: 10.1038/35068624. doi:10.1038/35068624 [DOI] [PubMed] [Google Scholar]
  6. Chave J, Rie´ra B, Dubois M.-A. Estimation of biomass in a neotropical forest of French Guiana: spatial and temporal variability. J. Trop. Ecol. 2001;17:79–96. doi:10.1017/S0266467401001055 [Google Scholar]
  7. Chave J, et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia. 2005;145:87–99. doi: 10.1007/s00442-005-0100-x. doi:10.1007/s00442-005-0100-x [DOI] [PubMed] [Google Scholar]
  8. Chave, J. et al. Submitted. Changes in tropical forest biomass across plant functional groups.
  9. Clark D.A. Sources or sinks? The responses of tropical forests to current and future climate and atmospheric composition. Phil. Trans. R. Soc. B. 2004;359:477–491. doi: 10.1098/rstb.2003.1426. doi:10.1098/rstb.2003.1426 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Clark D.A. Detecting tropical forests' responses to global climatic and atmospheric change: current challenges and a way forward. Biotropica. 2007;39:4–19. doi:10.1111/j.1744-7429.2006.00227.x [Google Scholar]
  11. Cramer W, et al. Global response of terrestrial ecosystem structure and function to CO2 and climate change: results from six dynamic global vegetation models. Glob. Change Biol. 2001;7:357–373. doi:10.1046/j.1365-2486.2001.00383.x [Google Scholar]
  12. Curtis P.S, Wang X. A meta-analysis of elevated CO2 effects on woody plant mass, form, and physiology. Oecologia. 1998;113:299–313. doi: 10.1007/s004420050381. doi:10.1007/s004420050381 [DOI] [PubMed] [Google Scholar]
  13. DeFries R.S, Houghton R.A, Hansen M.C, Field C.B, Skole D, Townshend J. Carbon emissions from tropical deforestation and regrowth based on satellite observations for the 1980s and 1990s. Proc. Natl Acad. Sci. USA. 2002;99:14 256–14 261. doi: 10.1073/pnas.182560099. doi:10.1073/pnas.182560099 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Denman K.L, et al. Couplings between changes in the climate system and biogeochemistry. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt K.B, Tignor M, Miller H.L, editors. Climate change 2007: the physical science basis. Contribution of working group I to the fourth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press; Cambridge, UK; New York, NY: 2007. pp. 499–587. [Google Scholar]
  15. Fearnside P.M. Global warming and tropical land-use change: greenhouse gas emissions from biomass burning, decomposition and soils forest in conversion, shifting cultivation and secondary vegetation. Clim. Change. 2000;46:115–158. doi:10.1023/A:1005569915357 [Google Scholar]
  16. Feeley K.J, Wright S.J, Nur Supardi M.N, Kassim A.R, Davies S.J. Decelerating growth in tropical forest trees. Ecol. Lett. 2007;10:461–469. doi: 10.1111/j.1461-0248.2007.01033.x. doi:10.1111/j.1461-0248.2007.01033.x [DOI] [PubMed] [Google Scholar]
  17. Granados J, Körner C. In deep shade, elevated CO2 increases the vigor of tropical climbing plants. Glob. Change Biol. 2002;8:1109–1117. doi:10.1046/j.1365-2486.2002.00533.x [Google Scholar]
  18. Gurney K.R, et al. Towards robust regional estimates of CO2 sources and sinks using atmospheric transport models. Nature. 2002;415:626–630. doi: 10.1038/415626a. doi:10.1038/415626a [DOI] [PubMed] [Google Scholar]
  19. Hubbell S.P, Foster R.B, O'Brien S.T, Harms K.E, Condit R, Wechsler B, Wright S.J, de Lao S.L. Light-gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science. 1999;283:554–557. doi: 10.1126/science.283.5401.554. doi:10.1126/science.283.5401.554 [DOI] [PubMed] [Google Scholar]
  20. Körner C. Slow in, rapid out—carbon flux studies and Kyoto targets. Science. 2003;300:1242–1243. doi: 10.1126/science.1084460. doi:10.1126/science.1084460 [DOI] [PubMed] [Google Scholar]
  21. Körner C. Through enhanced tree dynamics carbon dioxide enrichments may cause tropical forests to lose carbon. Phil. Trans. R. Soc. B. 2004;359:493–498. doi: 10.1098/rstb.2003.1429. doi:10.1098/rstb.2003.1429 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Körner C, Asshoff R, Bignucolo O, Hattenschwiler S, Keel S.G, Pela´ez-Riedl S, Pepin S, Siegwolf R.T.W, Zotz G. Carbon flux and growth in mature deciduous forest trees exposed to elevated CO2. Science. 2005;309:1360–1362. doi: 10.1126/science.1113977. doi:10.1126/science.1113977 [DOI] [PubMed] [Google Scholar]
  23. Laurance W.F, et al. Pervasive alteration of tree communities in undisturbed Amazonian forests. Nature. 2004;428:171–175. doi: 10.1038/nature02383. doi:10.1038/nature02383 [DOI] [PubMed] [Google Scholar]
  24. Laurance W.F, Oliveira A.A, Laurance S.G, Condit R, Dick C.W, Andrade A, Nascimento H.E.M, Lovejoy T.E, Ribeiro J.E.L.S. Altered tree communities in undisturbed Amazonian forests: a consequence of global change? Biotropica. 2005;37:160–162. doi:10.1111/j.1744-7429.2005.00022.x [Google Scholar]
  25. Lewis S.L. Tropical forests and the changing earth system. Phil. Trans. R. Soc. B. 2006;361:195–210. doi: 10.1098/rstb.2005.1711. doi:10.1098/rstb.2005.1711 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lewis S.L, Malhi Y, Phillips O.L. Fingerprinting the impacts of global change on tropical forests. Phil. Trans. R. Soc. B. 2004a;359:437–462. doi: 10.1098/rstb.2003.1432. doi:10.1098/rstb.2003.1432 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lewis S.L, et al. Concerted changes in tropical forest structure and dynamics: evidence from 50 South American long-term plots. Phil. Trans. R. Soc. B. 2004b;359:421–436. doi: 10.1098/rstb.2003.1431. doi:10.1098/rstb.2003.1431 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lewis S.L, Phillips O.L, Baker T.R. Impacts of global atmospheric change on tropical forests. Trends Ecol. Evol. 2006;21:173–174. doi: 10.1016/j.tree.2006.02.001. doi:10.1016/j.tree.2006.02.001 [DOI] [PubMed] [Google Scholar]
  29. Losos E, Leigh E.G, editors. Tropical forest diversity and dynamism: findings from a large-scale plot network. The University of Chicago Press; Chicago, IL: 2004. [Google Scholar]
  30. Malhi Y, Wright J. Spatial patterns and recent trends in the climate of tropical rainforest regions. Phil. Trans. R. Soc. B. 2004;359:311–329. doi: 10.1098/rstb.2003.1433. doi:10.1098/rstb.2003.1433 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Melillo J.M, McGuire A.D, Kicklighter D.W, Moore B, Vorosmarty C.J, Schloss A.L. Global climate change and terrestrial net primary production. Nature. 1993;363:234–240. doi:10.1038/363234a0 [Google Scholar]
  32. Moorcroft P.R, Hurtt G.C, Pacala S.W. A method for scaling vegetation dynamics: the ecosystem demography model (ED) Ecol. Monogr. 2001;71:557–585. [Google Scholar]
  33. Nascimento H.E.M, Laurance W.F. Total aboveground biomass in central Amazonian rainforests: a landscape-scale study. Forest Ecol. Manage. 2002;168:311–321. doi:10.1016/S0378-1127(01)00749-6 [Google Scholar]
  34. Nelson B.W. Pervasive alteration of tree communities in undisturbed Amazonian forests. Biotropica. 2005;37:158–159. doi: 10.1038/nature02383. doi:10.1111/j.1744-7429.2005.00021.x [DOI] [PubMed] [Google Scholar]
  35. Norby R.J, et al. Forest response to elevated CO2 is conserved across a broad range of productivity. Proc. Natl Acad. Sci. USA. 2005;102:18 052–18 056. doi: 10.1073/pnas.0509478102. doi:10.1073/pnas.0509478102 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Phillips O.L. Long-term environmental change in tropical forests: increasing tree turnover. Environ. Conserv. 1996;23:235–248. [Google Scholar]
  37. Phillips O.L, Gentry A.H. Increasing turnover through time in tropical forests. Science. 1994;263:954–958. doi: 10.1126/science.263.5149.954. doi:10.1126/science.263.5149.954 [DOI] [PubMed] [Google Scholar]
  38. Phillips O.L, et al. Changes in the carbon balance of tropical forests: evidence from long-term plots. Science. 1998;282:439–442. doi: 10.1126/science.282.5388.439. doi:10.1126/science.282.5388.439 [DOI] [PubMed] [Google Scholar]
  39. Phillips O.L, et al. Changes in growth of tropical forests: evaluating potential biases. Ecol. Appl. 2002a;12:576–587. doi:10.1890/1051-0761(2002)012[0576:CIGOTF]2.0.CO;2 [Google Scholar]
  40. Phillips O.L, et al. Increasing dominance of large lianas in Amazonian forests. Nature. 2002b;418:770–774. doi: 10.1038/nature00926. doi:10.1038/nature00926 [DOI] [PubMed] [Google Scholar]
  41. Russo S.E, Davies S.J, King D.A, Tan S. Soil-related performance variation and distributions of tree species in a Bornean rain forest. J. Ecol. 2005;93:879–889. doi:10.1111/j.1365-2745.2005.01030.x [Google Scholar]
  42. Saleska S.R, et al. Carbon in Amazon forests: unexpected seasonal fluxes and disturbance-induced losses. Science. 2003;302:1554–1557. doi: 10.1126/science.1091165. doi:10.1126/science.1091165 [DOI] [PubMed] [Google Scholar]
  43. Schimel D.S, et al. Recent patterns and mechanisms of carbon exchange by terrestrial ecosystems. Nature. 2001;414:169–172. doi: 10.1038/35102500. doi:10.1038/35102500 [DOI] [PubMed] [Google Scholar]
  44. Stephens B.B, et al. Weak northern and strong tropical land carbon uptake from vertical profiles of atmospheric CO2. Science. 2007;316:1732–1735. doi: 10.1126/science.1137004. doi:10.1126/science.1137004 [DOI] [PubMed] [Google Scholar]
  45. Vieira S, et al. Forest structure and carbon dynamics in Amazonian tropical rain forests. Oecologia. 2004;140:468–479. doi: 10.1007/s00442-004-1598-z. doi:10.1007/s00442-004-1598-z [DOI] [PubMed] [Google Scholar]
  46. Watt A.S. Pattern and process in the plant community. J. Ecol. 1947;35:1–22. doi:10.2307/2256497 [Google Scholar]
  47. Wright S.J. Tropical forests in a changing environment. Trends Ecol. Evol. 2005;20:553–560. doi: 10.1016/j.tree.2005.07.009. doi:10.1016/j.tree.2005.07.009 [DOI] [PubMed] [Google Scholar]
  48. Wright S.J. Response to Lewis et al. the uncertain response of tropical forests to global change. Trends Ecol. Evol. 2006;21:174–175. doi:10.1016/j.tree.2006.02.003 [Google Scholar]
  49. Wright S.J, Calderon O. Seasonal, El Niño and longer term changes in flower and seed production in a moist tropical forest. Ecol. Lett. 2006;9:35–44. doi: 10.1111/j.1461-0248.2005.00851.x. doi:10.1111/j.1461-0248.2005.00851.x [DOI] [PubMed] [Google Scholar]
  50. Wright S.J, Calderon O, Hernandez A, Paton S. Are lianas increasing in importance in tropical forests? A 17-year record from Panama. Ecology. 2004;85:484–489. doi:10.1890/02-0757 [Google Scholar]
  51. Würth M.K.R, Winter K, Korner C.H. In situ responses to elevated CO2 in tropical forest understorey plants. Funct. Ecol. 1998;12:886–895. doi:10.1046/j.1365-2435.1998.00278.x [Google Scholar]
  52. Würth M.K.R, Peláez-Riedl S, Wright S.J, Körner C. Non-structural carbohydrate pools in a tropical forest. Oecologia. 2005;143:11–24. doi: 10.1007/s00442-004-1773-2. doi:10.1007/s00442-004-1773-2 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary tables and figures

Table S1. Pearson correlation (R) coefficients between the indexes of gap phase (GP) as calculated using various stem size criteria in each FDP. Table S2. Pearson correlation coefficients (R) between GP and various measures of forest maturity at the FDP. Table S3. Results of ANCOVA including all census intervals. Figure S1. Distribution of GP at the initial (filled symbols, solid line) and final census (open symbols, dashed line) at (a) BCI, (b) Pasoh, (c) Lambir and (d) HKK. Vertical lines indicate the median values in each census (nearly indistinguishable in a and c). GP decreased significantly at Pasoh (W=826 292, P=0.013). Figure S2. Variation in total basal area of trees ≥300 mm dbh per 10×10 m subplot versus GP (calculated per 20×20 m subplot) at (a) BCI, (b) Pasoh, (c) Lambir and (d) HKK. There is no evidence of increased variation at intermediate GP values

rspb20070954s12.doc (210KB, doc)

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES