Solid-State NMR and Density Functional Theory Studies of Ionization States of Thiamin

Abstract

Thiamin diphosphate (ThDP) is a key coenzyme in sugar metabolism. The 4′-aminopyrimidine ring of ThDP cycles through several ionization and tautomeric states during enzyme catalysis, but it is not fully understood which states are adopted during the individual steps of the catalytic cycle. Thiamin has been synthesized with labels selectively inserted into the C2 and C6′ positions, as well as into the amino group, creating [C2, C6′-¹³C₂] thiamin and [N4′-¹⁵N] thiamin. Magic angle spinning (MAS) NMR spectroscopy has been employed to record the ¹³C and ¹⁵N chemical shift anisotropy (CSA) tensors for C2, C6′ and N4′ atoms. Our results indicate that the isotropic chemical shifts as well as the principal components of the ¹³C and ¹⁵N CSA tensors are very sensitive to the protonation states in these compounds and therefore permit to differentiate between the two ionization states, 4-aminopyrimidine (AP) and 4-aminopyrimidinium (APH⁺). Using Density Functional Theory (DFT), we have calculated the magnetic shielding anisotropy tensors of C2, C6′ and N4′, and found excellent agreement between the computed and the experimental tensors. Our findings indicate that MAS NMR spectroscopy in conjunction with DFT calculations is a sensitive probe of ionization states in the thiamin cofactor. The results of this study will serve as a guide for characterization of ionization and tautomeric states of thiamin in complexes with thiamin-dependent enzymes.

INTRODUCTION

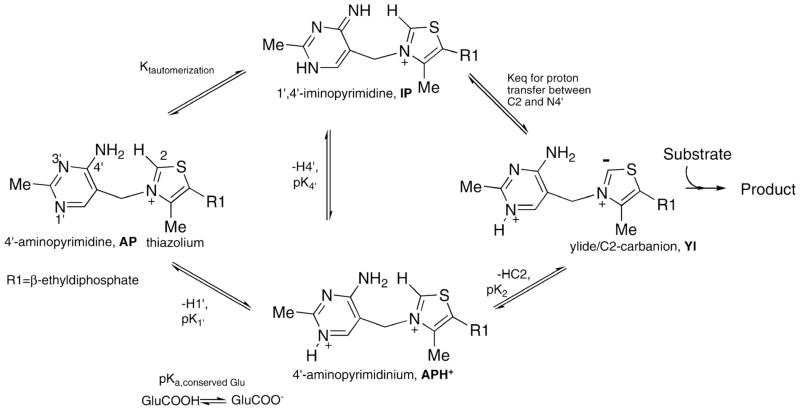
Thiamin diphosphate (ThDP) is an important coenzyme in a variety of enzyme systems that catalyze the transfer of aldehyde or acyl groups and the decarboxylation of α-keto acids. It is comprised of thiazolium and 4′-aminopyrimidine aromatic rings. Only recently has the participation of the 4′-aminopyrimidine group in enzyme catalysis gained wider acceptance.^1,2 During catalysis by the thiamin diphosphate (ThDP) superfamily of enzymes, the 4′-aminopyrimidine moiety of ThDP can interconvert among four ionization/tautomeric states: the positively charged N1′-protonated 4′-aminopyrimidinium (APH⁺), and the three neutral forms, 4′-aminopyrimidine (AP), 1′, 4′-iminopyrimidine (IP) and the ylide (Yl) (Scheme 1). However, not all of these ionization/tautomeric forms have been clearly characterized yet. In particular, previous research has shown that APH⁺ and the ylide forms are not directly detectable by other spectroscopic methods, such as circular dichroism³ or solution NMR.⁷ Therefore, central questions concerning the molecular basis for activation of C2-H bond of ThDP and how the enzymes favorably stabilize the IP form during various steps of the catalytic cycle still remain unanswered.^3–10 Solid-state NMR spectroscopy, which could provide atomic-level information in these large enzymes, would go the farthest in resolving such long-standing questions, due to the exquisite sensitivity of NMR chemical shifts to both the ionization and tautomeric states.^11–13

Scheme 1.

Various ionization and tautomerization states of ThDP bound to enzymes

While isotropic chemical shifts available from solution NMR spectra are in many cases sufficient to infer the ionization and tautomeric states,^14,15 chemical shift anisotropy (CSA) tensors recorded in the solid state provide much more detailed insight.^16–20 Furthermore, Density Functional Theory (DFT) calculations of the magnetic shielding anisotropy tensors and their analysis in light of the experimental NMR results yield comprehensive understanding of the electronic structure of a molecule.^21–23 Solid-state NMR measurements are often the only way to record chemical shifts and CSA tensors, for example, in large proteins, where solution lines are broadened beyond detection. The large molecular weight of the ThDP-dependent enzymes (varying between 160,000 and 250,000) has so far limited their solution NMR studies, while solid-state NMR spectroscopy presents a promising alternative for investigation of their catalytic mechanisms.

Despite this enormous potential of solid-state NMR methods, there have been no reports in the literature so far on the use of the CSA tensors as probes for various ionization/tautomeric forms of thiamin-dependent enzymes. Therefore, the focus of our work presented in the current report has been the investigation of ¹³C and ¹⁵N chemical shift anisotropy tensors for different ionization states of free thiamin in the solid state as a starting point for subsequent studies of ¹³C and ¹⁵N chemical shifts of several ionization and tautomeric states in a series of thiamin-enzyme complexes. This work represents the first step toward understanding the tautomeric and ionization states among which the protein-bound ThDP cofactor undergoes interconversion during the enzymatic cycle. We have synthesized thiamin molecules containing selective ¹³C and ¹⁵N isotopic labels at key positions of the 4′-aminopyrimidine ring (C6′, N4′) and of the thiazolium ring (C2). Protonated thiamin is in the 4′-aminopyrimidinium form (APH⁺) and unprotonated is in the 4′-aminopyrimidine form (AP), both on and off the enzymes. We have recorded the ¹³C and ¹⁵N CSA tensors for each ionization form by magic angle spinning (MAS) NMR spectroscopy and performed DFT calculations of the corresponding magnetic shielding anisotropy tensors. Our results indicate that the isotropic chemical shifts as well as the principal components of the ¹³C and ¹⁵N CSA tensors are very sensitive to the protonation states in thiamin and therefore permit to differentiate between the two forms (AP and APH⁺). The calculated magnetic shielding anisotropy tensors of C2, C6′ and N4′ exhibit excellent agreement with the experimental CSA tensors. Our findings indicate that MAS NMR spectroscopy in conjunction with DFT calculations is a sensitive probe of ionization states in the ThDP cofactor, and this approach can be applied to studies of the ionization and tautomeric forms in ThDP-dependent enzymes.

RESULTS AND DISCUSSION

Selective labeling

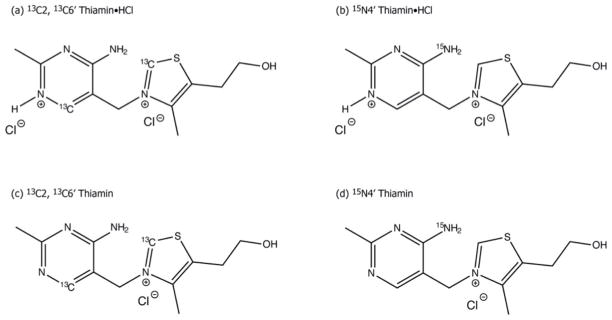
Thiamin (Th) and thiamin hydrochloride (Th•HCl) correspond to the AP and APH⁺ form of ThDP, respectively, in enzyme catalysis (Scheme 1). Since only the 4′-aminopyrimidinium ring undergoes change in ionization, we anticipated that between the two selectively labeled carbon atoms, C2 and C6′, the ¹³C CSA tensor of C6′ would be the prime reporter of the protonation state of the 4′-aminopyrimidine ring, along with the ¹⁵N CSA tensor of the N4′ atom. The chemical structures of Th and Th•HCl with selective ¹³C labels introduced at positions 2 and 6′, and with ¹⁵N label incorporated at N4′ are depicted in Figure 1.

Figure 1.

Chemical structures of Th•HCl and Th with ¹³C/¹⁵N enrichment at positions C2, C6′ and N4′.

Assignments of ¹³C Resonances in Different Ionization States of Thiamin

Since there are two ¹³C isotopically labeled sites (C2 and C6′) in both Th and Th•HCl, ambiguity arises in the resonance assignment of the ¹³C spectra of both samples in the absence of a priori knowledge about the two carbon chemical shifts. In order to resolve this ambiguity, we have measured the ¹J_13C-1H coupling constant for these two carbons by solution NMR, and compared the experimental results with the DFT computed J-couplings in Th•HCl and Th. The results are summarized in Table 1. Based on the DFT calculations, J_C2-H is larger than J_C6′-H by more than 22 Hz in Th•HCl and by 35 Hz in Th. The experimental J-couplings obtained from the proton-coupled ¹³C solution NMR spectra of Th•HCl and Th are in excellent agreement with the theoretical predictions, and immediately permit us to assign the two carbons in both ionization states; the corresponding isotropic solution chemical shifts are also indicated in Table 1.

Table 1.

Experimental and Computed J_CH Couplings for 2,6′-¹³C/4′-¹⁵N Th•HCl and Th.

Sample		JCH (Hz)		δiso (ppm)
		Solution NMR	DFT	Solution NMR
Th•HCl	C2	214.1	208.8	154.6
	C6′	185.6	186.7	145.1
Th	C2	213.6	210.0	157.8
	C6′	177.5	175.3	161.0

¹³C and ¹⁵N Chemical Shift Anisotropies in Different Ionization States of Thiamin: Solid-State NMR

The ¹³C CSA tensors were recorded by two methods: i) slow-MAS spectra at three different spinning frequencies with the subsequent Herzfeld-Berger analysis to extract the CSA tensor components;²⁴ ii) symmetry-based Recoupling Of Chemical Shift Anisotropy (ROCSA) method suitable for high MAS frequencies.²⁵ The ¹⁵N CSA parameters were determined using ROCSA because of the much smaller ¹⁵N CSA tensor resulting in rather weak sideband intensities even at slow-MAS frequencies and thus prohibiting their accurate measurement.

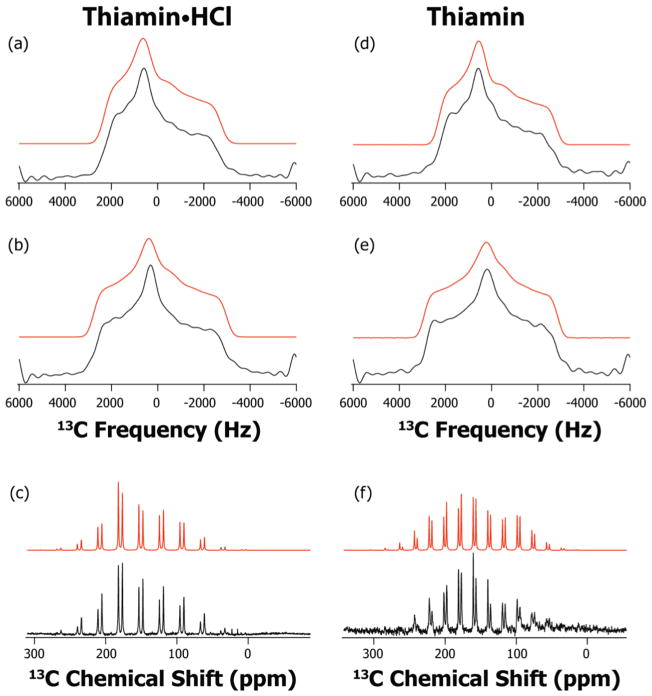
The ¹³C spectra, slow-MAS and ROCSA, are illustrated in Figure 2. From Table 2, it is obvious that the two methods give consistent results for ¹³C CSA tensors in both ionization states. The C2 CSA tensor is not very different in the two ionization forms. The three principal components (δ₁₁, δ₂₂ and δ₃₃) display a small shift of ca. 3 ppm in the upfield direction upon protonation, from Th to Th•HCl. As a result, the net change is only in the isotropic chemical shift, from 156.5 ppm to 153.4 ppm, while the reduced anisotropy δ_σ and the asymmetry parameter η_σ remain nearly the same in the two states. As expected, the CSA parameters of C6′ are significantly different in the two protonation states. The C6′ isotropic chemical shift changes by about 12.5 ppm upfield upon protonation, from Th to Th•HCl. The principal components of the CSA tensor, δ₁₁ and δ₃₃ also move upfield by 17 and 15 ppm, respectively. The δ₂₂ component displays only a small shift of 6 ppm. The resulting change in the reduced anisotropy δ_σ and the asymmetry parameter η_σ is negligible- these remain the same within the error bars in the two protonation states, as the difference between the relative shifts of δ_iso and δ₃₃ is small.

Figure 2.

¹³C ROCSA and slow-MAS spectra of Th•HCl and Th: experimental (black) and simulated (red). a) ROCSA spectrum of C2 of Th•HCl; b) ROCSA spectrum C6′ of Th•HCl; c) slow-MAS spectrum C2 and C6′ of Th•HCl at 2900 Hz rotor frequency; d) ROCSA spectrum of C2 of Th; e) ROCSA spectrum of C6′ of Th; and f) slow-MAS spectrum of C2 and C6′ of Th at 2075 Hz rotor frequency.

Table 2.

Experimental and Computed ¹³C and ¹⁵N CSA Parameters for 2,6′-¹³C/4′-¹⁵N Th•HCl and Th.

Sample	Atom	Method	δiso (ppm)	δσ (ppm)	ησ	δ11 (ppm)	δ22 (ppm)	δ33 (ppm)
Th•HCl	C2	Slow-MAS	153.4	−98.5 ± 1.6	0.59 ± 0.03	231.7	173.6	54.9
		ROCSA	153.4	−103.8 ± 5.0	0.61 ± 0.06	237.0	173.6	49.6
		DFT/with Cl−	154.9	−105.9	0.80	250.2	165.5	49.0
		DFT/without Cl−	158.7	110.3	1.00	269.0	158.7	48.4
	C6′	Slow-MAS	147.8	−109.6 ± 4.5	0.78 ± 0.03	245.3	159.9	38.2
		ROCSA	147.8	−111.3 ± 7.8	0.81 ± 0.08	248.5	158.4	36.5
		DFT/with Cl−	153.7	−114.0	0.87	260.3	161.1	39.7
		DFT/without Cl−	149.7	−110.2	0.88	253.3	156.3	39.5
	N4′	ROCSA	116.5	74.9 ± 3.5	0.27 ± 0.09	191.4	89.2	68.9
		DFT/with Cl−	113.1	70.8	0.11	183.9	81.6	73.8
		DFT/without Cl−	103.8	78.4	0.25	182.2	74.4	54.8
Th	C2	Slow-MAS	156.5	−100.8 ± 1.2	0.66 ± 0.05	240.2	173.6	55.7
		ROCSA	156.5	−103.1 ± 6.4	0.62 ± 0.08	240.0	176.1	53.4
		DFT/with Cl−	155.6	−107.0	0.75	249.2	169.0	48.6
		DFT/without Cl−	162.8	−114.9	0.80	266.2	174.3	47.9
	C6′	Slow-MAS	160.4	−107.8 ± 2.2	0.92 ± 0.03	263.9	164.7	52.6
		ROCSA	160.4	−108.7 ± 5.6	0.93 ± 0.07	265.3	164.2	51.7
		DFT/with Cl−	162.2	109.2	0.90	271.4	156.7	58.5
		DFT/without Cl−	163.4	−108.6	0.99	271.5	163.9	54.8
	N4′	ROCSA	91.2	59.6 ± 2.6	0.28 ± 0.06	150.8	69.7	53.1
		DFT/with Cl−	98.2	59.5	0.51	157.7	83.6	53.3
		DFT/without Cl−	70.2	−56.2	0.90	123.5	73.0	14.0

The ¹⁵N ROCSA spectra are presented in Figure 3. The N4′ CSA parameters are found to be even more sensitive to the protonation state than those for C6′. The isotropic chemical shift, δ_iso, differs by more than 25 ppm in the two forms. Of the three principal components of the CSA tensor, the δ₁₁ component of N4′ CSA tensor is observed to be the most sensitive to the protonation, moving downfield by ca. 40 ppm from Th to Th•HCl. As a result, the reduced anisotropy, δ_σ, increases by 15 ppm in Th•HCl. The δ₂₂ and δ₃₃ principal components also display considerable downfield shift of 20 and 16 ppm, respectively. We note that, it is not possible to accurately measure η_σ in our experiments, because this parameter has a strong correlation with the line-broadening parameter used in fitting the experimental ¹⁵N ROCSA lineshapes with nearly axial symmetry. As a consequence, the position of both δ₂₂ and δ₃₃ is not as well defined as that of δ₁₁ especially when η_σ is in the range of 0.1 – 0.4.²⁶

Figure 3.

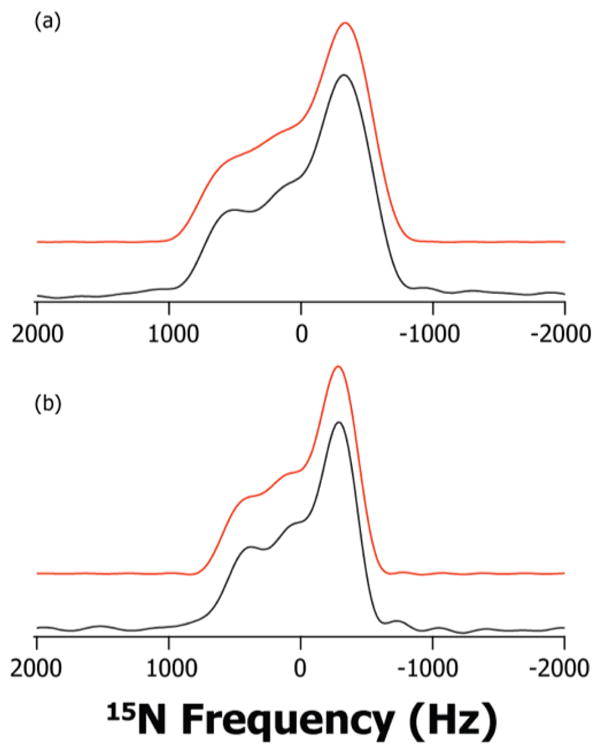
¹⁵N ROCSA spectra of Th•HCl and Th: experimental (black) and simulated (red). a) N4′ of Th•HCl; b) N4′ of Th.

¹³C and ¹⁵N Chemical Shift Anisotropies in Thiamin Hydrochloride: Density Functional Theory

Experimental results and DFT calculations are summarized in Table 2. DFT calculations performed on the geometry-optimized structure of Th•HCl predict the experimental trend very well in the following respects: i) C6′ is more shielded than C2; and ii) δ_σ of C6′ is larger than that of C2.

The calculations predict the principal components of the C2 CSA tensor to within 9 ppm. The calculated isotropic chemical shift of C2, 154.9 ppm, agrees well with the experimental value of 153.4 ppm. Maximum deviation is observed for δ₁₁ (13 ppm) and δ₂₂ (−8 ppm) with δ₃₃ showing no deviation at all. For C6′, the computed principal components of the magnetic shielding anisotropy tensor are in even better agreement with experiment, with the difference being only of the order of 7 ppm. Since for C6′ the three computed principal components deviate in the same direction (downfield) with respect to the experimental values, the isotropic chemical shift also differs by 6 ppm.

For N4′ CSA, the agreement between experiment and theory is excellent, and even tighter agreement is observed than for the ¹³C tensors. The average deviation of the three principal components is less than 7 ppm. The computed δ₁₁ and δ₂₂ are 7.5 ppm upfield, while the calculated δ₃₃ is downfield by 5 ppm compared with experiment. The calculated isotropic chemical shift is therefore only 3.4 ppm different from the experimental value.

We also addressed the effect of the presence of two chloride anions in the DFT calculations. We have performed an additional round of calculations with geometry optimization on the twice positively charged Th•HCl without the two chloride anions. The following trends were observed:

1. The predicted C6′ CSA tensor is in much better agreement with experiment without the two chloride anions, with the average deviations between experiment and theory of less than 4 ppm for the three principal components. The predicted isotropic chemical shift of 149.7 ppm is in much better agreement with the experimental value of 147.8 ppm.

2. At the same time, the computed principal components of the C2 CSA tensor show greater deviations from the experimental values (by more than 20 ppm on average). As observed in the calculations with chloride anions, this deviation can be largely attributed to changes in δ₁₁ (30 ppm) and to a lesser extent to δ₂₂ (−15 ppm) with δ₃₃ showing no deviation at all.

3. The computed N4′ CSA tensor deviates more from the experimental values without the chloride anions with an average difference of 13 ppm for the individual principal components. Both δ₂₂ and δ₃₃ display the maximum deviation from experiments as well as from their computed values in the presence of chloride ions. The δ₁₁ component of N4′ remains relatively unchanged upon the removal of the chloride ions.

¹³C and ¹⁵N Chemical Shift Anisotropies in Thiamin: Density Functional Theory

For the DFT calculations on thiamin, we used a starting model that was derived from the Th•HCl X-ray structure by removing the HCl, and performed further geometry optimization to obtain the final structure for magnetic shielding anisotropy tensor calculations.

As in the case of Th•HCl, DFT calculations on the geometry-optimized Th structure correctly predict that C6′ is more deshielded than C2, which is consistent with the experimental results. The calculated reduced anisotropy, δ_σ, of C6′ is higher than that of C2, as observed in experiments.

The calculated principal components of the C2 CSA tensor agree with their experimental values to within 7 ppm. As in the Th•HCl calculation, δ₁₁ of C2 shows greater deviation from experiment (9 ppm downfield), while δ₂₂ and δ₃₃ are upfield compared with experiment. As a result, the calculated isotropic chemical shift is different by only 1 ppm from experiment. For C6′, the average deviation of the calculated principal components is also less than 7 ppm. δ₁₁ and δ₃₃ are downfield compared with experiment (by 6.2 and 6.8 ppm, respectively), while δ₂₂ is upfield by 7.5 ppm. This results in the calculated isotropic chemical shift (162.2 ppm) in close agreement with the experimental value (160.4 ppm).

The calculated N4′ CSA components are also in close agreement with experiment, to within 9 ppm. As observed in the Th•HCl calculations, both δ₁₁ and δ₂₂ contribute to the difference between calculations and experiment with δ₃₃ showing no deviation.

The perturbation of the carbon CSA tensors due to the removal of the chloride anions in Th is nearly the same as in Th•HCl. The C6′ CSA tensor is observed to agree more closely with the experimental values, while C2 CSA tends to deviate to a greater extent from the experiment; nevertheless, the agreement between theory and experiment is still very good.

Conversely, the absence of the two chloride anions has a great effect on the N4′ CSA tensor in Th. The δ₁₁ and δ₃₃ components differ from their experimental values by −27 and −39 ppm, respectively. As a result, the computed isotropic chemical shift is off by more than 20 ppm upfield. Moreover, the calculations predict an almost rhombic tensor (η_δ = 0.90), whereas in experiments the tensor is close to axial (η_δ = 0.28).

The sensitivity of the C2 and N4′ CSA tensors to the absence of the chloride ions in both AP and APH⁺ forms can be attributed to the chloride ion located close to the sulfur atom in the thiazolium ring (see Figure S1 of the Supporting Information). The interatomic C2-Cl and N4′-Cl distances are ca. 3.7 Å and 3.2 Å, respectively, in the X-ray structure as well as in the geometry-optimized structures used in our shielding tensor calculations.

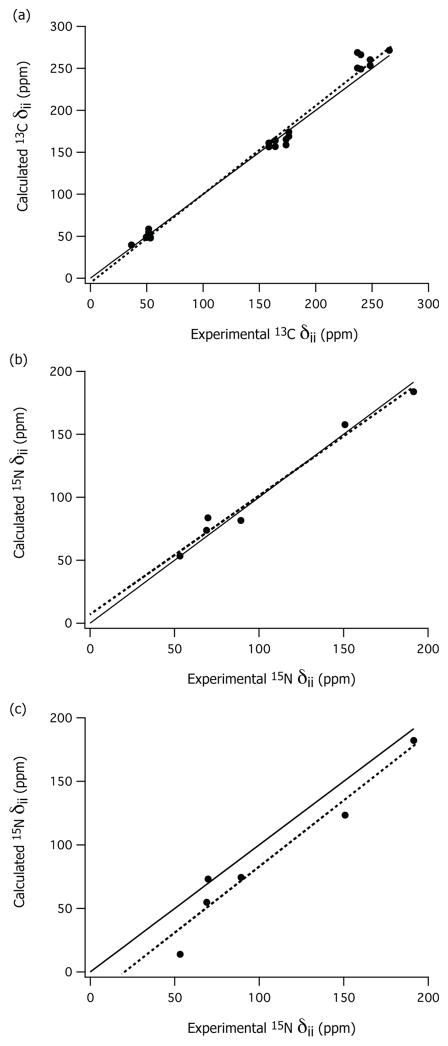
In summary, the calculations predict accurately the C2 and N4′ CSA tensors in the presence of the chloride anions, and the C6′ CSA tensor in the absence of chloride anions. This trend is observed to be the same for both Th as well as Th•HCl. The correlation between the computed and the experimental CSA components is shown in Figure 4 for both ¹³C and ¹⁵N atoms. As discussed, the correlation between the ¹⁵N CSA predictions and the experimental values is much better in the presence of the chloride anions than without chloride anions (see Figure 4b and 4c, respectively).

Figure 4.

Correlation between the principal components δ_ii of the calculated (DFT) and experimental (NMR) chemical shift anisotropy tensors of Th•HCl and Th: a) ¹³C of C2 and C6′; b) ¹⁵N of N4′ with chloride anions; and c) ¹⁵N of N4′ without chloride anions. The solid lines in both figures indicate perfect agreement (δ_cal = δ_exp), and the dotted lines are the least-square fits: (a) δ_cal = 1.05 * δ_exp − 4.88, R² = 0.99; (b) δ_cal = 0.94 * δ_exp + 7.86, R² = 0.98; and (c) δ_cal = 1.03 * δ_exp − 20.28, R² = 0.94.

In an effort to determine whether there is any marked difference in the orientation of CSA tensors of the key atoms in the two ionization states, we calculated the C6′ and N4′ tensor orientations with respect to the molecular frame. We observed that the N4′ and C6′ CSA orientations are relatively unchanged in both AP and APH⁺ forms in the presence of the chloride anions. However, in the absence of the chloride ions, the N4′ CSA orientation changes significantly. Further details are presented in the Supporting Information.

CONCLUSIONS

Our work demonstrates that the ¹³C and the ¹⁵N CSA tensors of C2, C6′ and N4′ atoms are sensitive probes of ionization states of thiamin. Both the principal components of the CSA tensors and the isotropic chemical shifts exhibit significant changes upon protonation/deprotonation. The Density Functional Theory calculations are in excellent agreement with the experimental findings. The predicted C6′ and N4′ isotropic chemical shifts are within 6.0 ppm and 7.0 ppm of the experimental values, respectively. Considering that the isotropic chemical shift difference of these atoms in the two ionization states far exceeds this range of deviation, we conclude that the DFT calculation of CSA parameters can be used in conjunction with MAS NMR measurements for characterization of the different ionization states of thiamin. Our conclusions can be extended to thiamin diphosphate (ThDP), the biologically active form of thiamin since the β-diphosphate moiety in ThDP is located too far from the heterocyclic rings to make any contribution to the chemical shifts, nor does the diphosphate come near to the key atoms under consideration in the enzyme-bound forms. The results of this work are expected to guide future investigations of thiamin ionization and tautomeric states in thiamin-dependent enzymes, which will address some of the remaining open questions about their enzymatic mechanisms.

EXPERIMENTS AND METHODS

Synthesis of [C2, C6′ – ¹³C2] thiamin chloride hydrochloride is reported elsewhere.²⁸

Synthesis of [N4′ – ¹⁵N] thiamin chloride hydrochloride

Compounds I, II & III (ref. Scheme S1) were synthesized with some minor modifications to the previously described methods.²⁹ Compound IV was synthesized according to a method described by Uray et al.³⁰; and compounds V, VI & VII were synthesized with minor modifications to the method described by Contant et al.³¹ and Nicewonger et a.l³² The details are described in Supporting Information.

[N4′– ¹⁵N] Thiamin and [C2, C6′-¹³C₂] Thiamin were prepared by neutralization of [N4′ – ¹⁵N] thiamin chloride hydrochloride and [C2, C6′-¹³C₂] thiamin chloride hydrochloride respectively under anhydrous conditions (See Supporting Information section).

[N4′– ¹⁵N] Thiamin was also prepared using a chemo-enzymatic approach by the Begley group.⁵⁵

Preparation of solid-state NMR samples

Crystalline [C2, C6′-¹³C₂] thiamin chloride hydrochloride (10.4 mg, 0.031 mmol) or [N4′-¹⁵N] thiamin chloride hydrochloride (9.0 mg, 0.027 mmol) were packed into 3.2 mm MAS rotors and used in the subsequent MAS NMR experiments as models for the N1′ protonated form (Figure 1a, 1b).

[C2, C6′-¹³C₂] thiamin (8.0 mg, 0.027 mmol) or [N4′-¹⁵N] thiamin (6.7 mg, 0.022 mmol) were packed into 3.2 mm MAS rotors and used in the subsequent MAS NMR experiments as models for the N1′ unprotonated form (Figure 1c, 1d).

Solid-state NMR spectroscopy

All ¹³C and ¹⁵N MAS spectra presented in this work were acquired at 9.4 T (400.17 MHz ¹H Larmor frequency) on a Tecmag Discovery spectrometer outfitted with a 3.2 mm wide bore Varian HXY T3 probe. The actual sample temperature includes a correction because of sample spinning which is about +5° C for 10 kHz spinning frequency. The temperature was calibrated for this probe at different MAS frequencies using a PbNO₃ temperature sensor³³, and the actual temperature at the sample was 18° C maintained to within ±1 °C throughout the experiments using the Tecmag temperature controller. ¹³C chemical shifts were referenced to the downfield peak of adamantane (38.56 ppm with respect TMS). ¹⁵N chemical shifts were referenced to ammonium chloride (39.2 ppm with respect to liquid NH₃).

The low spinning-frequency ¹³C CPMAS spectra were acquired on Th•HCl at ω_r/2π = 2900, 4070 and 5980 Hz. The MAS frequency was controlled with Tecmag MAS controller: within ±5 Hz at 2900 kHz, while at 4070 and 5980 Hz the variation was up to ±100 Hz. The standard CP sequence was used with 1 ms contact time; the ¹H radio frequency field strength was 60 kHz, the ¹³C field was linearly ramped 80–100% with the center of the ramp being 50 kHz. The ¹H 90° pulse width was 2.5 μs. The same experimental parameters were used at every spinning frequency. The ¹H decoupling was performed using TPPM³⁴ with 100 kHz ¹H radio frequency field strength maintained for the duration of the acquisition period, 25.6 ms. The CPMAS spectra were acquired with either 32 scans (at ω_r/2π = 2900 Hz) or with 4 scans (ω_r/2π = 4070 and 5080 Hz); the recycle delay was 10 s. The spectra were processed without any line broadening, and the intensities of each sideband were extracted for the two carbons in the 2, 6′-¹³C Th•HCl sample.

The low spinning-frequency ¹³C CP-MAS spectra of 2, 6′-¹³C Th were acquired at ω_r/2π = 2075, 3810, and 5973 Hz. The rest of the experimental conditions were the same as for the thiamin hydrochloride sample. At all MAS frequencies, 16 scans were used with 10 sec pulse delay.

The Herzfeld-Berger analysis²⁴ was performed to calculate the CSA parameters from the intensities of the spinning side-band envelopes for the two carbon atoms in both forms of thiamin.

The ¹⁵N CP-MAS NMR spectra of 4′-¹⁵N Th•HCl and Th were acquired at the spinning frequency of 10 kHz. The standard CP sequence was used with 1 ms contact; the ¹H radio frequency field strength was 60 kHz, the ¹⁵N field was linearly ramped 80–100% with the center of the ramp being 50 kHz.100 kHz. TPPM decoupling was applied during the acquisition time (30 ms); ¹H radio frequency field strength was 100 kHz. 32 scans were acquired with a recycle delay of 10 s.

ROCSA (Recoupling Of Chemical Shift Anisotropy) pulse sequence²⁵ was used to recouple the ¹³C and ¹⁵N CSA interaction at MAS frequencies above 10 kHz. The ¹³C ROCSA spectra were collected at the MAS frequency of 12 kHz. The ¹³C radio frequency field strength during the ROCSA period was 51.3 kHz, and that of the ¹H decoupling was 122 kHz. The ¹⁵N ROCSA spectra were collected at the MAS frequency of 10 kHz. The ¹⁵N rf field strength during the ROCSA period was 42.8 kHz and that of the ¹H decoupling was 100 kHz. 16 transients were added up with a recycle delay of 10 sec for each t₁ point. 32 and 24 t₁ points were acquired using the States method³⁵ for ¹⁵N and ¹³C ROCSA spectra, respectively. The CSA dimension was zero-filled to 512 points; no apodization was applied prior to the Fourier transformation.

CSA tensor convention

In this work, we use two conventions for reporting CSA tensors. 1) Standard convention with the three principal components defined as follows: δ₁₁ ≥ δ₂₂ ≥ δ₃₃. 2) Haeberlen-Mehring-Spiess convention where the CSA tensor is characterized by three parameters: i) isotropic chemical shift (δ_iso) ii) reduced anisotropy (δ_σ) iii) asymmetry parameter (η_σ). The relation between the two conventions is as follows: The isotropic chemical shift is defined as δ_iso = (δ₁₁ + δ₂₂ + δ₃₃)/3. The reduced anisotropy (δ_σ) and the asymmetry parameter (η_σ) are defined as: δ_σ = δ₁₁ − δ_iso and η_σ = (δ₂₂ − δ₃₃)/δ_σ if |δ₁₁ − δ_iso| ≥ |δ₃₃ − δ_iso| ≥ |δ₂₂ − δ_iso| (positive anisotropy), or δ_σ = δ₃₃ − δ_iso and η_σ = (δ₂₂ − δ₁₁)/δ_σ if |δ₃₃ − δ_iso| ≥ |δ₁₁ − δ_iso| ≥ |δ₂₂ − δ_iso| (negative anisotropy). The asymmetry parameter is always in the range between 0 and 1.

NMR spectra simulations

The slow spinning frequency ¹³C MAS spectra were simulated in SIMPSON³⁶ using the CSA parameters obtained from HB analysis. An exponential line broadening of 88 Hz was applied to the simulated spectra to match the natural line width. SIMPSON was also used to simulate ¹³C and ¹⁵N ROCSA lineshapes. The MINUIT procedure embedded in SIMPSON was applied for fitting the experimental ROCSA spectra using three variable parameters: δ_σ, η_σ and the line-broadening parameter. The uncertainties for the fitting parameters δ_σ and η_σ were determined from the corresponding values of δ_σ and η_σ giving ${\chi }^2=2{\chi }_{min}^2$.

Density Functional Theory calculations

Quantum chemistry calculations were carried out using the DFT method in Gaussian03.³⁷ Geometry optimization³⁸ was employed using the B3LYP functional^39–41 and tzvp bais set.^{42,43 13}C/¹⁵N shielding tensor calculations were performed using the same functional and the basis set and GIAO approximation.^44–47 The starting structure for Th•HCl geometry optimization was obtained from the X-ray structure of Th•HCl.⁴⁸ The starting structure for the unprotonated thiamin used in the subsequent geometry optimization was derived from the crystal structure of Th•HCl by removing the HCl. Two sets of calculations were performed for both Th•HCl and Th: one with chloride anions, the other one- without the anions (charge +1 for Th and charge +2 for Th•HCl). The J-coupling constant calculations were performed using B3LYP and IGLO-III basis set⁴⁹ with the polarizeable continuum model (PCM).^50–52 Most of the calculations were performed under GridChem computational resources and services, Computational Chemistry Grid⁵³ (www.gridchem.org)

The ¹³C chemical shifts were referenced with respect to adamantane (the downfield resonance at 38.56 ppm) whose absolute magnetic shielding tensor was calculated at the same level of theory as those for the thiamin models. The ¹⁵N chemical shift was referenced with respect to 244.6 ppm according to the previously described procedure.⁵⁴