Two processes support visual recognition memory in rhesus monkeys

Abstract

A large body of evidence in humans suggests that recognition memory can be supported by both recollection and familiarity. Recollection-based recognition is characterized by the retrieval of contextual information about the episode in which an item was previously encountered, whereas familiarity-based recognition is characterized instead by knowledge only that the item had been encountered previously in the absence of any context. To date, it is unknown whether monkeys rely on similar mnemonic processes to perform recognition memory tasks. Here, we present evidence from the analysis of receiver operating characteristics, suggesting that visual recognition memory in rhesus monkeys also can be supported by two separate processes and that these processes have features considered to be characteristic of recollection and familiarity. Thus, the present study provides converging evidence across species for a dual process model of recognition memory and opens up the possibility of studying the neural mechanisms of recognition memory in nonhuman primates on tasks that are highly similar to the ones used in humans.

In humans, dual process models of recognition memory, although different in detail, share the core idea that both recollection and familiarity contribute to this mnemonic function (1–5). Recollection is characterized by the retrieval of contextual information about the episode in which an item was encountered, whereas familiarity lacks this context, relying solely on knowledge of prior occurrence. The possibility that nonhuman animals also use separable memory processes to solve recognition memory tasks has begun to be experimentally addressed (6–8), an important shift, inasmuch as an understanding of how the brain gives rise to different memory functions in various species is critical for relating molecular and cellular findings in animals to behavioral and neuroimaging research conducted in humans.

Recollection and familiarity are commonly viewed as retrieval processes that support potentially independent routes of cognitive access to stored information. This distinction has been operationalized based on the analysis of receiver operating characteristics (ROCs) (5). ROCs in recognition memory relate the proportion of correctly recognized repeated or old items (hit rate) to the proportion of incorrectly recognized novel distracters (false alarm rate) as a function of response criterion (bias to respond “old”). In a typical recognition memory test aimed at characterizing ROCs, subjects would encounter a list of previously studied items intermixed with new items and be asked to rate how confidently they recognize each item on an arbitrary scale [e.g., ranging from one (sure that it is new) to six (sure that it is old), with two to five reflecting less confident judgments]. These confidence ratings represent different decision criteria, and an ROC curve is produced by plotting the hit rate against the corresponding false alarm rate as a function of decision criterion.

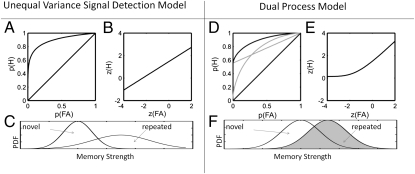
Recognition memory ROCs in humans are typically curvilinear and asymmetrical to the negative diagonal (9–11) (Fig. 1). Some investigators have proposed that the asymmetry in the ROC curve arises from a single signal detection process in which the variance of the old-item distribution is greater than the variance of the new-item distribution (12). This proposal is referred to here as the unequal variance signal detection (UVSD) model. Others have suggested that the ROC asymmetry arises from two underlying processes (5): familiarity, thought to reflect a continuum of item memory strength that is well-described by an equal variance signal detection model, and recollection, thought to reflect a threshold process. When an item is recognized based on familiarity, the memory strength of this item is judged relative to a particular decision criterion. However, when associated information is available, an item can also be recognized based on recollection. The process of recollection can be thought of as a recall process that succeeds for some items but completely fails for others (i.e., the memory falls below threshold). This alternative suggestion is here referred to as the dual process (DP) model. These two models make contrasting predictions regarding the shape of the z-transformed ROC curves (zROC). Specifically, the DP model predicts that the zROC is characterized by a slight U shape, whereas the UVSD model predicts that the zROC is well-described by a linear function with a slope smaller than one (Fig. 1).

Fig. 1.

ROCs (A and D), zROCs (B and E), and probability density functions (C and F) for the unequal variance signal detection (UVSD) and dual process (DP) models, respectively. Recognition memory ROCs in humans are typically curvilinear and asymmetrical to the negative diagonal (black curves in A and D). The UVSD model assumes that novel and repeated (old) items are represented by two Gaussian functions along the dimension of memory strength, with the variance of the old-item distribution being greater than the variance of the novel-item distribution (C). The DP model assumes that two independent processes, recollection and familiarity, contribute to recognition memory functions. Recollection is assumed to be a threshold process, whereas familiarity is assumed to be an equal variance signal detection process (F). Specifically, a certain proportion of old items (the distribution of all old items is indicated by the gray shading in F) is assumed to exceed that threshold and, therefore, is recognized with high confidence on the basis of recollection. When recollection fails, recognition is assumed to be based on familiarity. Purely on their own, an equal variance signal detection process will produce an ROC that is curvilinear and symmetrical to the negative diagonal, and a threshold process will produce a linear ROC (D; both ROCs shown in gray). The UVSD model predicts linear zROCs (B), with a slope smaller than one, reflecting the ratio of the SDs of the new- and old-item distributions. The DP model predicts U-shaped zROCs (E) as a result of the threshold process.

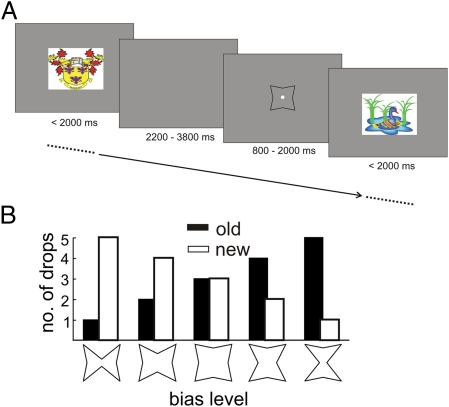
Previous studies in monkeys have treated recognition memory as a unitary phenomenon in that they have been agnostic to the possibility that different processes may underlie this mnemonic ability. To test whether ROCs in monkeys are qualitatively comparable with what is typically observed in humans and also, whether evidence can be found for two qualitatively different processes supporting recognition memory in monkeys, we trained four male rhesus monkeys (Macaca mulatta) on a visual running-recognition task with trial-unique, complex images (Fig. 2A). Monkeys were required to pull a lever on their left with their left hand if the image had been shown before (old image) and pull a lever on their right with their right hand if the image was being shown for the first time (new image). For every correct response, the monkey obtained a juice reward. Old and new images were of equal probability. The number of stimuli intervening between the first presentation of a particular stimulus and its later repetition was variable. Critically, ROCs were obtained by manipulating the monkeys’ bias to respond “old” or “new” by varying the relative amount of juice dispensed for correct old and correct new responses across five discrete levels (Fig. 2B).

Fig. 2.

(A) Timing of the running recognition task. Images were presented on a computer screen, one at a time, with equally probable presentation of old and new images. (B) Response bias was pseudorandomly manipulated in blocks of 200 stimuli. The histogram shows the juice reward (in number of drops; y axis) obtainable for correct “old” (black) and correct “new” (white) responses as a function of the five experimental bias manipulations (x axis). The symbols at the bottom indicate the cues that were presented immediately before each image as a function of bias level in effect on that block (Methods, Behavioral Procedure).

Results

Performance.

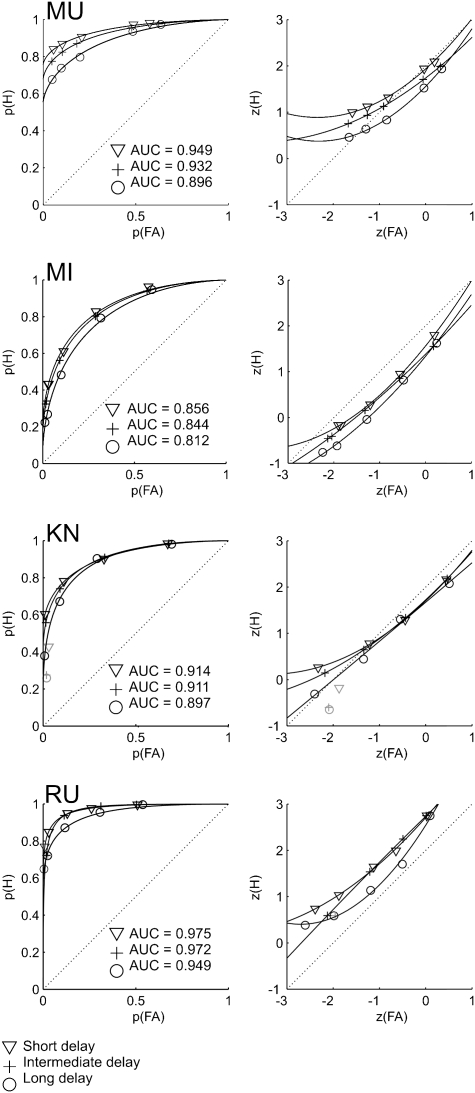
Fig. 3 shows the ROCs (Fig. 3, Left) and zROCs (Fig. 3, Right) for all four monkeys. Performance was assessed for each monkey and each delay separately by calculating the area under each ROC curve (AUC). The results are shown in Fig. 3.

Fig. 3.

ROCs (Left) and zROCs (Right) for each of the four monkeys. Areas under the ROC curves (AUCs) are given in Left. (Monkey MU) For the long interval, the ROC was significantly curvilinear (F = 117, P < 0.005), and the zROC was significantly nonlinear (F = 45, P < 0.05). For the medium interval, the ROC was significantly curvilinear (F = 75456, P < 0.001), and the zROC was significantly nonlinear (F = 89, P < 0.05). For the short interval, the ROC was significantly curvilinear (F = 184, P < 0.001), and the nonlinearity of the zROC approached significance (F = 18, P = 0.052). (Monkey MI) For the long interval, the ROC was significantly curvilinear (F = 268, P < 0.001), and the nonlinearity of the zROC approached significance (F = 11, P < 0.079). For the medium interval, the ROC was significantly curvilinear (F = 10518, P < 0.001), and the zROC was significantly nonlinear (F = 19, P < 0.05). For the short interval, the ROC was significantly curvilinear (F = 225, P < 0.001), and the zROC was significantly nonlinear (F = 30, P < 0.05). (Monkey KN) The most extreme “new” bias level was associated with a lower hit rate and higher false alarm rate than the neighboring bias level for all intervals. Because analyzing ROCs assumes constant discriminability across bias levels, which is not the case here, these extreme data points (shown in gray) were excluded from analysis. For the long interval, the ROC was significantly curvilinear (F = 334, P < 0.005), and the zROC was not significantly nonlinear (F = 0.004, P > 0.9). For the medium interval, the ROC was significantly curvilinear (F = 7118, P < 0.001), and the zROC was significantly nonlinear (F = 34191, P < 0.005). For the short interval, the ROC was significantly curvilinear (F = 1326, P < 0.001), and the nonlinearity of the zROC approached significance (F = 87, P = 0.068). (Monkey RU) For all delays, hit rate was 1.0 for the extreme “old” bias level and was set to 0.997 for analysis. For the long interval, the ROC was significantly curvilinear (F = 353, P < 0.001), and the zROC was significantly nonlinear (F = 22, P < 0.05). For the medium interval, the most extreme “new” bias level (shown in gray) was excluded from analysis because of a lower hit rate and higher false alarm rate than the neighboring bias level (see Monkey KN for rationale). The ROC was significantly curvilinear (F = 19188, P < 0.001), and the zROC was not significantly nonlinear (F = 3.9, P > 0.25). For the short interval, the ROC was significantly curvilinear (F = 2115, P < 0.001), and the nonlinearity of the zROC approached significance (F = 15, P = 0.06).The data points that were excluded from analysis are displayed in gray.

ROC Curvilinearity.

We asked whether recognition memory ROCs in monkeys are curvilinear, which is typically the case in human experiments. According to the DP model described above, both R and F (R denoting the model parameter for recollection and F denoting the model parameter for familiarity) contribute to recognition memory (Methods). Specifically, recognition of an item is said to be based on R if a threshold is exceeded, with R corresponding to the probability of old items exceeding that threshold. If old items are not recognized based on R, recognition is said to be based on F, estimated as d′, with the memory strength contributed by F reflecting the distance between the new and old item distributions in units of SD. The contribution of F to recognition performance will lead to a curvilinear ROC. Nested F-tests indicated that all 12 empirical ROCs (four monkeys with three intervals each) were fit significantly better by a DP model using both R and d′ as parameters than by a model using R alone, suggesting that a signal detection F process contributed to performance (details in Fig. 3).

ROC Asymmetry.

Recognition memory ROCs in human experiments are typically asymmetrical to the negative diagonal (Fig. 1). The UVSD model accounts for this asymmetry by assuming that the variance of the old item distribution is greater than the variance of the new item distribution. By contrast, the DP model accounts for this asymmetry by assuming that a threshold R process contributes to recognition memory. Using a least squares approach to fit the UVSD model to the empirical ROCs, we found that the variance ratio (VR) of the old vs. new item distributions was significantly greater than one (VR = 1.43, SD = 0.3, t₁₁ = 4.98, P < 0.001), suggesting that, as in humans, recognition memory ROCs in rhesus monkeys are asymmetrical to the negative diagonal. Using a least squares approach to fit the DP model to the empirical ROCs, we found that, as a population, parameter estimates for R were significantly greater than zero (R = 0.39, SD = 0.27, t₁₁ = 4.97, P < 0.001), corroborating the finding obtained by applying the UVSD model. Thus, to this point, the results are consistent with both models.

Contrasting the DP and UVSD Models.

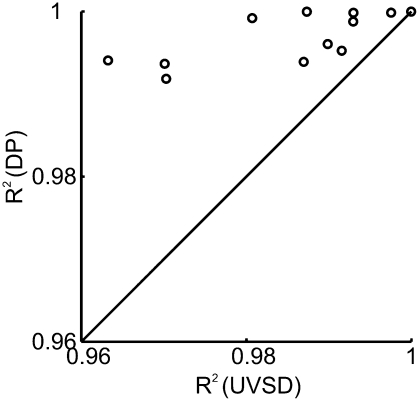
In the next step, we asked which model, DP or UVSD, provides a better fit to the empirical ROCs. Because both models have two free parameters, R² as a measure of goodness of fit can be directly compared between the two models. Eleven of the twelve ROCs were better fit by the DP model than by the UVSD model, and one was fit equally well by both models (Fig. 4). However, because ROCs were fit exceptionally well by both models (mean R² = 0.997 for the DP model, mean R² = 0.985 for the UVSD model), we used a more direct test to contrast the two models. A pure signal detection process, as in the UVSD model, always predicts that ROCs will be linear in z-space (zROCs). Therefore, if zROCs are nonlinear, a pure signal detection process cannot explain the empirical data. By contrast, the DP model predicts that the influence of a threshold R process will lead to U-shaped zROCs. To test these two predictions, we fit second-order polynomials to the zROCs. Eleven of twelve nonlinear coefficients were positive. To test whether the population of zROCs was significantly nonlinear, we used a mixed model ANOVA on the z-transformed hit rates [z(H)] for each bias level, with monkey (four levels) as a random effect, delay (three levels) as a fixed effect, and x and x² as continuous variables [where x is the z-transformed false alarm rate corresponding to each z(H)]. There was a significant main effect of x² (F_1,4 = 27, P < 0.01), showing that the zROCs were significantly U-shaped. Furthermore, nested F-tests were used to test whether individual zROCs were fit significantly better by a second-order polynomial than by a first-order polynomial. Of 12 analyzed zROCs, 6 were significantly U-shaped, and 4 of the other 6 approached significance (details in Fig. 3). Together, our data suggest that a signal detection model alone cannot account for the empirical data, whereas the DP model can do so.

Fig. 4.

Comparison of R² as goodness of fit measures for the UVSD (x axis) and DP models (y axis). Eleven of twelve ROCs were better fit by the DP model than by the UVSD model, and one was fit equally well by both models.

Parameter Estimates of R and F as a Function of Delay.

Recognition memory performance decreased as a function of increasing delay for all four monkeys (Fig. 3). We, therefore, asked whether this performance decrease was because of a selective decrease in either R or F or both. Table 1 shows the parameter estimates for R and F for all four monkeys. The mean parameter estimate for R was 0.4 (SD = 0.25), and the mean parameter estimate for F was 1.5 (SD = 0.48). For two of the four monkeys, both R and F estimates decreased as a function of increasing delay; for one monkey, R decreased and F increased; one monkey showed no systematic relationship. Correlation analysis across all four animals revealed no significant relationship between delay and the parameter estimates for either R (r = −0.3, P > 0.3) or F (r = −0.1, P > 0.75).

Table 1.

Estimates for R and F as a function of delay for all four monkeys

	Short	Medium	Long
R estimates
MU	0.7568	0.6785	0.5548
MI	0.2071	0.1525	0.0700
KN	0.5351	0.4217	0.2048
RU	0.5786	0.0618	0.5580
F estimates
MU	1.1651	1.1507	1.0409
MI	1.2945	1.2846	1.1863
KN	1.2796	1.4580	1.6074
RU	2.2592	2.5941	1.7225

Control Experiment to Test Whether Reward Size at Encoding Affects Recognition Accuracy.

In our running recognition task, novel items are encoded in the context of the test phase, whereas in most previous ROC experiments, which used study lists followed by test lists, the encoding phase was separated from the test phase. Because the monkeys’ bias was manipulated by using different reward ratios for old and new items, different amounts of reward are administered for novel (and old) items as a function of bias level. If the reward magnitude influences encoding, the shape of the ROCs could be influenced through different levels of performance across bias levels. We, therefore, conducted a control experiment with three monkeys, in which reward magnitudes for new and old items was pseudorandomized instead of being separated in different blocks. All other parameters, such as timing and delays, were the same as in the main experiment. This experiment allowed us to test whether old-item performance changes as a function of reward delivered during this item's first presentation. A two-way ANOVA with the factors delay (short, medium, and long) and reward at encoding (1, 2, 3, 4, and 5 drops of juice) was performed for each monkey. There was no significant interaction for any of the three monkeys (M1: F = 0.68, P > 0.7; M2: F = 0.66, P > 0.7; M3: F = 1.07, P > 0.35) and no significant main effect of reward (M1: F = 1.09, P > 0.35; M2: F = 0.62, P > 0.6; M3: F = 0.9, P > 0.45), arguing against the possibility that the running-recognition task used in the present experiment influenced ROC shape through an influence of reward magnitude during encoding on overall performance. All three monkeys showed a significant main effect of delay (M1: F = 5.51, P < 0.005; M2: F = 5.54, P < 0.005; M3: F = 23.6, P < 0.001).

Discussion

In this study, we showed that recognition memory ROCs in rhesus monkeys have the same features—curvilinearity and asymmetry to the negative diagonal—characteristic of ROCs observed in human studies. This observation leads directly to the ongoing debate about the process(es) underlying ROC asymmetry and, by implication, underlying recognition memory. Two opposing views make fundamentally different claims about the variable responsible for ROC asymmetry. The DP model claims that R, a threshold process, can be used independently of F, an equal variance signal detection process, to support recognition memory functions. According to this view, R should lead to an asymmetrical ROC as opposed to the symmetrical one that would be observed with F alone. The UVSD model claims that ROC asymmetry arises from the variance of the old-item distribution being greater than the variance of the new-item distribution. Critically, these two models make different predictions about the shape of z-transformed ROCs. The DP model predicts U-shaped zROCs because of the threshold R process, whereas the UVSD model predicts linear zROCs. In the present study, we found that zROCs were significantly U-shaped. Thus, a single signal detection process, as in the UVSD model, cannot account for the empirical data. Conversely, the data show that visual recognition memory in monkeys is well-described by an equal variance signal detection process together with a threshold process.

Related to the study presented here are studies in rats that used ROCs to dissociate recollection and familiarity in item (8) and associative memory (13). These studies tested odor recognition in rats and showed that selective lesions of the hippocampus impair what the authors (8, 13) termed “recollection-like” memory, whereas familiarity-based memory was unimpaired. The findings show the great potential that such research in experimental animals has for furthering our understanding of the neural basis of human recognition memory processes. However, comparison of recognition processes across species clearly benefit from comparability of experimental procedures, and human and rodent task designs are inherently difficult to match. The present study in nonhuman primates advances the goal of procedural comparability by using, as in studies conducted in humans, visual presentation of stimulus material together with a setup that allowed for subsecond manual responding. At the same time, despite differences in task design, stimulus material, type of responding, and species used, the main conclusions of the rodent studies described above and the present one are similar, suggesting that the processes underlying recognition memory are fundamental building blocks of memory function that are shared across species.

The vast majority of studies using ROCs to investigate recognition memory processes have been conducted in humans (10, 11). The findings from the present study show that recognition memory ROCs in monkeys share the same features with those obtained from human studies, namely curvilinearity and asymmetry to the negative diagonal. However, unlike the present study, most studies on item recognition in humans have not reported U-shaped zROCs. It is possible that the large number of trials that we collected (on average, nearly 2,000 trials per monkey per bias level) together with the within-subject and -delay analyses contributed to the detection of U-shaped zROCs, but the large number of studies that have failed to show nonlinear zROCs in humans argues against this proposal. Another possible explanation of the difference is that we obtained ROCs by manipulating the monkeys’ bias through differential reward payoffs in a block design using a running-recognition task, whereas in humans, ROCs are typically obtained by asking subjects, in a study/test design, to rate their recognition confidence on a continuous scale; however, several arguments speak against this explanation. First, a recent study in humans showed that ROCs obtained using a bias method are comparable in shape to ROCs obtained using the confidence method (14). Second, our control experiment suggests that the running recognition task in conjunction with differential reward payoffs did not influence accuracy differentially for the different bias levels. Third, overall reward availability and accessibility were constant across bias levels in the present experiment, arguing against the possibility that either could have influenced ROC shape through a differential effect on accuracy.*

Perhaps the most plausible explanation for the differences in zROC shape between the present study and the majority of human studies is that, in the present experiment, we used trial-unique images that the monkey had never seen before, whereas most human studies of recognition memory use highly familiar words. Consistent with this possibility are the findings from several studies in humans that have reported U-shaped zROCs for item recognition when images were used as the stimulus material (17–19). The use of trial-unique images could also have contributed to the high levels of performance observed in the present experiment. However, high performance alone does not produce U-shaped zROCs (20).

In the present study, we contrasted two extensively investigated models of recognition memory, namely, the DP and UVSD models. The greatest difference between them is that the DP model assumes that the contribution of recollection to recognition memory is an independent threshold process (i.e., it succeeds for some items but completely fails for others). It is worth noting in this connection that recent evidence raises the possibility that recollection could be a continuous process just like familiarity (18, 21). However, the proposal that recollection is a threshold process is not inconsistent with the idea that recollective strength can vary for above-threshold items, and the results presented here—curvilinear and asymmetrical ROCs together with nonlinear zROCs—are perfectly compatible with this proposal. Thus, the issue of whether recollection, when it occurs, is a continuous process does not affect the study's main conclusion, namely, that two processes support recognition memory in rhesus monkeys.

Recollection is often thought of as a retrieval process that enables access to episodic memory. Episodic memory (22) enables an organism to remember specific episodes of the past and is characterized by a specific phenomenological state involving the re-experiencing of personally experienced past episodes (4). It is this awareness of the self in past, present, and future that has been widely assumed to be a uniquely human faculty, perhaps in part because of the difficulty of assessing metamnemonic awareness in nonlinguistic animals (but see ref. 23). However, whereas episodic memory may rely on recollection, recollection as a neural process may support memory function independently of episodic memory, and thus, it could exist even in animals without the ability to remember episodes from the past. The assumption that animals use familiarity in recognition memory tasks seems to be much less controversial, despite the fact that familiarity in humans is also thought to be accompanied by a characteristic form of phenomenological awareness (a feeling of knowing) (4). Consequently, just as metamnemonic awareness in humans may be as intimately linked with familiarity as it is with recollection, the neural processes underlying familiarity, just like those processes underlying recollection, could operate independently of such awareness in nonhuman animals.

In summary, our results suggest that recognition memory in monkeys can be supported by two processes. The data are in line with previous work in humans arguing that a threshold recollection process and a signal detection familiarity process independently support recognition memory. The finding not only provides converging evidence across species for the DP model but also opens up the possibility of studying the neural mechanisms of visual recognition memory processes in primates, including the contributions of different regions in the medial temporal lobe, to performance on tasks that are highly similar to the ones used in humans.

Methods

Subjects and Testing.

Four experimentally naïve rhesus monkeys (M. mulatta; all male and 5.0–7.0 kg) were used in this study. They were housed singly or in pairs and fed a diet of primate chow and fruit. Fluid intake was controlled. On testing days, monkeys received apple juice as a reward for correct responses, and no water was supplemented. On nontesting days, monkeys received water in their home cage. All procedures were carried out in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and approved by the Animal Care and Use Committee of the National Institute of Mental Health. Monkeys were tested 5–7 d/wk, and, during testing, their heads were restrained.

Behavioral Procedure.

Monkeys were trained on a visual running-recognition task (e.g., ref. 24). The task was automated and programmed using LabView (http://www.ni.com/labview/). Monkeys sat in front of a computer monitor on which complex clipart images (size of library, ∼160,000) were displayed, one at a time, with an average interstimulus interval of about 5 s (range ∼3,300–6,800 s). First and repeat presentations were of equal probability within subsequent blocks of 108 stimuli (called randomization blocks below). The proportion of images that were second presentations was 41.7% of all images, with an equal likelihood of 5, 16, 17, 18, and 26 images intervening between first and second presentation. For subsequent analysis, the different numbers of intervening stimuli (IS) were grouped according to short delay (5 IS), intermediate delay (16, 17, and 18 IS), and long delay (26 IS). The recognition delays represented by these different numbers of intervening stimuli were ∼30 s for the short delay, 90 s for the intermediate delay, and 135 s for the long delay. All subsequent analyses are based on these trials together with the corresponding first presentations of the stimuli in these trials. For randomization purposes and to keep the proportion of first and repeat presentations equal, 8.3% of the images were never repeated, and 8.3% of the images consisted of third presentations; the responses to these single- and third-presentation images were not analyzed.

Monkeys were trained to pull a lever on their left with their left hand if the image had been shown before (“old” response) and pull a different lever on their right with their right hand if the image was being shown for the first time (“new” response). The stimulus was extinguished immediately after the monkey responded. For every correct response, the monkey obtained a juice reward. The monkeys’ bias to respond “old” or “new” was manipulated by varying the relative amount of juice that they could obtain for correct “old” and correct “new” responses across five discrete levels (Fig. 2B). Each level was used for 200 stimuli at a time, and the monkeys performed one to three blocks each day, with a different bias level for each block. In our running recognition task, the first images in each randomization block (see above) are necessarily novel, which could potentially influence the results in some way (e.g., because of lower levels of interference at the beginning of blocks). Excluding the first 15 stimuli of each block from analysis did not change the overall results, and we, therefore, used all trials for all analyses. Each stimulus was preceded by a cue, indicating the current bias level (Fig. 2B) to provide the monkeys with information about the bias level in effect before each stimulus presentation. Independently of the cues, however, the current bias level became evident after the first correct response was made and the reward for it was received. ROC curves were generated for each monkey separately by first averaging data across blocks for each reward ratio. zROCs were generated by computing the z-score for the hit and false alarm rate at each bias level.

ROC Analyses.

All analyses were performed using Matlab. Model fitting to the empirical data was performed by using a least squares approach as well as a maximum likelihood approach. Because the two methods yielded virtually identical results, we show only the results from the least squares analysis. According to the DP model, recognition can be based on a recollection process (R) or an independent familiarity process (d′) (25). This model can be formalized by the following equations (Eq. 1):

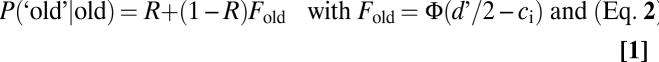where P(‘old’|old) refers to the probability of responding “old” to old items (hit rate) and P(‘old’|new) refers to the probability of responding “old” to new items (false alarm rate). The variable R reflects the probability of an item being recognized based on recollection (the threshold process). The variable d′ reflects the distance between the equal variance Gaussian strength distributions for old and new items (i.e., the discrimination sensitivity of the signal detection process); c_i reflects the response criterion at point i, which was experimentally obtained by manipulating the monkey's bias, and Φ is the cumulative response function.

Where indicated in Results, nested F-tests were used to statistically compare models of the empirical ROCs and zROCs according to (Eq. 3)

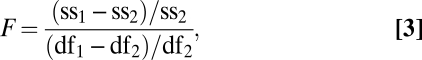where ss stands for sum of squares and df stands for degrees of freedom. The subscripts 1 and 2 stand for the simpler and more complex models, respectively. Specifically, when testing for ROC curvilinearity, the simpler model is the threshold model with one free parameter (R), and the more complex model is the DP model with two free parameters (R and d′). When testing for zROC nonlinearity, the simpler model has two free parameters, and the more complex model, adding a quadratic coefficient, has three parameters.

To test zROC nonlinearity on the population data, we used a mixed model ANOVA on the z-transformed hit rates [z(H)], with monkey (four levels) as a random effect, delay (three levels) as a fixed effect, and x and x² as continuous variables [where x is the z-transformed false alarm rate corresponding to each z(H)]. A significant main effect of x² would indicate nonlinearity of the zROCs.

AUCs were calculated using the parameters from a fit of the DP model to the individual ROCs.