Metacommunity theory explains the emergence of food web complexity

Abstract

Food webs are highly complex ecological networks, dynamic in both space and time. Metacommunity models are now at the core of unified theories of biodiversity, but to date they have not addressed food web complexity. Here we show that metacommunity theory can explain the emergence of species-rich food webs with complex network topologies. Our analysis shows that network branching in the food web is maximized at intermediate colonization rates and limited dispersal scales, which also leads to concomitant peaks in species diversity. Increased food web complexity and species diversity are made possible by the structural role played by network branches that are supported by omnivore and generalist feeding links. Thus, in contrast to traditional food web theory, which emphasizes the destabilizing effect of omnivory feeding in closed systems, metacommunity theory predicts that these feeding links, which are commonly observed in empirical food webs, play a critical structural role as food webs assemble in space. As this mechanism functions at the metacommunity level, evidence for its operation in nature will be obtained through multiscale surveys of food web structure. Finally, we apply our theory to reveal the effects of habitat destruction on network complexity and metacommunity diversity.

The science of networks is deepening our understanding of biodiversity in complex ecosystems (1). Food webs are archetypal ecological networks that have important temporal and spatial dimensions crucial to their assembly and persistence (2). Spatial food web data reveal patterns of species interactions that are structured in space, and theory suggests that this spatial structure may underlie a general explanation of food web complexity (3–7). Recently metacommunity theory has successfully invoked spatial processes such as dispersal to explain patterns of biological diversity from local to regional scales (8–11). However, to date metacommunity theory has focused on communities structured by competitive interactions, and although attempts have been made to extend the approach to the study of simple trophic interactions (12, 13), the study of larger, more complex trophic networks has largely remained—with rare exceptions (14, 15)—outside its purview (2).

The need for a general spatial theory of food webs is acute given current rates of biodiversity loss under global environmental change. Habitat destruction and fragmentation are changing not only species richness, but also the diversity and patterns of species interactions that link them in networks (16). Over time food webs disassemble in nonrandom patterns as the spatial network of interconnected patches of habitat is altered, eroded, and isolated (17). Shifts in food web interactions arising from spatial habitat compression also perturb the ecosystem functions at local and metacommunity scales (18). Efforts to restore functional food webs in fragmented landscapes will require an explicit theory of how food webs assemble and disassemble in space and how their complexity varies with habitat connectivity and spatial scale.

Here we extend metacommunity theory to show that the scale and rate of dispersal can explain the emergence of food web complexity. Our theory explains how food web complexity is assembled and maintained at regional scales despite simple rules that strongly constrain its structure and diversity at small scales (Fig. 1). We show that dispersal in the metacommunity mediates food web branching and diversity and that, at the metacommunity scale, network branching arises due to the structural support provided by omnivore and generalist feeding modules. Here generalist feeding refers to the ability of a consumer to switch its feeding between different resources from distinct food chains in different patches within the metacommunity. Omnivory, on the other hand, is defined when a consumer is able to switch its feeding between different resources within a single food chain—that is, to feed on species at different trophic levels within the same food chain. Our demonstration of the role of omnivory in sustaining complex network topologies and maintaining high-diversity communities stands in stark contrast to previous theoretical predictions that suggested omnivory should destabilize food webs (19). Finally, we show that habitat destruction can lead to reorganization of the trophic network which can, despite ultimately causing the collapse of the food web, bring about surprising transient increases in diversity. This effect is explained by our theory and could be tested in the field. These results provide a foundation for a metacommunity theory of food webs.

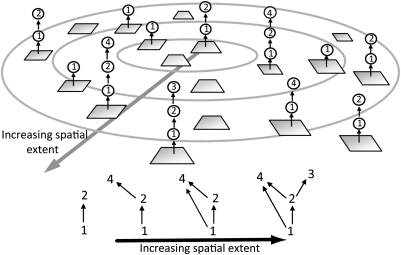
Fig. 1.

A simple example of how food web complexity might emerge at large spatial scales through the spatial aggregation of local food chain networks with increasing spatial extent within a metacommunity. (Upper) Numerous local habitat patches, represented by squares, contain various local food chains. The concentric circles show different sample sizes, and the large arrow shows the direction of increasing spatial extent. As spatial scale increases, and as more species and potential feeding interactions are sampled, the observed trophic complexity of the regionally aggregated food web [depicted by the network diagrams (Lower)] increases despite the complexity within local patches being constrained to simple network configurations—in this case, simple food chains. (Lower) The observed regional food web networks that correspond to increasing spatial extent. In this paper we assume complete competitive exclusion of inferior competitors from a given resource within patches, such that the only way two species that potentially feed on a common resource can coexist within a patch (e.g., species 2 and 4 competing for species 1) is if one species is an omnivore capable of switching its feeding to another species in the local food chain, as when species 4 switches its feeding predominantly toward species 2 when 2 excludes 4 from resource species 1.

Modeling Framework

We use a spatially explicit patch-dynamic model to represent a set of local patches, each of which can contain subpopulations of several trophically interacting species. Each species subpopulation produces colonizers to establish new subpopulations in available patches at a rate c. Subpopulations of each species also suffer extinction locally within patches at a rate e. Long-term or equilibrium patch occupancy of each species is determined by the balance between patch colonization and extinction. Our metacommunity model is thus a spatially explicit version of an extended metapopulation patch-dynamic model (20), capable of tracking the patch occupancy of multiple species competing for habitat patches and feeding on each other within patches (14, 15). This approach allows us to investigate the role of space in determining the equilibrium structural properties—specifically the network complexity and diversity—of spatial food webs assembled by colonization-extinction dynamics at the metacommunity scale.

We consider food webs as directed graphs or networks, with species represented by vertices and feeding links by directed arrows from resources to consumers. This approach enables us to define network complexity by the degree to which the food web is characterized by the branching of feeding links at forks in the network—that is, the degree to which multiple consumers are able to regionally persist by sharing common resources at the metacommunity scale. At any given fork in a network we define the link from a resource vertex to the competitively superior consumer as a “primary link” and any additional links to other independent consumers as “branching links”. We refer to the consumer at the end of a branching link as the “branching consumer”. Thus, a primary link refers to the dominant (or only) feeding link directed away from a given species vertex, whereas branching links refer to any additional feeding links directed away from a species vertex toward the various consumer vertices. In this paper we define food web branching, and hence complexity, by using the minimum number of branching links that would be required to connect all species in the metacommunity food web. Specifically, we define branching in the food web by the minimum number of branching links that a spanning tree or subnetwork of the food web would require to be able to span or connect all species nodes in the food web after all its omnivore links have been removed (SI Appendix). The minimum number of branching links required to connect all species in a food web then gives a measure of the degree of resource sharing by consumers at the metacommunity scale.

To isolate the effects of spatial processes on food web assembly we remove the confounding effects of other, nonspatial, coexistence mechanisms that can lead to network branching, such as the ability of consumers to partition and share resources within patches. Thus, linear chains are the most complicated network topology possible within a patch, although more complicated topologies can emerge across patches. We also assume that all species in the metacommunity have the same life-history trait parameter values (i.e., colonization, c, and extinction, e, rates), although they may differ in their competitive ability to displace other species from a given resource within a patch. Thus, trophic complexity cannot arise in our study because of innate differences in life-history strategies related to colonization or extinction rates between species (e.g., competition–colonization trade-offs) (21–23) or because of local mechanisms of coexistence (24), even though these are likely to play a role in nature. We do, however, consider differences that arise when species that feed on fewer resources (more specialized consumers) are competitively superior at excluding their more generalist competitors from local resource patches. Previous work suggests that specialists have higher fitness and competitive ability than generalists when both are constrained to a shared local resource (25, 26). Our approach is thus tailored to identifying how colonization rate and scale influence food web structure, and how network structure, in turn, affects realized species richness in the metacommunity.

We first present analytical results that derive the conditions for the emergence of trophic complexity at the metacommunity level. We then report the results of numerical simulations based on spatially explicit lattice models that demonstrate the range of food web structures that emerge within large metacommunities where dispersal rate and scale are varied. We also present the effects of habitat destruction on spatial food web diversity and complexity.

Results

The Role of Omnivore and Generalist Feeding Links in Simple Metacommunity Networks.

We first analytically demonstrate, for simple trophic configurations, how a simple patch-dynamic framework can be used to explain the spatial emergence of network branching and food web complexity despite all species having identical extinction, e, and colonization, c, rates. In a patch-dynamic metapopulation (20) the equilibrium patch occupancy, or fraction of the total available patches occupied, 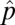, of a single species is 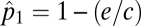. If a consumer, denoted as species 2, feeds exclusively on the original species (species 1), the patches suitable as habitat for colonization by species 2 are those patches already occupied by species 1. Assuming there is no added extinction rate due to top–down effects, species 2's equilibrium patch occupancy is 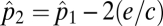(15). In general a species at the nth trophic level has an equlibrium patch density of 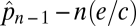, which is found by simply solving the equation 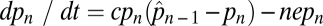after setting dp_n/dt = 0 (15). Here negative values of the equilibrium patch occupancy, 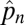, are equivalent to a patch occupancy of zero.

Note that in the equilibrium expression for the nth trophic level, 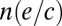represents the fraction of available habitat left at trophic level n − 1 after a species at the nth trophic level has reached equilibrium. It also represents the minimum habitat threshold required to allow an nth-trophic–level consumer to establish itself and maintain a positive equilibrium density. As a result, there are not enough suitable habitat patches remaining for an inferior competitor to occupy a given trophic level after a superior competitor has already established itself—the inferior competitor is prevented from establishing itself due to competitive exclusion from the trophic level at the metacommunity scale by the superior competitor. Coexistence of competitor species, and thus network branching, appears impossible in the absence of life-history trade-offs. However, it may still arise if subordinate competitors are capable of feeding in the leftover habitat on more than one trophic level. We can investigate this particular coexistence mechanism by studying the simple omnivory module in Fig. 2A to determine when species 4 is able to regionally coexist with species 3 on a common resource species 2 by feeding on multiple trophic levels. Assuming species 4 is the inferior competitor, we can calculate under what conditions 4 can regionally coexist with 3 at the metacommunity scale.

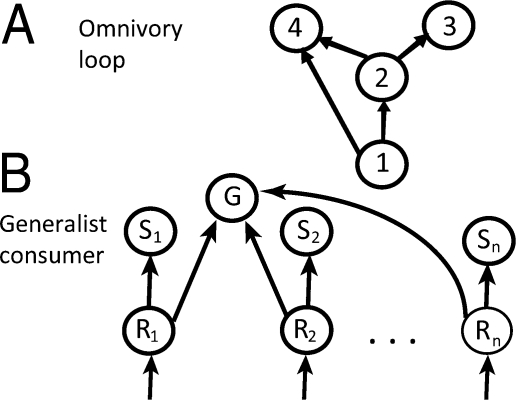
Fig. 2.

Simple omnivory and generalist food web modules. (A) Omnivore module showing an omnivore's (species 4's) feeding links to intermediate consumer 2 and basal resource 1. (B) Generalist module showing a generalist consumer G and its feeding links to its numerous resources (R_i). Each resource R_i has a competitively dominant specialist consumer S_i that feeds on it. As a result, generalist G experiences competition at the regional scale for occupancy of each R_i resource patch from competitively dominant specialist S_i.

We assume that species 4, as an omnivore species, can switch its feeding from species 1 onto species 2 if species 2 (a superior competitor for resource 1) is present in the same patch. Thus, 4 can switch its feeding locally between 1 and 2 depending on the local presence or absence of 2. The metapopulation equation tracking the change in total patch occupancy of species 4, p₄, is then

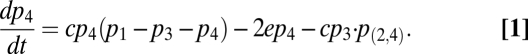Here p_(2,4) represents the density of patches where species 4 feeds specifically on species 2 (SI Appendix). Solving for equilibrium values when 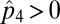and 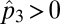gives us the conditions under which coexistence of 3 and 4 becomes possible:

When c/e is below the lower threshold, species 4, but not species 3, is able to persist in the metacommunity; above the upper threshold, species 3's patch density is high enough that it competitively displaces species 4 from the regional landscape. Increasing the colonization rate c reduces the coexistence window by allowing the superior competitor 3 to more efficiently exclude species 4. Inferior competitors, and hence network branches, can persist at the metacommunity scale in the face of competition from superior competitors as long as the patch occupancy of the superior competitor is small enough that it does not exert too much pressure on the inferior species.

In a similar way, generalist consumer behavior can allow inferior competitors to coexist at the regional level by allowing them to feed on resources in distinct food chains. If we consider the case where m distinct resources are being fed upon by m distinct specialists (generalist feeding module in Fig. 2B), and where the patch densities of the resources and specialists are given by R_i and P_i (where 1 ≤ i ≤ m), a competitively inferior generalist, with patch density G, should be able to coexist with its m specialist competitors at the metacommunity scale as long as the following condition is met:

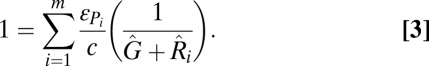Here refers to the total extinction rate experienced by the specialist i, which includes not only its own extinction rate, 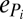, but also the effects of all species extinctions farther down each of its various food chains (15). Assuming the simple case where R_i increases with increasing c for all i, and 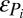has little or no response to increasing c, an instantaneous increase in the colonization rate c can be shown to decrease the equilibrium patch occupancy of the generalist given that, from Eq. 3,

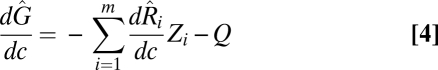(Q > 0, and Z_i > 0 for all i; SI Appendix). When regional coexistence occurs, increasing the total resource availability by increasing c reduces the generalist's regional abundance because of the increase in competitive pressure and loss of available habitat arising from increases in the patch occupancy of its specialist competitors.

The simple spatial network model demonstrates how, even in the absence of colonization or extinction trade-offs, generalist and omnivore feeding modules can facilitate the regional coexistence of competitors and thus provide the structural support for network branching in food webs. We also demonstrated that competitive coexistence and branching arising from omnivory and generalist feeding are sensitive to species colonization rate. Increases in the general colonization rate—which otherwise might have been expected to benefit all species—can, in the case of omnivores and generalists, actually drive down regional densities leading to the possibility of metacommunity-wide extinctions and hence the elimination of any associated network branches. We now use numerical simulations to show how the operation of these effects scales up to more complex food web networks at the metacommunity scale.

Numerical Simulations of Complex Food Webs.

We used simulation to study the change in equilibrium properties of metacommunity food webs subject to colonization–extinction dynamics when the rate and scale of dispersal were varied, as described in Materials and Methods.

Because we assumed that all species in the food webs we study here have identical life-history parameters, no classic competition–colonization trade-off allowing consumer coexistence is possible (23), and we might expect that the only long-term or equilibrium metacommunity food webs possible would be nonbranching networks, because only one competitively superior species can regionally exist by feeding on any given resource species within the network at equilibrium (23). Our simulations show that this is, in fact, what is observed at relatively high species colonization rates. However, at intermediate colonization rates more complex metacommunity food webs exhibiting significant network branching emerge (Fig. 3A).

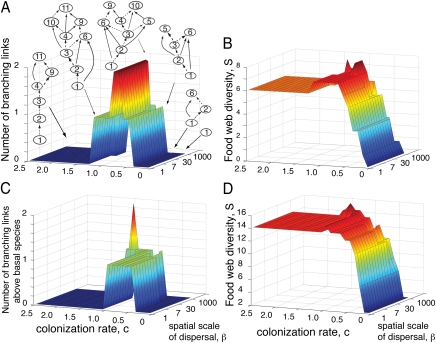
Fig. 3.

(A–D) Food web complexity and diversity across varying colonization rates, c, and dispersal scales for a potential network (A and B) and for the Benguela ecosystem (27) (C and D). (A) Network complexity, measured by food web branching in the realized metacommunity food web shown for different colonization rates and dispersal scales. Scale of dispersal is determined by a dispersal kernel on the basis of a modified β-distribution (with α = 1). The β-parameter determines the scale of dispersal: β = 1 represents global dispersal, whereas local (nearest-neighbor) dispersal is approximated when β = 1,000. Shown above the 3D plot are examples of realized metacommunity webs for various colonization rates when dispersal scale is relatively limited (β = 200). Dashed lines show a spanning tree for each of the realized food webs. (B) Food web diversity, S, as a function of colonization rate, c, and dispersal scale, β, for the same potential food web simulations shown in A. (C and D) Network complexity (C) (measured by minimum number of branching links above the two basal species) and food web diversity (D), S, of the realized food web as colonization and dispersal scale varied for the Benguela pelagic food web. All simulations were run for 15,000 time steps, with extinction rate e = 0.05.

When we initiated our simulations with a sufficiently complex potential (regional) food web (i.e., the network defining the initial set of species and potential trophic interactions), the realized equilibrium food web that arises from the play of colonization and extinction dynamics shows a peak in network complexity (measured by food web branching) at intermediate colonization rates (see SI Appendix, Fig. S3 for the potential food web used). The graph in Fig. 3A shows a general pattern: Network complexity is always maximal at intermediate colonization rates. This peak in network complexity can be associated with a peak in diversity (Fig. 3B). The peak in diversity itself follows from the presence of increased branching at intermediate colonization rates; more specifically, branching increases the opportunities available for feeding on one or more of the branching consumers in the food web and thus leads to enhanced opportunities for the buildup of species along new food chain paths in the network. A similar pattern is observed when the Benguela pelagic food web (27) is used as a potential food web (Fig. 3 C and D; see figures in SI Appendix for network and diversity responses when other empirical food webs are used).

We showed analytically that the existence of branching links in the network arising from regional coexistence of consumers on common resources relies on the structural support provided by omnivore and generalist feeding links. This result implies that, when a complex potential network is subjected to colonization–extinction dynamics, each of the branching links in the realized network should be accompanied for support by at least one omnivore or generalist trophic module (illustrated in SI Appendix, Figs. S5 and S9). However, the density or number of omnivore and generalist modules that are associated with both branching and nonbranching links changes at different spatial scales when dispersal is limited to adjacent or nearest-neighbor patches. For metacommunity food webs resolved at small spatial scales the average number of omnivore and generalist modules supporting each branching feeding link falls below the minimum threshold of 1 (SI Appendix, Figs. S6 and S10). Thus, sampling a metacommunity food web at small spatial scales could potentially lead to the conclusion that branching links appear to persist without any support and without any obvious signature of our proposed mechanism at play. These results suggest that revealing the signature of the underlying mechanisms responsible for the emergence of spatial food web complexity requires sampling at multiple spatial scales.

Effects of Habitat Destruction.

The effects of increasing habitat destruction and fragmentation can also reveal the role of omnivores and generalists in assembling food webs at the metacommunity scale. Fig. 4 shows the results of increasing habitat destruction on the realized network branching and diversity, S, when both the potential web used in Fig. 3 (Fig. 4 A and B) and the Benguela pelagic food web (Fig. 4 C and D) are subject to colonization–extinction dynamics for various fractions of unavailable habitat, d (d = 0–0.95).

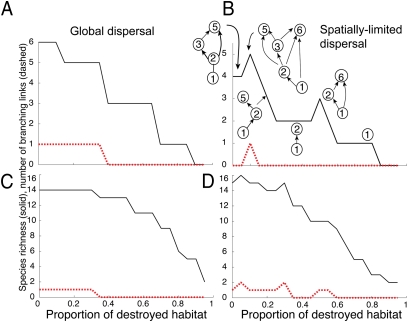
Fig. 4.

Effects of increasing habitat destruction on food web diversity (solid line) and network branching above basal species (dashed line) as fraction of habitat destroyed increases (d = 0–0.95). (A and B) Response of the potential web used in Fig. 3 to increasing habitat loss when (A) dispersal is global (β =1) and when (B) dispersal is spatially limited (β = 500). (C and D) Response of the Benguela food web when (C) dispersal is global (β = 1) and when (D) dispersal is spatially limited (β = 1,000). For all simulations c = 1.0. For A and B, e = 0.1; for C and D, e = 0.05.

With increasing habitat loss we would expect diversity to decrease monotonically, as predicted by previous studies (28). However, because of the role of omnivore and generalist consumers, limited habitat loss can lead to increases in network branching and a subsequent rise in biodiversity. In the case of global dispersal for both food webs, increasing habitat loss leads to an expected monotonic decrease in species richness (28) and a decrease in network complexity, measured by the minimum number of branching links. In the case of spatially limited dispersal, although the overall trend is for species richness to decline as habitat destruction increases, the response is not monotonic, as can be seen by the fact that habitat loss can at times lead to increases in diversity (Fig. 4). This response appears to be caused by the disproportionate effect of habitat loss or fragmentation on specialist consumers, decreasing their ability—particularly when dispersal is spatially limited—to access and exclude competitively inferior generalists from their required resource patches.

In Fig. 4B the metacommunity food webs that correspond to different habitat destruction rates are shown. The role that increased branching plays in facilitating diversity is illustrated by the first peak in branching that arises from the metacommunity coexistence of species 6 (inferior competitor) with species 5 (superior competitor). The second peak in diversity (at d = 0.5) also demonstrates the greater sensitivity of superior competitors to habitat loss: Here the rapid extinction of species 5 caused by habitat loss prevents it from driving other consumers (species 6) from the metacommunity before it itself becomes extinct.

Discussion

We have extended the metacommunity framework to show how under very simple assumptions complex food webs can emerge in space. We have uncovered a simple, empirically testable, mechanism for assembling complex food webs in space, even when local coexistence on a single resource is assumed impossible. Furthermore we have shown how omnivorous feeding links, far from being destabilizing as previous theory predicted (19), can be critical for the assembly of complex food webs. An ecologically important consequence of the spatial assembly mechanism elucidated here is that food web complexity and consequently diversity depend upon colonization rate: in particular, how both appear to be maximized at intermediate colonization rates. These results are of relevance for the conservation of biodiversity in fragmented landscapes.

The peak observed in food web complexity and species diversity at intermediate colonization rates in metacommunities arises from a balance between two contrasting effects of increasing colonization rate: (i) Increasing colonization increases the number of species that can stack vertically up individual chains, which tends to increase diversity (12); (ii) but also, high colonization rates cause branching links to be eliminated from the network, thus eliminating the food chains built upon branching consumers, which tends to decrease overall diversity. Thus, intermediate colonization rates can facilitate both a food web's vertical and horizontal diversity, whereas high colonization rates will lead to the collapse of its horizontal diversity while still maintaining its vertical diversity. The balance between these contrasting effects on horizontal and vertical diversity explains the variation in the pattern of diversity responses to colonization rate that can be observed when we start with different initial or potential food webs. If the potential food web is insufficiently complex—for instance, a network consisting primarily of one or more parallel food chains—then increasing colonization simply causes the vertical diversity to rise until it plateaus at its maximum. Most (although not all) empirical food webs contain enough potential omnivore and generalist feeding links to generate these effects of colonization rate on network complexity and species diversity (Figure S4 in SI Appendix).

What allows food web complexity to emerge is the ability of some, competitively inferior, branching consumers to offset their competitive disadvantage by feeding on different trophic levels or on resources in different branches of the food web across the landscape. This ability of branching consumers (i.e., inferior competitors) to regionally persist in the face of competitive pressure results from the trade-off between generalist feeding and competitive ability that is assumed in our model. Although this trade-off does not allow competing consumers to coexist locally, it makes their regional coexistence possible. Feeding on different trophic levels (omnivores) or alternate resources in different chains of the network (generalists) increases the number of available habitat patches accessible to inferior competitors, thus offering added opportunities for spatial refuge from superior competitors. Omnivores, by feeding on more than one trophic level in a given food chain, can invade a system at lower colonization rates than specialists because they can feed and persist in a potentially wider range of resource patches. The same holds for generalist consumers. However, because specialist consumers are superior competitors, increasing the general colonization rates of all species will eventually lead to their ability to invade the trophic metacommunity and, as colonization rates increase further, to competitively exclude their omnivore and generalist competitors. For a given trophic level within a food chain regional coexistence of competitors occurs only so long as colonization rates are within a narrow range: high enough to allow specialist consumers to invade, but low enough to keep them from competitively excluding omnivores and generalists from habitat patches (see Results, The Role of Omnivore and Generalist Feeding Links in Simple Metacommunity Networks).

Network branching in food webs is sustained by generalist and omnivore feeding links across space with dispersal limitation. This prediction of metacommunity theory stands in sharp contrast to traditional food web theory, which generally predicts destabilizing effects of omnivory in local food webs (19, 29). In metacommunities, omnivore and generalist feeding links provide the structural support that allows network branching, and hence the emergence of complexity and diversity, as food webs assemble in space. Given the prevalence of omnivory and generalist feeding in natural food webs (30), the role of space in shaping local food web structure should receive much more attention.

The emergence of network complexity made possible by omnivore and generalist feeding links occurs regardless of the scale of dispersal. When dispersal is spatially limited (restricted to nearby patches), however, the resource metacommunity for higher-level consumers becomes patchier, restricting local movement and making it more difficult to track resources. The result is that, although inferior consumers may be slower at arriving to their required resources, superior competitors will be even less efficient at finding and excluding them from their resource patches. This outcome accounts for the higher peak in network complexity and diversity that is sometimes observed with dispersal limitation compared with global dispersal.

The observed role of generalist and omnivore feeding modules in facilitating network branching and biodiversity may have important consequences for how habitat destruction and fragmentation affect biodiversity loss. It is possible, for example, that habitat loss and fragmentation, by disproportionately affecting the regional abundance of specialist consumers, may create opportunities for generalists and omnivores to establish themselves in the metacommunity, provided they are available to take advantage of the newly created niche. Although habitat loss was found to ultimately lead to food web collapse, the decrease in diversity was not monotonic as shown by previous studies (28). Habitat loss, at least to some degree, can lead to increases in network branching and consequently to increases in diversity (Fig. 4). This prediction could be validated with field data or experiments with natural microcosms (31).

In natural food webs spatial dynamics and omnivore and generalist feeding links are likely to operate in conjunction with other coexistence mechanisms, such as competitive life-history trade-offs, forms of resource partitioning within local habitats, keystone predation, etc. One future task will be to see whether the effects of spatial mechanisms like the one outlined here can leave a telltale signature of their operation in empirical data. This will likely involve the use of models that relax the simple assumptions made in this paper for isolating the effects of space on network complexity by allowing more complex local network topologies to occur within local patches (15). Similarly, the robustness of the ascribed role of space and network branching in structuring food webs should be tested using other modeling frameworks that relax the assumptions of the dynamic patch-occupancy approach, in particular the assumption that population dynamics in individual patches are relatively independent of each other, and by allowing for different scales of movement for different species in the food web (6, 7).

Extending metacommunity theory to complex food webs is a critical step in the development of a unified theory of biodiversity. Experimental tests of our results are possible with natural or laboratory-based model systems that allow the direct manipulation of metacommunity size and connectivity (32). One important implication of these results is that habitat fragmentation could prevent cross-patch trophic linkages by reducing the rate and scale of dispersal. However, restoration of even modest levels of spatial connectivity to maintain habitat colonization in networks of protected areas would facilitate the branching structure of natural food webs that appear to be essential for the maintenance of biodiversity.

Materials and Methods

Defining Branching Using a Food Web's Spanning Tree.

We define branching in the food web by the minimum number of branching links that a spanning tree or subnetwork of the food web would require to be able to span or connect all species nodes in the food web after all its omnivore links have been removed (SI Appendix). We determine this number by removing all omnivory links from the food web and then reduce the food web to a minimal subnetwork capable of linking all species by repeatedly removing links following the algorithm described in SI Appendix.

Simulation Methods.

Simulations involved subjecting potential food web communities (which were randomly generated or based on empirical food web datasets) to colonization–extinction dynamics on a 256 × 256-cell lattice with periodic boundary conditions, where each of the cells represented a distinct habitat patch. Each cell or patch could either be empty or contain any number of species that feed on each other in a food chain. Only the presence or absence of a species in a given patch was scored, not its local density or local dynamics.

The cells in the lattice were updated asynchronously at every time step. Updating cells involved allowing different migrant colonizer species to arrive at a given cell from other cells with a frequency of c and allowing each species in a given cell to go extinct with a frequency of e. Successful colonization of a cell depended upon whether the colonizer's required resource species was present in the cell and whether the colonizer was a superior competitor, capable of displacing any potential resident competitors currently occupying the resource. Colonization and extinction events within cells resulted in the local food chain rearranging itself according to the possible feeding relations defined in the potential food web graph.

Dispersal scale between cells was based on a β-distribution, with α = 1. Dispersal scale was determined by varying the β-parameter in the distribution between β = 1 (global dispersal) and β = 1,000 (nearest neighbor). See SI Appendix for more details on simulation methods.