Dynamic social networks promote cooperation in experiments with humans

Abstract

Human populations are both highly cooperative and highly organized. Human interactions are not random but rather are structured in social networks. Importantly, ties in these networks often are dynamic, changing in response to the behavior of one's social partners. This dynamic structure permits an important form of conditional action that has been explored theoretically but has received little empirical attention: People can respond to the cooperation and defection of those around them by making or breaking network links. Here, we present experimental evidence of the power of using strategic link formation and dissolution, and the network modification it entails, to stabilize cooperation in sizable groups. Our experiments explore large-scale cooperation, where subjects’ cooperative actions are equally beneficial to all those with whom they interact. Consistent with previous research, we find that cooperation decays over time when social networks are shuffled randomly every round or are fixed across all rounds. We also find that, when networks are dynamic but are updated only infrequently, cooperation again fails. However, when subjects can update their network connections frequently, we see a qualitatively different outcome: Cooperation is maintained at a high level through network rewiring. Subjects preferentially break links with defectors and form new links with cooperators, creating an incentive to cooperate and leading to substantial changes in network structure. Our experiments confirm the predictions of a set of evolutionary game theoretic models and demonstrate the important role that dynamic social networks can play in supporting large-scale human cooperation.

Cooperation is central to the success of human societies and is widespread (1–5). However, cooperation poses a challenge in both the social and biological sciences: How can this high level of cooperation be maintained in the face of possible exploitation? One answer involves networked interactions and population structure. Accounting for the fact that individuals are embedded in a social network and interact only with others in their neighborhood can lead natural selection to support even unconditional cooperation in evolutionary game theoretic models (6–11). The reason is that these local, nonrandom interactions can lead to the clustering of strategy types, so that cooperators are more likely to interact with other cooperators and therefore earn higher payoffs. However, empirical investigations using behavioral experiments have found little effect of network structure on promoting cooperation (12–15), despite evidence that cooperation and defection (as well as other, related behaviors) can spread among experimental subjects (15–17).

A key element missing from most prior network experiments is that real social networks typically are dynamic (18, 19). People often have control over whom they interact with, and interaction patterns change over time. This possibility of rewiring ties fundamentally alters the role of the network: Dynamic networks not only afford the opportunity for the clustering of strategy types but also make it possible for population structure to vary in response to cooperation. This variability creates a new form of conditional action, one that occurs via changes in network structure rather than via changes in cooperation behavior.

Behavioral reciprocity is a central mechanism for the evolution of cooperation (1, 20, 21). In evolutionary game theory, reciprocity is defined as occurring when my actions toward you depend on your actions in the past. Reciprocity traditionally has been conceptualized in two-player game theory as the emergence of concordant behaviors within dyads. For example, the “tit-for-tat” strategy engages in reciprocity by cooperating only if the opponent cooperated in the previous round. Reciprocity creates future consequences for one's choices and has been shown experimentally to promote cooperation in repeated two-player interactions (22–25). However, reciprocity is problematic in group interactions involving more than two players: If the only way to sanction defectors is to defect, this action also harms the other cooperators in one's group (26).

Strategic tie formation and dissolution in dynamic networks offer a solution to this problem by providing players with an additional method of responding to the past actions of others. Players can reciprocate not only by changing their cooperation behaviors but also by creating or dissolving ties. Thus, cooperators need not switch to defection to punish defectors in their group; instead they can establish and maintain links with cooperators but sever connections with defectors, engaging in what we call “link reciprocity.” (Note that this reciprocity is different from the use of the term in social network analysis, where reciprocity refers to the existence of tie concordance in directed graphs—that is, if ego nominates alter, alter also nominates ego, and a mutually reciprocated tie exists.)

In recent years, a number of evolutionary game theory models have demonstrated the ability of link reciprocity to promote the evolution of cooperation in group interactions (27–32). Although these articles differ in the details of their methods and assumptions, several qualitative results emerge consistently across dynamic network models (see ref. 33 for a review). Most importantly, these models predict that rapid rewiring of the network supports cooperation. If the network updates too slowly, the threat of severed links cannot be carried out often enough to make defection maladaptive. In addition, several other predictions arise regularly across models: Rapidly updating networks are predicted to have more variation across individuals in the number of connections (i.e., a greater degree heterogeneity) than static or slowly updating networks; connections between two cooperators are predicted to be more stable than connections involving defectors in rapidly updating networks; and cooperators are predicted to acquire more connections than defectors in rapidly updating networks.

Despite the considerable body of theoretical work exploring the ability of dynamic networks to promote multilateral cooperation, this issue thus far has received relatively little attention empirically. Here we evaluate these theoretical predictions by leveraging tools for running economic games online (12, 34–36) to conduct a series of large-scale behavioral cooperation experiments using dynamic networks. We randomly assigned 785 participants to one of four conditions in a series of 40 realizations of our network experiments (average network size = 19.6; SD, 6.4). In all conditions, subjects play a repeated cooperative dilemma with other subjects in an artificial social network created in the virtual laboratory.

We aim to capture the essential elements of the family of evolutionary game theory models exploring dynamic networks, and to do so using the simplest possible experimental design. To that end, our subjects lie on a nonweighted graph, and each subject interacts with her neighbors (determined as described below). As in most theoretical models, every subject chooses a single action simultaneously toward all neighbors, either cooperation (C) or defection (D). In our experiment, cooperation entails paying 50 units for each neighbor and results in each neighbor gaining 100 units; defection involves paying no costs and generating no benefits. Before making each decision, subjects are reminded of their number of neighbors and the neighbors’ previous decisions. At the end of each turn, subjects are informed about the decisions of their neighbors, along with their own payoff. Subjects also are informed that, after every round, the probability that another round will occur is 0.8.

At the beginning of the experiment, the social network is initialized with 20% of possible links being formed at random. We examine three kinds of network conditions: random link updating, fixed links, and strategic link updating. In the random-link condition, the social network is regenerated randomly after every round, creating a well-mixed population. In the fixed-link condition, the network is static and remains in its initial conformation for the duration of the experiment.

In the strategic link updating conditions, each cooperation round is followed by a rewiring round in which subjects choose whether to alter their network connections. Previous theoretical models have investigated a wide range of strategic updating rules. In our experiments, we aim to implement the simplest rewiring process: In each round, a percentage k of subject pairs are picked at random to have their connections updated. If a connection already exists between the pair of subjects, one of the two (picked at random) is offered the chance to break the connection. If no connection already exists, one of the two (again picked at random) is offered the chance to form a new connection. In both cases, before choosing to break or form a connection, the deciding subject is informed of the other's action in the preceding round. We inform subjects about the previous play of potential new partners to investigate whether different conditional strategies affect the making versus breaking of connections. We do not inform subjects about the structure of the network or how many of their neighbors are connected to the player they currently are evaluating. At the end of every rewiring round, each subject is told the number of others who chose to break links with her and the number of others who formed new links with her. Note that a particular subject may be part of multiple selected subject pairs and thus have the chance to update multiple links in a given round.

We examine two strategic updating scenarios. In the viscous condition, the network updates relatively infrequently, with k = 10% of pairings potentially changing each round. In the fluid condition, the network updates relatively frequently, with k = 30% of pairings potentially changing each round.

Results

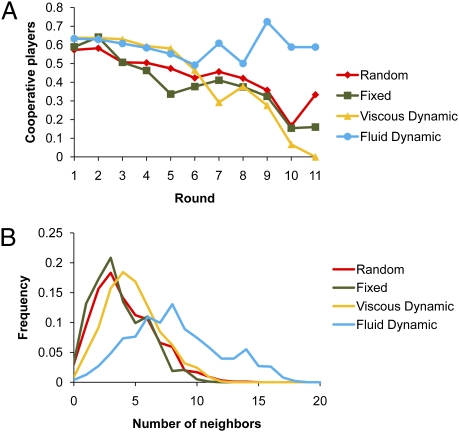
We begin by evaluating the central prediction of the theoretical models, that rapid network updating can support cooperation. To do so, we examine how cooperation varies across our four conditions (Fig. 1A). Unless otherwise noted, all statistical analyses use logistic regression with robust SEs clustered on subject and session (see Methods for details). We see that cooperation declines steeply over time in the random network condition (coeff = −0.11, P < 0.001), recreating the classic tragedy of the commons (37–39). In line with previous experimental results on static networks (12–15), we find the same pattern in the fixed network condition (coeff = −0.19, P < 0.001). This result is also consistent with theoretical predictions (11), given that the average number of neighbors exceeds the benefit-to-cost ratio of cooperation. Static interaction networks do not facilitate cooperation in our experiments.

Fig. 1.

(A) Dynamic social networks prevent the tragedy of the commons. The fraction of players choosing to cooperate is stable in fluid dynamic networks (blue) but declines over time in random networks (red), fixed networks (green), and viscous dynamic networks (yellow). Game length is stochastic and varies across sessions, with a constant 80% chance of a subsequent round. Although one might expect to see more cooperation in the viscous condition than in the static condition and more cooperation in the static condition than in the random condition, any differences in cooperation across these conditions are far from statistical significance (considering either all rounds or only rounds 7–11; P > 0.45 for all comparisons). (B) As predicted, there is greater variation in the number of connections in the rapidly updating fluid dynamic condition than in the other conditions. The fraction of individuals having each possible number of connections is shown by condition, across all sessions and rounds.

What, then, is the effect of allowing subjects to alter their interaction structure? In the viscous dynamic network condition, where 10% of connections update each round, we again see that cooperation decreases over time (coeff = −0.22, P = 0.013). Subjects cannot update their partnerships quickly enough to incentivize cooperation. However, in the fluid dynamic network condition, where 30% of connections update each round, we see a qualitatively different outcome: Cooperation is robust and stable (coeff = −0.04, P = 0.386).

These differences in cooperation across conditions emerge over time. Initially, as expected, there is no difference in cooperation between the fluid network condition and the other three conditions (P > 0.30 for all comparisons). However, over subsequent rounds of play, cooperation persists in the fluid condition and hence becomes increasingly more common relative to the other conditions. Thus, we find significantly more cooperation in the fluid condition than in the other conditions in the later rounds (rounds 7–11, P = 0.006). This result is demonstrated further by a significant positive interaction between round number and a variable indicating membership in the fluid condition when predicting cooperation (coeff = 0.135, P = 0.006). This interaction indicates that cooperation in the fluid condition increases, relative to the other conditions, as round number increases. Thus, we find strong support for the prediction that rapid network updating promotes cooperation.

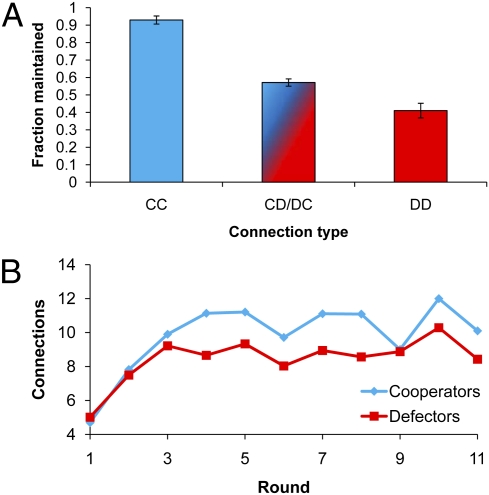
We now evaluate the three additional theoretical predictions (33), all of which are supported by our data. As predicted, we find greater variation in the number of connections (i.e., a greater degree of heterogeneity in the network) in the fluid condition than in the other conditions (Fig. 1B). For each session, we calculate the variance of number of connections across all subjects and rounds. Comparing these session-level variances shows significantly higher average variance in the fluid condition (Wilcoxon rank-sum; fluid vs. random, P = 0.0002; fluid vs. static, P = 0.0002; fluid vs. viscous, P = 0.0003). We also find that links between two cooperators are much more stable (i.e., less likely to be broken) in the fluid condition than are links between a cooperator and a defector or links between two defectors (P < 0.001 for both comparisons; Fig. 2A). Furthermore, we find that cooperators have more connections than defectors on average in the fluid condition (P = 0.021; Fig. 2B).

Fig. 2.

(A) In the fluid dynamic condition, connections between two cooperators (CC links) are much more likely to be maintained during rewiring than connections between a cooperator and a defector (CD/DC links) or between two defectors (DD links). Interestingly, CD/DC links also are significantly more stable than DD links (P = 0.009). Error bars indicate SEMs, clustered on subject and session. (B) In the fluid dynamic condition, cooperators come to have more connections on average than defectors.

Having evaluated the theoretical predictions, we turn next to exploring the behavioral mechanisms underlying the success of cooperation in the fluid dynamic networks. We begin by examining how subjects change their cooperation decisions in response to the cooperation and defection of the individuals with whom they have interacted in the prior round. Across all conditions, we see the same intuitive pattern: The greater the percentage of a subject's partners that defected in the previous period, the less likely the subject is to cooperate (random, coeff = −0.44, P = 0.001; fixed, coeff = −1.8, P < 0.001; viscous, coeff = −3.62, P < 0.001; fluid, coeff = −2.01, P < 0.001; see SI Appendix for further analysis). This behavior represents classical reciprocation via changing one's cooperative action in response to the actions of one's interaction partners. However, despite the presence of this form of reciprocation in all conditions, cooperation fails in the random, fixed, and viscous dynamic conditions and succeeds only in the fluid dynamic condition. Thus, reciprocation through changing one's cooperation action is not enough to stabilize cooperation in our experiments, most likely because of the large number of simultaneously interacting partners.

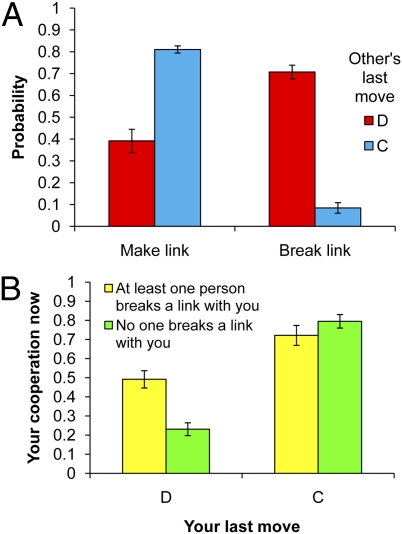
Instead, what differentiates the fluid condition from the others is the ability to reciprocate effectively by forming or breaking social ties. Consistent with the assumptions of many of the theoretical models, we find that subjects seek connections with cooperators and shun defectors (Fig. 3A). Subjects are more likely to form new links with those who cooperated in the previous round than with those who defected (P < 0.001), and they are more likely to break existing links with those who defected than with those who cooperated (P < 0.001). Interestingly, subjects are more discriminating when breaking links than when making links: the likelihood of making a link with a defector is significantly higher than the likelihood of breaking a link with a cooperator (P < 0.001). That is, although subjects almost never break links with cooperators, they sometimes make new links with defectors. This observation suggests that subjects are willing to give potential new partners the benefit of the doubt, which is reminiscent of a form of forgiveness or leniency (20, 25).

Fig. 3.

(A) Subjects are more likely to make new links with players who cooperated in the previous round than with those who defected, and are more likely to break existing links with partners who defected than with partners who cooperated. (B) Subjects who defected in the previous last round are more likely to switch to cooperation if other players break links with them. Conversely, the breaking of links does not affect the behavior of cooperators. Interestingly, subjects’ cooperation is not affected by whether others made new links with them. Error bars indicate SEMs, clustered on subject and session. Data from the fluid dynamic condition is shown. C, cooperation; D, defection. See SI Appendix for further analysis.

How subjects respond to alterations in the network is also important for cooperation. We find that a defector's probability of switching to cooperation increases with the number of players that broke links with her following her decision to defect, but is unaffected by the number of players that formed new links with her following her defection (logistic regression including both number of links broken, coeff = 0.19, P < 0.001, and number of new links formed, coeff = −0.03, P = 0.82; difference between the two coefficients, P = 0.016). Thus, breaking links serves to discipline defectors, but forming new links with defectors does not encourage cooperation (Fig. 3B). Unlike defectors, cooperators are not affected by either the breaking or forming of new links (logistic regression including both number of links broken, coeff = −0.14, P = 0.25, and number of new links formed, coeff = −0.41, P = 0.26). See SI Appendix for further analysis.

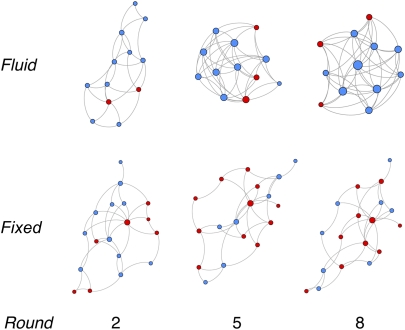
Thus, we find in our fluid dynamic network condition that subjects preferentially break links with defectors and form links with cooperators; that defectors switch to cooperation after links are broken; and that as a result stable cooperation emerges. Note that allowing frequent network updates does not necessarily mean that the network structure actually changes frequently but only that the opportunity for change often exists. Indeed, we find that the probability of a player altering the network when given the option decreases significantly over time (coeff = −0.146, P < 0.001) as the network structure equilibrates. To give an intuitive feel for how the development of behavior and network structure are related in our experiments, we show a series of snapshots from fluid and static networks in Fig. 4 (see SI Appendix for further analysis).

Fig. 4.

Structure and strategy snapshots over time in two representative experimental sessions. Blue nodes represent cooperating subjects; red nodes represent defecting subjects. Individual connections are shown as gray lines. The network is arranged using a force-based algorithm where the edges act like springs, so that nodes in a more highly connected network are drawn more closely together. In addition, the nodes are sized according to their number of connections, and nodes with no connections are omitted. In the fluid dynamic condition, cooperation is stable, the network evolves from being relatively spare to being quite dense, and cooperators come to have more connections than defectors. In the fixed condition, conversely, cooperation declines, and subjects with many connections are mostly defectors. Note that the connections do not change in the static network although the visualization algorithm alters the position of the nodes.

Discussion

We have shown that allowing subjects to update their social network connections dynamically can stabilize cooperation in groups, where cooperation otherwise is difficult to maintain solely through traditional reciprocation via changes in cooperative behavior. Despite having to choose the same action toward an average of 8.2 other players, subjects in our fluid condition maintained a high level of cooperation by strategically making and breaking social ties. As predicted by evolutionary game theory models, our experiments show that rapid network updating promotes cooperation and leads to greater degree heterogeneity; that connections between two cooperators are longer lived than connections involving defectors; and that cooperators acquire more connections than defectors.

Our fixed-condition results are consistent with several recent experimental studies on static networks (12–15), which find no effect on cooperation. Although theoretical models suggest that static networks can promote cooperation (6–11), these models often consider networks that are substantially larger than those typical of laboratory experiments. Exploring cooperation on very large static networks experimentally is an important direction for future study, particularly given the large scale of real-world social networks (18). The failure of static networks to promote cooperation experimentally also may be the result of subjects engaging in high rates of experimentation (or “mutation”) (15). Clustering is key to the success of cooperation in static networks, and the random variation introduced by mutation breaks up clusters. In dynamic networks, however, clustering may be maintained in the face of mutation by players rewiring the network. Should a well-connected cooperator mutate into a defector, her neighbors will sever their ties, and she will be excluded from the cooperative cluster. Exploring the effect of high mutation rates in dynamic networks is a promising area for future theoretical and empirical research.

Our results showing the ability of dynamic networks to promote cooperation in group interactions are complemented by a recent experimental study exploring pairwise interactions (24). There, it is shown that allowing subjects to choose a separate action toward each of three partners produces a substantial amount of cooperation, and that allowing subjects to break ties further improves cooperation. Similar results also are found in theoretical models of repeated two-player games on dynamic networks (40, 41). Our results also are consistent with the possibility that humans may have evolved to manipulate aspects of their social network structure to maximize their fitness (42, 43).

In an effort to use the simplest possible experimental set-up, we do not impose an explicit cost on forming, maintaining, or breaking ties in our experiment (although having more ties makes cooperating more costly, because one pays a cost for each neighbor to provide her with a benefit); and we do not limit the number of connections a subject can have. Exploring the effect of such costs and limits is an interesting direction for future empirical research. We also do not normalize payoffs across subjects with different numbers of connections, creating an incentive to increase the number of cooperative partners (the most efficient outcome is a fully connected network of cooperators). Cooperators, however, still have an incentive to avoid defecting partners in our experiments, because cooperation is costly, and the cost increases with each additional connection (unlike settings in which the lowest possible payoff is 0; e.g., ref. 8). Furthermore, although the average number of connections is higher in the fluid condition than in the other conditions, we find that cooperators accrue more connections than defectors in the fluid condition even when we restrict analysis to subjects whose degree is in the range of those observed in the other conditions (SI Appendix). Experimental investigation of interaction protocols with payoff normalization or asynchronous decisions is a promising direction for future research.

Following the convention of most dynamic network models from evolutionary game theory, network updating in our experiment is dyadic. When deciding whether to make or break a link with another player, subjects do not know how many neighbors they have in common with the other player. Therefore, a subject cannot be influenced explicitly by the behaviors her partners exhibit toward each other, a topic that has received considerable attention outside evolutionary game theory (44, 45). To the extent that cooperation and defection can be taken as forms of positive and negative ties, respectively, our experimental set-up can allow future exploration of the role of positive and negative valence as related to balance theory (46). Integrating information about relationships among partners in our experimental framework is a promising direction for future research.

Breaking links with defectors in our dynamic networks can be seen as a form of punishment. Most previous studies of cooperation and punishment have focused on costly punishment, in which players can pay a cost to cause others to incur a cost. Costly punishment can promote cooperation (37, 38, 47–50) but reduces the payoffs for both parties and can be used against cooperators as well as defectors, often as part of retaliatory vendettas (23, 51–55). Breaking links, on the other hand, is not costly to either party and cannot be used by defectors to harm cooperators.

Another form of punishment which has been shown to promote cooperation effectively is ostracism (56, 57). In these studies, players can choose to eject each other from the group using various voting schemes, with ejected players being universally excluded from the benefits of any cooperation undertaken by nonejected group members. Breaking links in our experiments represents a form of decentralized ostracism, where each subject makes her own decisions about whom to exclude from the benefits of her individual cooperation decisions. The success of cooperation in our experiments shows that ostracism need not be coordinated to be effective.

Opting out in voluntary social dilemmas is also related to the breaking of links. In voluntary games, players can choose to not interact with their partner or group, typically earning a fixed loner's payoff instead. It has been shown both experimentally (58–60) and theoretically (61, 62) that allowing opting out promotes cooperation. However, although voluntary games are characterized by a continual cycling between cooperators, defectors, and loners, dynamic networks can lead to stable high levels of cooperation.

In the same way that breaking links can be construed as punishment, forming new links is similar to costly rewarding (but only if the player forming the new link is a cooperator). Previous experimental studies have typically found that costly rewards have mixed effects in one-shot games or in the final period of finite-length games but effectively promote cooperation as long as future interactions are possible (39, 47, 48, 63, 64; see ref. 65 for further discussion). Whereas costly rewarding typically involves a separate stage following the cooperation game, forming new links allows the rewarding of good behavior within the single framework of the cooperation game, without the addition of a second, positively non–zero-sum interaction.

In summary, we provide empirical evidence regarding cooperation in dynamic networks, confirming the predictions of a family of evolutionary game theoretic models. Our experiments demonstrate that dynamically updating social networks can support cooperation in large groups. When social ties are fluid, people need not abandon cooperation to punish free-riders. Instead we can shun them, excluding them from the benefits of future cooperation and disincentivizing defection. It pays to cooperate today, lest you find yourself alone tomorrow.

Methods

A total of 785 subjects participated in our incentivized economic game experiments. Subjects were recruited using the online labor market Amazon Mechanical Turk (12, 34, 36) and interacted anonymously over the internet using custom software playable in a browser window. Subjects were not allowed to participate in more than one session of the experiment. In all, 40 sessions were conducted in March 2010. Each session lasted approximately 1 h on average. In each session, the subjects were paid a $3 show-up fee. Each subject's final score summed over all rounds was converted into dollars at an exchange rate of $1 = 1,000 points. For further discussion of the validity of experiments conducted using Mechanical Turk, as well as the details of our experiment setup, see SI Appendix. This research was approved by the Harvard University Committee on the Use of Human Subjects.

Unless otherwise noted, all statistical analyses are conducted at the level of the individual decision (cooperate/defect, break/maintain link, or create/do not create link) using logistic regression. Because multiple observations from the same subject are not independent, and observations from multiple individuals within the same session are not independent, we cluster the SEs in our regressions on both subject and session, as per ref. 66. Differences in cooperation between any two conditions are assessed by setting one of the conditions as the baseline, including a binary (“dummy”) variable to indicate decisions from the other condition, and examining the P value associated with the binary variable.