Dynamical freezing of active matter

When collections of interacting particles are externally driven, they typically form strongly fluctuating states with short-lived structures or patterns that are continually created and destroyed, such as those found in turbulent fluids (1) or fluctuating granular matter (2). In some cases, however, such driven systems do not remain in a strongly fluctuating state but instead organize into a peculiar dynamical state in which the fluctuations are strongly reduced or even completely lost. Such states typically involve the formation of some type of pattern, and they are considered to be dynamically “frozen” because the motion that does occur appears in a repeatable fashion or is confined only to specific localized regions. When the system has reached one of these states, the lack of significant fluctuations means that it becomes dynamically trapped or absorbed; hence, entry into such a state is termed an absorbing transition (3, 4). A broader question is whether this type of nonequilibrium phase transition is limited to a select few types of system or whether it is much more common and arises under generic nonequilibrium conditions such as those relevant to biology. In PNAS (5), Schaller et al. show that active matter systems with simple ingredients can indeed undergo a transition into an absorbing state.

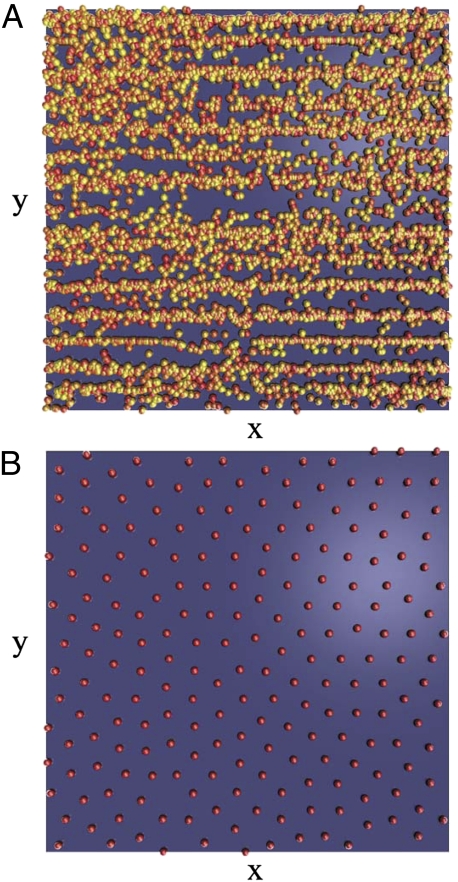
Examples of systems exhibiting dynamically frozen states include driven particles such as vortices in dirty superconductors. Under a moderate external drive, the vortices fluctuate strongly in a turbulent fashion (6, 7); however, under a strong drive, the vortices organize into a weakly fluctuating pattern characterized by a moving smectic structure or into some other repeatable pattern that exists only in the driven system (7–10). Fig. 1 shows an example of an assembly of vortices periodically driven over a rough landscape with the positions of the vortices at the end of a drive cycle marked for a series of consecutive cycles. In Fig. 1A, at moderate drives, the vortices return to different positions after each drive cycle, showing that the system is fluctuating. In Fig. 1B, at high drive, the vortices are moving but have organized into a dynamically frozen state in which they return to the same positions after every cycle. Such dynamically frozen states do not require the formation of an ordered or quasi-ordered pattern. Instead, the system may evolve into what is called a randomly organized state, which appears spatially random but that lacks dynamic fluctuations. Randomly organized states in which the particles return to the same position after each drive cycle were observed for sheared colloidal assemblies in a previous work (11).

Fig. 1.

An illustration of the difference between a fluctuating dynamical state and a dynamically frozen state for periodically driven vortices in a dirty type-II superconductor, from the system described by Mangan et al. (8). The vortices move under an ac current over a rugged landscape created by inhomogeneities in the superconductor. The vortex positions at the end of a driving cycle are plotted for a series of consecutive cycles. The image window is 64λ × 64λ, where λ is the London penetration depth; for the case of a Nb sample, the image window would be 3.3 μm on a side. (A) A system under a moderate external drive is in a strongly fluctuating liquid like state, and the positions of the vortices change after each cycle in an anisotropic random walk. (B) The same system under a strong external drive. Even through the vortices are in motion, they form a dynamically frozen state in which almost all the vortices return to the same position after each cycle.

In all the nonequilibrium systems in which absorbing phase transitions have been studied, the driving comes from some external source such as an applied current, shear, or periodic shaking, and in many cases the dynamically frozen state takes advantage of properties of the external drive such as the spatial symmetry breaking in the direction of drive. There is, however, another class of nonequilibrium systems known as active matter (12), in which the particles are self-driven rather than externally driven. Active matter systems include swimming bacteria (13, 14), pedestrian motion (15), systems exhibiting flocking (16), and self-propelled colloids (17). Despite the ubiquity of such systems, it is not known whether this class of system can also exhibit a dynamically frozen or absorbing phase. Because self-driven systems do not have the directional symmetry breaking associated with an external drive, it might be expected that dynamically frozen states would be much harder to form and that they might form only under rather complicated conditions. In the report by Schaller et al. (5), the authors demonstrate that active matter systems with simple ingredients can indeed form dynamically frozen or absorbing phases, opening the way to apply a similar analysis to this class of systems as performed for the nonactive driven systems. This result could be important for materials applications by permitting fabrication of patterns that form dynamically and for the further development of more generalized versions of nonequilibrium statistical mechanics, and could give insights into how living systems might use dynamically frozen states for biological function.

Schaller et al. (5) consider a canonical system of active transport consisting of a 2D system of actin filaments that can be simply understood as long flexible rods propelled by motor proteins. A combination of active directed motion and steric repulsion causes the system to produce dynamic patterns in the form of density fluctuations and waves; however, these are short-lived structures that appear and disappear, so the system has similarities to other fluctuating nonequilibrium liquid states. All this changes when an extra ingredient—a growth mechanism—is included by adding a critical amount of a protein that leads to cross-linking between actin filaments. Under these new conditions, the system organizes into a distinct moving state characterized by all the hallmarks of an absorbed or dynamically frozen state. All the filaments form rotating rings that are stable and do not break apart and reform, while the fluctuations within each filament are lost or completely absent. Because the system lacks large fluctuations, the ring structure cannot suddenly change to a liquid state and back or turn into some other type of constantly changing pattern; thus, the system is essentially trapped in a pattern from which it cannot escape, just as for an absorbing state. The ring formation arises from a competition between the growth as a result of the cross-linkers and the self-driven motion, which allows rings to form but provides no mechanism for them to dissociate. The characteristics of the resulting rings are set by the coarsening process, and the population of open or closed rings is varied with the biased growth process or the transport process. To confirm that pattern formation in the experiment can be explained with these few simple ingredients, the group also conducted agent based simulations that clearly capture the observed phenomena (5).

Active matter systems with simple ingredients can indeed undergo a transition into an absorbing state.

There are still many questions that remain, such as whether critical exponents can be extracted at the point at which there is a critical density of cross-linkers. This would be important in determining the universality class of the absorbing phase transition (3, 4). Although there has been a wealth of theoretical and numerical studies examining the critical properties of absorbing phase transitions, there are only a few experimentally realizable systems in which such transitions have been carefully studied. This active matter system provides another type of experimental system in which to study absorbing phase transitions, and it would be interesting to understand if the absorbing phase transition in this system falls in the same universality class found for theoretical studies of absorbing phase transitions or whether it is an entirely different type of transition.

As the dynamically frozen state proved so robust even with a small number of ingredients, another intriguing question is whether dynamically frozen states occur in other biological systems and whether they play any role in biological functions. For example, a swarm of agents in an environment with large fluctuations might be able to reduce dispersion by forming a dynamically frozen state. In materials science, it may be possible to use or control active agents to form stable dynamical patterns that could be harnessed for applications such as the creation of dynamic substrates or the formation of substances with materials properties that can be changed on the fly, or for making the system more robust against external perturbations.