Abstract
Two-dimensional paper networks (2DPNs) hold great potential for transcending the capabilities and performance of today's paper-based analytical devices. Specifically, 2DPNs enable sophisticated multi-step chemical processing sequences for sample pretreatment and analysis at a cost and ease-of-use that make them appropriate for use in settings with low resources. A quantitative understanding of flow in paper networks is essential to realizing the potential of these networks. In this report, we provide a framework for understanding flow in simple 2DPNs using experiments, analytical expressions, and computational simulations.
Keywords: two-dimensional paper networks, paper microfluidics, fluid transport
1.1 Introduction
Lately there has been an upsurge in interest in the use of capillary flow-based devices for performing biomedical diagnostic tests in low-resource settings (Zhao and van den Berg 2008; Martinez, Phillips et al. 2010). Such devices have the potential to perform many of the sophisticated processes that have been demonstrated for microfluidic systems, but with far less complexity or cost. For example, Martinez et al. (Martinez, Phillips et al. 2007; Martinez, Phillips et al. 2008; Martinez, Phillips et al. 2008) and Fenton et al. (Fenton, Mascarenas et al. 2009) have demonstrated the capability of paper networks to detect multiple analytes using three- and two-dimensional patterns in paper to link a single inlet with multiple detection regions.
Recently, we demonstrated the capability of 2DPNs to perform multi-step processes by linking multiple inlets to a detection region. We presented a series of tools to control the transport of fluids in 2DPNs and demonstrated the sequential delivery of multiple reagents to a detection region (Fu, Lutz et al. 2010). The capability of 2DPNs to perform sophisticated processes, while requiring only a single activation step, could enable a wide range of applications in paper-based devices. In order to fully realize the potential of 2DPNs, it is essential to develop a quantitative understanding of the principles of transport in these networks.
There exists an extensive body of literature on understanding capillary flow in paper. The majority of the work has focused on the investigation of imbibition in one-dimension, i.e. straight paper strips (Takahashi 1950; Fujita 1952) (for a review on the physics of paper see (Alava and Niskanen 2006)). Much less attention has been focused on two-dimensional patterns in paper. More relevant to the current study, Medina et al. (Medina, Perez-Rosales et al. 2001) investigated imbibition in triangular shapes of blotting paper and characterized the deviation from Washburn flow. More recently Mendez et al. (Mendez, Fenton et al. 2010) performed a study of imbibition in nitrocellulose paper1 composed of straight strips connected to two-dimensional shapes of increasing cross sectional area. They showed that the transport of fluid in the straight portion transitioned from Washburn flow to quasi-steady state flow as the position of the fluid front moved from the straight segment to the two-dimensional section such that the wicking pad in a conventional lateral flow strip could be replaced by the use of the single two-dimensional nitrocellulose piece.
In this paper, we extend this previous work, with the goal of providing a basic framework for understanding transport in 2DPNs and enabling engineering design for optimal performance. Specifically, we investigate basic transport in simple two-dimensional geometries consisting of multiple constant width segments in nitrocellulose during wet-out of the paper (i.e. fluid front is in the paper) and after the paper is fully wetted (i.e. fluid has filled the paper and capillary flow in the wicking pad affects transport in the paper). We use experiments, analytical expressions, and computational simulations to provide simple design rules for predicting transport times for the two-dimensional geometries. Finally, the use of input legs of different geometries to perform sequential delivery of multiple reagents is demonstrated.
2.1 Materials and Methods
The channels of the paper devices were cut from backed nitrocellulose (Hi-Flow Plus 135, Millipore, Billerica, MA) using a CO2 laser (Universal Laser Systems, Scottsdale, AZ) as described previously (Spicar-Mihalic, Stevens et al. 2007). Reagents were introduced into source pads (Millipore, Billerica, MA, Whatman, Maidstone, Kent) that had been placed in contact with network inlets. Similar absorbent material was used for wicking pads. The nitrocellulose 2DPNs and the pads were adhered to a glass substrate (Thermo Fisher Scientific, Waltham, MA) using double-sided tape (3M, St. Paul, MN) for the experiments of Figures 1, 2, and 4. In the case of the fully wetted flow experiments of Figure 4, small polycarbonate weights were placed on the source and wicking pads in order to produce uniform coupling of the absorbent material to the nitrocellulose. For the experiment of Figure 5, the 2DPN was first adhered to an adhesive-coated Mylar layer (Fraylock Inc., San Carlos, CA), which was then adhered to a glass substrate for support. The source pads were first adhered to a Mylar layer (Fraylock, San Carlos, CA) using double-sided foam tape (3M, St. Paul, MN), and then to a glass substrate for support. The effects of evaporation were minimized by enclosing the “loaded” paper devices in a covered dish containing a water source.
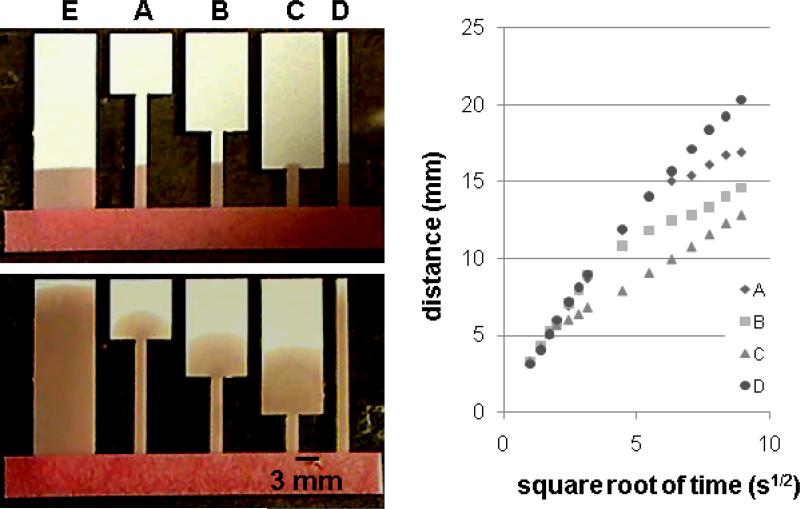
Figure 1.
Transport of fluids during wet-out for uniform-width and sudden-expansion strip geometries. Transport of the fluid front is the same for all strips initially (up to the time of the top image). For a strip in which there is an expansion, the fluid front moves more slowly in the greater-width segment as compared to if it had continued in a constant width strip (bottom image). The plot shows distance vs. the square root of time for strips A through D.
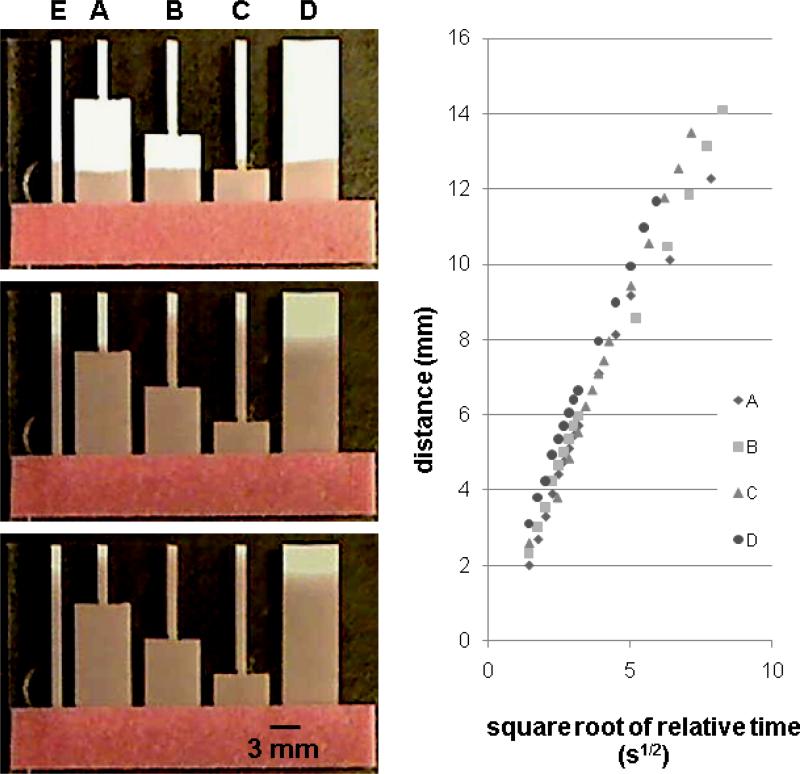
Figure 2.
Transport of fluids during wet-out for strips in which there is a sudden - contraction of the width of the strip. The plot shows the distance moved by the fluid front vs. in the first segment and distance vs. in the second segment for each strip. Comparison of the positions of the fluid fronts between the different strips in the image series and the plot indicate that the fluid front moves the fastest for the configuration in which the two lengths are closest to being equal, strip B at the time of the middle image (see Supplementary Information, Section C). The data indicate that fluid front displacement in the smaller-width segment follows a Washburn equation in terms of the relative time since the fluid front passed the segment transition, with a slope that is similar to the Washburn slope in the wider segment.
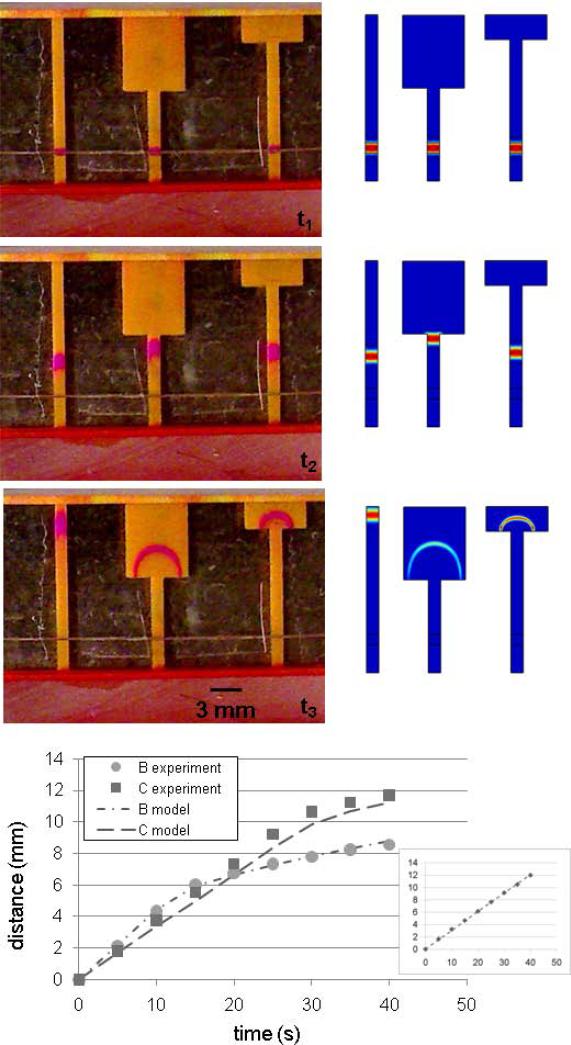
Figure 4.
Experimental and modeling results for transport in fully wetted strips of different geometries. The images (corresponding to 0, 12 s, and 40 s) indicate that the transport time was the fastest for the tracer species in strip A, then C, and then B. The main plot shows a quantitative comparison of the experimental and modeling results for the transport of tracer species in strips B and C, while the inset plot shows the comparison for strip A. The data indicate good agreement between the experimental and modeling results for the transport times and the qualitative shapes of the tracer species in the different geometries.
Figure 5.
Demonstration of sequential delivery of reagents to a detection region using input legs of different dimensions. The image at t1 shows the source pads filled with fluids. The images at t2 through t4 were taken at the approximate times of 9 s, 2.3 min, and 9.0 min, respectively, after the single activation step of placing the 2DPN in contact with the pre-wetted source pads. Clear fluid in the center leg arrived at the detection region (labeled in the image at t2) first, next yellow fluid from the right leg arrived at the detection region, and finally red fluid from the left leg arrived at the detection region.
Measurements of flow during wet-out were made using solutions of food coloring (containing FD&C Red #40 and Yellow #5) in water. Measurements of flow in fully wetted devices were made using the following method. Briefly, the devices were fully wetted with a 1 mg/ml solution of phenol red in phosphate buffered saline. A local increase in the pH of the solution was created at the visible wire electrode (the other electrode was placed beneath the source pad2), producing a color change of the phenol red from yellow to fuchsia in a band that was subsequently imaged. The pulses of tracer species were approximately 1 s in duration.
Images were acquired using a web camera (Logitech, Fremont, CA) and the software Handyavi (AZcendant Software, Tempe, AZ). ImageJ (Rasband) was used to measure the position of the front of the tracer species (in the center region of the channel) with respect to time. Images were subsequently adjusted for brightness and contrast for display purposes.
Computational simulations of fully wetted flow were performed using a model of the system constructed in the finite element software package COMSOL Multiphysics (Burlington, MA). The model was first solved for the steady-state velocity field assuming Darcy's law flow. Then the time-varying concentration of the tracer species was calculated using the convection and diffusion module. The parameters used in the model were as follows. The fluid was assumed to have a density of ρ = 1000 kg/m3 and a viscosity of μ = 0.001 kg/(s·m), corresponding to water. The permeability of the paper to water, κ, was assumed to be 10-12 m2 (in the range of experimental measurements of the permeability of nylon fibers to water (Jackson and James 1986)). The tracer species was assumed to have a diffusivity, D = 5×10-10 m2/s, consistent with that of a small molecule (Holde 1985) (molecular weight of phenol red is ~350 g/mol). A pressure difference, δP, of 4.5×10-2 atm was chosen for consistency with the experimentally observed flow velocity in the constant width strip. ImageJ was again used to measure the position of the tracer species with respect to time. Note that the model simulates the spreading of the tracer species as due to diffusion only and does not incorporate the process of reprotonation of the phenol red due to equilibration of the high and adjacent lower pH bands (Cabrera, Finlayson et al. 2001) (so underestimates the rate of spreading of the tracer species as compared to that in the experimental system). This is not a significant factor in our use of the model to provide a comparison with the transport times and the general shapes of the concentration profiles obtained in experiments.
3.1 Results and Discussion
3.1.1 Flow during the paper wet-out process
The one-dimensional transport of the fluid front in a porous matrix like a paper strip during wet-out follows the Washburn equation (Washburn 1921),
| (1) |
where L is distance moved by the fluid front, t is time, D is the average pore diameter, γ is the effective surface tension (which includes the effect of any contact angle dependence), and μ is viscosity (Peek and McLean 1934; Williams 1980). Thus, Washburn-like flow is characterized by . This implies that the fluid front velocity is decreasing with time. The force due to the surface tension pulls the fluid further into the paper. Counteracting this is the viscous resistance, which is proportional to the velocity with a coefficient, , that increases as the fluid column lengthens. This results in a decrease in flow velocity of the fluid front as the fluid penetrates the porous media. In the case of strips with different constant widths fed by a non-limiting fluid reservoir, e.g., strips D and E in the images of Figure 1, the fluid fronts obey the same decreasing velocity function and have the same transport time as given by the Washburn Equation. Thus, for constant-width inlet legs, the flux of reagent delivered relative to other inlet legs is proportional to the leg width; the length of the fixed-width inlet legs can be used to vary the time of delivery of reagent relative to other inlet legs.
The experiments of Figures 1 and S1 demonstrate the effect of a strip width expansion on the velocity of the fluid front. In Figure 1, the two images show the flow during wet-out of colored fluid in strips in which the transition from smaller to greater widths takes place at different downstream positions in the strips (A through C). The plot in Figure 1 shows distance vs. the square root of time for each case. Initially, advancement of the fluid front is the same for all strips (while the fluid front is within the smaller-width segment of the width-expanding strips), with fluid front advancement in all strips following the Washburn equation. When the width increases within a strip, first in C, then B, then A, the Washburn equation assumptions of a non-limiting source fluid and a constant cross-sectional area are violated. The fluid front slows significantly during progression through the narrow segment of the strip. Assuming incompressibility of the fluid, this decrease in the average linear velocity in the segment of larger width can be understood in terms of the greater time required for the fluid to “fill a volume element of length Δy (where y is the direction of fluid flow) within the greater width segment than a volume element of length Δy within the smaller width segment. As consistent with the data shown, the fluid front has the greatest transport time in strip C, then B, then A, and the shortest transport time in the two strips of constant width, strips D and E. Supplementary Figure S1 (for details, see Supplementary Information, Section A) shows images of transport during wet-out for two strips in which the width of the expansion is varied (and a constant-width strip is included for comparision). As expected, transport of the fluid front is slowed to a greater extent in the strip with the larger width expansion. Thus, an expansion in the width of an inlet leg can be used to vary the transport time of reagent delivered relative to other inlet legs, with the width of the expansion and the downstream location of the transition being two adjustable parameters.
In the case of a contraction in strip width, the constant cross-sectional area assumption of the Washburn equation is again violated. However, in contrast to the case of an expansion, in a contraction, the first segment of larger width acts as a non-limiting source of fluid for the second segment of smaller width. The result is that advancement of the fluid front in the second segment follows the Washburn relation as in the first segment, but with the relative time, t − t1 in place of (here, t1 is the time that the fluid front reaches the end of the first segment). Thus, a contraction within a strip can be used as a design tool to decrease the overall transport time of the fluid front with respect to a constant width strip. It is useful to determine the ratio of segment lengths that will produce the minimum overall transport time in a contraction composed of two constant width strips. A straightforward derivation indicates that the minimum transport time occurs for segments satisfying the relation , where d1 is the length of the first segment of constant width, and dT is the total length of the strip (see Supplementary Information, Section B).
The experimental results are in agreement with the above calculation, as shown in Figure 2. The images show the flow, during wet-out, of colored fluid in strips where the transitions from greater to smaller widths take place at different downstream positions. Constant-width strips are included for comparison (D = wide; E = narrow). The fluid front moves the fastest overall for the case of approximately equal segment lengths. The plot in Figure 2 shows the distance moved by the fluid front vs. in the first segment and distance vs. in the second segment for each strip. The data indicate that fluid front displacement in the smaller-width segment is governed by a Washburn equation in terms of the relative time since the fluid front passed the segment transition, with a slope that is similar to the Washburn slope for fluid front advancement in the wide segment. Thus, within an inlet leg, a contraction geometry, composed of a sudden transition from a greater width segment to a smaller width segment, can be used to decrease the overall transport time with respect to a constant width strip. In addition, the transport time is minimized for the case in which the lengths of the two constant width segments are equal.
3.1.2 Fully wetted flow
Flow in a straight paper channel of constant width can be conveniently described by Darcy's law,
| (2) |
where Q is the volumetric flow rate, κ is the permeability of the paper to the fluid, μ is the viscosity of the fluid, WH is the area of the channel perpendicular to flow, and ΔP is the pressure difference along the direction of flow over the length L. Darcy's law was originally derived phenomenologically (Darcy 1856) to describe flow in porous media, but follows from the Navier Stokes equation by assuming homogenization (Auriault, Borne et al. 1985; Nordbotten, A. et al. 2007).
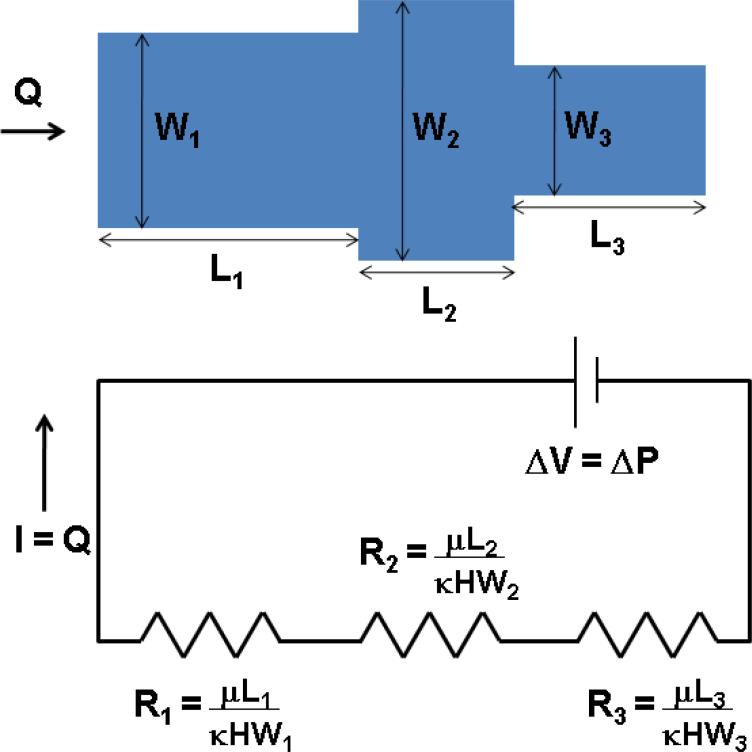
Flow in N connected straight channels of varying widths can be understood by straightforward extension of the simplest case of flow in a straight channel of constant width by imposing equality of the volumetric fluxes at the boundaries of the segments of different widths, Q1 = Q2 ... = QN.
| (3) |
where WiHi is the area of segment i of the channel perpendicular to flow, Li is the length of segment i of the channel in the direction of flow, and ΔP is the pressure difference across the total length of the channel in the direction of flow. Thus, the total volumetric flux through a straight paper device of N segments in series, during fully wetted flow, follows the same form as Ohm's law for computing the electric current through a circuit with N resistors in series, with ΔP the fluidic counterpart to voltage change, Q the fluidic counterpart to current, and the fluidic counterpart to the resistance for each segment i. As a consequence of Darcy's law, the electrical circuit analogy also holds for fluidic elements in parallel, where the fluidic resistances add in reciprocals.
The transport time for flow through a strip with a multi-segment geometry can be calculated from t = V/Q, where V is the volume of the geometry, and substituting in Darcy's law to obtain,
| (4) |
where (and ΔP is taken to be the absolute magnitude of the pressure difference for the remainder of the discussion). Assuming that permeability, viscosity, and pressure difference are constant (i.e. is constant), differences in the transport times of fluids in two strips will be solely due to geometric factors. For single-width strips, and predicts that all single-width strips of the same length will have the same transport time regardless of the other dimensions of the strip. The velocity for fully-wetted flow in a constant-width strip is constant (consistent with the experimental data for the inset plot of Figure 4). For strips that contain two constant-width segments of lengths L1 and L2 and widths W1 and W2, respectively, the transport time is given by . It is assumed that the heights of the segments are the same. The equation is symmetric in L1 and L2, and a local maximum exists at L1 = L2, indicating that for non-equal area values, the greatest transit time will be obtained in a strip with equal length segments. For a given combination of lengths and W2>W1, a greater transport time will be obtained for greater (for details, see Supplementary Information, Section C).
The relative transport times for each of the strips in Figure 4 can be calculated using the above analysis. The prediction is that transport should be the fastest in strip A, and for the strips of varying widths, the transport time should be faster in strip C than in strip B. This is consistent with the experimental results in the left panel of Figure 4. A time series comparison of experimental and simulation results for flow in the strips of different geometries is also shown in Figure 4. The model parameter of pressure difference across the strips was chosen to be consistent with the experimentally observed flow velocity in the constant width strip (~3×10-4 m/s of the inset plot of Figure 4). The simulation results show good agreement with the experimental results in the transport times of the tracer species for the geometries of strips B and C (images and plot of Figure 4), as well as in the shapes of the concentration profiles after transition from the smaller to greater width segments. The slight discrepancy between the experimental and modeling results for strip C may be due to small variations in the pressure difference across strips B and C in the experimental system.
The use of different leg geometries to produce sequential delivery of reagents was demonstrated in the experiment of Figure 5. A previous demonstration of sequential delivery to a detection region did not utilize different leg geometries, but instead used a configuration of multiple staggered inlets to a common segment containing the detection region (Fu, Lutz et al. 2010). In the demonstration shown here, the 2DPN consisted of three legs of different geometry (length and width) that fed to a centrally located detection region. The geometry of the middle leg was designed to have the shortest transport time, so was the shortest in length and was composed of a constant width. The rightmost leg was designed to deliver fluid to the detection region second, so was longer and contained a segment of greater width in order to slow the transport of fluid from that leg relative to the middle leg. The leftmost leg was designed to deliver fluid to the detection region last, so was the longest and contained the longest segment of greater width. The series of images show the transport of different colored fluids within the device to the detection region after a single activaton step. In the activation step, different size source pads, pre-wetted with colored fluids (6 μl clear fluid, 11 μl yellow fluid, and 18 μl red fluid), were brought into contact with the respective inlets of the three legs of the 2DPN. The different colored fluids, clear, yellow, and red, were sequentially delivered to the detection region at the intersection of the inlet legs. Note that in this network design, the first fluid delivered to the detection region also wet out portions of the other legs of the device closest to the detection region (see image at t2). Depending on the device application, the delivery of the first fluid could serve as a buffer rinse of the central portions of the device. Extension to additional reagents can be accommodated through the straightforward addition of legs. The amount of overlap in the delivery times of the different fluids to the detection region is influenced by the release properties of the source pad, such as the release volume and release profile, in addition to the dimensions of the network. The release profile of the source pad will affect the timescale over which the release volume flows into the inlet leg, as well as the shut-off time of fluid flow into that inlet. The release profile of the source pad is determined both by the inherent properties of the material and subsequent surface treatments.
4.1 Conclusion
Controlling the transport of multiple reagents in 2DPNs is key to utilizing their potential for expanding the capabilities and performance of paper-based analytical devices. We present a framework for understanding both wet-out and fully wetted fluid flow in simple 2DPNs that is useful for the design and implementation of multi-step sequences using these networks.
Supplementary Material
Supplementary Information
A. Flow during wet-out in strips with expansions of different widths
For a strip containing an expansion, the width of the expansion can be used to vary the transport time of the fluid front through the strip. Figure S1 shows a series of images of transport of the fluid front in strips with different width expansions. The transport time of the fluid front in the strip of constant width is shortest. The transport time of the fluid front is greatest in the strip containing the expansion to a greater width. Thus, an expansion in the width of an inlet leg can be used to vary the transport time of reagent delivered relative to other inlet legs.
Figure S1. Transport of fluids during wet-out for strips with expansions of different widths. A constant width strip is also shown for comparison. The effect of an expansion of greater width is to slow the advancement of the fluid front through the strip relative to that in a strip with an expansion of smaller width.
B. Minimizing Transport Time in a Contraction
This can be understood through a straightforward analysis of transport based on the Washburn equation, assuming a simple velocity function in the first constant width segment that is consistent with the Washburn equation,
| (S1) |
where ν0 is the initial velocity, τ is the timescale over which the fluid column progression becomes linear, and the expression is valid for 0 < t < t1. It is assumed . The distance traveled in this section is described by,
| (S2) |
Assuming that the fluid front travels a distance d1 to the end of the first segment of constant width at t1,
| (S3) |
and
| (S4) |
Analogous equations to (S2) though (S5), describe flow of the fluid front in the second segment of constant width. A velocity function consistent with Washburn behaviour at is,
| (S5) |
where (here, the prime does not denote a derivative), and again τ is the timescale over which the behaviour becomes Washburn-like. The expression is valid for t > t1, and the relative time is t – t1. The distance traveled in the second segment of constant width is,
| (S6) |
Assuming that the fluid front travels a total distance dT along both segments of constant widths in tT,
| (S7) |
and
| (S8) |
Imposing and solving for the d1 that minimizes tT, results in,
| (S9) |
C. Darcy's Law Flow in Strips of Two Constant Width Segments
For a strip composed of two constant width segments, with lengths L1 and L2, widths W1 and W2, and equal heights H, the volume of the strip is V = L1W1H + L2W2H and the resistance of the strip is . From equation (4), the transport time is proportional to,
| (S10) |
Note that the expression is symmetric in L1 and L2. Assuming and , δ can be rewritten as,
| (S11) |
Taking the derivative with respect to β, results in,
| (S12) |
Setting , and simplifying, results in γ = 1. This condition L1 = L2 corresponds to a local maximum, indicating that for any fixed non-equal width values, the greatest transport time can be obtained for equal length segments (and assuming the same ).
For γ = 1 or L1 = L2 = L, in the limit of , δ~L2β, or . Thus, longer transport times can be obtained by increasing the ratio in the widths of the segments (again assuming the same ).
Figure 3.
Schematic of the fluidic network analogy to electrical resistance. The total volumetric flux through a 2DPN of N segments in series, during fully wetted flow, follows the same form as Ohm's Law for a circuit with N resistors in series. The pressure difference ΔP is the fluidic counterpart to voltage change, the volumetric flow rate Q is the fluidic counterpart to current, and the length of the segment divided by the cross-sectional area to flow multiplied by , is the fluidic counterpart to the resistance for each segment i.
Acknowledgements
We thank Benedict Hui for assistance with the fabrication of 2DPNs. We gratefully acknowledge the support of NIH Grant No. RC1EB010593.
Footnotes
Though nitrocellulose is not formed in the manner traditionally used for papermaking, and may not be considered by some to be a true paper, here we use a more inclusive definition of paper with respect to 2DPNs that includes related thin porous materials.
Note that electrophoresis was not an issue with respect to transport of the pulse of tracer species due to the upstream placement of both electrodes.
References
- Alava M, Niskanen K. The physics of paper. Reports on Progress in Physics. 2006;69:669–723. [Google Scholar]
- Auriault J, Borne L, et al. Dynamics of porous saturated media, checking of the generalized law of Darcy. Journal of the Acoustical Society of America. 1985;77:1641–1650. [Google Scholar]
- Cabrera C, Finlayson B, et al. Formation of Natural pH Gradients in a Microfluidic Device under Flow Conditions: Model and Experimental Validation. Analytical Chemistry. 2001;73:658–666. doi: 10.1021/ac000495a. [DOI] [PubMed] [Google Scholar]
- Darcy H. Les Fontaines Publiques de la Ville de Dijon. V. Dalmont. Paris. 1856.
- Fenton E, Mascarenas M, et al. Multiplex lateral-flow test strips fabricated by two-dimensional shaping. Applied Materials and Interfaces. 2009;1:124–129. doi: 10.1021/am800043z. [DOI] [PubMed] [Google Scholar]
- Fu E, Lutz B, et al. Controlled reagent transport in disposable 2D paper networks. Lab on a Chip. 2010;10:918–920. doi: 10.1039/b919614e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujita H. On the Distribution of Liquid Ascending in a Filter Paper. Journal of Physical Chemistry. 1952;56:625–629. [Google Scholar]
- Holde KEV. Physical Biochemistry. Englewood Cliffs; Prentice Hall: 1985. [Google Scholar]
- Jackson G, James D. The permeability of fibrous porous materials. The Canadian Journal of Chemical Engineering. 1986;64:364–374. [Google Scholar]
- Martinez AW, Phillips ST, et al. Patterned paper as a platform for inexpensive, low-volume, portable bioassays. Angewandte Chemie-International Edition. 2007;46:1318–1320. doi: 10.1002/anie.200603817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez AW, Phillips ST, et al. Three-dimensional microfluidic devices fabricated in layered paper and tape. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:19606–19611. doi: 10.1073/pnas.0810903105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez AW, Phillips ST, et al. Diagnostics for the Developing World: Microfluidic Paper-Based Analytical Devices. Analytical Chemistry. 2010;82:3–10. doi: 10.1021/ac9013989. [DOI] [PubMed] [Google Scholar]
- Martinez AW, Phillips ST, et al. FLASH: A rapid method for prototyping paper-based microfluidic devices. Lab on a Chip. 2008;8:2146–2150. doi: 10.1039/b811135a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medina A, Perez-Rosales C, et al. Imbibition in pieces of paper with different shapes. Revista Mexicana De Fisica. 2001;47:537–541. [Google Scholar]
- Mendez S, Fenton EM, et al. Imbibition in Porous Membranes of Complex Shape: Quasi-stationary Flow in Thin Rectangular Segments. Langmuir. 2010;26:1380–1385. doi: 10.1021/la902470b. [DOI] [PubMed] [Google Scholar]
- Nordbotten JM, C. M. A., et al. Interpretation of macroscale variables in Darcy's law. Water Resources Research. 2007;43:W08430. [Google Scholar]
- Peek RL, McLean DA. Capillary penetration of fibrous materials. Industrial & Engineering Chemistry. 1934;6:85–90. [Google Scholar]
- Rasband WS. ImageJ. U. S. National Institutes of Health; Bethesda, Maryland, USA: 1997-2010. http://rsb.info.nih.gov/ij/ [Google Scholar]
- Spicar-Mihalic P, Stevens D, et al. MicroTAS Proceedings. 2007.
- Takahashi A. Kagaku. 1950;20:41. [Google Scholar]
- Washburn EW. The dynamics of capillary flow. Physical Review. 1921;17:273–283. [Google Scholar]
- Williams R. The capillary without walls. Journal of Colloid and Interface Science. 1980;79:287–288. [Google Scholar]
- Zhao WA, van den Berg A. Lab on paper. Lab on a Chip. 2008;8:1988–1991. doi: 10.1039/b814043j. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information
A. Flow during wet-out in strips with expansions of different widths
For a strip containing an expansion, the width of the expansion can be used to vary the transport time of the fluid front through the strip. Figure S1 shows a series of images of transport of the fluid front in strips with different width expansions. The transport time of the fluid front in the strip of constant width is shortest. The transport time of the fluid front is greatest in the strip containing the expansion to a greater width. Thus, an expansion in the width of an inlet leg can be used to vary the transport time of reagent delivered relative to other inlet legs.
Figure S1. Transport of fluids during wet-out for strips with expansions of different widths. A constant width strip is also shown for comparison. The effect of an expansion of greater width is to slow the advancement of the fluid front through the strip relative to that in a strip with an expansion of smaller width.
B. Minimizing Transport Time in a Contraction
This can be understood through a straightforward analysis of transport based on the Washburn equation, assuming a simple velocity function in the first constant width segment that is consistent with the Washburn equation,
| (S1) |
where ν0 is the initial velocity, τ is the timescale over which the fluid column progression becomes linear, and the expression is valid for 0 < t < t1. It is assumed . The distance traveled in this section is described by,
| (S2) |
Assuming that the fluid front travels a distance d1 to the end of the first segment of constant width at t1,
| (S3) |
and
| (S4) |
Analogous equations to (S2) though (S5), describe flow of the fluid front in the second segment of constant width. A velocity function consistent with Washburn behaviour at is,
| (S5) |
where (here, the prime does not denote a derivative), and again τ is the timescale over which the behaviour becomes Washburn-like. The expression is valid for t > t1, and the relative time is t – t1. The distance traveled in the second segment of constant width is,
| (S6) |
Assuming that the fluid front travels a total distance dT along both segments of constant widths in tT,
| (S7) |
and
| (S8) |
Imposing and solving for the d1 that minimizes tT, results in,
| (S9) |
C. Darcy's Law Flow in Strips of Two Constant Width Segments
For a strip composed of two constant width segments, with lengths L1 and L2, widths W1 and W2, and equal heights H, the volume of the strip is V = L1W1H + L2W2H and the resistance of the strip is . From equation (4), the transport time is proportional to,
| (S10) |
Note that the expression is symmetric in L1 and L2. Assuming and , δ can be rewritten as,
| (S11) |
Taking the derivative with respect to β, results in,
| (S12) |
Setting , and simplifying, results in γ = 1. This condition L1 = L2 corresponds to a local maximum, indicating that for any fixed non-equal width values, the greatest transport time can be obtained for equal length segments (and assuming the same ).
For γ = 1 or L1 = L2 = L, in the limit of , δ~L2β, or . Thus, longer transport times can be obtained by increasing the ratio in the widths of the segments (again assuming the same ).