Prediction with measurement errors in finite populations

Abstract

We address the problem of selecting the best linear unbiased predictor (BLUP) of the latent value (e.g., serum glucose fasting level) of sample subjects with heteroskedastic measurement errors. Using a simple example, we compare the usual mixed model BLUP to a similar predictor based on a mixed model framed in a finite population (FPMM) setup with two sources of variability, the first of which corresponds to simple random sampling and the second, to heteroskedastic measurement errors. Under this last approach, we show that when measurement errors are subject-specific, the BLUP shrinkage constants are based on a pooled measurement error variance as opposed to the individual ones generally considered for the usual mixed model BLUP. In contrast, when the heteroskedastic measurement errors are measurement condition-specific, the FPMM BLUP involves different shrinkage constants. We also show that in this setup, when measurement errors are subject-specific, the usual mixed model predictor is biased but has a smaller mean squared error than the FPMM BLUP which point to some difficulties in the interpretation of such predictors.

1 Introduction

Mixed models have a long history in the statistical literature and have been used to analyze data from many fields, like Agriculture, Genetics, Medicine etc. They are not only extremely exible and useful to model the covariance structure of correlated data but also allow both subject-specific and population-averaged analyses as indicated in Verbeke and Molenberghs (2001), for example. The importance of mixed models is clearly demonstrated by the variety of texts that have been recently published on the subject. Verbeke and Molenberghs (2001), Diggle et al. (2002), Demidenko (2004), Fitzmaurice et al. (2008) are excellent examples.

The linear mixed model may be expressed as

$$\mathbf{Y}=\mathbf{X}\mathit{\alpha }+\mathbf{ZB}+\mathbf{E}$$ (1)

where Y is an n × 1 response vector, X and Z are, respectively, n × p and n × q known model specification matrices, α is a p × 1 vector of unknown parameters (fixed effects), B is a q × 1 vector of random elements (random effects) such that 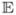(B) = 0 and 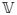(B) = Γ, E is an n×1 vector of random errors such that 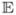(E) = 0 and 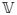(E) = Σ and is not correlated with B. This implies that

$$\mathbb{V}(\mathbf{Y})=\mathbf{\Omega }={\mathbf{Z}\mathbf{\Gamma }\mathbf{Z}}^{\top }+\mathbf{\sum }.$$ (2)

In many practical situations, we are interested not only in estimating α but also in predicting B. The best linear unbiased estimator (BLUE) of α and the best linear unbiased predictor (BLUP) of B are respectively given by

$$\begin{array}{l}\widehat{\mathit{\alpha }}={({\mathbf{X}}^{\top }{\mathbf{\Omega }}^{-1}\mathbf{X})}^{-1}{\mathbf{X}}^{\top }{\mathbf{\Omega }}^{-1}\mathbf{Y}\\ \widehat{\mathbf{B}}=\mathbf{\Gamma }{\mathbf{Z}}^{\top }{\mathbf{\Omega }}^{-1}(\mathbf{Y}-\mathbf{X}\widehat{\mathit{\alpha }})\end{array}$$ (3)

which is the solution to the well-known Henderson equations [see Verbeke and Molenberghs (2001), for example]

$$\left(\begin{array}{cc}{\mathbf{X}}^{\top }{\mathbf{\sum }}^{-1}\mathbf{X}& {\mathbf{X}}^{\top }{\mathbf{\sum }}^{-1}\mathbf{Z}\\ {\mathbf{Z}}^{\top }{\mathbf{\sum }}^{-1}\mathbf{X}& {\mathbf{Z}}^{\top }{\mathbf{\sum }}^{-1}\mathbf{Z}+{\mathbf{\Gamma }}^{-1}\end{array}\right)\left(\begin{array}{c}\widehat{\mathit{\alpha }}\\ \widehat{\mathbf{B}}\end{array}\right)=\left(\begin{array}{c}{\mathbf{X}}^{\top }{\mathbf{\sum }}^{-1}\mathbf{Y}\\ {\mathbf{Z}}^{\top }{\mathbf{\sum }}^{-1}\mathbf{Y}\end{array}\right).$$ (4)

It follows that the BLUP of

$$Q={\mathbf{k}}_1^{\top }\mathit{\alpha }+{\mathbf{k}}_2^{\top }\mathbf{B}$$ (5)

where k₁ and k₂ are known p × 1 and q × 1 vectors is $\widehat{Q}={\mathbf{k}}_1^{\top }\widehat{\mathit{\alpha }}+{\mathbf{k}}_2^{\top }\widehat{\mathbf{B}}$. Although many derivations of these results are available, it is possible, as indicated in Harville (1990), to obtain the BLUP assuming only the existence of the first and second moments as considered above. An outline of this derivation is given in Appendix A. The reader is also referred to Robinson (1991) for an excellent account on the subject.

Linear mixed models may be used to predict latent values in the presence of heteroskedastic measurement errors, as seen in Stanek et al. (1999), for example. Specification of the appropriate mixed model for such purposes may be tricky, as we show by the following example.

With the objective of evaluating the impact of physical activity on gestational diabetes, suppose that a single measurement of fasting serum glucose (sg) level is made on each of n pregnant women sampled from a hospital practice. Women with sufficiently elevated fasting sg-levels are to be referred to a physician for further evaluation. The accuracy of the prediction is important to ensure high sensitivity and specificity of the referrals. However, since fasting sg-levels may vary from day to day, and the variance may differ among women, we plan to predict latent fasting sg-levels for women in the sample appropriately accounting for this heterogeneous subject-specific measurement variability.

A model usually employed for this problem is

$$Y_i=\mu +B_i+E_i,i=1,\dots ,n$$ (6)

where Y_i is the observed fasting sg-level for the i-th selected woman, μ is the population mean, B_i, assumed to have null mean and variance γ², represents the random effect of the i-th selected woman and E_i, assumed to have null mean and variance ${\sigma }_i^2$, denotes the corresponding measurement error; we also assume that B_i and E_i are uncorrelated. This model may be expressed as (1) by letting X = 1_n, where 1_n denotes an n×1 vector with all elements equal to 1, α = μ, Z = I_n, with I_n denoting the identity matrix of order n, B = (B₁,…,B_n)^⊤, Γ = γ²I_n and $\mathbf{\sum }={\oplus }_{i=1}^n{\sigma }_i^2$ where ${\oplus }_{i=1}^n{\sigma }_i^2$ denotes an n × n diagonal matrix with the ${\sigma }_i^2$ along the main diagonal, i.e,

$$\mathbf{Y}={\mathbf{1}}_n\mu +{\mathbf{I}}_n\mathbf{B}+\mathbf{E}.$$ (7)

Under this setup, the BLUP for the latent fasting sg-level of the i-th selected woman, namely, μ+B_i, which corresponds to (5) with k₁ = 1 and k₂ = e_i where e_i denotes an n×1 vector with a single nonnull element equal to 1 in the i-th position, may be obtained from (3) and simplifies to

$${\widehat{Y}}_i=\widehat{\mu }+k_i(Y_i-\widehat{\mu })$$ (8)

where $\widehat{\mu }={\sum }_{i=1}^n(w_i/{\sum }_{i=1}^n{w}_i)Y_i$ is a weighted mean with $w_i={({\gamma }^2+{\sigma }_i^2)}^{-1}$ and $k_i={\gamma }^2/({\gamma }^2+{\sigma }_i^2)$ is the corresponding shrinkage constant. Details are presented in Appendix A.

For simplicity, to see how the mixed model is used in the context of our finite population example, suppose that a physician has N = 3 pregnant women in her practice and that we plan to take a simple random sample of n = 2 women, and make a single measurement of fasting sg-level on each woman. Normal fasting sg-levels are 4–8 mmoles/l; levels above 11.1 mmoles/l indicate a diagnosis of diabetes. We assume that the population parameters (latent fasting sg-levels and subject-specific measurement error variances) are those summarized in Table 1.

Table 1.

Fasting serum glucose levels, subject-specific measurement error variances and shrinkage constants for a population of 3 women

Subject	Latent sg-level	Measurement error variance	Shrinkage constant
Daisy	10	1	0.950
Lily	3	100	0.160
Rose	2	4	0.826
Average	μ = 5	σ̄2 = 35
Variance	γ2 = 19

We assume further that the variances are known and that the subject-specific measurement error can take on only two possible equally likely values given by plus or minus the subject-specific standard deviation. We wish to predict the latent fasting sg-level of each woman in the sample and use the subject-specific variance components to define the shrinkage constants. The observed response, Y_i and the values of the predictor (8) are listed in Table 2 for all 24 possible samples corresponding to the 4 possible combinations of response for each of the 6 possible sample sequences. We also tabulate the squared difference between the value of each predictor and the corresponding latent value; the averages over all samples are presented in the bottom row.

Table 2.

Mixed model predictor (based on subject-specific measurement errors) of fasting latent sg-levels for selected women and squared errors for all possible samples

Sample	Woman (latent sg-level)		Measurement error		Observed response*		Predictor (8)		Squared error
	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2
1	Daisy (10)	Lily (3)	1	10	11	13	11.0	11.6	1.03	73.29
2	Daisy (10)	Lily (3)	1	−10	11	−7	10.9	5.9	0.76	8.70
3	Daisy (10)	Lily (3)	−1	10	9	13	9.0	10.1	0.94	50.73
4	Daisy (10)	Lily (3)	−1	−10	9	−7	8.9	4.5	1.24	2.28
5	Daisy (10)	Rose (2)	1	2	11	4	10.8	4.7	0.70	7.03
6	Daisy (10)	Rose (2)	1	−2	11	0	10.7	1.0	0.55	0.95
7	Daisy (10)	Rose (2)	−1	2	9	4	8.9	4.5	1.25	6.08
8	Daisy (10)	Rose (2)	−1	−2	9	0	8.8	0.8	1.46	1.35
9	Lily (3)	Daisy (10)	10	1	13	11	11.6	11.0	73.29	1.03
10	Lily (3)	Daisy (10)	10	−1	13	9	10.1	9.0	50.73	0.94
11	Lily (3)	Daisy (10)	−10	1	−7	11	5.9	10.9	8.70	0.76
12	Lily (3)	Daisy (10)	−10	−1	−7	9	4.5	8.9	2.28	1.24
13	Lily (3)	Rose (2)	10	2	13	4	6.7	4.3	13.41	5.08
14	Lily (3)	Rose (2)	10	−2	13	0	3.8	0.4	0.71	2.67
15	Lily (3)	Rose (2)	−10	2	−7	4	0.7	3.7	5.08	2.86
16	Lily (3)	Rose (2)	−10	−2	−7	0	−2.1	−0.2	25.71	4.83
17	Rose (2)	Daisy (10)	2	1	4	11	4.7	10.8	7.03	0.70
18	Rose (2)	Daisy (10)	2	−1	4	9	4.5	8.9	6.08	1.25
19	Rose (2)	Daisy (10)	−2	1	0	11	1.0	10.7	0.95	0.55
20	Rose (2)	Daisy (10)	−2	−1	0	9	0.8	8.8	1.35	1.46
21	Rose (2)	Lily (3)	2	10	4	13	4.3	6.7	5.08	13.41
22	Rose (2)	Lily (3)	2	−10	4	−7	3.7	0.7	2.86	5.08
23	Rose (2)	Lily (3)	−2	10	0	13	0.4	3.8	2.67	0.71
24	Rose (2)	Lily (3)	−2	−10	0	−7	−0.2	−2.1	4.83	25.71
Average					5.0	5.0	5.8	5.8	9.11	9.11

^*Observed response = latent sg-level ± measurement error

The average value of predictor (8) is 5.8 and surprisingly it is not equal to the population mean (5.0) although it was presumably derived under an unbiasedness assumption. Clearly, in the setting where there is subject-specific measurement error, this predictor is not a BLUP since the unbiasedness property does not hold. Our objective is to clarify such apparent inconsistency.

In Section 2 we discuss the nature of measurement errors and show that in this context, (8) is a BLUP when measurement errors are heterogeneous, but not subject-specific. In Section 3, we introduce a finite population mixed model that may be formulated as (1) but with a different covariance structure depending on the nature of the measurement errors. We also show that for heteroskedastic subject-specific measurement errors, the corresponding BLUP is not given by (8). We conclude with a discussion in Section 4.

2 Sources of measurement errors

In many situations, the actual measurement of a latent value is not possible because it may be affected by many sources of variability. Such variability is termed measurement error by Cochran (1977) or observation error by Sukhatme (1984). Measurement errors may arise in different ways which can be classified into two types of sources. The first is subject-specific and is associated to the natural variability of the response around a fixed value (the latent value); it is called inherent variability by Buonaccorsi (2006). The second is associated with the measurement process, i.e., measurement instruments or interviewers. With the same spirit generally employed in the Econometric literature [see Kennedy (2008), for example], where variables may be classified as endogenous or exogenous, we refer to the first type of measurement errors as endogenous measurement errors and the second, exogenous measurement errors. Using this terminology, the measurement errors considered in Table 2 are endogenous.

Now suppose that in our example, the measurement errors are exogenous, i.e., related to the measurement condition associated with the position (i = 1 or i = 2) in the sample, instead of endogenous (subject-specific). Let us also assume that the exogenous measurement error variance is 1 when i = 1 or 4 when i = 2 and for simplicity, that the measurement error may take only two possible values, given by plus or minus the corresponding standard error. The results are presented in Table 3.

Table 3.

Mixed model predictor (based on exogenous measurement errors) of fasting latent sg-levels for selected women and squared errors for all possible samples

Sample	Woman (latent sg-level)		Measurement error		Observed response*		Predictor (8)		Squared error
	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2
1	Daisy (10)	Lily (3)	1	2	11	5	10.9	5.6	0.74	6.54
2	Daisy (10)	Lily (3)	1	−2	11	1	10.8	1.9	0.59	1.14
3	Daisy (10)	Lily (3)	−1	2	9	5	8.9	5.4	1.19	5.63
4	Daisy (10)	Lily (3)	−1	−2	9	1	8.8	1.7	1.41	1.58
5	Daisy (10)	Rose (2)	1	2	11	4	10.8	4.7	0.70	7.03
6	Daisy (10)	Rose (2)	1	−2	11	0	10.7	1.0	0.55	0.95
7	Daisy (10)	Rose (2)	−1	2	9	4	8.9	4.5	1.25	6.08
8	Daisy (10)	Rose (2)	−1	−2	9	0	8.8	0.8	1.46	1.35
9	Lily (3)	Daisy (10)	1	2	4	12	4.2	11.3	1.41	1.58
10	Lily (3)	Daisy (10)	1	−2	4	8	4.1	7.6	1.19	5.63
11	Lily (3)	Daisy (10)	−1	2	2	12	2.2	11.1	0.59	1.14
12	Lily (3)	Daisy (10)	−1	−2	2	8	2.1	7.4	0.74	6.54
? 13	Lily (3)	Rose (2)	1	2	4	4	4.0	4.0	1.00	4.00
14	Lily (3)	Rose (2)	1	−2	4	0	3.9	0.4	0.82	2.65
15	Lily (3)	Rose (2)	−1	2	2	4	2.0	3.8	0.91	3.29
16	Lily (3)	Rose (2)	−1	−2	2	0	2.0	0.2	1.10	3.29
17	Rose (2)	Daisy (10)	1	2	3	12	3.2	11.2	1.46	1.35
18	Rose (2)	Daisy (10)	1	−2	3	8	3.1	7.5	1.25	6.08
19	Rose (2)	Daisy (10)	−1	2	1	12	1.3	11.0	0.55	0.95
20	Rose (2)	Daisy (10)	−1	−2	1	8	1.2	7.3	0.70	7.03
21	Rose (2)	Lily (3)	1	2	3	5	3.0	4.8	1.10	3.29
22	Rose (2)	Lily (3)	1	−2	3	1	3.0	1.2	0.91	3.29
23	Rose (2)	Lily (3)	−1	2	1	5	1.1	4.6	0.82	2.65
24	Rose (2)	Lily (3)	−1	−2	1	1	1.0	1.0	1.00	4.00
Average					5.0	5.0	5.0	5.0	0.98	3.63

^*Observed response = latent sg-level ± measurement error

Since the average value of predictor (8) is 5.0 (the true value), it is clearly unbiased and the results indicate that the specification of the measurement errors in model (1) may help in deciding whether (8) is or is not the BLUP and consequently in choosing the covariance structure. Although we considered only a simple example, the conclusion holds in general as shown in Appendix B.

To better understand this result, we follow the lines given in Stanek, Singer and Lencina (2004) and Stanek and Singer (2004), and consider a finite population mixed model (FPMM) that is directly connected to the physical problem it represents and show that it is useful in identifying the appropriate model specification.

3 The finite population mixed model with measurement error

Let a population consist of N labeled subjects and let the latent value for subject s correspond to a fixed (but unknown) constant, y_s. We assume that the potentially observable response for subject s is Y_s = y_s + W_s and that it differs from the latent response y_s by the endogenous measurement error W_s. Defining $\mu =N^{-1}{\sum }_{s=1}^N{y}_s$, we express the latent value in terms of a subject effect β_s as

$$y_s=\mu +{\beta }_s.$$ (9)

Adding endogenous measurement error to (9) we obtain the measurement error model for subject s, namely

$$Y_s=\mu +{\beta }_s+W_s.$$ (10)

We assume that 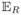(W_s) = 0 and ${\mathbb{E}}_R(W_s{W}_{s^{\prime }})={\sigma }_s^2$ for s = s′ and 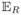(W_sW_s′) = 0 otherwise. The subscript R indicates expectation with respect to the distribution of the endogenous measurement error. We also define ${\gamma }^2={(N-1)}^{-1}{\sum }_{s=1}^N{(y_s-\mu )}^2$.

To formalize the selection of a simple random sample (without replacement) we first represent a permutation of subjects by a set of random variables, and assume that each permutation is equally likely. Without loss of generality we may assume that the sample corresponds to the set of the first n random variables in a permutation, with each random variable identified by its position. Each of these is defined via a set of N indicator random variables U_is that take on a value of one with probability 1/N if subject s is selected in position i, i = 1,…,N and zero otherwise. For the response in position i, we specify the model that includes both sampling and endogenous measurement error by

$$Y_i^{\ast }=\mu +B_i+W_i^{\ast }$$ (11)

where $Y_i^{\ast }={\sum }_{s=1}^N{U}_{is}{Y}_s,B_i={\sum }_{s=1}^N{U}_{is}{\beta }_s$ and $W_i^{\ast }={\sum }_{s=1}^N{U}_{is}{W}_s$. The assumption that sampling is without replacement implies that 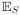(U_isU_i′s′) = 0 if i = i′, s ≠ s′ or i ≠ i′, s = s′ but 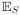(U_isU_i′s′) = 1/[N(N − 1)] if i ≠ i′, s ≠ s′ where the subscript S indicates expectation with respect to sampling. The random variables $Y_i^{\ast }$, i = 1,…,N, represent the permutations of the N subjects in the population. The latent value for the subject selected in position i in a sample is

$$Y_i^{+}=\sum _{s=1}^N{U}_{is}{y}_s=\mu +B_{i}i=1,\dots ,n.$$ (12)

Although model (11) has the same form as model (6), it explicitly accounts for random sampling with indicator random variables that underlie the definition of the random variables B_i and $W_i^{\ast }$. When endogenous measurement error variances differ between subjects, the term corresponding to E_i in (6), namely $W_i^{\ast }$, is such that

$$\mathbb{V}(W_i^{\ast })={\mathbb{E}}_S(\sum _{s=1}^N{U}_{is}{\sigma }_s^2)=N^{-1}\sum _{s=1}^N{\sigma }_s^2={\overline{\sigma }}^2.$$

In other words, taking the expectation over sampling effectively averages the measurement error variances over subjects in the population.

We can represent the FPMM for the sample as (7) with ${\mathbf{Y}}^{\ast }={(Y_1^{\ast },\dots ,Y_n^{\ast })}^{\top }$ in lieu of Y and ${\mathbf{W}}^{\ast }={(W_1^{\ast },\dots ,W_n^{\ast })}^{\top }$ in lieu of E. The variances of B and W^* emerge directly from the finite population mixed model development and are respectively given by Γ = γ²(I_n − N⁻¹J_n) where J_n = 11^⊤ and Σ = σ̄²I_n.

The corresponding BLUP for the latent fasting sg-level of the i-th selected woman, (12), may be computed as in the mixed model setup and simplifies to

$${\widehat{Y}}_i^{\ast }={\overline{Y}}^{\ast }+k(Y_i^{\ast }-{\overline{Y}}^{\ast })$$ (13)

where ${\overline{Y}}^{\ast }=n^{-1}{\sum }_{i=1}^n{Y}_i^{\ast }$ is the sample mean and k = γ²/(γ² + σ̄²). Details are given in Appendix B.

The inclusion of the additional finite population term in the variance of B has no impact on the expression for the predictor and even though the endogenous measurement error variances ${\sigma }_s^2$ are heterogeneous, the BLUP is based on the average endogenous measurement error variance σ̄². In the setup of Table 1, it follows that the predictor (13) is unbiased, and therefore, it is the BLUP, as expected.

In Table 4, we show the results for the FPMM BLUP with heteroskedastic endogenous measurement errors applied to the same setup considered in Table 2. Differently from the mixed model predictor, the average value of the FPMM predictor is equal to the population mean.

Table 4.

FPMM predictor (based on subject-specific measurement errors) of fasting latent sg-levels for selected women and squared errors for all possible samples

Sample	Woman (latent sg-level)		Measurement error		Observed response*		Predictor (13)		Squared error
	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2	i = 1	i = 2
1	Daisy (10)	Lily (3)	1	10	11	13	11.7	12.4	2.72	87.46
2	Daisy (10)	Lily (3)	1	−10	11	−7	5.2	1.2	23.36	17.36
3	Daisy (10)	Lily (3)	−1	10	9	13	10.3	11.7	0.09	75.75
4	Daisy (10)	Lily (3)	−1	−10	9	−7	3.8	−1.8	38.26	23.18
5	Daisy (10)	Rose (2)	1	2	11	4	8.7	6.3	1.61	18.22
6	Daisy (10)	Rose (2)	1	−2	11	0	7.4	3.6	6.58	2.45
7	Daisy (10)	Rose (2)	−1	2	9	4	7.4	5.6	6.87	13.11
8	Daisy (10)	Rose (2)	−1	−2	9	0	6.1	2.9	15.34	0.84
9	Lily (3)	Daisy (10)	10	1	13	11	12.4	11.7	87.46	2.72
10	Lily (3)	Daisy (10)	10	−1	13	9	11.7	10.3	75.75	0.09
11	Lily (3)	Daisy (10)	−10	1	−7	11	−1.2	5.2	17.36	23.36
12	Lily (3)	Daisy (10)	−10	−1	−7	9	−1.8	3.8	23.18	38.26
13	Lily (3)	Rose (2)	10	2	13	4	10.1	6.9	50.17	24.17
14	Lily (3)	Rose (2)	10	−2	13	0	8.8	4.2	33.49	4.90
15	Lily (3)	Rose (2)	−10	2	−7	4	−3.4	0.8	41.41	2.45
16	Lily (3)	Rose (2)	−10	−2	−7	0	−4.7	−2.3	59.78	18.22
17	Rose (2)	Daisy (10)	2	1	4	11	6.3	8.7	18.22	1.61
18	Rose (2)	Daisy (10)	2	−1	4	9	5.6	7.4	13.11	6.87
19	Rose (2)	Daisy (10)	−2	1	0	11	3.6	7.4	2.45	6.58
20	Rose (2)	Daisy (10)	−2	−1	0	9	2.9	6.1	0.84	15.34
21	Rose (2)	Lily (3)	2	10	4	13	6.9	10.1	24.17	50.17
22	Rose (2)	Lily (3)	2	−10	4	−7	0.4	−3.4	2.45	41.41
23	Rose (2)	Lily (3)	−2	10	0	13	4.2	8.8	4.90	33.49
24	Rose (2)	Lily (3)	−2	−10	0	−7	−2.3	4.7	18.22	59.78
Average					5.0	5.0	5.0	5.0	23.66	23.66

^*Observed response = latent sg-level ± measurement error

Now we consider situations where there are only exogenous measurement errors. We begin with (9) and use a simple random sampling argument to obtain (12). Using the position in the sample sequence, i = 1,…, n, to index the measurement conditions, we assume that the exogenous measurement error for condition i is given by $W_i^{•}$ with ${\mathbb{E}}_R(W_i^{•})=0$ and ${\mathbb{E}}_R(W_i^{•}{W}_{i^{\prime }}^{•})={\sigma }_i^2$ when i = i′ and is zero otherwise. The model that accounts for sampling when there is only exogenous measurement error is defined by adding $W_i^{•}$ to (12), i.e.,

$$Y_i^{•}=\mu +B_i+W_i^{•}.$$ (14)

This model may also be expressed as (7) with Y replaced by ${\mathbf{Y}}^{•}={(Y_1^{•},\dots ,Y_n^{•})}^{\top }$ and E replaced by ${\mathbf{W}}^{•}={(W_1^{•},\dots ,W_n^{•})}^{\top }$. Once again, the variance of B is given by Γ = γ²(I_n − N⁻¹J_n), but now, $\mathbf{\sum }={\oplus }_{i=1}^n{\sigma }_i^2$. The heterogeneous variance is associated with the measurement condition, i.e., position in the sample sequence, not with the realized subject. Proceeding as in the previous cases, we obtain the BLUP of (12) which simplifies to (8) with the Y_i replaced by $Y_i^{•}$ and the results of Table 3 are reproduced. Once again, there is no impact of including the additional finite population term in the variance of B on the expression for the predictor. Details are given in Appendix B.

4 Discussion

At a first sight, it may appear that predictor (8) is the most appropriate when endogenous measurement error variances differ among subjects since its expression accounts for the different variances. This problem has been recently examined by Buonaccorsi (2006) in the context of estimating the population mean in a two-stage heteroskedastic model. He concludes that when the endogenous measurement error variance (which he terms inherent variability) is heterogeneous, the best linear unbiased estimator should be constructed using an average variance instead of subject-specific variances. He also notes that a weighted estimator may have smaller mean squared error (MSE), commenting that this result deserves further study since the weighted estimator is not justified by the context of the problem. We face a similar situation when predicting the latent value of a randomly selected subject. Our results are consistent with the conclusions of Buonaccorsi (2006) and illustrate additional problems generated by a weighted estimator. We strengthen the foundation for our conclusions by explicitly linking the finite population to the sample via a mixed model that arises directly from the incorporation of sampling and measurement errors.

Both the predictors given by (8) and (13) can be derived under the standard mixed model (7) through the specification of the variance components. If there is heteroskedastic endogenous measurement error, then 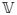(E) = σ̄²I_n; otherwise, if there is heteroskedastic exogenous measurement error, $\mathbb{V}(\mathbf{E})={\oplus }_{i=1}^n{\sigma }_i^2$. In the first case, the BLUP will be (13) and in the second, it will be (8). The basic problem is that in a standard mixed model, response for the set of labelled subjects in the data could be assigned in n! different orders (or sequences) to represent realizations of the vector Y in (7). The index i for for the random variable Y_i does not identify the realized subject, but rather simply its position in the vector Y. It is easy to mistake interpretation of this index and to consider it to be the realized subject’s label as outlined in Stanek, Singer and Lencina (2004). If misinterpreted, the heterogeneous position-specific (exogenous) variances in (7) will be falsely attributed to heterogeneous subject-specific (endogenous) variances. Since the step that links a subject’s label to the position of the subject in a response vector is omitted in the usual mixed model (unlike the models developed in Section 3), this mistake is easily made. The models developed in Section 3 prevent such erroneous switch of concepts. This is aggravated by the fact that (13) corresponds to the BLUP obtained when exogenous heteroskedastic measurement errors are considered.

Harville (1978) shows that the mixed model may be formulated in different ways. In particular, model (1) may also be viewed as arising from the first n of N superpopulation random variables as in Voss (1999). In fact, if N is very large, the covariance terms divided by N may be taken as zero and the simple mixed model (7) with appropriate covariance matrices can be used to approximate the FPMM for the simple settings considered. The FPMM framework is able to capture different physical situations corresponding to endogenous or exogenous measurement error even for very large (essentially infinite) populations.

In many practical situations, both endogenous measurement error that is associated with labeled subjects and exogenous measurement error that is associated with positions in the sample sequence can occur concurrently. For example, in a typical nutritional epidemiologic study, information on study participants’ daily dietary intake is collected using 24 hour recalls through telephone interviews. The accuracy of the collected information depends on the accuracy of a participant’s memory (endogenous, subject-specific, measurement error) as well as the experience of the staff assigned to conduct the interview (i.e., exogenous measurement error). Extensions to such settings involve additional investigation which are currently being conducted.

Our development was limited to settings where a single measure was made on each sample subject. Buonaccorsi (2006) introduced the idea of variability in sampling effort to describe situations where a different number of measures are made on a subject, limiting consideration to settings where a single random variable represented response for each sample subject. He discussed the possibility of the sampling effort being fixed or random, but stopped short of characterizing the problem via subject labels and measurement conditions associated with positions in a sample sequence. Settings where the number of measures on a subject differ are more complex. This problem has been discussed by Stanek and Singer (2008) in clustered population settings where sampling effort is part of the study design, but they included neither endogenous nor exogenous measurement errors. Equal size clustered populations with balanced two stage sampling and endogenous measurement error have been discussed by Stanek and Singer (2004), and yield predictors similar to (8). Since in practice, variance components are rarely known, empirical predictors based on method of moment estimates of variance components are commonly used. Simulation studies were reported in San Martino, Singer, and Stanek (2008) to evaluate the performance of the resulting empirical predictors and indicated some loss in the expected MSE reduction, especially when variance component estimates have low reliability. However, they still outperform the weighted least squares competitor in the majority of cases.

An intriguing feature of the analysis in Table 2 is that the MSE (= 9.1) for the biased predictor (8) is smaller than the MSE (= 23.7) for the FPMM BLUP (13) applied in the same setting. A similar result occurred when other examples were investigated, and in each case, the MSE of (8) was smaller, even though it is based on an inappropriate model. This counter-intuitive result may be explained by the fact that the miss-specified model-based predictor falls outside the class of linear unbiased predictors that are defined for the correctly specified problem, a result alluded to by Buonaccorsi (2006). Given that the MSE may be a more important property than (average) unbiasedness when prediction of latent values of realized subjects is in perspective, it seems that the search for best predictors in broader classes may be an important avenue for research.

Appendix A

In the context of the mixed model (1), we follow the development of Goldberger (1962) as reviewed by Robinson (1991) to obtain a predictor of $Q={\mathbf{k}}_1^{\top }\mathit{\alpha }+{\mathbf{k}}_2^{\top }\mathbf{B}$ where k₁ and k₂ are respectively p × 1 and q × 1 known vectors. We require the predictor to be the unbiased linear function of Y that has minimum expected MSE within this class. We first note that

$$\mathbb{E}\left(\begin{array}{c}\mathbf{Y}\\ Q\end{array}\right)=\left(\begin{array}{c}\mathbf{X}\\ {\mathbf{k}}_1^{\top }\end{array}\right)\mathit{\alpha }\text{and}\mathbb{V}\left(\begin{array}{c}\mathbf{Y}\\ Q\end{array}\right)=\left(\begin{array}{cc}\mathbf{\Omega }& {\mathbf{Z}\mathbf{\Gamma }\mathbf{k}}_2\\ {\mathbf{k}}_2^{\top }\mathbf{\Gamma }{\mathbf{Z}}^{\top }& {\mathbf{k}}_2^{\top }\mathbf{\Gamma }{\mathbf{k}}_2\end{array}\right).$$

Then we consider linear predictors of the form q = c^⊤Y and note that i) the unbiasedness constraint implies ${\mathbf{c}}^{\top }\mathbf{X}-{\mathbf{k}}_1^{\top }=\mathbf{0}$ and ii) the variance of the predictor is $\mathbb{V}(q-Q)={\mathbf{c}}^{\top }\mathbf{\Omega }\mathbf{c}-2{\mathbf{c}}^{\top }{\mathbf{Z}\mathbf{\Gamma }\mathbf{k}}_2+{\mathbf{k}}_2^{\top }\mathbf{\Gamma }{\mathbf{k}}_2$. Minimizing the variance with respect to c subject to the unbiasedness constraint results in

$$\widehat{Q}={\mathbf{k}}_1^{\top }\widehat{\mathit{\alpha }}+{\mathbf{k}}_2^{\top }\mathbf{\Gamma }{\mathbf{Z}}^{\top }{\mathbf{\Omega }}^{-1}(\mathbf{Y}-\mathbf{X}\widehat{\mathit{\alpha }})$$ (15)

where α̂ = (X^⊤Ω⁻¹X)⁻¹X^⊤Ω⁻¹Y.

For the special case (7) with Γ = γ²I_n and $\mathbf{\sum }={\oplus }_{i=1}^n{\sigma }_i^2$, it follows that ${\mathbf{\Omega }}^{-1}={\oplus }_{i=1}^n{({\gamma }^2+{\sigma }_i^2)}^{-1}$ so that using (15), we obtain (8).

Appendix B

The predictor of a sample subject’s latent value in the FPMM may be obtained from the results in Appendix A. We first consider the setting with heteroskedastic endogenous measurement errors. In such a case, Γ = γ²(I_n − N⁻¹J_n) and Σ = σ̄²I_n and it follows that Ω⁻¹ = (γ² + σ̄²)⁻¹[I_n + k/(N − nk)J_n] where k = γ²/(γ² + σ̄²). Again, using (15), we obtain (13).

Next we consider the heteroskedastic exogenous measurement error case. Here, Γ = γ²(I_n − N⁻¹J_n) and $\mathbf{\sum }={\oplus }_{i=1}^n{\sigma }_i^2$, so that ${\mathbf{\Omega }}^{-1}=1/{\gamma }^2[{\oplus }_{i=1}^n{k}_i+{(N-n\overline{k})}^{-1}\mathbf{k}{\mathbf{k}}^{\top }]$ where k = (k₁,…, k_n)^⊤ with $k_i={\gamma }^2/({\gamma }^2+{\sigma }_i^2)$ and $\overline{k}=n^{-1}{\sum }_{i=1}^n{k}_i$. Then (8) follows directly from (15).