Abstract
Assessing the quality of predicted models is essential in protein tertiary structure prediction. In the past Critical Assessment of Techniques for Protein Structure Prediction (CASP) experiments, consensus quality assessment (QA) methods have shown to be very effective, outperforming single-model methods and other competing approaches by a large margin. In the consensus QA approach, the quality score of a model is typically estimated based on pair-wise structure similarity of it to a set of reference models. In CASP8, the differences among the top QA servers were mostly in the selection of the reference models. In this paper, we present a new consensus method SelCon based on two key ideas: 1) to adaptively select appropriate reference models based on the attributes of the whole set of predicted models and 2) to weight different reference models differently, and in particular not to use models that are too similar or too different from the candidate model as its references. We have developed several reference selection functions in SelCon and obtained improved QA results over existing QA methods in experiments using CASP7 and CASP8 data. In the recently completed CASP9 in 2010, the new method was implemented in our MUFOLD-WQA server. Both the official CASP9 assessment and our in-house evaluation showed that MUFOLD-WQA performed very well and achieved top performances in both the global structure QA and top-model selection category in CASP9.
Keywords: Protein tertiary structure prediction, protein model quality assessment, protein model selection, consensus method, CASP
1 Introduction
Protein structure prediction is one of the challenging problems in bioinformatics. Determining accurate protein structures quickly and at low-cost will benefit many life science fields, such as medicine and biotechnology. To increase the speed and bring down the cost, computational methods for protein structure prediction have been actively developed and significant progress has been achieved in recent years [1], [2], [3], [4], [5], [6], [7], [8], [9], [10]. To facilitate the research and development of computational prediction methods, a bi-annual community-wide experiment for protein structure prediction, Critical Assessment of Techniques for Protein Structure Prediction (CASP), has been held since 1994. CASP experiments have been served as a place for research groups to rigorously test and evaluate their techniques for protein 3D structure prediction and model quality assessment [11] [12].
Protein structure prediction software generates a large number of models and, as a result, the ability of picking out the good ones directly affects the final prediction result. Currently, protein structure prediction tools often can generate good structural models but have difficulty picking them out [13] [14]. Thus, a Quality Assessment (QA) category was created in CASP7 in 2006 to facilitate the development of QA methods. For a predicted model, a good QA method should produce a quality score that is strongly correlated with the true quality of the model.
Major approaches for protein model quality assessment (QA) can be divided into three categories: energy or scoring functions, clustering-based methods, and consensus methods. Energy or scoring functions have long been used in QA, especially for single model QA. They estimate the quality of a given protein model based on its physical or statistical properties. Physics-based energy functions have been constructed based on physical properties at molecule levels [17] [18]. Their advantages include sound theoretical foundations and the ability to estimate the quality of a single model. Their drawbacks include being too sensitive to small structural errors and expensive computation due to the large amount of information involved, such as atomic interactions of protein molecules and solvent [20]. More recently, knowledge-based statistical scoring functions have gained popularity. They are designed based on statistical knowledge of experimentally known protein structures [21] [22]. These functions are faster, simpler and sometimes more accurate than physics-based functions [23] [24].
The second approach for protein structure selection is clustering based. The idea of using clustering to discriminate protein structures suggests that near-native structures have more structural neighbors than poor structures [27]. Some clustering methods, e.g. SCAR [28], apply k-means clustering algorithm and use cluster centroids as representative models for clusters. A centroid is the average of all the structures in a cluster and is constructed by minimizing distance constraint between each pair of residues. Some clustering methods, e.g. SPICKER [30] and its variant [29], find clusters by looking for one or more structures with the largest number of neighbors within a certain clustering radius. Surrounding a structure with most neighbors, a cluster is formed and the cluster center is constructed. SPICKER also uses cluster centroids as the candidates of near-native conformations. Though a centroid is more robust than an individual structure in a cluster, it often contains significant atomic clashes and needs additional structure refinement.
The third approach utilizes consensus information [15] [25] [31]. This approach assumes predicted models as samples around a native conformation and a model that is more similar to others is closer to the native conformation. Different from clustering-based methods, consensus methods do not find clusters, but instead compute the quality score of a candidate model as the average of pair-wise similarities between it and other predicted models [25]. For example, 3D-Jury [15] and Pcons [39] use the average of pairwise similarity between all models. 3D-Jury drops some bad models according to a predetermined cutoff value, and computes the final score of a model by averaging its similarity scores against the remaining models. In order to get further improvement, many methods, e.g. CASP8 QA servers QMEANclust [32], MULTICOM [34], ModFOLDclust [40], and SAM-T08-MQAC [41], also combine consensus techniques with scoring functions. A drawback of consensus methods is that they need a large number of predicted models, usually in hundreds, that consist of a sufficient number of good models, and do not work for single-model QA. As demonstrated in previous CASP experiments, consensus QA methods have been very effective, outperforming single-model methods by a large margin [13] [14]. A basic consensus QA method RefAll [37] [38], referred to as total consensus QA in this paper, is to use all available models as the reference set. In CASP8, the main differences of the top QA servers were mostly in the reference models used. Despite significant efforts by the CASP8 QA teams in developing various sophisticated consensus QA methods, the simple total consensus QA was shown to perform better than the top CASP8 QA servers on the CASP8 data [37] [38], which indicates that improving over the total consensus QA is non-trivial.
In our work, through systematic and in-depth analysis of different reference selection strategies, we have developed a new adaptive consensus method based on two key ideas: 1) adaptively select appropriate reference models based on the attributes of the whole set of predicted models and 2) weight different reference models differently, and in particular not to use the ones that are too similar or too different from the candidate models as references. The method can work with any reasonable pairwise similarity measurement between two 3D models, such as GDT_TS [16] and Q-score [53], [54]. Within a general framework, we have developed several reference selection functions and studied their performances empirically using CASP7 and CASP8 data. Extensive experimental results show the new method outperforms state-of-the-art consensus methods and scoring functions in both quality assessment and top model selection. In CASP9, the new method was implemented in our QA server, MUFOLD-WQA, which was ranked No. 1 in both the global QA category and the top-model selection category in term of the average GDT_TS loss.
2 Materials and Methods
2.1 Quality Assessment Problem Definition
Let S be a set of predicted models for a target protein, T, and p be the size of S, S = {si, 1 ≤ i ≤ p}. Let Y = {yi, 1 ≤ i ≤ p} be the true quality of each predicted model si, which is usually measured as its GDT_TS value to the native structure, GDT_TS(si, T). Our goal is to compute a quality assessment (QA) score xi for each si, 1 ≤ i ≤ p, such that X = {xi, 1 ≤ i ≤ p} correlates strongly with Y.
Specifically, a commonly used performance metric of QA is the Pearson correlation coefficient ρ between X and Y:
| (1) |
The range of ρ is [−1, 1], with a perfect correlation being 1. Then, the problem objective is to generate QA score X that maximizes the correlation ρ:
| (2) |
Another important problem in protein structure prediction is to select the best model from a pool of predicted models. The QA score X can be used for this purpose too. In this case, the top-model selection problem becomes to select si with the largest xi value. Note that the structure si with the largest xi value may not have the highest GDT_TS score. Unfortunately, in practice, the native structures of proteins, hence yi, are not available, and thus the selection is based on xi.
2.2 Similarity Measure and Consensus Algorithms
Our consensus method is based on pairwise similarity between predicted protein structures. Any reasonable similarity metrics, such as RMSD, GDT_TS [16], and Q-score [53], [54], can be used. For CASP data, we used GDT_TS simply because it is the main metrics used in the official CASP evaluation [35]. GDT_TS stands for Global Distance Test Total Score and measures global similarity between two protein structures si and sj as follows.
| (3) |
where Pd is the percentage of residues from si that can be superimposed with corresponding residues from sj under selected distance cutoffs d, d ∈ {1, 2, 4, 8} [16]. GDT_TS values are in the range of 0 to 1. The larger the GDT_TS score between two structures, the more similar they are. In this paper, GDT_TS score is computed using software TM-score [36].
The GDT_TS value defined above depends on structure lengths. For example, for two predicted structures si and sj of a protein, if Len(si) < Len(sj), where Len(si) and Len(sj) are the lengths of si and sj respectively, then from the definition of GDT_TS, GDT_TS(si, sj) < GDT_TS(sj, si).
The sensitivity of the pairwise GDT_TS to structure size complicates algorithm design. To remove the dependency of GDT_TS on model length, we normalize GDT_TS by scaling with the lengths of the compared structures as follows
| (4) |
where Len(seq) is the length of the query protein sequence, for which 3-D structures are predicted.
The normalized score nGDT_TS has several nice properties. First, it is between 0 and 1, because Len(si) ≤ Len(seq) holds for any predicted structure si. Second, with nGDT_TS(si, sj) = nGDT_TS(sj, si), it is symmetric. More importantly, being independent of model lengths, nGDT_TSs of different pairs of models are directly comparable. In the remainder of this paper, nGDT_TS is used to measure structure similarity. However, for the convenience of description, GDT_TS instead of nGDT_TS is used to denote normalized structural similarity.
The total consensus method, called RefAll as shown in Algorithm 1, uses all predicted models in computing a consensus score. Given a set of predicted models, RefAll computes the QA score of a given model as the average of all pair-wise similarity measures between it and each of the other models.
Algorithm 1.
RefAll
| Require: Predicted protein models, S = {si, 1 ≤ i ≤ p}. | |
| for all si ∈ S do | |
|
| |
| where sim(a, b) is a similarity measure between a and b, e.g., GDT_TS. | |
| end for | |
| return QA score for each model, X = {xi, 1 ≤ i ≤ p}. |
RefAll and the other consensus algorithms presented in this paper are based on similarity between a pair of 3D protein models. The algorithm GRefAll is RefAll using GDT_TS.
Though simple, GRefAll performs very well on CASP data sets. Table 1 compares the performance of GRefAll with those of the top five QA servers in CASP8, which are all consensus based and mainly differ in the selection of reference models and the choice of pair-wise similarity metrics. Pcons_Pcons [39] is similar to GRefAll, but used LGscore and S-score as their similarity metrics. SAM-T08-MQAC [41] first uses their in-house single-model QA tool Undertaker to evaluate the models, then computes GDT_TS of each server model against the top model that was labeled model 1 by the same server, and then takes the median GDT_TS as their consensus cost function. QMEANclust [32] ranks the models using the QMEAN scoring function [33] and chooses the top 20% of models as the reference set for likely template-based modeling (TBM) targets and top 10% of models for likely free modeling (FM) targets. MULTICOM [34] uses their single model scoring function MULTICOM-CMFR to rank the models, and selects top five models as references.
TABLE 1.
QA performance comparison of GRefAll and the top five QA servers in CASP8 on 122 CASP8 targets.
As shown in Table 1, GRefAll outperforms the top CASP8 QA servers in terms of per target Pearson correlation ρ. We were surprised at this result in the beginning and double-checked our experiments to make sure that the methods were indeed run on the same set of models with the same target structures as references and same method to calculate GDT_TS. We even thought about using this method in one of our QA servers in CASP9. We did not do it because some other teams could have discovered the same result and implemented it as their servers. Also we had developed other QA methods, including the SelCon method in this paper, that were slightly better than GRefAll based on our testing.
Even though GRefAll performs well on the CASP8 dataset, it can be improved. First, different weights may be given to different reference models. The predicted CASP models were usually generated from servers with different biases. Redundant models may be given unnecessarily high weights in computing the QA score. Secondly, not all predicted models need to be used as references and better strategies in choosing appropriate references can be developed.
2.3 A New Selective Consensus Method - SelCon
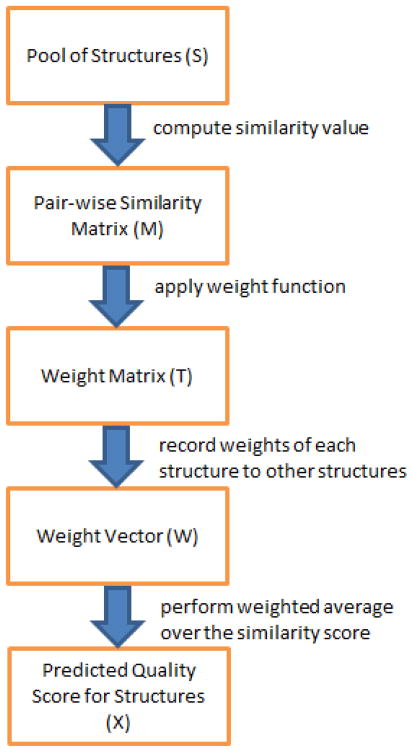
The new consensus method SelCon, which stands for Selective Consensus, differs from previous consensus methods in how to adaptively select and weight reference models based on structure similarities. Given a set of predicted models for a protein target, SelCon computes a QA score for each model based on its similarity to other models. The similarity measurement can be any commonly used metric, such as GDT_TS, TM-score, or Q-score. For each model, after computing its similarity to all other models, we perform a weighted averaging of the similarity measurements. The major steps of SelCon is shown in Fig. 1 and its pseudo-code in Algorithm 2.
Fig. 1.
Major steps of the proposed consensus method, SelCon.
Algorithm 2.
A New Selective Consensus Method, SelCon
| Require: Predicted protein models S = {si, 1 ≤ i ≤ p} and a weight function W. | ||
| For each si ∈ S | ||
| ||
| return QA score for each structure, X = {xi, 1 ≤ i ≤ p}. |
A key part of SelCon is the weight function W that determines the relative importance of the reference models. We have tried many different functions in our work and in this section present three that are simple, yet effective functions.
2.3.1 Sigmoid Weight Function
The sigmoid weight function, Sig(x), is defined as follows:
| (6) |
where x is the similarity measure between a pair of structures, sim(si, sj), and c is a constant, controlling the steepness of the sigmoid function. This function de-emphasizes similar models by giving them smaller weights. The idea comes from our observation that there are very similar or redundant models among the server predicted models and their effects should not be double-counted [37] [38]. Through experiments, we determine appropriate c values.
2.3.2 Step Weight Function
The step weight function is defined based on a step transition threshold θ as follows:
| (7) |
Again, argument x in the equation is the pair-wise similarity measure as in Eq. (6). The function value is 0 when the similarity between two models is greater than or equal to θ and is 1 otherwise. The result is that similar models, including redundant ones, are not counted when computing the consensus QA scores. Although the step weight function is simpler than the sigmoid weight function, our experimental results showed it can perform equally well or better. We tested different values of θ using CASP8 data in our experiments to find appropriate ones.
2.3.3 Band Weight Function
The band weight function is a generalization of the step weight function. In addition to discounting very similar structures, very dissimilar structures are also discounted. The band weight function is defined based on two threshold parameters, a and b, as follows:
| (8) |
The weight is 1 when the similarity of a pair of models is between a and b, and 0 otherwise. Again, we experimentally find appropriate values of a and b using CASP8 data. The performance is tested in CASP9 using previously unknown CASP9 data.
Although the idea of redundancy and outlier removal is widely used, designing an effective method to improve existing QA techniques is non-trivial, as demonstrated in extensive previous work. We have experimented with many different algorithms before coming up with the seemingly simple method SelCon, which was ranked at the top in CASP9. A detailed analysis of why and how redundancy removal improves the consensus approach is available in our previously published/accepted papers [37] and [38]. In this paper, a new redundancy and outlier removal method, i.e. a general framework of similarity-based weighting functions, with specialization as the sigmoidal, step, and band function, was devised to assign weights to reference models, which is different from existing algorithms in literature and is also different from the RefSelect algorithm in papers [37] and [38].
2.4 Determining SelCon Parameters
We used CASP8 targets as training set to determine appropriate parameters for the sigmoid weight function, step weight function, and band weight function of SelCon. Originally, CASP8 provided 128 targets. Some of them were canceled and the final list of targets was composed of 122 targets. Candidate models were submitted by different protein prediction servers and archived at CASP8 official website [12].
First, for the sigmoid weight function, we tried different c values in the range of [2, 50] on a subset of 23 randomly selected CASP8 targets. Experimental result shows that SelCon with the sigmoid weight function is slightly better than GRefALL. Larger c values are slightly better. For the step weight function, we tested different threshold values from 0 to 1 with increment 0.1. For the band weight function, we tested the lower and upper cutoffs from 0 to 1 with increment 0.1, respectively, and used the values that gave the best QA result in the rest of the experiments.
Table 2 compares the QA results of GRefAll, SelCon with step weight function (SelCon-GStepW), and SelCon with band weight function (SelCon-GBandW) on all 122 CASP8 targets. The targets are divided into 8 subsets based on the average pair-wise GDT_TS values of the predicted models of each target. The values in the table are the average QA Pearson correlations for each subset of targets.
TABLE 2.
QA results of GRefAll, SelCon with step weight function (SelCon-GStepW), and SelCon with band weight function (SelCon-GBandW) using 122 CASP8 targets. The targets are divided into 8 subsets based on the average pair-wise GDT_TS values of the predicted models.
| Target Subset | #targets | GRefAll | SelCon-GStepW | SelCon-GBandW |
|---|---|---|---|---|
| 0 ≤ GDT_TS < 0.1 | 1 | 0.7525 | 0.7547 | 0.8265 |
| 0.1 ≤ GDT_TS < 0.2 | 14 | 0.8026 | 0.8060 | 0.8449 |
| 0.2 ≤ GDT_TS < 0.3 | 15 | 0.9150 | 0.9158 | 0.9169 |
| 0.3 ≤ GDT_TS < 0.4 | 9 | 0.9459 | 0.9508 | 0.9527 |
| 0.4 ≤ GDT_TS < 0.5 | 29 | 0.9542 | 0.9619 | 0.9629 |
| 0.5 ≤ GDT_TS < 0.6 | 32 | 0.9782 | 0.9792 | 0.9804 |
| 0.6 ≤ GDT_TS < 0.7 | 18 | 0.9797 | 0.9811 | 0.9812 |
| 0.7 ≤ GDT_TS < 1 | 4 | 0.6266 | 0.6657 | 0.6658 |
The results show that SelCon-GBandW is better than SelCon-GStepW, which in turn is better than GRefAll. The improvement of SelCon-GBandW is significant on the harder targets, i.e., the subsets of targets with small average pair-wise GDT_TS values. The last subset (0.7 ≤ GDT_TS < 1) has low average QA values because there are only 4 targets in this subset and one of them is T0498, which gave very low QA values for all consensus methods: −0.4624, −0.3010, and −0.3010, for GRefAll, SelCon-GStepW, and SelCon-GBandW, respectively.
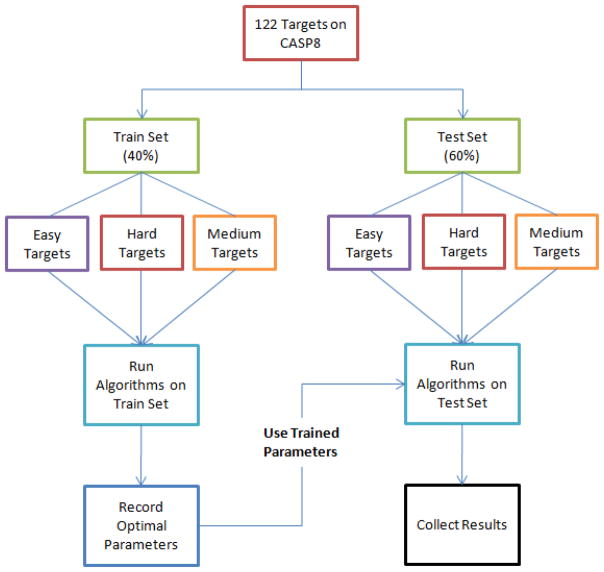
Because SelCon-GSigW, SelCon-GStepW and SelCon-GBandW have different optimal parameters for different classes of targets, we divided the CASP8 targets into three categories, Easy, Medium and Hard, based on the average pair-wise GDT_TS values of the predicted models of each target. Table 3 shows the classification criteria and the number of targets in each category. Then, we randomly selected 40% of CASP8 targets in each category as the training set to determine the best SelCon-GSigW, SelCon-GStepW and SelCon-GBandW parameters for each category. The other 60% targets formed the test set to test the performance of the algorithms with predetermined parameters. The experimental scheme is shown in Fig. 2.
TABLE 3.
The three subsets of 122 CASP8 targets.
| Group | # targets | Criteria: average pair-wise GDT_TS |
|---|---|---|
| Hard | 30 | (0, 0.3] |
| Medium | 38 | (0.3, 0.5] |
| Easy | 54 | (0.5, 1] |
Fig. 2.
Experimental scheme for SelCon-GStepW and SelCon-GBandW.
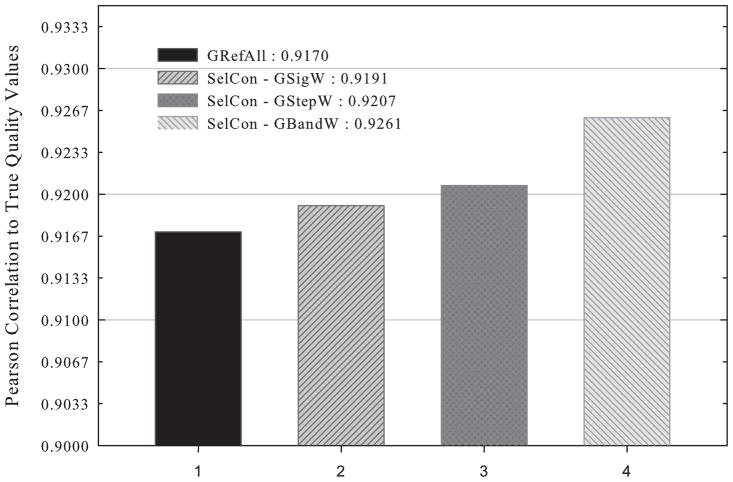
With the parameters determined based on the training set, we evaluated QA results of the three new algorithms, SelCon-GSigW, SelCon-GStepW, and SelCon-GBandW, on the test set and compared them with the result of RefAll, the total consensus method. Fig. 3 shows that all three new algorithms outperform GRefAll and SelCon-GBandW is the best.
Fig. 3.
QA results of GRefAll and three new algorithms, SelCon-GSigW, SelCon-GStepW, and SelCon-GBandW, on the randomly selected test set of CASP8 targets.
Table 4 compares the QA results of SelCon-GBandW with those of GRefAll and the top five QA servers in CASP8 on all 122 CASP8 targets, including their results for each official target category and overall average QA scores. In CASP8, the CASP organizers divided targets into 5 categories: free modeling (FM), which is the most difficult group to predict by current computational methods, fold recognition (FR), comparative modeling-hard (CM_H), comparative modeling-medium (CM_M), and comparative modeling-easy (CM_E). The numbers of targets in the modeling difficulty bins FM, FR, CM_H, CM_M, and CM_E are 7, 23, 22, 40, 30, respectively [42] [43]. Table 4 shows the overall QA score of GBandW is 0.9368, significantly better than the CASP8 top servers, and is also slightly better than GRefAll.
TABLE 4.
QA results of GRefAll, the top five QA servers in CASP8, and SelCon-GBandW on all 122 CASP8 targets.
| Official category | MULTICOM | Pcons | SAM-T08-MQAC | ModFOLDclust | QMEANclust | GRefAll | GBandW |
|---|---|---|---|---|---|---|---|
| FM | 0.7387 | 0.7806 | 0.8150 | 0.7280 | 0.8304 | 0.7981 | 0.8084 |
| FR | 0.7980 | 0.8473 | 0.8433 | 0.8549 | 0.7890 | 0.8657 | 0.8945 |
| CM_H | 0.8653 | 0.8623 | 0.8541 | 0.8699 | 0.8580 | 0.8806 | 0.8962 |
| CM_M | 0.9558 | 0.9599 | 0.9579 | 0.9629 | 0.9521 | 0.9726 | 0.9731 |
| CM_E | 0.9730 | 0.9845 | 0.9749 | 0.9763 | 0.9738 | 0.9856 | 0.9807 |
|
| |||||||
| Overall | 0.9029 | 0.9168 | 0.9144 | 0.9156 | 0.9021 | 0.9290 | 0.9368 |
3 Results and Discussion
In CASP9 in 2010, we implemented SelCon-GBandW in our automated QA server MUFOLD-WQA. CASP9 originally provided 129 targets, from T0515 to T0643. But later 12 targets were canceled and the remaining 117 targets were used for QA.
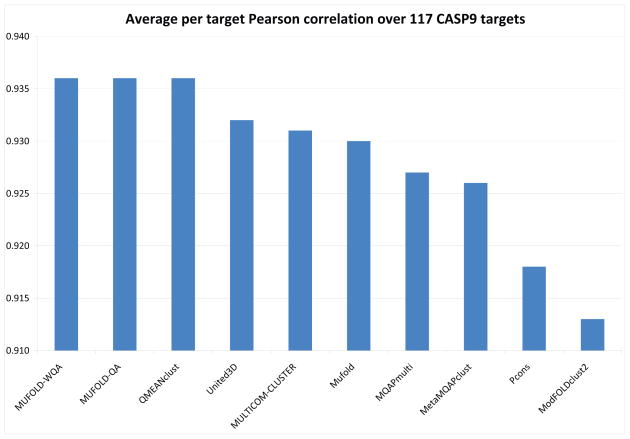
Fig. 4 shows the quality estimates of whole models based on per-target correlation between predicted model quality and GDT_TS of the QA servers participated in CASP9, which is consistent with the official QA assessment presentation at the CASP9 meeting [51]. The servers are ranked according to their average QA scores, i.e., Pearson correlations of estimated quality values to the true quality values per target. MUFOLD-WQA is tied with two other servers at the first place, with average per target Pearson’s correlation coefficient 0.936. The paired t-test results for MUFOLD-WQA against the other top 7 servers are 0.98, 0.95, 0.43, 0.26, 0.21, 0.05, 0.16, respectively, and thus the improvement of MUFOLD-WQA over them is not statistically significant based on paired t-test of p value 0.01. The p-values of MUFOLD-WQA against the rest of QA servers are less than 0.01.
Fig. 4.
Quality estimates of whole models (Pearson correlation coefficient) of top 10 QA servers on 117 targets in CASP9.
Table 5 shows the average Spearman’s correlations of the top CASP servers, in which MUFOLD-WQA is the first, although the difference between the servers is small.
TABLE 5.
Average Spearman’s rank correlations of the top 10 QA servers in CASP9.
| QA server | Spearman’s rank correlations |
|---|---|
| MUFOLD-WQA | 0.856 |
| MUFOLD-QA | 0.852 |
| QMEANclust | 0.850 |
| United3D | 0.839 |
| MULTICOM-cluster | 0.846 |
| Mufold | 0.840 |
| MQAPmulti | 0.841 |
| MetaMQAPclust | 0.852 |
| Pcons | 0.829 |
| ModFOLDclust2 | 0.832 |
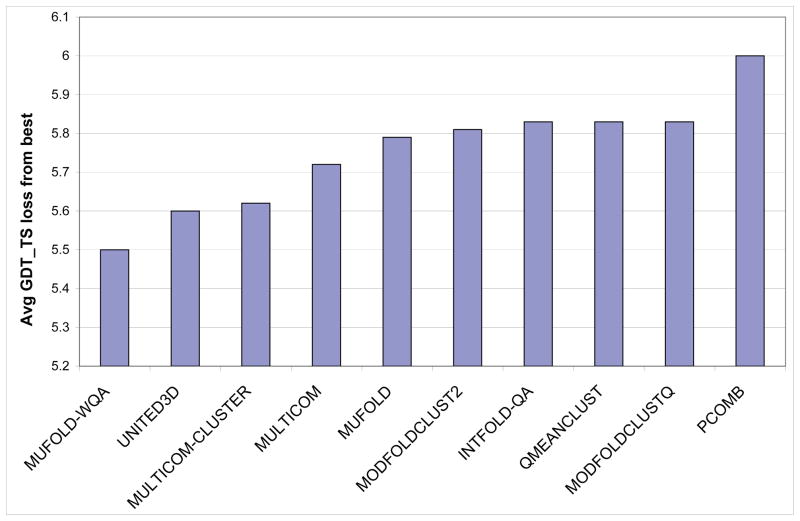
Next, we present the top-one-model selection result of MUFOLD-WQA. Fig. 5 shows our evaluation of the ability of CASP9 QA servers for selecting the best model, which is also consistent with the official QA assessment presentation at the CASP9 meeting [51]. The QA servers are ranked by the average GDT_TS loss from the best predicted models and the top 10 servers are provided in Fig. 5. Again, MUFOLD-WQA is ranked No. 1, although the difference of the top few servers is not statistically significant.
Fig. 5.
Comparison of top 10 CASP9 QA servers on top-one-model selection.
We also compared MUFOLD-WQA with the state-of-the-art single-model scoring functions and the Zhang server, one of the best automatic prediction servers in the past CASPs, on top-model selection. The average GDT_TS scores of the best models selected by MUFOLD-WQA were compared with seven scoring functions, OPUS-Ca, ModelEvaluator, DFIRE, RAPDF, OPUS-PSP, DFIRE2.0, and DOPE, as well as GRefAll. OPUS-CA is a knowledge-based potential function for Cα models [44]. ModelEvaluator is a machine-learning based scoring function using support vector machines and 1D and 2D structural features. DFIRE is a statistical energy function based on the reference state of distance-scaled, finite ideal gases [45]. DFIRE2.0 is an improved DFIRE that evaluates energy by ab initio refolding of fully unfolded terminal segments with secondary structures [46]. RAPDF is a residue-specific all-atom probability discriminatory function [47]. OPUS-PSP is an all-atom potential derived from side-chain packing [48]. Finally, DOPE is an atomic distance-dependent statistical potential calculated from a sample of native protein structures [49].
In Table 6, the first column, True Best, shows the average GDT_TS score of the true best model from the predicted pool for each target. The results show that MUFOLD-WQA is the best overall and its improvement over the other methods is statistically significant. On CASP9 targets, its overall value 0.5855 is significantly better than OPUS-PSP at 0.5418, which is the best among the scoring functions on CASP9 targets, an improvement of 7.4%. The overall average loss of MUFOLD-WQA from the true best model is 0.0547, 8.5%. MUFOLD-WQA also outperforms the first models of Zhang-Server.
TABLE 6.
Average GDT_TS of the top selected models of MUFOLD-WQA, various single-model scoring methods, and Zhang server, on CASP8 and CASP9 targets.
| (a) Results on 122 CASP8 targets | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| True Best | OPUS-Ca | ModelEvaluator | DFIRE | RAPDF | OPUS-PSP | DFIRE2.0 | DOPE | Zhang-Server_TS1 | MUFOLD-WQA |
| 0.6799 | 0.4985 | 0.5613 | 0.5627 | 0.5856 | 0.5239 | 0.5331 | 0.5196 | 0.6280 | 0.6292 |
| (b) Results on 117 CASP9 targets | |||||||||
| True Best | OPUS-Ca | ModelEvaluator | DFIRE | RAPDF | OPUS-PSP | DFIRE2.0 | DOPE | Zhang-Server_TS1 | MUFOLD-WQA |
| 0.6402 | 0.4430 | 0.4578 | 0.4714 | 0.4552 | 0.5418 | 0.5080 | 0.5149 | 0.5746 | 0.5855 |
Finally, MUFOLD-WQA was evaluated against quality measures MaxSub [52], TM-score [36], Q-score [53], [54], S-score [39], [40] and RMSD. MaxSub and TM-score of each CASP9 model to native were calculated using software TM-score [36] while other three used our in-house program. We computed per-target Pearson correlation of CASP9 QA servers against these five scores and then for each score selected 10 servers with the highest average correlation. Table 7 provides the names of the top 10 servers under different measures and the corresponding average correlation sorted in decreasing order of correlation. It indicates that out of the top 10 CASP9 QA servers that have higher correlation than all other QA methods in CASP9, only one server, i.e. MODFOLDCLUST2, is ranked top, if RMSD is used as model quality measure. In addition, MUFOLD-WQA is among the tops under the quality measures MaxSub, TM-score and S-score. If a QA server is ranked based on the times it is among top 10, then out of 46 CASP9 QA servers, MUFOLD-WQA is only inferior to MUFOLD-QA, MQAPMULTI, MULTICOM-CLUSTER, METAMQAPCLUST and QMEANCLUST, which are atop four times.
TABLE 7.
Top 10 QA servers and corresponding average per-target Pearson coorelations under five model quality measures MaxSub, TM-score, Q-score, S-score and RMSD on 117 CASP9 targets. The servers are ordered based on their average correlations.
| Ranking | MaxSub | TM-score | Q-score | S-score | RMSD |
|---|---|---|---|---|---|
| 1 | UNITED3D 0.9022 |
MUFOLD-QA 0.9145 |
MODFOLDCLUST2 0.8984 |
AOBA 0.6955 |
MODCHECK-J2 0.7809 |
| 2 | MUFOLD-WQA 0.8985 |
QMEANCLUST 0.914 |
INTFOLD-QA 0.8963 |
MULTICOM 0.6938 |
SIFT_SA 0.7529 |
| 3 | QMEANCLUST 0.8977 |
MULTICOM-CLUSTER 0.9115 |
MUFOLD 0.8918 |
QMEANCLUST 0.6968 |
MODFOLDCLUSTQ 0.6975 |
| 4 | MUFOLD-QA 0.8962 |
MUFOLD 0.9104 |
MUFOLD-QA 0.8897 |
METAMQAPCLUST 0.686 |
MODFOLDCLUST2 0.6822 |
| 5 | MULTICOM-CLUSTER 0.8916 |
UNITED3D 0.9103 |
QMEANCLUST 0.8875 |
MUFOLD-QA 0.6851 |
INTFOLD-QA 0.6787 |
| 6 | METAMQAPCLUST 0.8906 |
MUFOLD-WQA 0.9096 |
MULTICOM-CLUSTER 0.8866 |
MODCHECK-J2 0.6846 |
AOBA 0.678 |
| 7 | PCONS 0.889 |
MQAPMULTI 0.9071 |
AOBA 0.8851 |
MQAPMULTI 0.6843 |
SPLICER 0.6679 |
| 8 | MUFOLD 0.8888 |
MODFOLDCLUST2 0.9022 |
MQAPMULTI 0.8829 |
MULTICOM-REFINE 0.6821 |
DISTILL_NNPIF 0.6613 |
| 9 | MQAPMULTI 0.8871 |
INTFOLD-QA 0.9017 |
METAMQAPCLUST 0.8812 |
MULTICOM-CLUSTER 0.682 |
PCOMB 0.6544 |
| 10 | PCONSM 0.8847 |
METAMQAPCLUST 0.9009 |
MODCHECK-J2 0.8796 |
MUFOLD-WQA 0.6806 |
SPLICER_QA 0.6541 |
4 Conclusion
In this paper, we presented a new consensus method SelCon with various reference selection functions for QA in protein structure prediction and selection. The method is simple, yet effective. Experimental results using CASP targets showed that the new method outperforms previous consensus methods and scoring/potential functions. The adaptive consensus algorithm with band weight function, GBandW, is robust and performed well, not only in correlation-based QA, but also in top-model selection. In the global structure QA category of CASP9, the MUFOLD-WQA that implemented GBandW was the top performer, finishing as the #1 in the correlation-based QA and #1 in top-model selection among all CASP9 QA servers and manual QA predictions.
In the future work, we will further improve the consensus methods for QA and model selection. The CASP data sets consist of high-quality models generated from some of the best prediction servers, a situation especially suitable for consensus methods. Without a pool of high-quality models, existing consensus methods may not perform as well. A promising direction is to develop new methods to combine the strengths of scoring/energy functions and consensus methods to improve the QA and selection result on collections of commonly available prediction models, e.g., those generated by individual prediction servers such as Rosetta. We plan to experiment with SelCon on non-CASP models, such as I-TASSER models and Rosetta decoys. With better understanding of conditions under which the consensus approach achieves good performance, SelCon could be improved to perform well outside CASP. Another issue of consensus methods is the high computational overhead in computing pair-wise similarity measures, which makes them impractical on large data set, e.g., thousands of models. Efficient algorithms will be developed to address this problem.
Acknowledgments
This work has been supported by National Institutes of Health Grant R21/R33-GM078601.
Footnotes
The work was performed at the University of Missouri-Columbia.
Contributor Information
Qingguo Wang, Email: qwp4b@mail.missouri.edu, Department of Computer Science, University of Missouri, Columbia, Missouri 65211.
Kittinun Vantasin, Email: kvr43@mail.missouri.edu, Department of Computer Science, University of Missouri, Columbia, Missouri 65211.
Dong Xu, Email: xudong@missouri.edu, Department of Computer Science and the Christopher S. Bond Life Sciences Center, University of Missouri, Columbia, Missouri 65211.
Yi Shang, Email: shangy@missouri.edu, Department of Computer Science, University of Missouri, Columbia, Missouri 65211.
References
- 1.Soding J. Protein homology detection by HMM-HMM comparison. Bioinformatics. 2005;21(7):951–60. doi: 10.1093/bioinformatics/bti125. [DOI] [PubMed] [Google Scholar]
- 2.Peng J, Xu J. A multiple-template approach to protein threading. Proteins. 2011 doi: 10.1002/prot.23016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234(3):779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- 4.Arnold K, Bordoli L, Kopp J, Schwede T. The SWISS-MODEL workspace: a web-based environment for protein structure homology modelling. Bioinformatics. 2006;22(2):195–201. doi: 10.1093/bioinformatics/bti770. [DOI] [PubMed] [Google Scholar]
- 5.Soding J, Biegert A, Lupas AN. The HHpred interactive server for protein homology detection and structure prediction. Nucleic Acids Res. 2005;33(Web Server issue):W244–8. doi: 10.1093/nar/gki408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kim DE, Chivian D, Baker D. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Research. 2004;32(suppl 2):W526–W31. doi: 10.1093/nar/gkh468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baker D, Sali A. Protein Structure Prediction and Structural Genomics. Science. 2001;294 (5540):93–96. doi: 10.1126/science.1065659. [DOI] [PubMed] [Google Scholar]
- 8.Zhang Y. Template-based modeling and free modeling by I-TASSER in CASP7. Proteins: Structure, Function, and Bioinformatics. 2007;S8:108–117. doi: 10.1002/prot.21702. [DOI] [PubMed] [Google Scholar]
- 9.Floudas C. Computational methods in protein structure prediction. Biotechnology and Bioengineering. 2007;97:207–213. doi: 10.1002/bit.21411. [DOI] [PubMed] [Google Scholar]
- 10.Zhang J, Wang Q, Barz B, He Z, Kosztin I, Shang Y, Xu D. MUFOLD: A New Solution for Protein 3D Structure Prediction. Proteins: Structure, Function, and Bioinformatics. 2009;78:1137–1152. doi: 10.1002/prot.22634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cozzetto D, Kryshtafovych A, Tramontano A. Critical assessment of methods of protein structure prediction-Round VIII. Proteins: Structure, Function, and Bioinformatics. 2009;77:1–4. doi: 10.1002/prot.22589. [DOI] [PubMed] [Google Scholar]
- 12.Protein Structure Prediction Center [Internet] Protein Structure Prediction Center; c1994–2010. Available from: http://predictioncenter.org/index.cgi/ [Google Scholar]
- 13.Cozzetto D, Kryshtafovych A, Ceriani M, Tramontano A. Assessment of predictions in the model quality assessment category. Proteins: Structure, Function, and Bioinformatics. 2007;69:175–183. doi: 10.1002/prot.21669. [DOI] [PubMed] [Google Scholar]
- 14.Cozzetto D, Kryshtafovych A, Tramontano A. Evaluation of casp8 model quality predictions. Proteins: Structure, Function, and Bioinformatics. 2009;77:157–166. doi: 10.1002/prot.22534. [DOI] [PubMed] [Google Scholar]
- 15.Ginalski K, Elofsson A, Fischer D, Rychlewski L. 3d-jury a simple approach to improve protein structure predictions. Bioinformatics. 2003;19:1015–1018. doi: 10.1093/bioinformatics/btg124. [DOI] [PubMed] [Google Scholar]
- 16.Zemla A. Lga: a method for finding 3d similarities in protein structures. Nucleic Acids Research. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathann S, Karplus M. Charmm a program for macromolecular energy, minimization, and dynamics calculations. Journal of Computational Chemistry. 1982;4:187–217. [Google Scholar]
- 18.Duan Y, Wu C, Chowdhury S, Lee MC, Xiong G, Zhang W, Yang R, Cieplak P, Luo R, Lee T, Caldwell J, Wang J, Kollman P. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. Journal of Computational Chemistry. 2003;24(16):1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 19.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical treatment of solvation for molecular mechanics and dynamics. Journal of The American Chemical Society. 1990;112:6127–6129. [Google Scholar]
- 20.Duan Y, Kollman PA. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science. 1998;282:740–744. doi: 10.1126/science.282.5389.740. [DOI] [PubMed] [Google Scholar]
- 21.Lu H, Skolnick J. A distance-dependent atomic knowledge-based potential for improved protein structure selection. Proteins: Structure, Function, and Bioinformatics. 2001;44:223–232. doi: 10.1002/prot.1087. [DOI] [PubMed] [Google Scholar]
- 22.Gohlkea H, Hendlicha M, Klebe G. Knowledge-based scoring function to predict protein-ligand interactions. Journal of Molecular Biology. 2000;295:337–356. doi: 10.1006/jmbi.1999.3371. [DOI] [PubMed] [Google Scholar]
- 23.Jones DT, Taytor WR, Thornton JM. A new approach to protein fold recognition. Nature. 1992;358:86–89. doi: 10.1038/358086a0. [DOI] [PubMed] [Google Scholar]
- 24.Zhou Y, Zhou H, Zhang C, Liu S. What is a desirable statistical energy functions for proteins and how can it be obtained? Cell Biochemistry and Biophysics. 2006;46:165–174. doi: 10.1385/cbb:46:2:165. [DOI] [PubMed] [Google Scholar]
- 25.Qiu J, Sheffler W, Baker D, Noble WS. Ranking predicted protein structures with support vector regression. Proteins: Structure, Function, and Bioinformatics. 2007;71:1175–1182. doi: 10.1002/prot.21809. [DOI] [PubMed] [Google Scholar]
- 26.Wang Z, Tegge AN, Cheng J. Evaluating the absolute quality of a single protein model using structural features and support vector machines. Proteins: Structure, Function, and Bioinformatics. 2008;75:638–647. doi: 10.1002/prot.22275. [DOI] [PubMed] [Google Scholar]
- 27.Shortle D, Simons KT, Baker D. Clustering of low-energy conformations near the native structures of small proteins. Proceedings of the National Academy of Sciences of the United States of America. 1998;95:11158–11162. doi: 10.1073/pnas.95.19.11158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Betancourt MR, Skolnick J. Finding the needle in a haystack: educing native folds from ambiguous ab initio protein structure predictions. Journal of Computational Chemistry. 2000;22:339–353. [Google Scholar]
- 29.Wang Q, Shang Y, Xu D. A new clustering-based method for protein structure selection. IEEE International Joint Conference on Neural Networks.2008. [Google Scholar]
- 30.Zhang Y, Skolnick J. Spicker: a clustering approach to identify near-native protein folds. Journal of Computational Chemistry. 2004;25:865–871. doi: 10.1002/jcc.20011. [DOI] [PubMed] [Google Scholar]
- 31.Venclovas C, Margelevicius M. Comparative modeling in casp6 using consensus approach to template selection, sequence-structure alignment, and structure assessment. Proteins: Structure, Function, and Bioinformatics. 2005;7:99–105. doi: 10.1002/prot.20725. [DOI] [PubMed] [Google Scholar]
- 32.Benkert P, Tosatto SCE, Schwede T. Global and local model quality estimation at casp8 using the scoring functions qmean and qmeanclust. Proteins: Structure, Function, and Bioinformatics. 2009;77:173–180. doi: 10.1002/prot.22532. [DOI] [PubMed] [Google Scholar]
- 33.Benkert P, Tosatto SCE, Schomburg D. QMEAN: A comprehensive scoring function for model quality assessment. Proteins: Structure, Function, and Bioinformatics. 2008;71:261–277. doi: 10.1002/prot.21715. [DOI] [PubMed] [Google Scholar]
- 34.Cheng J, Wang Z, Tegge AN, Eickholt J. Prediction of global and local quality of casp8 models by MULTICOM series. Proteins: Structure, Function, and Bioinformatics. 2009;77:181–184. doi: 10.1002/prot.22487. [DOI] [PubMed] [Google Scholar]
- 35.Moult J, Fidelis K, Kryshtafovych A, Rost B, Hubbard T, Tramontano A. Critical assessment of methods of protein structure prediction - round VII. Proteins: Structure, Function, and Bioinformatics. 2007;69:3–9. doi: 10.1002/prot.21767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang Y, Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins: Structure, Function, and Bioinformatics. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- 37.Wang Q, Shang Y, Xu D. Protein structure selection based on consensus. Proc. IEEE Congress on Evolutionary Computation; Barcelona, Spain. July 2010.2010. [Google Scholar]
- 38.Wang Q, Shang Y, Xu D. Improving Consensus Approach for Protein Structure Selection by Removing Redundancy. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2011 doi: 10.1109/TCBB.2011.75. (in press) [DOI] [PubMed] [Google Scholar]
- 39.Larsson P, Skwark MJ, Wallner B, Elofsson A. Assessment of global and local model quality in casp8 using pcons and proq. Proteins: Structure, Function, and Bioinformatics. 2009;77:167–172. doi: 10.1002/prot.22476. [DOI] [PubMed] [Google Scholar]
- 40.McGuffin LJ. Prediction of global and local model quality in casp8 using the MODFOLD server. Proteins: Structure, Function, and Bioinformatics. 2009;77:185–190. doi: 10.1002/prot.22491. [DOI] [PubMed] [Google Scholar]
- 41.Archie JG, Paluszewski M, Karplus K. Applying undertaker to quality assessment. Proteins: Structure, Function, and Bioinformatics. 2009;77:191–195. doi: 10.1002/prot.22508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shi S, Pei J, Sadreyev RI, Kinch LN, Majumda I, Tong J, Cheng H, Kim BH, Grishin NV. Analysis of casp8 targets, predictions, and assessment methods. Database (Oxford) 2009:Article ID: bap003. doi: 10.1093/database/bap003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tress ML, Ezkurdia I, Richardson JS. Target domain definition and classification in casp8. Proteins: Structure, Function, and Bioinformatics. 2009;77:10–17. doi: 10.1002/prot.22497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wu Y, Lu M, Chen M, Li J, Ma J. Opus-cα: A knowledge-based potential function requiring only c-alpha positions. Protein Sci. 2007;16:1449–1463. doi: 10.1110/ps.072796107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhou H, Zhou Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 2002;11:2714–2726. doi: 10.1110/ps.0217002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yang Y, Zhou Y. Ab initio folding of terminal segments with secondary structures reveals the fine difference between two closely related all-atom statistical energy functions. Protein Science. 2008;17:1212–1219. doi: 10.1110/ps.033480.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Samudrala R, Moult J. An all-atom distance-dependent conditional probability discriminatory function for protein structure prediction. Journal of Molecular Biology. 1998;275:895–916. doi: 10.1006/jmbi.1997.1479. [DOI] [PubMed] [Google Scholar]
- 48.Lu M, Dousis AD, Ma J. Opus-psp: An orientation-dependent statistical all-atom potential derived from side-chain packing. Journal of Molecular Biology. 2008;273:283–298. doi: 10.1016/j.jmb.2007.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Shen M, Sali A. Statistical potential for assessment and prediction of protein structures. Protein Sci. 2006;15:2507–2524. doi: 10.1110/ps.062416606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Protein Structure Prediction Center; 1994–2010. 9th community wide experiment on the critical assessment of techniques for protein structure prediction [Internet] Available from: http://predictioncenter.org/casp9/qaanalysis.cgi/ [Google Scholar]
- 51.Kryshtafovych A, Tramontano A, Fidelis K, Moult J. Automatic evaluation of the QA category [Internet] 2011 Available from: http://predictioncenter.org/casp9/doc/presentations/CASP9QA.pdf.
- 52.Siew N, Elofsson A, Rychlewski L, Fischer D. MaxSub: an automated measure for the assessment of protein structure prediction quality. Bioinformatics. 2000;16:776785. doi: 10.1093/bioinformatics/16.9.776. [DOI] [PubMed] [Google Scholar]
- 53.Ben-David M, Noivirt-Brik O, Paz A, Prilusky J, Sussman JL, Levy Y. Assessment of CASP8 structure predictions for template free targets. Proteins: Structure, Function, and Bioinformatics. 2009;77(s9):50–65. doi: 10.1002/prot.22591. [DOI] [PubMed] [Google Scholar]
- 54.McGuffin LJ, Roche DB. Rapid model quality assessment for protein structure predictions using the comparison of multiple models without structural alignments. Bioinformatics. 2010;26(2):182–188. doi: 10.1093/bioinformatics/btp629. [DOI] [PubMed] [Google Scholar]