Coping with time scales in disease systems analysis: application to bone remodeling

Abstract

In this study we demonstrate the added value of mathematical model reduction for characterizing complex dynamic systems using bone remodeling as an example. We show that for the given parameter values, the mechanistic RANK-RANKL-OPG pathway model proposed by Lemaire et al. (J Theor Biol 229:293–309, 2004) can be reduced to a simpler model, which can describe the dynamics of the full Lemaire model to very good approximation. The response of both models to changes in the underlying physiology and therapeutic interventions was evaluated in four physiologically meaningful scenarios: (i) estrogen deficiency/estrogen replacement therapy, (ii) Vitamin D deficiency, (iii) ageing, and (iv) chronic glucocorticoid treatment and its cessation. It was found that on the time scale of disease progression and therapeutic intervention, the models showed negligible differences in their dynamic properties and were both suitable for characterizing the impact of estrogen deficiency and estrogen replacement therapy, Vitamin D deficiency, ageing, and chronic glucocorticoid treatment and its cessation on bone forming (osteoblasts) and bone resorbing (osteoclasts) cells. It was also demonstrated how the simpler model could help in elucidating qualitative properties of the observed dynamics, such as the absence of overshoot and rebound, and the different dynamics of onset and washout.

Introduction

The objective of disease system analysis is to characterize and predict the status of biological systems under physiological and pathophysiological conditions as well as the impact of therapeutic interventions [1–3]. Models characterizing this dynamic behavior can be established at different levels of complexity, ranging from data driven and descriptive to completely mechanistic approaches (systems pharmacology) [3, 4]. Descriptive approaches usually start at a clinical observation level and become increasingly more complex in order to understand the system better, whereas systems pharmacology approaches start at the molecular level and provide a full description of the pathways involved. While descriptive models may not predict the clinical response beyond the data on which they were established, completely mechanistic approaches may face problems with the identifiability of model parameters [3, 4]. To obtain a sufficient understanding of a biological system, its dynamics, and the impact of therapeutic interventions, a compromise between the descriptive and the systems approach is frequently needed. This compromise results in mechanisms-based disease system models, which strive to characterize a system’s behavior rather than its complexity [5].

One important challenge to be met when developing mechanism-based disease system models is the appropriate handling of the different time scales present in biological systems. While processes on the molecular level, such as receptor binding or enzymatic reactions, are usually fast (within milliseconds), it can take months or even years before clinical signs and symptoms of chronic, progressive diseases become manifest. The design of mechanism-based disease system models consequently relies on a sufficient understanding of the relative speeds of the underlying (patho)physiological processes. Acquiring this information requires familiarity with various mathematical analysis techniques including dimensional analysis, dynamical systems analysis, and mathematical model reduction approaches (i.e., singular perturbation theory (see, e.g. [6]). When applying these techniques for the analysis of complex dynamic systems, the relative importance and speed of the different processes involved can be determined. Information on the system’s dynamic properties thus obtained can then be used to derive simpler models. Such reduced models yield dynamic properties that are very similar to those of completely mechanistic models but require the identification of fewer parameters. They also yield important insights into the impact of different parameters on the full system and often explicit expressions and quantitative estimates for drug-, system-, and/or disease-specific characteristics, such as clearance or the area under the curve of different compounds [6, 7].

The objective of this article is to demonstrate the added value of mathematical model reduction for establishing mechanism-based disease system models, using bone remodeling as an example. Bone remodeling is a physiological process that allows continuous renewal and repair of bone structure [8]. It is accomplished by groups of osteoblasts (bone forming cells) and osteoclasts (bone resorbing cells), which closely collaborate in so-called basic multicellular units (BMU) [9, 10]. The interaction between osteoblasts and osteoclasts is highly regulated and provides the basis for a temporally and spatially coordinated bone remodeling process. Disturbances in the regulation of these cell–cell interactions can result in pathophysiological conditions, such as osteoporosis [11].

The RANK-RANKL-OPG signaling pathway is one of the key players involved in the osteoblast-osteoclast regulation [12]. This regulatory pathway consists of three main components: (i) the receptor activator of nuclear factor κB (RANK), which is expressed on the surface of osteoclasts, (ii) the RANK ligand (RANKL), a polypeptide expressed on the surface of osteoblasts, and (iii) osteoprotegerin (OPG), a soluble decoy receptor for RANKL released by osteoblasts [12]. To date, multiple conceptual bone cell interaction models have been established [10, 13–18] some of which specifically incorporate the RANK-RANKL-OPG pathway [10, 13, 16]. Of these conceptual frameworks, Lemaire et al. were the first to propose a model, where the interaction between the different types of bone cells within a BMU (responding osteoblasts (R), active osteoblasts (B), and active osteoclasts (C)) is mediated by the RANK-RANKL-OPG regulatory pathway [13].

It will be shown how the mechanistic bone cell interaction model proposed by Lemaire et al. [13] may be mathematically reduced for the parameter values quoted in [13] and for physiologically and therapeutically relevant time scales. The dynamic properties of the full and the reduced model will then be compared using simulations, in which the response of both models to changes in physiological states and/or therapeutic interventions will be evaluated using physiologically meaningful scenarios. Estrogen (deficiency and replacement therapy) will be used as the primary example. In addition, the effects of Vitamin D, ageing, and chronic glucocorticoid treatment on the bone cell dynamics will be evaluated. The reduced model will then be used to obtain answers to questions about qualitative properties of response curves, such as the possibility of overshoot and rebound. Finally, we will conclude with a discussion of the advantages and limitations of mathematical model reduction as well as its implications for clinical situations.

Materials and methods

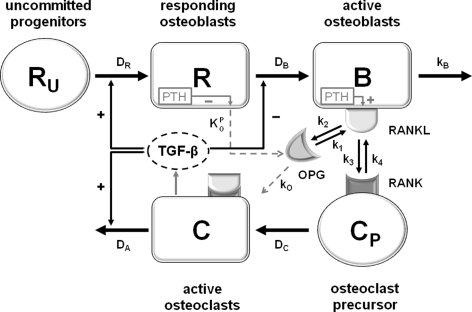
In the conceptual bone cell interaction model proposed by Lemaire et al. [13], both the osteoblastic and the osteoclastic cell line consist of cells at different levels of maturation (cf. Fig. 1). Responding osteoblasts (R) are recruited from a large pool of uncommitted osteoblast progenitor cells (R _u), which then differentiate into active, bone-forming osteoblasts (B). Active, bone-removing osteoclasts (C), on the other hand, are recruited from a pool of osteoclast progenitor cells (C _P) upon stimulation of RANK by its ligand. In addition to this receptor-mediated osteoblast-osteoclast interaction, a number of local and systemic hormones play a role in the regulation of bone remodeling. Of these factors, transforming growth factor beta (TGF-β) and parathyroid hormone (PTH) have been incorporated into the Lemaire model [13]. TGF-β is released from the bone by active osteoclasts and promotes multiple mechanisms of action: (1) it stimulates the recruitment of responding osteoblasts, (2) it inhibits the differentiation of responding osteoblasts into active osteoblasts, and (3) it stimulates the apoptosis of active osteoclasts. PTH, on the other hand, promotes its effect on osteoblasts and osteoclasts through the RANK-RANKL-OPG pathway, where it stimulates the expression of RANKL and suppresses the secretion of OPG.

Fig. 1.

Schematic illustration of the bone-cell interaction model. R _u uncommitted osteoblast progenitor, R responding osteoblast, B active osteoblast responsible for bone formation, C _p osteoclast progenitor, C active osteoclast responsible for bone resorption, PTH parathyroid hormone, TGF-β transforming growth factor-β, OPG osteoprotegerin, RANK receptor activator of NF-κB, RANKL receptor activator of NF-κB ligand. RANK-RANKL-OPG regulatory pathway: RANKL binds to RANK and promotes osteoclast differentiation, while OPG inhibits this differentiation by binding RANKL. Definitions and values of the rate constants are provided in Tables 1 and 2. This figure and its legend are taken from Ref. [13] and were slightly modified

Mathematically, this scheme of reactions translates into the following set of differential equations:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} \frac{{{\text{d}}R}}{{{\text{d}}t}} = D_{R} \pi_{C} (C) - \frac{{D_{B} }}{{\pi_{C} (C)}}R \hfill \\ \frac{{{\text{d}}B}}{{{\text{d}}t}} = \frac{{D_{B} }}{{\pi_{C} (C)}}R - k_{B} B \hfill \\ \frac{{{\text{d}}C}}{{{\text{d}}t}} = D_{C} \pi_{L} (R,B) - D_{A} \pi_{C} (C)C \hfill \\ \end{gathered} \right., $$\end{document} 1

where D _R represents the differentiation rate of osteoblast progenitors, D _B the differentiation rate of responding osteoblasts, D _C the differentiation rate of osteoclast precursors, π _C(C) the TGF-β receptor occupancy, and π _L(R,B) the RANK receptor occupancy. While π _C(C) is dependent on the amount of TGF-β released from bone by active osteoclasts, π _L(R,B) is determined by the amount of RANKL attached to the surface of active osteoblasts (K ^P_L) and the OPG production rate of responding osteoblasts (K ^P_O) as shown in Eqs. 2–4.

Since binding of TGF-β to its receptor is faster than any changes in the active osteoclast population, π _C(C) can be expressed as a function of C, i.e.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{C} (C) = \frac{{C + f_{0} C^{s} }}{{C + C^{s} }} = f_{0} \left( {1 + \frac{{1 - f_{0} }}{{f_{0} }}\frac{C}{{C + C^{s} }}} \right) \left( {0 \, < f_{0} < { 1}} \right) $$\end{document} 2

where f ₀ equals the minimum receptor occupancy and C ^s is half the value of C necessary to obtain maximum TGF-β receptor occupancy (cf. Eq. 2). For the dependence of π _L on R and B we have the expression,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{L} (R,B) = \frac{\alpha B}{1 + \beta R}\quad\left( {\alpha > 0,\beta > 0} \right) $$\end{document} 3

where α and β can be computed from equation (4) in which π _P represents the fraction of occupied PTH receptors,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \alpha = \frac{{k_{3} }}{{k_{4} + k_{3} K}}K_{L}^{P} \pi_{P} \;{\text{and}}\;\beta = \frac{{k_{1} }}{{k_{2} \cdot k_{O} }}\frac{{k_{4} }}{{k_{4} + k_{3} K}}\frac{{K_{O}^{P} }}{{\pi_{P} }}. $$\end{document} 4

The impact of changes in the underlying physiology or therapeutic interventions is reflected in changes of some of the parameters in Eqs. 1–4. Specifically, estrogen affects \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ K_{O}^{P} $$\end{document} and hence β, Vitamin D affects \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{P} $$\end{document} and hence α and β, ageing affects C ^s and hence \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{C} \left( C \right) $$\end{document}, and glucocorticoid treatment affects D _R. As a result, physiological processes and therapeutic interventions will cause these parameters to change with time (cf. Evaluation of model behavior).

We assume that initially, the values of all the parameters are those given by Lemaire et al. [13] (cf. Table 1), and that the system starts from the baseline values R ₀, B ₀, and C ₀ for those parameters:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R(0) = R_{0} ,\quad B(0) = B_{0} ,\quad C(0) = C_{0} . $$\end{document} 5

Table 1.

Parameter values provided by Lemaire et al. [13]

Symbol	Unit	Value	Description
D R	pM day−1	7 × 10−4	Differentiation rate of osteoblast progenitors
D B	day−1	0.7	Differentiation rate of responding osteoblasts
k B	day−1	0.189	Elimination rate of active osteoblasts
D C	pM day−1	2.1 × 10−3	Differentiation rate of osteoclast precursors
D A	day−1	0.7	Osteoclast apoptosis rate due to TGF-β
f 0	Dimensionless	0.05	Positive constant characterizing the minimum TGF-β receptor occupancy
C s	pM	5 × 10−3	About half the value of C to get maximum TGF-β receptor occupancy
k 1	pM−1 day−1	10−2	Rate of OPG-RANKL binding
k 2	day−1	10	Rate of OPG-RANKL dissociation
k 3	pM−1 day−1	5.8 × 10−4	Rate of RANK-RANKL binding
k 4	day−1	1.7 × 10−2	Rate of RANK-RANKL dissociation
k 5	pM−1 day−1	0.02	Rate of PTH binding to its receptor
k 6	day−1	3	Rate of PTH dissociation from its receptor
K	pM	10	Fixed concentration of RANK
K PL	pM/pM cells	3 × 106	Maximum number of RANKL attached to the cell surface of each active osteoblast
k O	day−1	0.35	Elimination rate of OPG
K PO	pM day−1/pM cells	2 × 105	Minimum OPG production rate per responding osteoblast
I P	pM day−1	0	Rate of PTH administration
S P	pM day−1	250	Rate of PTH synthesis
k P	day−1	86	Rate of PTH elimination

Plainly, R ₀, B ₀, and C ₀ satisfy the algebraic equations

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} D_{R} \pi_{C} (C_{0} ) - \frac{{D_{B} }}{{\pi_{C} (C_{0} )}}R_{0} = 0 \hfill \\ \frac{{D_{B} }}{{\pi_{C} (C_{0} )}}R_{0} - k_{B} B_{0} = 0 \hfill \\ D_{C} \frac{{\alpha B_{0} }}{{1 + \beta R_{0} }} - D_{A} \pi_{C} (C_{0} )C_{0} = 0 \hfill \\ \end{gathered} \right. , $$\end{document} 6

in which the parameters that change with time are taken at their initial values, i.e., their values at time t = 0. The respective values of the parameters used in Eqs. 1–6, as given by Lemaire et al. [13], are presented in Table 1. Numeric values for the baseline concentrations are computed in Appendix A:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R_{0} = 1.82 \times 10^{ - 4}\,{\text{pM}},\quad B_{0} = 1.58 \times 10^{ - 3}\,{\text{pM}},\quad C_{0} = 3.285 \times 10^{ - 3}\,{\text{pM}} . $$\end{document} 7

Mathematical model reduction

When attempting to gain insight into the dynamics of the system of Eq. 1 and identify its characteristic properties, it is important to assess the relative importance of the individual terms in the three equations and the relative speed and time scales of the different processes involved. In order to do so, we cast the system into dimensionless form. Using the baseline values R ₀, B ₀ and C ₀ as reference values for the concentrations, we put

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ x = \frac{R}{{R_{0} }},\quad y = \frac{B}{{B_{0} }},\quad z = \frac{C}{{C_{0} }} $$\end{document} 8

and we introduce the dimensionless function related to π _C(C):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{z} (z) = \frac{{z + f_{0} z^{s} }}{{z + z^{s} }}\quad {\text{where}}\quad z^{s} = \frac{{C^{s} }}{{C_{0} }}. $$\end{document} 9

In terms of these new variables, the system (1) becomes

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} \frac{{{\text{d}}x}}{{{\text{d}}t}} = \frac{{D_{R} }}{{R_{0} }}\pi_{z} (z) - D_{B} \frac{x}{{\pi_{z} (z)}} \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}t}} = D_{B} \frac{{R_{0} }}{{B_{0} }}\frac{x}{{\pi_{z} (z)}} - k_{B} y \hfill \\ \frac{{{\text{d}}z}}{{{\text{d}}t}} = D_{C} \frac{{B_{0} }}{{C_{0} }}\frac{\alpha y}{{1 + \beta R_{0} x}} - D_{A} \pi_{z} (z)z \hfill \\ \end{gathered} \right. $$\end{document} 10

and the baseline is given by

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ x(0) = y(0) = z(0) = 1. $$\end{document} 11

For the sake of transparency, we derive the Reduced Model for the estrogen scenario, where β is the only parameter that changes with time, i.e. β = β(t). We denote the initial value of β by β ₀, i.e. β(0) = β ₀, and write

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \beta (t) = \beta_{0} f(t),\quad {\text{where}}\quad f\left( 0 \right) \, = { 1}. $$\end{document} 12

For the other scenarios we obtain the same Reduced Model. For these scenarios the derivation is very similar and we shall not reproduce it here.

We use the three equations in (6) to eliminate the baseline concentrations B ₀ and C ₀ and the parameter α, which is constant in this scenario. This results in the system

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} \frac{{{\text{d}}x}}{{{\text{d}}t}} = \frac{{D_{R} }}{{\pi_{z} (1)}}\left( {\sigma (z) - \frac{x}{\sigma (z)}} \right) \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}t}} = k_{B} \left( {\frac{x}{\sigma (z)} - y} \right) \hfill \\ \frac{{{\text{d}}z}}{{{\text{d}}t}} = D_{A} \pi_{z} (1) \cdot \left( {\frac{{1 + \beta_{0} R_{0} }}{{1 + \beta_{0} f(t)R_{0} x}}y - \sigma (z)z} \right) \hfill \\ \end{gathered} \right.\quad \sigma (z) = \frac{{\pi_{z} (z)}}{{\pi_{z} (1)}} $$\end{document} 13

where π _z(1) is the baseline value of π _z(z).

To complete the transformation to dimensionless variables, it remains to make the independent variable, time, dimensionless as well. This involves selecting a characteristic time scale for the system (13). Since the elimination rate of y or B is given by k _B, with a corresponding half-life of ln(2)/k _B, a characteristic time scale T = 1/k _B was chosen. The new dimensionless time τ is consequently defined as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \tau = \frac{t}{T} = k_{B} t . $$\end{document} 14

When τ is incorporated into (13), the system becomes

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} \varepsilon \frac{{{\text{d}}x}}{{{\text{d}}\tau }} = \sigma (z) - \frac{x}{\sigma (z)} \hfill \\ \frac{{{\text{d}}y}}{{{\text{d}}\tau }} = \frac{x}{\sigma (z)} - y \hfill \\ \frac{{{\text{d}}z}}{{{\text{d}}\tau }} = \mu \left( {\frac{{1 + \beta_{0} R_{0} }}{{1 + \beta_{0} \overline{f} (\tau )R_{0} x}}y - \sigma (z)z} \right) \hfill \\ \end{gathered} \right.\quad {\text{with}}\;\overline{f} (\tau ) = f(t) $$\end{document} 15

where we have introduced the dimensionless numbers:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \varepsilon = \frac{{k_{B} }}{{D_{B} }}\pi_{z} (1)\;{\text{and}}\;\mu = \frac{{D_{A} }}{{k_{B} }}\pi_{z} (1). $$\end{document} 16

For the parameter values used by Lemaire et al. [13] (cf. Appendix A), we obtain ε = 0.11 and μ = 1.58. The small value of ε, relative to the other coefficients in the system, implies that x(τ) rapidly converges to a zero of the right hand side of the first equation of (15), while z(τ) changes only slowly. Thus, after a brief initial period, x(τ) and z(τ) are to good approximation related by the equation

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sigma (z) - \frac{x}{\sigma (z)} = 0 $$\end{document} 17

i.e., x and z are in quasi-equilibrium or quasi-steady state. For more details of this “quasi-steady state approximation” we refer to [6, 7, 19, 20].

Equation 17 can now be used to eliminate x from the second and third equation of the system (13) and so to obtain a simpler system, which only involves the dimensionless concentrations y and z:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} \frac{{\text{d}}y}{{{\text{d}}\tau }} = \sigma (z) - y \hfill \\ \frac{{{\text{d}}z}}{{{\text{d}}\tau }} = \mu \left( {\frac{{1 + \beta_{0} R_{0} }}{{1 + \beta_{0} \overline{f} (\tau )R_{0} \sigma^{2} (z)}}y - \sigma (z)z} \right) \hfill \\ \end{gathered} \right.. $$\end{document} 18

Returning to the original variables, we obtain the Reduced System (see Appendix C for details),

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} \frac{{{\text{d}}B}}{{{\text{d}}t}} = D_{R} \pi_{C} (C) - k_{B} B \hfill \\ \frac{{{\text{d}}C}}{{{\text{d}}t}} = D_{C} \frac{\alpha B}{1 + \beta R} - D_{A} \pi_{C} (C)C \hfill \\ \end{gathered} \right., $$\end{document} 19

in which the function R = R(C) is defined by the expression:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R(C)\mathop = \limits^{\text{def}} \frac{{D_{B} }}{{D_{R} }}\pi_{C}^{2} (C), $$\end{document} 20

obtained by equating the right-hand side of the first equation in (1) to zero.

Thus, we have shown that for the parameter values used in Lemaire et al. [13], after a brief initial period we may put the right-hand side of the equation for dR/dt to zero and use the resulting equation to express R in terms of C, which allows one to reduce the original system involving the three dependent variables R, B, and C to one of two with the dependent variables B and C. We refer to the latter system as the Reduced System.

For the other three scenarios we arrive at the same Reduced System (19) and (20). However, different parameters may vary with time. Thus, in the Vitamin D scenario, both α and β vary with time, in the ageing scenario it is π _c(C) that changes and in the glucocorticoid scenario D _R changes with time.

The reduced system (19), is of a type recently discussed by Zumsande et al. [21]. However, in their study they focused on the stability of steady states. As we shall see, this is no issue in our study because for the parameter values from Lemaire et al. the baseline is stable, and remains so when it slowly changes under the impact of disease progression and therapeutic interventions.

Reduction to a two-dimensional system opens the way for a transparent discussion of its dynamics. The state of a system at a given time t, is given by the pair (B(t), C(t)), which can be represented by a point in the (B, C)-plane (in terms of dimensionless variables this is the (y, z)-plane), often referred to as the Phase Plane. In Appendix B we describe how the state (B(t), C(t)) moves through the phase plane as time progresses and show what information about the system we can derive from it.

Evaluation of the model behavior

To evaluate the dynamic properties of both models, the four physiologically meaningful scenarios outlined by Lemaire et al. [13] (estrogen deficiency, Vitamin D deficiency, ageing, and chronic glucocorticoid treatment) were used for simulations. Simulation parameters are provided in Table 2. It should be noted that estrogen deficiency, Vitamin D deficiency, and ageing characterize changes in physiological states, whereas chronic glucocorticoid treatment leads to drug-induced side effects.

Table 2.

Simulation parameters

Scenario	Parameter	Unit	Value	Description
Estrogen	β 0	pM−1	21985	Value of β at time zero
	I max	Dimensionless	0.9994	Maximum inhibition of OPG production
	k dis	day−1	0.0015	Rate at which estrogen production declines
	k int	day−1	0.015	Rate at which estrogen production increases during estrogen replacement therapy
	∆β	pM−1	3000	Maximum increase in β
Vitamin D	α 0	pM−1	1479	Value of α at time zero
	α 1	pM−1	1460	Maximum value of α at maximum deficiency (6 months)
	β 0	pM−1	21985	Value of β at time zero
	β 1	pM−1	22274	Value of β at maximum deficiency (6 months)
Ageing	C s0	pM	5 × 10−3	Value of C s at time zero
	λ	Dimensionless	5.5	Factor by which C s increases
	k age	day−1	6 × 10−4	Rate at which C s increases
Glucocorticoids	D R(0)	pM day−1	7 × 10−4	Differentiation rate of osteoblast progenitors at time zero
	D R(∞)	pM day−1	1.7 × 10−4	Differentiation rate of osteoblast progenitors at time infinity
	k dis	day−1	7.8 × 10−4	Rate of onset of glucocorticoid-induced side effects
	k wash	day−1	7.8 × 10−3	Rate at which glucocorticoid-induced side effects wash out

Estrogen

Estrogen promotes its action, at least in part, through the RANK-RANKL-OPG pathway by stimulating the production of OPG [13]. As estrogen production increases significantly during menarche, the RANKL/OPG ratio decreases resulting in a relative decrease in osteoclast activity leading to a substantial increase in longitudinal and radial bone growth as well as rapid skeletal mineralization [22]. On the other hand, a decrease in estrogen production by 85–90% during menopause results in rapid bone loss and subsequently in an increased risk of bone fracture [22]. The decrease in estrogen production during menopausal transition does not occur instantaneously but slowly evolves over a period of several years.

For this analysis, it was assumed that the main decrease in estrogen production takes place during early post menopause over a period of 5 years [23]. It is further assumed that this decrease in estrogen corresponds to a decrease of the OPG production rate (K ^P_O) [8]. It was assumed for this simulation that K ^P_O decreases from 2 × 10⁵ pM day⁻¹/pM cells to 158 pM day⁻¹/pM cells [13], resulting in a corresponding drop in β (cf. (4)). We assume a mono-exponential decline of β over a period of 5 years (which corresponds to a t _1/2 of 1.25 years and k _dis = 0.0015 day⁻¹),

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \beta (t) = \beta_{\text{bas}} (t) = \beta_{0} \left[ {1 - I_{\max } \left( {1 - e^{{ - k_{\text{dis}} t}} } \right)} \right] $$\end{document} 21

where β _bas(0) = β ₀ is the initial baseline value and β _bas(∞) = β ₀(1-I _max) with I _max = 0.9994 as the maximum inhibition of OPG production.

The increasing lack of endogenous estrogen in post-menopausal women can be compensated for by supplying exogenous estrogen (hormone replacement therapy). Studies have shown that hormone replacement therapy is usually well tolerated by women during the first few years of treatment, whereas the risk for cardio vascular disease, stroke, venous thromboembolic events and possibly breast cancer is increased after more than 5 years of treatment [24–26]. For this analysis, treatment with estrogen was started 1 year post menopause and continued for 3 years. Respective changes in bone cell populations were simulated using Eq. 22 to account for the natural decline in estrogen production as well as the effect of hormone replacement therapy on the OPG production rate,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \beta (t) = \beta_{\text{bas}} (t) + \beta_{\text{int}} (t) $$\end{document} 22

where β _bas(t) is the baseline value of β as it evolves with time, given by (21), and β _int(t) the change in β caused by the therapeutic intervention. An additive term was used for characterizing the therapeutic intervention, where the loss of endogenous estrogen is balanced by a supply of exogenous estrogen:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \beta_{\text{int}} (t) = \Updelta \beta \left\{ {\left( {1 - e^{{ - k_{\text{int}} \left( {t - t_{1} } \right)}} } \right) \cdot \left[ {H\left( {t - t_{1} } \right)} \right] - \left( {1 - e^{{ - k_{\text{int}} \left( {t - t_{2} } \right)}} } \right) \cdot \left[ {H\left( {t - t_{2} } \right)} \right]} \right\}. $$\end{document} 23

In this equation, ∆β represents the maximum increase in β due to estrogen replacement, k _int the rate at which the corresponding OPG production increases, t ₁ the time at which treatment with exogenous estrogen starts, t ₂ the time at which treatment is discontinued (t ₁ = 1 year and t ₂ = 4 years), and H the Heaviside function.1

Vitamin D

Vitamin D plays an important role in maintaining the body’s calcium and phosphate homeostasis and is consequently important for the formation as well as the maintenance of bone [27]. While recent morphogenetic studies also suggest a direct effect on the osteoblastic phenotype expression [28], Vitamin D promotes its main effect on bone by regulating PTH levels and thus the RANKL/OPG ratio. At physiological levels, Vitamin D decreases the synthesis and secretion of PTH [29] as well as the number of PTH receptors [30, 31] resulting in a decrease in RANKL expression and an increase in OPG secretion. In case of Vitamin D deficiency, this inhibiting effect on PTH diminishes leading to an increased RANKL/OPG ratio and increased bone resorption.

Calcitriol, the bioactive form of Vitamin D, is formed from mainly two biologically inert precursors, cholecalciferol and ergocalciferol, via biotransformation in the liver and the kidneys [27]. Cholecalciferol is formed in the skin when 7-dehydrocholesterol is exposed to ultraviolet B light (UVB, 290–320 nm), whereas ergocalciferol is produced by plants and taken up by diet. Assuming that the dietary intake of ergocalciferol does not significantly change during the course of 1 year, changes in Vitamin D levels, and thus changes in bone mineral density, are correlated with seasonal differences in sunlight exposure [32].

For this analysis, it was assumed that these seasonal differences in Vitamin D production result in periodic changes in PTH production (S _P) of the following form:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ S_{P} (t) = \frac{1}{2}\left\{ {\left( {S_{P,\max } + S_{P,\min } } \right) - \left( {S_{P,\max } - S_{P,\min } } \right)\cos \left( {\frac{2\pi t}{365}} \right)} \right\}, $$\end{document} 24

where S _P,min = 250 pM/day is the normal value and S _P,max = 3765 pM/day is the value characterizing maximal Vitamin D deficiency (cf. Lemaire et al.). If no additional PTH is administered, the PTH receptor occupancy π _P is proportional to S _P (cf. (Appendix A, Eq. 28)) This fluctuation in S _P results in periodic changes in the values of α and β.

Ageing

Ageing is associated with significant bone loss in both men and women [33]. The extent of this loss can differ between the different bone sites and has been associated with a decrease in TGF-β production as well as its release from bone [34–36]. Once TGF-β levels decrease, their stimulating effect on osteoclast apoptosis decrease resulting in increased osteoclast activity and increased bone resorption. In addition, the differentiation of OPG-secreting responding osteoblasts to RANKL-expressing active osteoblasts is no longer inhibited. This gradual loss of regulatory feedback leads to an increased RANKL/OPG ratio and further stimulation of osteoclasts.

The age-dependent loss of the bone’s TGF-β content was modeled by Lemaire et al. [13] by decreasing the value of π _C(C) by a factor of 5.5. However, π _C(C) is a non-linear function, which depends on C, f ₀, and C ^s as shown in Eq. 2. Decreasing this function by a constant factor does consequently require additional assumptions. For this analysis, it was assumed that the decrease in π _C is caused by an increase in C ^s (about half the value of C necessary to obtain maximum TGF-β receptor occupancy) since more bone needs to be resorbed to yield the same amount of TGF-β. It was further assumed that these age-dependent changes in TGF-β become clinically relevant for individuals aged 65 and older and manifest themselves over a period of approximately 12.5 years (average life expectancy in Western World: 75–80 years). The change of the bone’s TGF-β content over time (C ^s(t)) can be computed according to Eq. 25,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ C^{s} (t) = C_{0}^{s} \left\{ {\lambda - \left( {\lambda - 1} \right) \cdot e^{{ - k_{\text{age}} t}} } \right\}, $$\end{document} 25

where C ^s₀ represents the bone’s TGF-β content at the age of 65, k _age the rate and λ > 1 the extent by which C ^s increases in the elderly.

Glucocorticoids

Bone loss and increased fracture risk due to long-term glucocorticoid therapy is the most common cause of drug-induced osteoporosis [37]. The extent of this drug-induced side effect seems to be dependent on the cumulative glucocorticoid dose and affects trabecular bone more than cortical bone [37, 38]. Although glucocorticoid receptors are present in almost every vertebrate cell, glucocorticoids seem to primarily affect bone formation by decreasing the expression of osteoblastic differentiation factors, such as core binding factor A1 [39–41].

Glucocorticoid-induced effects on bone were modeled by Lemaire et al. [13] by decreasing the differentiation rate of osteoblast progenitors (D _R). Since these drug-related adverse effects only emerge after a chronic treatment with glucocorticoids, it was assumed for this simulation that D _R decreases slowly from 7 × 10⁻⁴ to 1.7 × 10⁻⁴ pM/day at a rate k _dis over 5 years as shown in Eq. 26 [13]. In this simulation we take k _dis = 0.00078 day⁻¹.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ D_{R} (t) = D_{R} (\infty ) + \left[ {D_{R} (0) - D_{R} (\infty )} \right] \cdot e^{{ - k_{\text{dis}} t}} $$\end{document} 26

Once treatment with glucocorticoids is discontinued after 6 years (T = 2190 days), the system completely recovers and equilibrates at its original baseline D _R(0). Results from a study in patients with rheumatoid arthritis receiving low-dose prednisone suggest that this recovery process is relatively fast and occurs within 1 year [42]. Respective changes in bone cells during (0 < t ≤ T) and after (T < t < ∞) treatment with glucocorticoids can be computed according to Eq. 27.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ D_{R} (t) = \left\{ \begin{gathered} D_{R} (\infty ) + \left[ {D_{R} (0) - D_{R} (\infty )} \right] \cdot e^{{ - k_{\text{dis}} t}} \quad (0 < t \le T) \hfill \\ D_{R} (0) + \left[ {D_{R} (T) - D_{R} (0)} \right] \cdot e^{{ - k_{\text{wash}} (t - T)}} \quad (T < t < \infty ) \hfill \\ \end{gathered} \right. $$\end{document} 27

Here, T represents the time at which treatment with glucocorticoids was discontinued and k _wash represents the first-order rate constant characterizing the offset of the glucocorticoid effect.

Software

Simulations were performed in MatLab version R2011a. In light of the stiffness of the system, the ode-solver “ode23s” was used.

Results

Application of dimensional analysis to the conceptual bone cell interaction model by Lemaire et al. [13] allowed us to evaluate (i) the relative importance of its model terms, (ii) the relative speeds of the processes involved, and (iii) the critical dimensionless numbers (often combinations of parameters), which determine the qualitative character of the dynamics of the system. In particular, we were able to show mathematically that responding osteoblasts (R) rapidly reach a quasi-steady state with active osteoclasts (C) for the model parameters provided in [13]. Thus, for R and C the quasi-steady state assumption was shown to hold and the original three-dimensional system containing R, B, and C could be reduced to a simpler, two-dimensional system, whose dynamics is determined by B and C. Reduction to a two-dimensional system further allowed for a graphical representation of its dynamics in the planar State Space. While the state of the system can be depicted as a point in the state space, its evolution is characterized by a respective curve parameterized by the time t (the orbit, cf. Fig. 9 in Appendix B). Representation in the state space also enables a transparent discussion of the system’s dynamics and readily reveals qualitative properties, such as the absence of overshoot and rebound.

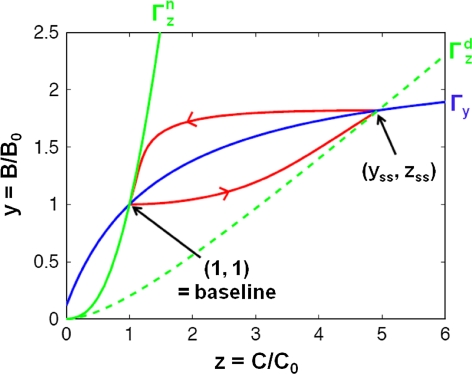
Fig. 9.

Orbit of the reduced system (34) (in red) in the (z,y)-plane. At normal estrogen levels, the system is at baseline (y,z) = (1,1), which is characterized by the intersection point of the solid blue line (Г_y) and the solid green line (Г_z (normal)). Once estrogen levels change, Г_z changes and the system starts moving towards a new steady-state (y _ss,z _ss). In case of a sudden drop in estrogen levels, realized here by a step-decrease in β, y _ss,z _ss is now determined by the intersection point of Г_y and the new Null Cline Г_z(decreased) (dashed green line). As a result, the system starts moving from (1,1) towards (y _ss,z _ss). Once estrogen concentrations return to their baseline levels, the system moves back to its original baseline (1,1)

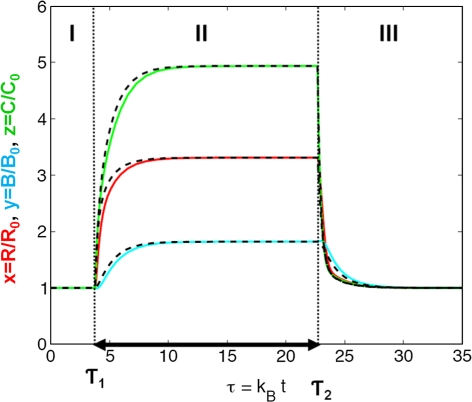
When evaluating the performance of both the full Lemaire model and the reduced model following rapid interventions, such as a sudden decrease or increase in estrogen levels (Appendix B), our findings show that the dynamic properties of both models are very similar but not identical (Fig. 8 in Appendix B). Small discrepancies between the dynamic properties of the two models exist during the first 10–20 days after the rapid intervention. Once the speed of the onset and/or offset of these interventions decreases to more (patho)physiological/therapeutic levels, the profiles of both models become more and more similar. On the time scale of disease progression and therapeutic intervention both the full Lemaire model and the mathematically reduced model show negligible differences in their ability to characterizing the dynamic interaction between osteoclasts and osteoblasts.

Fig. 8.

Effect of rapidly changing estrogen concentrations on bone cell dynamics (I) at normal (non-deficient) estrogen levels, (II) following a step-decrease to a constant, deficient estrogen level, and (III) following a step-increase back to normal (non-deficient) estrogen levels. Solid red lines represent simulated changes in responding osteoblasts (x), solid blue lines those in active osteoblasts (y), and solid green lines those in active osteoclasts (z) based on the full model, whereas dashed lines represent the respective changes based on the mathematically reduced model. The duration of the step-change is depicted by a black solid arrow. Note that the time t can be computed as t = τ/k _b

Estrogen

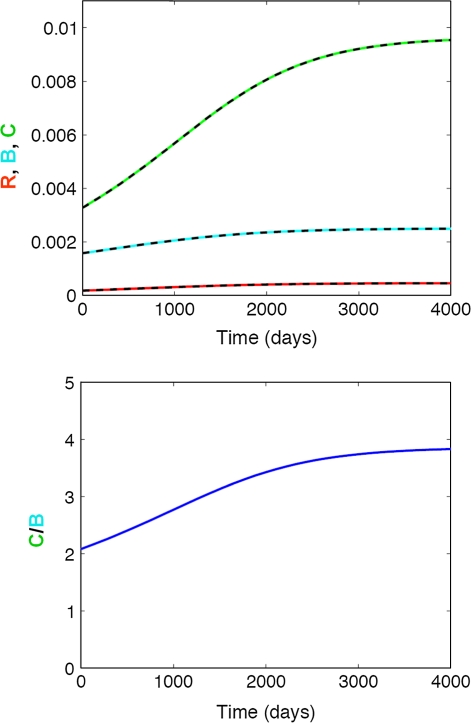
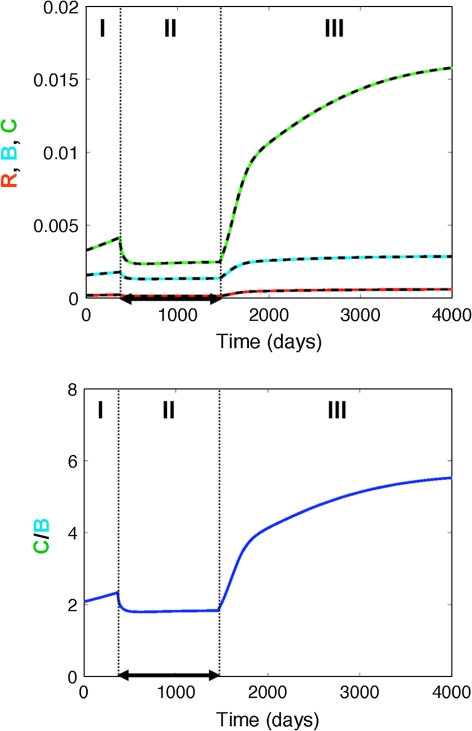
In particular, results of our first scenario (estrogen deficiency) indicate that once estrogen levels are declining, their inhibiting effect on bone cell proliferation is gradually lost, leading to an increased differentiation and activation of both osteoblasts and osteoclasts. This estrogen-mediated effect is more pronounced for C than for R and B resulting in an elevated C/B ratio (high turnover) and thus increased bone resorption (Fig. 2). On the other hand, the system equilibrates at a new steady-state upon start of the estrogen replacement therapy (Fig. 3, “Materials and methods” section), which is different from its original baseline. The establishment of a new steady-state results in a slow-down or even halt of osteoporotic processes. It should be noted though that for symptomatic therapeutic interventions, such as estrogen replacement therapy, the underlying disease is still progressing at its natural rate [3]. The status of patients having received symptomatic treatments will consequently be indistinguishable from that of untreated patients once the treatment has been discontinued and the drug effect has washed out.

Fig. 2.

Effect of slowly decreasing endogenous estrogen production on bone turnover. Top panel Impact on responding osteoblasts (R, red), active osteoblasts (B, blue), and active osteoclasts (C, green); Bottom panel Impact on the active osteoclasts/osteoblast (C/B) ratio. An increase in the C/B ratio results in bone loss, whereas a decrease results in bone gain. The solid lines represent the simulated change in bone cells using the full model, whereas the dashed lines represent the respective changes using the mathematically reduced model

Fig. 3.

Effect of estrogen replacement therapy on the dynamics of bone cells (I) prior to the start of treatment (disease progression due to estrogen deficiency), (II) during treatment, and (III) after treatment cessation. Top panel Impact on responding osteoblasts (R, red), active osteoblasts (B, blue), and active osteoclasts (C, green); Bottom panel Impact on the active osteoclasts/osteoblast (C/B) ratio. The solid lines represent the simulated change in bone cells using the full model, whereas the dashed lines represent the respective changes using the mathematically reduced model. Treatment starts after 1 year (t = 365 days) and is discontinued after 4 years (t = 1460 days) and is depicted by a black solid arrow

Vitamin D

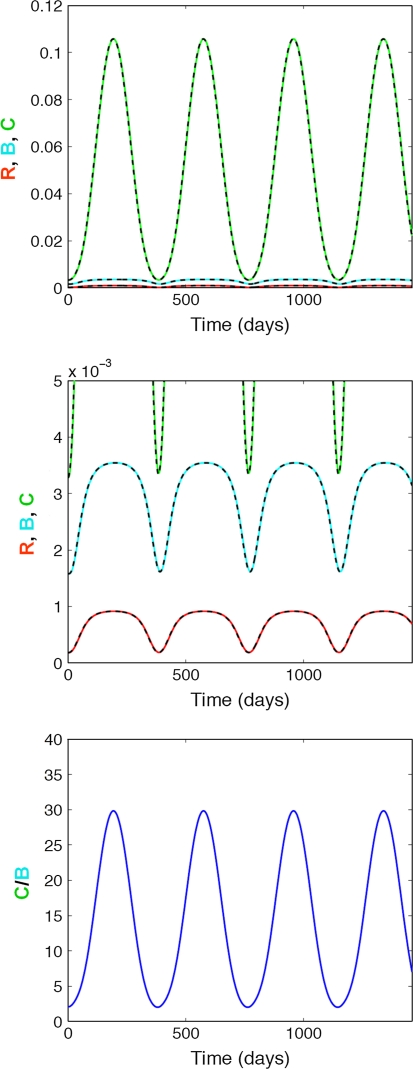
In comparison, changes in Vitamin D exposure have a bigger impact on osteoclasts than on osteoblasts (Fig. 4). The seasonal nature of these changes leads to a periodically elevated C/B ratio, which is maximally elevated during the winter when Vitamin D levels are lowest.

Fig. 4.

Effect of seasonal changes in Vitamin D exposure on bone turnover. Top panel: Impact on responding osteoblasts (R, red), active osteoblasts (B, blue), and active osteoclasts (C, green); Middle panel Impact on responding osteoblasts (R, red), active osteoblasts (B, blue), and active osteoclasts (C, green) with focus on R and B; Bottom panel Impact on the active osteoclasts/osteoblast (C/B) ratio. The solid lines represent the simulated change in bone cells using the full model, whereas the dashed lines represent the respective changes using the mathematically reduced model. The simulation starts at the highest Vitamin D exposure in the summer and peaks during the winter

Ageing

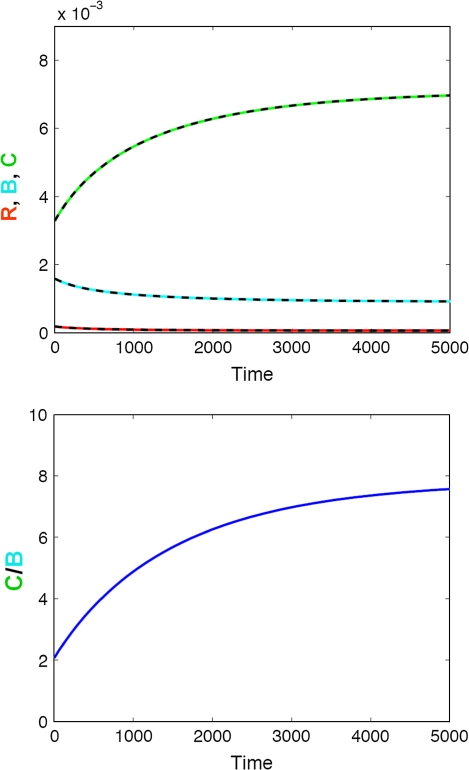
Changes in the bone’s TGF-β content due to ageing also result in a rapid increase of the active osteoclast to active osteoblast ratio as shown in Fig. 5. Our findings further indicate that these changes in the C/B ratio are non-reversible and lead to a rapid increase in the breakdown of bone in subjects 65 and older.

Fig. 5.

Effect of ageing on bone turnover. Top panel Impact on responding osteoblasts (R, red), active osteoblasts (B, blue), and active osteoclasts (C, green); Bottom panel Impact on the active osteoclasts/osteoblast (C/B) ratio. The solid lines represent the simulated change in bone cells using the full model, whereas the dashed lines represent the respective changes using the mathematically reduced model

Glucocorticoids

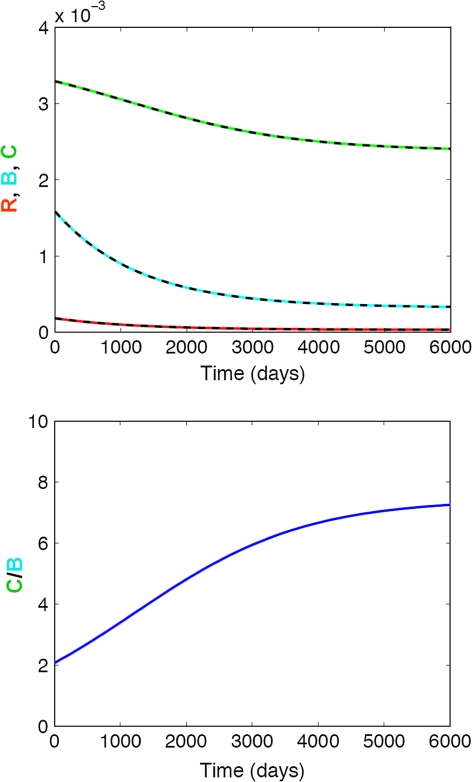
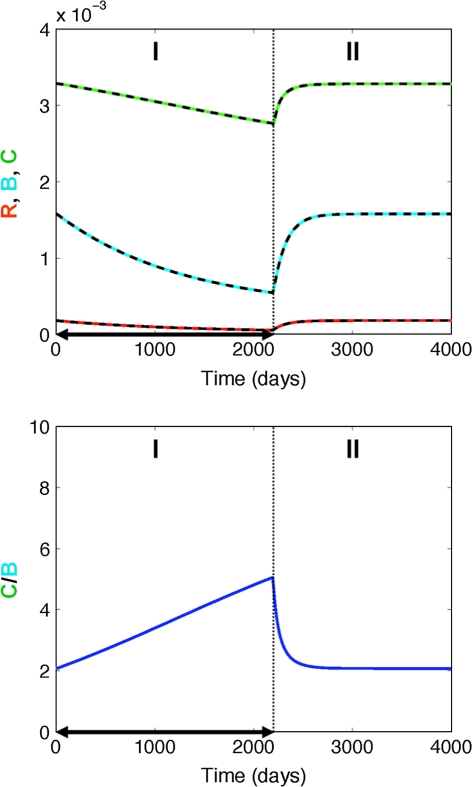
Finally, simulated profiles for the chronic glucocorticoid treatment scenario (Fig. 6) show that a drug-mediated decrease of the osteoblast precursor differentiation has a much bigger effect on the maturation and activation of osteoblasts than that of osteoclasts. These differences in effect size result in a rapid increase in the C/B ratio (i.e., high bone turnover) and a subsequent decrease in bone mass. However, these glucocorticoid-induced site effects are reversible as the maturation of osteoblast progenitors can recover upon termination drug treatment (Fig. 7, “Materials and methods” section). The system’s recovery also results in the reestablishment of the original C/B ratio and subsequently no further bone loss.

Fig. 6.

Effect of chronic glucocorticoid treatment on bone turnover. Top panel Impact on responding osteoblasts (R, red), active osteoblasts (B, blue), and active osteoclasts (C, green); Bottom panel Impact on the active osteoclasts/osteoblast (C/B) ratio. The solid lines represent the simulated change in bone cells using the full model, whereas the dashed lines represent the respective changes using the mathematically reduced model

Fig. 7.

Effect of glucocorticoid treatment on bone turnover before (I) and after (II) treatment cessation. Top panel Impact on responding osteoblasts (R, red), active osteoblasts (B, blue), and active osteoclasts (C, green); Bottom panel Impact on the active osteoclasts/osteoblast ratio (C/B) during treatment/washout. The solid lines represent the simulated change in bone cells using the full model, whereas the dashed lines represent the respective changes using the mathematically reduced model. Treatment with glucocorticoids is discontinued after 6 years (t = 2190 days) and is depicted by a black solid arrow

Discussion

The effects of both local and systemic control mechanisms on the regulation of bone remodeling result in the establishment of a complex framework that contains multiple spatial and temporal levels. To obtain a sufficient understanding of this framework, its dynamics, and the impact of therapeutic interventions and disease processes, the use of mathematical models is required (for a more elaborate conceptual discussion of the role of mathematical modeling for characterizing bone turnover see also [43]). Mathematical modeling provides a powerful tool as it allows incorporation of information from different in vitro and in vivo experiments into a single approach. Once developed and validated, these models can be used in silico to explore the cause-effect relationship and to assist the formulation of new hypotheses as well as the design of new experimental studies. However, as these frameworks become more complex, problems with identifying the key mechanisms that cause a system to undergo pathophysiological changes may arise [3, 4]. To identify these key components, sufficient understanding of a system’s dynamic properties is often more informative than characterizing its complexity. One way of exploring a system’s dynamic properties is to mathematically reduce completely mechanistic models in order to evaluate (1) the relative importance of the various model components and (2) the relative speed of the processes involved for the overall performance of the system.

To demonstrate the benefits and limitations of model reduction, we analyzed the well-known bone-cell interaction model proposed by Lemaire et al. [13], which is based on the RANK-RANKL-OPG signaling pathway. By performing a dimensional analysis, we identified critical properties, such as overall and relative time scales, on the basis of the parameter values quoted in [13]. We found that for these parameter values the dynamics of the responding osteoblasts was relatively fast compared to that of active osteoblasts and osteoclasts. The dynamics of the system were thus primarily driven by changes in osteoclasts and active osteoblasts, whilst responding osteoblasts follow their lead. Although not all of the parameter values provided in [13] seem to have been previously validated, corresponding model-predicted bone cell dynamics are in agreement with clinical observations [44], where rapid changes in bone resorption markers during/after treatment with conjugated estrogen and/or alendronate are followed by respective changes in bone formation markers.

Based on these findings, the conceptual bone cell interaction model by Lemaire et al. [13] could be reduced from a three- to a two-dimensional system. Reducing the model’s complexity allowed for a transparent discussion of its dynamics and also opened the way for a geometric, two-dimensional analysis. This approach added significantly to the transparency of the system as it allowed its representation in the Phase Plane. Results of this geometric analysis indicate that there can be no overshoot at onset and no rebound at washout for the reduced model. Given the proximity of the concentration curves of the reduced and full model this implies that any overshoot or rebound the full model might exhibit will be very small (cf. Appendix B).

When simulating the response of both the full Lemaire model and the mathematically reduced model to rapid changes, such as a sudden onset/offset of effect, we showed that there is overall a good match between the two models (cf. Fig. 8). Small discrepancies in their dynamic properties were only observed during the first 10–20 days after the onset/offset of the effect. However, once the relative speeds of the underlying (patho)physiological processes and therapeutic interventions were taken into account, both models were at any time at quasi-equilibrium (Figs. 2, 3, 4, 5, 6, 7). Consequently, both models can be used interchangeably for characterizing bone cell dynamics on the time scale of disease progression and therapeutic intervention. From a data analysis point of view, the use of the simpler model is advantageous as fewer parameters have to be identified and estimated. This aspect becomes particularly important for the analysis of clinical data, where usually only few samples per subject are available. On the other hand, the development and validation of disease system models heavily depends on current knowledge about the biological system, the availability of sufficient data on different spatial/temporal levels, and the availability of appropriate software tools that allow running and visualizing these models based on widely accepted modeling standards [4, 45].

The application of advanced mathematical and statistical tools, such as mathematical model reduction, can guide the development of disease system models as it allows one to identify the rate-limiting steps within complex, dynamic systems. The joint use of systems pharmacology and mathematical model reduction approaches provides, therefore, a powerful combination as it can guide the identification of drug-, system-, and disease-specific parameters, informative biomarkers as well as the generation of data, where such information can be obtained from. In particular, knowledge on the system’s dynamics and the time scales involved in the establishment of disease and drug effects can guide clinical trial design as it allows to identifying its maximal susceptibility to changes in the underlying physiology and/or therapeutic interventions. For example, the response of the reduced model to a step-decrease in estrogen suggests that in this case a washout design would be superior to a delayed start design for characterizing the impact of this physiological change on bone remodeling. This is due to the fact that in this case equilibrium is reached much faster after washout of the intervention than following its onset (cf. Appendix B; Figs. 8, 9). These findings are in agreement with those of Ploeger and Holford, who found a washout design superior to a delayed start design for characterizing and distinguishing treatment effect types in Parkinson’s disease [46].

In conclusion, mathematical model reduction is a valuable approach for analyzing disease systems and simplifying complex models while maintaining their dynamic properties. A significant decrease in the number of parameters to be identified and estimated in addition to an increased system transparency qualifies reduced models as tools to evaluate the impact of changes in physiological states and/or therapeutic interventions with respect to the different time scales involved.

Appendix A: Model parameters

From the parameter values provided by Lemaire et al. (Table 1) [13], the fraction of occupied PTH receptors (π _P) can be computed according to Eq. 28:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{P} = \frac{{\overline{P} + P^{0} }}{{\overline{P} + P^{s} }} = 0.019,\quad \overline{P} = \frac{{I_{P} }}{{k_{P} }} = 0\,{\text{pM}},\quad P^{0} = \frac{{S_{P} }}{{k_{P} }} = 2.9\,{\text{pM}},\quad P^{s} = \frac{{k_{6} }}{{k_{5} }} = 150\,{\text{pM}} $$\end{document} 28

where \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \overline{P} $$\end{document} is the amount of externally administered PTH, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ P^{0} $$\end{document} is the amount of endogenous produced PTH, which is produced at a rate S _P, and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ P^{s} $$\end{document} is the amount of PTH at which 50% of the receptors are occupied. The baseline values of α and β are given by α ₀ and β ₀ (cf. Eq. 29).

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \alpha_{0} = \frac{{k_{3} }}{{k_{4} + k_{3} K}}K_{L}^{P} \pi_{P} \approx 1479\,{\text{pM}}^{ - 1} ,\;\beta_{0} = \frac{{k_{1} }}{{k_{2} \cdot k_{O} }}\frac{{k_{4} }}{{k_{4} + k_{3} K}}\frac{{K_{O}^{P} }}{{\pi_{P} }} \approx 21985\,{\text{pM}}^{ - 1} , $$\end{document} 29

Based on these values, we find the following baseline concentrations R ₀, B ₀, and C ₀ for the full as well as for the reduced system:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R_{0} = 1.82\, \times \,10^{ - 4} \,{\text{pM}},\quad B_{0} = 1.58\, \times \,10^{ - 3} \,{\text{pM}},\quad C_{0} = 3.285\, \times \,10^{ - 3} \,{\text{pM}} . $$\end{document} 30

When the internal PTH production increases (from 250 pM/day to 3765 pM/day) due to decreased Vitamin D exposure, corresponding values for α and β are given by α ₁ and β ₁:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \alpha_{1} \approx 22274\,{\text{pM}}^{ - 1} ,\;\beta_{1} \approx 1460\,{\text{pM}}^{ - 1} , $$\end{document} 31

and the baseline changes accordingly.

Appendix B: Systems analysis

In this paper we have shown that the full Lemaire model and the mathematically reduced model show negligible differences in their dynamic properties for relatively slow processes that occur on the time scale of disease progression and/or therapeutic intervention. In this appendix we compare the performance of the full and the reduced model on the time scale of very rapid interventions, such as a temporary drop in estrogen levels, where onset and offset are instantaneous and have no dynamics of their own. This sudden drop and equally sudden rebound of estrogen levels results in a function for β that has the form

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \beta (\tau ) = \beta_{0} I(\tau ) $$\end{document} 32

where

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ I(\tau ) = \left\{ \begin{array}{ll} 1\quad for\quad 0 < \tau < \tau_{1} \quad {\text{and}}\quad \tau > \tau_{2} \hfill \\ 1 - I_{\max } \quad for\quad \tau_{1} < \tau < \tau_{2} \hfill \\ \end{array} \right.\;{\text{with }}0 < I_{ \max } < 1. $$\end{document} 33

Thus, the estrogen level drops instantaneously from a normal to a constant, deficient level at τ = τ ₁ and abruptly returns to the normal level at τ = τ ₂. (Throughout this appendix we use the dimensionless variables.)

Although physiologically unrealistic, we choose this form of exposure because it focuses attention on the dynamics of the two systems we wish to compare and challenges them maximally because of the sudden changes at onset and offset.

In Fig. 8 we show graphs of the dimensionless concentrations computed with the full model (drawn; in color) and with the reduced model (dashed; black). Clearly, the match is very good, even after onset and offset.

It is interesting to note that (i) after onset the concentrations increase monotonically to their new steady-state values, i.e., there is no overshoot, and similarly, after washout, they drop monotonically back to baseline without any rebound, and (ii) after onset, the time to equilibrium is much longer than after washout.

To understand how this comes about, we turn to a geometric analysis of the reduced system, which we restate below

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left\{ \begin{gathered} \frac{{{\text{d}}y}}{{{\text{d}}\tau }} = \sigma (z) - y \hfill \\ \frac{{{\text{d}}z}}{{{\text{d}}\tau }} = \mu \left( {\frac{{1 + \beta_{0} R_{0} }}{{1 + \beta_{0} I(\tau )R_{0} \sigma^{2} (z)}}y - \sigma (z)z} \right) \hfill \\ \end{gathered} \right.. $$\end{document} 34

Because this system consists of only two equations involving the concentrations y and z, we can describe its dynamics by following the state of the system (y,z) as a point in the (y,z)-plane, also called the Phase Plane, as it moves with time [47].

In the phase plane one can identify two useful curves, the Null Clines Г_y and Г_z, along which dy/dτ = 0 and dz/dτ = 0, respectively. We readily see from (34) that the null clines are given by:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{y} :y = \sigma (z) $$\end{document} 35

the blue curve in Fig. 9 and, depending on whether the value of β is normal (I(τ) = 1) or decreased (I(τ) = 1−I _max),

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{n} :y = z\sigma (z)\frac{{1 + \beta_{0} R_{0} \sigma^{2} (z)}}{{1 + \beta_{0} R_{0} }}\quad {\text{normal}} $$\end{document} 36

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{d} :y = z\sigma (z)\frac{{1 + \beta_{0} (1 - I_{\max } )R_{0} \sigma^{2} (z)}}{{1 + \beta_{0} R_{0} }}\quad {\text{decreased}} $$\end{document}

the green curves in Fig. 9 (\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{n} $$\end{document}solid and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{d} $$\end{document} dashed).

Plainly, at any point of intersection of Г_y and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{n} $$\end{document} or \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{d} $$\end{document}, both dy/dτ = 0 and dz/dτ = 0, so that such a point is an equilibrium point. When I(τ) = 1, the null clines Г_y and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{n} $$\end{document} intersect at the point (y,z) = (1,1), the baseline. We see that when β is decreased Г_y and the new null cline \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{d} $$\end{document} still intersect, but now at the point (y _ss,z _ss) and that y _ss > 1 and z _ss > 1.

At each point in the (y,z)-plane we can read off from the system of Eq. 34 the values of dy/dτ and dz/dτ and hence the direction of the orbit. Thus, we see that the orbit leaves the baseline point (1,1) in a horizontal direction and thereafter moves up and towards the right. We also see that it cannot cross Г_y and the new \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Upgamma_{z}^{d} $$\end{document} so that it must move towards the new equilibrium point (y _ss,z _ss). Thus, both y(t) and z(t) are increasing and hence there is no overshoot. Similarly, at washout the orbit leaves (y _ss,z _ss) in a horizontal direction, moving down and to the left. Again, y(t) and z(t) are monotone and there is no rebound.

Appendix C Transformation of (18) into (19)

In this appendix we show how the system (18) expressed in terms of dimensionless variables results in the system (19), which is written in terms of the original variables. Recall that

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ x = \frac{R}{{R_{0} }},\quad y = \frac{B}{{B_{0} }},\quad z = \frac{C}{{C_{0} }},\quad \tau = k_{B} t $$\end{document} 37

The first equation of ( 18 ): When converting the original variables R, B, and C in the first equation of (18) we obtain

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{{{\text{d}}B}}{{{\text{d}}t}} = B_{0} k_{B} \frac{{{\text{d}}y}}{{{\text{d}}\tau }} = B_{0} k_{B} \left( {\sigma (z) - \frac{B}{{B_{0} }}} \right) = B_{0} k_{B} \sigma (z) - k_{B} B $$\end{document} 38

where σ(z) = π _z(z)/π _z(1). Note that

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{z} (z) = \frac{{z + f_{0} z^{s} }}{{z + z^{s} }} = \frac{{C + f_{0} C^{s} }}{{C + C^{s} }} = \pi_{C} (C) $$\end{document}

and

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \pi_{z} (1) = \frac{{1 + f_{0} z^{s} }}{{1 + z^{s} }} = \frac{{C_{0} + f_{0} C^{s} }}{{C_{0} + C^{s} }} = \pi_{C} (C_{0} ) $$\end{document}

Thus, Eq. 39 can be written as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{{{\text{d}}B}}{{{\text{d}}t}} = B_{0} k_{B} \frac{{\pi_{C} (C)}}{{\pi_{C} (C_{0} )}} - k_{B} B $$\end{document} 39

By definition, the baseline values B ₀ and C ₀ are related through the equation

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ D_{R} \pi_{C} (C_{0} ) - k_{B} B_{0} = 0 $$\end{document}

When we use this expression in (39) we obtain

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{{{\text{d}}B}}{{{\text{d}}t}} = D_{R} \pi_{C} (C) - k_{B} B , $$\end{document} 40

which establishes the first equation of (19).

The second equation of ( 18 ): Proceeding as with the first equation, we now obtain

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{{{\text{d}}C}}{{{\text{d}}t}} = C_{0} k_{B} \frac{{{\text{d}}z}}{{{\text{d}}\tau }} = C_{0} k_{B} \cdot \frac{{D_{A} }}{{k_{B} }}\pi_{C} (C_{0} ) \cdot \left( {\frac{{1 + \beta R_{0} }}{1 + \beta R}\frac{B}{{B_{0} }} - \frac{{\pi_{C} (C)}}{{\pi_{C} (C_{0} )}}\frac{C}{{C_{0} }}} \right) $$\end{document} 41

Since σ ²(z) = x = R/R ₀ and μ = (D _A/k _B)π _C(C ₀), this equation can be further simplified to

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{{{\text{d}}C}}{{{\text{d}}t}} = C_{0} D_{A} \pi_{C} (C_{0} )\left( {\frac{{1 + \beta R_{0} }}{1 + \beta R}\frac{B}{{B_{0} }} - \frac{{\pi_{C} (C)}}{{\pi_{C} (C_{0} )}}\frac{C}{{C_{0} }}} \right) $$\end{document} 42

By definition, the baseline values B ₀ and C ₀ are related through the equation

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ D_{C} \frac{{\alpha B_{0} }}{{1 + \beta R_{0} }} - D_{A} \pi_{C} (C_{0} )C_{0} = 0 $$\end{document}

This means that

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\frac{{1 + \beta R_{0} }}{{B_{0} }} = \frac{{D_{C} }}{{D_{A} }}\frac{\alpha }{{\pi_{C} (C_{0} )C_{0} }} $$\end{document}

Substitution into (42) yields

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{{{\text{d}}C}}{{{\text{d}}t}} = D_{C} \frac{\alpha B}{1 + \beta R} - D_{A} \pi_{C} (C)C $$\end{document} 43

Finally, since

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R = R_{0} x = R_{0} \sigma (z) = R_{0} \frac{{\pi_{z}^{2} (z)}}{{\pi_{z}^{2} (1)}} = R_{0} \frac{{\pi_{C}^{2} (C)}}{{\pi_{C}^{2} (C_{0} )}} $$\end{document} 44

and R ₀ and C ₀ are related through the equation

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ D_{R} \pi_{C} (C_{0} ) - \frac{{D_{B} }}{{\pi_{C} (C_{0} )}}R_{0} = 0\;{\text{or}}\;\pi_{C}^{2} (C_{0} ) = \frac{{D_{R} }}{{D_{B} }}R_{0} $$\end{document}

we can write (44) as

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R = R(C)\mathop = \limits^{def} \frac{{D_{B} }}{{D_{R} }}\pi_{C}^{2} (C) $$\end{document} 45

This completes the transformation of the two equations of the system (18) into those of the system (19).