Anticorrelations in resting state networks without global signal regression

Abstract

Anticorrelated relationships in spontaneous signal fluctuation have been previously observed in resting-state functional magnetic resonance imaging (fMRI). In particular, it was proposed that there exists two systems in the brain that are intrinsically organized into anticorrelated networks, the default mode network, which usually exhibits task-related deactivations, and the task-positive network, which usually exhibits task-related activations during tasks that demands external attention. However, it is currently under debate whether the anticorrelations observed in resting state fMRI were valid or were instead artificially introduced by global signal regression, a common preprocessing technique to remove physiological and other noise in resting-state fMRI signal. We examined positive and negative correlations in resting-state connectivity using two different preprocessing methods: a component base noise reduction method (CompCor, Behzadi et al., 2007), in which principal components from noise regions-of-interest were removed, and the global signal regression method. Robust anticorrelations between a default mode network seed region in the medial prefrontal cortex and regions of the task-positive network were observed under both methods. Specificity of the anticorrelations was similar between the two methods. Specificity and sensitivity for positive correlations were higher under CompCor compared to the global regression method. Our results suggest that anticorrelations observed in resting-state connectivity are not an artifact introduced by global signal regression and might have biological origins, and that the CompCor method can be used to examine valid anticorrelations during rest.

1. Introduction

Coherent low frequency fluctuations in the resting state of the blood oxygenation level-dependent (BOLD) signal in functional magnetic resonance imaging (fMRI) are thought to reflect the intrinsic organization of the brain [see (Buckner et al., 2008; Fox and Raichle, 2007) for review]. Resting-state fMRI has revealed that signals in functionally related brain regions correlate with each other even in the absence of external stimuli (Beckmann et al., 2005; Biswal et al., 1995; De Luca et al., 2006; Fox et al., 2005a; Fransson, 2005; Greicius et al., 2003). Functional networks identified by resting-state fMRI have been shown to be robust and reliable (Damoiseaux et al., 2006; Shehzad et al., 2009; Van Dijk et al., 2010; Zuo et al., 2010), and can thus provide useful information about brain organization differences across different clinical populations (Dosenbach et al., 2010; Seeley et al., 2009) and during development (Dosenbach et al., 2010).

It has been proposed that some systems in the brain are intrinsically organized into anticorrelated networks in resting-state fMRI. Specifically, the default mode network, which consists of a set of brain regions that are commonly deactivated during tasks that demand external attention, has been found to be anticorrelated with regions of the task-positive network, which consists of a set of regions that are commonly activated in tasks that demand attention and mental control (Fox et al., 2005b; Fransson, 2005; Greicius et al., 2003; Kelly et al., 2008; Uddin et al., 2009). The strength of the negative correlation between the default mode network regions and task-positive network regions has been linked to variability in task performance (Hampson et al., 2010; Kelly et al., 2008) and individual differences in task-induced BOLD activity (Mennes et al., 2010). Abnormalities in these two anticorrelated networks have been found in patients with schizophrenia (Whitfield-Gabrieli et al., 2009), ADHD (Castellanos et al., 2008), bipolar disorder (Chai et al., 2011), and Alzheimer's disease (Wang et al., 2007).

However, it remains unclear whether the anticorrelations observed in resting-state fMRI are neurobiologically valid or are instead artificially introduced by global signal regression, a preprocessing technique for removing physiological and other noise in fMRI BOLD time series (Aguirre et al., 1997, 1998; Desjardins et al., 2001; Macey et al., 2004; Zarahn et al., 1997). Global signal, the average signal across all voxels in the brain, is removed in some fMRI studies to correct for physiological noise, such as respiratory and cardiac noise, under the assumption that global signal is not correlated with task-induced signal. However, when global signal is influence by experimental manipulations, removing global signal can decrease task-related activation in fMRI studies (Aguirre et al., 1998; Junghofer et al., 2005). In seed-based resting-state fMRI analysis, physiological noise and signal fluctuation caused by residual motion and other artifacts can introduce spurious correlation among brain regions and result in overestimation of connectivity. Global signal is commonly removed using a general linear model (GLM) technique to improve the specificity of functional connectivity analysis (Fox et al., 2005b; Van Dijk et al., 2010; Weissenbacher et al., 2009). However, global signal regression shifts the distribution of the correlation values of a seed region toward the negative direction such that they must sum to less than zero (Murphy et al., 2009). It has been suggested that anticorrelations in resting-state connectivity are most likely artificially introduced by global signal regression, calling into question of the functional significance of anticorrelations observed in resting-state connectivity (Murphy et al., 2009). Previous studies have not reached a consistent conclusion on this issue (Chang and Glover, 2009; Fox et al., 2009; Hampson et al., 2010; Van Dijk et al., 2010; Weissenbacher et al., 2009).

In the present study, we examined positive and negative correlations in resting-state connectivity using a component base noise reduction method (CompCor) (Behzadi et al., 2007). The CompCor method corrects for physiological noise by regressing out principal components from noise regions-of-interest (ROI), such as the white matter and cerebral spinal fluid (CSF) regions, in which signal is unlikely to be related to neural activity. Compared to the average signal from white matter and CSF regions, principal components derived from these noise ROIs can better account for voxel-specific phase differences in physiological noise. Applying CompCor to BOLD time series significantly reduced noise from physiological and other sources (Behzadi et al., 2007). Here we compared functional connectivity from a default mode network seed region in the medial prefrontal cortex (MPFC) under two separate preprocessing streams: the CompCor approach that does not remove global signal, and the whole brain regression method in which the global signal was removed. We hypothesized that anticorrelations from the MPFC seed should emerge without global signal regression, when physiological and other spurious noise is effectively removed using the CompCor approach.

2. Materials and Methods

2.1 Participants

Fifteen healthy participants (mean age: 37.3±2.4, 9 males) were included in the study. All participants were right-handed, had no history of psychiatric or neurological illness as confirmed by a psychiatric clinical assessment. The study was approved by the institutional review boards of McLean Hospital. Signed informed consent was obtained prior to participation.

2.2 Imaging procedure

Data were acquired on a 3T Siemens scanner using a standard head coil. T1-weighted whole brain anatomy images (MPRAGE sequence, 256×256 voxels, 1×.3-mm inplane resolution, 1.3-mm slice thickness) were acquired. In addition, all participants underwent a resting functional MRI scan of 10 mins with the instructions “keep your eyes open and think of nothing in particular”. Resting scan images were obtained in 42 3.5-mm thick transverse slices, covering the entire brain (interleaved EPI sequence, T2*-weighted images; 3.5-mm inplane resolution, repetition time = 2.5 s, echo time = 24 ms, flip angle = 82, 64×64 voxels).

2.3 Data Analysis

Resting-state fMRI data were first preprocessed in SPM5 (Wellcome Department of Imaging Neuroscience, London, UK; http://www.fil.ion.ucl.ac.uk/spm), using standard spatial preprocessing steps. Images were slice-time corrected, realigned and resliced into 2mm isotropic voxels, normalized, smoothed with a 4-mm kernel.

Connectivity analysis

Functional connectivity analysis was performed using a seed-driven approach with in-house, custom software “Conn toolbox” (Whitfield-Gabrieli and Nieto-Castanon) (http://web.mit.edu/swg/software/). We defined the MPFC seed following the literature (Fox et al., 2005a; Whitfield-Gabrieli et al., 2009) as a 10-mm sphere around the coordinates (−1, 49, −2) in Montreal Neurological Institute (MNI) space. Physiological and other spurious sources of noise were removed using two separate preprocessing approaches described below (Fig. 1). A temporal band-pass filter of 0.009 Hz to 0.08 Hz was applied. Residual head motion parameters (3 rotation and 3 translation parameters, plus another 6 parameters representing their first-order temporal derivatives) were regressed out.

Fig. 1.

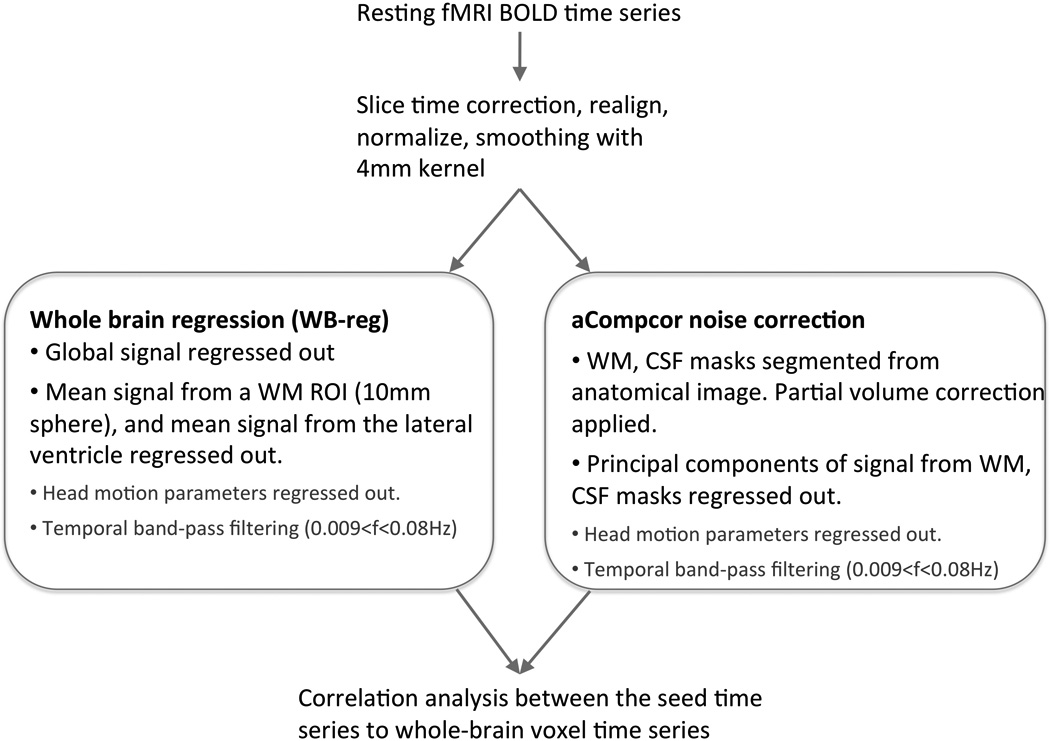
Illustration of the data analysis methods. The two preprocessing methods are shown in the boxes.

a) Whole brain signal regression (WB-reg)

The average signal over all voxels (global mean) was computed for each time point and used as a temporal covariate and removed using linear regression. In addition, signal from a 10-mm sphere ROI located in the center of the white matter and signal from the lateral ventricle were also removed (Fox et al., 2005b; Vincent et al., 2006).

b) Anatomical CompCor (without global signal regression)

Instead of removing the global signal, non-neuronal sources of noise were estimated and removed using the anatomical CompCor method (aCompCor) (Behzadi et al., 2007). The anatomical image for each participant was segmented into white matter (WM), grey matter, and CSF masks using SPM5. To minimize partial voluming with grey matter, the WM and CSF masks were eroded by one voxel and used as noise regions of interest (ROI) (Fig. S1a). The average volume of the white matter ROI before and after the one-voxel erosion was 622 cm³ and 198 cm³, respectively (68% of white matter voxels were removed by the erosion process). The average CSF ROI volume before and after the one-voxel erosion was 436 cm³ and 20 cm³, respectively (96% of CSF voxels were removed by erosion). The average volume of the whole-brain mask that was used to estimate global signal was 1831 cm³. Principal components of the signals from WM and CSF noise ROIs were removed with regression. Signals from the WM and CSF ROIs were always extracted from the unsmoothed functional volumes.

We examined the connectivity maps after removing 1, 3, 5, or 10 principal components (PCA1 – PCA10) from the WM and CSF noise ROIs in order to determine the optimal configuration of the aCompCor approach for resting-state connectivity analysis.

Correlation maps were produced by extracting the residual blood oxygen level–dependent (BOLD) time course from the MPFC seed and computing Pearson’s correlation coefficients between that time course and the time course of all other voxels. Correlation coefficients were converted to normally distributed z-scores using the Fisher transformation to allow for second-level General Linear Model analyses. For each preprocessing stream, the group connectivity map was created by performing a random effects one-sample t-test across all participants.

Creation of ROIs

To compare across different preprocessing methods, we created ROIs for representative regions that were positively correlated or anticorrelated with the MPFC seed, following Fox et al., (2005). The positively correlated ROIs included major nodes of the default mode network, the medial prefrontal cortex (MPFC), posterior cingulate cortex (PCC), left lateral parietal cortex (LLP), and right later parietal cortex (RLP). Anticorrelated ROIs included the left and right dorsolateral prefrontal cortex (DLPFC), left and right inferior parietal lobule (IPL), supplementary motor area (SMA), and frontal eye field (FEF). The ROIs were created using the following steps: 1) Group-level connectivity maps from each method (whole brain regression, and 4 aCompCor preprocessing streams with 1, 3, 5, and 10 PCA components from the noise ROIs) were created. 2) A mask for positively-correlated regions and a mask for anticorrelated regions were created for each method from the connectivity map with the threshold of p < .001, uncorrected. 3) A union operation was performed in SPM Imcalc on masks from all methods to create a combined mask for correlated regions and a combined mask for anticorrelated regions across different methods. 4) Each ROI was restricted with the corresponding Brodmann area(s) from Fox, et al. (2005). These ROIs for positively correlated and anticorrelated regions with MPFC (Fig. 3) were later used to further examine the connectivity magnitude and specificity of different preprocessing approaches via pair-wise t-tests. The rationale for using the union masks was to make sure we include regions that were only present for a subset of the methods. Since the CompCor approach which regressed out one principal noise signal component did not result in significant negative correlations in several task-positive regions, a union mask was used to examine the differences among the different analyses. To examine the positive connectivity strengths in more restricted ROIs, we re-created the MPFC and PCC ROIs as intersections of the correlation maps from different methods, using a more strict threshold (p < .05 FWE-corrected) (Fig. S4).

Fig. 3.

Functional connectivity maps from the MPFC seed across all participants. a) whole brain regression b) aCompCor, regressing out 5 principal components of the noise ROIs signal.

Specificity comparison of the different preprocessing streams

To examine the specificity of each preprocessing approach, we compared group-level connectivity values from regions showing significant correlation or anticorrelation with the MPFC seed with the connectivity values from two reference regions in the visual cortex (Van Dijk et al., 2010) to the MPFC seed in which no correlation is expected with the MPFC. The reference regions were 10-mm spheres that were centered around MNI coordinates (−30, −88, 0) and (30, 88, 0). Following Weissenbacher et al. (2009), we define specificity as

$$S_{\text{target}}=\frac{\left|Z_{\text{target}}\right|-\left|Z_{\text{reference}}\right|}{\left|Z_{\text{target}}\right|+\left|Z_{\text{reference}}\right|}$$

Z_target is the group-level fisher’s Z score from the MPFC to the anticorrelated or positive correlated ROIs described above. Z_reference represents the average fisher’s z scores from MPFC to the left and right visual reference regions. Specificity of the target ROI S_target ranges from −1 to 1.

To compare the specificity for different methods, we use a bootstrapping procedure (resampling with replacement). The resampling technique consisted of creating a high number (10^6) of new datasets from the original dataset by resampling with replacement across subjects. Each new dataset consists of 15 data points, obtained from the original data by choosing 15 subjects at random. Then for each of these new dataset, specificity from the group-level averages was computed. The resulting distribution of values represents the expected distribution of specificity values in the population. Hypothesis test p-values were obtained by computing the corresponding percentages in the obtained distributions (e.g. the p-value for comparing the specificity for one PCA method vs. the specificity for the whole brain regression method was obtained by computing the percentage of times, from the multiple datasets, where the specificity resulting from one PCA method was higher than the specificity resulting from the whole brain regression method). p-values of two-sided tests are reported.

3. Results

Distribution of the correlation values before and after whole brain signal regression or aCompCor preprocessing is shown in Fig 2. Correlation values were predominantly in the positive range before whole brain regression or aCompCor. Whole brain regression shifted the distribution towards the negative range.

Fig. 2.

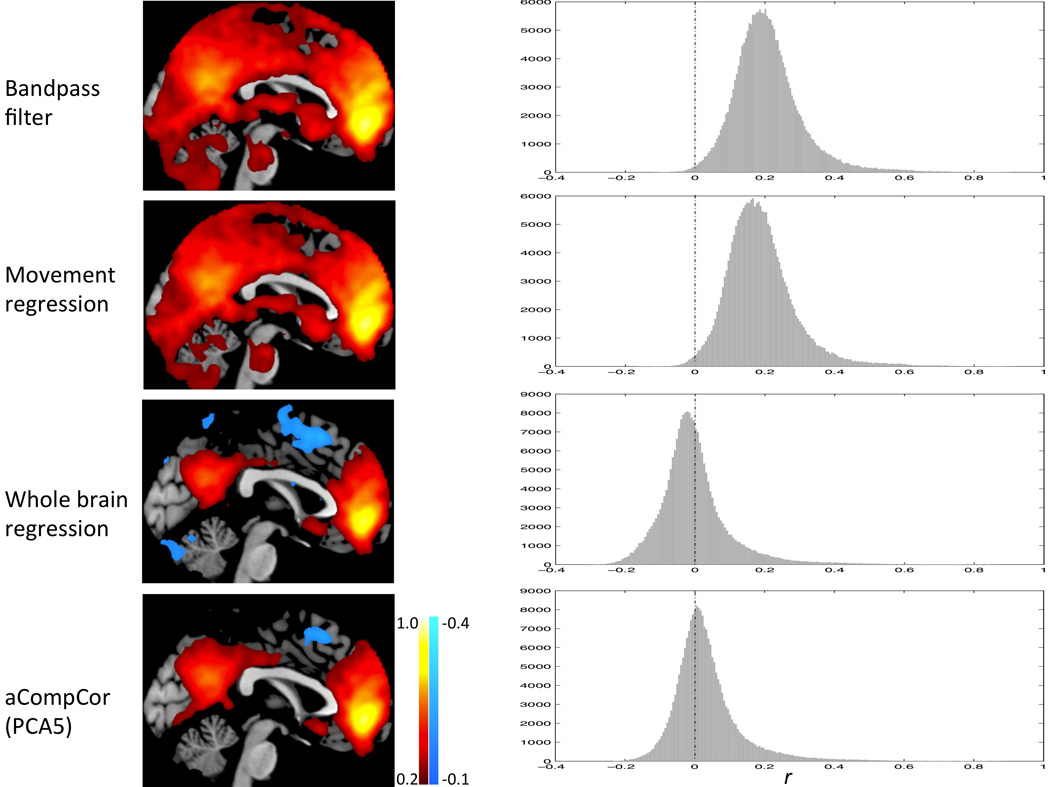
Connectivity maps (left panel) and correlations values distribution (right panel) after each preprocessing step.

Regions positively correlated with the MPFC seed, including the posterior cingulate cortex, left and right lateral parietal cortices, bilateral parahippocampal gyri, bilateral inferior temporal cortices, were consistent across the both the whole brain regression and aCompor approaches. Regions anticorrelated with the MPFC, including bilateral DLPFC, bilateral IPL, SMA, and FEF, were present under both the whole brain regression approach and the aCompCor processing streams when more than one PCA components were removed (Table 1, Fig. 3). These positively and negatively correlated regions corresponded closely to previously reported default mode network and task-positive networks (Fox et al., 2005b; Fransson, 2005).

Table 1.

Group-level peak t-values of the regions negatively (top) and positively (bottom) correlated with the MPFC seed.

		Standard method	aCompCor
			PCA1	PCA3	PCA5	PCA10
Anticorrelated regions	L DLPFC	10.84	n.s.	7.02	9.67	7.92
	R DLPFC	9.73	n.s.	8.17	7.23	6.44
	L IPL	10.53	8.76	8.67	10.21	12.25
	R IPL	8.18	6.07	7.55	7.90	6.96
	SMA	8.02	n.s.	5.40*	6.48	5.87
	R FEF	7.44	n.s	5.79*	5.93*	6.06
Positive- correlated regions	MPFC	22.06	24.19	22.78	24.65	20.72
	PCC	14.58	18.03	16.24	15.91	13.83
	L LP	8.47	9.76	10.66	8.53	6.79
	R LP	7.18	12.88	10.16	8.81	7.80
	L PHG	9.96	11.13	10.41	9.63	8.75
	R PHG	8.08	10.02	11.19	11.34	9.15
	L IT	10.50	10.07	9.51	7.35	8.22
	R IT	9.40	11.48	8.92	8.36	10.32

The aCompCor results are shown separately after regressing out 1, 3, 5, or 10 principal components (PCA1, PCA3, PCA5, and PCA10) from noise ROIs. Regions listed survived a height threshold of p < 0.001, and an extent threshold of FWE-corrected p < 0.05 at the cluster-level, unless noted otherwise by *.

^*These clusters did not pass the cluster-level correction but survived voxel-wise FDR correction at p < 0.05.

We further investigated the magnitude and specificity of the connectivity values of each processing stream in subsequent ROI analysis, using masks for correlated and anticorrelated regions described above (Fig. 4).

Fig. 4.

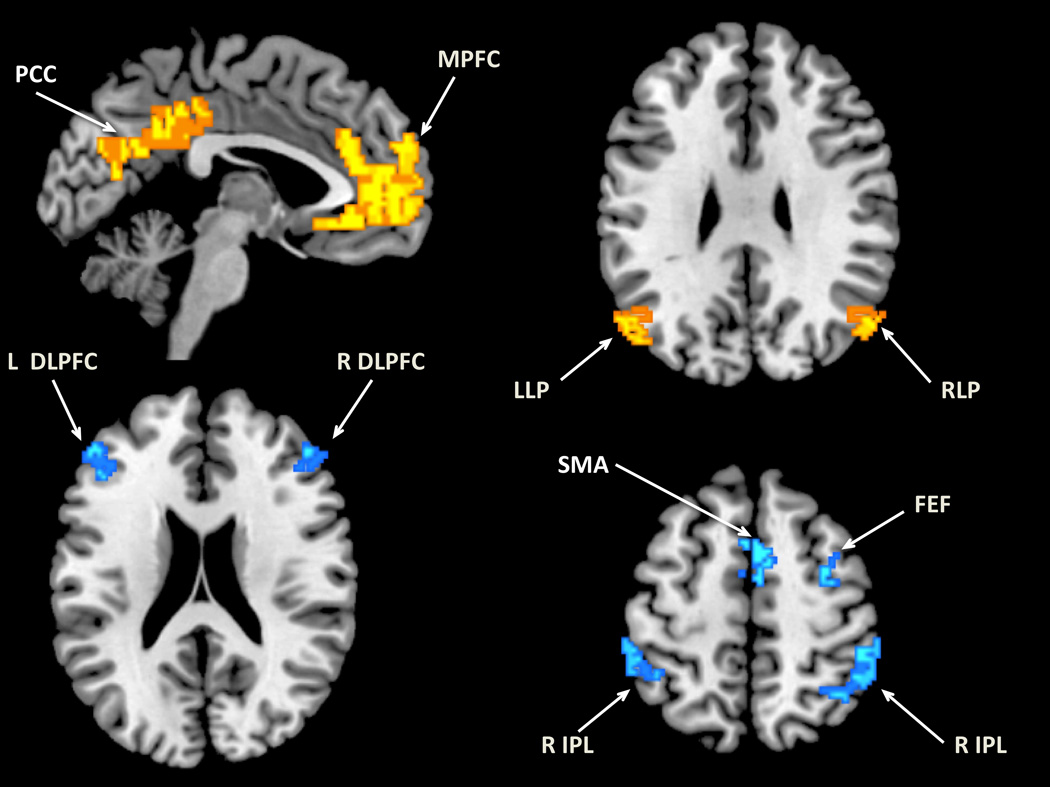
Regions of interest used in the comparison of different analysis methods. Yellow: positively-correlated ROIs. Blue: anticorrelated ROI.

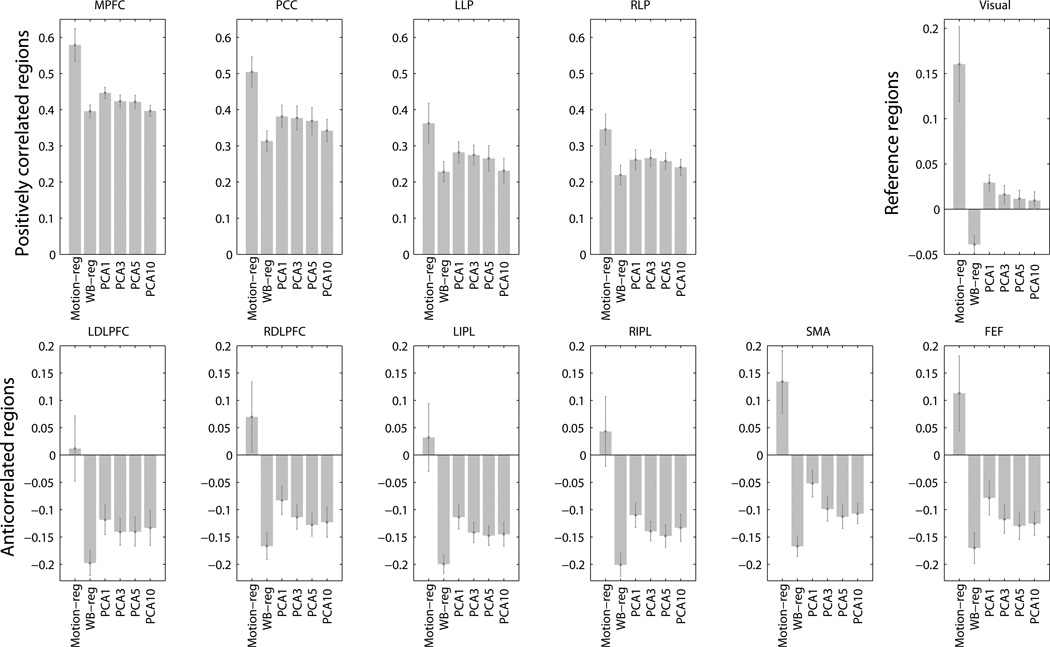
3.1 Magnitude of connectivity (Fig. 5)

Fig. 5.

Connectivity from the MPFC seed to the positively correlated ROIs (top left panel), anticorrelated ROIs (bottom panel), and functional related reference ROIs (top right panel). Motion-reg: motion regression, without global regression or aCompCor. WB-reg: whole brain regression. PCA1 – PCA10: aCompCor processing streams after regressing out 1 – 10 principal components of noise ROI signal. Bars represent the mean of the group. Error bars are standard errors.

Positively correlated regions

Compared to the whole brain regression method, positive correlations were significantly higher or trended toward significance with the aCompCor approach when 1 (PCA1: MPFC, p = .0002, PCC, p = .0004, LLP, p = .003, RLP p = .008), 3 (PCA3: MPFC, p = .018, PCC, p = .003, LLP, p = .009, RLP p = .004), or 5 (PCA5: MPFC, p = .06, PCC, p = .02, LLP: p = .1, RLP, p = .07) principal components from the noise ROIs were removed. When neither global signal nor principal components of the signal from aCompCor noise ROI was regressed out, positive correlations were much higher, which reflected the overestimation of correlations due to noise.

Anticorrelated regions

Compared to the whole brain regression approach, anticorrelation strengths were less strong under the aCompCor processing streams (ps < .05). Nevertheless, anticorrelations between the MPFC seed and all 6 anticorrelation ROIs were significant with the aCompCor approach when 3, 5, or 10 PCA components were removed (PCA3 – 5) (ps < 0.001). When only the first noise PCA component was removed (PCA1), inferior parietal lobule ROIs (left and right IPL) were anticorrelated with the MPFC seed at p < .001 level, while the anticorrelation between MPFC and DLPFC regions (ps < .005) and FEF (p =. 03) were less strong. The SMA anticorrelation with MPFC seed was not significant when only the first principal component was removed (p = .11). No negative correlations emerged when neither global signal nor principal components of the signal from aCompCor noise ROI were regressed out,

Reference regions

Connectivity from MPFC to functionally unrelated regions (in which neither positive nor negative correlations were expected) was assessed using the average connectivity between the MPFC and the two visual reference regions (10-mm spheres around (−30, −88, 0) and (30, 88, 0)) (Van Dijk et al., 2010). There was artifactual anticorrelation between MPFC and the reference regions when the whole brain regression approach was applied (t(14) = 3.99, p = .001). With the aCompCor approach, connectivity between MPFC and the reference regions not significant when 3, 5, or 10 noise principal components were removed (PCA3 – 10) (ps > .14). When a single principal component from noise ROIs was removed (PCA1), there was artifactual connectivity between MPFC and the reference regions (t(14) = 3.21, p = .006). When neither global signal nor principal components of the signal from aCompCor noise ROI was regressed out, we also observed artifactual connectivity between the MPFC and the reference regions (t(14) = 3.71, p = .002).

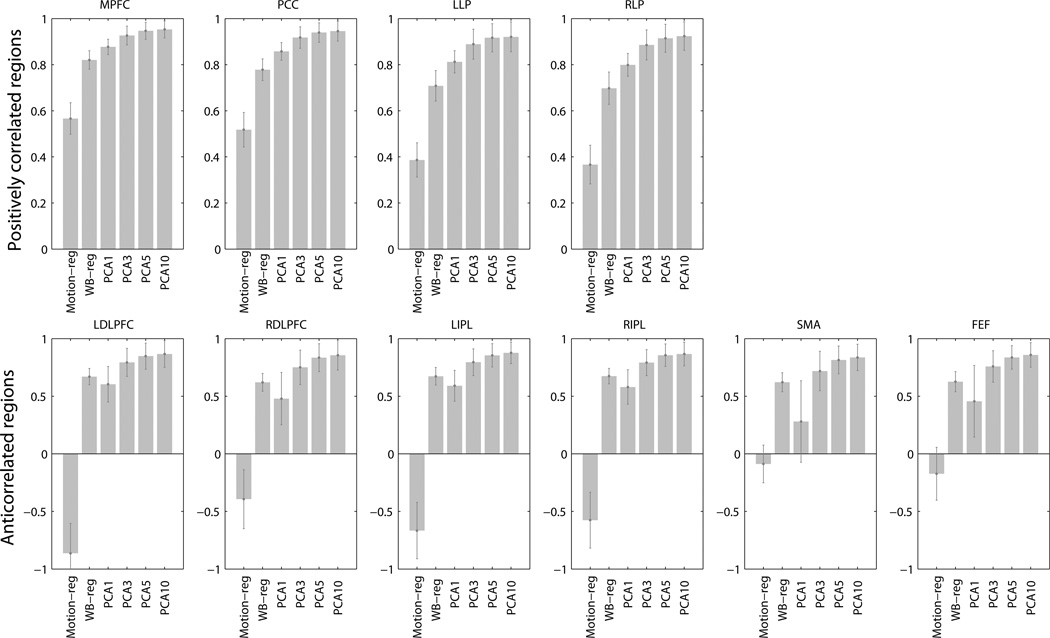
3.2 Specificity (Fig. 6)

Fig. 6.

Specificity for positively correlated (top) and anticorrelated (bottom) ROIs. Motion-reg: motion regression, without global regression or aCompCor. WB-reg: whole brain regression. PCA1 – PCA10: aCompCor processing streams after regressing out 1 – 10 principal components of noise ROI signal. Error bars are standard errors.

Specificity of the whole brain regression approach was compared against specificity of the aCompCor approach using the resampling simulation procedure described above (N = 10^6 iterations). Compared to the whole brain regression approach, specificity for positively correlated regions was higher with the aCompCor approach when 5 or 10 PCA components from noise ROI signal were removed (PCA5: PCC, p = .022, LLP, p = .028, RLP, p = .022, MPFC, p = .038; PCA10: PCC, p = .032; LLP, p = .05; RLP; p = .032, MPFC, p = .046). There was a trend for higher specificity for positively correlated regions when 3 PCA components were removed compared to the whole brain regression approach (PCC, p = .060, LLP, p = .066, RLP, p = .058, MPFC, p = .1). There was no difference in specificity for these regions between whole brain regression and the aCompCor approach when only 1 PCA noise component was removed. Specificity for anticorrelated regions did not differ between aCompCor approach and the whole brain regression approach (ps > .1). Specificity was the lowest when neither global signal nor principal components of the signal from aCompCor noise ROI was regressed out.

Results from more conservative white matter and CSF noise ROIs, created by further erosion of the white matter/CSF masks by two voxels, are presented in supplementary material (Table S1; Fig. S2). To further compare the whole brain regression approach with the aCompCor approach, we ran an additional analysis which included 5 or 10 principal components of the global signal. Results from this additional analysis are included in the supplementary material (Fig. S3).

4. Discussion

We examined the magnitude and specificity of resting-state connectivity using two different data processing methods, to test the hypothesis that anticorrelation during rest is not artificially introduced by global signal regression. Our results highlight that the global regression can result in artifactual anticorrelations (as found between MPFC and functionally unrelated reference regions). In contrast, the aCompCor approach correctly removes these effects (no associations found between MPFC and reference areas) when sufficient number of representative components are extracted from noise ROIs (3 or above components) without incurring in artifactual anticorrelations. Robust anticorrelations between the default and task-positive network regions emerged when the aCompCor method was applied. Our results suggest that aCompCor is more effective in correcting for spurious noise sources compared to global regression, and that anticorrelations observed in resting-state connectivity cannot be fully attributed to artifacts introduced by global signal regression and might be neuronal in origin.

Several lines of evidence from human and animal research also support the functional significance of resting-state anticorrelations. First, global signal does not distribute specifically to regions in the anticorrelated networks (Fox et al., 2009), but anticorrelation between the two networks that typically show the opposite activation patterns during task performance, the default mode network and the task-positive network, has been consistently reported by multiple studies (Fox et al., 2005b; Fransson; Kelly et al., 2008; Uddin et al., 2009). Second, anticorrelated relationships between the default mode and executive attention components of the resting-state networks have been found using an independent component analysis (ICA) approach, which does not involve global signal regression (Cole et al., 2010; Zuo et al., 2010). Third, computational simulations of monkey and human brains suggest existence of spontaneous anticorrelated networks (Deco et al., 2009; Honey et al., 2007; Izhikevich and Edelman, 2008). Finally, neuronal origins of the anticorrelated fluctuations in the BOLD signals have been explored by electrophysiological work in cats, in which anticorrelated fluctuations of local field potential have been shown between homologs of the task-positive and default mode systems in cats (Popa et al., 2009).

Compared to the whole brain regression preprocessing method, our results suggest that a preprocessing stream using aCompCor, combined with the bandpass filtering and modeling of movement parameters, may provide better sensitivity and specificity to detect positive correlations in resting-state networks, while anticorrelations under the aCompCor approach are similar to those with global signal regression. Physiological and subject-movement noise sources are known to introduce artifactual positive associations between potentially unconnected areas. When attempting to correct for these spurious effects our analyses show, in agreement with Murphy et al (2009)’s rationale, that the global signal regression method can effectively overshoot and introduce artifactual negative associations (as found between MPFC and functionally unrelated reference regions), while the aCompCor method provides a more valid control (showing no associations between MPFC and reference regions). Also in agreement with Murphy et al’s rationale, the connectivity between positively associated regions (e.g., MPFC and PCC) seems to be undersestimated when using global signal regression, compared to the aCompCor method. One possible explanation for the higher positive correlations under aCompor is that the global signal may contain neural signal (Scholvinck et al., 2010), and therefore removing the global signal will reduce the estimated effects as well as the power to detect positive correlations. Moreover, the non-homogeneous distribution of noise in the brain is not captured by the global signal, but is potentially represented by the higher order principal components from the noise ROIs, which is consistent with our results showing that a single principal component from the noise ROIs only partially but not fully removes artifactual associations between MPFC and the reference regions. Since global signal regression shifts the correlation coefficients distribution to the more negative range, it is also not surprising to see anticorrelation strengths to be the strongest under global signal regression.

Alternative physiological noise correction methods have been used to examine anticorrelations in resting-state fMRI data (Chang and Glover, 2009). Chang and Glover (2009) tested the effects of removing time-locked cardiac and respiratory artifacts (RETROICOR) (Glover et al., 2000) and low-frequency respiratory and heart rate effects (Birn et al., 2008; Chang et al., 2009). Physiological noise correction enhanced the extent of negative correlations. Here we showed that aCompCor was effective in characterizing noise of non-neural origin, yielding robust group-level anticorrelations. It is possible that other physiological noise not modeled by Chang and Glover (2009), such as nonlinear interactions between respiratory and cardiac effects, may be captured in aCompCor. The two approaches combined together might provide even better noise correction in resting-state fMRI data analysis.

Negative correlations are in general weaker in magnitude than positive correlations. This could be due to the more varied temporal dynamics of anticorrelations compared to positive correlations in resting-state BOLD connectivity. Chang and Glover (Chang and Glover, 2010) showed that the degree of anticorrelation between the default mode network and the task-positive network exhibited considerable fluctuation within the course of a single session. Furthermore, the dynamic interactions between the default mode and executive control network have been shown to be modulated by nicotine administration in abstinent smokers (Cole et al., 2010). Variability in the strength of the anticorrelation between the default mode and executive control networks was linked with individual differences in symptom improvement after nicotine replacement therapy, suggesting the functional significance of state-dependent dynamics in anticorrelations between the two networks (Cole et al., 2010). The majority of the studies so far have only tested stationary relationships in resting state connectivity. Future studies are needed to better understand the temporal dynamics between brain regions in the resting state.

When higher numbers of principal components from the noise ROIs were regressed out, artifactual connectivity between the MPFC and functionally unrelated (reference) regions was reduced, suggesting that removing higher number of PCA components resulted in more effective noise correction. Residual confounding effects introduced by physiological and subject motion are not spatially homogeneous enough to be captured by a single temporal component. Higher number of PCA components allows these noise effects to be characterized by a more complex set of temporal series and effectively removed, which eliminated the artifactual correlations in the reference regions. However regressing out too many PCA components (10 components) seemed to reduce correlation strengths, especially positive correlations, at a similar rate as the reduction observed in the reference region. This is reflected in the approximate saturation of the specificity results (Fig. 6) when extracting 5 or above components from each noise ROI, consistent with the findings from Behzadi et al. (2007) which estimated the number significant components for to be around 6. It is possible that higher PCA components from the noise ROI may share spectral characteristics with the neural signal which, paired with the associated reduction in degrees of freedom, may limit the benefits of removing additional components from the noise ROIs. It is possible the noise signal estimated from the WM/CSF masks still overlapped in a small portion with signal from grey matter. However the extent of the contamination from grey matter signal should be minimal compared to the global regression method. If the WM/CSF regressors share a significant portion of its variance with the global signal regressor, one would expect similar patterns of correlations when comparing the aCompCor method to a method that removes principal components obtained from whole-brain voxels. In contrast we observe (Fig. S3) faster reduction in spurious correlations with reference regions and slower decay of correlations with positively and negatively correlated areas when using the aCompCor method compared to regressing out principal components of the global signal. This suggests important qualitative differences between those signals represented by the aCompCor components and the global signal. Using more restrictive noise ROIs masks created by eroding the WM/CSF masks by two voxels, we showed that significant anticorrelations to task-positive regions still emerged when higher number of principal components were regressed out (Fig. S2). Therefore we believe the CompCor method is a reasonable alternative to the global regression method, which mathematically creates artifactual negative correlations, as shown by Murphy et al., 2009. Based on the present analysis, we propose that removing 5 principal components from noise ROIs, modeling residual motion, and performing temporal pass-filtering are recommended in a resting-state connectivity preprocessing stream.

In conclusion, we demonstrated that when physiological and other noise sources were effectively removed, anticorrelations between the default network and task-positive network were present without global signal regression and therefore may be of biological importance. Future work in resting state connectivity should consider noise correction methods without global signal regression, such as the one presented in the present study, possibly in combination other physiological noise correction methods such as the ones described in Chang & Glover (2009).

• Resting-state connectivity analysis without global signal regression.

• Principal components from noise regions-of-interest were regressed out (CompCor).

• Robust anticorrelations were observed under CompCor.

• Specificity was equal or higher under CompCor compared to global signal regression.