An fMRI Study of Magnitude Comparison and Exact Addition in Children

Abstract

By contrast to the adult literature, in which a consistent parieto-frontal network for number processing has been identified, the data from studies of number processing in children have been less consistent, probably due to differences in study design and control conditions. Number processing was examined using functional MRI in 18 right-handed children (8–12 years) from the Cape Coloured community in Cape Town, South Africa using Proximity Judgment (PJ) and Exact Addition (EA) tasks. The findings were consistent with the hypothesis that, as in adults, the anterior horizontal intraparietal sulcus (HIPS) plays a major role in the representation and manipulation of quantity in children. The posterior medial frontal cortex, believed to be involved in performance monitoring in more complex arithmetic manipulations in adults, was extensively activated even for relatively simple symbolic number processing in the children. Other areas activated to a greater degree in the children included the left precentral sulcus, which may mediate number knowledge, and, for EA, the head of the caudate nucleus, which is part of a fronto-subcortical circuit involved in the behavioral execution of sequences. Two regions that have been linked to number processing in adults—the angular gyrus and posterior superior parietal lobule—were not activated in the children. The data are consistent with the inference that, although the functional specialization of the anterior HIPS may increase as symbolic number processing becomes increasingly automatic, this region and other elements of the parieto-frontal network identified in adults are already reliably and robustly activated by middle childhood.

Introduction

A reproducible set of parietal and frontal areas has been identified in adults that is systematically activated during the manipulation of numerical quantities (Chochon, Cohen, van de Moortele, & Dehaene, 1999; Dehaene, Piazza, Pinel, & Cohen, 2003; Zago, Petit, Turbelin, Andersson, Vigneau, & Tzourio-Mazoyer, 2008). The frontal activations do not appear to be specific to numerical processing and are believed to relate to the integration and management of numerical operations in working memory, response decision and execution, and error monitoring. Thus, for example, intensity of inferior frontal activation is directly proportional to the time pressure imposed during a number processing task rather than the complexity of the numerical calculation per se (Menon, Rivera, White, Glover, & Reiss, 2000). By contrast, three parietal areas—the anterior horizontal segment of the intraparietal sulcus (HIPS), the posterior superior parietal lobule (PSPL), and the angular gyrus— relate to quantity representation and manipulation. Data from lesion and functional Magnetic Resonance Imaging (fMRI) studies have linked bilateral activation of the anterior HIPS with representation of semantic information about magnitude, whether presented as Arabic numbers, sequences of words, or analogically (e.g., by numbers of dots) (Dehaene & Cohen, 1995; Naccache & Dehaene, 2001). Activations in the anterior HIPS are seen in response to numbers even when no arithmetic manipulation is required (Eger, Sterzer, Russ, Giraud, & Kleinschmidt, 2003) and are sensitive to the “distance effect,” that is, they are activated more in a number comparison task when the participant makes the more difficult discrimination between two close numbers (e.g., 3 and 4) than when s/he compares two more distant numbers (e.g., 3 and 12) (Pinel, Dehaene, Riviere, & Le Bihan, 2001).

The neural circuitry crucial for abstract representation of quantity is based in parietal regions that overlap closely with neural circuits involved in visuo-spatial representation (Hubbard, Piazza, Pinel, & Dehaene, 2005; Simon, Mangin, Cohen, Le Bihan, & Dehaene, 2002). The anterior HIPS, which is activated by semantic representation of quantity and distance relations, is believed to be homologous to the ventral intraparietal area in the macaque monkey, which contains neurons that fire in response to specific numerosities (Dehaene, Molko, Cohen, & Wilson, 2004; Nieder & Miller, 2003)) and is adjacent to the lateral intraparietal area, which mediates shifts in visuospatial attention (Hubbard et al., 2005). A second parietal area involved in number processing, the PSPL, is activated during counting (Piazza, Giacomini, Le Bihan, & Dehaene, 2003) and during a variety of visual-spatial tasks, including attention orienting and mental rotation. The third parietal area, the left angular gyrus, which participates in the adjacent perisylvian language processing network, is activated during retrieval of addition and multiplication facts (Delazer et al., 2005; Simon et al., 2002; Stanescu-Cosson, Pinel, van de Moortele, Le Bihan, Cohen, & Dehaene, 2000) and in other language-mediated processes, such as phoneme detection. Within this frontoparietal network, researchers have noted dissociations between two distinct aspects of number processing: magnitude comparison (e.g., Number Comparison—"Which number is larger?"; Proximity Judgment—"Which of two numbers is closer to a third?") and calculation (e.g., Addition) (Dehaene & Cohen, 1997; Menon et al., 2000).

Several recent studies have used fMRI to compare the neural networks that are activated during number processing in adults and children. Using an event-related odd ball task, in which the standard was a 16-dot array, Cantlon, Brannon, Carter and Pelphrey (2006) compared brain activations during deviant trials in which the number of dots was varied (32 instead of 16) and in deviant trials where shape was varied (squares instead than dots). When compared with the standard, the deviant number condition elicited strikingly similar increased activations in the right anterior HIPS in both 4-year-old children and adults, indicating that this region is recruited for magnitude comparison early in development, well before formal school training in number processing is begun.

Rivera, Reiss, Eckert and Menon (2005) compared simple addition and subtraction in 17 children ranging from 8 to 19 years of age, using a correlational design. Activations of two brain regions increased as the children grew older—the left supramarginal gyrus extending into the intraparietal sulcus, which corresponds to Dehaene et al.’s (2003) anterior HIPS; and the left lateral occipital cortex, a region believed to be involved in the transfer of lexical arithmetic symbols to the parietal cortex (Pinel et al., 2001). Activations of five areas decreased with age—prefrontal cortex, including anterior cingulate cortex and left precentral sulcus; left medial temporal lobe (hippocampus and parahippocampus); basal ganglia; left insula; and brain stem. Although these correlational data provide important information about age-related changes in the neural activations involved in simple arithmetic calculation, Rivera et al. did not directly examine which regions are activated during exact addition and subtraction in childhood.

Several studies have examined the role of the anterior HIPS and other brain structures in number processing in elementary school age children, but their findings are inconsistent. In one study involving simple addition, subtraction, and multiplication, activations were seen within the intraparietal sulcus but fell short of statistical significance, possibly due to small sample size (Kawashima et al., 2004). In another study of exact addition, bilateral activations of the HIPS were reported (Kucian, Loenneker, Dietrich, Dosch, Martin, & von Aster, 2006), but none of the activations in the anterior cingulate, precentral sulcus, basal ganglia, or other regions that would be expected in childhood based on Rivera et al.’s (2005) correlational data were seen. Three studies comparing small vs. large numerical distances (the “distance effect”) in children found no activation of the anterior HIPS (Ansari & Dhital, 2006; Ansari, Garcia, Lucas, Hamon, & Dhital, 2005; Kaufmann et al., 2006), yet a fourth study examining nonsymbolic magnitude comparison reported greater anterior HIPS activations in children than adults (Kaufmann et al., 2008). Most recently, Davis et al. (2009) examined neural correlates of simple and complex versions of exact and approximate addition in adults and third grade children and reported significantly weaker activations in posterior parietal brain regions in the children. While they reported inferior parietal activations, corresponding to Dehaene et al.’s (2003) anterior HIPS, in the children in three of their tasks, the children exhibited no significant parietal activations during simple single-digit exact calculation. One important limitation that could account for some of these inter-study differences is that several of the studies used a fixation point or gray scale stimulus rather than numbers or number-like symbols as control conditions.

This study was designed to examine the role of the HIPS and other brain structures that have been identified in number processing studies with adults in a sample of healthy, normally developing elementary school age children engaged in tasks involving magnitude comparison and exact addition. The activation of a parieto-fronto-cingular network generally similar to that identified in previous studies with adults was predicted. One focus of this study was to attempt to clarify the role of the anterior HIPS in number processing in childhood in light of the inconsistent evidence that has emerged from the developmental studies conducted to date.

Methods

Participants

Participants were 18 right-handed, 8- to 12-year-old children from the Cape Coloured community in Cape Town, South Africa, who were recruited to serve as typically developing controls for neurodevelopmental studies of children with fetal alcohol spectrum disorder. The Cape Coloured is a mixed ancestry population, comprised of descendants of white European settlers, Malaysian slaves, Khoi-San aboriginals, and black African ancestors. All the participating children were healthy with no history of neurological or psychiatric illness, and none was on medication. Demographic and sample characteristics are summarized in Table 1 for the 16 children who provided usable data on either or both fMRI tasks. Although the sample was economically disadvantaged, the families were intact and stable.

Table 1.

Demographic Background and Sample Characteristics (N = 16^*)

	N (%)	Mean (SD)	Range
Socioeconomic status (Hollingshead Scale)
V. Unskilled	10 (62.5)
IV. Semi-skilled	3 (18.8)
III. Skilled craftsmen, clerical, sales	3 (18.8)
Maternal education (years)		8.6 (2.1)	6.0 – 12.0
Child’s gender
Male	6 (37.5)
Female	10 (62.5)
Child’s age at assessment (years)		10.5 (1.2)	8.2 – 12.6

^*16 children provided usable data on either or both of the fMRI tasks

Procedure

A staff driver and research nurse transported the mother and child from their home to the University of Cape Town for a neuropsychological assessment. Each child was assessed on 7 of the 10 subtests from the Wechsler Intelligence Scale for Children, third edition (WISC-III)—Similarities, Arithmetic, Digit Span, Symbol Search, Coding, Block Design, and Picture Completion—and Matrix Reasoning from the WISC-IV. IQ was estimated from these subtests using Sattler’s (1992) formula for computing Short Form IQ; validity coefficients for Sattler Short Form IQ based on five or more subtests consistently exceed r = .90. Handedness was assessed on the Annett (1970) Behavioral Handedness Inventory. Only right-handed children were recruited for scanning. Each child was also administered an assessment of Number Processing developed in collaboration with Dehaene (Jacobson, Dodge, Dehaene, Chiodo, Sokol, & Jacobson, 2003; Kopera-Frye, Dehaene, & Streissguth, 1996), which included 16-item subtests focusing on Exact Addition, Proximity Judgment, and Number Comparison. The mothers were interviewed to provide information regarding demographic background and the child’s health history. The child was rated by his/her classroom teacher for behavioral symptoms of attention deficit hyperactivity disorder (ADHD) on the Disruptive Behavior Disorders Scale (Pelham, Gnagy, Greenslade, & Millich, 1992). Within a few weeks after the neuropsychological assessment, the mother and child were transported to Groote Schuur Hospital, which is adjacent to the University of Cape Town Faculty of Health Sciences campus, for a neuroimaging assessment. Written informed consent was obtained from the mothers and oral assent from the children. Approval for human research was obtained from the Wayne State University Human Investigation Committee and University of Cape Town Research Ethics Committee. Mothers and children were given breakfast and a snack during the visit. The mother received a small monetary compensation and photograph of her child, and the child was given a small gift.

Magnetic Resonance Imaging protocol

All scans were acquired using a 1.5T Magnetom Symphony MRI scanner (Siemens Medical Systems, Erlangen, Germany). High-resolution anatomical images were acquired in the sagittal plane using a three-dimensional inversion recovery gradient echo sequence (72 slices, TR = 1900 ms, TE = 3.93 ms, TI = 1100 ms, slice thickness 2 mm), 250 × 250 mm field of view, resolution 1.4 × 1.0 × 2 mm. During the fMRI protocol, 154 functional volumes sensitive to blood oxygen level dependent contrast were acquired with a T2*-weighted gradient echo, echo planar imaging sequence (TR = 2000 ms, TE = 50 ms, 20 interleaved slices, 5 mm thick, gap 1 mm, 230 × 230 mm field of view, resolution 3.6 × 3.6 × 5 mm).

Functional MRI experimental tasks

Two fMRI tasks involving number processing were administered: Exact Addition (EA) and Proximity Judgment (PJ) ("Which of two numbers is closer to a third number?”). Each child practiced these tasks initially in a mock scanner built for this study, which was important in reducing anxiety and facilitating completion of the MRI scans. The experimental tasks were programmed using E-Prime software (Psychology Software Tools, Inc., Pittsburgh, USA) and were presented using a data projector and a rear projection screen mounted at the foot of the patient bed. Subjects held a Lumitouch response system (Photon Control Inc., Burnaby, Canada) in their right hand and responded using their right index and middle fingers. The child was able to talk to the examiner using an intercom that is built into the scanner and could stop the scan at any time by squeezing a ball held in his/her left hand.

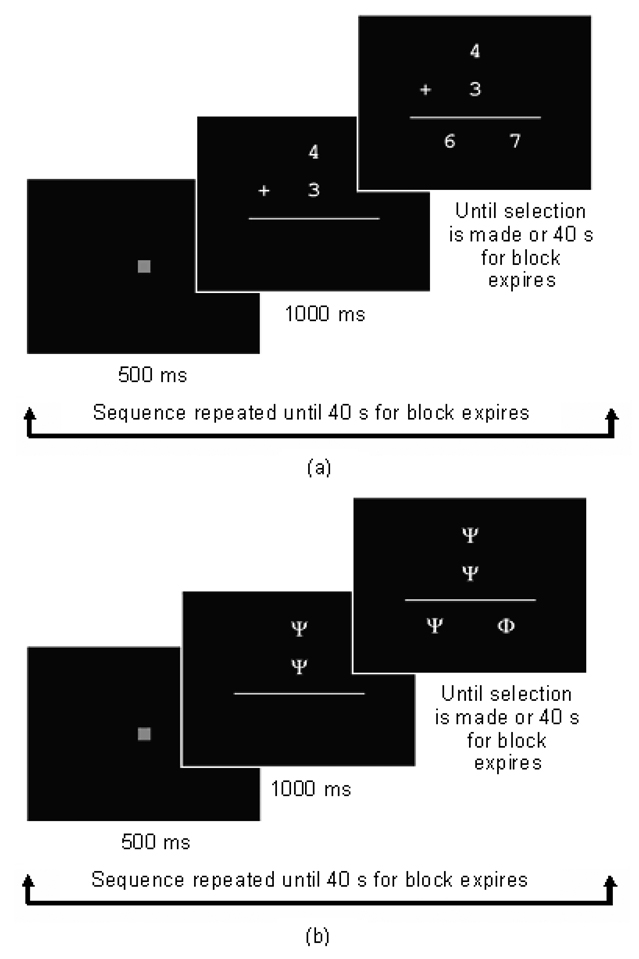
The EA and PJ tasks were administered using a self-paced block design, in which the child completes as many problems as possible during each 40s block. In the active blocks, a fixation square is displayed for 500ms prior to each problem (Fig 1a). In EA, two numbers are displayed one above the other for 1000ms, after which two possible solutions appear horizontally below the two numbers. The display remains on the screen until either the child makes a selection or the 40s time limit for the block expires. Sums were selected randomly from a list in which the solution was never greater than 12 and from which tie problems (e.g., 2+2) and sums involving unity had been excluded. The child is instructed to add the top two numbers together and select the correct answer from the two choices displayed below. The child makes a selection by pressing the button on the same side as the correct answer. The EA control (EACTL) blocks follow the same format, but with two identical Greek symbols displayed vertically initially for 1000ms (Fig 1b). Two different symbols are then displayed horizontally below the vertical symbols, and the child selects the one that is identical to the initial two by pressing the button on the side of that symbol. Each block is repeated three times in the following order: EA, EACTL, rest, EA, EACTL, rest, EACTL, EA, rest. In the rest blocks the fixation square is displayed for 20s, resulting in a total task duration of 5 min.

Figure 1.

Schematic of task design showing the format and timing for blocks of (a) Exact Addition trials, and (b) control trials. The same format and timing was used for the Proximity Judgment task.

The PJ task follows the same format, the only difference being that a single number (the “target”) is now displayed for 1000ms, and the child is instructed to select from the two numbers displayed horizontally below it, the one that is numerically closer to the target. Problems were selected randomly from a list of 1- and 2-digit numbers. In the PJ control blocks (PJCTL) the target consists of a single Greek symbol, which is displayed initially for 1000ms, followed by two Greek symbols displayed horizontally below it. The child is instructed to press the button on the same side as the symbol that is identical to the target. Each block is repeated three times in the order PJ, PJCTL, rest, PJ, PJCTL, rest, PJCTL, PJ, rest, with the fixation square displayed for 20s during the rest blocks, for a total task duration of 5 min.

Data analysis

Responses for the number processing tasks were recorded on a computer. Exclusion criteria were inconsistent task rates between active blocks within a task, markedly faster responses compared with practice sessions in the mock scanner, repeatedly pressing the same button, alternately pressing each of the two buttons, or overall task accuracy less than 66%.

All fMRI analyses were performed using Brain Voyager QX (Brain Innovation, Maastricht, The Netherlands). Four dummy images were acquired in each run that were excluded from all analyses. Images were motion corrected relative to the first volume of the functional run acquired at the middle of the imaging session with trilinear estimation and interpolation. Images were corrected for different slice acquisition times and linear trends, spatially smoothed using a Gaussian filter (FWHM 4 mm), and temporally smoothed with a high pass filter of 3 cycles/point. All data exceeding movement criteria 3 mm displacement, 3.0° rotation within a functional run, were rejected. Each child’s functional data sets were co-registered to his/her high-resolution iso-voxeled anatomical MRI (1×1×1 mm³ resolution), rotated into the AC–PC plane and normalized to Talairach space using a linear transform calculated on the anatomical images. The 3.6 × 3.6 × 5 mm³ fMRI voxels were interpolated during Talairach normalization to 3×3×3 mm³. After applying the above exclusion criteria based on performance and motion correction, we present fMRI data for 16 children, 13 of whom provided usable data for both tasks, one only for EA, and two only for PJ.

Whole-brain group analyses were first performed for each task separately with a random effects analysis of variance using the general linear model with predictors based on the known experimental blocks convolved by the standard hemodynamic function. The six motion correction parameters were added as predictors of no interest. Beta maps were created for each subject for each predictor for each task (i.e., PJ, PJCTL; EA, EACTL) and analyzed for each task separately at the second level using a single-factor repeated measures ANOVA. We report clusters that are greater than 200 contiguous voxels (1×1×1 mm³ resolution of the iso-voxeled structural images) at p<0.05, voxel-wise corrected for whole-brain multiple comparisons using the false discovery rate method. For large clusters that span different functionally distinct regions at the threshold specified above, activation peaks were isolated by increasing the threshold until distinct regions could be identified. The thresholds are reported for these sub-regions, as well. In an additional analysis, the number of PJ or EA trials completed during the run was added as a covariate in the single-factor repeated measures ANOVA to explore the degree to which number of trials completed was related to the signal increase during the number processing task compared to the symbol matching task.

We examined differences in brain activation between the tasks, by performing whole-brain analyses for the 13 children that provided usable fMRI data on both tasks with a random effects analysis of variance, using the general linear model with predictors for EA and PJ and their respective control tasks, based on the known experimental blocks convolved by the standard hemodynamic function. The motion correction parameters were again added as predictors of no interest. Beta maps were analyzed at the second level using a single-factor repeated measures ANOVA. Brain activation between EA and PJ relative to their respective control tasks were compared by examining activations for the contrast (EA - EACTL) vs. (PJ - PJCTL).

Region of interest (ROI) analyses were performed for all the clusters that emerged in the whole-brain analyses shown in Table 3 and Table 4. Random effects analysis of variance was performed of the average signal in each cluster for each child using the general linear model with the same predictors described above. The beta values generated by this analysis reflect the mean percent signal change for each condition. The mean percent signal change for the numeric task compared to the control task was computed for each ROI for each child. Pearson correlation analysis was used to examine percent signal change in the ROIs that comprise the parieto-frontal number processing network identified in previous studies in relation to child performance on the tasks.

Table 3.

Regions Showing Greater Activity during Proximity Judgment Compared to the Control Task

Region	Mean x	Mean y	Mean z	Number of voxelsa	Max t
Parietal
R horizontal intraparietal sulcus; anterior	39	−47	43	673	6.3
R horizontal intraparietal sulcus; posterior	31	−68	33	868	7.4
R,L precuneus extending into cuneus and    L posterior HIPS	−10	−68	29	15426	9.4
R,L precuneusb	−5	−65	35	1720	9.4
L horizontal intraparietal sulcus; posteriorb	−29	−66	35	249	7.7
R cuneusb	3	−85	14	184	8.2
Frontal
R middle frontal gyrus	30	20	33	1154	11.8
R middle frontal gyrus	37	31	25	204	5.4
L middle frontal gyrus	−21	26	21	854	7.9
R, L posterior medial frontal cortex extending    bilaterally into superior frontal sulci	5	19	41	8205	7.9
L precentral sulcus	−43	14	32	1394	8.5
Occipital
R parieto-occipital sulcus	11	−66	25	276	5.8
R cuneus	11	−73	11	215	5.6
Insula
R anterior insula	27	19	7	773	6.5
L anterior insula	−26	19	5	779	6.7
Basal ganglia
R tail of caudate nucleus	31	−45	15	440	6.7
L head of caudate nucleus	−18	−1	19	298	6.0

Threshold set at p<0.05, corrected for multiple comparisons using the false discovery rate.

^aVoxel size refers to the 1×1×1 mm³ resolution of the iso-voxeled structural images.

^bDiscrete area within the larger region that is revealed when threshold is increased to p<0.02, corrected for multiple comparisons using the false discovery rate.

Table 4.

Regions Showing Greater Activity during Exact Addition Compared to the Control Task

Region	Mean x	Mean y	Mean z	Number of voxelsa	Max t
Parietal
R horizontal intraparietal sulcus; posterior	33	−58	30	269	7.0
L horizontal intraparietal sulcus; anterior and    posterior	−33	−54	32	4018	9.0
L horizontal intraparietal sulcus; anteriorb	−39	−45	31	888	10.0
L horizontal intraparietal sulcus; posteriorb	−29	−63	33	962	7.7
R precuneus	3	−60	28	339	6.2
L precuneus	−10	−63	28	348	5.2
R central sulcus	25	−22	39	642	6.9
Frontal
R middle frontal gyrus	38	20	31	222	5.9
R dorsolateral prefrontal cortex	30	48	22	345	6.5
L dorsolateral prefrontal cortex	−18	46	19	225	5.6
L superior frontal sulcus	−26	4	46	1291	8.5
R, L posterior medial frontal cortex extending bilaterally into the cingulate gyrus	1	20	36	8845	7.8
R,L posterior medial frontal cortexb	2	20	40	3275	7.8
L cingulate gyrusb	−7	21	19	600	7.4
L cingulate gyrusb	−9	17	33	342	7.4
L cingulate gyrus; middle section	−1	−7	29	213	6.2
L precentral sulcus	−42	18	26	1199	7.1
L precentral sulcus	−34	7	30	489	5.9
Insula
R anterior insula	31	17	5	538	6.2
Cerebellum
R cerebellar cortex	32	−58	−36	217	6.5
R,L deep cerebellar nuclei	3	−44	−29	576	7.6
Basal ganglia
R head of caudate nucleus	15	5	9	929	6.9
L head of caudate nucleus	−15	2	11	735	6.6
R tail of caudate nucleus	29	−42	18	281	6.2
Diencephalon
R thalamus	20	−17	10	497	7.4

Threshold set at p<0.05, corrected for multiple comparisons using the false discovery rate.

^aVoxel size refers to the 1×1×1 mm³ resolution of the iso-voxeled structural images.

^bDiscrete area within the larger region that is revealed when threshold is increased to p<0.04, corrected for multiple comparisons using the false discovery rate.

Results

Behavioral Performance

The behavioral performance of the 16 children who provided usable fMRI data on either or both tasks is summarized in Table 2. Of these, 13 children provided usable fMRI data on both tasks, another child was included in the EA analysis only (N=14 for EA), and two additional children were included in the PJ analyses only (N=15 for PJ). Although the IQ scores are low, presumably reflecting socioeconomic deprivation, intellectual competence was homogeneous within the sample, as indicated by the relatively small standard errors on all the assessments. All the children performed well on the Dehaene Number Processing subtests administered prior to the scan. They also all performed well (≥ 70% correct) on the PJ and EA tasks administered in the scanner. None met DSM-IV criteria for either the inattentive or hyperactive subtypes of ADHD based on the rating scales completed by their classroom teachers.

Table 2.

Behavioral Performance

	N	Mean	Standard error
Estimated IQ	16*	77.3	2.8
Dehaene Number Processing Test
Exact Addition
% correct	16	93.8	1.7
Reaction time (s)	16	6.6	0.6
Proximity Judgment
% correct	16	91.8	1.9
Reaction time (s)	16	3.6	0.4
Number Comparison
% correct	16	96.1	1.7
Reaction time (s)	16	1.6	0.1
fMRI Exact Addition
Number of problems attempted	14**	30.0	2.2
% correct	14	87.7	2.1
Reaction time (s)	14	2.5	0.2
fMRI Proximity Judgment
Number of problems attempted	15***	38.7	1.7
% correct	15	88.9	2.7
Reaction time (s)	15	1.5	0.1

^*16 children provided usable data on either or both of the fMRI tasks.

^**14 children provided usable fMRI data the Exact Addition task.

^***15 children provided usable fMRI data on the Proximity Judgment task.

Neuroimaging Assessments

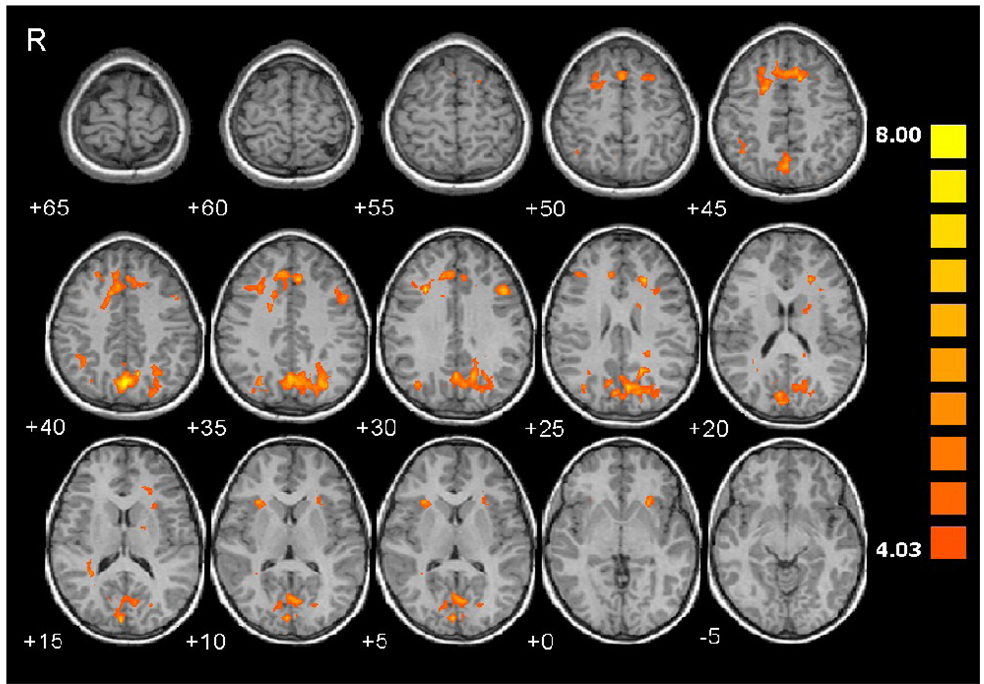
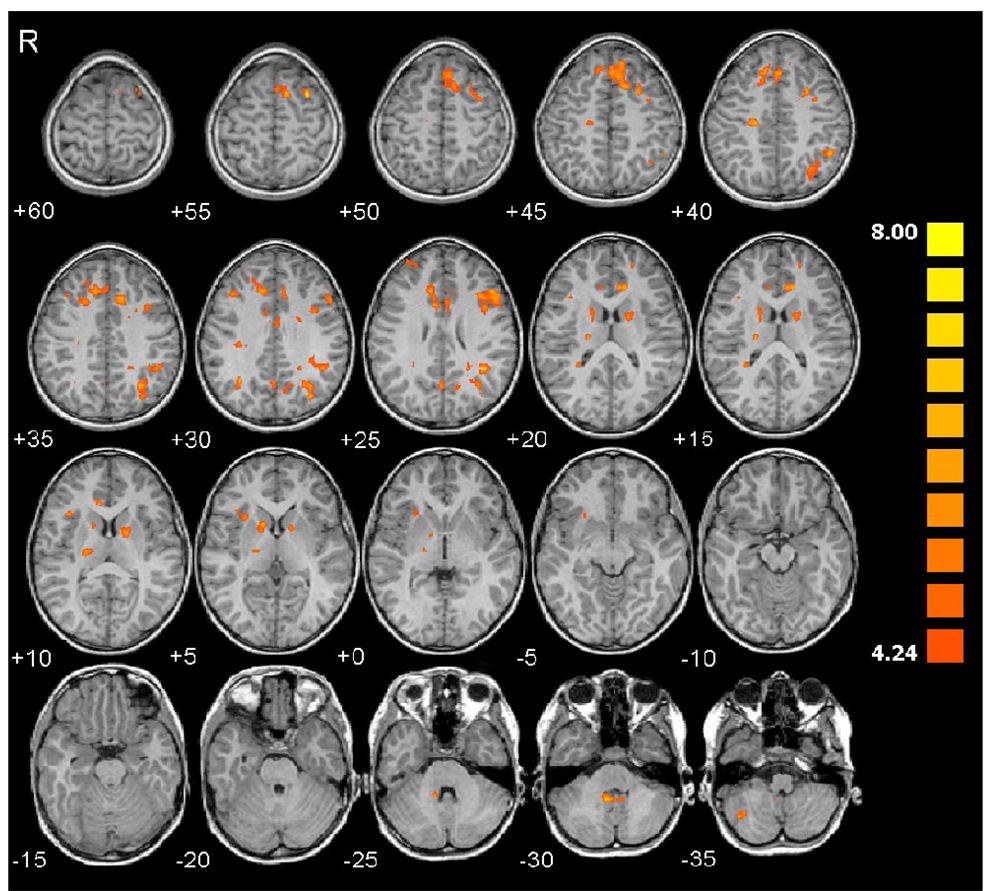
Table 3 and Table 4 list all the ROIs, their mean Talairach coordinates, statistics, and size for regions showing increased brain activation during the number processing tasks compared to the control tasks at p<0.05 (voxel-wise corrected for whole-brain multiple comparisons using the False Discovery Rate) with a minimum cluster size of 200 contiguous voxels. For PJ, the children activate the expected fronto-parietal network, namely right anterior HIPS, bilateral posterior HIPS, bilateral precuneus, bilateral posterior medial frontal cortex (pMFC), bilateral middle frontal gyrus, and left precentral sulcus (Table 3 and Fig. 2). A bilateral activation of the anterior insula is also seen. For EA, the children show increased activity in the same fronto-parietal network, including left anterior HIPS, bilateral posterior HIPS, bilateral precuneus, bilateral pMFC, right middle frontal gyrus, and left precentral sulcus (Table 4 and Fig. 3). The principal differences are that the activation of the anterior HIPS is on the left rather than on the right, the activation within the middle frontal gyrus is right lateralized and smaller, and there are added bilateral activations of dorsolateral prefrontal cortex and head of caudate nucleus. For the 13 children who completed both tasks, the contrast (EA - EACTL) vs. (PJ - PJCTL) yields no significant activations at the threshold used in Table 3 and Table 4, providing additional evidence that these tasks activate essentially the same number processing network.

Figure 2.

Activation maps show greater activity during Proximity Judgment compared to the control task in the posterior medial frontal cortex (pMFC) that extends bilaterally into the superior frontal sulci, right anterior horizontal intraparietal sulcus (HIPS), right posterior HIPS, a large bilateral activation in the precuneus that extends continuously into the left posterior HIPS and right cuneus, right parieto-occipital sulcus, left precentral sulcus, right and left middle frontal gyrus, right tail of caudate and left head of caudate, and right and left anterior insula.

Figure 3.

Activation maps show greater activity during Exact Addition compared to the control task in the left superior frontal sulcus, posterior medial frontal cortex, right central sulcus, left anterior and posterior HIPS, right posterior HIPS, bilateral precuneus, left precentral sulcus, bilateral activations in the dorsolateral prefrontal cortex, left cingulate gyrus, right and left head of caudate, right thalamus, right anterior insula, right and left deep cerebellar nuclei, and right cerebellar cortex.

Pearson correlation was used to examine for PJ and EA, respectively, the relation of number of PJ or EA trials attempted to signal change (i.e., task minus control task) at each voxel. At the threshold used in the analyses reported in Table 3 and Table 4, no regions are activated in relation to number of trials attempted for either task, indicating that these activations are not influenced by the number of problems the child performs during the task.

Relation of ROIs Associated with the Number Processing Network to Task Performance

Mean percent signal change was computed for the numeric task compared with the control task for the ROIs from Table 3 and Table 4 that have been identified most consistently in studies of number processing in adults. Table 5 examines the relation of percent signal change in these ROIs with the children’s behavioral performance on the tasks. Greater activation of this parieto-fronto-insular network was associated with significantly better performance on the PJ task. By contrast, during EA there was a nonsignificant inverse correlation between activation of the parieto-frontal network and performance accuracy.

Table 5.

Relation of Activation of ROIs from the Parieto-frontal Number Processing Network to Task Performance

Region	Proximity Judgment (N = 15)	Exact Addition (N = 14)
Horizontal intraparietal sulcus; anteriora	.35	−.28
Horizontal intraparietal sulcus; posteriora	.65**	−.21
L precentral sulcus	.46†	−.37b
R, L posterior medial frontal cortex	.24	−.45†
R anterior insula	.66**	−.18
L anterior insula	.25	−− c
Composite measured	.57**	−.36

Values are Pearson r. Regional activations are based on mean % signal change (task minus control task) for ROIs derived from the Proximity Judgment (PJ) task for the correlations with PJ performance and from the Exact Addition (EA) task for the correlations with EA performance. Performance is measured by number of problems answered correctly.

^aRight anterior horizontal intraparietal sulcus for PJ; left, for EA.

^bThe larger of the two ROI clusters emerging at the left precentral sulcus for EA (−42, 18, 28) was examined here.

^cROI did not reach threshold in the whole brain analysis.

^dFactor scores derived from factor analyses of the mean % signal change values for the PJ and EA ROIs listed in this table, respectively.

^†p < .10

^*p < .05

^**p < .01

Discussion

The children in this study showed greater activations on both the PJ and EA tasks (compared with symbol matching) in the anterior segment of the HIPS, which has been shown to play a crucial role in the semantic representation of quantity, size, and distance in studies with adults (Dehaene et al., 2004; Eger et al., 2003). These data extend previous findings that activation of the anterior HIPS is well established for nonsymbolic magnitude comparison in the preschool (Cantlon et al., 2006) and school age (Kaufmann et al., 2008) periods to show that this area is clearly involved in symbolic magnitude comparison and simple calculation by middle childhood. Although the anterior HIPS are often activated bilaterally in magnitude comparison, our findings are consistent with data from several studies indicating greater right activation during magnitude comparison tasks, such as PJ, and greater left activation in calculation tasks, such as EA (Ansari, 2007; Cantlon et al., 2006; Chochon et al., 1999; Ischebeck, Zamarian, Egger, Schocke, & Delazer, 2007; Kaufmann et al., 2006; Pesenti, Thioux, Seron, & De Volder, 2000; Price, Holloway, Rasanen, Vesterinen, & Ansari, 2007; Rivera et al., 2005; Zago, Pesenti, Mellet, Crivello, Mazoyer, & Tzourio-Mazoyer, 2001).

A second area within the intraparietal sulcus that is activated by the children in both tasks is in the posterior segment of the HIPS. The activation is bilateral for both tasks, but with greater left lateralization for EA. A bilateral activation in this region was seen during nonsymbolic addition problems using arrays of dots (Venkatraman, Ansari, & Chee, 2005) and during a counting task (Piazza et al., 2003); a left lateralized activation was seen in tasks involving exact calculation (Chochon et al., 1999; Venkatraman et al., 2005; Zago et al., 2008). In studies with children, left posterior HIPS activations were seen during algebra equation solving (Qin et al., 2004), subtraction (Kong, Wang, Kwong, Vangel, Chua, & Gollub, 2005), and nonsymbolic number comparison (Ansari & Dhital, 2006); right activations, during nonsymbolic magnitude comparison and approximate addition (Kucian et al., 2006). The mean coordinates for this region correspond closely to a bilateral area within the intraparietal sulcus identified as an important neural locus of visual working memory storage in a study in which memory load was varied parametrically (Todd & Marois, 2004; see also Xu & Chun, 2006). This activation may, therefore, relate to the involvement of short-term visual memory storage in both the PJ and EA tasks (see Leroux, Bergman, & Klingberg, 2007). This posterior HIPS activation, which is contained within the banks of the intraparietal sulcus, is inferior to the posterior superior parietal lobule (PSPL) region, which was activated in four number processing studies with adults—one involving subtraction and three involving magnitude comparison (Dehaene et al., 2003). The absence of PSPL activations in the children in this study is consistent with Kaufmann et al.’s (2008) report that this region is activated in nonsymbolic magnitude comparison in adults but not in children, although PSPL activations were seen in three studies in children—one involving nonsymbolic number comparison (Cantlon et al., 2006); the other two, exact addition (Kucian et al., 2006; Davis et al., 2009). It is not clear which task parameters influence activation of this region, which Dehaene et al. (2003) suggest support the engagement of attention during number processing (Dehaene et al., 2003; Menon et al., 2000; Pinel et al., 2001). This interpretation is supported by Davis et al. (2009), who found activations in this region in third grade children during computationally demanding double-digit exact calculation, but not during single-digit exact calculation.

The left angular gyrus, which was activated during exact calculation in five studies of adults (Dehaene et al., 2003) was also not activated in children in either of the tasks administered in this study. No activation of the angular gyrus (AG) was predicted in the PJ task since AG activation appears to depend on the degree to which the task involves verbal processing, which is not generally required for magnitude comparison (Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Lee, 2000). Rivera et al. (2005) note a nonsignificant increase in activation in the AG with age, which is consistent with activations in this region seen in some, although not all, adult studies involving retrieval of addition and multiplication facts (cf. Grabner, Ansari, Reishofer, Stern, Ebner, & Neuper, 2007; Simon et al., 2002; Stanescu-Cosson et al., 2000, with Pesenti et al., 2000; Venkatraman et al., 2005; Zago et al., 2001). Venkatraman et al. suggest that verbally-mediated processes are not required for simple exact addition and that other strategies can be employed, including finger counting or counting on from the larger addend (Geary & Wiley, 1991), or, as Pesenti et al. (2000) suggest, computation strategies involving magnitude comparison, which would presumably be mediated by the anterior HIPS. Vankatraman et al,’s interpretation is consistent with Davis et al.’s (2009) finding of increased activity in the angular gyrus in double-digit exact calculation compared to simple single-digit exact calculation.

In addition to the age-related increases in activation in the anterior HIPS, Rivera et al. (2005) found age-related increases in a region of the left lateral occipital-temporal cortex (including the inferior and middle occipital gyrus and the inferior and middle temporal gyrus), which is believed to be involved in the transfer of lexical arithmetic symbols to the parietal cortex in a format that facilitates numerical calculation and computation (Pinel et al., 2001). Consistent with Rivera et al.’s correlational data, activations in this region have been reported in three number processing studies with adults (Menon et al., 2000; Venkatraman et al., 2005; Zago et al, 2001) but in none of the studies with children, including the data reported here.

Rivera et al. (2005) found age-related decreases in prefrontal cortex, including anterior cingulate cortex and left precentral sulcus. Ridderinkhof, Ullsperger, Crone and Nieuwenhuis (2004) have identified the posterior medial frontal cortex (pMFC), which includes the dorsal anterior cingulate, as important for performance monitoring, including detection of response errors, response conflict, and decision uncertainty, across a broad range of cognitive tasks. The significant activations seen in the pMFC and other frontal areas, including the precentral and superior frontal sulci and middle frontal gyrus, during the EA and PJ tasks in our study are consistent with the hypothesis that number processing engages fronto-cingular activations that are involved in performance monitoring and cognitive control (Chochon et al., 1999; Zago et al., 2008). In one study with adults, activations of the pMFC were reported only in more complex addition and subtraction tasks involving carrying and borrowing (Kong et al., 2005). In adolescents, this region was activated during algebra equation solving, particularly for problems involving a greater number of transformations (Qin et al., 2004). In studies with children, by contrast, pMFC activations are often seen in relatively simple tasks (Davis et al., 2009; Kaufman et al., 2006; Kucian et al., 2008), suggesting that activation of regions mediating error monitoring and cognitive control may be required even for less complex number processing tasks in children.

Activations in the left precentral and lateral superior frontal sulcus areas have also been reported in several adult number processing studies (Pesenti et al., 2000; Piazza et al., 2003; Stanescu-Cosson et al., 2000; Zago et al., 2001) and in three other studies of number processing in children—one involving exact addition (Kucian et al., 2006); one, approximate calculation (Davis et al., 2009); the third, exact subtraction (Kawashima et al., 2004). Zago et al. point out that this activation overlaps with the premotor strip at the coordinates of finger representation and that activations in this location have been observed during learning of finger movement sequences (Seitz & Roland, 1992) and hand manipulation of objects (Binkofski, Buccino, Posse, Seitz, Rizzolatti, & Freund, 1999). Activations during tasks involving grasping and pointing are also seen in an area in the anterior HIPS adjacent to the area that is activated in number processing tasks (Hubbard et al., 2005). It has been suggested that a fronto-parietal finger movement network involved in finger counting, a spontaneous numerical learning strategy that has been observed cross-culturally (Butterworth, 1999), may develop in the skilled user to become a substrate that mediates numerical knowledge (Pesenti et al., 2000; Zago et al., 2001). Although Rivera et al. (2005) reported that activations in this region decreased with age, Davis et al. (2009) found greater activation in adults compared to third grade children in this area in both exact and approximate calculation tasks.

Rivera et al. (2005) also found age-related decreases in activation in medial temporal lobe, basal ganglia (including caudate nucleus), insula, and brain stem. Although no medial temporal or brain stem activations were observed in our study, bilateral activations of head of caudate were seen in the EA task and insular activations were seen in both tasks. The basal ganglia are part of a fronto-subcortical circuit known to be involved in the behavioral execution of sequences (Dehaene & Cohen, 1997). Patients with focal basal ganglia lesions are selectively impaired in tasks requiring a multi-step sequence procedure and/or retrieval of addition or multiplication facts but perform normally on magnitude comparison and subtraction (Benke, Delazer, Bartha, & Auer, 2003: Delazer, Domahs, Lochy, Karner, Benke, & Poewe, 2004). Caudate nucleus activations have been observed in studies of adults engaged in relatively challenging number processing tasks, including addition of four 2-digit numbers (Zago et al., 2008), learning a novel set of multiplication facts involving 2-digit × 1-digit numbers (Ischebeck et al., 2007; 2006), and solving addition and subtraction problems with three operands within a short time period (Menon et al., 2000). Left head of caudate was also activated during equation solving in adolescents who were learning algebra for the first time (Qin et al., 2004). It is of interest that caudate nucleus was activated even for problems involving retrieval of simple arithmetic facts in our healthy but economically disadvantaged South African sample.

Several studies that have focused on counting and simple addition have found activations of the left and/or right insula similar to those that we found for the PJ and EA tasks (Davis et al., 2009; Pesenti et al., 2000; Piazza et al., 2003; Venkatraman et al., 2005; Zago et al., 2001). In the Pesenti et al. study the insular activation was seen when digit matching was compared to matching unfamiliar abstract characters and also in problems requiring retrieval of simple addition facts. A right insula activation was also reported in two symbolic number processing studies with children – one involving number comparison (Ansari et al., 2005); the other, single-digit exact calculation (Davis et al., 2009). Zago et al. (2001) note that the insula is also activated in studies involving the naming of simple familiar objects in which neither Broca’s or Wernicke’s areas are activated (Etard et al., 1999; Martin, Wiggs, Ungerleider, & Haxby, 1996). Etard et al. point out that Broca’s area is more likely to be activated when several alternative names might be applied to a given object and Wernicke’s area, when the object might have multiple alternative meanings. Thus, these data suggest that retrieval of the names of familiar digits may not require activation of left frontal, language-related areas but may be mediated by insular activations associated with the retrieval of the names of familiar objects. Activations were also seen for both tasks in the precuneus, a medial parietal region that is activated by shifting of visual attention between different locations in space and in episodic memory retrieval involving events that are sequentially ordered in time (Cavanna & Trimble, 2006). Although activations in the anterior precuneus have also been found in other studies involving magnitude comparison and calculation in both adults (Dehaene et al., 1999; Kong et al., 2005; Lee, 2000; Stanescu-Cosson et al., 2000) and children (Davis et al., 2009; Kucian et al., 2006; Ansari et al., 2005), there has been very little consideration in the literature regarding the role this region may play in number processing.

Behavioral performance on EA and PJ was examined in relation to activation in six prominent ROIs from the parieto-fronto-insular network identified in studies of number processing with adults. As predicted, greater activation of these ROIs was associated with significantly better performance on the PJ task. Although these regions were also activated during EA in the whole brain analysis (Table 4), degree of activation did not predict EA performance accuracy for individual children. Because proficiency in solving simple addition problems often relies on recall of over learned addition facts, the most proficient children may not need to activate this number processing network as strongly when performing this task. We suspect that degree of activation would predict better performance in an exact addition task with more computationally challenging problems.

In summary, by contrast to the adult literature, in which a distinctive parieto-frontal network for number processing has been repeatedly identified, the findings from the initial studies of number processing in children have been less consistent, possibly due to differences in study design (i.e., comparison groups) and control conditions. The data in this study extend the findings on nonsymbolic magnitude comparison in preschool and school age children to demonstrate robust activation of the anterior HIPS in the context of symbolic magnitude comparison and simple calculation in school age children. In addition, our data are consistent with reports by Rivera et al. (2005) of age-related decreases in activations in pMFC, left precentral sulcus, caudate nucleus, and insula during number processing. pMFC activations are frequently seen in number processing studies with adults, particularly when more complex arithmetic manipulations are involved. The very extensive activations in this region on both tasks in our study are consistent with the inference that even relatively simple symbolic number processing requires more extensive performance monitoring and cognitive control in middle childhood than for adults. Rivera et al. suggest that their finding of age-related increased activation of the anterior HIPS may be due to greater functional specialization of this region as symbolic number processing becomes increasingly automatic, a claim supported by the findings of Davis et al. (2009). Our data demonstrate that, despite this age-related increase, when appropriate (letter/symbol matching) control conditions are used, the anterior HIPS are already reliably and robustly activated for symbolic number processing by middle childhood.