Abstract
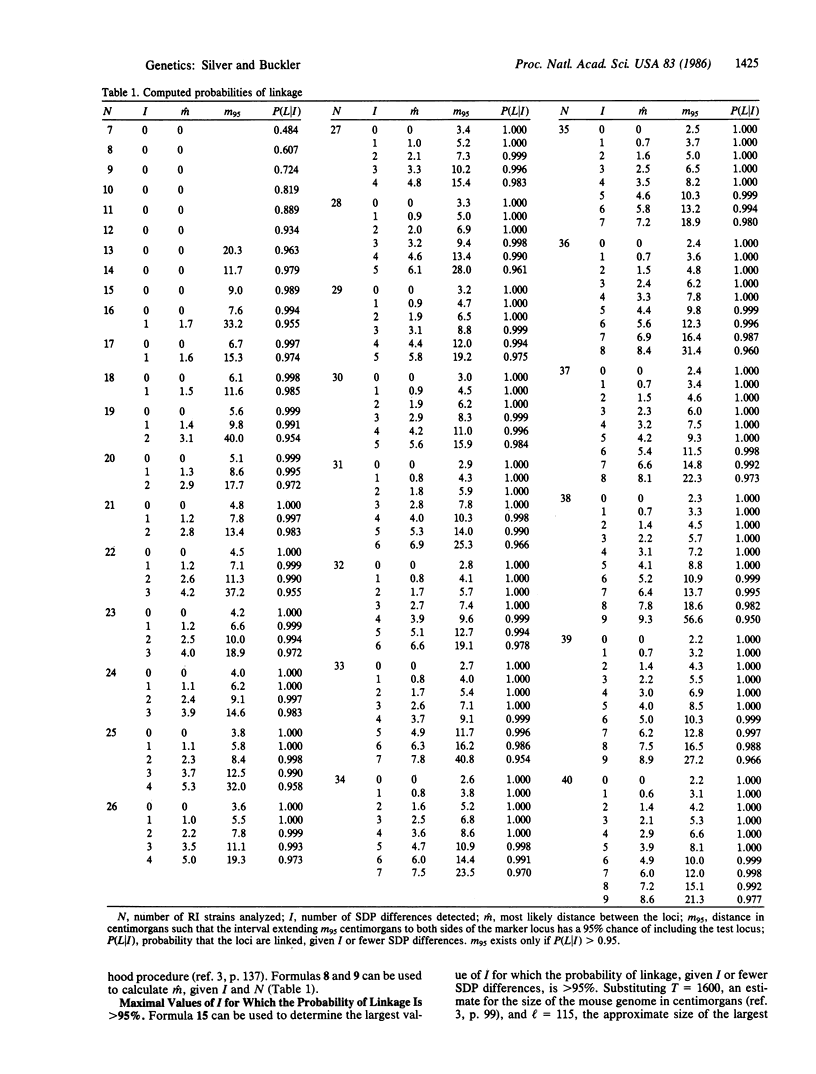
Recombinant inbred (RI) mouse strains are extremely useful for gene mapping, especially for establishing preliminary map positions for new loci. However, the usual statistical analysis applied to such experiments may lead to erroneous conclusions about linkage unless unusually stringent criteria are adopted for rejecting the null hypothesis. We describe a Bayesian statistical approach for determining the probability of linkage when no prior information is available about the location of the gene to be mapped (the test locus). We present a table that gives the probability of linkage, the most likely position of the test locus with respect to a marker locus, and the interval around the marker locus that has a 95% chance of containing the test locus, for all possible experimental results suggesting linkage in sets of up to 40 RI strains. These results show that for the probability of linkage to be greater than 95%, the number of RI strains inheriting chromosomes recombinant for the test and marker loci must be smaller than previously assumed. The formulas derived for RI strains can be applied, with only minor modifications, to the analysis of Mendelian backcrosses. Differences between the Bayesian approach advocated here and the more traditional analysis of linkage are discussed in detail.
Full text
PDF



Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Haldane J B, Waddington C H. Inbreeding and Linkage. Genetics. 1931 Jul;16(4):357–374. doi: 10.1093/genetics/16.4.357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver J. Confidence limits for estimates of gene linkage based on analysis of recombinant inbred strains. J Hered. 1985 Nov-Dec;76(6):436–440. doi: 10.1093/oxfordjournals.jhered.a110140. [DOI] [PubMed] [Google Scholar]


