Comparative Performance of Cell Life Span and Cell Transit Models for Describing Erythropoietic Drug Effects

Abstract

Prolonged time delay in response to drug action is a common feature of hematological responses to pharmacotherapy such as erythropoiesis. The objective of this study was to compare the performance of two competing modeling approaches for delayed drug effects, mechanistic cell life span models, and semi-mechanistic cell transit models. The comparison was performed with an experimental dataset from multiple dose administrations of an erythropoietin mimetic to Cynomolgus monkeys. Comparative performance measures include visual predictive checks, goodness-of-fit plots, model estimation time, estimation status, and estimation error. The analysis revealed that both models resulted in a similarly good description of the erythropoietic drug effect, with precision and bias of the model-based predictions of red blood cell counts of less than 11%. The cell transit model needed slightly longer time to converge compared to the cell life span model. The system and drug effect parameters were similar in both models indicating that the models can be interchangeably used to describe the current data. Thus, model selection would be dependent on the purpose of the modeling exercise, the available data, and the time allocated for model development.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-011-9302-9) contains supplementary material, which is available to authorized users.

INTRODUCTION

Prolonged time delays between drug action and physiologic response are common features in the hematological response to drug treatment, both for therapeutic efficacy (e.g., stimulation of the formation of blood cell subpopulations) as well as toxicity (e.g., myelosuppression). Traditionally used pharmacokinetic–pharmacodynamic (PK/PD) models to describe dissociated time courses of drug concentration and response intensity such as effect compartment models (1) and indirect response or turnover models (2) have commonly been employed to describe the delay in drug effects in the order of minutes to hours, but fail to handle prolonged delays in drug effects in the order of days to months.

Thus, over the recent years, numerous mathematical models became available in the literature for specifically modeling the effect of delayed drug responses, especially for the stimulation or suppression of the generation of blood cells (3–13). Of these approaches, cell life span and cell transit models have been widely used to describe drug effects on hematopoiesis (9–21). The common theme of these models is that the extensive time delay in drug effect due to maturation of cells is described by a series of compartments connected in a chain like fashion.

Cell life span models are mechanism-based and physiological in nature. The currently published models assume that cells are produced at a constant rate, persist for a certain time period at a maturational cell type, and are then converted to a different cell type or are lost due to natural senescence (5,10,12). The rate of cell loss is equal to their production rate but with a delay which is equal to the cell life span. The individual compartments represent cell types at various stages of hematopoiesis and the duration of persistence or life span of each cell type is different and unique. Cell life span models allow estimating the physiological or system parameters along with drug-related parameters depending on the richness of the available data. The regulatory role of hematopoietic growth factors and cytotoxic agents on cellular processes such as proliferation, differentiation, and maturation are described by modulating system parameters (5). The multicompartmental structure of the cell life span models allows inclusion of cell types at multiple defined stages of a blood cell maturation pathway in the same model structure.

The cell transit models can be considered semiphysiological or empirical in nature since the time delay for a cell to transfer from one compartment to the next due to continuous maturational processes is lumped into a single parameter called mean transit time (3,17,20,22,23). The mean transit time (MTT) is modeled as a first-order rate constant (K_tr = NRBC/MTT, where K_tr is the transit rate constant and NRBC is the number of red blood cell (RBC) compartments) that is the same for all the compartments. The RBC count is calculated as the sum of cells in all RBC compartments. As a result, the MTT in this model represents cell aging and is equivalent to RBC life span. The chain of the compartments is necessary to account for delay between the drug action on the progenitor cells and its effect in the circulating cell compartments. Thus, the cell transit model does not assign a specific maturational cell type or status to any of its compartments other than the mature cell in peripheral blood. The system parameters are usually estimated along with the drug effect parameters. The regulatory role of hematopoietic growth factors and cytotoxic agents can be implemented on system related parameters.

Both of these models offer flexibility in implementing drug action in terms of stimulating cell growth or cell death. The major difference between the two approaches is that the maturation or transit between different compartments is modeled with a zero-order process for the cell life span models and a first-order process for the cell transit models. The number of compartments for describing the growth or implementing delay in drug effect is flexible in both of these models.

Here, we compared the performance of the cell life span and cell transit models with respect to their ability in describing a stimulatory drug effect on erythropoiesis, including estimation time and performance/stability, using an experimental dataset obtained from a preclinical study with multiple administrations of an investigational erythropoiesis stimulating agent (EPO mimetic) to Cynomolgus monkeys.

The EPO mimetic stimulates erythropoiesis by binding to erythropoietin receptors by the same mechanism as endogenous erythropoietin. The receptors are expressed on the surface of erythroid progenitor cells in the bone marrow. Erythropoietin and thus also the EPO mimetic stimulate the division and differentiation of these progenitor stem cells to increase red blood cell production.

METHODS

Study Design

The EPO mimetic serum concentrations and red blood cells data were obtained from two studies performed by Merck KGaA, Darmstadt, Germany. In the first study, 40 Cynomolgus monkeys were divided into four groups with 10 (5 male and 5 female) animals per group. The animals received biweekly intravenous doses of 10, 30, 100 μg/kg of EPO mimetic or placebo for 6 months. Blood samples were collected predose and up to 48 h after administration of the first, third, seventh, and the last (13th) dose of EPO mimetic. Similarly, in the second study, 24 monkeys were divided into four groups with six (3 male and 3 female) animals per dose group. These animals received a weekly intravenous dose of EPO mimetic of 10, 30, 100 μg/kg or placebo for 1 month. Blood samples were collected in the first and last dosing interval predose and up to 168 h postdose. All obtained blood samples were analyzed for RBC counts and serum concentrations of the EPO mimetic using a validated assay procedure.

Pharmacokinetics

The serum concentration data from the two preclinical studies were combined for pharmacokinetic model building. After IV administration, the EPO mimetic serum concentrations declined in a biexponential manner, and therefore a two-compartment pharmacokinetic model was used to describe the data. Further, the EPO mimetic exposure increased more than proportional relative to dose as observed in a previously performed noncompartmental analysis, and hence a saturable clearance pathway was implemented to characterize its elimination. Thus, the PK model was described with the following set of differential equations,

1

2

3

4

where, A(1) and A(2) are the amounts and C₁ and C₂ are the concentrations in the central and peripheral compartments, respectively. V₁ and V₂ are the volume parameters for central and peripheral compartment, respectively; V_max is the maximum rate of the saturable elimination, K_m is the concentration at which saturable elimination is at half maximal rate, and Q is inter-compartmental clearance. A population PK model was fitted simultaneously to the EPO mimetic concentration–time data from all dose groups to obtain a common set of parameters. The Bayesian post hoc individual parameter estimates from the PK model for each study animal were used to drive the PD models.

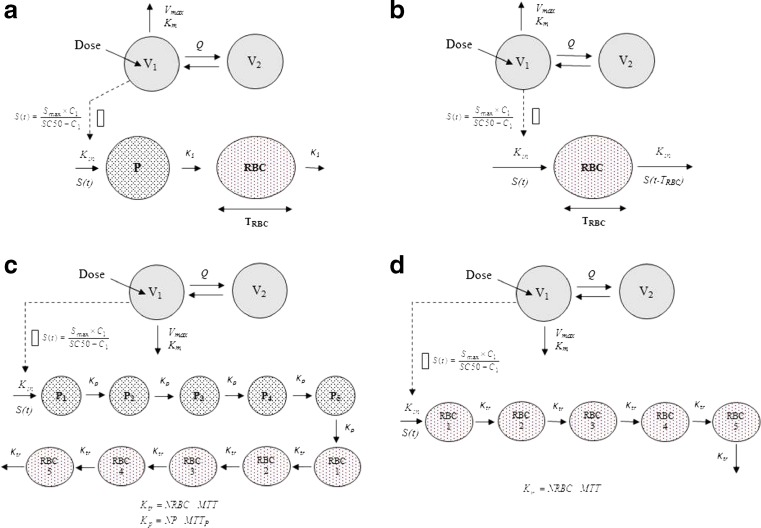
Cell Life Span Model

A modified cell life span indirect response model with or without a precursor cell compartment, and a circulating RBC compartment (5,10,24) was linked to a two-compartment PK model for describing the pharmacodynamic effect of the EPO mimetic (Fig. 1a and b). According to the model, the population of cells in the RBC compartment is assumed to be produced as a consequence of conversion of precursor cells. The precursor cells P are produced at the zero-order rate K_in, and transformed to the RBC at the first-order rate K₁. In the alternative model without a precursor compartment, the RBCs are produced at the zero-order rate K_in. The cells in the RBC compartment remain in this maturation state for a fixed duration of time, T_RBC, before being removed from the circulation through the natural aging process. The EPO mimetic was assumed to stimulate production of precursor cells or RBCs via an E_max-type function. For simplicity, it was assumed that the life span of RBCs remains unchanged with time and was not affected by the EPO mimetic. The differential equations determining the cell populations in the precursor and RBC compartments and their initial conditions are as follows:

5

6

Fig. 1.

Schematic diagrams of the compared models describing erythropoietic drug effects: a cell life span model with a precursor compartment, b cell life span model with no precursor compartment, c cell transit model with a precursor compartment chain, d cell transit model with no precursor compartment chain

The differential equation and associated initial condition for the life span model without a precursor compartment are as follows:

7

The delayed differential equations of both life span models (Eqs. 6 and 7) were converted to ordinary differential equations by using an approach called “method of steps” for an easy implementation in NONMEM as described earlier (5).

Cell Transit Model

A modified cell transit model linked to a two-compartment PK model was used to describe the time course of RBCs following the multiple doses of the EPO mimetic (9,17,22,23,25). The transit model (Fig. 1c) consists of a series of precursor compartments (P_1–5) and RBC compartments (RBC_1–5) linked in a catenary fashion with the first-order transfer rate constants, K_p (5/MTT_P) and K_tr (5/MTT), respectively (15,17,23,26). The MTT_P and MTT represents the mean transit time for precursors and RBC, respectively. The precursor compartment chain accounts for the development and maturation of RBC precursor cells in bone marrow whereas the RBC compartment chain accounts for the release and aging of RBCs in blood. The alternative transit model (Fig. 1d) consists of only one series of compartments (RBC_1–5) linked in a catenary fashion to account for release and aging of RBCs in blood (25). A first-order rate constant, K_tr (NRBC/MTT) was used to describe the transfer rate between the compartments. Models with higher number of compartments (up to 10) did not show any improvement in the model predictions (results not shown). A zero-order rate constant K_in was used to describe the rate of cell formation in the first compartment. The number of circulating RBC at any time is calculated as the sum of RBCs in all five compartments for both transit models (25). No random loss of cells was assumed in any of the compartments. The stimulatory drug effect was implemented on the production of precursors or RBC using an E_max-type function. The overall cell transit structural models were parameterized in terms of baseline RBC count (RBC₀), mean transit time (MTT = NRBC/K_tr), precursor transit rate constant (K_p = 5/MTT_P), maximal stimulatory effect (S_max), and the concentration required to produce the half-maximal drug effect (SC₅₀). The zero-order rate constant of RBC formation, K_in, was a secondary parameter calculated from the steady-state condition (RBC₀/MTT) for both transit models. The equations governing the transit compartment model with precursor chain were as follows:

8

9

10

11

Similarly, the equations governing the alternative transit model without precursor chain were as follows:

12

13

For both models, the number of circulating RBCs is the sum of RBCs in all compartments, according to Eq. 14,

14

Common Modeling Steps for All Four Models (Transit and Life Span)

Between-animal variance (BAV) in the PK and PD parameters was implemented assuming log-normal distributions of individual parameters.

15

TVP is the population typical value of a parameter, P_i is the individual parameter value, and η_i represents the individual deviation. Additive, proportional and combined additive and proportional residual error models were evaluated.

Initial values for the model parameters are provided in the online supplemental material. Endogenous erythropoietin concentrations were not available for analysis and had this be assumed to remain unchanged during administration of the EPO mimetic.

A sequential model analysis approach was used for fitting the PK/PD model to the PK and PD data for all the cell transit and cell life span models. The EPO mimetic serum concentration data from the two studies were pooled for developing the population PK model. The individual post hoc PK parameters derived from this analysis step were used in the subsequent second analysis step to calculate the EPO mimetic concentrations that drive the drug effect in the PD model. Changes in the minimum value of the objective function, the Akaike Information Criterion (AIC), the precision of the parameter estimates, visual inspection of standard goodness-of-fit plots, and reduction in between-subject and residual variability were used for model selection.

Data Analysis

The nonlinear mixed effects modeling approach was used for both cell life span and cell transit models. Modeling was performed using NONMEM software version 6.0 level 2 (Globomax, Ellicott City, MD, USA) installed on Windows XP and the GNU Fortran g77 compiler. The first-order conditional estimation method with interaction between residual and between-animal variability was used during the model building process for both life span and transit models. Graphical representations and simulations for visual predictive checks were performed using the software R version 2.8.1.

Performance Measures

Estimation Time

CPU time needed for fitting the PD model was used for comparison. The time taken for fitting the PK model was not considered since a sequential approach was used in the analysis.

Estimation Status

The convergence criterion in NONMEM was used for designating the estimation status. It was also recorded whether the covariance step was completed successfully.

Estimation Error

The difference between the observed value and the model prediction at selected time points was calculated as percent prediction error.

16

Bias and precision of model predictions were calculated at all time points for all cell life span and transit models by summarizing the percent prediction errors. Bias was calculated as the median percent prediction error (MPE), and precision was calculated as the median absolute percent prediction error (MAPE) as shown below,

17

18

The bias and precision of the model predictions (RBC) were used to assess the model performance. Since the comparison uses actually observed preclinical data rather than simulated datasets, the bias and precision should be considered as relative measures as there is no “true” underlying model and both tested modeling approaches are simplifications of the underlying real physiologic processes. For calculating these relative measures, the RBC data for 1,000 animals were simulated in each dose group using the final parameter estimates, BAV, and residual variability for both of the final models. The uncertainty in the parameter estimates was not taken into account in these simulations. The model was also evaluated using the normalized prediction distribution error (NPDE) assessment (27). The NPDE was calculated for both models from the 1,000 simulated animal data using an add-on package for the statistical software R version 2.8.1 (28). According to this assessment, the NPDE should follow a normal distribution when data are adequately described by the model.

Predictive Check

Visual predictive checks were performed to assess whether the predictions deviate significantly from the observed data. For purposes of the predictive check, 1,000 datasets were simulated in each dose group using the final parameter estimates from both models. The median and 90% prediction interval of the simulated data was plotted against the observed data.

RESULTS

Population PK Model

A total of 48 Cynomolgus monkeys, 30 from study 1 and 18 from study 2, provided 888 evaluable serum concentrations of the EPO mimetic for the pharmacokinetic analysis. The EPO mimetic serum concentrations were best described by a two-compartment model with nonlinear elimination based on AIC values and goodness-of-fit plots. Addition of a second linear elimination pathway to the nonlinear model resulted in no significant change in the objective function value. The goodness-of-fit plots between the both competing models were similar. Thus, the more parsimonious model was used for the further analysis. The individual post hoc PK parameters from the model were used to predict the individual concentrations, which were then used to describe the erythropoietic effects of the EPO mimetic via a cell life span or a transit model. The PK parameters from the final population PK model are provided in Table I. Additional goodness-of-fit plots and a visual predictive check for the PK model are available in the online supplemental material (Figure S1 and Figure S2).

Table I.

Population Pharmacokinetic Model Parameters

Parameter		Estimate (% SE)	BAV (%SE)
K m	μg/L	515 (17.2)	27.6 (44.4)
V max	μg/h	3.84 (12.5)	26.3 (59.1)
V 1	L	0.118 (2.1)	11.4 (34.3)
V 2	L	0.0439 (18.2)	NE
Q	L/h	0.000501 (16.7)	NE
σ_prop	%	33.6 (11.7)	–

Cell Life Span Model

RBC data from the two studies provided 576 observations for the analysis. The time course of the RBC data was analyzed with life span models (5). The drug effect was implemented on the production of precursor cells or RBCs. Though a life span model could describe the data from multiple cell types, for the purpose of comparison with the transit model, only RBC data was used in the current life span models. The life span model fit to the data was assessed via goodness-of-fit plots and a visual predictive check. No significant improvement in the model fit or objective function was observed when feedback inhibition parameter was included in the model.

Between-animal variance was estimated on parameters SC₅₀, RBC₀, and K₁ for the life span model with a precursor compartment and SC₅₀ and RBC₀ of the life span model without a precursor compartment. BAV was not estimated on all parameters due to the complexity of these models. The parameters from the final life span models are provided in Table II. Based on the goodness-of-fit plots (online supplemental material Figure S3 and Figure S4) and visual predictive check (Figure S5 and Figure S6), both the cell life span models described the RBC data well.

Table II.

Model Parameters for the Cell Life Span and Cell Transit Models (NE = not estimated)

Parameter	Units	Estimate (% SE)	BAV (%SE)	Estimate (% SE)	BAV (%SE)
Life span model		With precursor compartment		No precursor compartment
TRBC	h	1540 (4.4)	NE	1650 (1.1)	NE
S max		0.848 (8.8)	NE	0.876 (7.1)	NE
SC50	μg/L	3.17 (45.4)	137 (43.4)	3.85 (40.5)	128 (45.2)
K 1	h−1	0.0122 (63.0)	132 (125)	–	–
RBC0	1012/L	6.05 (2.0)	7.7 (24.0)	5.99 (1.3)	8.3 (33.1)
σ_additive (RBC)	1012/L	0.326 (7.5)	–	0.342 (6.9)	–
Transit model
MTT	h	1380 (1.07)	19.8 (30.7)	1450 (0.8)	19 (32.0)
K p	h−1	0.0757 (43.3)	NE	–	–
S max		0.91 (3.04)	NE	0.895 (1.0)	NE
SC50	μg/L	3.56 (1.79)	154 (44.1)	2.91 (1.3)	172 (37.1)
RBC0	1012/L	5.92 (1.11)	8.1 (34.8)	5.89 (0.9)	8.2 (35.4)
σ_additive (RBC)	1012/L	0.303 (6.5)	–	0.305 (8.3)	–

Cell Transit Model

The time course of the RBC data described in the previous section was also described by two versions of cell transit models parameterized in terms of RBC₀, MTT, S_max, and SC₅₀. The drug effect was implemented on the production rate of cells in the first compartment for both transit models. As described earlier, the number of RBCs was estimated as sum of cell numbers in all transit compartments (25). Models with increased number of transit compartments (up to 10) did not result in improved model fit. Model fits resulting from variations to transit models reported in the literature such as models to describe neutrophils and leucocytes were not satisfactory (3,22). No obvious improvement in the model fit or the objective function value was obtained with the inclusion of a negative feedback parameter. Similar to the life span models, a high condition number was observed when the feedback inhibition was implemented in the model structure. Between-animal variability was estimated on the parameters RBC₀, MTT, and SC₅₀ for both transit models. The final parameters for both transit models are given in Table II. Based on the goodness-of-fit plots (Figure S7 and Figure S8) and plots from a visual predictive check (Figure S9 and Figure S10), the final transit model also described the RBC data well.

It should be noted that the estimated SC₅₀ in both models is substantially lower than the K_m value for the pharmacokinetic model. This suggests that the saturable elimination pathway is either not representative of a receptor-mediated endocytosis via the target of the EPO mimetic or that the maximum pharmacodynamic effect could be achieved with less than 50% of receptors occupied. This is in line with a recent finding suggesting that erythropoietic stimulating agents need only about 10% of receptor occupancy for producing maximal stimulatory effects (29).

Performance Measures

Estimation Time

The cell transit model with precursor compartment chain took longer to converge, 38 min compared to 26 min for the life span model with precursor compartment. Similarly, the cell transit model without a precursor chain took longer to converge, 14 min compared to 8 min for the life span model without a precursor compartment. Only the RBC data was used for estimation of the model parameters with life span and transit models. Cell life span models with more precursor cell compartments would likely result in slower convergence due to their complex model structure; however, such models were not used in the current study.

Estimation Status

Model convergence was achieved easily for both the cell transit and life span models. The covariance step was successful for all life span and transit models.

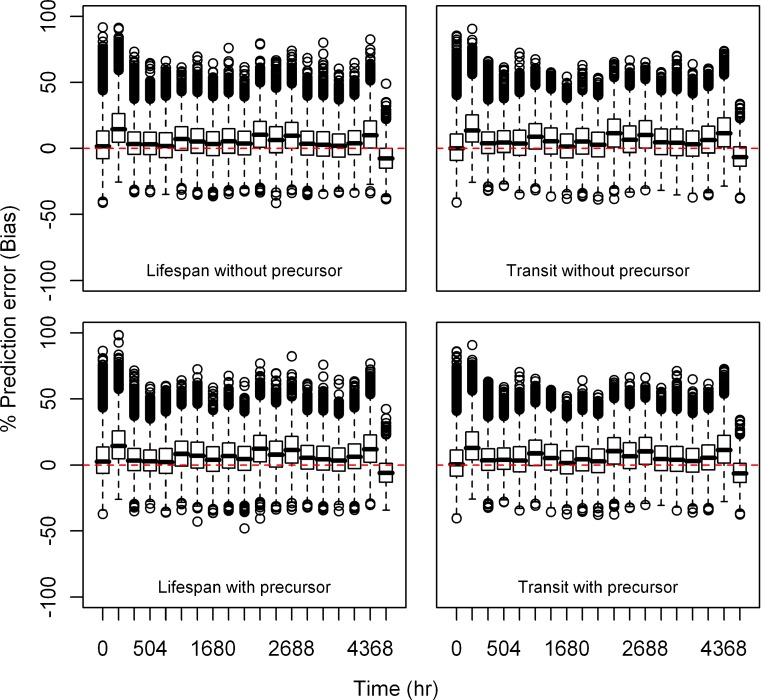
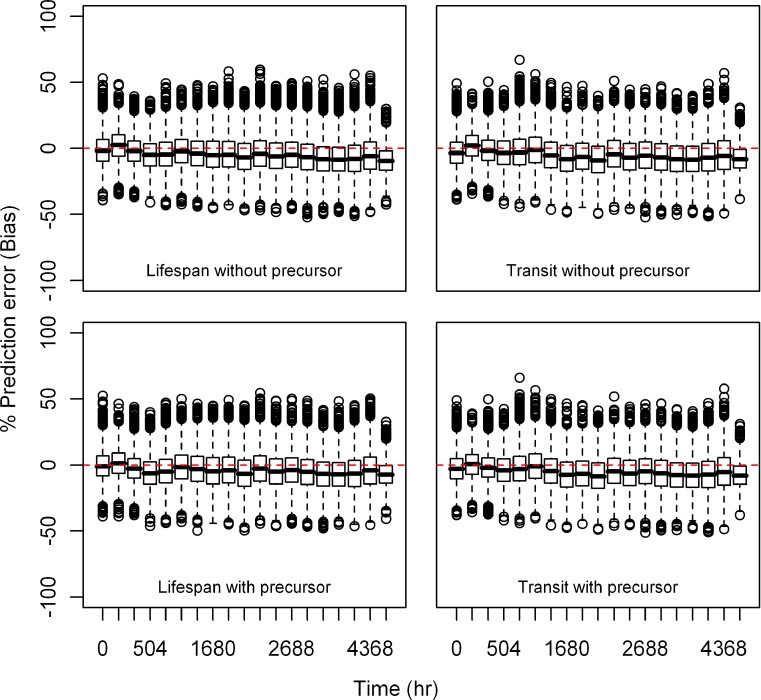
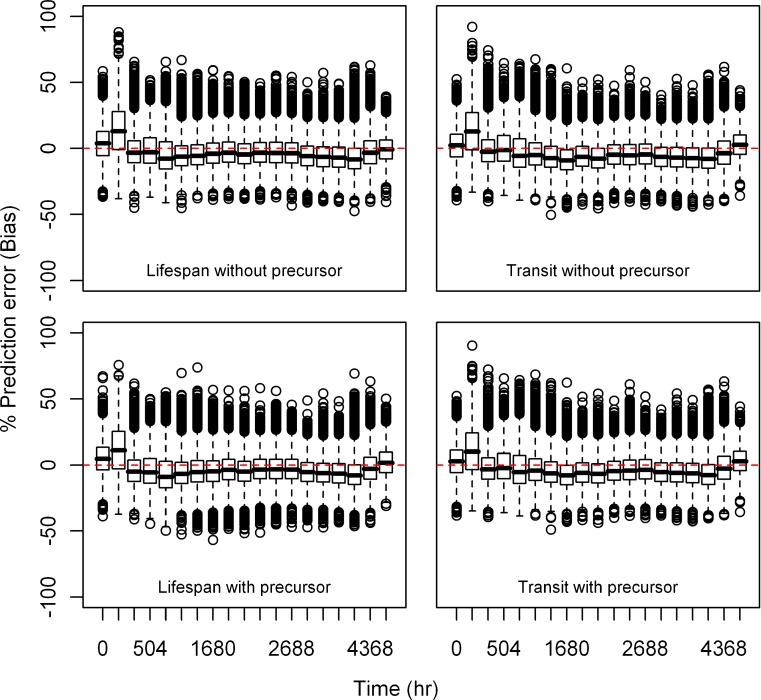
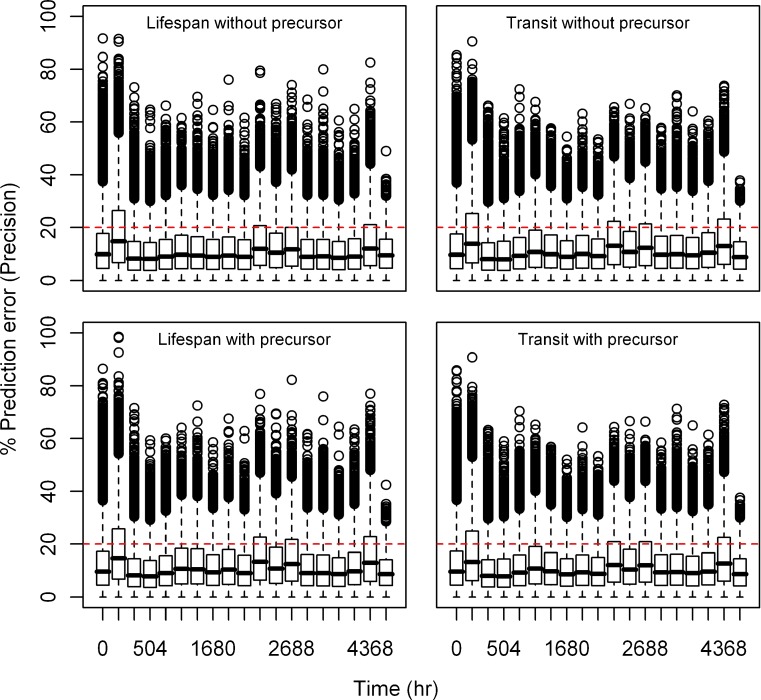
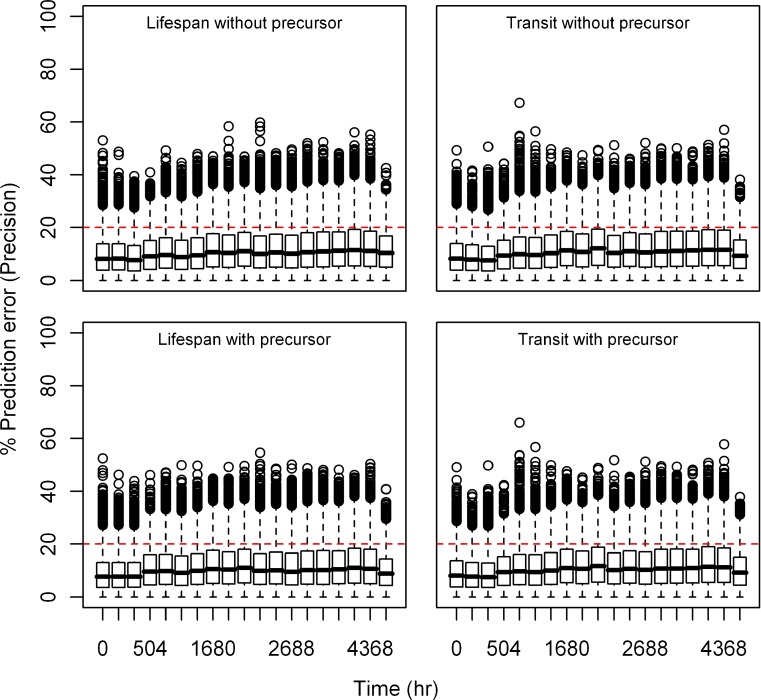
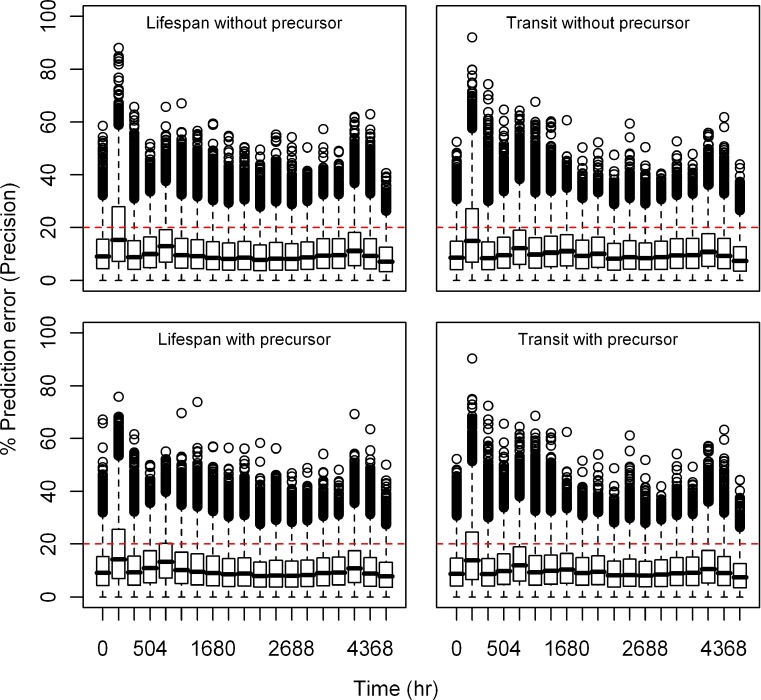
Estimation Error

Relative bias and precision of the model prediction at selected time points for both types of models from 1,000 replicate datasets is listed in Table III. Box plots showing the% prediction error are provided in Figs. 2, 3, 4, 5, 6, and 7. Overall, both cell life span and cell transit models performed well with respect to predicting the RBC data. The mean NPDE is 0.0242 and 0.0312 and the variance is 1.028 and 1.028 for the life span model with and without a precursor compartment, respectively. Similarly, the mean NPDE is −0.0266 and −0.0263 and the variance is 1.011 and 1.010 for the transit model with and without a precursor compartment chain, respectively. The mean NPDE and variance for all models is not different from 0 and 1, respectively, as determined by the Wilcoxon signed-rank test and Fisher’s test for variance. Additional details on the NPDE are available in the online supplemental material (Figures S11, S12, S13 and S14).

Table III.

Bias (Median Percent Estimation Error) and Precision (Median Absolute Percent Estimation Error) in the Model Predictions (RBC) at Selected Time Points for the Cell Transit and Life Span Models

Time (h)	Bias (MPE) (%)				Precision (MAPE) (%)
	Life span		Transit		Life span		Transit
	Precursor	No precursor	Precursor	No precursor	Precursor	No precursor	Precursor	No precursor
336	−1.4	−0.72	−0.69	−0.18	8.4	8.3	8.1	8.1
1,848	−0.51	−1.0	−3.0	−2.9	9.7	9.3	9.7	10.0
1,992	−2.2	−2.4	−4.1	−4.7	9.6	9.5	9.9	10.4
2,184	1.3	0.37	−0.31	−0.25	10.0	9.8	10.0	10.3
3,864	−3.4	−4.4	−3.8	−3.7	10.6	10.6	10.6	11.0
6,384	−4.2	−5.9	−3.9	−4.0	8.4	8.9	8.5	8.5

Fig. 2.

Box plots of percent prediction errors (bias) for model predictions (RBC) at 10 μg/kg dose for all the models. Predictions for four models are shown in four different panels

Fig. 3.

Box plots of percent prediction errors (bias) for model predictions (RBC) at 30 μg/kg dose for all the models. Predictions for four models are shown in four different panels

Fig. 4.

Box plots of percent prediction errors (bias) for model predictions (RBC) at 100 μg/kg dose for all the models. Predictions for four models are shown in four different panels

Fig. 5.

Box plots of percent prediction errors (precision) for model predictions (RBC) at 10 μg/kg dose for all the models. Predictions for four models are shown in four different panels

Fig. 6.

Box plots of percent prediction errors (precision) for model predictions (RBC) at 30 μg/kg dose for all the models. Predictions for four models are shown in four different panels

Fig. 7.

Box plots of percent prediction errors (precision) for model predictions (RBC) at 100 μg/kg dose for all the models. Predictions for four models are shown in four different panels

DISCUSSION

Delays in response to pharmacotherapy can occur due to a multitude of different mechanisms. Various models have been described in the literature to describe these delays (30), e.g., Sheiner’s link model (1) and Jusko’s indirect response model (2). These models account for delays due to drug distribution to the target site or the time needed for changes in production or removal of the measured biosignal (31,32). However, long delays in pharmacodynamic response due to time-consuming transduction processes and/or cell maturation processes can be better described by transit compartment models (9) and life span models (5,12). Characterization of these delays in response using mechanistic or semi-mechanistic models allows characterizing system level pharmacological properties independent of drug-specific properties. The derived system parameters can then be utilized in modeling and simulation of response profiles for drug candidates under development that affect the same or a similar pharmacodynamic response system (33,34).

While both cell life span and cell transit models have been widely used in the literature for similar systems, a formal head-to-head comparison of both modeling approaches had so far been lacking other than in abstract format from presentations at scientific meetings (25,35). Thus, we compared both approaches in terms of describing the erythropoietic drug effect in a real dataset obtained by multiple administrations of an EPO mimetic to Cynomolgus monkeys. Both of these models integrate the concept of cell maturation processes as a mechanism underlying the temporal dissociation in the time courses of concentration and response. One key assumption both models share is that the cell compartments are homogeneous and the PK processes do not affect the maturation process via the cell compartments. In the cell life span model, the delay is modeled using effect propagation through a series of compartments in a zero-order fashion. The time needed for the transfer of signal between the compartments, which is equal to the life span of cells, is allowed to be different. This kind of model structure offers great flexibility to describe the maturation processes in blood cells and other similar systems. Furthermore, the cell life span model also offers extra flexibility to estimate the distribution for life span parameters, which is a more physiological approach for describing the hematopoietic processes when the suitable data is available (11,12).

In contrast, the signal transduction cascade in the transit model is simplified to a varying number of compartments having a mean transit time for the signal to pass through the compartments. With the use of one parameter, MTT, this approach allows to use any different number of compartments to capture the delay in response. This kind of empirical fitting of data comes with simplicity and increased speed of analysis (34). The transit model also allows the drug effect to be implemented on the rate of signal transduction along with effects on precursor or progenitor cells.

The baseline cell number estimates (RBC₀) in our analyses are similar for both types of models, 5.92 × 10¹² and 5.89 × 10¹²/L for the two transit models versus 6.05 × 10¹² and 5.99 × 10¹²/L for the two life span models. Similarly, the drug effect parameters S_max and SC₅₀ are comparable for both types of models (Table II). The MTT estimates of the transit model with and without precursor chain are 1,380 and 1,450 h, respectively. Interestingly, the MTT of the transit model with precursor chain is shorter by 70 h, which is very similar to the MTT of precursor cells (∼66 h). Similarly, the T_RBC of the life span model with precursor compartment (1,540 h) is shorter by 110 h when compared to the life span model without a precursor compartment (1,650 h). The life span for the precursor compartment (∼82 h) explains the difference in the T_RBC estimates for the life span models. The MTT estimate of the transit models, 1,380–1,450 h (∼58–60 days) is very similar to the reported average life span of RBCs in the Cynomolgus monkey, 70–90 days (36). Similarly, the T_RBC estimate from the life span model, 1,540–1,650 h (∼64–69 days) is comparable to the reported average life span of RBCs in Cynomolgus monkeys (36) and the estimates obtained by the transit models. This is in agreement with the previously reported finding that in cell transit models with 5–20 compartments, the mean transit time is similar to the life span of the cells with a point life span distribution. Further, when the number of compartments approaches infinity, the MTT approaches the life span (37). Though the parameter estimates from the two modeling approaches are not directly comparable because of differences in their implementation, the similarity in estimates implies the interchangeability of these models for describing the tested data set. However, for the simultaneous description of data from multiple cell types, life span models are more useful than the transit models.

The parameter estimates from the two life span models (Table II) are very similar, indicating that the inclusion of the precursor compartment can be optional based on the data available for modeling. Similarly, the parameter estimates from two transit models (Table II) are very similar. The two versions of life span and transit models differed only in one aspect, i.e., the time needed for convergence.

The life span models use the “ALAG” function in NONMEM for converting the delayed differential equations to ordinary differential equations via the “method of steps” approach for implementation in NONMEM (5). In contrast, transit models are relatively simple to implement without the need for delayed differential equations. However, both life span models (with and without precursor compartment) needed shorter time for convergence when compared to the corresponding transit models. This finding indicates that the simplest life span models, i.e., life span models describing data from only one cell type, can perform equally well or better than the transit models with respect to time needed for model convergence.

It is intuitive that simulated data obtained from a specific model will usually be well described by the model they were generated with. Consequently, describing observed data would be ideal for comparing the performance and suitability of competing modeling approaches. Since the true underlying physiologic processes may not be completely understood, the measures (MPE and MAPE) used for the comparison of the tested modeling approaches are relative measures. Good and comparable precision was observed for both types of models, as the MAPE was less than 11% (range, 8–11%) at time points selected for comparison. Similarly, bias was low for both types of models ranging from −4.7 to +1.3% at the time points selected for comparison. The NPDE was not significantly different from zero and NPDE distribution for the two types of models followed the normal distribution indicating that all models explain the observed data well. The NPDE provides information on the accuracy of model prediction of median observed data and the variability in the observed data. The two types of models could have performed differently if the corresponding data for reticulocytes as a precursor cell population for RBC would have been available as in many other datasets reported in the literature. With regard to the observed data, both types of models seemed to slightly over predict the median RBC time course and variability in the 10 μg/kg group and under predict it in the 30 μg/kg group. This suggests that both types of models miss an aspect in the PK/PD relationship of the specific EPO mimetic used for this comparison, but that this feature is unrelated to the basic structure and performance of the cell life span and the cell transit models.

CONCLUSIONS

In summary, both cell life span and cell transit models were able to adequately describe the time course of RBC following multiple doses of an EPO mimetic. Due to the use of delayed differential equations for describing the cell maturation process, cell life span models are more challenging to implement in routinely used software such as NONMEM as compared to transit models (5). In spite of their complexity, cell life span models allow to study the system parameters as well as drug effects simultaneously as they resemble physiologically based PD models. In contrast, cell transit models seem to be more useful to describe drug effects and answer routine drug development questions when short turn-around times are needed. The life span models describing the data from a single-cell type converge similarly or faster than the corresponding transit models. Thus, both of these models have unique advantages that may justify their application based on the associated modeling purpose. The factors determining their selection for describing drug effects include the data available at hand, the questions to be answered, and finally the time available for model development.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.