Abstract
We consider a Gaussian copula model for multivariate survival times. Estimation of the copula association parameter is easily implemented with existing software using a two-stage estimation procedure. Using the Gaussian copula, we are able to test whether the association parameter is equal to zero. When the association term is positive, the model can be extended to incorporate cluster-level frailty terms. Asymptotic properties are derived under the two-stage estimation scheme. Simulation studies verify finite sample utility. We apply the method to a Children’s Oncology Group multi-center study of acute lymphoblastic leukemia. The analysis estimates marginal treatment effects and examines potential clustering within treatment institution.
Keywords: Copula model, Correlated survival data, Proportional hazards model, Semiparametric normal transformation
1 Introduction
In some correlated survival data settings, practitioners have two primary interests: determining the effect of treatment and assessing potential dependence between subjects. For example, in many multi-center clinical trials, data are clustered within treatment center. Athough institutions participating in clinical trials follow trial-specific protocols, differences can still exist in outcomes between institutions. The dependence among patients treated at the same institution is an important component of a multi-center clinical trial analysis (Fleiss, 1986; Gray, 1994; Jones, Teather, Wang, and Lewis, 1998; Senn, 1998; Anello, O’Neill, and Dubey, 2005; Vierron and Giraudeau, 2007; Logan, Nelson, and Klein, 2008; Zheng and Zelen, 2008).
Our motivating data arise from a large multi-center clinical trial for children with acute lymphoblastic leukemia. The goal of the clinical trial was to test whether either an increase in the strength or an increase in the duration of the standard chemotherapy regimen was associated with improved survival. We are interested in evaluating whether there exists correlation between survival outcomes within an institution while concurrently assessing the efficacy of the new treatment regimens.
A variety of statistical models are available for correlated survival data. Marginal models treat within-cluster correlations as a nuisance (Wei, Lin, and Weissfeld, 1989; Prentice and Cai, 1992; Cai and Prentice, 1995; Cai, Wei, and Wilcox, 2000, among others). Parameters from marginal models have population-average interpretations. Frailty models are used when within-cluster inferences are desired because the parameters from these models have interpretations conditional on the value of the frailty (Clayton, 1978; Oakes, 1989; Murphy, 1994, 1995; Parner, 1998; Cai, Cheng, and Wei, 2002; Lam, Lee, and Leung, 2002; Glidden and Vittinghoff, 2004; Zeng and Lin, 2007, among others). The positive stable frailty model (Fine, Glidden, and Lee, 2003) allows for marginal proportional hazards interpretation of parameters within a frailty model framework. Copula models (Shih and Louis, 1995; Glidden, 2000; Li, Prentice, and Lin, 2008, among others) embed marginal survival functions within a copula function parametrized by an association term.
For our application, we would like to: (1) test whether either of the two new chemotherapy schedules is associated with improved marginal survival and (2) test whether there is a non-zero correlation between survival outcomes within institutions while controlling for known prognostic factors. Few existing models for multivariate survival data accommodate both semiparametric marginal distributions and unrestricted pairwise dependence.
Consider, for example, Clayton (1978)’s model for a pair of survival times. The dependence term for this model, θ, takes values in (0, ∞). When θ = 1 the model reduces to the independence model, while θ > 1 induces positive association and θ < 1 induces negative association. When θ ≥ 0.5, the distribution is absolutely continuous, but for θ ≤ 0.50, a singular distribution is concentrated on a curve (Oakes, 1989). Hougaard (2000) noted that frailty models cannot yield unrestricted marginal distributions with unrestricted pairwise parameters. Hence, it will be of substantial interest to specify a semiparametric likelihood model that allows for arbitrary modeling of the marginal survival functions and a flexible and interpretable correlation structure.
The goal of this project is to develop a model for multivariate survival data that addresses points (1) and (2) above. To this end we use a semiparametric normal transformation that establishes a Gaussian copula for survival data. The marginal survival function follows a proportional hazards model. The Gaussian copula includes a parameter that summarizes the within-cluster correlation. The correlation parameter can take positive and negative values, which allows for straightforward testing of whether the correlation parameter is equal to zero.
We note that there have been two previous articles using the semiparametric normal transformation model, but neither is applicable to our setting and the proposed model extends the range of data to which the idea can be applied. In contrast to Li et al (2008), our model can accommodate varying cluster sizes and allows for covariates. Li and Lin (2006) assume a specific spatial correlation structure on the entire dataset. In contrast, our method explicitly allows for correlated survival times within independent clusters.
The rest of the paper is structured as follows: in Section 2 we define notation and describe the model; Section 3 summarizes inference procedures; Section 4 outlines an extension of the model when the correlation term is postive; we provide a summary of asymptotic results in Section 5; simulations are presented in Section 6; Section 7 contains an analysis of a Children’s Oncology Group multi-center clinical trial; and we finish with a brief discussion in Section 8. Regularity conditions and proofs of theorems are contained in the Appendix.
2 Model Specification
Let Tij and Cij denote potentially unobserved failure and censoring times for subject j in cluster i, where j = 1, …, ni and i = 1, …, m. The observed data are Xij = min(Tij, Cij) and Δij = I(Tij ≤ Cij). Let Zij(t) denote an external time-dependent covariate vector (Kalbfleisch and Prentice, 2002, page 197) of length p and write its covariate path up to time t as Z̄ij(t) = {Zij(s) | 0 ≤ s ≤ t}. Assume that Tij, conditional on the covariate process Z̄ij(Tij), is independent of Cij. Also, assume that, conditional on each individual’s covariate path, the hazard of Tij, denoted λ{t | Z̄ij(t)}, follows a proportional hazards model:
| (1) |
Here β is a vector of regression coefficients and λ(t) is an unspecified baseline hazard function with cumulative hazard function Λ. Equation (1) is a marginal model for each Tij, hence β has a population-average interpretation not a cluster-specific interpretation.
To model the clustering of the Tij, consider the semiparametric normal transformation:
| (2) |
where Φ is the standard normal distribution function and S is the survival function associated with Equation (1). By the probability integral transform, 1 – S{Tij | Z̄ij(Tij)} has a Uniform(0, 1) distribution. It necessarily follows that T̃ij ~ Normal(0, 1). The transformation takes Tij with support on (0, ∞) and transforms it to a standard normal random variable, T̃ij.
Denote the correlation of (T̃i1, …, T̃ini) with Σi. We consider an exchangeable correlation structure for Σi, where the diagonal terms are equal to 1 and off-diagonal terms are equal to σ. In this model σ can take positive and negative values. The value zero is an interior point of the parameter space for σ so this model can be used to test whether potentially clustered survival data have non-zero correlation. The Gaussian copula model of Li et al (2008) is a special case of this model with no covariates and cluster size fixed at two.
The term σ can be considered a summary measure for the correlation between two subjects within the same cluster after controlling for the covariates included in model (1). Known prognostic factors can be included in the proportional hazards model, and the estimate of the correlation will be based on Cox-Snell type residuals as defined with Equation (2). The term σ can viewed as a generalization of Kenall’s τ and Spearman’s ρ to allow for covariates. For bivariate data, a direct relationship between σ and Kendall’s τ and Spearman’s ρ is straightforward to establish (Li et al, 2008). We can relate σ to the original time scale using the cross-ratio, a local dependence measure (Kalbfleisch and Prentice, 2002). A derivation of this result can be found in Li and Lin (2006, Section 3.1).
3 Inference
3.1 Likelihood Development
Let Yij be a potentially censored version of T̃ij (Equation (2)). The semiparametric normal transformation is monotone and thus preserves censoring patterns. To simplify the presentation, define and order the observations such that Δi1 = … = ΔiΔi = 1. First consider 1 ≤ Δi ≤ ni − 1. Let and .
Let Σi be the covariance matrix for the transformed failure times. Write Σi as a partitioned matrix:
where Σi11 has dimension Δi × Δi. The vector follows a multivariate normal distribution with mean 0 and covariance matrix Σi11. It follows that is a censored observation from a normal distribution with mean and covariance matrix .
Because the semiparametric normal transformation is monotonic, the likelihood for the observed data, Xij, can be written in terms of the transformed terms, Yij. To do so, we use the fact that P(Xij < x) = P(Yij < y), where y is the semiparametric normal transformation of x. Write the likelihood based on the observed data as L(σ, β, Λ). The likelihood contribution from cluster i is
| (3) |
where φΔi is the multivariate normal density corresponding to its argument, Φ̃ni−Δi is the multivariate normal survival function corresponding to its argument, f is the density corresponding to Equation (1), and φ is the standard normal density function. If σ = 0, L(σ, β, Λ) reduces to the usual proportional hazards likelihood. A derivation of this likelihood is provided in the Appendix.
When Δi = 0 (all subjects in cluster i are censored) define φΔi = 1 and . When Δi = ni (all subjects in cluster i have been observed to fail) define Φ̃ni−Δi = 1. With these conventions, Equation (3) holds also for Δi = 1 and Δi = ni. L(σ, β, Λ) is the product of Equation (3) over i = 1, …, m.
To make the likelihood L(σ, β, Λ) more transparent, we consider an example likelihood contribution from a cluster of size two where one subject is observed to be censored at time CA1 and one subject is observed to fail at time TA2. The covariate process for each subject is denoted Z̄A1(CA1) and Z̄A2(TA2). The normally transformed observed failure times are YA1 = Φ−1[1– S{CA1 | Z̄A1(CA1)}] and YA2 = Φ−1[1 − S{TA2 | Z̄A2(TA2)}]. In this case
The first term of L(σ, β, Λ) can be written
| (4) |
while the second term can be written
| (5) |
Equation (4) is the density of a standard normal random variable, while Equation (5) corresponds to, conditional on YA2 = yA2, the probability that a Normal(σyA2, 1−σ2) random variable is greater than yA1.
3.2 Estimation
We propose a two-stage method to estimate (σ, β, Λ). First we estimate β̂ and Λ̂ from the marginal proportional hazards model. We then solve maxσ L(σ, β̂, Λ̂) for σ̂. Formulas for the standard errors of β̂ and Λ̂ that account for clustering can be found using a sandwich formula (Spiekerman and Lin, 1998). The formula for β has been implemented in many statistical programs. The analytic standard error of σ̂ is complicated because it needs to account for the variability from β̂ and Λ̂. In practice the standard error can be estimated using a resampling scheme. To maintain the correlated structure of the failure times, the clusters should be the unit of removal for the resampling calculations (Cai et al, 1997; Cai and Shen, 2000). We choose to use the jackknife for resampling because theoretical validation of the method exists (Lipsitz, Dear, and Zhao, 1994; Lipsitz and Parzen, 1996).
This estimation procedure is computationally straightforward. Marginal estimates of the survival function are available in all standard computing programs, while the likelihood for σ, L(σ, β̂, Λ̂), is proportional to a product of multivariate normal terms, quickly computable using existing software (e.g., R package MVTNORM).
4 A Frailty Model Extension
4.1 A marginalized frailty model
When σ > 0, the model for T̃ij can be extended to allow for a frailty term:
| (6) |
where bi is a cluster-level frailty and εij is an error term. We assume that cluster-level frailties bi have a standard normal distribution and the error terms εij are independent and identically distributed N(0, 1 – σ) random variables that are independent of bi. The cluster-level frailties bi can be used to assess cluster-level differences. The β parameters in Equation (1) have marginal interpretation, while σ and bi from Equation (6) characterize the cluster effect.
Equation (6) merges elements of frailty models with the marginal model, and so will take a moment to review the interpretation of the components of this model. Larger values of σ imply that the frailty terms explain a larger portion of the variance in the T̃ij compared to smaller values for σ. Larger values of σ provide evidence for a stronger cluster effect compared to smaller values for σ. In the context of a multi-center clinical trial, the cluster-level frailties (bi) characterize the center effect. For a fixed set of covariates, smaller or more negative values for bi are associated with shorter survival times (on the original untransformed scale) compared to larger or more positive values for bi.
4.2 Prediction of the frailty terms
If σ̂ > 0, prediction of bi and the associated standard error can be found using Laplace approximations to the bi’s first two moments. Denote the observed data for the ith cluster, (Xi1, …, Xini, Δi1, …, Δini, Z̄i1(Xi1), …, Z̄ini (Xini)), with Ψi. The conditional density of bi given the observed data Ψi, denoted g(bi | Ψi; σ, β, Λ), can be written
where Li is the likelihood for Ψi | σ, β, Λ. Define ki such that . Using the Laplace approximations to the first two moments of g(bi | Ψi; σ, β, Λ) (Booth and Hobert, 1998), the predicted estimate and variance of bi are taken to be:
| (7) |
| (8) |
where double superscript dots denote second derivatives.
The prediction of the shared frailties is straightforward. The expression for ki(bi | σ̂, β̂, Λ̂, Ψi) involves ni normal terms and can be maximized using any standard optimization routine. The estimate of the variance of bi has a closed form expression and can be found by plugging in relevant estimated quantities.
5 Theoretical Results
The following theorems establish the theoretical properties of (σ̂, β̂, Λ̂) where their true values are denoted with (σ0, β0, Λ0).
Theorem 1
Under Conditions C.1 – C.6 in the Appendix, (σ̂, β̂, Λ̂) converges in probability to (σ0, β0, Λ0) as m → ∞.
Theorem 2
Under Conditions C.1 – C.7 in the Appendix Report, as m → ∞, and converge to zero-mean normal distributions and converges to a zero-mean Gaussian process.
Proofs of Theorems 1 and 2 can be found in the Appendix. The proofs of both theorems for σ̂ adjust for the two-stage estimating procedure. These theorems verify that σ̂ is consistent and asymptotically normal when plug-in estimates of β and Λ are used in the likelihood function.
6 Simulation Results
Simulations were conducted to evaluate the efficacy of the proposed method. The presented simulations have marginal survival times from a proportional hazards model with a constant baseline hazard function equal to 1 and with two covariates: one Bernoulli(0.5) covariate with parameter equal to log(0.5) (denoted β1) and one Uniform(0,1) covariate with parameter equal to 0.75 (denoted β2). Censoring times were taken from the Exponential(median=3) distribution and produced about a 25% censoring rate. Correlated survival times were created by first generating random correlated multivariate normal values. The normal values were transformed to the survival scale using Equation (2). Each simulation is based on 250 replications.
In order to focus on the novel elements of the method, we present results for β1 and β2 in the Appendix. As has been shown by other authors, our simulations verify that estimates of β1 and β2 have little bias and appropriate coverage probability.
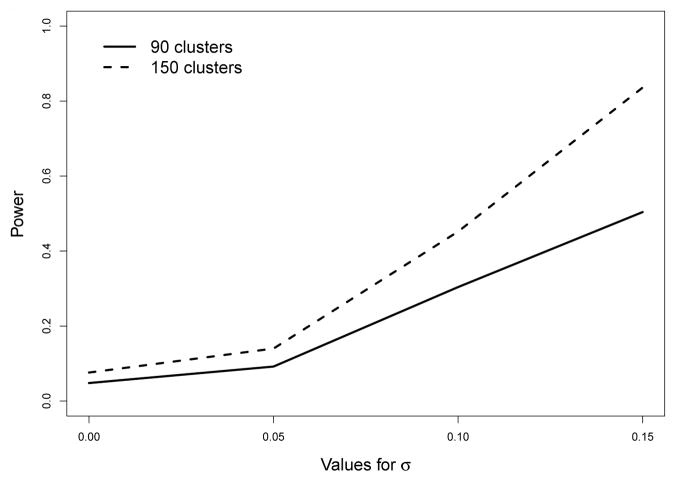
For our results for σ, we summarize scenarios with 45, 60, and 90 clusters. Within each replication, clusters varied in size between 2 and 7 units. Standard errors (SEs) for σ were found using the jackknife. We chose to use the jackknife for resampling because theoretical validation of the method exists for multivariate survival data (Lipsitz, Dear, and Zhao, 1994; Lipsitz and Parzen, 1996). Bias, SEs, and coverage probabilities are summarized in Table 1. Power results are summarized in Figure 1.
Table 1.
Simulation results for the correlation terms
| Estimate | Jackknife SE | Monte Carlo SE | Coverage Probability | |
|---|---|---|---|---|
| 45 clusters | ||||
| σ = 0 | −0.001 | 0.091 | 0.091 | 0.904 |
| σ = 0.05 | 0.058 | 0.104 | 0.099 | 0.924 |
| σ = 0.10 | 0.108 | 0.110 | 0.100 | 0.932 |
| σ = 0.15 | 0.160 | 0.112 | 0.118 | 0.888 |
| 60 clusters | ||||
| σ = 0 | 0.000 | 0.076 | 0.078 | 0.942 |
| σ = 0.05 | 0.049 | 0.086 | 0.082 | 0.928 |
| σ = 0.10 | 0.104 | 0.094 | 0.083 | 0.944 |
| σ = 0.15 | 0.154 | 0.096 | 0.091 | 0.964 |
| 90 clusters | ||||
| σ = 0 | 0.002 | 0.060 | 0.059 | 0.952 |
| σ = 0.05 | 0.049 | 0.067 | 0.067 | 0.900 |
| σ = 0.10 | 0.108 | 0.072 | 0.068 | 0.960 |
| σ = 0.15 | 0.151 | 0.075 | 0.077 | 0.944 |
| σ = 0.50 | 0.523 | 0.045 | 0.044 | 0.924 |
| σ = −0.10 | −0.109 | 0.067 | 0.068 | 0.930 |
Fig. 1.
Power curves as a function of σ and number of cluster.
The estimates of σ have little bias across the simulations. The jackknife SE is close to the Monte Carlo SE across the scenarios. In clusters of size 45, parameter estimates remain unbiased, but the coverage probability drops below nominal levels. As expected, as sample size and correlation increases, the power for testing whether σ ≠ 0 increases.
We also conducted simulations to assess the performance of our frailty estimation method (Equations (7) and (8)). In these simulations, we took σ = 0.5 to ensure all estimates of σ were positive so that frailties could be predicted. Data were generated using Equation (6), to provide true values for the frailty terms. The parameters σ and β were estimated using our proposed two-stage method and their estimates were used in Equations (7) and (8) to predict frailty values and calculate standard errors. We summarize results for simulations with 90 clusters and a range of cluster sizes: cluster sizes varying between 3 and 10 with median size 5, cluster sizes varying between 7 and 20 with median size 10, cluster sizes varying between 10 and 33 with median size 15, and cluster sizes varying between 13 and 50 with median size 20. Results are summarized in Table 2.
Table 2.
Summary of frailty simulations. Relative bias=bias/predicted value
| Median relative bias | SE | |
|---|---|---|
| Median cluster size = 5 | 0.06 | 1.07 |
| Median cluster size = 10 | −0.05 | 1.02 |
| Median cluster size = 15 | −0.05 | 1.01 |
| Median cluster size = 20 | −0.06 | 1.01 |
The method performs well even with small cluster sizes. The relative bias is small. As the cluster sizes increase, the likelihood SEs approach 1, their true value.
7 Data Application: Children’s Oncology Group Study 1961
7.1 Is there evidence of correlation between the survival times of patients within the same institution?
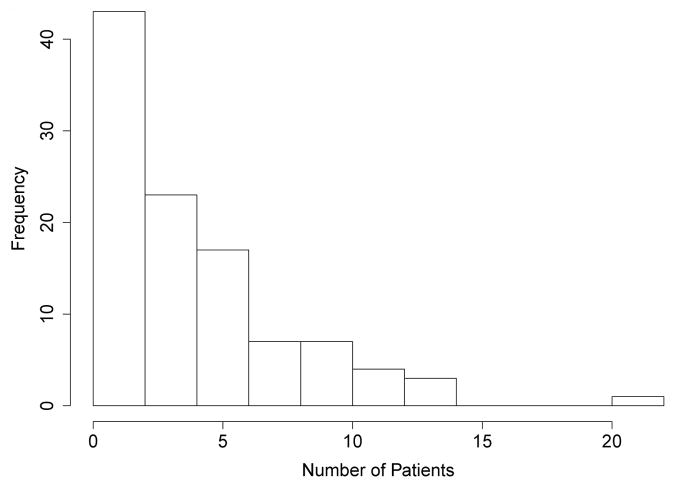
We applied our method to a Children’s Oncology Group (COG) study (protocol number 1961) (Seibel et al, 2008). We analyzed 460 children with enlarged livers from 104 institutions. The goal of the clinical trial was to test whether either an increase in the strength or an increase in the duration of the standard chemotherapy regimen was associated with improved survival for “higher risk” acute lymphoblastic leukemia patients. A 2×2 factorial design was used. The distribution of subjects with enlarged livers among the four arms is presented in Table 3. The number of subjects in each of the 104 institutions is summarized in the histogram in Figure 2. We analyzed the overall survival endpoint.
Table 3.
Distribution of patients with enlarged livers across treatment arms
| Strength | Duration | Number of Patients |
|---|---|---|
| Standard | Standard | 119 |
| Standard | Double | 104 |
| Increased | Standard | 117 |
| Increased | Double | 120 |
Fig. 2.
A histogram of the number of patients in each institution.
We present regression results in Table 4. Standard errors for the marginal survival covariates were found using three methods: a sandwich formula, the jackknife, and a naïve estimate ignoring potential clustering. Standard errors for σ were found using the jackknife. P-values were found using the jackknife standard errors.
Table 4.
Data analysis results using proposed model
| Parameter | Estimate | SEJ | P-value | SES | Naive SE |
|---|---|---|---|---|---|
| Treament Only Model | |||||
| Correlation | 0.173 | 0.159 | 0.279 | - | - |
| Increased Strength | −0.430 | 0.231 | 0.063 | 0.225 | 0.247 |
| Increased Duration | 0.419 | 0.231 | 0.070 | 0.226 | 0.245 |
| Larger Model | |||||
| Correlation | 0.207 | 0.200 | 0.300 | - | - |
| Increased Strength | −0.249 | 0.482 | 0.605 | 0.440 | 0.374 |
| Increased Duration | 0.551 | 0.387 | 0.154 | 0.360 | 0.326 |
| Interaction | −0.321 | 0.704 | 0.648 | 0.646 | 0.498 |
| Age | |||||
| 1–9 | (ref) | ||||
| 10–15 | 0.353 | 0.234 | 0.132 | 0.227 | 0.256 |
| 16+ | 0.485 | 0.739 | 0.512 | 0.565 | 0.451 |
| Platelets (×103/mm2) | |||||
| 1–49 | (ref) | ||||
| 50–150 | 0.397 | 0.305 | 0.193 | 0.290 | 0.258 |
| 150+ | −0.145 | 0.651 | 0.824 | 0.574 | 0.528 |
Estimate = log hazard ratios and estimates of σ
SEJ = jackknife based standard errors
P-value = two-sided p-value using SEJ
SES = sandwich-formula based standard errors (only for β)
Naive SE = SE assuming independence (only for β)
In a model with two covariates for treatment, there was some evidence that increased duration of chemotherapy was associated with worse overall survival compared to the standard duration. There was also evidence that overall survival was improved for patients with increased strength of chemotherapy compared to standard strength. The estimate for the correlation of the transformed failure times was 0.173 with a standard error of 0.159.
We also considered a larger model including the two treatment covariates, their interaction, and the prognostic factors of age and platelet count at registration. In this larger model, none of the covariates appeared to be associated with overall survival. The correlation term of this larger model was of similar magnitude as the treatment only model: the estimate was 0.207 with a standard error of 0.200.
7.2 Is there further information that can be gained by considering frailty terms?
The standard errors for the correlation term (σ̂) were large in both models summarized in Table 4, so we felt it would be useful to investigate whether there were any outliers contributing to the large standard error. In both regression models presented, the estimate of the correlation (σ̂) was positive, so we were able to predict frailty terms for each institution. The predicted frailty values were very similar between the two models, so we only present the frailties from the larger model.
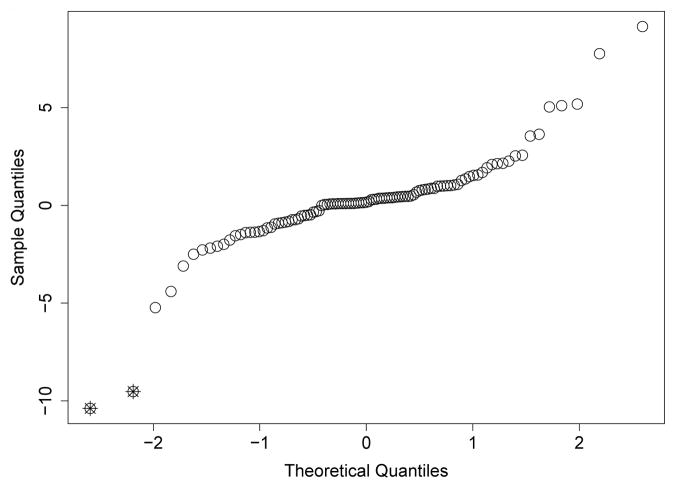
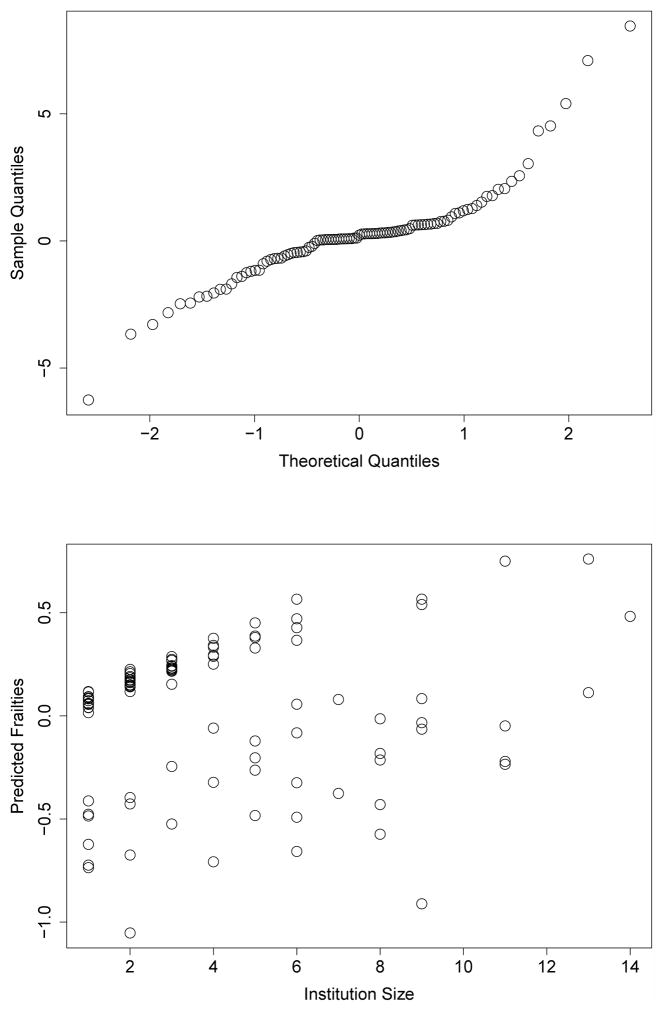
A qq-plot for frailty values standardized by their standard errors indicated several potential outliers (Figure 3). The largest positive standardized frailties were from institutions with only one patient, so we disregarded those institutions as potential outliers. The largest negative frailties were from institutions with 10 and 22 patients, so we investigated these institutions further.
Fig. 3.
A qq-plot of frailties from proposed model standardized by their standard errors. Two potential outlier frailties are marked with crosses.
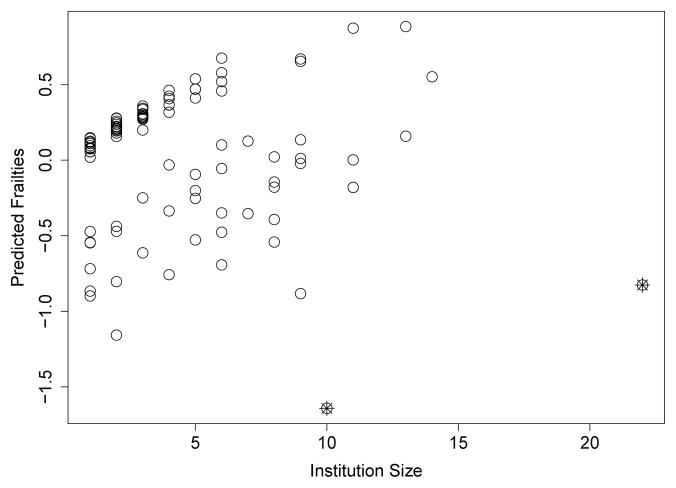
A plot of the predicted frailty values by institution size is provided in Figure 4. The two institutions identified as potential outliers in the qq-plot are marked in Figure 4, and the institutions still appear to be outliers. Among the other institutions there appears to be a positive trend, where institutions that contributed more patients had larger frailty values. Both of the institutions that are potential outliers do not follow this trend.
Fig. 4.
A plot of institution size by frailty value from proposed model. The two frailties marked with crosses in Figure 3 are marked with crosses in this Figure.
Given these results, we were interested in whether these trends could be explained by the type of patients at the two institutions. We used Fisher’s Exact test to compare known prognostic factors between each of the potential outlying institutions and all other patients. Given the limited sample sizes, we recognized that the power of the tests may be limited. We compared the following baseline characteristics: spleen enlargement, race, nodes (normal, moderately enlarged, significantly enlarged), mediastinal mass, white blood cell count (less than 50, 50–199, 200 or more; all ×103/mm2), hemoglobin count (1 to 7.9, 8.0 to 10.9, 11.0 or more; all g/dL), platelet count (1 to 49, 50 to 149, 150 or more; all ×103/mm3), and age (1–9, 10–15, 16 and older). Only one test had a p-value < 0.05, the comparison of age with the institution with ten patients.
The larger regression model in Table 4 controls for age, and age was not significantly associated with survival in the model. Given this result, there may be other factors beyond the available patient data that explain why these institutions have unusual frailty values.
To evaluate the impact of these two institutions on the estimate of the correlation, we refit our models excluding patients from the two institutions marked in Figures 3 and 4. A summary of the original and refit correlation estimates (σ̂) is provided in Table 5. The correlation estimate was smaller in the subset compared to the full dataset, though the change was more pronounced in the treatment only model.
Table 5.
Correlation estimates from proposed model for the full data and for data excluding two potential outliers.
| Treatment Only Model | Larger Model | |||
|---|---|---|---|---|
| All Data | Subset | All Data | Subset | |
| Correlation | 0.17 | 0.03 | 0.21 | 0.12 |
| SE | 0.16 | 0.13 | 0.20 | 0.16 |
| P-value | 0.28 | 0.81 | 0.30 | 0.44 |
The correlation estimates for the subset data are positive and so frailty terms were able to be predicted for each of the institutions. A qq-plot of the frailties standardized by their standard errors and a plot of the frailty terms versus the institution size is provided in Figure 5. There do not appear to be any outliers in the model fit with the subset of the data. The frailty results look very similar to the results in Figures 3 and 4 excluding the two marked values.
Fig. 5.
A qq-plot of standardized frailties from proposed model (left) and a plot of institution size by frailty value from proposed model (right) for the subset data.
In this subset of the data, there is not evidence that survival times are correlated within institution. Our available data does not explain why two institutions may be outliers.
7.3 An alternative analysis using a gamma frailty model
We applied the gamma frailty model to the COG dataset. Results from an analysis with the two treatment covariates and an analysis including a treatment interaction and controlling for age and platelet count is provided in Table 6. The estimate for covariates is the log hazard ratio.
Table 6.
Data analysis results using gamma frailty model
| Parameter | Estimate | SE | P-value |
|---|---|---|---|
| Treament Only Model | |||
| Frailty variance | 0.440 | 0.374 | 0.12 |
| Increased Strength | −0.455 | 0.251 | 0.071 |
| Increased Duration | 0.498 | 0.252 | 0.048 |
| Larger Model | |||
| Frailty variance | 0.443 | 0.361 | 0.11 |
| Increased Strength | −0.324 | 0.383 | 0.40 |
| Increased Duration | 0.594 | 0.337 | 0.08 |
| Interaction | −0.256 | 0.512 | 0.62 |
| Age | |||
| 1–9 | (ref) | ||
| 10–15 | 0.418 | 0.264 | 0.11 |
| 16+ | 0.558 | 0.457 | 0.24 |
| Platelets (×103/mm2) | |||
| 1–49 | (ref) | ||
| 50–150 | 0.361 | 0.266 | 0.17 |
| 150+ | −0.087 | 0.541 | 0.11 |
In the gamma frailty model, the strength of the correlation is measured by the variance of the gamma frailties. In both the treatment only and larger models, the estimate for the frailty variance variance is not significant. As with our results, these two gamma frailty models do not show evidence of clustering within institution.
The covariate parameter values from the proposed model are the same as would be found using a marginal proportional hazards model treating the potential clustering as a nuisance. Therefore the parameters from the proposed model have population interpretation as an average effect across all the patients in the study.
In contrast, due to the functional specification of the gamma frailty hazard function, covariate parameters values from a gamma frailty model are interpreted as conditional on the value of the frailty and do not represent an average effect. When there is no correlation within clusters, the proposed model and the gamma frailty model both reduce to the proportional hazards model. Given the low evidence of clustering in this dataset, it is not surprising that the covariate parameter estimates are close in Tables 4 and 6. Given that the COG study was interested in population averaged hazard ratios, the parameters in Table 4 provide a more appropriate interpretation.
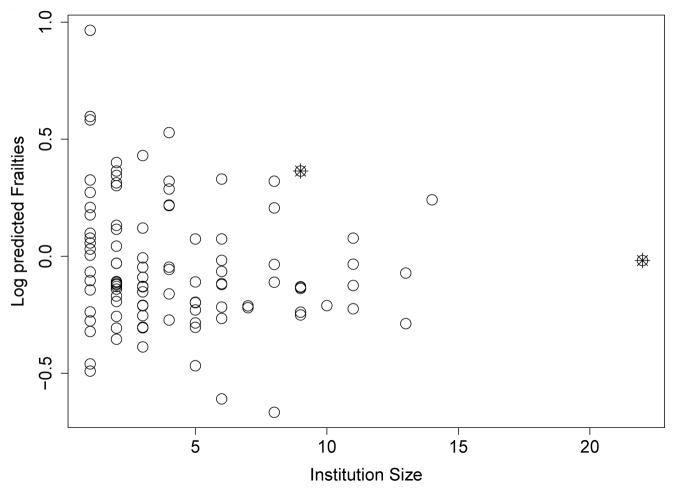
As with the proposed method, we looked plotted the log frailty values from the gamma frailty model versus the institution size in Figure 6. We note that the with the proposed method large, positive frailties are associated with improved survival, in contrast to the gamma frailty model in which large frailties are associated with increased hazards. The two institutions identified as potential outliers with the proposed method are marked with crosses. In Figure 6 there does not appear to be a relationship between log frailty value and institution size. The two marked institutions do not appear to have unusual frailty values given the trends in the data.
Fig. 6.
A plot of institution size by the log frailty value from gamma frailty model. Institutions identified as outliers in proposed methods are marked with crosses.
8 Discussion
There is a need for flexible survival regression models that allow for marginal interpretations of treatment or exposure, while concurrently evaluating potential clustering. The method proposed here establishes a general likelihood framework for this type of analysis. Marginal treatment or exposure effects are modeled with a proportional hazards model, while the correlation between survival times is described by a Gaussian copula. When the correlation between the transformed survival times is positive, the model can be extended to incorporate frailties. We believe this model can provide an easy graphical method to identify potentially “abnormal” clusters.
When the model was applied to a Children’s Oncology Group dataset, we were able to identify two potential outlying institutions. Baseline patient characteristics were unable to explain the observed trends. More information on patients or on the institutions may be needed to understand the underlying issues.
One area of future research is investigating the relative efficiency of using a non-parametric maximum likelihood approach in contrast to the two-stage approach used in this paper. Also, it might be useful to develop a more flexible frailty model that allows for covariates so that factors influencing correlation can be examined within a regression framework.
Acknowledgments
This work was supported in part by National Cancer Institute grants R01 CA95747 and CA09337-25. The authors thank Jim Anderson for providing the Children’s Oncology Group dataset and advice he gave for the data application.
A Regularity Conditions and Notation
Assume the following regularity conditions where τ > 0 is a constant (for example, study duration):
-
C.1
β is in a compact subset of ℝp
-
C.2
Λ(τ) < ∞
-
C.3
σ ∈ ν, where ν is a compact subset of (−1, 1)
-
C.4
P(Cij ≥ t ∀t ∈ [0, τ] | Zij) > δc > 0 for j = 1, …, ni and i = 1, …, m
-
C.5
Write Zij(t) = {Zij1(t), …, Zijp(t)}. almost surely for some constant BZ and i = 1, …, m, j = 1, …, ni, k = 1, …, p
-
C.6
E[log{L(σ1; β, Λ)/L(σ2; β, Λ)}] exists for all σ1, σ2 ∈ (−1, 1)
-
C.7Let Yij(t) = I(Xij ≥ t), K = maxi ni, a⊗0 = 1, a⊗1 = a, a⊗2 = a′a,
Assume is positive definite
Condition C.3 allows us to avoid boundary issues. Condition C.5 assumes that all the covariates are of bounded variation, which is necessary to ensure the Hadamard differentiability of the likelihood and score function. Condition C.6 is useful to help prove that the expected likelihood is maximized at σ0. Condition C.7 is a technical condition from Spiekerman and Lin (1998) that is needed for the results for β̂ and Λ̂.
Before providing technical results, we will provide a brief description of how the likelihood in Equation (3) can be derived. Let Sij (x) = S{x | Z̄ij (Xij)}. We consider a cluster of size ni with Δi subjects who are not censored. The contribution to the likelihood will be the density function for Xi1, …, XiΔi and the survival function for XiΔi+1, …, Xini. We have specified a copula structure, so we can write the survival function for (Xi1, …, Xini) as follows:
We can write the density of (Xi1, …, XiΔi), denoted fΔi (xi1, …, xiΔi) = f(xi1, …, xiΔi | Z̄i1(xi1), …, Z̄ini (xini)), in terms of YΔi using the chain-rule:
For j = 1, …, Δi:
The rest of Equation (3) can be found by combining these calculations with survival terms for subjects who are censored.
To simplify the presentation of the proofs we define several terms. Define
where L(σ, β, Λ) = c*L*(σ, β, Λ) and c* does not depend on σ. Let
Expectations are with respect to the true distributions of all random variables involved. Let || · || denote the Euclidean norm and let || · ||∞ denote the supremum norm on [0, τ]. Let BV [0, τ] denote the class of functions with bounded total variation on [0, τ]. Let single superscript dots denote first derivatives and double superscript dots denote second derivatives.
B Proof and Associated Lemmas for Theorem 1
For ease of presentation we state several lemmas used in the proof of Theorem 1, but defer their proof until Appendix D.
To account for the fact that plug-in estimates of β and Λ are used in the likelihood for σ, we will need to take a Taylor series expansion of the likelihood of σ around β0 and Λ0. Since Λ0 is an unspecified function, this expansion will need to include a functional expansion term. An expansion using Hadamard derivatives is appropriate for this situation. In order to use the functional expansion, we first need to verify that the log-likelihood is Hadamard differentiable with respect to Λ, which is done in Lemma 1.
Lemma 1
Under conditions C.1–C.5, the log-likelihood lm(σ) is Hadamard differentiable with respect to Λ.
After we have an expansion of the log-likelihood we will need the first order terms to be bounded by a random variable with finite expectation. We provide this verification in Lemma 2.
Lemma 2
Write the Hadamard derivative of lm(σ) with respect to Λ at ϒ ∈ BV [0, τ] as and let ζm(β, σ) = ∂lm(σ)/∂β. Under conditions C.1–C.5, ||ζm(Λ, σ) ||∞ and ||ζm(β, σ)|| are bounded. Expressions for ζm(β, σ)|| and ζm(Λ, σ) are provided in the proof.
In order to prove σ̂ is consistent we will need to verify the uniform convergence of the log-likelihood with plug-in estimates of β and Λ to the expected value of the log-likelihood evaluated at the true values of β and Λ, denoted lm0(σ). We accomplish this, using the results of Lemmas 1 and 2, in Lemma 3.
Lemma 3
Under conditions C.1–C.5, as m → ∞,
Finally, in order to verify that σ̂ is consistent, we will need to show that the expected log-likelihood is maximized at the truth, which is done in Lemma 4.
Lemma 4
Under conditions C.1–C.6, for any σ ≠ σ0,
Proof of Theorem 1
The results for β̂ and Λ̂ follow from arguments along the lines of Spiekerman and Lin (1998). We use the results of Lemmas 3 and 4 to prove the result for σ̂.
Since σ̂ maximizes l̂m(σ), Lemma 3 implies that
Therefore E{lm0(σ0)} ≤ l̂m(σ̂) + op(1). Subtract E{lm0(σ̂)} from each side of the inequality to write
| (9) |
where the last equality comes from Lemma 3.
Take σ such that |σ−σ0| ≥ ε for any fixed ε > 0. By Lemma 4 there must exist some γε > 0 such that E{lm0(σ)} + γε < E{lm0(σ0}). It follows that P(|σ̂−σ0| ≥ ε) ≤ P[E{lm0(σ)}+ γε< E{lm0(σ0)}[. Equation (9) implies that P[E{lm0(σ̂)} + γε < E{lm0(σ0)}] converges to 0 as m → ∞. Therefore P(|σ̂−σ0| ≥ ε) converges to 0 as m → ∞.
C Proof and Associated Lemmas for Theorem 2
For ease of presentation we state several lemmas used in the proof of Theorem 2, but defer their proof until Appendix D.
To account for the fact that plug-in estimates of β and Λ are used in the likelihood and score function for σ, we will need to take a Taylor series expansion of the score function for σ around β0 and Λ0. To do so we first need to verify that the score function is Hadamard differentiable with respect to Λ, which is done in Lemma 5.
Lemma 5
Under conditions C.1–C.5, the score function Um(σ) is Hadamard differentiable with respect to Λ.
After we have an expansion of the score function for σ, we will need the first order terms to be bounded by a random variable with finite expectation. We provide this verification in Lemma 6.
Lemma 6
Write the Hadamard derivative of Um(σ) with respect to Λ at ϒ ∈ BV [0, τ] as and let ξm(β, σ) = ∂Um(σ)/∂β. Under conditions C.1–C.5, ||ξm(σ, Λ)||∞ and ||ξm(σ, β)|| are bounded. Expressions for ξm(σ, β) and ξm(σ, Λ) are provided in the proof.
Proof of Theorem 2
The result that converges to mean zero normal distribution and that converges to mean zero Guassian process follows from arguments along the lines of Spiekerman and Lin (1998). This proof needs to verify that converges to a normal distribution with mean zero after accounting for the extra variance induced by the two-stage estimation procedure. The variance of σ̂ should be adjusted compared to a model where β0 and Λ0 are used to take into account the estimation of β̂ and Λ̂.
First we will show that the score equation associated with l̂m evaluated at σ0 follows a normal distribution. This result coupled with a first order expansion of the score equation associated with l̂m around σ0 will finish the proof.
Using Lemma 5, a Taylor series expansion of Ûm(σ) around β0 and Λ0 gives
where Gm is a remainder term for the Taylor series. Since Λ̂ and β̂ are -consistent it can be shown that Gm = op(m−1/2). Define the pointwise limit of ξm(σ, Λ)(t) as ξ(σ, Λ)(t) and let ξ(σ, β) = E{ξm(σ, β)}. From Lemma 6, ||ξ(σ0, Λ)||∞ and ||ξ(σ, β)|| are bounded. It follows that
| (10) |
Using the results of Spiekerman and Lin (1998), we can write Equation (10) as a sum of independent and identically distributed random variables, , where E(Ξ1) = 0 and V(Ξ1 < ∞. The central limit theorem implies that converges to a normally distributed random variable with mean zero and variance equal to the variance of Ξ1.
Next, we take a first order Taylor series expansion of Ûm(σ̂) around σ0:
where Ŵm(σ) = ∂Ûm(σ)/∂σ and σ* is between σ̂ and σ0. It must be the case that Ûm(σ̂) = 0 since σ̂ was taken to be the maximum of L(σ, β̂, Λ̂). Theorem 1 showed that σ̂ consistently estimates σ0, so the the law of large numbers implies that Ŵm(σ*) converges in probability to W(σ0) = limm→∞ Wm(σ0). Finally, using the central limit theorem and Slutsky’s theorem, converges to a normal distribution with mean zero and variance equal to W(σ0)−2V(Ξ1)
D Proofs of Lemmas
Proof of Lemma 1
Define Yij(t) = I(Xij ≥ t). The log-likelihood can be written
where . By condition C.5 the term
is Hadamard differentiable. Using multiple iterations of the chain rule for Hadamard derivatives (van der Vaart, 1998, Theorem 20.9), we conclude that lm(σ) is Hadamard differentiable.
Proof of Lemma 2
First we find expressions for ζm(σ, Λ) and ζm(β, σ), starting with ζm(σ, Λ). To make the argument more concrete express lm(σ) as a function of Λ by writing lm(σ, Λ) = lm(σ). Let Γ BV[0, τ]. Denote
By conditions C.1 and C.2, for j = 1, …, ni and i = 1, …, m, Hij > 0 and |X̃ij| < B* < ∞ for some constant B*.
To find the expression for the derivative, take a Taylor series expansion of lm{σ, Λ + t(Γ − Λ)} around t = 0 and evaluate the result at t = 1. The final expression is
where ζm(σ, Λ)(u) is equal to and is equal to
Therefore the Hadamard derivative for ϒ ∈ BV[0, τ] is . Direct calculation verifies that ζm(σ, β) is equal to
We need to check whether each of the terms in is bounded and also that the terms unique to ζm(σ, β) and ζm(σ, Λ) are bounded. First,
for some constant B1 since for , |X̃ij| < B*. Therefore, for i =1, …, m, .
Let wα(j) denote the vector of length α where the jth element is 1 and the rest of the vector is 0. Using the chain rule, for j = 1, …, Δi and i = 1, …, m,
The multivariate normal density is bounded and for , |X̃ij| < B*. Hence, for j = 1, …, Δi and i =1, …, m, for some constant B2.
Next consider , which for i = 1, …, m is equal to
where Mi = {t(Δi+1) > X̃i, (Δi+1), …, tni > X̃i,ni}, tni − Δi = (t(Δi+1), …, tni), , and . Since |X̃ij| < B* for , it must be the case that for i = 1, …, m. for some constant B3.
Let be equal to tni − Δi but with the component corresponding to the (j − Δi)th component replaced by X̃ij. Let be equal to tni − Δi but with the (j − Δi)th element removed. Let Mi,−j denote Mi but with the ( ) inequality removed. Consider , which, for j = Δi + 1, …, ni, i = 1 …, m, can be written
for some constant B4 < ∞ since |X̃ij| < B* for .
Using the definition of the derivative of an inverse function,
where φ is the density of the standard normal distribution and Φ−1 is the inverse of the distribution function of the standard normal distribution. Since |X̃ij| < B*, 0 < B5 < Hij < B6 < 1 for some constants B5 and B6. Therefore, for j = 1, …, ni and i = 1, …, m, |∂Φ−1(Hij)/∂Hij| < B7 < ∞ for some constant B7. By condition C.5, for j = 1, …, ni and i = 1, …, m, ||Yij exp(β′Zij)||∞ < B8 < ∞ and for some constants B8 and B9. Hence ||ζm(σ, Λ)||∞ and ||ζm(β, σ)|| are bounded are bounded by (B1B2 + B3B4)B7(B8 + B9) < ∞
Proof of Lemma 3
An expansion of l̂m(σ) around Λ0 and β0 can be written:
where R is a remainder term of order op{max(||Λ̂ − Λ0||∞, ||β̂ − β0||)} and ζm(β, σ) and ζm(σ, Λ)(t) are defined in Lemma 2. Since Λ̂ is uniformly consistent and β̂ is consistent (Spiekerman and Lin, 1998), R = op(1). The result follows from the law of large numbers, the uniform consistency of Λ̂, the consistency of β̂, and the fact that ||ζm(β, σ)|| and ||ζm(σ, Λ)||∞ are bounded (Lemma 2).
Proof of Lemma 4
The log-likelihood, lm(σ), can be written as a sum of independent and identically distributed random variables . Take σ ≠ σ0. The law of large numbers and Jensen’s inequality imply that E{lm0(σ)} − E{lm0(σ0)} = limm→∞ lm0(σ) − lm0(σ0) which is strictly less than log[E{L*(σ, β0, Λ0)/L*(σ0, β0, Λ0)}] = 0.
Proof of Lemma 5
Let N(t, d, μ, Σ†) be defined as (2π)−d/2 det(Σ†)−1/2 exp{−(t − μ)′(Σ†)−1(t − μ)/2} [tr{(Σ†)−1 W̃d} − {−(t − μ)′(Σ†) −1 W̃d(Σ†)−1(t − μ)/2}]/2, where W̃d is the d dimensional square matrix with zeros along the diagonal and ones off the diagonal. Let 0d denote a vector of length d of zeros. The score function can be written
Using the results of Lemma 1 and multiple iterations of the chain rule for Hadamard derivatives (van der Vaart, 1998, Theorem 20.9), we conclude that Um(σ) is Hadamard differentiable.
Proof of Lemma 6
First we find expressions for ξm(σ, Λ) and ξm(σ, β), starting with ξm(σ, Λ). To make the argument more concrete express Um(σ) as a function of Λ by writing Um(σ, Λ) = Um(σ). Let Γ ∈ BV [0, τ].
To find the expression for the derivative, take a Taylor series expansion of Um{σ,Λ + τ(Γ – Λ)} around t = 0 and evaluate the result at t = 1. The final expression is , where ξm(σ, Λ)(u) is equal to
and
Therefore the Hadamard derivative for ϒ ∈ BV [0, τ] is . Direct calculation verifies that ξm(σ, β) is equal to
In Lemma 2 we showed that, for i = 1, …, m, and . Also, for j = 1, …, ni, i = 1, …, m, |∂Φ−1(Hij)/∂Hij| < B7 < ∞, ||Yij exp(β′Zij)||∞ < B8 < ∞ and .
We tackle each of the remaining terms. First, using results from Lemma 2, for j = 1, …, Δi, i = 1, …, m, is equal to for some constant B11.
Since Σi11 has an exchangeable structure, and det(Σi11)−1/2 are both bounded by some constant B10 < ∞. Therefore for i = 1, …, m, for some constant B12.
Next, we consider for j = 1, …, Δi and i = 1, …, m, which is equal to
and, by the results of the previous paragraph and the results of Lemma 2, is bounded by some constant B13 < ∞.
Using results from Lemma 2, for j = Δi + 1, …, ni and i = 1, …, m, is equal to
for some constant B14.
Using similar arguments as above one can directly show that for i = 1, …, m,
for some constant B15.
Also, for j = Δi + 1, …, ni and i = 1, …, m,
for some constant B16.
Hence ||ξm(σ, Λ)||∞ and ||ξm(β, σ)|| are bounded by (B11B12+B1B13+B14B15+B3B16)B7(B8+B9) < ∞.
E Extended simulation results
In the interest of space, the simulation results in the main body of the manuscript focus on the novel results for σ. We summarize the performance of β in Table 7. The true values for β1 and β2 are log(0.5) and 0.75, respectively. In all scenarios investigated, both the robust sandwich standard error and the jackknife standard error perform well. The jackknife standard error (SE) appears to match the Monte Carlo SE more closely compared to the robust SE, but the coverage probabilities are very similar and indicate appropriate coverage. Power for a Wald-type test with the jackknife SE is high across all the scenarios.
Table 7.
Simulation results for marginal parameters from the proportional hazards model. CP denotes coverage probability and SE denotes standard error.
| Estimate | Jackknife SE | Monte Carlo SE | Robust SE | Jackknife CP | Robust CP | Power | ||
|---|---|---|---|---|---|---|---|---|
| 90 clusters | ||||||||
| σ = 0 | β1 | −0.700 | 0.140 | 0.136 | 0.182 | 0.964 | 0.960 | 0.996 |
| β2 | 0.765 | 0.237 | 0.236 | 0.185 | 0.956 | 0.944 | 0.912 | |
| σ = 0.05 | β1 | −0.711 | 0.138 | 0.124 | 0.183 | 0.964 | 0.964 | 1.000 |
| β2 | 0.800 | 0.237 | 0.212 | 0.198 | 0.956 | 0.952 | 0.948 | |
| σ = 0.10 | β1 | −0.696 | 0.140 | 0.140 | 0.185 | 0.952 | 0.944 | 1.000 |
| β2 | 0.769 | 0.241 | 0.241 | 0.197 | 0.948 | 0.944 | 0.884 | |
| σ = 0.15 | β1 | −0.710 | 0.141 | 0.127 | 0.182 | 0.972 | 0.960 | 1.000 |
| β2 | 0.756 | 0.240 | 0.236 | 0.178 | 0.960 | 0.948 | 0.884 | |
| 150 clusters | ||||||||
| σ = 0 | β1 | −0.689 | 0.106 | 0.108 | 0.139 | 0.944 | 0.936 | 1.000 |
| β2 | 0.743 | 0.182 | 0.173 | 0.141 | 0.956 | 0.956 | 0.988 | |
| σ = 0.05 | β1 | −0.679 | 0.106 | 0.101 | 0.138 | 0.952 | 0.952 | 1.000 |
| β2 | 0.770 | 0.182 | 0.172 | 0.141 | 0.968 | 0.968 | 0.996 | |
| σ = 0.10 | β1 | −0.699 | 0.106 | 0.107 | 0.146 | 0.956 | 0.948 | 1.000 |
| β2 | 0.753 | 0.183 | 0.178 | 0.144 | 0.964 | 0.952 | 0.988 | |
| σ = 0.15 | β1 | −0.702 | 0.107 | 0.109 | 0.143 | 0.940 | 0.936 | 1.000 |
| β2 | 0.742 | 0.183 | 0.178 | 0.138 | 0.948 | 0.940 | 0.964 |
Contributor Information
Megan Othus, Email: mothus@fhcrc.org, Fred Hutchinson Cancer Research Center, Seattle, WA 98109, Tel.: 206-667-5749.
Yi Li, Harvard University and Dana Farber Cancer Institute, Boston, MA 02115.
References
- Anello C, O’Neill R, Dubey S. Multicentre Trials: A US Regulatory Perspective. Statistical Methods in Medical Research. 2005;14(3):303–318. doi: 10.1191/0962280205sm398oa. [DOI] [PubMed] [Google Scholar]
- Booth J, Hobert J. Standard Errors of Prediction in Generalized Linear Mixed Models. Journal of the American Statistical Association. 1998;93(441):262–272. [Google Scholar]
- Cai J, Prentice R. Estimating Equations for Hazard Ratio Parameters Based on Correlated Failure Time Data. Biometrika. 1995;82(1):151–164. [Google Scholar]
- Cai J, Shen Y. Permutation Tests for Comparing Marginal Survival Functions with Clustered Failure Time Data. Statistics in Medicine. 2000;19(21):2963–2973. doi: 10.1002/1097-0258(20001115)19:21<2963::aid-sim593>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Cai J, Zhou H, Davis C. Estimating the Mean Hazard Ratio Parameters for Clustered Survival Data with Random Clusters. Statistics in Medicine. 1997;16(17):2009–2020. doi: 10.1002/(sici)1097-0258(19970915)16:17<2009::aid-sim606>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- Cai T, Wei L, Wilcox M. Semiparametric Regression Analysis for Clustered Failure Time Data. Biometrika. 2000;87(4):867–878. [Google Scholar]
- Cai T, Cheng S, Wei L. Semiparametric Mixed-effects Models for Clustered Failure Time Data. Journal of the American Statistical Association. 2002;97(458):514–522. [Google Scholar]
- Chen X, Fan Y, Tsyrennikov V. Efficient Estimation of Semiparametric Multivariate Copula Models. Journal of the American Statistical Association. 2006;101(475):1228–1240. [Google Scholar]
- Clayton D. A Model for Association in Bivariate Life Tables and its Application in Epidemiological Studies of Familial Tendency in Chronic Disease Incidence. Biometrika. 1978:141–151. [Google Scholar]
- Fine J, Glidden D, Lee K. A Simple Estimator for a Shared Frailty Regression Model. Journal of the Royal Statistical Society Series B, Statistical Methodology. 2003;65(1):317–329. [Google Scholar]
- Fleiss J. Analysis of Data from Multiclinic Trials. Controlled Clinical Trials. 1986;7(4):267–275. doi: 10.1016/0197-2456(86)90034-6. [DOI] [PubMed] [Google Scholar]
- Glidden D. A Two-Stage Estimator of the Dependence Parameter for the Clayton-Oakes Model. Lifetime Data Analysis. 2000;6(2):141–156. doi: 10.1023/a:1009664011060. [DOI] [PubMed] [Google Scholar]
- Glidden D, Vittinghoff E. Modelling Clustered Survival Data from Multicentre Clinical Trials. Statistics in medicine. 2004;23(3):369–388. doi: 10.1002/sim.1599. [DOI] [PubMed] [Google Scholar]
- Gray R. A Bayesian Analysis of Institutional Effects in a Multicenter Cancer Clinical Trial. Biometrics. 1994;50(1):244–253. [PubMed] [Google Scholar]
- Hougaard P. Analysis of Multivariate Survival Data. Springer Verlag; 2000. [Google Scholar]
- Jones B, Teather D, Wang J, Lewis J. A Comparison of Various Estimators of a Treatment Difference for a Multi-centre Clinical Trial. Statistics in Medicine. 1998;17:1767–1777. doi: 10.1002/(sici)1097-0258(19980815/30)17:15/16<1767::aid-sim978>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Kalbfleisch J, Prentice R. The Statistical Analysis of Failure Time Data. 2. Wiley; 2002. [Google Scholar]
- Klaassen C, Wellner J. Efficient Estimation in the Bivariate Normal Copula Model: Normal Margins are Least Favourable. Bernoulli. 1997;3(1):55–77. [Google Scholar]
- Lam K, Lee Y, Leung T. Modeling Multivariate Survival Data by a Semipara-metric Random Effects Proportional Odds Model. Biometrics. 2002;58(2):316–323. doi: 10.1111/j.0006-341x.2002.00316.x. [DOI] [PubMed] [Google Scholar]
- Li Y, Lin X. Semiparametric Normal Transformation Models for Spatially Correlated Survival Data. Journal of the American Statistical Association. 2006;101(474):591–603. [Google Scholar]
- Li Y, Prentice R, Lin X. Semiparametric Maximum Likelihood Estimation in Normal Transformation Models for Bivariate Survival Data. Biometrika. 2008;95(4):947–960. doi: 10.1093/biomet/asn049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipsitz S, Parzen M. A Jackknife Estimator of Variance for Cox Regression for Correlated Survival Data. Biometrics. 1996;52:291–298. [PubMed] [Google Scholar]
- Lipsitz S, Dear K, Zhao L. Jackknife Estimators of Variance for Parameter Estimates from Estimating Equations with Applications to Clustered Survival Data. Biometrics. 1994;50:842–846. [PubMed] [Google Scholar]
- Logan B, Nelson G, Klein J. Analyzing Center Specific Outcomes in Hematopoietic Cell Transplantation. Lifetime Data Analysis. 2008;14:389404. doi: 10.1007/s10985-008-9100-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy S. Consistency in a Proportional Hazards Model Incorporating a Random Effect. Annals of Statistics. 1994;22(2):712–731. [Google Scholar]
- Murphy S. Asymptotic Theory for the Frailty Model. Annals of Statistics. 1995;23:182–198. [Google Scholar]
- Oakes D. Bivariate Survival Models Induced by Frailties. Journal of the American Statistical Association. 1989;84(406):487–493. [Google Scholar]
- Parner E. Asymptotic Theory for the Correlated Gamma-frailty Model. Annals of Statistics. 1998;26(2):183–214. [Google Scholar]
- Prentice R, Cai J. Covariance and Survivor Function Estimation Using Censored Multivariate Failure Time Data. Biometrika. 1992;79(3):495–512. [Google Scholar]
- Seibel N, Steinherz P, Sather H, Nachman J, Delaat C, Ettinger L, Freyer D, Mattano L, Jr, Hastings C, Rubin C, Bertolone K, Franklin J, Heerema N, Mitchell T, Pysemany A, La M, Edens C, Gaynon P. Early Post-induction Intensification Therapy Improves Survival for Children and Adolescents with High-risk Acute Lymphoblastic Leukemia: A Report from the Children’s Oncology Group. Blood. 2008;11(5):2548–2555. doi: 10.1182/blood-2007-02-070342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senn S. Some Controversies in Planning and Analysing Multi-centre Trials. Statistics in Medicine. 1998;17(15–16):1753–1765. doi: 10.1002/(sici)1097-0258(19980815/30)17:15/16<1753::aid-sim977>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- Shih J, Louis T. Assessing Gamma Frailty Models for Clustered Failure Time Data. Lifetime Data Analysis. 1995;1(2):205–220. doi: 10.1007/BF00985771. [DOI] [PubMed] [Google Scholar]
- Spiekerman C, Lin D. Marginal Regression Models for Multivariate Failure Time Data. Journal of the American Statistical Association. 1998;93(443):1164–1175. [Google Scholar]
- Therneau T, Grambsch P. Modeling Survival Data: Extending the Cox Model. Springer Verlag; 2000. [Google Scholar]
- van der Vaart A. Asymptotic Statistics. Cambridge University Press; 1998. [Google Scholar]
- Vierron E, Giraudeau B. Sample Size Calculation for Multicenter Randomized Trial: Taking the Center Effect into Account. Contemporary Clinical Trials. 2007;28(4):451–458. doi: 10.1016/j.cct.2006.11.003. [DOI] [PubMed] [Google Scholar]
- Wei L, Lin D, Weissfeld L. Regression Analysis of Multivariate Incomplete Failure Time Data by Modeling Marginal Distributions. Journal of the American Statistical Association. 1989;84(408):1065–1073. [Google Scholar]
- Zeng D, Lin D. Maximum Likelihood Estimation in Semiparametric Regression Models with Censored Data. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2007;69(4):507–564. [Google Scholar]
- Zheng L, Zelen M. Multi-center Clinical Trials: Randomization and Ancillary Statistics. Annals of Applied Statistics. 2008;2(2):582–600. doi: 10.1214/07-AOAS151. [DOI] [PMC free article] [PubMed] [Google Scholar]