Abstract
Adult Bengalese finches generate a variable song that obeys a distinct and individual syntax. The syntax is gradually lost over a period of days after deafening and is recovered when hearing is restored. We present a spiking neuronal network model of the song syntax generation and its loss, based on the assumption that the syntax is stored in reafferent connections from the auditory to the motor control area. Propagating synfire activity in the HVC codes for individual syllables of the song and priming signals from the auditory network reduce the competition between syllables to allow only those transitions that are permitted by the syntax. Both imprinting of song syntax within HVC and the interaction of the reafferent signal with an efference copy of the motor command are sufficient to explain the gradual loss of syntax in the absence of auditory feedback. The model also reproduces for the first time experimental findings on the influence of altered auditory feedback on the song syntax generation, and predicts song- and species-specific low frequency components in the LFP. This study illustrates how sequential compositionality following a defined syntax can be realized in networks of spiking neurons.
Keywords: HVC, Reafferent, Feed-forward network, Efference copy, Syntax generation, Synfire chains, Bengalese finch, Spike synchrony, Motor control, Compositionality
Introduction
Several experimental studies have shown that the song of the Bengalese finch relies on auditory feedback. The Bengalese finch typically produces a set of ordered sequences of syllables, but after deafening this song syntax is disrupted, i.e. the sequence becomes more random and unstable (Okanoya and Yamaguchi 1997, 1997; Woolley and Rubel 1999; Watanabe and Aoki 1998). In a subsequent experiment Woolley and Rubel (2002) reversibly deafened Bengalese finches and showed that normal vocal behavior can be restored when hearing is restored. They argued that a template of the song exists independently of auditory input. Yamada and Okanoya (2003) reported that the song syntax is also reversibly changed if the Bengalese finch is singing in a helium atmosphere. More recently, studies have demonstrated that the vocal motor control system of the Bengalese finch relies on real time auditory feedback (Sakata and Brainard 2006) and that the HVC activity (caudal nucleus of the ventral hyperpallium or high vocal center, nowadays used as proper name) is influenced instantaneously by feedback perturbance (Sakata and Brainard 2008). These experimental findings suggest an auditory reafferent signal to be necessary for the generation of correct song syntax.
Early experimental studies on the songbird suggested that HVC neurons projecting to the pre-motor nucleus RA (robust nucleus of the arcopallium) only encode for the temporal structure within the song and that a sequence of fixed motor commands is replayed within the RA (Yu and Margoliash 1996; Hahnloser et al. 2002; Nottebohm 2002). Recent results using moderate local cooling (Long and Fee 2008; Glaze and Troyer 2008) have changed our understanding of this motor pathway. Temporal coding not only of the song elements but on all timescales (motif, syllable, note) is located in the HVC, whilst the RA serves to encode the HVC commands into firing rates suitable for the muscles needed to control the vocal output (Yu and Margoliash 1996; Fee et al. 2004). During singing the HVC neurons projecting to RA (HVCRA) show bursting activity that is time locked with sub-millisecond precision to the stereotyped song motif (Hahnloser et al. 2002).
How the HVCRA neurons are able to generate the activity pattern with sub-millisecond precision can be explained by two different approaches. The first hypothesis explains the pattern by rhythmic drive to the HVCRA neurons from an afferent nucleus, based on studies suggesting temporal structuring originating from the Uva (nucleus uvaeformis) or NIf (nucleus interface of the nidopallium) (McCasland 1987; Williams and Vicario 1993; Vu et al. 1994; Coleman and Vu 2005). Several model studies are based on this assumption (Troyer and Doupe 2000a; Drew and Abbott 2003; Katahira et al. 2007; Yamashita et al. 2008; Gibb et al. 2009b). The second hypothesis is that the activity pattern originates from circuits intrinsic to the HVC. Models of neural circuits known as synfire chains that are composed of divergently and convergently connected feed-forward structures can reliably produce activity patterns on a sub-millisecond time scale (Abeles 1991; Herrmann et al. 1995; Diesmann et al. 1999). Mooney and Prather (2005) reported convergent and divergent connection structures in the HVC, which provides supporting evidence for the involvement of such assemblies in song production. Additionally, a recent experiment has revealed that the subthreshold dynamics visible in the intracellular recordings in HVCRA of freely behaving zebra finches exhibits large and rapid depolarization before spiking, and that spike times are only weakly affected by injected currents. These findings also provide strong support for the hypothesis that HVC contains feed-forward networks (Long et al. 2010). This insight has been influential; a number of recent theoretical studies investigate the functional consequences of synfire chain involvement in HVC (Li and Greenside 2006; Jin et al. 2007; Jin 2009) or the development of the chains themselves (Fiete et al. 2010).
Similarly, there are two hypotheses to account for the generation of sequences of syllables. In the simplest realization the syllable sequence is predefined by the HVC connectivity. This ‘motor tape’ in the HVC is able to reproduce the highly stereotyped sequences generated by adult zebra finches. A simple example is a song starting with an introductory note ‘i’ that is followed by a repeating sequence of syllables ‘ABC’, resulting in ‘iABC − ABC’ (Bottjer and Arnold 1984; Drew and Abbott 2003; Weber and Hahnloser 2007). This can be extended to a more complex realization that reproduces stochastic branching as observed in the song of the Bengalese finch (e.g. ‘iABCD − ABD’; Katahira et al. 2007; Yamashita et al. 2008; Jin 2009). The major shortcoming in predefining the song syntax in the HVC connectivity is that it is static, whereas multiple experimental findings demonstrate that the syntax can be transiently altered, and even entirely lost and regained. An alternative approach is based on the assumption that syntax generation is controlled by a state signal. This signal can be either an efference copy of the motor command (e.g. within HVC; Troyer and Doupe 2000b), a neural feedback signal (e.g. from the brain stem; Gibb et al. 2009a) or a reafferent cue (e.g. from the auditory system; Sakata and Brainard 2006).
Here, we investigate for the first time the reafferent hypothesis in a functional network model. To account for the findings on both undisturbed and disturbed song syntax, we combine the feed-forward model of Jin (2009) with the reafferent hypothesis of Sakata and Brainard (2006) to a unified model. We present a functional network model of spiking neurons with feed-forward circuits in HVC and a reafferent state signal that reproduces key experimental findings on Bengalese finches. We assume all-to-all interconnections between the chains in HVC such that all transitions between syllables are possible. A specific syntax is then generated by priming the transition sites of the synfire chains with auditory feedback generated from the perception of the bird’s own song (BOS). This mechanism is called reafference (the afference evoked by the efference; Holst and Mittelstaedt 1950) and has been suggested to explain the influence of the auditory feedback by Sakata and Brainard (2006).
Our model is able to reproduce the normal sequence generation and the main findings of experiments on auditory feedback disturbance of the Bengalese finch. In the absence of the auditory feedback more random sequences of syllables are produced, whilst perturbing the auditory feedback by playing the bird a syllable different from the one sung results in a stereotyped change in sequencing (Okanoya and Yamaguchi 1997; Watanabe and Aoki 1998; Sakata and Brainard 2006). Moreover, by postulating synaptic plasticity within the model we can reproduce the finding that syntax is gradually lost over a period of days after deafening, but is regained when hearing is restored (Woolley and Rubel 2002).
In our model we investigate two plasticity hypotheses to explain the gradual loss of syntax. If the transition sites between the synfire chains are plastic, an imprinting of the more frequently used syllable transitions occurs. After feedback suppression the syntax is approximately maintained by the imprinted structure until it is eroded. If plastic outgoing connections of HVCRA realize an efference copy of the song syntax, the causal relationship between the efferent and reafferent signals can be learned. In the absence of the reafferent signal, the efference copy stabilizes the song syntax for a period of time. Interactions of an efference copy with a reafferent signal have previously been reported, for example in the electric sense of the weakly electric fish (Bell 1981).
From a theoretical point of view our study investigates the compositionality of sequences. The syllables of the song are elementary building blocks, called primitives, which are combined following a defined syntax. Previous studies have investigated the generation of sequences of primitives without syntax, i.e. any primitive can follow any other primitive (Chang and Jin 2009; Schrader et al. 2010). A syntax can be imposed on the selection of the next primitive by using a higher level controller (Yamashita and Tani 2008), a pre-defined connectivity within the same level (Jin 2009; Schrader et al. 2010; Hanuschkin et al. 2010c), or a combination of both. Here, we generate the syntax using a combination of a pre-defined all-to-all connectivity between the primitive syllables encoded in HVC together with higher level signals from the auditory system. The all-to-all connectivity allows the system to realize any syntax defined in terms of transitions between pairs of syllables; the control signal consists of the system’s reafferent input and constrains the set of possible syntaxes to a specific one.
The paper is organized as follows; in the last part (Section 1.1) of this introduction we briefly review the relevant song bird anatomy and the neurophysiological details of the HVC neurons. In Section 2 we explain the concept of synfire chains, the details of the numerical simulations and the evaluation of song syntax. In Section 3 we introduce the model and demonstrate its functional consequences. Experimental predictions arising from our study and its limitations and possible future extensions are presented in Section 4.
Preliminary results have been published in abstract form (Hanuschkin et al. 2010a, b, 2011).
Songbird anatomy
In the adult songbird three main brain regions play key roles in the production and learning of songs. The motor pathway consists of two nuclei: HVC and RA. The anterior forebrain pathway (AFP) resembles a basal ganglia/ thalamus equivalent structure and consists of three nuclei: Area X (Area X of the medial striatum), which projects to DLM (dorsolateral thalamic nucleus) which in turn projects to LMAN (lateral magnocellular nucleus of the anterior nidopallium). The two pathways are interconnected; Area X receives input from HVC and LMAN projects to RA and back to Area X. Both Area X and LMAN receive input from dopamine neurons (Brainard and Doupe 2002; Gale and Perkel 2010). The AFP is necessary for song learning but not for reproduction of the learned song (Bottjer et al. 1984; Sohrabji et al. 1990; Scharff and Nottebohm 1991), however it is responsible for variability in syllable structure (Sakata et al. 2008; Hampton et al. 2009). The third brain region related to the song is the sensory input area consisting of field L (avian primary forebrain auditory area; roughly equivalent to mammalian primary auditory cortex) which projects to HVC via CM (caudal mesopallium) and NIf (Roy and Mooney 2009). NIf and HVC also receive dopaminergic input (Brainard and Doupe 2002). For a review of songbird anatomy and its revised nomenclature, see Brainard and Doupe (2002) and Jarvis et al. (2005).
The HVC neurons can be subdivided into three populations with distinct morphological and neural properties: interneurons (HVCI) and neurons that project to RA (HVCRA) or Area X (HVCX) (Dutar et al. 1998; Mooney 2000). Experiments by Mooney and Prather (2005) on the HVC network structure revealed projections from HVCRA to HVCX via HVCI and divergent connections from HVCI to HVCRA and HVCX. Furthermore, they describe convergent and divergent connection structures. Activity synchrony between the population of interneurons and HVCX, and weak synchrony between individual HVCI neurons has been observed during singing (Kozhevnikov and Fee 2007). All three HVC populations increase their firing rate in response to BOS playback due to common excitatory input from NIf or CM (Cardin et al. 2005; Rosen and Mooney 2006; Shaevitz and Theunissen 2007; Bauer et al. 2008; Roy and Mooney 2009; Akutagawa and Konishi 2010) but exhibit differentiated sub-threshold activity. HVCX neurons show hyper-polarization (Lewicki 1996) while HVCRA neurons exhibit BOS-specific depolarization (Mooney 2000). The different sub-threshold behaviors can be explained by the local HVC interaction of direct inhibition from HVCI and indirect inhibition of the HVCX neurons by the HVCRA neurons (Mooney 2000; Rosen and Mooney 2003; Mooney and Prather 2005; Rosen and Mooney 2006). It should be noted that nearly all studies on the HVC network structure (Lewicki 1996; Mooney 2000; Rosen and Mooney 2003; Mooney and Prather 2005; Rosen and Mooney 2006; Kozhevnikov and Fee 2007; Poirier et al. 2009) were carried out with zebra finches and that the role of local inhibition in the HVC might be more elaborate in the Bengalese finch, due to its more variable song syntax (Sakata and Brainard 2008).
Materials and methods
Synfire chains
The concept of a convergent and divergent connected feed-forward structure that allows the propagation of synchronous spiking activity was originally introduced to explain precise spike timing patterns in cortical tissue (Abeles 1991). In its simplest realization, neurons are organized in successive pools and each neuron is connected to all neurons in the following pool. The resultant structure of neuronal assemblies is known as a synfire chain (SFC). Activity volleys reliably propagate along a synfire chain under quite general conditions (Herrmann et al. 1995; Diesmann et al. 1999; Goedeke and Diesmann 2008). Here, we consider chains of 20 pools containing 100 neurons each, which is similar to the number of neurons estimated to be active at each moment during song (Fee et al. 2004; Fiete et al. 2010). The number of feed-forward connections made by each neuron is governed by a dilution factor p = 0.5 (Abeles et al. 2004). This is illustrated schematically in Fig. 1a. The activation period of a chain is around 160 ms, which is comparable to the characteristic length of birdsong syllables (Brainard and Doupe 2001; Leonardo and Fee 2005; Sakata and Brainard 2006). Additionally, each SFC neuron makes connections to random targets in a population of inhibitory neurons, which in turn globally inhibits the synfire chains with short synaptic delays (Jin 2009). The neurons in the final pool of each chain make feed-forward connections to the initial pools of each of its potential successor chains. This fundamental architecture is shown in Fig. 1b. Due to the global inhibition, activity in a single chain is the unique attractor so reliable switching from one synfire chain to exactly one of its potential successor chains is assured (Chang and Jin 2009). By applying additional priming in the form of an excitatory stimulus to the initial pool of a chain, the probability of selecting that chain during competition can be increased.
Fig. 1.
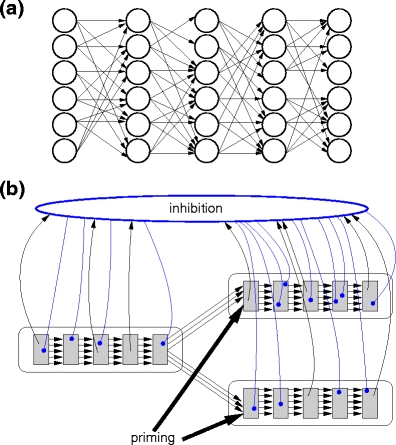
Synfire chains, global inhibition and priming. (a) Sketch of a synfire chain. Excitatory neurons (open circles) are organized in pools. Each neuron in pool j makes connections (black arrows) to the neurons in pool j + 1 in a feed-forward manner employing a random divergent connection schema with a dilution rate of p = 0.5. (b) Synfire chain switching in the presence of global inhibition and priming. The final pool of one chain establishes excitatory feed-forward connections to the initial pools of two potential successor chains. When the synfire activity reaches the end of the first chain, both potential successor chains are stimulated. The synfire chains are reciprocally connected with a population of inhibitory neurons. The simultaneous activity in the potential successor chains thus leads to an increase of inhibition in the network. Due to the dominant and fast global inhibition, activity can only propagate in one of the potential successor chains. Priming is induced by additional excitation to one or both of the successor chains, altering the switching probability. Excitatory connections are represented by black arrows, inhibitory connections by blue arrows
The synfire chain connectivity is described in detail in Table 1, the corresponding parameters are specified in Table 3.
Table 1.
Summary of model structure after Nordlie et al. (2009)
| Model summary | |||
|---|---|---|---|
| Populations | One network of interconnected synfire chains and recurrent connected interneurons (HVC), one network of recurrent connected neurons (auditory network; AN) | ||
| Connectivity | HVC: excitatory feed-forward (FF) connections within each chain and between final and initial groups of all pairs of chains, excitatory connections to interneurons, recurrent inhibitory connections within group of interneurons, global random inhibition from the interneurons to the chains. AN: balanced networks of excitatory and inhibitory neurons with random connectivity. HVC to AN: excitation from the individual chains. AN to HVC: selective excitatory connections to the first pool of the chains (priming). All connections realized using random divergent (RD) or random convergent (RC) wiring. | ||
| Neuron model | Leaky integrate-and-fire (IaF), fixed voltage threshold, fixed absolute refractory time | ||
| Synapse model | Static α-current or spike-timing dependent plasticity with α-current | ||
| Input | Independent fixed-rate Poisson spike trains to all neurons | ||
| Measurements | Spike activity, membrane potential, synaptic weights | ||
| Populations | |||
|---|---|---|---|
| Name | Elements | Size | |
| HVC | SFCN, group of inter neurons IN | 1 SFCN,1 IN | |
| AN | Auditory sub networks j Au | 4 | |
| SFCN | Synfire chains SFCj | 4 SFCs | |
| SFCj | SFC groups E i,j | 20 | |
| IN | Neuron populations I | 1 population | |
| j Au | Neuron populations |
2 populations per subnet j | |
|
|
Excitatory IaF neuron | 100 | |
|
|
Inhibitory IaF neuron | 1000 | |
|
|
Excitatory IaF neuron | 336 | |
|
|
Inhibitory IaF neuron | 84 | |
| Connectivity | |||
|---|---|---|---|
| Name | Source | Target | Pattern |
| FF |
|
|
RD, 1→C Ex, weight J RA,RA, delay d RA,RA |
|
|
|
|
RC, C Ex→1, weight J RA,RA or plastic, delay d RA,RA |
| Ch inh |
|
I | RD, 1→C RA,I, weight J RA,I, delay d RA,I |
| I global | I |
|
RD, 1→C I,RA, weight J I,RA, delay d I,RA |
| I recurrent | I | I | RC, C I,I→1, weight J I,I, delay d I,I |
| E reafferent |
|
|
RC, C reaff→1, weight J reaff, delay d reaff |
| E prime |
|
|
RC, C prime→1, weight J E,AN, delay d AN |
|
|
|
|
RC, C E,AN→1, weight J E,AN, delay d AN |
|
|
|
|
RC, C E,AN→1, weight J E,AN, delay d AN |
|
|
|
|
RC, C I,AN→1, weight J I,AN, delay d AN |
|
|
|
|
RC, C I,AN→1, weight J I,AN, delay d AN |
|
|
|
|
Not connected by default; RC, C e.c.→1, plastic weight J e.c., delay d e.c. |
Connections marked with stars might be plastic as described in Section 3.2.
Table 3.
Specification of connectivity parameters
| Name | Value | Description |
|---|---|---|
| C Ex | 93 | Number of feed-forward connections from each excitatory neuron |
| J RA,RA | 65 pA | Synaptic weight in feed-forward connections |
| d RA,RA | 3 ms | Synaptic transmission delay |
| C RA,I | 50 | Number of connections from each of HVCRA to the pool of interneurons |
| J RA,I | 60 pA | Synaptic weight |
| d RA,I | 0.1 ms | Synaptic transmission delay |
| C I,RA | 720 | Number of connections from each inhibitory HVCI neuron to the HVCRA neurons |
| J I,RA | − 50 pA | Synaptic weight |
| d I,RA | 0.1 ms | Synaptic transmission delay |
| C I,I | 10 | Number of connections from the pool of HVCI neurons to each HVCI neuron |
| J I,I | − 5 pA | Synaptic weight |
| d I,I | 1 ms | Synaptic transmission delay |
| C reaff | 20 | Reafferent input: connections from the HVCRA neurons of one syllable to each of the neurons of the corresponding auditory subnetwork |
| J reaff | 30 pA | Synaptic weight |
| d reaff | 40 ms | Synaptic transmission delay is chosen large to take auditory perception into account |
| C prime | 250 | Priming: number of connections from the pool of the auditory subnetwork to each neuron of the first pool of the chain to prime |
| C E,AN | 33 | Number of connections drawn from the pool of excitatory neurons |
| C I,AN | 8 | Number of connections drawn from the pool of inhibitory neurons |
| J E,AN | 3.33 pA | Synaptic weight |
| J I,AN | − 20.81 pA | Synaptic weight |
| d AN | 1 ms | Synaptic transmission delay |
| C e.c. | 0 or 10 | Efference copy: number of connections drawn from the pool of SFCs neurons in the implementation with efference copy |
| J e.c. | – | Synaptic weight (plastic) |
| d e.c. | 3 ms | Synaptic transmission delay |
Neuron and synapse model
We perform numerical simulations of leaky integrate-and-fire model neurons (Lapicque 1907; Abbott 1999) with post synaptic currents (PSCs) described by the alpha-function. This neuron model reproduces the basic features of cortical nerve cells and can be efficiently simulated (Rotter and Diesmann 1999; Plesser and Diesmann 2009). This enables us to simulate large networks with biologically realistic connectivity, which is necessary for the investigation of collective phenomena such as the propagation of ensemble firing of neuronal groups.
In the experiments involving synaptic plasticity the synaptic weights are altered according to an additive spike-timing dependent plasticity (STDP) rule (Song et al. 2000). The change of weight is defined as
| 1 |
where λ defines a step size and τ + and τ − are the time constants of the STDP window for potentiation and depression, respectively. The time difference Δt = t post − t pre is given by the timing of the post-synaptic and pre-synaptic spikes. Between spike times, the synaptic weights decay exponentially with time constant τ decay:
| 2 |
Synapses are bounded within a range
All simulations were performed using NEST revision 1.9.8718 (see www.nest-initiative.org and Gewaltig and Diesmann 2007) with a computational step size of
To avoid synchrony artefacts (Hansel et al. 1998), all simulations without plasticity were performed employing precise simulation techniques with the bisectioning method in a globally time driven framework (Morrison et al. 2007b; Hanuschkin et al. 2010d). A description of the neuronal and synaptic dynamics and the corresponding parameters are provided in Tables 2, 4 and 5. To allow other researchers to perform their own experiments, at the time of publication we are making a module available for download at www.nest-initiative.org containing all relevant scripts.
Table 2.
Summary of model dynamics after Nordlie et al. (2009)
| Neuron models | ||
|---|---|---|
| Name | HVCRA, HVCI and auditory neurons (precise) | |
| Type | Leaky integrate-and-fire, α-current input | |
| Subthreshold dynamics |
|
|
| Spiking |
If V(t − ) < V th ∧ V(t + ) ≥ V th 1. calculate retrospective threshold crossing with bisectioning method (Hanuschkin et al. 2010d) 2. set 3. emit spike with time stamp t * |
|
| Neuron models | ||
|---|---|---|
| Name | HVCRA, HVCI and auditory neurons (grid constrained) | |
| Type | Leaky integrate-and-fire, α-current input | |
| Subthreshold dynamics |
|
|
| Spiking | If V(t − ) < V th ∧ V(t + ) ≥ V th emit spike with time stamp t + | |
| Synapse Model | ||
|---|---|---|
| Name | STDP synapse | |
| Type | Simple STDP with additive update rule for potentiation and depression. Exponential decay of weights. | |
| Spike pairing scheme | All-to-all (for nomenclature see Morrison et al. 2008) | |
| Pair-based update rule | Δw
+ = |
|
| Weight dependence | Fixed upper W
max and lower W
min bounds. Exponential decay: |
|
| Inputs | ||
|---|---|---|
| Type | Target | Description |
| Poisson generator | SFCj | Independent for all targets, rate ν x, weight J x |
| Poisson generator | IN | Independent for all targets, rate ν IN,ext, weight J IN,ext |
| Poisson generator | j Au | Independent for all targets, rate ν AN, weight J E,AN |
| Measurements | Spike activity of all neurons, synaptic weights if plasticity is present | |
Table 4.
Specification of neuron model parameters
| Name | Value | Description |
|---|---|---|
| Neuron model of HVCRA | ||
| τ m | 20 ms | Membrane time constant |
| C m | 250 pF | Membrane capacitance |
| V th | 20 mV | Fixed firing threshold |
| V 0 | 0 mV | Resting potential |
| V reset | − 50 mV | Reset potential |
| τ ref | 5 ms | Absolute refractory period |
| τ α | 3 ms | Rise time of post-synaptic current |
| I e | 0 pA | External DC current applied to each neuron |
| Neuron model of HVCI | ||
| τ m | 5 ms | Membrane time constant |
| C m | 250 pF | Membrane capacitance |
| V th | 20 mV | Fixed firing threshold |
| V 0 | 0 mV | Resting potential |
| V reset | 0 mV | Reset potential |
| τ ref | 0.5 ms | Absolute refractory period |
| τ α | 1 ms | Rise time of post-synaptic current |
| I e | 800 pA | External DC current applied to each neuron |
| Neuron model of the auditory neurons | ||
| τ m | 20 ms | Membrane time constant |
| C m | 250 pF | Membrane capacitance |
| V th | 20 mV | Fixed firing threshold |
| V 0 | 0 mV | Resting potential |
| V reset | 0 mV | Reset potential |
| τ ref | 2 ms | Absolute refractory period |
| τ α | 5 ms | Rise time of post-synaptic current |
| I e | 100 pA | External DC current applied to each neuron |
Table 5.
Specification of synapse parameters and applied input
| Name | Value | Description |
|---|---|---|
| STDP synapse model (imprinting) | ||
| λ | 10 − 3 | Learning rate |
| τ decay | 104 s | Decay time constant |
| τ + | 15 ms | Time constant of potentiation window |
| τ − | 20 ms | Time constant of depression window (unused) |
| W max | 75 pA | Upper bound of weights |
| W min | 65 pA | Lower bound of weights |
| W start | 65 pA | Start value of weights |
| STDP synapse model (efference copy) | ||
| λ | 10 − 3 | Learning rate |
| τ decay | 5·103 s | Decay time constant |
| τ + | 20 ms | Time constant of potentiation window |
| τ − | 20 ms | Time constant of depression window |
| W max | 80 pA | Upper bound of weights |
| W min | 0 pA | Lower bound of weights |
| W start | 35 pA | Start value of weights |
| Input | ||
| ν x | 7 kHz | External Poisson rate |
| J x | 26 pA | Synaptic weight |
| ν IN,ext | 2 kHz | External Poisson rate |
| J IN,ext | 28 pA | Synaptic weight |
| ν AN | 2.9 kHz | External Poisson rate |
Analysis of stochastic sequences
We use the song definition of Woolley and Rubel (1997) who define a stereotype set of separated acoustic elements to be one syllable and each song to consist of several syllables. This is, the song starts with an introductory note ‘i’ followed by a sequence of syllables ‘ABC..’. For alternative definitions, see Okanoya and Yamaguchi (1997), Sakata and Brainard (2006), Katahira et al. (2007).
To evaluate the syntax of the song produced by our model, we consider transitions between syllables. For a specific syntax, a transition between two syllables can be deterministic, stochastic or forbidden. We use two measures to characterize the song structure. The sequence stereotype score S ⋆ is defined as the average of sequence linearity and sequence consistency (Scharff and Nottebohm 1991; Woolley and Rubel 1997). The sequence linearity is given by the ratio between the number of different syllables per bout and the number of transition types per bout. The sequence consistency is given by the ratio of the sum over allowed transitions per bout and the sum over total transitions per bout.
Another measure used to describe the syllable sequencing is the transition entropy
| 3 |
where p
i is the probability that when syllable j occurs it is followed by syllable i (Sakata and Brainard 2006). The average transition entropy
Results
A reafferent and feed-forward model of song syntax generation
The feed-forward model of the Bengalese finch HVC recently proposed by Jin (2009) is motivated by the resemblance of synfire activity to the activity of HVCRA neurons: each syllable is represented as a synfire chain, and excitatory connections from the final pools of chains to the initial pools of specific other chains dictate the song syntax. If a chain projects to only one other chain, stereotypical sequences are produced (e.g. ‘CD’ in Fig. 2b), whereas if multiple successor chains are activated, this results in stochastic branching (e.g. ‘AA’ or ‘AB’). Here, we consider only distinguishable states and the transitions between them; an even better fit to the statistics of song syntax can be obtained by including hidden states in the first order Markov process (Jin 2009; Katahira et al. 2010).
Fig. 2.
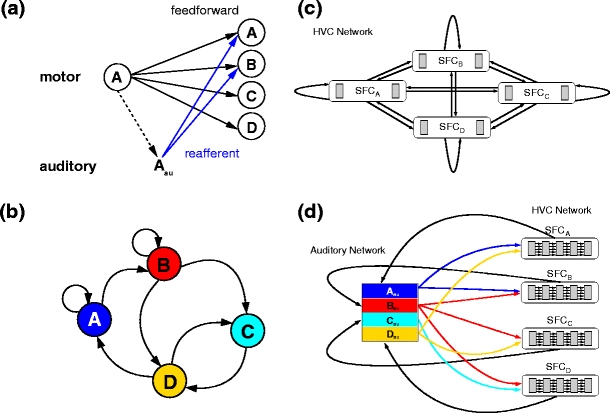
A reafferent and feed-forward model of song syntax generation (a) Combination of reafferent and feed-forward models. Each syllable (open circle) is connected in a feed-forward fashion (black arrows) to every syllable in the motor system, potentially allowing all syllable transitions. During syllable output the syllable is perceived by the auditory system (Aau), which responds by priming the activation of the next syllable in the motor system (blue arrows). The reafferent connections realize a specific song syntax; here, the perception of syllable ‘A’ results in excitatory input to syllables ‘A’ and ‘B’, thus sequences ‘AA’ and ‘AB’ will occur, but not ‘AC’ or ‘AD’. (b) Transition diagram for an example of Bengalese finch song syntax (Jin 2009). Each syllable is represented by a node, the black arrows connecting the nodes indicate possible transitions. (c) HVC interconnectivity. Each syllable is represented by a synfire chain. The final group of each chain makes feed-forward connections to the initial group of every chain, as shown for syllable ‘A’ in (a). (d) Auditory priming. Each synfire chain makes excitatory connections to the corresponding auditory sub-network. Each auditory sub-network makes excitatory connections to specific synfire chains to realize a song syntax. Color coding and syntax as in (b)
However, the feed-forward model neither explains the loss of syntax of the Bengalese after deafening and the recovery of the song syntax after the auditory feedback is restored (Okanoya and Yamaguchi 1997; Woolley and Rubel 1997, 1999; Watanabe and Aoki 1998), nor the instantaneous modifications of syntax due to auditory feedback perturbations (Sakata and Brainard 2006, 2008). These findings suggest a sparse song template of syllables where the song syntax is generated by reafferent cues of the auditory system (Sakata and Brainard 2006).
To account for the findings on both undisturbed and disturbed song syntax, we combine the feed-forward model of Jin (2009) with the reafferent hypothesis of Sakata and Brainard (2006) to a unified model as illustrated in Fig. 2a. To produce the syntax shown in Fig. 2b, 4 synfire chains {SFCA, SFCB, SFCC, SFCD} as described in Section 2.1 code for the four different syllables {A,B,C,D}. The final pool of each synfire chain projects to the initial pool of every chain with the same feed-forward excitatory connectivity as within the chains, thus potentially allowing all syllable transitions (see Fig. 2c). As in the model proposed by Jin (2009), the excitatory neurons are reciprocally connected with the population of fast spiking HVCI interneurons with short synaptic delays. The activity of the HVCI interneurons (referred to in the following as the inhibition network, IN) results in dominant global inhibition that stabilizes the HVC network. Supra-threshold input to the neurons of the synfire chain network leads to the spontaneous ignition of synfire activity, but the numerous fast connections from IN to the synfire chains suppress the synfire activity in all but one chain. Consequently, activity in a single chain is the only attractor in the network and ensures reliability of the switching.
The reafferent hypothesis suggests that the vocal output determines or influences the next vocalization mediated by immediate auditory feedback. For the sake of simplicity, we reduce the complex auditory system of the finch to a single network which we will call auditory network (AN) in the following. The auditory network consists of a set of four balanced networks (Brunel 2000) representing auditory perceptions of the four syllables {Aau,Bau,Cau,Dau}. As the spiking activity of individual HVCRA neurons is locked to specific syllables (Hahnloser et al. 2002), we approximate the reafferent signal to the auditory system by the HVCRA activity, assuming a long propagation delay to account for the production and perception of the syllable. Thus, when syllable i is sung excitatory connections from SFCi to i au lead to an increase in firing rate in the auditory subnetwork i au. The excitatory neurons of the auditory sub-networks project to the first pool of the synfire chains selected for priming. The priming of individual synfire chains modifies the switching probabilities (Jin 2009; Hanuschkin et al. 2010c) such that only one of the primed synfire chains can win the competition. The interaction between the synfire chains representing the syllables and the auditory network is illustrated in Fig. 2d.
The interactions between the networks comprising the reafferent and feed-forward model are illustrated in Fig. 3. A tabular description of our model is given in Tables 1 and 2; unless otherwise stated, model parameters are as given in Tables 3, 4 and 5.
Fig. 3.
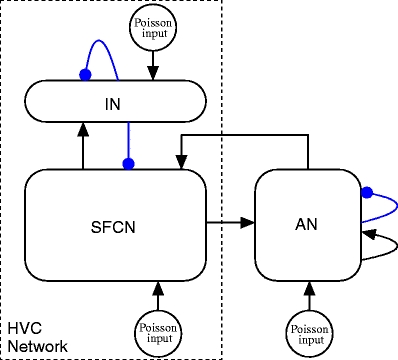
Interaction within and between the two networks of the reafferent and feed-forward model. Song syllables are produced in the HVC network. This network contains a synfire chain network (SFCN) comprising four synfire chains consisting of excitatory HVCRA neurons that are interconnected as shown in Fig. 2c. The SFCN makes reciprocal connections with a recurrently connected population of inhibitory HVCI neurons (IN). The SFCN is reciprocally connected with the recurrently connected sub-networks of the auditory network (AN) as shown in Fig. 2d. All neurons receive supra-threshold Poissonian input. Excitatory connections are shown as black arrows and inhibitory connections as blue arrows with rounded heads
Synaptic plasticity
In the absence of auditory feedback the Bengalese finch loses the song syntax within days. This implies that the song system of the finch does not exclusively rely on auditory feedback for the generation of the song syntax. We extend our network model to realize two different hypotheses of how the syntax is gradually lost.
The first hypothesis is that the song syntax is imprinted on the synfire chain network (SFCN). We therefore incorporate spike-timing dependent plasticity (STDP) at the transition sites between the synfire chains as illustrated in Fig. 4a. The syntax is determined by the priming from the auditory network (see Fig. 2). For example, in the syntax given in Fig. 2b, the transition from ‘A’ to ‘B’ occurs often, whereas the transition from ‘A’ to ‘C’ is not observed. Consequently, the synaptic strengths between SFCA and SFCB are potentiated, imprinting the sequence ‘AB’, but the synaptic strengths between SFCA and SFCC are depressed. If the reafferent priming is removed, the sequence ‘AB’ is initially more likely but occasionally ‘AC’ occurs. After a period of time the imprinting vanishes, resulting in a more random syntax.
Fig. 4.
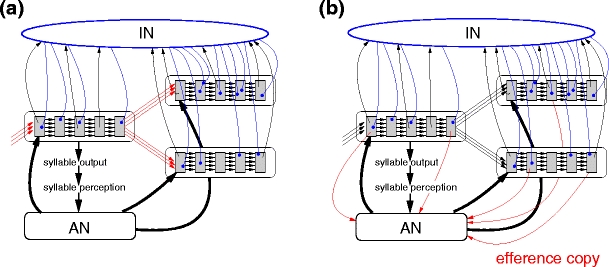
Alternative synaptic plasticity hypotheses in the reafferent and feed-forward model (a) The feed-forward connections between the final pool of a chain and the initial pools of its successor chains are modeled with an additive spike-timing dependent plasticity rule with additional exponential decay (red arrows). Transitions that occur more often are imprinted. (b) Additional random connections from the synfire chain networks to the corresponding auditory sub-networks are modeled with the same plasticity rule as in (a). The auditory network develops an efference copy of the motor signal. In both cases an excerpt of the full network is shown for clarity
The second hypothesis is based on the argument that an efference copy of the song has to be present to allow learning of the song syntax (Troyer and Doupe 2000a). We propose that such an efference copy could also be used to keep the song syntax stable after the auditory feedback is disrupted. We do not elaborate on the site of the efference copy, but simply postulate that the auditory input converges with the efference copy in the auditory network. We therefore assume plastic connections from the SFCN to the auditory network as illustrated in Fig. 4b. The correlation between the activity in the synfire chains representing the syllables and the elevation of activity in the corresponding auditory sub-networks causes these connections to be potentiated. Consequently, if the auditory input is removed, activity in an individual synfire chain still results in elevated activity in the corresponding auditory sub-network and thus in the correct priming behavior. Over time the absence of external reinforcement weakens the connections, leading to a gradual loss of syntax.
Both hypotheses can be realized with an additive STDP rule (Song et al. 2000) with additional depression on a long timescale. The details of the plasticity model are described in Section 2.2 and the parameters are given in Table 5.
Song generation
The reafferent and feed-forward model generates sequences of syllables with a syntax determined by the excitatory priming connections from the auditory network. A 5 s example of a generated sequence following the song syntax in Fig. 2c is shown in Fig. 5a. Reliable switching is achieved throughout the simulation in accordance with experimental findings that the combination of syllables is a rare error in intact bird (Woolley and Rubel 1997). The syllable distribution is p
A = 0.17, p
B = 0.17, p
C = 0.33 and p
D = 0.33. In order to quantify the quality of the song produced by the model, we calculate the stereotype score and the average transition entropy as described in Section 2.3. For the syntax shown in Fig. 2c the allowed transitions are ‘AA’, ‘AB’, ‘BB’, ‘BC’, ‘BD’, ‘CD’, ‘DC’ and ‘DA’. A perfect reproduction of the example song syntax would therefore result in
Fig. 5.
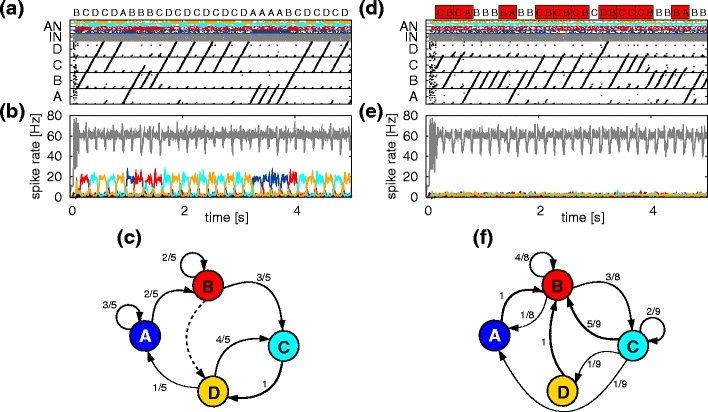
Song sequences generated by the reafferent and feed-forward model with and without auditory feedback. (a) Lower panel: spiking activity of the different auditory sub-networks (AN: Aau, blue; Bau, red; Cau, cyan; Dau, yellow), the HVCI neurons (IN, gray) and the HVCRA synfire chains (black) when auditory feedback is present. Upper panel: generated sequence of syllables. (b) Average Gaussian filtered firing rate of HVCI neurons and neurons of the different auditory subnetworks. Color coding as in (a). (c) Transition diagram for the song sequence in (a). Numbers and arrow thicknesses give transition probabilities. The song syntax given in Fig. 2c is followed; the dashed line indicates that the sequence ‘BD’ is allowed but does not occur in the sample. (d–f) As in (a–c) but without auditory feedback. In the upper panel of (d) forbidden transitions are highlighted in red. In (a, b, d, e) 10% of the network spiking activity is plotted and evaluated
Figure 5b shows the modulation in the firing rate in the auditory and HVC networks during song production. The instantaneous firing rate is estimated from the spike data using a Gaussian filter (σ = 5 ms). The firing rate of the auditory sub-networks follows the generated syllables since it is driven by the reafferent input. The song initiation is triggered by a synfire activity ignition in the HVCRA neurons which results in a brief increase in firing rate of the HVCI network. Furthermore, at each SFC transition site (i.e. change from one syllable to the other) a local increase in firing rate results from the competition between the chains. These dynamical features of the model activity are in good agreement with experimental findings that HVC activity modulation is locked to the structure of the song: before song initiation the activity rises and at the beginning of each syllable an increase in firing rate is observed (Sakata and Brainard 2008). The synfire chains in our model have an activation period of 160 ms resulting in periodic modulations with a frequency of approximately 6 Hz. We have shown in a model of the motor cortex of the monkey that such modulations evoked by synfire chain competition may be observable in mesoscopic signals such as the LFP (Hanuschkin et al. 2010c).
Figure 5d shows a 5 s example of a generated sequence with no auditory feedback. For example, after the syllable ‘C’ is sung there is no auditory perception of the syllable and thus no increase in the firing rate of the auditory sub-network Cau (compare Fig. 5b and e). As a consequence, the temporal cue for the next element in the song sequence is missing. All chains are activated by the final pool of SFCC due to the all-to-all feed-forward connectivity illustrated in Fig. 2c. As syllable ‘D’ is not primed by the auditory network, all synfire chains compete to follow syllable ‘C’. Since activity of a single chain is the only attractor, only a single one will be selected. Due to the heterogeneities in the connectivity some sequences are still more likely than others, and some sequences may never occur. As a result of the increased number of possible sequences, the original song syntax is lost. Figure 5f shows the transition probabilities measured over the 5 s song sample. The upper panel of Fig. 5d highlights the occurrence of the forbidden transitions ‘BA’, ‘CA’, ‘CB’, ‘CC’ and ‘DB’. The average transition entropy
Gradual loss of syntax
After deafening the Bengalese finch song becomes distorted within 7 days (Okanoya and Yamaguchi 1997; Watanabe and Aoki 1998; Woolley and Rubel 1999). In this section we test the ability of two different hypotheses to reproduce this behavior. (see Section 3.2).
We first consider the case that the feed-forward connections from the final pool of each synfire chain to the initial pools of every synfire chain are plastic such that transitions that occur often tend to strengthen those connections, whereas transitions that do not occur often lead to weakened connections (Fig. 4a). In other words, song repetition results in imprinting the song structure on the transition sites between the synfire chains encoding the individual syllables. The details of the spike-timing dependent plasticity rule with additional decay term can be found in Section 3.2 and the parameters in Table 5. In Fig. 6a the average synaptic weight for each transition SFCi→SFCj is shown for a time period of 12,000 s. In the presence of auditory feedback the weights converge reflecting the song syntax, i.e. transitions allowed by the syntax have stronger synaptic weights than those of forbidden transitions (compare the right panel of Figs. 6a and 2b). For example, the average weights from the final pool of SFCA split into two groups. The average strengths of the synapses to the initial pools of SFCA and SFCB are greater than the average strengths of the synapses to the first pools of SFCC and SFCD, reflecting the song syntax which permits the sequences ‘AA’ and ‘AB’ but forbids the sequences ‘AC’ and ‘AD’. The outgoing synaptic weights from SFCC are small compared to the outgoing connections from the other chains. This is a result of the uneven syllable distribution during auditory feedback (p
A = 0.27±0.02, p
B = 0.37±0.02, p
C = 0.06±0.02, p
D = 0.30±0.01) due to the unbalanced random connectivity of the network. Figure 6b shows the development of the sequencing stereotype and the average transition entropy. While the auditory feedback is present, the sequencing stereotype S
⋆ = 0.75±0.02 shows that the song syntax is produced accurately (S
⋆ = 0.75 for perfect syntax). The average transition entropy reaches a stable value (
Fig. 6.
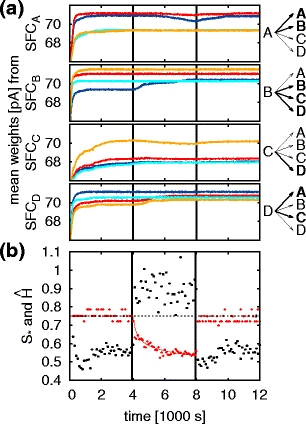
Gradual loss of syntax with imprinted transitions. (a) Left panel: average synaptic weights for the feed-forward connections from the final pool of each synfire chain (SFCA-SFCD) to the initial pools of all chains (SFCA, blue; SFCB, red; SFCC, cyan; SFCD, yellow). The auditory feedback is suppressed at t
df = 4,000 s and restored at 8,000 s (vertical black lines). Right panel: connections that are potentiated before auditory feedback is suppressed are highlighted by broader arrows and bold letters. (b) Sequencing stereotype (S
⋆ , red dots) and average transition entropy (
At t
df = 4,000 s the auditory feedback is suppressed. After this point the average synaptic weights slowly begin to equalize, since in the absence of the priming cue transitions that were previously forbidden can now occur by chance (see for example Fig. 5d). The sequencing stereotype decreases gradually and can be fitted with a power law (
Note that the slow weight decay term in the synaptic plasticity model (Eq. 2) is a necessary condition for the symmetry breaking in the outgoing connections of the synfire chains and also for the gradual loss of syntax. This is because the neurons in the synfire chains only fire when a volley of activity travels through the chain. Hence, the only activity pattern that occurs between a neuron in the final pool of one chain and a neuron in the initial pool of a successor chain is a pre-synaptic spike before a post-synaptic spike (i.e Δt > 0). This pattern results in an increase in synaptic strength; in the absence of an additional decay term all synaptic weights converge to the maximum value W max.
The second hypothesis to be tested is that additional plastic excitatory connections exist between the synfire chains encoding the syllables and the corresponding auditory sub-networks (Fig. 4b). Through song repetition the connections are strengthened, thus realizing an efference copy of the song in the auditory network. For the sake of simplicity, we assume the same synaptic plasticity model as above. Figure 7a shows that in the presence of auditory feedback, the average synaptic weights converge to stable values. The sequencing stereotype S
⋆ = 0.749±0.003 and the average transition entropy
Fig. 7.
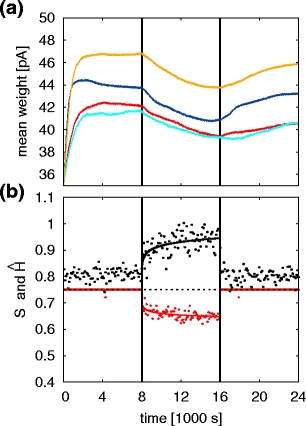
Gradual loss of syntax with efference copy connections. (a) Mean synaptic weights of the efference copy connections from each synfire chain (SFCA, blue; SFCB, red; SFCC, cyan; SFCD, yellow) to the corresponding auditory sub-networks. The auditory feedback is suppressed at t
df = 8,000 s and restored at 16,000 s (vertical black lines). (b) Sequencing stereotype (S
⋆ , red dots) and average transition entropy (
Auditory feedback perturbations
In our reafferent model of the songbird the auditory feedback is responsible for the correct sequence generation. By additional and specific excitation from the auditory network, the SFCs in the HVC network are primed to be active in the desired sequence (see Fig. 8a, b). However, at the stochastic branching points of the song the auditory feedback does not completely determine the next syllable, it simply reduces the competition to the syllables allowed by the given song syntax. In this section, we investigate the behavior of the model when the auditory network is disturbed resulting in inconsistent priming cues.
Fig. 8.
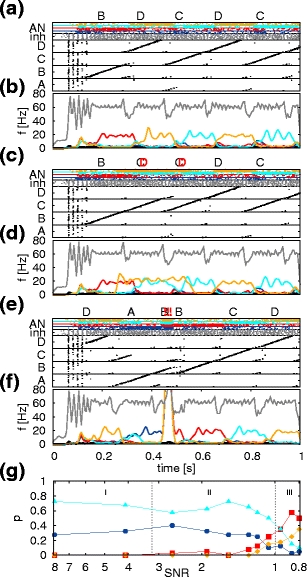
Effects of auditory feedback perturbations on song syntax. (a) Song production without feedback perturbations. Lower panel: spiking activity of the different auditory sub-networks (AN: Aau, blue; Bau, red; Cau, cyan; Dau, yellow), the HVCI neurons (IN, gray) and the HVCRA synfire chains (black) when auditory feedback is present. Upper panel: generated sequence of syllables: the sequence ‘BDCDC’ is generated. (b) Average Gaussian filtered firing rate of HVCI neurons and neurons of the different auditory subnetworks. Color coding as in (a). (c, d) As in (a, b) with altered auditory feedback. From t = 250 ms until 550 ms additional input to the auditory network Dau is applied to mimic the additional perception of syllable ‘D’ (indicated by bold red letter). The syllable sequence is changed to ‘BCCDC’. The sequence ‘BD’ has been changed to ‘BC’ and the forbidden transition ‘CC’ has been introduced. (e, f) As in (a, b) but for a brief burst of noise (10 ms) applied at t = 450 ms to all auditory sub-networks (indicated by bold red exclamation marks). The song is briefly interrupted. (g) Probabilities of transition from syllable ‘D’ to ‘A’ (blue), ‘B’ (red), ‘C’ (cyan) and ‘D’ (yellow) as a function of the signal-to-noise ratio (SNR) controlled by additional synaptic input to Aau, Bau and Cau. Vertical dashed lines indicate three regimes with different characteristic ratios of forbidden to allowed transitions
Sakata and Brainard (2006) observed that perturbing the auditory feedback by playing the bird a syllable different from the one sung results in a stereotyped change in sequencing. The effect of altered auditory feedback (AAF) can easily be demonstrated in our model by stimulating a specific auditory sub-network with additional Poisson input. This can activate an auditory feedback cue for a syllable that would not be activated in the usual song sequence. In Fig. 8c, d the auditory sub-network Dau is stimulated with an excitatory Poissonian spike train at 1 kHz with a synaptic strength of 5 pA to mimic the additional perception of syllable ‘D’. In the syntax given in Fig. 2b the sequence ‘CC’ is not possible in the presence of the correct auditory feedback because the auditory sub-network Cau just primes SFCD. Due to the additional input to Dau, chains SFCA and SFCC are also primed so the selection of SFCC becomes possible (compare Fig. 8a and c). The syntax alteration induced by an additional and unique syllable playback of sufficient amplitude is entirely determined by the pre-defined syntax transition diagram (Fig. 2b).
An alternative hypothesis for how AAF induces syntax change is that the feedback reduces the signal-to-noise ratio (SNR) in the auditory perception of the bird, such that the bird cannot unambiguously identify which syllable it perceived. We simulate this by providing an additional stimulus to the auditory subnetworks Aau, Bau and Cau (excitatory Poissonian spike train at 1 kHz for 200 ms with a variable synaptic strength μ) whenever syllable ‘D’ is sung. We estimate the transition probabilities for a 10 s song excerpt (compare Fig. 5a) where the syllable ‘D’ is sung 20 times, averaged over 2 trials. The SNR is given by the ratio between the firing rate of Dau and the mean firing rate of the auditory subnetworks Aau, Bau and Cau. Increasing the synaptic weight μ decreases the SNR and reveals distinct regions of characteristic transition changes (Fig. 8g). In the first region (I) the probability of the primary transition decreases while the probability of the second transition increases. In the second region (II) forbidden transitions arise with finite probability. The right border of this region is given by SNR = 1, i.e. the point at which all auditory subnetworks receive the same mean excitatory input (μ ≈ 3.75 pA). Increasing the strength of the AAF further has the net effect of suppressing the allowed transitions from ‘D’ as defined in Fig. 2b, such that forbidden transitions become more likely than allowed transitions.
Experimental findings suggest that a strong feedback perturbation results in the song being broken off and restarted later (Cynx and von Rad 2001; Sakata and Brainard 2006). In Fig. 8e,f we test the response of the system to a brief burst of noise to the auditory system. All neurons in the auditory sub-networks receive additional Possonian input at 10 kHz with a synaptic strength of 25 pA for 10 ms. The song is immediately interrupted and restarts after a period of a few milliseconds due to the subthreshold drive to the HVCRA neurons. These results show that feedback perturbances to the auditory network change the sequence ordering and result in violation of the song syntax as observed in experiment.
Discussion
The discovery of the sub-millisecond precision of the sparse HVCRA activity pattern by Hahnloser et al. (2002) led to the hypothesis of a chain-like activity generation within HVCRA by Fee et al. (2004). This hypothesis has been recently strengthened by a report that the subthreshold dynamics of the HVCRA neurons in the freely behaving zebra finch exhibits features characteristic of chain-like structures (Long et al. 2010). Here, intrinsic HVC connectivity gives rise to the generation of the activity pattern within HVC rather then a rhythmically external drive. Additionally, Cynx (1990) and Seki et al. (2008) reported that a flash of light interrupts ongoing song at discrete locations in the song which almost always fall between song syllables. As it is difficult to interrupt the stable and reliable propagation of synfire activity within a chain, this observation supports the theory that individual syllables are represented by such feed-forward networks. This hypothesis has been influential in subsequent modeling studies of the HVC (Li and Greenside 2006; Jin et al. 2007; Jin 2009).
A feed-forward model of the HVC of the Bengalese finch was recently proposed by Jin (2009). This model accounts for the sparse sequences of HVCRA activity and is able to produce the song syntax of Bengalese finches with a fixed inter-chain connectivity. Moreover, Jin (2009) showed that priming can lead to changes in branching probabilities, however the influence of external areas that could generate such a priming signal was not explicitly modeled. Experimental studies on the effect of auditory feedback perturbations on the song syntax suggest a direct influence of the auditory feedback on syllable sequencing in the Bengalese finch (Woolley and Rubel 1997, 2002; Okanoya and Yamaguchi 1997; Watanabe and Aoki 1998; Sakata and Brainard 2006, 2008; Woolley 2008) and also in the zebra finch (Nordeen and Nordeen 1992, 2010; Leonardo and Konishi 1999; Lombardino and Nottebohm 2000; Cynx and von Rad 2001; Brainard and Doupe 2001; Hough and Volman 2002; Roy and Mooney 2009). These results led to the development of a reafferent model of syntax generation (Sakata and Brainard 2006). In the reafferent model, immediate auditory feedback cues the motor system to generate the correct song syntax. In the current study we merge the feed-forward and the reafferent models. The combined model is able to explain key result of the experimental studies on the adult Bengalese finch song production and enables us to investigate hypotheses which are beyond the scope of today’s experiments. In the following we summarize and motivate the model assumptions and then outline the experimental findings that are reproduced by the model together with its specific predictions. Finally, we discuss the model’s limitations and possible extensions.
Model assumptions
The spiking of individual HVCRA neurons is time locked with sub-millisecond precision to distinct song syllables (Hahnloser et al. 2002), motivating our key assumption of feed-forward HVC circuitry. However, whether the observed spiking pattern originates from such intrinsic structures or are rhythmically driven from outside HVC (e.g. Uva) remains an unresolved question (Fee et al. 2004). As we use predefined synfire chains, our study also implicitly assumes that such structures can be developed by the brain. Some studies on the basis of Hebbian synaptic plasticity have reported the development of feed-forward sub-networks (Izhikevich et al. 2004; Buonomano 2005; Doursat and Bienenstock 2006; Jun and Jin 2007; Masuda and Kori 2007; Hosaka et al. 2008; Liu and Buonomano 2009; Waddington et al. 2010), but these findings have so far not been verified by investigations of large-scale model networks with biologically realistic numbers of synapses per neuron (Morrison et al. 2007a; Kunkel et al. 2010). Recently, Fiete et al. (2010) showed that the combination of STDP with heterosynaptic plasticity in a small network generates wide chains with a length distribution similar to the one estimated in the zebra finch HVC. This finding further supports our assumption that HVCRA neurons are organized into synfire chains.
The neural activity of the HVCRA is characterized by zero firing rate in the absence of singing or playback of BOS (Hahnloser et al. 2002). We have therefore made the assumption of robust winner-takes-all chain switching on the basis of dominant global inhibition (Chang and Jin 2009). An advantage of this approach is that the presence of superthreshold drive to the HVCRA neurons assures ongoing song activity. Previously, we have also shown reliable switching from one to several potential successor chains in a model of the motor cortex by combining mutual cross-inhibition and global inhibition (Hanuschkin et al. 2010c). In this case, global dominant inhibition is not a plausible assumption, because the motor cortex is characterized by asynchronous and irregular neural activity (Burns and Webb 1976; Softky and Koch 1993; van Vreeswijk and Sompolinsky 1996; Ponce-Alvarez et al. 2009) which can be reproduced by balanced, rather than dominant, inhibition (Brunel 2000).
We further assume that many biological details of the neurons are not critical for the network function. In general, a specific network behavior can be achieved by completely different parameter sets (Prinz et al. 2004). In our model of the HVC, the feed-forward network structure (reviewed in Kumar et al. 2010) is crucial whereas the precise details of the neuron model are not. It has been shown that synfire chains can reliably propagate pulse packages in the presence of noise (Diesmann et al. 1999; Goedeke and Diesmann 2008), an intra-dilution rate (Hayon et al. 2005), distributed delays (private observation) or unreliable synapses (Guo and Li 2010) and for various forms of neural models such as leaky integrate-and-fire neurons with conductance- or current-based synapses (Kumar et al. 2006; Schrader et al. 2010), intrinsic bursting neurons (Teramae and Fukai 2008) or compartmental bursting neurons (Jin et al. 2007). Hence, we do not model the neurons in the HVC or the auditory network neurons in detail because our level of description is sufficient to draw conclusions on the functional level of the song syntax production.
We have not included the AFP in our model, which is the second major pathway in the song system. The AFP is crucial for song learning in young birds, since lesion of LMAN leads to an early crystallization of the song whereas lesion of Area X prevents song stabilization (Bottjer et al. 1984; Sohrabji et al. 1990; Scharff and Nottebohm 1991). In the adult zebra finch it has been reported that the activity in LMAN drives variability in either syllable structure in isolation (Kao et al. 2005; Aronov et al. 2008; Horita et al. 2008) or together with changes in song sequencing (Brainard and Doupe 2000; Ölveczky et al. 2005; Nordeen and Nordeen 2010). However, in the Bengalese finch only changes in syllable structure have been experimentally verified (Kao and Brainard 2006; Hampton et al. 2009). Furthermore, as song sequencing is fixed in the adult zebra finch, it is difficult to draw conclusions from studies on zebra finch as to the role of LMAN in the variability of sequences (Hampton et al. 2009). As we are investigating song sequencing and not song learning, these experimental results motivate our model assumption that the AFP is not responsible for the song syntax generation in the adult Bengalese finch and thus need not be modeled.
We assume that the song sequence is controlled directly by the means of state cues delivered by the auditory system. The state cue consists of only the last syllable produced, based on the assumption that the song syntax can be fully characterized by a first order Markov process. This assumption has been used explicitly in several model studies (Katahira et al. 2007; Jin 2009) and implicitly in numerous transition diagrams (e.g. Yamada and Okanoya 2003; Sakata and Brainard 2006; Wohlgemuth et al. 2010). Recent investigations of the song syntax statistics reveal additional hidden states and adaptation in the first order Markov process (Jin 2009; Katahira et al. 2010; Jin and Kozhevnikov 2010). Common excitatory drive to the HVC from NIf or CM in response to BOS has been found experimentally (Rosen and Mooney 2006; Roy and Mooney 2009). In our model these reafferent signals are directly used to generate the correct song syntax via priming the synfire chain transition sites. Indirect reafferent influence on local circuits within the HVC or on a possible brain stem feedback loop are not investigated because they would neither change the function of the model nor deliver further insight into the song system based on current knowledge.
We test two different hypotheses of how synaptic plasticity could generate a gradual loss of syntax when the auditory feedback is depressed. We either assume plasticity in the HVCRA synapses to imprint the song syntax or the interaction of an efference copy with the reafferent signal. The latter is realized in the model by assuming additional plastic connections from the HVC to the auditory network. An efference copy in field L and CM neurons of zebra finches has recently been found by Keller and Hahnloser (2009). An additional efference copy could also be situated in the HVC itself (Troyer and Doupe 2000a); recent experiments on swamp sparrows indicate that an efference copy is established in the connections from HVCRA to HVCX via HVCI (Prather et al. 2008, 2009). The specific site of the interaction of the efference copy or alternatively the brain stem feedback with the reafferent signal does not alter the conclusions we draw from our model. In both cases the synaptic plasticity is modeled by additive STDP with fixed upper and lower bound of the weights in order to prevent runaway excitation or the disconnection of the chains. A weight-dependent STDP rule would behave similarly, as the results do not depend on symmetry breaking properties; only the causal relationship of the pre- and post-synaptic activity plays a role. STDP coupled to hard synaptic weight boundaries has been shown to prevent the destabilization of network activity by Hebbian plasticity (Abbott and Nelson 2000; Turrigiano and Nelson 2004). Additionally, we assume an exponential decay of weights over time. This is needed to introduce depression, as typically only the pre-before-post spiking pattern is found in the activity of feed-forward networks.
Reproduction and predictions of experimental findings
By combining the reafferent and feed-forward model it is possible to reliably produce a predefined song syntax that is stored in the excitatory afferent connections from auditory sub-networks to the HVC. In our model each syllable is represented by the synfire activity propagating through one chain in the HVC network; the transformation into sounds via RA and the vocal organs is not modelled. Consequently, the reafferent signal consists of temporal rather than spectral cues, which is in accordance with experimental findings (Woolley and Rubel 1999). The population activity of the HVCI neurons in our simulated network is modulated with song structure as observed in experiments by Kozhevnikov and Fee (2007) and Sakata and Brainard (2008).
Our model reproduces for the first time the loss of song syntax when the auditory feedback is suppressed and its recovery when the auditory feedback is restored (see Section 3.3) as observed in experiments (e.g. reviewed in Woolley 2008). The model song exhibits an increase in transition entropy (Sakata and Brainard 2006) and a decrease in sequence score (Woolley and Rubel 1997) in the absence of auditory feedback. We test two hypotheses for how plasticity in the model could result in a gradual loss of syntax after the auditory feedback is suppressed (see Section 3.4). Both hypotheses, imprinting of song syntax in the HVC or maintaining an efference copy in additional connections from the HVC to the auditory network, are able to reproduce the experimental observation that the song syntax deteriorates over a long period after deafening (Okanoya and Yamaguchi 1997; Watanabe and Aoki 1998; Woolley and Rubel 1999).
In Section 3.3 we have shown that the heterogeneities in the HVC connectivity result in sequences where some transitions are more likely than others, a typical song property (Katahira et al. 2007). When the auditory feedback is suppressed these heterogeneities prevent the song syntax from becoming completely randomized. This effect has also been reported in experiments, compare Fig. 5 with, for example, Figure 1 of Sakata and Brainard (2006). We therefore conclude that transition probabilities are partly determined by the network connectivity and that the suppression of the auditory feedback reveals this underlying network heterogeneity. By comparing the transition probabilities before and after deafening, the priming bias of the auditory feedback could be quantified.
In order to investigate the gradual loss of syntax we introduced plasticity to the model (see Section 3.4). Both hypotheses presented, efference copy and imprinting of the syntax, can account for the gradual loss of syntax after deafening. Hence, we predict the presence of Hebbian synaptic plasticity in the adult bird’s HVCRA interconnections or connections from the HVCRA to the auditory system, with a depressing component on a time scale similar to the ‘loss of syntax period’. This can be investigated by future electrophysiological experiments on the HVC and will reveal whether either of the hypotheses is correct. Independent of which mechanism takes place in the Bengalese finch, it has significant impact on the behavior level of the bird because it reduces the reliance on auditory feedback and keeps the syntax correct in the absence or perturbance of a constant reafferent input. We therefore predict that birds within the same species that show longer lasting stability in the song syntax will be less affected by online perturbations. Across species such experiments have already been conducted. Indeed, the zebra finch, which maintains its song syntax over several weeks after deafening, is less affected by feedback perturbances than the Bengalese finch, which loses its song syntax within a week (Sakata and Brainard 2008). Additionally, it has been shown that the age at deafening determines the time period over which the song syntax is lost (Lombardino and Nottebohm 2000). The younger the bird, the earlier and faster the song syntax is lost, suggesting that experienced singers possess a more robust memory. This is in accordance with our findings that a memory of the song syntax develops over a substantial period of time, irrespective of the plasticity hypothesis assumed.
An active process of song decrystallization in the adult bird by unlearning or renewed vocal plasticity has been suggested by Roy and Mooney (2009). In our study we show that at least the loss of song syntax can be completely explained by the gradual and passive depression of synaptic weights due to the lack of auditory cues in the deafened bird. Whether the syllable structure is actively altered or passively disturbed by the LMAN in the absence of auditory feedback is beyond the scope of the current study but is an interesting question to be addressed in future research.
The syntax can be changed online with altered auditory feedback (see Section 3.5) resembling experimental findings by Sakata and Brainard (2006, 2008). These experimental studies report the occurrence of novel transitions in response to selective AAF, and also a decrease of primary transition and an increase of secondary transition probabilities. The former effect can be reproduced by our model if an additional syllable is overlaid on the sung syllable. To reproduce the second effect, it is necessary to lower the signal-to-noise ratio of the sung syllable by stimulating the auditory sub-networks of all syllables. These results suggest that in the experiment the bird cannot classify the artificial syllable playback uniquely and that multiple, conflicting syllable responses in BOS selective neurons are generated by the stimulus. An experimental prediction arising from these results is that the type and amount of transition probability changes depend on the value of the signal-to-noise ratio and that distinct regions of different AAF effects can be defined. To observe these regions experimentally, the auditory feedback would have to be manipulated in such a way that the bird’s classification of the feedback into distinct syllables can be controlled. For example, artificial syllables could be generated by gradually superimposing syllables of the BOS or using a combination of notes from different syllables.
We previously reported that synfire chain competition of motor primitives can lead to low frequency oscillations in collective signals such as the LFP (Hanuschkin et al. 2010c). The frequency of these oscillations depends on the characteristic length of competing motor primitives. Experiments have already revealed modulations of the HVC activity with song structure (Kozhevnikov and Fee 2007; Sakata and Brainard 2008). Our model predicts the existence of a low frequency component of the LFP that is characteristic for a given song bird species, where the characteristic frequency is given by the inverse of the characteristic song syllable length. Assuming that the mean syllable length is a fair approximation of the modal syllable length, for the zebra finch (mean syllable duration ∼100 ms, Brainard and Doupe 2001; Leonardo and Fee 2005) we predict a 10 Hz component and in the case of the Bengalese finch (mean syllable duration ∼64 ms, Sakata and Brainard 2006) a 15 Hz component. However, a sharp peak is not to be expected, due to the distribution of syllable lengths (Seki et al. 2008; Fiete et al. 2010) and masking of the effect as a result of the spatial distribution of neurons coding for different syllables and the activity of HVCX neurons. Moreover, the amplitude of the low frequency component will be reduced in the presence of a strong priming bias or imprinting, as this reduces the competition between the chains. We therefore predict that the low frequency component has a greater amplitude in deafened birds. The discovery of a species characteristic low frequency component would be strong supporting evidence for our model assumption of competing synfire chains for motor pattern construction and hence may shed light on the mechanism of motor pattern generation in general.
Limitations and extensions
The investigation of auditory responses in the HVC revealed common BOS selective excitation from NIf or CM which results in sparse bursts of HVCRA and HVCX neurons, depolarized HVCRA neurons, and hyperpolarized HVCX neurons (Rosen and Mooney 2006; Roy and Mooney 2009). Due to the superthreshold drive to the HVCRA and the auditory input to only the initial pools of the synfire chains, no spontaneous BOS selective spiking responses occur in our model. In order to reproduce the results of the playback of BOS and delayed BOS more accurately, we would need to model the drive from the auditory network in a more elaborate fashion. For example, projections to neurons within the chains in addition to the priming projections would elicit HVCRA activity without synfire ignition.
Sakata and Brainard (2008) showed that the HVCI activity decreases in response to feedback perturbations. This is not observed in our simulations, since the auditory input to the HVCRA is excitatory and followed by an increase in HVCI activity. This leads to an increase of the total HVC activity. The effect introduced by the feedback perturbations is marginal but strong in the case of a flash of sound (compare Fig. 8a, c, e). However, decrease in total HVC activity could be reproduced if the HVCX neurons were included in the model, as they are suppressed by increasing HVCI activity. Alternatively, a modulation of the external drive to the HVC neurons could be assumed.
While pools of neurons in the HVCI do increase their firing rate in response to specific syllables, the model does not create neurons that are selective for temporal order (Lewicki and Konishi 1995). This feature selectivity has been shown for a model with large time constants in the HVCI neurons and an appropriately chosen connectivity of the HVC network (Drew and Abbott 2003); it is likely that temporal order selectivity would naturally emerge from our network model if we also made these assumptions. Recently, Nishikawa et al. (2008) reported population coding of the song element sequences rather then temporal order selective neurons in the HVC. We have yet to determine whether such syllable sequence selective assembles could be extracted from our simulated neuron populations.
We made the assumption that the Bengalese song syntax can be fully characterized by a first order Markov process. However, it has recently been shown that a partially observable Markov model (POMM) provides a better account of the higher-order state dependencies of transition probabilities observed in the Bengalese song syntax (Jin 2009; Katahira et al. 2010). The POMM is an extension of a first order Markov model introducing hidden states which provide multiple encodings of the same syllable but with different transition probabilities. Hidden states are indistinguishable for the observer and can only be deduced from an analysis of the transitions. The model presented here can be trivially extended from a first order Markov process to the POMM. Moreover, it could be extended to include adaptation; Jin and Kozhevnikov (2010) showed that when adaptation is introduced to the POMM the reproduction of the song syntax statistics is improved further and the number of hidden states is substantially reduced.
The sequencing stereotype S
⋆ and the average transition entropy
Our model predicts that the duration of individual song syllables remain constant after deafening. A shortening of syllables has been reported (Brainard and Doupe 2001), but a more recent study did not reproduce these findings (Nordeen and Nordeen 2010). Similarly, reduction of song tempo as a result of altered auditory feedback has been observed (Sakata and Brainard 2006). Such effects could be reproduced by manipulating the external drive to the neurons of the synfire chain (Wennekers and Palm 1996). Dropping syllables and the emergence of new or unrecognizable syllables have previously been reported (Woolley and Rubel 1997; Watanabe and Aoki 1998; Leonardo and Konishi 1999; Horita et al. 2008), but are not observed in our model even though the activation probability can become low. Increasing the total number of syllables would probably result in the loss of some syllables after deafening.
We postulate synaptic plasticity in the HVC to account for the gradual loss of syntax. The plastic connections either imprint the song structure within HVCRA or construct an efference copy of the song. Both hypotheses reproduce the loss of syntax over a period of time. Unfortunately, in the current study we cannot further distinguish between these hypotheses. Even though the trajectories of S
⋆ and
It has been shown that lesion of the Uva in the zebra finch evokes changes in the syllable sequencing (Williams and Vicario 1993). The original syllable sequencing recovers after a period of time if the Uva is only unilaterally lesioned (Coleman and Vu 2005). These and other experiments on interhemispherical interaction suggest that the Uva delivers nonauditory feedback information during singing (Wild 1994; Vu et al. 1994). Our model does not include the Uva influence on the song syntax generation because we assume the influence of auditory feedback to be the major source of priming in the Bengalese finch. In further extensions to our model an additional source of priming from the Uva to the HVC network via NIf would have to be incorporated.
In the model a constant suprathreshold drive is applied to the HVC network. This ensures ongoing synfire activity; the presence of dominant global inhibition creates a strong competition between the chains that results in robust winner-takes-all competition (Jin 2009). However, this approach introduces some limitations because the drive has to be controlled from outside HVC. The reproduction of behavior states such as periods of silence, sleep, habituation to AAF (Sakata and Brainard 2006) or even the relevance of the social context (Jarvis et al. 1998; Sakata et al. 2008) or motivation is beyond the scope of the presented model. By introducing a variable drive to the HVC such behavior states could be incorporated in the model. This drive could originate in other functional brain areas, such as the Uva or the auditory network (Rosen and Mooney 2006; Akutagawa and Konishi 2010) and may also be controlled by neuromodulation (Dave et al. 1998; Sakata et al. 2008), context-dependent gene expression (Jarvis et al. 1998) and hormones (Pröve 1974).
A further limitation is the lack of defined song initiation and termination by introductory notes and terminal states respectively. Additional drive to a synfire chain representing the initial note would ensure that the song always starts at that point, but the termination would have to be controlled by reducing the common external drive to the HVC. The constant high drive also results in shorter interruptions following bursts of noise than are observed experimentally (Sakata and Brainard 2006), which further demonstrates that the constant drive is over-simplified.
The finding that zebra finch song is most interruptable between song syllables (Cynx 1990) fits nicely to the concept that individual syllables are represented by propagating synfire activity, because the interruption of such activity is generally difficult. Recently, Seki et al. (2008) showed that flashes of light also tend to interrupt the Bengalese finch song between syllables, with high probability transitions exhibiting greater robustness. However, modeling the HVC with synfire chains that are driven by a suprathreshold input masks the robustness of the synfire propagation, as any failure in propagating activity leads to a direct restart of the same or another chain in the network.
An alternative approach to the suprathreshold drive is to apply a subthreshold drive to the individual neurons that raises their average membrane potential to the proximity of the threshold. Synfire activity in the network is initiated by applying a synchronous stimulus to the initial pool of an individual chain or a set of competing chains. In a model of the motor cortex of a monkey performing 2-dimensional movements, we have shown that robust competition can be achieved in such a network, but that it requires fine tuning of the mutual cross-inhibition between competing chains. The working regime can be enlarged by priming signals, but the probability that activity fails to propagate from a chain to one of its successor chains rises with increasing number of possible successor chains (Hanuschkin et al. 2010c). In such a network, the song would automatically stop after some repetitions of the song motif and it would predict that substantially shorter songs are produced in the absence of auditory priming. Additional predictions of such an approach would be that interruptions occur between syllables (Cynx 1990; Seki et al. 2008), that altered auditory feedback is most effective at a specific delay (Sakata and Brainard 2006) and that combinations of syllables can occur in some circumstances (Woolley and Rubel 1997).
In the investigation of the song syntax generation in the adult Bengalese finch presented here we have not touched upon the question of the acquisition of the song syntax of the juvenile bird. Our key assumption is that the song syntax is stored in the afferent connections from the auditory system to the HVC. This syntax is probably learned through the interplay of AFP, auditory network and synaptic plasticity within HVC. Dopaminergic input to NIf, HVC and the AFP nuclei Area X and LMAN has been reported (Brainard and Doupe 2002; Gale and Perkel 2010), which could represent a reinforcement signal (Hollerman and Schultz 1998; Potjans et al. 2010). Our model could therefore be extended to incorporate dopaminergic reinforcement signals to investigate song syntax learning. A similar approach to learning syllable structure has already yielded promising results (Fiete et al. 2007).
In summary, our findings support the theory that song syntax memory after song crystallization is stored in the connections from auditory related areas to the HVC. Our combined model is not only capable of reproducing a variety of experimental findings and generating specific predictions for future experiments, but also lends itself to extensions that allow many other aspects of song learning and production to be studied.
Acknowledgments
Partially funded by DIP F1.2, BMBF Grant 01GQ0420 to BCCN Freiburg, EU Grant 15879 (FACETS), EU Grant 269921 (BrainScaleS), Helmholtz Alliance on Systems Biology (Germany), Next-Generation Supercomputer Project of MEXT (Japan), Neurex, and the Junior Professor Program of Baden-Württemberg. The authors would like to thank Jun Nishikawa and Kentaro Katahira for stimulating and fruitful discussions. The computations were conducted on the high performance computer cluster of the CNPSN group at RIKEN BSI, Wako, Japan.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Abbott LF. Lapicque’s introduction of the integrate-and-fire model neuron (1907) Brain Research Bulletin. 1999;50(5/6):303–304. doi: 10.1016/S0361-9230(99)00161-6. [DOI] [PubMed] [Google Scholar]
- Abbott LF, Nelson SB. Synaptic plasticity: Taming the beast. Nature Neuroscience. 2000;3:1178–1183. doi: 10.1038/81453. [DOI] [PubMed] [Google Scholar]
- Abeles M. Corticonics: Neural circuits of the cerebral cortex. 1. Cambridge: Cambridge University Press; 1991. [Google Scholar]
- Abeles M, Hayon G, Lehmann D. Modeling compositionality by dynamic binding of synfire chains. Journal of Computational Neuroscience. 2004;17(2):179–201. doi: 10.1023/B:JCNS.0000037682.18051.5f. [DOI] [PubMed] [Google Scholar]
- Akutagawa E, Konishi M. New brain pathways found in the vocal control system of a songbird. Journal of Comparative Neurology. 2010;518:3086–3100. doi: 10.1002/cne.22383. [DOI] [PubMed] [Google Scholar]
- Aronov D, Andalman AS, Fee MS. A specialized forebrain circuit for vocal babbling in the Juvenile songbird. Science. 2008;320(5876):630–634. doi: 10.1126/science.1155140. [DOI] [PubMed] [Google Scholar]
- Bauer EE, Coleman MJ, Roberts TF, Roy A, Prather JF, Mooney R. A synaptic basis for auditory-vocal integration in the songbird. Journal of Neuroscience. 2008;28(6):1509–1522. doi: 10.1523/JNEUROSCI.3838-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell C. An efference copy which is modified by reafferent input. Science. 1981;214(4519):450–453. doi: 10.1126/science.7291985. [DOI] [PubMed] [Google Scholar]
- Bottjer S, Arnold A. The role of feedback from the vocal organ. I. Maintenance of stereotypical vocalizations by adult zebra finches. Journal of Neuroscience. 1984;4(9):2387–2396. doi: 10.1523/JNEUROSCI.04-09-02387.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bottjer S, Miesner E, Arnold A. Forebrain lesions disrupt development but not maintenance of song in passerine birds. Science. 1984;224(4651):901–903. doi: 10.1126/science.6719123. [DOI] [PubMed] [Google Scholar]
- Brainard MS, Doupe AJ. Interruption of a basal ganglia-forebrain circuit prevents plasticity of learned vocalizations. Nature. 2000;404:762–766. doi: 10.1038/35008083. [DOI] [PubMed] [Google Scholar]
- Brainard MS, Doupe AJ. Postlearning consolidation of birdsong: Stabilizing effects of age and anterior forebrain lesions. Journal of Neuroscience. 2001;21(7):2501–2517. doi: 10.1523/JNEUROSCI.21-07-02501.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard MS, Doupe AJ. What songbirds teach us about learning. Nature. 2002;417:351–358. doi: 10.1038/417351a. [DOI] [PubMed] [Google Scholar]
- Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. Journal of Computational Neuroscience. 2000;8(3):183–208. doi: 10.1023/A:1008925309027. [DOI] [PubMed] [Google Scholar]
- Buonomano DV. A learning rule for the emergence of stable dynamics and timing in recurrent networks. Journal of Neurophysiology. 2005;94:2275–2283. doi: 10.1152/jn.01250.2004. [DOI] [PubMed] [Google Scholar]
- Burns BD, Webb AC. The spontaneous activity of neurones in the cat’s visual cortex. Proceedings of the Royal Society of London. 1976;B 194:211–223. doi: 10.1098/rspb.1976.0074. [DOI] [PubMed] [Google Scholar]
- Cardin JA, Raksin JN, Schmidt MF. Sensorimotor nucleus NIf is necessary for auditory processing but not vocal motor output in the avian song system. Journal of Neurophysiology. 2005;93(4):2157–2166. doi: 10.1152/jn.01001.2004. [DOI] [PubMed] [Google Scholar]
- Chang W, Jin DZ. Spike propagation in driven chain networks with dominant global inhibition. Physical Review E. 2009;79(5):51917. doi: 10.1103/PhysRevE.79.051917. [DOI] [PubMed] [Google Scholar]
- Coleman MJ, Vu ET. Recovery of impaired songs following unilateral but not bilateral lesions of nucleus uvaeformis of adult zebra finches. Journal of Neurobiology. 2005;63:70–89. doi: 10.1002/neu.20122. [DOI] [PubMed] [Google Scholar]
- Cynx J. Experimental determination of a unit of song production in the zebra finch (taeniopygia guttata) Journal of Comparative Psychology. 1990;104(1):3–10. doi: 10.1037/0735-7036.104.1.3. [DOI] [PubMed] [Google Scholar]
- Cynx J, von Rad U. Immediate and transitory effects of delayed auditory feedback on bird song production. Animal Behaviour. 2001;62(2):305–312. doi: 10.1006/anbe.2001.1744. [DOI] [Google Scholar]
- Dave AS, Yu AC, Margoliash D. Behavioral state modulation of auditory activity in a vocal motor system. Science. 1998;282(5397):2250–2254. doi: 10.1126/science.282.5397.2250. [DOI] [PubMed] [Google Scholar]
- Diesmann M, Gewaltig M-O, Aertsen A. Stable propagation of synchronous spiking in cortical neural networks. Nature. 1999;402(6761):529–533. doi: 10.1038/990101. [DOI] [PubMed] [Google Scholar]
- Doursat R, Bienenstock E. 10th international conference on cognitive and neural systems (ICCNS) Massachusetts: Boston University; 2006. The self-organized growth of synfire patterns. [Google Scholar]
- Drew PJ, Abbott LF. Model of song selectivity and sequence generation in area HVc of the songbird. Journal of Neurophysiology. 2003;89(5):2697–2706. doi: 10.1152/jn.00801.2002. [DOI] [PubMed] [Google Scholar]
- Dutar P, Vu HM, Perkel DJ. Multiple cell types distinguished by physiological, pharmacological, and anatomic properties in nucleus HVC of the adult zebra finch. Journal of Neurophysiology. 1998;80(4):1828–1838. doi: 10.1152/jn.1998.80.4.1828. [DOI] [PubMed] [Google Scholar]
- Fee MS, Kozhevniko AA, Hahnloser RH. Neural mechanisms of vocal sequence generation in the songbird. Annals of the New York Academy of Sciences. 2004;1016:153–170. doi: 10.1196/annals.1298.022. [DOI] [PubMed] [Google Scholar]
- Fiete IR, Fee MS, Seung HS. Model of birdsong learning based on gradient estimation by dynamic perturbation of neural conductances. Journal of Neurophysiology. 2007;98(4):2038–2057. doi: 10.1152/jn.01311.2006. [DOI] [PubMed] [Google Scholar]
- Fiete IR, Senn W, Wang CZH, Hahnloser RHR. Spike-time-dependent plasticity and heterosynaptic competition organize networks to produce long scale-free sequences of neural activity. Neuron. 2010;65:563–576. doi: 10.1016/j.neuron.2010.02.003. [DOI] [PubMed] [Google Scholar]
- Gale SD, Perkel DJ. A basal ganglia pathway drives selective auditory responses in songbird dopaminergic neurons via disinhibition. Journal of Neuroscience. 2010;30(3):1027–1037. doi: 10.1523/JNEUROSCI.3585-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gewaltig M-O, Diesmann M. NEST (neural simulation tool) Scholarpedia. 2007;2(4):1430. doi: 10.4249/scholarpedia.1430. [DOI] [Google Scholar]
- Gibb L, Gentner TQ, Abarbanel HDI. Brain stem feedback in a computational model of birdsong sequencing. Journal of Neurophysiology. 2009;102(3):1763–1778. doi: 10.1152/jn.91154.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibb L, Gentner TQ, Abarbanel HDI. Inhibition and recurrent excitation in a computational model of sparse bursting in song nucleus HVC. Journal of Neurophysiology. 2009;102(3):1748–1762. doi: 10.1152/jn.00670.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaze CM, Troyer T. Neuroscience: Cool songs. Nature. 2008;456:187–188. doi: 10.1038/456187a. [DOI] [PubMed] [Google Scholar]
- Goedeke S, Diesmann M. The mechanism of synchronization in feed-forward neuronal networks. New Journal of Physics. 2008;10:15007. doi: 10.1088/1367-2630/10/1/015007. [DOI] [Google Scholar]
- Guo, D., & Li, C. (2010). Signal propagation in feedforward neuronal networks with unreliable synapses. Journal of Computational Neuroscience. doi:10.1007/s10827-010-0279-7. [DOI] [PubMed]
- Hahnloser RH, Kozhevnikov AA, Fee MS. An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature. 2002;419(6902):65–70. doi: 10.1038/nature00974. [DOI] [PubMed] [Google Scholar]
- Hampton CM, Sakata JT, Brainard MS. An avian basal ganglia-forebrain circuit contributes differentially to syllable versus sequence variability of adult Bengalese finch song. Journal of Neurophysiology. 2009;101(6):3235–3245. doi: 10.1152/jn.91089.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel D, Mato G, Meunier C, Neltner L. On numerical simulations of integrate-and-fire neural networks. Neural Computation. 1998;10(2):467–483. doi: 10.1162/089976698300017845. [DOI] [PubMed] [Google Scholar]
- Hanuschkin, A., Diesmann, M., & Morrison, A. (2010a). Functional compositionality realized in biological realistic spiking neural networks by synfire chain competition. Proceedings of the 40th annual meeting of the Society for Neuroscience.
- Hanuschkin, A., Diesmann, M., & Morrison, A. (2010b). A reafferent model of song syntax generation in the Bengalese finch. BMC Neuroscience, 11(Suppl 1), P33. [DOI] [PMC free article] [PubMed]
- Hanuschkin, A., Diesmann, M., & Morrison, A. (2011). Plasticity in the HVC of the Bengalese finches is crucial for song syntax stability. Proceedings of the 9th Göttingen Meeting of the German Neuroscience Society.
- Hanuschkin A, Herrmann JM, Morrison A, Diesmann M. Compositionality of arm movements can be realized by propagating synchrony. Journal of Computational Neuroscience. 2010 doi: 10.1007/s10827-010-0285-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanuschkin A, Kunkel S, Morrison A, Diesmann M. A general and efficient method for incorporating precise spike times in globally time-driven simulations. Frontiers in Neuroinformatics. 2010;4:113. doi: 10.3389/fninf.2010.00113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayon G, Abeles M, Lehmann D. A model for representing the dynamics of a system of synfire chains. Journal of Computational Neuroscience. 2005;18:41–53. doi: 10.1007/s10827-005-5479-1. [DOI] [PubMed] [Google Scholar]
- Herrmann M, Hertz JA, Prügel-Bennett A. Analysis of synfire chains. Network. 1995;6:403–414. doi: 10.1088/0954-898X/6/3/006. [DOI] [Google Scholar]
- Hollerman JR, Schultz W. Dopamine neurons report an error in the temporal prediction of reward during learning. Nature Neuroscience. 1998;1:304–309. doi: 10.1038/1124. [DOI] [PubMed] [Google Scholar]
- Holst E, Mittelstaedt H. Das Reafferenzprinzip. Naturwissenschaften. 1950;37(20):464–476. doi: 10.1007/BF00622503. [DOI] [Google Scholar]
- Horita H, Wada K, Jarvis ED. Early onset of deafening-induced song deterioration and differential requirements of the pallial-basal ganglia vocal pathway. European Journal of Neuroscience. 2008;28:2519–2532. doi: 10.1111/j.1460-9568.2008.06535.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hosaka R, Araki O, Ikeguchi T. STDP provides the substrate for igniting synfire chains by spatiotemporal input patterns. Neural Computation. 2008;20:415–435. doi: 10.1162/neco.2007.11-05-043. [DOI] [PubMed] [Google Scholar]
- Hough GEII, Volman SF. Short-term and long-term effects of vocal distortion on song maintenance in zebra finches. Journal of Neuroscience. 2002;22(3):1177–1186. doi: 10.1523/JNEUROSCI.22-03-01177.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM, Gally JA, Edelman GM. Spike-timing dynamics of neuronal groups. Cerebral Cortex. 2004;14:933–944. doi: 10.1093/cercor/bhh053. [DOI] [PubMed] [Google Scholar]
- Jarvis ED, Gunturkun O, Bruce L, Csillag A, Karten H, Kuenzel W, et al. Avian brains and a new understanding of vertebrate brain evolution. Nature Reviews Neuroscience. 2005;6:151–159. doi: 10.1038/nrn1606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarvis ED, Scharff C, Grossman MR, Ramos JA, Nottebohm F. For whom the bird sings: Context-dependent gene expression. Neuron. 1998;21(4):775–788. doi: 10.1016/S0896-6273(00)80594-2. [DOI] [PubMed] [Google Scholar]
- Jin DZ. Generating variable birdsong syllable sequences with branching chain networks in avian premotor nucleus HVC. Physical Review E. 2009;80(5):51902. doi: 10.1103/PhysRevE.80.051902. [DOI] [PubMed] [Google Scholar]
- Jin, D. Z., & Kozhevnikov, A. A. (2010). A compact statistical model of the song syntax in Bengalese finch. arXiv. 1011.2998v1 [q-bio.NC]. [DOI] [PMC free article] [PubMed]
- Jin DZ, Ramazanoglu FM, Seung HS. Intrinsic bursting enhances the robustness of a neural network model of sequence generation by avian brain area HVC. Journal of Computational Neuroscience. 2007;23(3):283–299. doi: 10.1007/s10827-007-0032-z. [DOI] [PubMed] [Google Scholar]
- Jun JK, Jin DZ. Development of neural circuitry for precise temporal sequences through spontaneous activity, axon remodeling, and synaptic plasticity. PLoS ONE. 2007;2(8):723. doi: 10.1371/journal.pone.0000723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kao MH, Brainard MS. Lesions of an avian basal ganglia circuit prevent context-dependent changes to song variability. Journal of Neurophysiology. 2006;96(3):1441–1455. doi: 10.1152/jn.01138.2005. [DOI] [PubMed] [Google Scholar]
- Kao MH, Doupe AJ, Brainard MS. Contributions of an avian basal ganglia-forebrain circuit to real-time modulation of song. Nature. 2005;433:638–643. doi: 10.1038/nature03127. [DOI] [PubMed] [Google Scholar]
- Katahira K, Okanoya K, Okada M. A neural network model for generating complex birdsong syntax. Biological Cybernetics. 2007;97(5–6):441–448. doi: 10.1007/s00422-007-0184-y. [DOI] [PubMed] [Google Scholar]
- Katahira, K., Suzuki, K., Okanoya, K., & Okada, M. (2010). Complex sequencing rules of birdsong can be explained by simple hidden Markov processes. arXiv. 1011.2575v1 [q-bio.NC]. [DOI] [PMC free article] [PubMed]
- Keller GB, Hahnloser RHR. Neural processing of auditory feedback during vocal practice in a songbird. Nature. 2009;457:187–190. doi: 10.1038/nature07467. [DOI] [PubMed] [Google Scholar]
- Konishi M. The role of auditory feedback in birdsong. Annals of the New York Academy of Sciences. 2004;1016:463–475. doi: 10.1196/annals.1298.010. [DOI] [PubMed] [Google Scholar]
- Kozhevnikov A, Fee MS. Singing-related activity of identified HVC neurons in the zebra finch. Journal of Neurophysiology. 2007;97:4271–4283. doi: 10.1152/jn.00952.2006. [DOI] [PubMed] [Google Scholar]
- Kumar, A., Rotter, S., & Aertsen, A. (2006). Propagation of synfire activity in locally connected networks with conductance-based synapses. In Computational and Systems Neuroscience (Cosyne) 2006.
- Kumar A, Rotter S, Aertsen A. Spiking activity propagation in neuronal networks: Reconciling different perspectives on neural coding. Nature Reviews Neuroscience. 2010;11:615–627. doi: 10.1038/nrn2886. [DOI] [PubMed] [Google Scholar]
- Kunkel S, Diesmann M, Morrison A. Limits to the development of feed-forward structures in large recurrent neuronal networks. Frontiers in Computational Neuroscience. 2010;4:160. doi: 10.3389/fncom.2010.00160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapicque L. Recherches quantitatives sur l’excitation electrique des nerfs traitee comme une polarization. Journal de physiologie et de pathologie générale. 1907;9:620–635. [Google Scholar]
- Leonardo A, Fee MS. Ensemble coding of vocal control in birdsong. Journal of Neuroscience. 2005;25(3):652–661. doi: 10.1523/JNEUROSCI.3036-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leonardo A, Konishi M. Decrystallization of adult birdsong by perturbation of auditory feedback. Nature. 1999;399:466–470. doi: 10.1038/20933. [DOI] [PubMed] [Google Scholar]
- Lewicki MS. Intracellular characterization of song-specific neurons in the zebra finch auditory forebrain. Journal of Neuroscience. 1996;16(18):5854–5863. [PubMed] [Google Scholar]
- Lewicki MS, Konishi M. Mechanisms underlying the sensitivity of songbird forebrain neurons to temporal order. PNAS. 1995;92(12):5582–5586. doi: 10.1073/pnas.92.12.5582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Greenside H. Stable propagation of a burst through a one-dimensional homogeneous excitatory chain model of songbird nucleus HVC. Physical Review E. 2006;74(1):11918. doi: 10.1103/PhysRevE.74.011918. [DOI] [PubMed] [Google Scholar]
- Liu JK, Buonomano DV. Embedding multiple trajectories in simulated recurrent neural networks in a self-organizing manner. Journal of Neuroscience. 2009;29(42):13172–13181. doi: 10.1523/JNEUROSCI.2358-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lombardino AJ, Nottebohm F. Age at deafening affects the stability of learned song in adult male zebra finches. Journal of Neuroscience. 2000;20(13):5054–5064. doi: 10.1523/JNEUROSCI.20-13-05054.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long MA, Fee MS. Using temperature to analyse temporal dynamics in the songbird motor pathway. Nature. 2008;456:189–194. doi: 10.1038/nature07448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long MA, Jin DZ, Fee MS. Support for a synaptic chain model of neuronal sequence generation. Nature. 2010;468:394–399. doi: 10.1038/nature09514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masuda N, Kori H. Formation of feedforward networks and frequency synchrony by spike-timing-dependent plasticity. Journal of Computational Neuroscience. 2007;22:327–345. doi: 10.1007/s10827-007-0022-1. [DOI] [PubMed] [Google Scholar]
- McCasland J. Neuronal control of bird song production. Journal of Neuroscience. 1987;7(1):23–39. doi: 10.1523/JNEUROSCI.07-01-00023.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mooney R. Different subthreshold mechanisms underlie song selectivity in identified HVC neurons of the zebra finch. Journal of Neuroscience. 2000;20(14):5420–5436. doi: 10.1523/JNEUROSCI.20-14-05420.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mooney R, Prather JF. The HVC microcircuit: The synaptic basis for interactions between song motor and vocal plasticity pathways. Journal of Neuroscience. 2005;25(8):1952–1964. doi: 10.1523/JNEUROSCI.3726-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison A, Aertsen A, Diesmann M. Spike-timing dependent plasticity in balanced random networks. Neural Computation. 2007;19:1437–1467. doi: 10.1162/neco.2007.19.6.1437. [DOI] [PubMed] [Google Scholar]
- Morrison A, Diesmann M, Gerstner W. Phenomenological models of synaptic plasticity based on spike-timing. Biological Cybernetics. 2008;98:459–478. doi: 10.1007/s00422-008-0233-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison A, Straube S, Plesser HE, Diesmann M. Exact subthreshold integration with continuous spike times in discrete time neural network simulations. Neural Computation. 2007;19(1):47–79. doi: 10.1162/neco.2007.19.1.47. [DOI] [PubMed] [Google Scholar]
- Nishikawa J, Okada M, Okanoya K. Population coding of song element sequence in the Bengalese finch HVC. European Journal of Neuroscience. 2008;27(12):3273–3283. doi: 10.1111/j.1460-9568.2008.06291.x. [DOI] [PubMed] [Google Scholar]
- Nordeen K, Nordeen E. Auditory feedback is necessary for the maintenance of stereotyped song in adult zebra finches. Behavioral and Neural Biology. 1992;57:58–66. doi: 10.1016/0163-1047(92)90757-U. [DOI] [PubMed] [Google Scholar]
- Nordeen KW, Nordeen EJ. Deafening-induced vocal deterioration in adult songbirds is reversed by disrupting a basal ganglia-forebrain circuit. Journal of Neuroscience. 2010;30(21):7392–7400. doi: 10.1523/JNEUROSCI.6181-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordlie E, Gewaltig M-O, Plesser HE. Towards reproducible descriptions of neuronal network models. PLoS Computational Biology. 2009;5(8):1000456. doi: 10.1371/journal.pcbi.1000456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nottebohm F. Birdsong’s clockwork. Nature Neuroscience. 2002;5:925–926. doi: 10.1038/nn1002-925. [DOI] [PubMed] [Google Scholar]
- Okanoya K, Yamaguchi A. Adult Bengalese finches (lonchura striata var. Journal of Neurobiology. 1997;33(4):343–356. doi: 10.1002/(SICI)1097-4695(199710)33:4<343::AID-NEU1>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- Ölveczky BP, Andalman AS, Fee MS. Vocal experimentation in the juvenile songbird requires a basal ganglia circuit. PLoS Biol. 2005;3(5):153. doi: 10.1371/journal.pbio.0030153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plesser HE, Diesmann M. Simplicity and efficiency of integrate-and-fire neuron models. Neural Computation. 2009;21:353–359. doi: 10.1162/neco.2008.03-08-731. [DOI] [PubMed] [Google Scholar]
- Poirier C, Boumans T, Verhoye M, Balthazart J, Van der Linden A. Own-song recognition in the songbird auditory pathway: Selectivity and lateralization. Journal of Neuroscience. 2009;29(7):2252–2258. doi: 10.1523/JNEUROSCI.4650-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponce-Alvarez A, Kilavik BE, Riehle A. Comparison of local measures of spike time irregularity and relating variability to firing rate in motor cortical neurons. Journal of Computational Neuroscience. 2009;29(1–2):351–365. doi: 10.1007/s10827-009-0158-2. [DOI] [PubMed] [Google Scholar]
- Potjans, W., Diesmann, M., & Morrison, A. (2011). An imperfect dopaminergic error signal can drive temporal-difference learning. PloS Computational Biology (in press). [DOI] [PMC free article] [PubMed]
- Prather JF, Nowicki S, Anderson RC, Peters S, Mooney R. Neural correlates of categorical perception in learned vocal communication. Nature Neuroscience. 2009;12:221–228. doi: 10.1038/nn.2246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prather JF, Peters S, Nowicki S, Mooney R. Precise auditory-vocal mirroring in neurons for learned vocal communication. Nature. 2008;451:305–310. doi: 10.1038/nature06492. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nature Neuroscience. 2004;7:1345–1352. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Pröve E. Der Einfluß von Kastration und Testosteronsubstitution auf das Sexualverhalten männlicher Zebrafinken (Taeniopygia guttata castanotis Gould) Journal für Ornithologie. 1974;115:338–347. doi: 10.1007/BF01644328. [DOI] [Google Scholar]
- Rosen MJ, Mooney R. Inhibitory and excitatory mechanisms underlying auditory responses to learned vocalizations in the songbird nucleus HVC. Neuron. 2003;39:177–194. doi: 10.1016/S0896-6273(03)00357-X. [DOI] [PubMed] [Google Scholar]
- Rosen MJ, Mooney R. Synaptic interactions underlying song-selectivity in the avian nucleus HVC revealed by dual intracellular recordings. Journal of Neurophysiology. 2006;95(2):1158–1175. doi: 10.1152/jn.00100.2005. [DOI] [PubMed] [Google Scholar]
- Rotter S, Diesmann M. Exact digital simulation of time-invariant linear systems with applications to neuronal modeling. Biological Cybernetics. 1999;81(5/6):381–402. doi: 10.1007/s004220050570. [DOI] [PubMed] [Google Scholar]
- Roy A, Mooney R. Song decrystallization in adult zebra finches does not require the song nucleus NIf. Journal of Neurophysiology. 2009;102(2):979–991. doi: 10.1152/jn.00293.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakata JT, Brainard MS. Real-time contributions of auditory feedback to avian vocal motor control. Journal of Neuroscience. 2006;26(38):9619–9628. doi: 10.1523/JNEUROSCI.2027-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakata JT, Brainard MS. Online contributions of auditory feedback to neural activity in avian song control circuitry. Journal of Neuroscience. 2008;26(38):11378–11390. doi: 10.1523/JNEUROSCI.3254-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakata JT, Hampton CM, Brainard MS. Social modulation of sequence and syllable variability in adult birdsong. Journal of Neurophysiology. 2008;99(4):1700–1711. doi: 10.1152/jn.01296.2007. [DOI] [PubMed] [Google Scholar]
- Scharff C, Nottebohm F. A comparative study of the behavioral deficits following lesions of various parts of the zebra finch song system: Implications for vocal learning. Journal of Neuroscience. 1991;11(9):2896–2913. doi: 10.1523/JNEUROSCI.11-09-02896.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrader S, Diesmann M, Morrison A. A compositionality machine realized by a hierarchic architecture of synfire chains. Frontiers in Computational Neuroscience. 2010;4:154. doi: 10.3389/fncom.2010.00154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seki Y, Suzuki K, Takahasi M, Okanoya K. Song motor control organizes acoustic patterns on two levels in Bengalese finches (lonchura striata var. domestica) Journal of Comparative Physiology. 2008;194(6):533–543. doi: 10.1007/s00359-008-0328-0. [DOI] [PubMed] [Google Scholar]
- Shaevitz SS, Theunissen FE. Functional connectivity between auditory areas field L and CLM and song system nucleus HVC in anesthetized zebra finches. Journal of Neurophysiology. 2007;98(5):2747–2764. doi: 10.1152/jn.00294.2007. [DOI] [PubMed] [Google Scholar]
- Softky WR, Koch C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. Journal of Neuroscience. 1993;13(1):334–350. doi: 10.1523/JNEUROSCI.13-01-00334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohrabji F, Nordeen EJ, Nordeen KW. Selective impairment of song learning following lesions of a forebrain nucleus in the juvenile zebra finch. Behavioral and Neural Biology. 1990;53(1):51–63. doi: 10.1016/0163-1047(90)90797-A. [DOI] [PubMed] [Google Scholar]
- Song S, Miller KD, Abbott LF. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nature Neuroscience. 2000;3(9):919–926. doi: 10.1038/78829. [DOI] [PubMed] [Google Scholar]
- Teramae J-n, Fukai T. Complex evolution of spike patterns during burst propagation through feed-forward networks. Biological Cybernetics. 2008;99(2):105–114. doi: 10.1007/s00422-008-0246-9. [DOI] [PubMed] [Google Scholar]
- Troyer TW, Doupe AJ. An associational model of birdsong sensorimotor learning I. Efference copy and the learning of song syllables. Journal of Neurophysiology. 2000;84(3):1204–1223. doi: 10.1152/jn.2000.84.3.1204. [DOI] [PubMed] [Google Scholar]
- Troyer TW, Doupe AJ. An associational model of birdsong sensorimotor learning II. Temporal hierarchies and the learning of song sequence. Journal of Neurophysiology. 2000;84(3):1224–1239. doi: 10.1152/jn.2000.84.3.1224. [DOI] [PubMed] [Google Scholar]
- Turrigiano GG, Nelson SB. Homeostasic plasticity in the developing nervous system. Nature Reviews Neuroscience. 2004;5:97–107. doi: 10.1038/nrn1327. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C, Sompolinsky H. Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science. 1996;274:1724–1726. doi: 10.1126/science.274.5293.1724. [DOI] [PubMed] [Google Scholar]
- Vu E, Mazurek M, Kuo Y. Identification of a forebrain motor programming network for the learned song of zebra finches. Journal of Neuroscience. 1994;14(11):6924–6934. doi: 10.1523/JNEUROSCI.14-11-06924.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waddington, A., Appleby, P. A., de Kamps, M., & Cohen, N. (2010). Triphasic spike-time-dependent plasticity organizes networks to produce robust sequences of neural activity. (submitted). [DOI] [PMC free article] [PubMed]
- Watanabe A, Aoki K. The role of auditory feedback in the maintenance of song in adult male Bengalese finches lonchura striata var. domestica. Zoological Science. 1998;15:837–841. doi: 10.2108/zsj.15.837. [DOI] [Google Scholar]
- Weber AP, Hahnloser RHR. Spike correlations in a songbird agree with a simple Markov population model. PLoS Computational Biology. 2007;3(12):249. doi: 10.1371/journal.pcbi.0030249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wennekers T, Palm G. Controlling the speed of synfire chains. In: von der Malsburg C, von Seelen W, Vorbrüggen JC, Sendhoff B, editors. Artificial neural networks – ICANN 96. Berlin: Springer-Verlag; 1996. pp. 451–456. [Google Scholar]
- Wild JM. Visual and somatosensory inputs to the avian song system via nucleus uvaeformis (Uva) and a comparison with the projections of a similar thalamic nucleus in a nonsongbird, columbia livia. Journal of Comparative Neurology. 1994;349:512–535. doi: 10.1002/cne.903490403. [DOI] [PubMed] [Google Scholar]
- Williams H, Vicario D. Temporal patterning of song production: Participation of nucleus uvaeformis of the thalamus. Journal of Neurobiology. 1993;24(7):903–912. doi: 10.1002/neu.480240704. [DOI] [PubMed] [Google Scholar]
- Wohlgemuth MJ, Sober SJ, Brainard MS. Linked control of syllable sequence and phonology in birdsong. Journal of Neuroscience. 2010;30(39):12936–12949. doi: 10.1523/JNEUROSCI.2690-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolley SM, Rubel EW. Bengalese finches lonchura striata domestica depend upon auditory feedback for the maintenance of adult song. Journal of Neuroscience. 1997;17(16):6380–6390. doi: 10.1523/JNEUROSCI.17-16-06380.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolley SM, Rubel EW. High-frequency auditory feedback is not required for adult song maintenance in Bengalese finches. Journal of Neuroscience. 1999;19(1):358–371. doi: 10.1523/JNEUROSCI.19-01-00358.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolley, S. M. N. (2008). Neuroscience of birdsong, Chapter 19. Auditory feedback and singing in adult birds, pp. 228–239. Cambridge University Press.
- Woolley SMN, Rubel EW. Vocal memory and learning in adult Bengalese finches with regenerated hair cells. Journal of Neuroscience. 2002;22(17):7774–7787. doi: 10.1523/JNEUROSCI.22-17-07774.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada H, Okanoya K. Song syntax changes in Bengalese finches singing in a helium atmosphere. Neuroreport. 2003;14(13):1725–1729. doi: 10.1097/00001756-200309150-00014. [DOI] [PubMed] [Google Scholar]
- Yamashita Y, Takahasi M, Okumura T, Ikebuchi M, Yamada H, Suzuki M, et al. Developmental learning of complex syntactical song in the Bengalese finch: A neural network model. Neural Networks. 2008;21(9):1224–1231. doi: 10.1016/j.neunet.2008.03.003. [DOI] [PubMed] [Google Scholar]
- Yamashita Y, Tani J. Emergence of functional hierarchy in a multiple timescale neural network model: A humanoid robot experiment. PLoS Computational Biology. 2008;4(11):1000220. doi: 10.1371/journal.pcbi.1000220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu AC, Margoliash D. Temporal hierarchical control of singing in birds. Science. 1996;273(5283):871–1875. doi: 10.1126/science.273.5283.1871. [DOI] [PubMed] [Google Scholar]


