Fast extraction of neuron morphologies from large-scale SBFSEM image stacks

Abstract

Neuron morphology is frequently used to classify cell-types in the mammalian cortex. Apart from the shape of the soma and the axonal projections, morphological classification is largely defined by the dendrites of a neuron and their subcellular compartments, referred to as dendritic spines. The dimensions of a neuron’s dendritic compartment, including its spines, is also a major determinant of the passive and active electrical excitability of dendrites. Furthermore, the dimensions of dendritic branches and spines change during postnatal development and, possibly, following some types of neuronal activity patterns, changes depending on the activity of a neuron. Due to their small size, accurate quantitation of spine number and structure is difficult to achieve (Larkman, J Comp Neurol 306:332, 1991). Here we follow an analysis approach using high-resolution EM techniques. Serial block-face scanning electron microscopy (SBFSEM) enables automated imaging of large specimen volumes at high resolution. The large data sets generated by this technique make manual reconstruction of neuronal structure laborious. Here we present NeuroStruct, a reconstruction environment developed for fast and automated analysis of large SBFSEM data sets containing individual stained neurons using optimized algorithms for CPU and GPU hardware. NeuroStruct is based on 3D operators and integrates image information from image stacks of individual neurons filled with biocytin and stained with osmium tetroxide. The focus of the presented work is the reconstruction of dendritic branches with detailed representation of spines. NeuroStruct delivers both a 3D surface model of the reconstructed structures and a 1D geometrical model corresponding to the skeleton of the reconstructed structures. Both representations are a prerequisite for analysis of morphological characteristics and simulation signalling within a neuron that capture the influence of spines.

Electronic supplementary material  The online version of this article (doi:10.1007/s10827-011-0316-1) contains supplementary material, which is available to authorized users.

Introduction

Morphology dictates the passive, and partly, the active, electrical properties of dendritic branches and thereby the entire dendritic compartment of a neuron. Fine structural details of dendrites must be determined to accurately model electrical behavior. Spines are prominent subcellular specializations of dendrites. They form the postsynaptic elements of excitatory synapses between neurons. To understand the contribution of different dendritic branches and spines to the electrical properties of a neuron it is essential to know their dimensions, their location, their density and their shapes in different compartments such as the basal dendrites, oblique dendrites and the tufts of pyramidal cells in e.g. the mammalian cortex. In order to obtain estimates of dendritic geometry and in particular of spine parameters one needs to accurately reconstruct, at a large scale, dendrites and spines at the EM level of morphologically or molecularly identified cell-types (Gong et al. 2003).

Serial Block-Face Scanning Electron Microscopy, SBFSEM (Denk and Horstmann 2004) enables fully automatic imaging of large specimen volumes at high resolution and small deformation of images. Due to the high voxel resolution of the SBFSEM imaging technique, imaging of large biological tissues will result in large amounts of image data. For example, the image data used in the work presented here have a voxel resolution of 25 nm × 25 nm × 50 nm or 25 nm × 25 nm × 30 nm. Images provided by SBFSEM are 8-bit gray-level value images. At this resolution a 5 GB image stack corresponds to a biological tissue volume of just 1.6·10^− 4 mm³. Typically, neuronal processes, including dendrites and spines, are manually reconstructed from EM data. The large size of SBFSEM datasets however, makes manual reconstruction laborious and time-consuming.

Several approaches have been presented for the automatic reconstruction of neural structures for SBFSEM. Jurrus et al. developed methods for axon tracking in SBFSEM volume data. In their method, users first specify axon contours in the initial image of a stack that are then tracked sequentially through the remaining stack using Kalman Snakes (Jurrus et al. 2006). This method focuses on axon tracking in SBFSEM volume data and has not been applied to the reconstruction of dynamic structures like spiny dendrites. Further work on the reconstruction of neural structures is presented by Macke et al. (2008) focusing on contour-propagation algorithms for semi-automated processing. Other proposals were made for the reconstruction of neural structure in electron microscopy data. Vázquez et al. proposed a segmentation method based on the computation of minimal weighted distance paths between user defined points of the neuron boundary for 2D slices (Vázquez et al. 1998). Sätzler et al. reported the 3D reconstruction of a giant synaptic structure from electron microscopy data in Sätzler et al. (2002). However, these approaches have proved ineffective for large datasets. Methods developed for the reconstruction of neuronal structures obtained using light microscopy (Urban et al. 2006; Al-Kofahi et al. 2002; Dima et al. 2002; Broser et al. 2004; Santamaria and Kakadiaris 2007) are not directly applicable to EM data, since both image quality and image characteristics differ substantially.

We describe a software system named NeuroStruct1 Neurostruct (2010) establishing an efficient and fully-automated workflow for the reconstruction of neural structures from large-scale SBFSEM image data stacks where neurons were filled with biocytin in vivo or in vitro (i.e. in tissue slices) and then visualized by osmium. Efficient reconstruction is enabled by applying highly parallelizable algorithms for CPUs with multiple cores, computing clusters, and GPUs. NeuroStruct’s algorithms enable the reconstruction of individual dendritic branches and dendrites of hundreds of μm in length at high resolution.

The paper is organized as follows: Section 2 presents the developed reconstruction methods including filtering, segmentation, padding, surface extraction, and skeletonization. Section 3 presents results achieved with the presented methods for three different datasets. Validation and discussion of the workflow are presented in Sections 4 and 5, respectively. Finally, in Section 6 conclusions are presented.

Methods

Three datasets are analyzed. Each dataset contained a neuron filled in vivo or in vitro with biocytin via a patch pipette. In the fixed tissue the neuron was visualized by osmium (Newman et al. 1983; Luebke and Feldmeyer 2007; Silver et al. 2003 and Supplementary Material). An SBFSEM image of a tangential section of the rat barrel cortex is shown in Fig. 1(A). Dendritic structures represented by dark regions are shown in the subfigures (A) and (C) in Fig. 1. With a resolution of 2,047 × 1,765 pixels, this image corresponds to a biological tissue covering a surface of 51.2 × 44.1 μm². The large SBFSEM dataset size in the range of several hundred gigabytes generated for whole cell tissue volumes, necessitates fast reconstruction algorithms.

Fig. 1.

SBFSEM images of rat barrel cortex. Image of dendritic structures with spines (a), (b) zoomed view of the dendrite in (a), (c) image of a dendrite (red arrows) and a blood vessel touching it (blue arrow)

In addition, three major difficulties were encountered in these datasets (i) a considerable decrease in contrast within connected regions is apparent especially in thin object areas as illustrated in Fig. 1(A), (B) and Fig. 2(d) even when staining is performed carefully; (ii) the extent of extracellular gaps between unconnected electron-dense structures can go below voxel size as illustrated in subfigure (C) of Fig. 1 where an electron-dense blood vessel touches a dendrite; (iii) the thickness of subdendritic structures such as that of specific spine types can be smaller than the extent of image stack voxels as for the spine shown in Fig. 7.

Fig. 2.

SBFSEM image properties. (a) image background signal along the red line in Fig. 1; (b) histogram of subfigure (A) in Fig. 1 where pixels marked by the red circle or with lower intensities correspond to the highlighted neural structures; (c) signal along the blue line with peaks of dark values indicating neural structures; (d) signal along the green line, arrow marks a spine neck with decreasing contrast

Fig. 7.

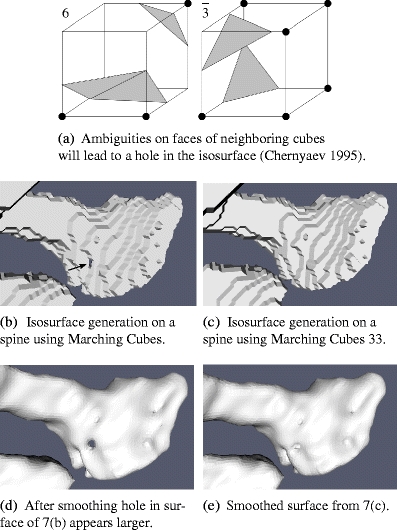
Surface reconstruction for a dendritic spine with Marching Cubes and Marching Cubes 33

Subfigure (A) in Fig. 1 illustrates the first situation. The gray values along the drawn lines of subfigure (A) are shown in Fig. 2 plots (a), (c), and (d), respectively. Arrows mark corresponding locations. The histogram Fig. 2(b) shows the gray value distribution of subfigure (A) and illustrates the signal-to-noise ratio of foreground information (red circle) and background with noise as gaussian curve. The second situation is shown in subfigure (C) of Fig. 1. Red and blue arrows point to anatomically distinct structures, whose gap is below voxel resolution. Thus, the robust and exhaustive detection of a continuous “membrane” with its complicated shape represents a challenge for image processing.

The main steps in NeuroStruct’s workflow are presented in Fig. 3. Before the sequence of algorithms is started the initial SBFSEM image data is inverted such that the neuronal foreground information is bright on a dark background. To highlight the neural structures in the SBFSEM images, the image stacks are first filtered. Next the SBFSEM image volumes are segmented. The segmentation output is a binary image volume, where the neural structures, namely the neuron membranes, are the white foreground. Several iterations of filtering and segmentation are possible until the desired segmentation result is achieved. During a padding step the segmented structures are prepared for visualization. The visualization is based on surface extraction from the binary volume. The last step in our workflow is the extraction of a skeleton from the 3D neuronal structures mainly to enable the use of neural structure morphologies for simulation.

Fig. 3.

NeuroStruct’s workflow for the extraction of neural structures from SBFSEM image data

The reconstruction steps are developed using the Visualization Toolkit VTK (Schroeder et al. 2006) and the CUDA2 toolkit (Nvidia 2008) for GPU-specific implementations as programming models. To accelerate the extraction pipeline, the basic workflow steps, i.e., filtering, segmentation, padding and surface extraction are already parallelized for GPU execution, in this paper for an Nvidia Tesla C1060 Graphics Processing Unit.

As a detailed presentation of the parallelization of the algorithms on GPU is beyond the scope of this paper, here we will discuss methodological aspects for reconstruction for large data volumes.

Definitions

Throughout this paper a 2D (digital) image is represented by a discrete function f, which assigns a gray-level value to a distinct pair of coordinates (x,y), f:(x,y) →G; x,y,G ∈ ℕ. f(x,y) is therefore the gray-level value of pixel at position (x,y). In a 3D image, the f(x,y,z) corresponds to the gray-level value of the volume element or voxel at position (x,y,z). The highest gray-level value is denoted as G _max = max{G}.

Objects of interest are represented by the image subset F (foreground): F = {v ∈ I ³ | f(v) = 255}. \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$\overline{F}$\end{document} is the complement of F, \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$\overline{F} = \{v \in I^3 | f(v) = 0\}$\end{document} represents the background.

For each voxel v at position (x,y,z) the neighborhood types N ₆(v), N ₂₆(v) and N ₁₈(v) are used (Fig. 4). Based on N ₂₆(v) two points/voxels in F are connected if there exists a 26-path (v _i, ⋯ , v _j) in F. A 6-(26-) connected component is a set of points in F, which are connected under 6-(26-) connectivity. In this work we apply 26-connectivity for F and 6-connectivity for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$\overline{F}$\end{document}.

Fig. 4.

Neighborhood types as described in Jähne (2005) and Lee et al. (1994)

Filtering

The filtering of the SBFSEM data itself consists of two steps: First the image data is inverted, a Top-Hat operation (Gonzalez and Woods 2002; Serra 1982) is then applied to the inverted SBFSEM images. Images in the image volume are processed sequentially and independently from their adjacent images.

The highlighted neuron corresponds in the image scale to peaks of brightness. To detect these peaks of brightness we apply the Top-Hat operation which is based on the morphological Opening and is defined as (Gonzalez and Woods 2002; Serra 1982):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ h = f - (f \circ b) $$\end{document} 1

where f is the input image, b is the structuring element function and (f ∘ b) is the morphological Opening of the image f by the structuring element b. The morphological Opening itself is the morphological erosion of f by b, followed by the dilation of the erosion result by b:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ f \circ b = (f \ominus b) \oplus b $$\end{document} 2

Filtering with Top-Hat Operation is done using a rectangular structuring element b of size 41 ×41 pixels. For the actual SBFSEM image data with a voxel resolution of 25 nm in x- and y- axes and 50 nm in the z-axis the size of b corresponds to a biological tissue size of 1 μm × 1 μm into which most dendritic spines fit.

In Fig. 5 the filtering result is shown. On an inverted image, Fig. 5(b), the Top-Hat operator as described by Eq. (1) is applied, Fig. 5(c). As shown in Fig. 5(c) and (d) Top-Hat subtracts image background and highlights the bright image elements which represent the neural structures of interest.

Fig. 5.

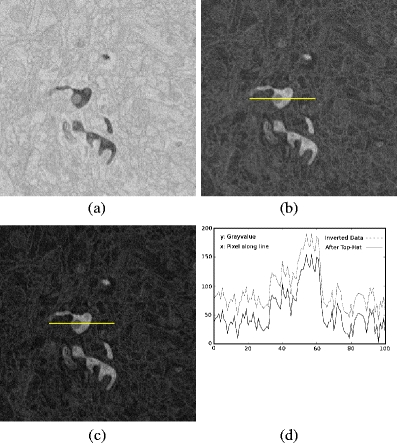
Filtering steps in the reconstruction workflow. A 300 × 300 pixel extract of an image of rat barrel cortex (a), inverted image (b), image after Top-Hat filtering with a rectangular structuring element b of size 41 × 41 pixel (c). Subtraction of image background through Top-Hat (d)

Top-Hat is a separable operation, thus the runtime increases linearly with the size of the structuring element b. Considering the data locality and the high density of arithmetic operations, Top-Hat is a highly parallelizable operation and especially suitable for execution on Single Instruction Multiple Data (SIMD) architectures. We implemented a parallelization of Top-Hat on an Nvidia Tesla C1060 GPU. This parallelization reduces the Top-Hat runtime for 3.6 MB of data (corresponding to an image size of 2047 × 1765 pixels) from 0.9 s on CPU to only 19 ms on GPU. More details on the performance of this operation can be found in Section 3.

Segmentation

During segmentation the neural structures, namely neuron volumes, are separated from the image background. The segmentation step results in a binary image volume. Several image segmentation methods have been proposed in the literature, e.g. thresholding, egde-finding, region growing (seeded or unseeded), watershed or Level Set (Adams and Bischof 1994; Gonzalez and Woods 2002; Jähne 2005; Lin et al. 2001; Serra 1988; Soille 2003). Thresholding segmentation techniques are often used due to their simplicity. In the SBFSEM image data of rat barrel cortex, the neuron is locally highlighted Fig. 5(a). The neural structures are local minima of the image function (respectively, local maxima of the image function for inverted images). A segmentation algorithm, using local properties of the image function and is well parallelizable, is suitable for this purpose.

For the segmentation of the Top-Hat transformed SBFSEM image data we developed a 3D local morphological thresholding operator as presented in Eq. (3). To enable automatic segmentation, the 3D operator uses histogram characteristics of the SBFSEM images, therefore no user interaction during the segmentation process is required:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ f_{\rm binary}(x,y,z) = \begin{cases} 255 & \text{if}~ [f (x,y,z)~>~Th_{\rm max}] \vee \\ ~& [ \left(Th_{\rm min}\le f(x,y,z)\le Th_{\rm max}\right) \\ ~& ~~\wedge \left(p(x,y,z)=1 \right) ] \\ 0 & \text{else}\\ \end{cases} \label{eq:segmentation} $$\end{document} 3

The threshold parameters Th _min and Th _max subdivide the image gray-value range into three subranges. All voxels v with gray value f(v) > Th _max are classified as foreground voxels: v ∈ F. All voxels with f(v) < Th _min are assigned to the background: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$v~\in \overline{F}$\end{document}. For the remaining voxels the local property function p(v) is evaluated:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ p(x,y,z) = \left( ( M > (Th_{\rm min}~+~\delta)) \wedge \left( \frac{|A|}{18}~>~\gamma \right) \right) $$\end{document}

Where M is the average gray-level value of the a ×b ×c neighborhood centered in (x,y,z):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ M~=~\frac{\sum\limits_{x-\frac{a}{2}}^{x+\frac{a}{2}} \sum\limits_{y-\frac{b}{2}}^{y+\frac{b}{2}} \sum\limits_{z-\frac{c}{2}}^{z+\frac{c}{2}}~f(x,y,z)} {a*b*c} $$\end{document}

and A represents the number of neighbors in N ₁₈ with gray-level values greater than the average gray-level value M of the a × b × c neighborhood.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ A~=~\lbrace voxel~v~\in ~\underbrace{N_{18}(x,y,z)}_{\text{18-neighborhood}}~|~f(v)~>~(M~+~\epsilon) \rbrace $$\end{document}

The evaluation of the mean gray-level, value M, of the neighborhood a ×b ×c for the segmentation operator is motivated by the idea that the mean gray-level value of image regions that belong to neural structures is higher than that of the background. For a reliable segmentation the closest neighbors in the 18 neighborhood of (x,y,z), N ₁₈, are also evaluated. Th _min and Th _max are obtained from the histogram characteristics of the first i images of the image stack.

The result of the segmentation operator are highlighted structures such as neuron surfaces. Figure 6(a) presents the segmentation result for the image of Fig. 5(c).

Fig. 6.

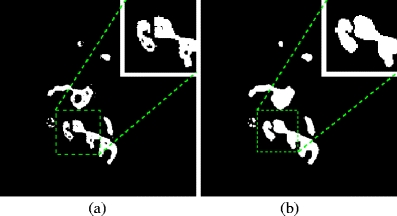
Segmentation result for a = b = 15, c = 3, δ = 15, γ = 0.25 and ϵ = 15 (a). M is calculated in the 15 × 15 × 3 neighborhood. Padding result after hole filling and smoothing of segmented data (b)

The presented 3D segmentation operator, f _binary(x, y, z), allows a rapid computation to determine, whether a pixel belongs to the foreground. It is applied to each voxel independently, therefore it is suitable for parallelization to enable a very fast segmentation of large image volumes. We implemented a parallelization of the segmentation operator on a GPU that performs segmentation of a data volume of several Gigabytes within seconds. Performance details are presented in Table 1, Section 3.

Table 1.

Algorithms performance in seconds on a single core of an AMD Opteron(tm) quad-core 8380 processor with 2.5 GHz CPU and 32 GB of RAM and a Nvidia Tesla C1060 GPU with 4 GB GDDR3 global memory

	Dataset I		Dataset II		Dataset III
Voxel volume	300 × 300 × 60		2047 × 1765 × 1000		2048 × 1768 × 6018
Cortical tissue size	7.5 × 7.5 × 3 μm3		102.4 × 88.2 × 50 μm3		51.2 × 44.2 × 180.6 μm3
Working data size	5.4 MB		3.6 GB		21.8 GB

	CPU (s)	GPU (ms)	CPU (s)	GPU (s)	CPU (s)	GPU (s)
Complete reconstruction	9.082 ±0.188	2074 ±88.1	4139 ±30.7	292.9 ±4.57	22391 ±114.0	2070.3 ±28.8
Filtering	1.799 ±0.010	46.86 ±1.00	1364 ±14.7	22.19 ±1.87	9100 ±19.1	151.0 ±0.38
Segmentation	3.083 ±0.097	28.15 ±1.27	119.2 ±2.12	10.30 ±0.564	164.8 ±0.45	50.7 ±0.015
Padding–holefilling	1.499 ±0.049	1369 ±67.7	1634 ±4.10	107.3 ±0.510	6664.3 ±12.1	464.5 ±2.1
Connectivity	0.104 ±0.008	N/A	121.3 ±1.1	N/A	1217 ±24.0	N/A
Padding–smoothing*	0.797 ±0.014	61.7 ±1.1	529.5 ±7.59	23.41 ±0.514	3230 ±43.1	141.6 ±2.2
Surface reconstruction**	1.80 ±0.01	464 ±9	371.3 ±1.1	8.365 ±0.007	2015 ±15.4	44.87 ±0.094

^*The morphological smoothing of the surface is an optional step of the working pipeline

^**The GPU version of the Marching Cubes processed the whole volume in substacks of 16 images in order to increase granularity

Padding and connectivity analysis

As only the neuron surface is segmented, holes inside the neural structures have to be filled. Holes are defined as those background components which are not connected to the image border (Soille 2003). Therefore, the complement of the background components which touch the image border results in an image with filled holes. The detailed algorithm that we apply to the segmented binary volume data for hole filling in 2D3 is presented in Soille (2003). By nature, this algorithm is highly sequential, since the decision to remove holes is defined with respect to the border of the image.

To separate the neural structure from other segmented structures, a connected component analysis in digital topology is applied to extract the largest components existing in the dataset. In addition to extraction using voxel weights, a selection of structures may also be defined using a voxel radius around a primary structure. There is currently no GPU implementation available, but this step can be parallelized using a shared or distributed memory programming model.

The image data can be smoothed in an optional padding step. Smoothing the binary image with dilation and erosion preserves the reliability of connectivity as shown for the (padded) images Fig. 6(a) and (b).

Surface extraction

Following the padding step, the surface of segmented neural structures is generated. This is a very important step in the workflow as it not only enables visual access to the biological data but also generates a 3D input for simulations.

The most popular surface extraction technique is the Marching Cubes (MC) algorithm designed by (Lorensen and Cline 1987). It generates a triangle mesh representation of an isosurface defined by a three-dimensional scalar field.

Marching Cubes subdivides the voxel volume into cubes of eight neighbor voxels. Marching through each cube, for each vertex it is determined whether it is within the isosurface or outside it. How a cube is tiled by the isosurface is approximated by triangles. Connecting all triangles from cubes on the isosurface boundary will result in a surface representation. A surface of a calyx-shaped spine from a L4 spiny dendrite generated using Marching Cubes is shown in Fig. 7(b).

The main drawback of the Marching Cubes algorithm, as presented by Lorensen and Cline (1987), are that ambiguities can appear on faces or inside a cube. Such ambiguities can lead to “holes” in the generated triangle mesh, as shown for the configurations presented in Fig. 7(a). A topologically correct isosurface generation cannot be guaranteed. The generation of topologically correct isosurfaces is of importance for the reconstruction of neuronal membranes. Despite the high voxel resolution of SBFSEM, we often have to deal with structures of less than 1 voxel thickness. Such structures can be seen only in one image. Figure 7(d) shows such a spine. After applying the MC, a hole results in the surface because of a face ambiguity. As the isosurface is smoothed, such artefacts will be intensified.

A proposed extension to the original Marching Cubes that generates topologically correct isosurfaces is the Marching Cubes 33 (Chernyaev 1995). It resolves ambiguities both on faces and inside the cell (Chernyaev 1995; Lewiner et al. 2003). We implemented the Marching Cubes algorithm for our application using the Look-Up-Table introduced by Lewiner et al. (2003) and applied it to the same data set as in Fig. 7(b). The result is a topologically correct isosurface reconstruction shown in Fig. 7(c) and (e) after smoothing.

In a last step to separate the neural structure from other segmented structures, a connected component analysis can be applied in object space. The generated triangle mesh is smoothed using a low pass filter. Both algorithms are available in VTK.

Figure 8(a) presents a projection of a dendrite with spines generated from a 300 × 300 × 60 voxel volume of a L4 spiny neuron from rat barrel cortex.

Fig. 8.

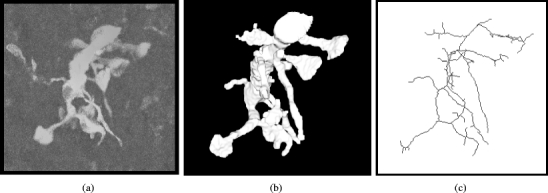
A L4 spiny dendrite from a 300 × 300 × 60 SBFSEM image volume of rat barrel cortex: projection of experimental data (a) and its corresponding reconstructed 3D smoothed surface model (b). The one-dimensional skeleton approximation of the dendritic surface is shown in (c)

This image stack correspond to a cortical tissue size of 7.5 × 7.5 × 3 μm³. The complete reconstruction of this volume from inversion to surface generation takes on a single core of a AMD Opteron(tm) quad-core 8380 processor with 2.5 GHz 1.8 s, whilst the GPU reconstruction needs only 464 ms.

Skeletonization

The last step in the reconstruction workflow is the extraction of neuronal morphology for simulation. This step is optional and is computed if a 1D skeleton model is needed for simulation.

Proposed methods for computing the skeleton of a 3D volume can be divided into three categories: (1) topological thinning, (2) distance transformation methods and (3) a Voronoi-based algorithm (Cornea et al. 2007; Sherbrooke et al. 1995; Jones et al. 2006; Gonzalez and Woods 2002; Soille 2003; Lee et al. 1994). 3D topological thinning methods are common because the skeleton is generated by iteratively removing simple points from the boundary of the 3D object (Lee et al. 1994; Manzanera et al. 1999; Soille 2003). Simple points are boundary points (voxels) that can be removed without changing the object topology.

We implemented a fast 3D thinning algorithm (Lee et al. 1994) to skeletonize our smoothed binary image volume. Starting from the 3D object boundary, at every iteration, a boundary voxel is removed if it meets a set of topological constraints that aim at preserving object topology: the number of connected components, object holes and cavities. These topological conditions are presented in the following Eqs. (4), (5) and (6):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\delta}\chi_{\rm local}(N_{26}(v)) = 0 $$\end{document} 4

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$${\delta}O(N_{26}(v)) = 0 $$\end{document} 5

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \forall v \in R: \text{connectivity re-check} $$\end{document} 6

As presented in Eq. (4), border voxels v, that are Euler invariant in N ₂₆, are removed. The number of connected components, holes and cavities in F does not change. But as Euler invariance alone does not ensure topology retainment (e.g. the removement of a voxel v does not only create a hole in the 3D object but also an additional object) we further require that the number of objects in N ₂₆ is invariant, see Eq. (5).

To avoid the removal of all object voxels when removing simple border voxels, the thinning iteration is subdivided into 6 subiterations according to six types of border points: N(orth), S(outh), W(est), E(ast), U(p), B(ottom)(Lee et al. 1994). For each subiteration simple border voxels are not directly removed, rather are just labeled. After labeling all simple border points \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$R = \{v \in F~|~v~\text{labeled}\}$\end{document}, a connectivity re-check in N ₂₆ for all v ∈ R is computed (Eq. (6)).

We applied the skeletonization method to the data volume with the reconstructed surface from Fig. 8(b). The skeletonization result is presented in Fig. 8(c). For simulation purposes the skeleton can also be stored into a file containing all topological and geometrical information.

Results

NeuroStruct’s reconstruction pipeline enables a fast and automatic extraction of neural structures from SBFSEM image stacks, assuming an appropriate parameterization of all necessary steps. One important issue regarding the reconstruction of large neural circuits from SBSFEM image data is the performance of reconstruction methods.

Table 1 presents the performance of our algorithms on three data sets. Dataset I, presented in Section 2.5, has a voxel volume of 300 × 300 × 60 (7.5 × 7.5 × 3 μm³). This reconstruction was generated on an AMD Opteron(tm) processor with 2.5 GHz in 9.082 s. For larger volumes, such as Dataset II and III (gigabytes), reconstruction time exceeded one hour. Computing the same data sets on a Nvidia C1060 GPU reduces the time for reconstruction to less than two seconds for Dataset I, and to few minutes for the others. This shows that significant acceleration can be achieved with GPU based algorithms.

The first two workflow steps, filtering and segmentation, are very well suited for parallel execution on a GPU. The padding step does not scale so well due to the sequential nature of the holefilling algorithm. The segmentation step takes 3.083 s on a CPU (60 images) or 51.4 ms per image. The segmentation process can be accelerated on a GPU to 0.47 ms per image. The parallelization of the algorithms is particularly profitable when reconstructing large image stacks. The reconstruction of neural structures from Dataset II, a 3.6 GB image volume corresponding to a cortical tissue size of 102.4 × 88.2 × 50 μm³, takes 1 h 8 m and 59 s on the same machine. The parameter values for the segmentation step were the following: Th _min = 95; Th _max = 180; γ = 0.15; δ = 0; ϵ = 3. These values resulted in the rough surface reconstruction shown in example in Fig. 9(a). For a fully detailed reconstruction, as shown in Fig. 9(b) and (c), segmentation parameters are iteratively fine-tuned taking advantage of the fast reconstruction cycle. With these values, the segmentation step on the CPU needs 119 s, which is about 0.12 s per image (image resolution of 2047 × 1765 pixels). A GPU based segmentation results in a 12-fold improvement in speed. Speed up factors of 190-fold have been achieved with optimized segmentation parameters. Reconstruction can be reduced to a few minutes if the basic workflow steps are executed on a GPU. Reconstruction results from Dataset II are presented in Fig. 9 and a zoom on a spiny dendrite section is shown in Fig. 9(c).

Fig. 9.

Surface reconstruction of a spiny L4 cell from Dataset II: (a) soma with dendrites. (b) details of the dendritic branch complex and spines in direct comparison with (d) a projection of the experimental data. (c) zoom of a spiny dendrite section. The area shown corresponds to the region that is marked green in (b). White length bars are 10 μm in (a), 1 μm otherwise

Dataset III corresponds to 21.8 GB of data with a cortical volume of 51.2 μm × 44.2 μm × 180.6 μm. In Table 1, we show the performance results from reconstruction of this stack. Although filtering and segmentation of this large data set could be performed on a fast CPU, the GPU parallelization enables an extraction of neural structures within 34 m and 30 s. If necessary, filtering and segmentation iterations could be performed in 201.7 s. Figure 10 presents images from the reconstruction of this data volume. The center pictures show the reconstructed surface on a labeled dendrite from a excerpt of the stack. A 10 voxel envelope around the principal dendrite was used during the connectivity step to generate this extraction. The left and right snapshot show zoomed dendrite areas with spines attached to them.

Fig. 10.

Surface reconstruction of a apical dendrite with spines from a L5 cell represented by Dataset III. Left and right pictures show two snapshots of areas with attached spines selected from the center picture. Length bars indicate 1 μm. Center picture shows an overview of the dendrite surface that corresponds to an extract of Dataset III. Length bar indicates 10 μm

Preliminary validation

The complexity inherent in the structure of a dendrite, including variant spine shapes, is amenable to reconstruction inaccuracies. We compared our automated image results to a reconstruction derived manually to validate completeness and accuracy.

Individual images of both approaches are presented in Fig. 11(a) and (d) and show a good agreement in count and shape of detected structures (spines). As shown in the image, Fig. 11(d), automatically segmented areas have rougher surfaces. This has a twofold origin: (1) during manual reconstruction the object is circumvented by a limited number of points without selecting each voxel on its own, (2) the automatic scheme does not benefit from objective consideration of the surrounding voxel neighborhood. Manual reconstruction of Dataset I is shown in Fig. 11(e) This manual reconstruction compares to the workflow generated version in Fig. 8(b). Both reconstructions include 11 spines. Spine shapes showed little variation between reconstructions. A critical issue in both manual and automated reconstruction of this dataset has been the detection of a single voxel during segmentation. The presence or absence of this voxel has direct influence on the length of a single spine, the one that extends diagonally in Fig. 8(b).

Fig. 11.

Comparison of several aspects regarding reconstruction accuracy and completeness: (a) manually traced image and (b) original image data after inversion. (c) zoomed MIP plot of Dataset II with original EM resolution. (d) automatically traced image corresponding to (a) and (b). (e) unsmoothed manual reconstruction of Dataset I. (f) reconstruction extract from Dataset II that corresponds to (c)

Additionally, we validated the spine skyline along the dendrite using a maximum intensity projection (MIP) shown in Fig. 11(c) for an extract of Dataset II. Spines of the represented dendrite, visible in the MIP plot, have proper correspondence to spines in the reconstruction shown in Fig. 11(f). Small artifacts can be seen on the subspine level. The rough spine surface shown in Fig. 9(c) is due to the voxel-based digital staircase approximation not to the fixation procedure. Optimization of surface smoothing will be required to remove these artifacts.

We consider the present validation as preliminary. A more profound validation must incorporate several datasets, larger regions of analysis, and a larger number of manual reconstructions for comparison.

Discussion

To obtain a complete morphology of a neuron’s dendritic branches, including its spines, at a sub-micrometer resolution, reconstruction of individually biocytin labeled neurons at the EM level is useful. With NeuroStruct’s approach, the geometry of dendritic branches, the total number of spines, and their density in different compartments of the cell can be determined for functionally, morphologically, and genetically identified cell types. Furthermore, each individual spine can be precisely described by its shape and volume as well as neck length and diameter. Accurate quantification of these parameters is essential for modeling the passive and active electrical properties of dendritic branches and of the entire dendritic compartment. This task requires a rapid method of image reconstruction therefore, this is the focus of the current study.

Utilizing the fast methods described here, the difficulties (i)–(iii), listed at the beginning of the Methods Section, were addressed. In summary, the situations (i) and (iii) have been solved to a degree that will not only enable our workflow to provide qualitative structural information on a large scale, but will also allow for a detailed quantitative spine-related analysis of large dendritic compartments. For unconnected electron-dense structures, whose gap is not resolved in the image stack data, situation (ii), at present, manual separation is required.

The reconstruction of a complete dendritic compartment will likely incorporate several large-scale datasets. Given the expected size of these data sets (hundreds of gigabytes) the presented GPU parallelization is a prerequisite to allow for a fast reconstruction cycle. Further difficulties have to be overcome, e.g. alignment of neuronal structures from different substacks.

Further development of NeuroStruct’s workflow will be required to deal with multiple image stacks. Our approach is limited by artifacts generated by segmentation such as high contrast structures from unlabelled neighboring elements. For example, when blood vessels directly touch dendritic structures as shown in Fig. 1, subfigure (C) these structures cannot be separated by the 3D segmentation operator. An extension to the reconstruction workflow to “correct” such segmentation errors will be based on the graph representation of the generated neural skeleton e.g. by eliminating branches after identifying them as non-dendritic. Both automatic and supervised removal can be considered for that purpose.

Computer simulations of electrical signals occuring in dendrites require high resolution skeletal representations as well as volume information. Such information can be retrieved more accurate by EM reconstructions because of the limited resolution of light microscopy. Since neighboring SBFSEM image stacks might be distorted towards each other the alignment will be a further crucial point for the reconstruction of larger tissue volumes. Surface reconstruction that meets the requirements for simulation purposes, such as triangle shape and aspect ratios, and further allows volume meshing of an entire dendritic compartment requires optimization of this process.

Obviously, the presented workflow is currently limited to the reconstruction of the dendritic compartment of an individually labeled neuron. Straightforward extension of the method will enable to simultaneous reconstructions of several stained cells. We aim first at clarifying the variation of spine shapes, including the cell-specific distribution densities of spines along a dendrite on a large scale. These distributions are required for morphologically detailed simulation of realistic circuits. In the future, large-scale reconstructions of spines in genetically identified cells will most likely reduce the variability of spine types due to the dependency of spine shapes on particular cell types.

Conclusion

This work presents NeuroStruct a fully automated reconstruction system for individually stained neurons from SBFSEM image data. NeuroStruct’s algorithmic workflow consists of a filtering step, segmentation, padding, surface extraction and skeleton generation. It allows fast and fully automated processing of image volumes without any user interaction, provided that the individual steps are parameterized properly. The developed 3D segmentation operator allows efficient processing of image data and enables reproducible segmentation results utilizing the large computing power of modern CPU and GPU hardware. Reconstructions of neurons from different image stacks show promising results and thus prove the variability and robustness of the proposed scheme. The output of NeuroStruct provides both a triangulated 3D surface representation of the neural structure and a 1D skeleton, which can be used for both structural analysis and simulation purposes. However, it also became obvious that an increase in resolution will depend on major improvements in EM staining techniques.

Electronic Supplementary Material

Below is the link to the electronic supplementary material.