Segmentation of Nerve Bundles and Ganglia in Spine MRI Using Particle Filters

Abstract

Automatic segmentation of spinal nerve bundles that originate within the dural sac and exit the spinal canal is important for diagnosis and surgical planning. The variability in intensity, contrast, shape and direction of nerves seen in high resolution myelographic MR images makes segmentation a challenging task. In this paper, we present an automatic tracking method for nerve segmentation based on particle filters. We develop a novel approach to particle representation and dynamics, based on Bézier splines. Moreover, we introduce a robust image likelihood model that enables delineation of nerve bundles and ganglia from the surrounding anatomical structures. We demonstrate accurate and fast nerve tracking and compare it to expert manual segmentation.

1 Introduction

Mapping and localization of nerve pathways is essential for diagnosis of spinal pathologies, treatment planning, and image-guided interventions. Recent developments in high-resolution MRI have enabled visualization of the nerve bundles within the dura, as they pass through the foramen, and exit the vertebral canal [16]. The bundles exhibit good contrast with fluids and bone, but are often of similar intensity to that of marrow and muscle. Manual segmentation of nerves and ganglia is quite challenging and time-consuming. In this paper, we develop and demonstrate a method for automatic segmentation of these nerves and ganglia in high-resolution MRI that requires minimal input from an expert.

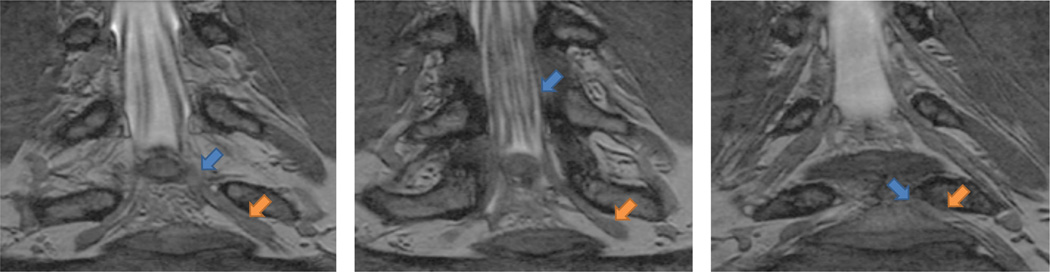
Nerve bundles and ganglia can be observed in high-resolution (0.3–0.6 mm voxels) MRI, as illustrated in Fig. 1. They start inside the spinal canal as dark grey bundles. The intensity contrast changes along the nerve; the neighboring tissues include cerebral spinal fluid, bone and other nerves. The bundles approximate cylinders, but change shape in the presence of a pathology such as disc herniation. As the bundles turn and exit through the foramen, they grow thicker, less regular and have lower contrast with their surroundings (e.g., fat, muscle or bone) as the nerve ganglia form. Automated nerve segmentation promises to significantly improve image-based diagnosis and therapy by providing fast tracing of the nerve bundles. In fact, the amount of time and effort currently required for manual tracing of the nerves precludes the practical construction of nerve maps, which could benefit surgery and minimally invasive interventions by reducing procedure duration and complications and improving outcomes of treatment of several degenerative conditions and spinal trauma.

Fig. 1.

Three slices from an example herniated disk MRI. All arrows point to the same nerve bundle. Blue arrows show examples of poor contrast between the nerve and surrounding tissue; orange arrows indicate the thickening of the nerve into a ganglion.

Prior work in segmentation of tubular structures, such as blood vessels, is clearly relevant to this task. Region-growing approaches, such as classical region-growing [5], competitive region-growing [20] and wave propagation [6], have been used successfully for vessel segmentation. Unfortunately, these methods suffer from leakage, where segmentation “leaks” into nearby structures, in areas with lack of contrast [11]. Active contours that evolve an initial boundary to segment the tubular targets offer a model-based approach [13,14]. Variational and level-set formulations have been successfully used for vascular segmentation [7,13]. However, these methods need good initializations and suffer from many local minima [11]. Moreover, false positive rate (or severe leakage) is certain to limit the usefulness of such methods in our application.

An alternative approach is to first extract the centerline, and to fill out the segmentation as a subsequent step. The target is modeled as a tubular structure – most often via circular cross-sections of inscribed cylinders or spheres – with a centerline in 3D [1,9]. In practice, these methods require a fair amount of user interaction to often re-seed tubes or branches [11]. Correction and re-centering during centerline propagation are affected substantially by neighboring tissues of similar intensities. Some methods require two end-points and employ variants of minimal path extraction [4,10], which often suffer from shortcut paths [12]. The high degree of required user input and the high false-positive rate in low contrast structures make these approaches inappropriate for our specific task. A recent study has demonstrated the feasability of using DTI and fiber tracking of lumbar nerves [2] to estimate differences of diffusion parameters between healthy and herniated discs. Our method can be readily extended to include diffusion information by incorporating directional information in the likelihood function.

In this paper, we present a tracking approach based on particle filtering, also known as sequential Monte-Carlo tracking. Tracking has also been demonstrated previously for segmentation of tubular structures [8,11,15]. Most vessel tracking methods model the state as a cross-sectional ellipse [3,8] or as a cylindroid [19]. In tracking nerve bundles, the regions of low contrast require the state to capture substantially longer segments of the track than what is represented by a cross-section. In addition, nerves tend to change direction, often sharply, which necessitates a use of more complex descriptors than cylinders. Enabling multiple hypotheses, flexible dynamics and diverse likelihood models, particle filtering is an ideal approach for our task.

To address the challenges of nerve tracking, we define a rich particle representation that captures the geometric behaviour of the nerve bundles. We use a Bézier spline [18] centerline with a quadratic radius function to characterize a nerve bundle. We devise a dynamics model for particle updates that enforces continuity and smoothness. Furthermore, we define an image likelihood model that compares gradient fields and intensities of predicted patches with image observations to evaluate the posterior distribution of the particles’ importance. Once tracking is completed, we remove spurious segmentations by measuring the quality of the entire tract. We demonstrate successful segmentations of nerves and evaluate them relative to expert manual segmentations. To the best of our knowledge, this is the first automatic segmentation of nerve bundles and ganglia.

2 Methods

Particle Filters

We start by providing a brief review of particle filters [17]. We let h_t be the particle, or state, representation at step t of the tracking algorithm, and assume the states respect a first order Markov chain, i.e.,

$$p({\mathbf{h}}_t|{\mathbf{h}}_{1:t-1})=p({\mathbf{h}}_t|{\mathbf{h}}_{t-1}),$$ (1)

where h_1:t−1 denotes the state history for step t. We let z_t be the image-based observation at step t, and further assume that given the state, the observations at different time points are independent:

$$p({\mathbf{z}}_{1:t}|{\mathbf{h}}_{1:t})=p({\mathbf{z}}_t|{\mathbf{h}}_t)·p({\mathbf{z}}_{1:t-1}|{\mathbf{h}}_{1:t-1}).$$ (2)

A step of the tracking algorithm estimates the posterior distribution p(h_t|z_1:t), represented non-parametrically via a set of K weigthed samples ${\{{\mathbf{h}}_t^{(k)},w_t^{(k)}\}}_{k=1}^K$. It can be readily shown that

$$p({\mathbf{h}}_t|{\mathbf{z}}_{1:t})\mathrm{\propto }p({\mathbf{z}}_t|{\mathbf{h}}_t)·p({\mathbf{h}}_t|{\mathbf{z}}_{1:t-1}),$$ (3)

i.e., the particle distribution depends on a likelihood function p(z_t|h_t) and a prior term p(h_t|z_1:t−1) [17].

A particle filter maintains the posterior distribution (3) by generating a set of samples ${\{{\mathbf{h}}_t^{(k)},w_t^{(k)}\}}_{k=1}^K$ at step t from the set ${\{{\mathbf{h}}_{t-1}^{(k)},w_{t-1}^{(k)}\}}_{k=1}^K$ generated at step t−1. Specifically, a sample 〈h_t−1, w_t−1〉 is drawn from the set $\{{\mathbf{h}}_{t-1}^{(k)},w_{t-1}^{(k)}\}$ according to the weights $\{w_{t-1}^{(k)}\}$, and is propagated to become $\langle {\mathbf{h}}_t^{(k)},w_t^{(k)}\rangle$. The state vector ${\mathbf{h}}_t^{(k)}$ is sampled from p(h_t|h_t−1), and its weight $w_t^{(k)}$ is computed by rescaling w_t−1 with likelihood $p({\mathbf{z}}_t|{\mathbf{h}}_t^{(k)})$. The weights are normalized at each step to sum to 1. It can be shown that the resulting sample set ${\{{\mathbf{h}}_t^{(k)},w_t^{(k)}\}}_{k=1}^K$ is an accurate representation of the state distribution p(h_t|z_1:t).

In the remainder of this section, we define our particle model h_t for the nerve bundle, our dynamics model p(h_t|h_t−1), and our likelihood measure p(z_t|h_t). Together, these elements fully define the tracking algorithm.

Particle Representation for Nerve Tracks

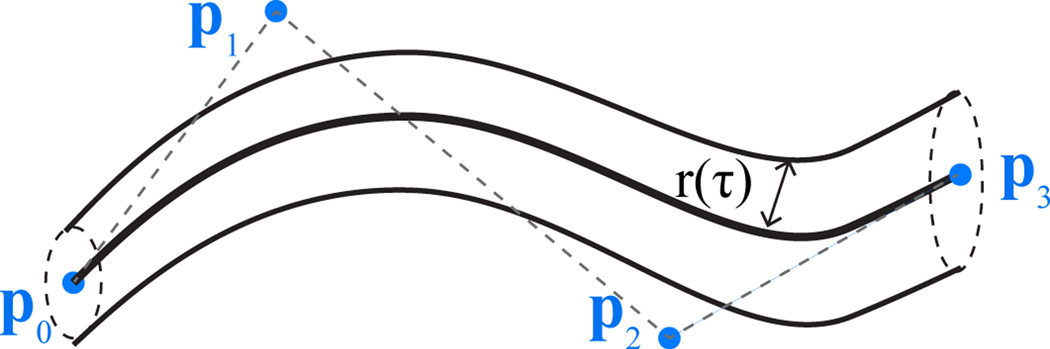
We model each particle as a tubular structure around a centerline curve in 3D. We design the centerline as a Bézier curve and form the tubular structure by introducing a radius function, as illustrated in Fig. 2. A n^th degree Bézier curve [18] is defined by n + 1 control points. The first and last control points define the endpoints of the curve. The interior control points can be thought of as “pulling” the curve towards them. We choose to work with cubic curves, i.e.,

$$\mathbf{c}(\tau )={(1-\tau )}^3{\mathbf{p}}_0+3{(1-\tau )}^2\tau {\mathbf{p}}_1+3(1-\tau ){\tau }^2{\mathbf{p}}_2+{\tau }^3{\mathbf{p}}_3,$$ (4)

where τ ∈ [0, 1] is the parameterization variable.

Fig. 2.

Nerve segment (particle) is defined as a Bézier curve centerline with four control points and a radius function r(·)

We allow the radius function r(·) to vary quadratically along the segment, and also define it via a Bézier curve:

$$r(\tau )={(1-\tau )}^2{r}_0+2(1-\tau )\tau r_1+{\tau }^2{r}_2,$$ (5)

for some control points r₀, r₁, and r₂. In addition, we maintain the mean image intensity μ inside the segment. The state vector

$$\mathbf{h}=({\mathbf{p}}_0,{\mathbf{p}}_1,{\mathbf{p}}_2,{\mathbf{p}}_3,r_0,r_1,r_2,\mu )$$ (6)

fully describes the corresponding segment. This construction can handle tubular structures with variable directionality, thickness and contrast, such as nerve bundles and ganglia.

Dynamics model

We now describe the construction of the state vector h_t from the state vector h_t−1 generated in a previous step of the algorithm. This step corresponds to sampling the probability p(h_t|h_t−1).

We set the first centerline control point of h_t to the last control point of h_t−1: p_0,t = p_3,t−1, which ensures continuity of the track. We place p_1,t along the line (p_2,t−1p_3,t−1). This maintains smoothness during the transition from the previous to the current particle, since for Bézier curves, the tangent of a curve at an endpoint p₀ is along the vector (p₀, p₁), and similarly the tangent at point p₃ is along the vector (p₂, p₃). The distance ℓ between p_0,t and p_1,t is drawn uniformly from [0, L] where L is a parameter of the algorithm. Formally,

$${\mathbf{p}}_{1,t}={\mathbf{p}}_{0,t}+\ell \widehat{\mathbf{n}},$$

where n̂ is the unit vector in the direction of (p_2,t−1, p_3,t−1).

We draw the direction of (p_1,t, p_2,t) from a von Mises-Fisher distribution on the unit sphere, centered on the direction of the initial tangent (p_0,t, p_1,t) with concentration $1/{\sigma }_{\alpha }^2$ (we call this new direction n̂₀₁ + Δn̂₁₂). We then sample the distance ℓ of p_2,t from p_1,t uniformly from [0, L]. Formally,

$${\mathbf{p}}_{2,t}={\mathbf{p}}_{1,t}+{\ell }_2({\widehat{\mathbf{n}}}_{\mathbf{01}}+\mathbf{\Delta }{\widehat{\mathbf{n}}}_{\mathbf{12}}).$$

Using the same procedure we generate p_3,t based on p_2,t and vector (p_1,t, p_2,t).

We set r_0,t = r_2,t−1 to maintain continuity of the radius function. We sample a distance d ∈ (0, 1), and we set r_1,t to the y-coordinate of a control point which is d away from r_0,t along the line (r_1,t−1, r_2,t−1). We choose r_2,t from a Gaussian distribution with mean r_1,t and variance ${\sigma }_r^2$. The intensity parameter μ_t is propagated via a Gaussian distribution with variance ${\sigma }_{\mu }^2$.

This construction depends on four parameters: L controls the length of the particle, ${\sigma }_{\alpha }^2$ determines the variation in the particle curvature, ${\sigma }_r^2$ describes the range of the radius, and ${\sigma }_{\mu }^2$ captures the intensity variation.

Likelihood Measure

Now we focus on the likelihood p(z_t|h_t). The contrast between the nerve bundle and surrounding tissue may change along the track, rendering ribbon measures [8,15] inappropriate. However, it still creates image gradients normal to the centerline. Therefore, to measure alignment of an observed image patch I with a hypothesis h_t, we simulate an image patch with a white nerve segment described by the particle h_t on a black background. We compare the directions of its gradients g^h with those of the observed patch g^I. We avoid using the gradient magnitude, since false hypotheses with partial but very strong contrasts are abundant. We express the distance $d_{\nabla }^2$ between the normalized particle gradient ĝ^h and the normalized observed gradient ĝ^I via their cross product:

$$d_{\nabla }^2({\mathbf{h}}_t,I)=\frac{1}{|V({\mathbf{h}}_t)|}{\displaystyle \sum _{\upsilon \in V({\mathbf{h}}_t)}}{({\mathbf{ĝ}}_{\upsilon }^h\times {\mathbf{ĝ}}_{\upsilon }^I)}^2=\frac{1}{|V({\mathbf{h}}_t)|}{\displaystyle \sum _{\upsilon \in V({\mathbf{h}}_t)}}{\text{sin}}^2({\mathbf{ĝ}}_{\upsilon }^h,{\mathbf{ĝ}}_{\upsilon }^I),$$ (7)

where V (h_t) is the set of voxels in the simulated patch that belong to the predicted nerve segment and υ is an image voxel.

To capture relatively constant nerve intensity, we include a term that measures the distance between the mean intensities in the observation and the particle prediction:

$$d_{\mu }^2({\mathbf{h}}_t,I)={\left[{\mu }_t-\frac{1}{|V({\mathbf{h}}_t)|}{\displaystyle \sum _{\upsilon \in V({\mathbf{h}}_t)}}{I}_{\upsilon }\right]}^2.$$ (8)

We form the likelihood model by combining equations (7) and (8):

$$p({\mathbf{z}}_t|{\mathbf{h}}_t)=\frac{1}{Z}\text{exp}\{-(d_{\nabla }^2+\lambda d_{\mu }^2)\},$$ (9)

where λ trades off between the two measures and Z is the partition function. In practice, Z does not need to be explicitly computed as the weights (likelihoods) of all samples are normalized at the end of each iteration.

Partial volume effects play a significant role in this computation. Most nerve bundle voxels also contain volume from surrounding anatomy. Modeling large segments of the nerve tracts, as opposed to cross-sections, improves the robustness of the method by increasing the number of voxels that contribute to the distance computations in (7) and (8).

Implementation Details

We initialize each nerve bundle with two nearby clicks that specify p_2,0 and p_3,0 for a single particle of weight w = 1 at time t = 0. We set parameters as follows: length L = 5, curvature σ_α = 0.4, radius σ_r = 1, intensity σ_μ = 2. The curvature variation only needs to be increased if sharp transitions are expected. In our experience, the length, radius and intensity parameters rarely need to be varied for similar contrast and resolution MR images. We also consider the intensity distance equally important to the gradient field, setting the tradeoff parameter λ in the likelihood model to 1.

We run the particle filter until all bundles reach the end of the volume. In each iteration, we sample 5, 000 particles and keep the ten top-weighed particles to form the sample set ${\{{\mathbf{h}}_t^{(k)},w_t^{(k)}\}}_{k=1}^{10}$. To identify the most appropriate of the surviving tracts, we simulate each tract V (h_1:t) in the volume, and compute the likelihood (9) for the whole tract. We retain the top three tracts. Note that due to the multi-hypothesis nature of particle filters, branching nerves are naturally handled. Typical runtime ranges from 10 to 30 CPU-minutes per nerve.

3 Results

We demonstrate our method on MRI scans of the spine in ten nerve bundles from five subjects (3D Wide-band Steady State Free Precession, in-plane resolution of 0.44–0.6mm, slice thickness of 1.2–1.8mm, TR=6.4–6.9ms, TE=2.1–2.4ms, Θ=25, ±32 KHz bandwidth, FOV=14 cm) [16]. These include four nerves in two pathologies where the nerves have been displaced by disc herniations. Fig. 3 illustrates an example automatic segmentation. We obtain both expert and automatic segmentations of nerve bundles and ganglia that were deemed traceable, and evaluate tracing accuracy for all bundles. Fig. 3 shows cumulative distributions of the distances between segmentations in terms of centerlines and surfaces.

Fig. 3.

Left: Example segmentation results – the rightmost nerve shows results without post-processing pruning, while the left segmentation was processed after completion of tracking. as described at the end of Section 2. Right: Cumulative distribution functions of distances (in voxels) between the automatically extracted and manual segmentations: centerline distances on top and surfaces on the bottom. Blue plots indicate differences from algorithm to expert segmentation voxels, red plots correspond to expert-to-algorithm distances. Error bars indicate standard deviations. Dotted vertical lines indicate mean (lower) and 90^th percentiles distances (higher).

The mean distance between automatically extracted centerlines and their manual counterparts is within 1 voxel (0.2 ± 0.1 and 1.0 ± 0.3 for automatic-to-manual and manual-to-automatic, respectively); 90% of automatically extracted centerlines are within 0.9 ± 0.3 voxels of the expert centerline, and 90% of expert centerlines are within 2.2 ± 0.5 voxels of the algorithm centerline. Visually, we find very good centerline alignment (≤ 1 voxel) inside the vertebral canal. The greater disagreement is present in the ganglia, where the algorithm tends to under-segment and may be off-center, thereby shifting the centerline by a couple of voxels.

We find that since the edges of nerve bundles and ganglia are subject to the partial volume effects and are often near other anatomical structures, the algorithm slightly over-estimates the extent of the nerves in some regions of the image. As mentioned above, inside the thick ganglia the algorithm under-segments due to the ganglia’s more irregular shape. The mean distance from the automatically extracted surface to the expert surface is 1.1 ± 0.4 voxels and the 90^th percentile is at 2.3 ± 0.6 voxels. Visual inspection reveals that the expert segmentation can be irregular and include small deformations or protrusions, especially in pathologies. Since the algorithm attempts to maintain the estimation within the ganglia, the correct outer surface voxels in areas of small irregularities will be more distant from the algorithm prediction. This occurs in cases where the nerve bundle is thicker, generally leading up to and including the ganglia, which can reach 15 voxels in diameter. This results in a mean distance between surfaces of 2.6 ± 0.8 voxels, with the 90^th percentile within 5.9 ± 1.9 voxels. We therefore conclude that the proposed segmentation may slightly over-segment (usually by no more than two voxels) in thin areas and under-segment in thick areas, but will give a very good estimation of the nerve core and location.

We also evaluated the algorithm on the nerves following the ganglia, where they split up into several thinner peripheral nerves. Here, the algorithm often loses some nerves due to loss of contrast and the small radii of the nerves. When the algorithm continues to track, we observe a fully estimated path (the segmentation follows the nerve), but with over-segmentation as the filter is driven by stronger edges from the neighboring anatomical structures.

4 Conclusion

We demonstrate tracking of nerve bundles in high-resolution spine MRI. The tracking method is based on particle filtering and requires minimal input from the user. We model nerve segments via Bézier curves and describe a dynamics model for propagating the segments. A new distance measure that utilizes gradient fields and nerve intensities is used to score nerve segments and whole bundles. We demonstrate the method’s capacity to handle nerves and ganglia in presence of both high and low contrast. Precisely estimating edges from the current segmentation and segmentation of much thinner peripheral nerves of lower contrast remain challenging problems for future work.