Role of structural anisotropy of biological tissues in poroelastic wave propagation

Abstract

Ultrasound waves have a broad range of clinical applications as a non-destructive testing approach in imaging and in the diagnoses of medical conditions. Generally, biological tissues are modeled as an homogenized equivalent medium with an apparent density through which a single wave propagates. Only the first wave arriving at the ultrasound probe is used for the measurement of the speed of sound. However, the existence of a second wave in tissues such as cancellous bone has been reported and its existence is an unequivocal signature of Biot type poroelastic media. To account for the fact that ultrasound is sensitive to microarchitecture as well as density, a fabric-dependent anisotropic poroelastic ultrasound (PEU) propagation theory was recently developed. Key to this development was the inclusion of the fabric tensor - a quantitative stereological measure of the degree of structural anisotropy of bone - into the linear poroelasticity theory. In the present study, this framework is extended to the propagation of waves in several soft and hard tissues. It was found that collagen fibers in soft tissues and the mineralized matrix in hard tissues are responsible for the anisotropy of the solid tissue constituent through the fabric tensor in the model.

1. Introduction

Ultrasound waves have a broad range of clinical applications as a non-invasive testing approach to imaging and the diagnoses of medical conditions. For instance, ultrasound elastography, intravascular ultrasound and quantitative ultrasound have been considered as attractive alternatives to the use of magnetic resonance imaging (MRI), computed tomography (CT) or dual-energy X-ray absorptiometry (DXA) to diagnose cancer, atherosclerosis or osteoporosis among many other diseases (Siffert & Kaufman, 2006; Hans, et al., 1996; Grimm & Williams, 1997). Ultrasound waves are elastic vibrations that can provide direct information on the mechanical properties of the medium in which they propagate. These waves have potential diagnostic information, they are non-ionizing, inexpensive to measure and non-invasive. On one hand, most clinical ultrasound systems use wave echography to compose images of tissues morphology or to estimate the mechanical properties of tissues based on their characteristic wave absorption and mass density. On the other hand, ultrasound bone densitometers use a through transmission approach to measure the speed of sound (SOS) and broadband ultrasound attenuation (BUA) in cancellous bone to diagnose bone loss and osteoporosis. Nevertheless, these two approaches in either soft or hard tissues consider tissues as a single-phase medium with an apparent density through which a single wave propagates, and in which only the first wave arriving at the ultrasound probe is used for the measurement of the SOS.

If only one wave is measured, the solid matrix structure cannot be distinguished from the fluid within the tissue. However, the existence of a second wave in cancellous bone has been reported (Hosokawa and Otani, 1997, 1998; Cardoso et al., 2001, 2003; Mizuno et al., 2008, 2009; Anderson et al., 2008, 2009). The existence of this wave is an unequivocal signature of a poroelastic medium. These two waves propagate with different velocities and have been shown to correspond to the fast and slow waves predicted by Biot’s poroelastic wave propagation theory (Biot 1941, 1955, 1956a&b and 1962a&b). Therefore, poroelastic wave propagation theory is conceptually more appropriate than the homogenized equivalent media approach to characterize the properties of a porous medium. Isotropic poroelasticity theory has been used for many years to analyze wave propagation in cancellous bone (Williams 1992; Hosokawa and Otani, 1997, 1998; Haire & Langton 1999; Kaczmarek et al., 2002; Fellah et al., 2004; Wear 2005, 2009, 2010; Pakula et al., 2008; Cardoso et al., 2008), but it is only recently that the role of microarchitecture (Xia et al., 2007; Cardoso et al., 2008; Sasso et al., 2008; Haïat et al., 2008; Pakula 2009; Lin et al., 2009; Nguyen et al., 2010) has been included in poroelasticity theory through the fabric tensor (Cowin and Cardoso 2011). The fabric-dependent anisotropic poroelastic ultrasound (PEU) approach developed by Cowin and Cardoso (2011) has the advantage of providing a theoretical framework to describe the relationship between measurable wave properties (i.e. wave velocity and attenuation) and the elastic constants of the porous structure. Key to the development of such a theory was the incorporation of the fabric tensor into the governing equations for wave motion in the linear theory of anisotropic poroelastic materials (Cowin 1985, 2004). Fabric is a quantitative stereological measure of the degree of structural anisotropy in the pore architecture of a porous medium (Hilliard, 1967; Whitehouse 1974a; Whitehouse and Dyson, 1974b; Cowin and Satake, 1978; Satake, 1982; Kanatani, 1983, 1984a&b, 1985; Harrigan and Mann, 1984; Odgaard, 1997a, 2001; Odgaard et al., 1997b, Matsuura et al., 2008). This new approach resulted in a poroelastic Christoffel equation for anisotropic poroelastic media represented by an eigenvalue problem with a characteristic polynomial equation of order six. Four of those six roots are nonzero, and correspond to the four wave modes of propagation in porous media, two of which are longitudinal and two are shear wave modes. Analytical expressions were given in Cowin and Cardoso (2011) and Cardoso and Cowin (2011) for the velocity and attenuation of each wave mode along an arbitrary direction in orthotropic porous media. Since this poroelastic wave propagation theory depends on anisotropy of the structure and tissue composition in addition to tissue’s mass density, it represents an alternative to improve over the characterization of biological tissue as provided by single-phase ultrasound elastography and quantitative ultrasound.

In the present study, the theoretical framework of Cowin and Cardoso (2011) is extended to the propagation of waves in several soft and hard tissues. The plane wave equation in an anisotropic fluid-saturated poroelastic medium developed in Cowin and Cardoso (2011) is reviewed in section 2. The fabric dependence of tensors appearing in the poroelastic model of wave propagation is summarized in section 3. The propagation of plane waves in an anisotropic, fabric dependent, saturated porous medium along an arbitrary direction is non-dimensionalized in section 4, and the practical application of these results to the wave propagation in soft and hard tissues is presented in section 5. Speed of sound of blood vessels, brain, breast, cartilage, eye lens, eye aqueous humor, adipose, heart, kidney, liver, skeletal muscle, skin, spleen, tendon, testis, tongue and uterus are compared with the predictions of the proposed poroelastic model of wave propagation. Among the hard tissues included are cortical bone, cancellous bone, tooth’s dentin and tooth’s enamel. In order to calculate the wave propagation in biological tissues, the material properties of tissues’ constituents, such as the elastic modulus and density of the tissue matrix, as well as the bulk modulus and density of the fluid were obtained from the literature. The final section, section 6, contains our discussion and concluding remarks.

2. Plane wave equation in an anisotropic fluid-saturated poroelastic medium

The field equations of motion in an anisotropic porous medium (Biot 1941) were obtained from the conservation of linear momentum and the conservation of mass by substituting constitutive equations for stress and fluid flux (Cowin and Cardoso, 2011). Einstein’s convention of summing over repeated indices is adopted for this presentation. The field equations describe the solid displacement field u and the displacement field w of the fluid relative to the solid (Cowin and Cardoso, 2011),

$$Z_{\mathit{ijkm}}\frac{{\partial }^2{u}_k}{\partial x_m\partial x_j}+M_{ij}\frac{{\partial }^2{w}_k}{\partial x_k\partial x_j}=\rho {\ddot{u}}_i+{\rho }_f{\ddot{w}}_i,$$ (1)

$$M_{km}\frac{{\partial }^2{u}_k}{\partial x_m\partial x_i}+M\frac{{\partial }^2{w}_k}{\partial x_k\partial x_i}={\rho }_f({\ddot{u}}_i+J_{ij}{\ddot{w}}_j)+\mu R_{ij}{\stackrel{.}{w}}_j,$$ (2)

where ρ is the bulk density of the solid matrix, ρ_f the density of the pore fluid, μ the viscosity of the pore fluid and M the constant of proportionality between the fluid pore pressure p and the variation in fluid content, ζ. The variation in fluid content ζ, a traditional Biot variable, is defined as the divergence of the displacement vector w of the fluid relative to the solid, ζ =−∇·w. Also, the Biot effective stress coefficient tensor A_ij represents the proportionality factor between the stress tensor T_ij and the pore fluid pressure p, $T_{ij}=C_{\mathit{ijkm}}^d{E}_{km}-A_{ij}p$, where T_ij are the components of the stress tensor and $C_{\mathit{ijkm}}^d$ represents the components of the drained elasticity tensor. The four constitutive tensors, Z_ijkm, M_ij, J_ij and R_ij, appearing in (1) and (2) are identified as follows: Z_ijkm is Biot’s elasticity tensor, M_ij is directly related to the Biot effective stress coefficient tensor A_ij and the scalar M by M_ij = MA_ij; The constant M is related to the effective drained elastic stiffness tensor $C_{\mathit{ijkm}}^d$, the drained compliance tensor $S_{\mathit{ijkm}}^d$ and the Biot’s effective stress tensor A_ij by

$$M={\left(C_{\mathit{eff}}^d-A_{ij}{S}_{\mathit{ijkm}}^d{A}_{km}\right)}^{-1}$$ (3)

J_ij is the micro-macro velocity average tensor - it functions as a density distribution function that relates the relative micro-solid-fluid velocity to its bulk volume average ẇ; and R_ij is the flow-resistivity tensor, the inverse of the permeability tensor K_ij. Note Z_ijkm differs from the drained elasticity tensor $C_{\mathit{ijkm}}^d$ by the term MA_ijA_km, which is the open product of the Biot effective stress coefficient tensor A_ij with itself.

The propagation of plane waves in an anisotropic fluid-saturated porous medium is represented kinematically by a direction of propagation, denoted by n = (n₁, n₂, n₃)^T a unit normal to the wave front. The directions of displacement for the wave fronts, a or b, are associated with u and w, respectively. These two plane waves are represented by

$$\mathbf{u}(\mathbf{x},t)={\mathbf{a}e}^{i(\stackrel{\sim }{\mathit{k}}·\mathbf{x}-\omega t)}\text{and}\mathbf{w}(\mathbf{x},t)={\mathbf{b}e}^{i(\stackrel{\sim }{\mathit{k}}·\mathbf{x}-\omega t)},$$ (4)

where x is the position vector, ω is the angular frequency, t is time, and k̃ is the complex wave vector,

$$\stackrel{\sim }{\mathit{k}}=(\mathit{\kappa }+i\mathit{\alpha })=\left(k_1,k_2,k_3\right)$$ (5)

where κ is the real valued wave vector, indicating the direction of wave propagation and α is the attenuation vector, indicating the direction of wave attenuation (Carcione, 2001; Cerveny, & Psencik, 2006; Sharma, 2010). For homogeneous waves, the propagation and attenuation directions coincide and the complex wave vector can be written as

$$\stackrel{\sim }{\mathit{k}}=(\kappa +i\alpha )\mathbf{n}=\stackrel{\sim }{k}\mathbf{n}$$ (6)

where

$$\mathbf{n}={(n_1,n_2,n_3)}^{\text{T}}$$ (7)

defines the propagation direction through the direction cosines n₁, n₂ and n₃. A transverse wave is characterized by a·n = 0, a longitudinal wave by a·n = 1. Substituting the relations (4) for the plane waves into the field equations (1) and (2) leads to the poroelastic Christoffel equation (8):

$$\left[\begin{array}{cc}\mathbf{Q}-\rho \stackrel{\sim }{z}\mathbf{1}& C-{\rho }_f\stackrel{\sim }{z}\mathbf{1}\\ {\mathbf{C}}^T-{\rho }_f\stackrel{\sim }{z}\mathbf{1}& \mathbf{H}-{\rho }_f\stackrel{\sim }{z}\stackrel{\sim }{\mathbf{S}}\end{array}\right]\left[\begin{array}{c}\mathbf{a}\\ \mathbf{b}\end{array}\right]=0,$$ (8)

where the complex valued quantity z̃ represents the square of the frequency to complex wave vector ratio

$$\stackrel{\sim }{z}={\left(\frac{\omega }{\stackrel{\sim }{k}}\right)}^2$$ (9)

and the notation Q_ik = Z_ijkmn_mn_j, C_ik = M_ijn_jn_k, H_ik = Mn_i ⊗ n_k, and ${\stackrel{\sim }{S}}_{ik}=J_{ik}+i\frac{\mu }{{\rho }_f\omega }{R}_{ik}$ has been introduced. The detailed algebraic structure of the tensors Q, C, H and S̃ as functions of the general direction of wave propagation n are recorded in Cardoso and Cowin (2011).

3. Fabric dependence of tensors appearing in the poroelastic Christoffel equation

The second rank fabric tensor F is a non-dimensional quantitative stereological measure of the degree of structural anisotropy in the pore architecture of a porous medium. The experimental procedure for the surface area orientation measurement of cancellous bone is described by Whitehouse (1974a&b), Harrigan and Mann (1984) and Turner et al., (1987, 1990). The work of these authors, and Odgaard (1997a; 2001), Odgaard et al., (1997b), van Rietbergen et al., (1996, 1998), Matsuura et al., (2008) and others, has shown that the fabric tensor is a good measure of the structural anisotropy in cancellous bone tissue (Cowin, 1997).

The second rank fabric tensor F is symmetric, therefore its invariants I_F, II_F and III_F are related to the traces of F, F² and F³ by the formulas recorded, for example, in Ericksen (1960):

$$I_F=tr\mathbf{F},{II}_F=\frac{1}{2}\left[{(tr\mathbf{F})}^2-{tr\mathbf{F}}^2\right],{\mathit{III}}_F=\frac{1}{6}\left(tr\mathbf{F}-3{tr\mathbf{F}}^2+2{tr\mathbf{F}}^3\right).$$ (10)

The fact that a matrix satisfies its own characteristic equation, the Cayley-Hamilton theorem, is then written in the form:

$${\mathbf{F}}^3-I_F{\mathbf{F}}^2+{II}_F\mathbf{F}-{\mathit{III}}_F\mathbf{1}=0.$$ (11)

The significance of this result is that any power of F of the order three or higher may be eliminated by repetitive use of this result. From the first and second equations of (10) one can see that trF² = I_F² − 2II_F. Using the Cayley-Hamilton theorem it is easy to show that

$${tr\mathbf{F}}^3={I_F}^3-3I_F·{II}_F+3{\mathit{III}}_F\text{and}{tr\mathbf{F}}^4={I_F}^4-3{I_F}^2·{II}_F+2I{I_F}^2+4I_F·{\mathit{III}}_F;$$ (12)

these results will be used below. Finally, we normalize the fabric tensor by setting I_F = trF = 1. Thus in the applications of the formulas trF² = I_F² − 2II_F and (11), I_F is replaced by 1. The Cayley-Hamilton theorem is here used not only on the fabric tensor, but on other second rank tensors such as R, K, M and J. Formulas relating the Biot’s elasticity tensor Z, the flow resistivity tensor R and the tensor M, representing the interaction of the velocity fields u and w, to the fabric tensor F were obtained in Cowin and Cardoso (2011).

Briefly, the dependence of the Biot’s elasticity tensor Z upon the fabric tensor F is described by the following relationships:

$$\begin{array}{c}{Z}_{\mathit{ijkm}}=\left[a_1^{cd}+M{\left(\frac{3K^m-a_o^d}{3K^m}\right)}^2\right]{\delta }_{ij}{\delta }_{km}+\left[a_2^{cd}-\frac{M\left(3K^m-a_o^d\right)a_I^d}{{\left(3K^m\right)}^2}\right]\left(F_{ij}{\delta }_{km}+{\delta }_{ij}{F}_{km}\right)+\\ \left[a_3^{cd}-M\frac{\left(3K^m-a_o^{cd}\right)a_{II}^{cd}}{{\left(3K^m\right)}^2}\right]\left({\delta }_{ij}{F}_{kq}{F}_{qm}+{\delta }_{km}{F}_{iq}{F}_{qj}\right)+\left[b_1^{cd}+M{\left(\frac{a_I^{cd}}{3K^m}\right)}^2\right]F_{ij}{F}_{km}+\\ \left[b_2^{cd}+M\frac{a_I^{cd}{a}_{II}^{cd}}{{\left(3K^m\right)}^2}\right]\left(F_{ij}{F}_{kq}{F}_{qm}+F_{km}{F}_{iq}{F}_{qj}\right)+\left[b_3^{cd}+M{\left(\frac{a_{II}^{cd}}{3K^m}\right)}^2\right]F_{is}{F}_{sj}{F}_{kq}{F}_{qm}+\\ c_1^{cd}\left({\delta }_{ki}{\delta }_{mj}+{\delta }_{mi}{\delta }_{kj}\right)+c_2^{cd}\left(F_{ki}{\delta }_{mj}+F_{kj}{\delta }_{mi}+F_{im}{\delta }_{kj}+F_{mj}{\delta }_{ki}\right)+\\ c_3^{cd}\left(F_{ir}{F}_{rk}{\delta }_{mj}+F_{kr}{F}_{rj}{\delta }_{mi}+F_{ir}{F}_{rm}{\delta }_{kj}+F_{mr}{F}_{rj}{\delta }_{ik}\right).\end{array}$$ (13)

The tensor M represents the elastic coupling between the solid and the fluid phases,

$$M_{ij}=M{\delta }_{ij}-\frac{M}{3K^m}\left(a_o^{cd}{\delta }_{ij}+a_I^{cd}{F}_{ij}+a_{II}^{cd}{F}_{iq}{F}_{qj}\right);$$ (14)

the micro-macro velocity average tensor J is related to the fabric by

$$J_{ij}=j_1{\delta }_{ij}+j_2{F}_{ij}+j_3{F}_{iq}{F}_{qj};$$ (15)

similarly, the flow-resistivity tensor R, is related to the fabric by

$$R_{ij}=r_1{\delta }_{ij}+r_2{F}_{ij}+r_3{F}_{iq}{F}_{qj},$$ (16)

where the quantities $a_1^{cd},a_2^{cd},a_3^{cd},b_1^{cd},b_2^{cd},b_3^{cd},c_1^{cd},c_2^{cd},c_3^{cd},a_o^{cd},a_I^{cd},a_{II}^{cd}$, j₁, j₂, j₃, r₁, r₂, and r₃ are scalar-valued functions of φ, II_F and III_F (Cowin, 1985; Cowin and Cardoso, 2011). R is the inverse of the second-rank intrinsic permeability tensor K and it represents dissipation phenomena due to viscous losses at low frequencies of fluid motion. The conception of K was extended to take into account the change in fluid flow regime occurring between low and high frequencies of wave propagation (Johnson et al., 1987):

$$K_{ij}(\omega )={\mathit{\kappa }}_0\left[1-2\frac{{\text{J}}_1(d\chi )}{d\chi {\text{J}}_0(d\chi )}\right]\left(K_1{\delta }_{ij}+K_2{F}_{ij}+K_3{F}_{iq}{F}_{qj}\right),$$ (17)

where the dynamic permeability tensor K is a function of the average intrinsic permeability κ₀, the fabric tensor and Bessel functions that characterize the dynamics of the oscillatory fluid flow inside a cylindrical channel. In this equation, J₁ and J₀ are, respectively, the first order and zeroth order Bessel functions of the first kind, and d corresponds to the average characteristic pore dimension. The inverse of the viscous skin depth χ is defined as a function of the angular frequency ω, the fluid mass density ρ_f and the dynamic viscosity of the fluid μ:

$$\chi ={\left(\frac{i\omega {\rho }_f}{\mu }\right)}^{1/2}.$$ (18)

4. Non-dimensional poroelastic Christoffel equation

Equation (8) is made dimensionless by dividing through by K_f, the bulk modulus of the fluid in the pores,

$$\left[\begin{array}{cc}{\mathbf{Q}}_o-{\rho }_o{\stackrel{\sim }{z}}_o\mathbf{1}& {\mathbf{C}}_o-{\stackrel{\sim }{z}}_o\mathbf{1}\\ {{\mathbf{C}}_o}^T-{\stackrel{\sim }{z}}_o\mathbf{1}& {\mathbf{H}}_o-{\stackrel{\sim }{z}}_o{\stackrel{\sim }{\mathbf{S}}}_o\end{array}\right]\left[\begin{array}{c}\mathbf{a}\\ \mathbf{b}\end{array}\right]=0,$$ (19)

where the fluid wave velocity, v_f, and the characteristic frequency, ω_c, were used to define the non dimensional complex quantity, z̃_o, non dimensional frequency ω_o, and non dimensional elastic coefficients Q_o, C_o, H_o, and S̃_o as

$$\begin{array}{l}{\stackrel{\sim }{z}}_o=\frac{\stackrel{\sim }{z}}{v_f^2},v_f=\sqrt{\frac{K_f}{{\rho }_f}},{\omega }_o=\frac{\omega }{{\omega }_c},{\omega }_c=\frac{\mu }{{\rho }_f},\\ {\mathbf{Q}}_o=\frac{\mathbf{Q}}{K_f},{\mathbf{C}}_o=\frac{\mathbf{C}}{K_f},{\mathbf{H}}_o=\frac{\mathbf{H}}{K_f},{\stackrel{\sim }{\mathbf{S}}}_o=\mathbf{J}+i\frac{\mathbf{R}}{{\omega }_o}\end{array}$$ (20)

and the non dimensional density ρ₀ is considered as a function of the porosity φ, the mass density of the solid tissue matrix, ρ_m, and the mass density of the fluid, ρ_f,

$${\rho }_o=\frac{\rho }{{\rho }_f}=\frac{(1-\phi ){\rho }_m+\phi {\rho }_f}{{\rho }_f}=\frac{{\rho }_m}{{\rho }_f}+\phi \left(1-\frac{{\rho }_m}{{\rho }_f}\right).$$ (21)

Equation (19) represent an eigenvalue problem, the non-dimensional complex quantity z̃_o representing the eigenvalues and the vectors a and b representing the eigenvectors. Since the right hand side of this linear system of equations is a zero 6D vector, it follows from Cramer’s rule that, in order to avoid the trivial solution, it is necessary to set the determinant of the 6 by 6 matrix equal to zero, thus

$$\left|\left[\begin{array}{cc}{\mathbf{Q}}_o& {\mathbf{C}}_o\\ {\mathbf{C}}_o^T& {\mathbf{H}}_o\end{array}\right]-{\stackrel{\sim }{z}}_o\left[\begin{array}{cc}{\rho }_o·\mathbf{1}& \mathbf{1}\\ \mathbf{1}& {\stackrel{\sim }{\mathbf{S}}}_o\end{array}\right]\right|=0.$$ (22)

The characteristic equation of system (22) is represented by a sixth order polynomial in z̃, given by

$$h_6{{\stackrel{\sim }{z}}_o}^6+h_5{{\stackrel{\sim }{z}}_o}^5+h_4{{\stackrel{\sim }{z}}_o}^4+h_3{{\stackrel{\sim }{z}}_o}^3+h_2{{\stackrel{\sim }{z}}_o}^2+h_1{\stackrel{\sim }{z}}_o+h_0=0,$$ (23)

from which six complex valued eigenvalues, z̃_om, (m = 1,…, 6) are obtained, and their square root,

$$\sqrt{{\stackrel{\sim }{z}}_{om}}=\frac{{\omega }_o}{{\stackrel{\sim }{k}}_{om}}={\stackrel{\sim }{v}}_{om},$$ (24)

is used to obtain the values of the phase velocity and attenuation for each wave mode in a fluid saturated porous medium. The complex wave vector is decomposed as below

$${\stackrel{\sim }{k}}_o=\frac{{\omega }_o}{{\stackrel{\sim }{v}}_o}=\frac{{\omega }_o(Re{\stackrel{\sim }{v}}_o)}{{(Re{\stackrel{\sim }{v}}_o)}^2+{(Im{\stackrel{\sim }{v}}_o)}^2}-i\frac{{\omega }_o(Im{\stackrel{\sim }{v}}_o)}{{(Re{\stackrel{\sim }{v}}_o)}^2+{(Im{\stackrel{\sim }{v}}_o)}^2}$$ (25)

from which the real valued phase velocity is obtained

$$v_o=\frac{{\omega }_o}{Re\stackrel{\sim }{k}}=\frac{{(Re{\stackrel{\sim }{v}}_o)}^2+{(Im{\stackrel{\sim }{v}}_o)}^2}{Re{\stackrel{\sim }{v}}_o},$$ (26)

as well as the attenuation

$$\alpha =-\frac{{\omega }_o(Im{\stackrel{\sim }{v}}_o)}{{(Re{\stackrel{\sim }{v}}_o)}^2+{(Im{\stackrel{\sim }{v}}_o)}^2}.$$ (27)

For each value of z̃_om substituted back into (8), two 3D polarization vectors, a and b, are determined subject to the condition that they are both unit vectors. For an isotropic medium, the complex wave vector k̃ becomes a scalar quantity (i.e. wave number) and the phase velocity v₀ is constant for any direction n of wave propagation. If the porous medium is anisotropic, the direction of phase propagation is described by the complex wave vector k̃ (Equation 5) and the associated phase velocity vector v₀ varies with the direction of wave propagation n.

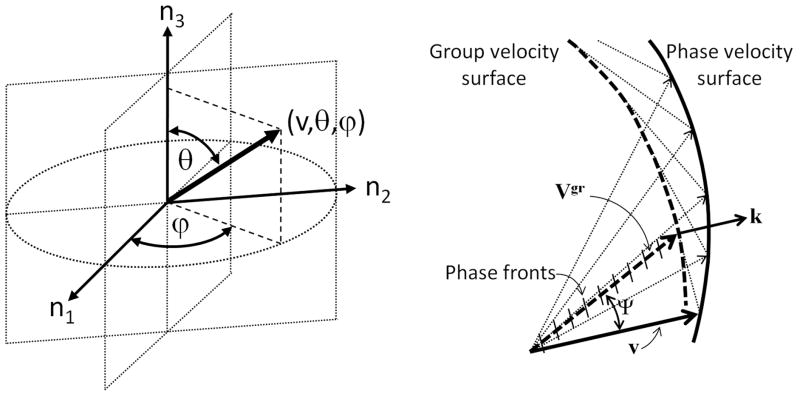
In a general direction n there will be six roots of which four are non-trivial wave speeds, two shear waves and two longitudinal modes, representing Biot’s fast and slow waves. Only waves propagating along the axes of symmetry are considered as pure wave modes (P1, P2, S1 and S2), while waves propagating off axes of symmetry are composed of mixed modes and called quasi-waves (qP1, qP2, qS1 and qS2). The two zero roots obtained from the poroelastic Christoffel equation indicate that the two possible “slow shear waves” have zero velocity. In other words, transverse wave modes in which the polarization of the solid and fluid displacements, a and b, are out of phase with each other, and orthogonal to the direction of wave propagation, n, have zero velocity of propagation. Using a spherical coordinate system, the phase velocity vector v₀ (v₀, θ, ϕ) along the direction n = (sinθ cosϕ, sinθ sinϕ, cosθ) is expressed in terms of its magnitude (radial distance from a fixed origin, v₀), its inclination angle (θ) measured from a fixed zenith direction (n₃), and the azimuth angle (ϕ) of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction (n₁) on that plane (Figure 1a).

Figure 1.

Spherical coordinate system, where the radial distance from a fixed origin, is the magnitude of v, θ is the inclination angle measured from a fixed zenith direction (n₃), and ϕ is the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction (n₁) on that plane (a). Phase (v) and group (V^gr) wave velocities of quasi-waves propagating in a dispersive anisotropic medium, exhibiting different magnitude and direction Ψ (b).

In anisotropic media, waves traveling off axes of symmetry propagate with a group velocity, slightly different from their phase velocity (Cardoso and Cowin, 2011). The group velocity V^gr propagates along a ray at an angle (θ^gr,ϕ^gr) to the phase propagation direction (θ_m,ϕ_m) for each mode of wave propagation (qP1, qP2, qS1, qS2). Different phase and group velocities may exist for each of the qP1, qP2, qS1 and qS2 wave modes. In isotropic, non-dispersive media, the phase and group velocities are the same. However, phase and group velocities may be different due to dispersion, or anisotropy or both. The group velocity is given by

$${\mathbf{V}}^{gr}=\frac{\partial \omega }{\partial \mathit{\kappa }}.$$ (28)

The wave vector magnitude is proportional to the ratio of the frequency and the wave phase velocity, and its direction is perpendicular to the wavefront. If the difference between the phase and group velocities depends only on the magnitude of k, the difference V^gr − v is caused by dispersion. In a dispersive medium, the phase and group velocities have the same direction but different magnitudes. If the difference between phase and group velocities depends only on the direction of κ, the difference V^gr − v is caused by anisotropy (Figure 1b), and the group velocity can be computed in cylindrical coordinates as

$${\mathbf{V}}^{gr}=\mathbf{\nabla }\mathbf{v}(v,\theta ,\varphi )=\frac{\partial \mathbf{v}}{\partial v}\widehat{\mathbf{v}}+\frac{1}{v}\frac{\partial \mathbf{v}}{\partial \theta }\widehat{\mathit{\theta }}+\frac{1}{vsin\theta }\frac{\partial \mathbf{v}}{\partial \varphi }\widehat{\varphi },$$ (29)

where the two angular components of the group velocity in (29) can be obtained by differentiation of the dispersion equation (8):

$${\mathbf{V}}_{\theta }^{gr}(\text{v},\theta ,\varphi )=\frac{\partial \mathbf{v}(\text{v},\theta ,\varphi )}{\partial \theta },{\mathbf{V}}_{\varphi }^{gr}(\text{v},\theta ,\varphi )=\frac{\partial \mathbf{v}(\text{v},\theta ,\varphi )}{\partial \varphi },$$ (30)

The magnitude and direction of phase and group velocities are both different in dispersive anisotropic media. In the case of anisotropy, the phase velocity is the projection of the velocity of energy transport in the direction of the wave normal (Figure 1b). The phase and group velocities are thus characterized by the phase direction (θ,ϕ) and ray direction (θ^gr,ϕ^gr) respectively. The difference between phase and ray directions is shown in Figure 1b by the angle Ψ. Anisotropy and dispersion may co-exist in biological tissues.

Alternate approaches to the solution of the poroelastic wave equation has been undertaken by Carcione (2001) and Sharma (2005, 2008, 2010). These authors solved the poroelastic wave equation for anisotropic media based on either the balance of elastic, kinetic, and dissipative energy, or based on the field equations of motion as presented in Cowin and Cardoso (2011). The approach by Sharma is restricted to the four nonzero roots of the poroelastic equation, while the approaches by Carcione as well as Cowin and Cardoso lead to four nonzero and two zero roots. This last approach by Cowin and Cardoso is the first to include a tensorial descriptor of the pore medium architecture, the fabric, and does not require a priori knowledge of the anisotropic drained elastic constants of the porous medium. The drained elastic constants are a function of the fabric, tissue matrix material properties and the volume fraction.

5. Results

5.1 Poroelastic wave propagation in biological tissues

The anisotropic poroelastic model of wave propagation is now applied to the case of several soft and hard (calcified) biological tissues. The soft tissues considered are blood vessels, brain, breast, cartilage, eye lens, eye aqueous humor, adipose, heart, kidney, liver, skeletal muscle, skin, spleen, tendon, testis, tongue and uterus. Among the hard tissues included are cortical bone, cancellous bone, tooth’s dentin and enamel. In order to calculate the wave propagation in such tissues, the theoretical model requires the material properties of tissues’ constituents, such as the elastic modulus and density of the tissue matrix, as well as the bulk modulus and density of the fluid. Soft tissues are mainly made of water, collagen, other proteins and fat. Therefore, water and fat will be considered part of the fluid phase, while proteins and collagen will be part of the anisotropic solid tissue matrix. The bulk modulus of the fluid constituent (Berryman, 1997) was calculated as

$$\frac{\phi }{K_f}=\frac{{\phi }_L}{K_L}+\frac{{\phi }_W}{K_W},$$ (31)

using measurements of the volume fraction of lipid and water (φ_L and φ_W) for each kind of soft tissue (Table 1) and the bulk modulus of lipid and water (K_L and K_W) reported in Table 2. The fluid volume fraction, or porosity φ, is given by

TABLE 1.

Volume fraction of main constituents of biological tissues from Goss et al., 1980a, Cowin and Cardoso 2011 and Turner at al., (1999).

Tissue	% total protein	% collagen	% lipid	% water
Blood vessel	24(23–27)	5.7(5–6.5)	1.8(1.5–1.9)	70
Brain	10(8–12)	0.16(0.05–0.28)	11(9–17)	77.4(76–78)
Breast	20		3	50–75
Cartilage	21(18–24)	15.5(14–17)	1.3	72(55–85)
Eye, lens Eye, aqueous	35.5 0.013(0.011–0.016)	0.01–0.05	1.7–2.3	68 99
Adipose Fat	5	-	80	15(10.0–21)
Heart	16.5(14–19)	1.7(1.4–2.0)	2.6(2.7–17)	72(63–83)
Kidney	17(14.7–19.3)	0.865(0.43–1.3)	5(1.8–7.2)	76(71–81)
Liver	18(16–22)	0.4(0.1–0.7)	6.9(1.1–11.5)	71(63.6–73.9)
Muscle	17.2(13–20)	0.6(0.4–0.8)	2.2(2.2–9.4)	79(68.9–80.3)
Skin	33(32–34)	30	0.3–19	62(53.7–72.5)
Spleen	19.5(18.8–20.2)	0.6	1.6(0.85–3)	77(72–79)
Tendon	37.5(35–40)	32	1	63
Testis	12		3	81
Tongue	16–18		15–24	60–72
Uterus	20	17	1.4(0.9–2.2)	79
Bone, cortical	1–3% of tissue matrix	30% Col & 65–70% mineral	-	(5–15)
Bone, trabecular	1–3% of tissue matrix	30% Col & 65–70% mineral	-	(60–95)
Tooth, dentin	2.5% of tissue matrix	25.5% Col & 48% mineral	-	24
Tooth, enamel	0.1% of tissue matrix	1% Col & 95% mineral	-	4

TABLE 2.

Physiological values of main constituents of biological tissues summarized from Fratzl (2008), Silver et al., (2000; 2001a,b,c; 2002a,b; 2003), Noda (1972), Cowin, (1986; 1999); Cowin and Mehrabadi (1997); Cowin and Cardoso (2011), and Turner at al., (1999).

Parameter	Symbol	Value	Units
Bulk modulus of lipid	KL	0.5	GPa
Bulk modulus of water	KW	2.25	GPa
Mass density of water	ρf	1000	Kg/m3
Viscosity of water	ν	1×10−3	Pa-s
Young’s modulus of collagen	EC	5.95 (4.2–7.69)	GPa
Young’s modulus of other proteins	EP	4.0	GPa
Shear modulus of collagen/protein matrix	GC	2.14	GPa
Poisson ratio of collagen/protein matrix	νC	0.4
Mass density of collagen	ρC	1430	Kg/m3
Young’s modulus of bone mineralized matrix	Em	18	GPa
Shear modulus of bone mineralized matrix	Gm	7.2	GPa
Poisson ratio of bone mineralized matrix	νm	0.25
Mass density of bone mineralized matrix	ρm	2000	Kg/m3

$$\phi ={\phi }_L+{\phi }_W$$ (32)

The elastic modulus of the solid tissue matrix, E_m, was estimated using the volume fraction of the solid constituents (φ_P and φ_C) of the soft tissue (Table 1), and the elastic properties of proteins and collagen (E_P and E_C) reported in Table 2 as

$$\frac{{\phi }_s}{E_m}=\frac{{\phi }_C}{E_C}+\frac{{\phi }_P}{E_P},$$ (33)

where the solid volume fraction is calculated as

$${\phi }_s={\phi }_C+{\phi }_P=1-\phi$$ (34)

The elastic properties estimated using equations 31 and 33 are summarized in Table 3. The bulk modulus of lipid and water, the Young’s elastic modulus of the collagen, E_C, and proteins, E_P, were obtained from Fratzl (2008), Silver et al., (2000; 2001a,b&c; 2002a&b; 2003), Noda (1972), Cowin, (1986; 1999); Cowin and Mehrabadi (1997); Cowin and Cardoso (2011), Turner at al., (1999) and are summarized in Table 2.

TABLE 3.

Mass density and speed of sound of biological tissues were obtained from the literature (Goldman & Richards 1954; Goldman & Hueter 1956; Chivers & Parry 1978; Goss et al., 1978; 1980a,b; Goss & Dunn, 1980; Hoffmeister et al., 1995; Mast 2000; Haïat et al., 2006). The fluid bulk modulus K_f and tissue matrix modulus E_m were computed using equations 31 and 33 respectively, and corresponding data from Table 1 and 2.

Tissue	Mass density (Kg/m3)	Speed of Sound (m/s)	Fluid Bulk Modulus Kf (GPa)	Tissue Matrix Modulus Em (GPa)
Blood vessel		1500–1532	2.069	6.15
Brain	1040	1540–1580	1.541	6.90
Breast	1020	1490–1530	1.846	7.00
Cartilage		1565–1770	2.100	5.31
Eye, lens Eye, aqueous	1070 1010	1635–1655 1597–1518	2.045 2.250	7.00 4.44
Fat	0950	1468–1488	0.570	7.00
Heart	1060	1526–1623	1.727	6.49
Kidney	1050	1530–1590	1.854	6.72
Liver	1060	1555–1635	1.644	6.89
Muscle	1050	1517–1600	1.980	6.83
Skin	1090	1595–1635	2.028	6.59
Spleen	1054	1537–1597	2.069	6.85
Tendon	1130	1654–1852	2.133	4.20
Testis	1044	1556–1535	2.010	7.00
Tongue		1500–1600	1.235	7.00
Uterus		1589–1669	2.071	4.19
Bone, Cortical	1800–2200	3200–4000	0.225	18.00
Trabecular	400–1600	1500–2400	1.22–2.20	1.00–15.00
Tooth, dentin	2000–2200	3800–4200	0.20	19.00–25.00
Tooth, enamel	2840–3000	5000–5900	0.02	16.00–23.00

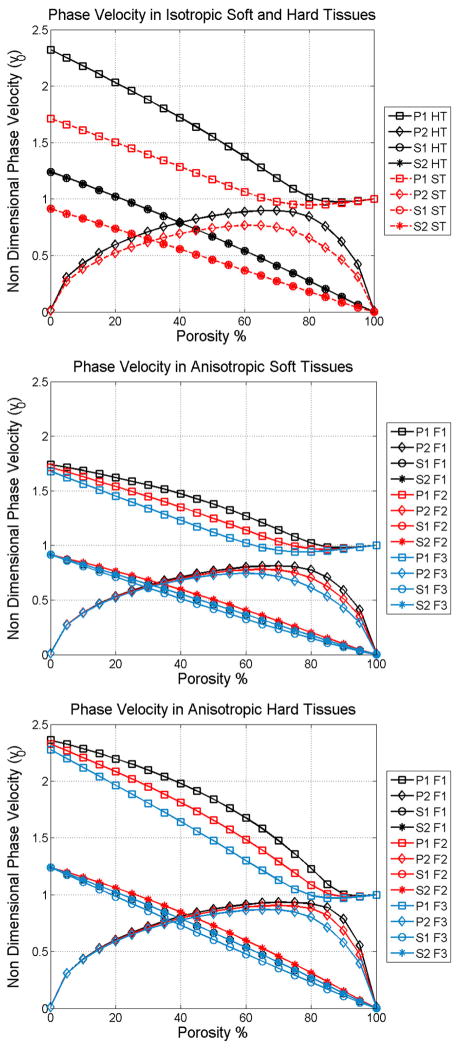
5.2 Phase velocity

The phase velocity of the two longitudinal modes of wave propagation in isotropic soft and hard tissues (Figure 2a), and along the axes of symmetry anisotropic on soft tissues (Figure 2b), as well as anisotropic hard tissues (Figure 2c) are shown as functions of the porosity in Figure 2. The fast wave velocity (squares) depicted in Figure 2 linearly decrease as the porosity increases at low porosities; conversely, the slow wave velocity (diamonds) increase with the porosity within the same range of porosity. However, this monotonic behavior changes drastically for porosities higher than about 80% in hard tissues, and 60% in soft tissues. The fast wave velocity becomes almost constant, reaching a value close to the velocity of sound in the fluid, v_f. At the same high porosity level, the slow wave velocity shows a clear inflexion, becoming inversely related to the porosity.

Figure 2.

Phase velocity as a function of porosity of the four wave modes in isotropic bone medium (a), along the axes of symmetry in anisotropic soft tissues (b), and in anisotropic hard tissues (c).

Figure 2b and 2c are presented to illustrate the much greater variability possible with an orthotropic matrix material compared to the isotropic material illustrated in Figure 2a. In Figure 2b the two longitudinal wave modes are shown propagating along all three axes of symmetry of an orthotropic hard tissue sample. Anisotropy is characterized by three distinct principal values of fabric, F₁, F₂ and F₃. The direction F₁ represents the direction parallel to the collagen fibers, matrix fibrils or bone trabeculae. The directions F₂ and F₃ are perpendicular to the fibers, and in the case of trabecular bone, F₂ • F₃. In Figure 2b note the variability of the fast wave for porosities lower than about 60% porosity for the three different directions, as well as in the variability of the slow wave at porosities higher than 60%, for the three directions. In contrast, the slow wave velocity below 60% porosity and fast wave velocity above 60%, are practically insensitive to the anisotropy of the collagen/matrix structure. A similar effect of the anisotropic mineralized matrix is observed for hard tissues but at a higher porosity value, of 75% approximately.

These theoretical results indicate that changes in both porosity and anisotropy are mainly shown in the fast wave velocity at low and mild porosities, while these changes are observed in the slow wave velocity mainly at high porosities. In contrast, the slow wave at low and mild porosities is slightly sensitive to changes in porosity and practically insensitive to bone anisotropy; and the fast wave at high porosities is independent of both porosity and anisotropy. All together, these findings indicate the existence of a wave mode transition between the longitudinal wave mode (fast or slow) that is most sensitive to changes in porosity and anisotropy. The wave mode transition occurs at the porosity level at which the drained elastic constant values of the solid fraction are equal to the bulk modulus of the fluid fraction. This wave mode transition occurs at a different value of porosity for soft and hard tissues, since the drained elastic constants are different in soft and hard tissues.

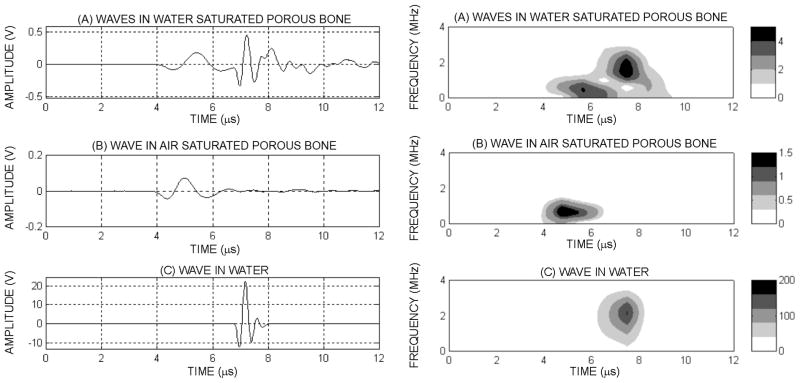
To further study the role of the structural anisotropy (fabric) of biological tissues, Figure 3 is analyzed. Figure 3 shows a typical set of signals obtained in a single direction of a human cancellous sample: (i) a well defined, single ultrasound wave excited the sample (Figure 3a), (ii) the signal received after propagating through the fluid-saturated cancellous bone sample (Figure 3b), (iii) the signal received through the sample when the water medium was removed (Figure 3c) and (iv) the signal received when the cancellous bone sample was removed, thus representing the propagation through the fluid alone (Figure 3d). From these figures, it is clear that propagation through the cancellous bone structure dramatically alters the waveform, which after propagation is made of at least two distinguishable waves. When removing the water from the sample (Figure 3c), only the very first part of the signal remains. On the contrary, when removing the sample while leaving the transducers in place, this first signal disappears and the remaining signal is very similar to the second part of the transmitted signal of Figure 3b. From these results, one may conclude that the two waves observed with fluid saturated cancellous bone correspond in general to: (i) a first propagation mode related to the presence of a solid phase within the biphasic material and (ii) a second wave highly related to the effect of the fluid phase.

Figure 3.

Ultrasound wave after propagation through a fluid saturated human cancellous bone sample (a) signal propagated through the same human sample after the water was removed from the pores (b), and detected pulse after propagating in water on a distance identical to the sample’s size (c). Corresponding spectrograms of a human signal showing the two waves having different frequency compounds and time localization (d), when the fluid is removed from the pores (e) and when the porous sample is removed and the wave propagates in the fluid only (f). The color bar indicates the respective power spectra density value (Vrms²)

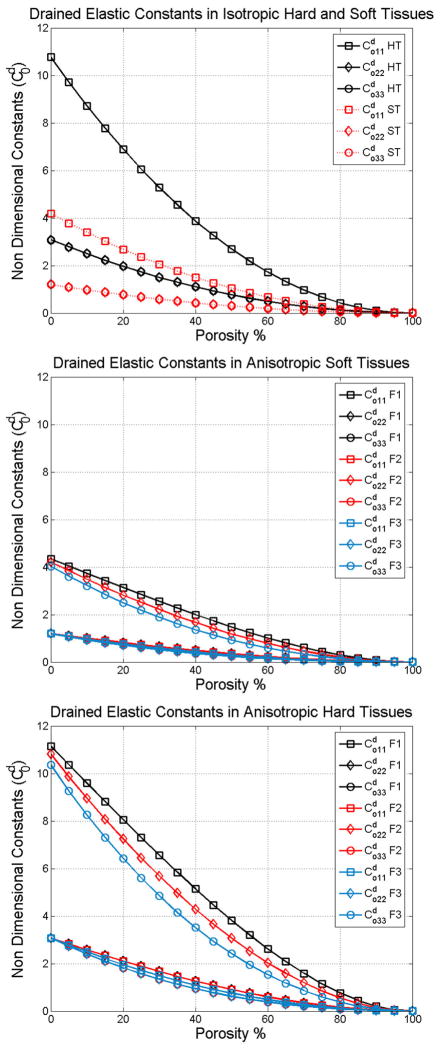
This observation is also verified by analyzing the drained elastic constants of the porous medium as a function of the fabric. Figure 4 shows the $C_{o11}^d,C_{o22}^d$, and $C_{o33}^d$ drained elastic constants for isotropic soft and hard tissues (Figure 4a), anisotropic soft tissues (Figure 4b) and anisotropic hard tissues (Figure 4c). Here, it can be observed that the value of $C_{o11}^d$ is equal to that of K_f at 50% porosity in soft tissues and 70% porosity in hard tissues. The transition in the ratio between $C_{o11}^d$ and K_f occurs at the same porosity as the change from solid wave to fluid wave observed in Figure 2.

Figure 4.

Non dimensional drained elastic constants as a function of porosity in isotropic tissues (a), along the axes of symmetry in anisotropic soft tissues (b) and in anisotropic hard tissues (c).

5.3 Comparison of the theory with reported measurements

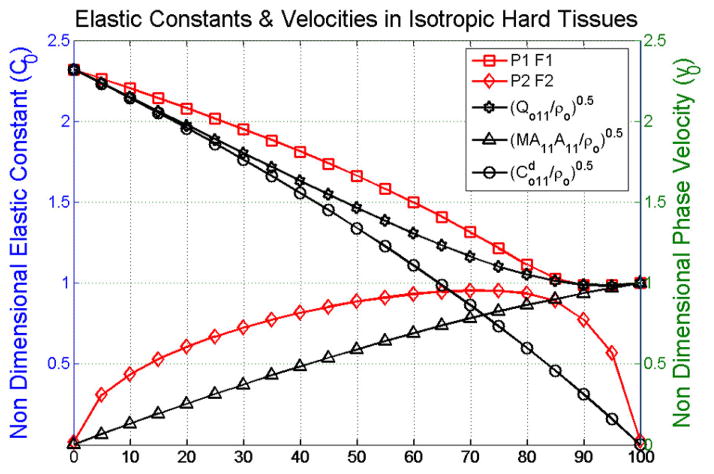
Figure 5 shows the behavior of the non-dimensional fast and slow waves (P1 & P2) as a function of porosity in isotropic hard tissues along the direction n = (1,0,0)^T, which are compared to the curves of non dimensional elastic-density ratios, $R_o^Q,R_o^{Cd}$, and $R_o^{\mathit{MAA}}$, involving the acoustic tensor Q_o11, the drained elastic constants $C_{o11}^d$ and the difference between them, MA₁₁A₁₁, namely the product of the constant M times the open product of the Biot’s effective stress tensor with itself,

Figure 5.

Comparison of non dimensional fast and slow wave velocities versus non dimensional acoustic modulus associated to the Biot elasticity tensor $R_o^Q$, to the drained elastic constants $R_o^{Cd}$ and to the fluid constituent $R_o^{\mathit{MAA}}$. It can be observed how the Biot elasticity tensor follows a trend similar to the drained elastic constants, and changes in behavior around 70% porosity to become similar to the fluid modulus $R_o^{\mathit{MAA}}$. The Biot elasticity tensor has a very similar behavior to the fast wave over the whole range of porosity.

$$R_o^Q=\sqrt{\frac{Q_{o11}}{{\rho }_o}},R_o^{\mathit{MAA}}=\sqrt{\frac{{MA}_{11}{A}_{11}}{{\rho }_o}},\text{and}{R}_o^{Cd}=\sqrt{\frac{C_{o11}^d}{{\rho }_o}}$$ (22)

Figure 5 illustrates how $R_o^{Cd}$ decreases linearly from a value of 2.3 to zero (circles), while the ratio $R_o^{\mathit{MAA}}$ increases linearly with the porosity from 0 to 1 (triangles). The former illustrates the behavior of the drained elastic constants as a function of the porosity, which depends on the properties of the solid phase, the anisotropic tissue matrix. The later $R_o^{\mathit{MAA}}$ ratio is related to the fluid fraction in the porous medium, and is equal to the fluid properties at 100% porosity. The $R_o^Q$ ratio (pentagrams) is in fact the combination of the $R_o^{\mathit{MAA}}$ and $R_o^{Cd}$ ratios since it follows the behavior of the drained elastic constants ratio $R_o^{Cd}$ from 0 to ~70% porosity, and then changing to the behavior of the $R_o^{\mathit{MAA}}$ ratio from 70% to 100% porosity. Therefore, $R_o^Q$ changes in behavior from solid-like to fluid-like as a function of the porosity. Importantly, when these non dimensional ratios are compared to the non dimensional fast and slow wave velocities, it shows how the fast wave exhibits a behavior similar to the drained elastic constants at low porosity, but it changes in behavior around 70% porosity to become much more like a fluid material from 70 to 100% porosity.

Speed of sound of blood vessels, brain, breast, cartilage, eye lens, eye aqueous humor, adipose, heart, kidney, liver, skeletal muscle, skin, spleen, tendon, testis, tongue and uterus are compared with the predictions of the proposed poroelastic model of wave propagation. Such values of speed of sound were obtained from the literature (Goldman & Richards 1954; Goldman & Hueter 1956; Chivers & Parry 1978; Goss et al., 1978; 1980a,b; Goss & Dunn, 1980; Hoffmeister et al., 1995; Mast 2000; Haïat et al., 2006) and summarized in Table 3. Ultrasound wave velocities reported in Table 3 are shown as different regions for enamel, cortical bone, dentine, cancellous bone and soft tissues (Figure 6a). The soft and hard tissues regions overlap slightly at high porosities. Importantly, the speed of sound of either soft or hard tissues at high porosity is very similar to the speed of sound in water, due to the high fluid content in soft tissues and cancellous bone at high porosity. Therefore, at high porosities (i.e. 90% porosity), the fast wave velocity is practically indicative of the fluid phase of biological tissues, as opposed to the tissue matrix. Figure 6b shows a magnified view of the region corresponding to the soft tissues, in which each of them is located based on their porosity and speed of sound. Reported values of speed of sound fall between the theoretical predictions by the model for most of them, except for brain and testis.

Figure 6.

Mapping of different types of soft and hard tissues within the plot of anisotropic fast wave velocity in anisotropic tissues (a), and comparison of experimental ultrasound wave velocities against theoretical model predictions (b). Good qualitative agreement between theory and reported wave velocities was observed.

The predictions of the fast and slow wave velocities using this theoretical model are now compared with experimental measurements in trabecular bone previously reported (Cardoso et al., 2003). Briefly, fourteen bovine and sixty human trabecular bone samples were retrieved from bovine femoral heads, human femoral heads and femoral and tibial condyles. Samples of approximately 1×1×1 cm in size were prepared, followed by removal of fat and marrow, and saturated with water under vacuum for 30 minutes. Group velocities of quasi-wave modes were measured in immersion with distillated water at room temperature, using two broadband ultrasound transducers (Panametrics V323-SU) at a central frequency of 2.25 MHz (0.25 in diameter). The emitter was excited by a damped single pulse generated by an ultrasonic source (Panametrics 5052 UA) operated in a transmission mode. The signal was amplified in 40 dB, digitized by a 100 MHz Digital Oscilloscope (Tektronic model 2430), and analyzed in MatLab. Importantly, bone cubes were cut without aligning their orthogonal faces with the planes of symmetry of the sample. Since bone samples were interrogated along the normal direction to each face of the sample (e.g. arbitrary directions labeled as A, B and C), which do not coincide with the normals to the planes of symmetry of the sample, it was considered that propagated signals correspond to quasi-wave modes for each of the three interrogated directions. It was shown in that study that the wavelengths of the fast and slow waves are significantly different and that this property can be used to separate the two waves using digital filtering. Therefore, acquired signals were filtered out using bandpass filters with a frequency bandwidth of 0.5±0.25 MHz for the fast wave and a frequency bandwidth of 1.6±0.6 MHz for the slow wave. The fabric tensor describing the microarchitecture of each sample was measured using the Mean Intercept Length (MIL) approach as described in Whitehouse (1974a&b), Harrigan and Mann (1984) and Turner et al (1987, 1990). The phase angles θ, ϕ were determined as the relative orientation of the principal axes of fabric in respect to the measurement directions A, B and C of the cube samples.

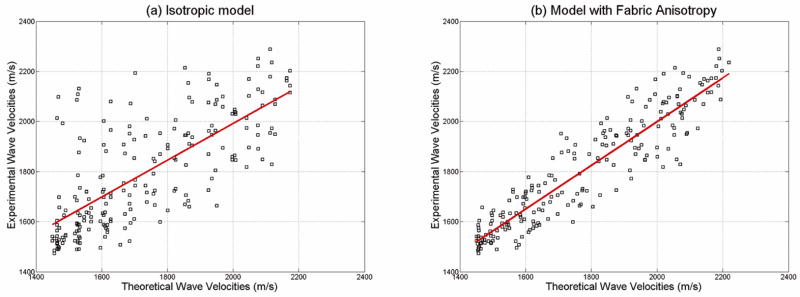
In order to investigate the effect of fabric on the fast and slow wave velocity measurements, two cases were analyzed by comparing experimental values with theoretical predictions. First, the theoretical phase velocities for qP1 and qP2 were computed using the experimental values of porosity, tissue density, and without taking into account the fabric anisotropy, but considering the fabric as isotropic (F₁ = F₂ = F₃ = •). Then, the ray direction and group velocity were calculated for each quasi-longitudinal mode. Figure 7a shows a comparison between the group velocities predicted from the model (under the assumption of isotropy) and the experimental wave velocity measurements obtained on three orthogonal directions on each sample. In the second case, the theoretical phase velocities for qP1 and qP2 were computed as in the previous case, but this time using the images-derived fabric anisotropy values for each sample. Again, the ray direction and group velocity were calculated for each quasi-longitudinal mode. Figure 7b shows the comparison between experimental group wave velocities, for all three directions A, B and C and predicted wave velocity values when the fabric was taken into account. The correlation coefficient between experimental and theoretical predictions when the fabric anisotropy is not taken into account was R² = 0.53, and R² = 0.86 when the fabric anisotropy was included in the theoretical model. This analysis indicates a much higher quantitative agreement between experimental and theoretical values of group quasi-wave velocity when the fabric anisotropy is included in the model.

Figure 7.

Comparison of experimental ultrasound wave velocities against theoretical model predictions when considering (a) isotropic fabric and (b) anisotropic fabric measurements. The predictability of experimental values by the poroelastic theory is much increased when the fabric anisotropy is taken into account (color online).

6. Discussion

A theoretical framework for analysis of anisotropic poroelastic wave propagation in a porous medium was recently developed by introducing the dependence of the wave motion equations upon fabric, a tensorial descriptor of the porous microarchitecture (Cowin and Cardoso, 2011). Solution of the constitutive equations for harmonic displacements of the solid and fluid constituents leads to a modified Christoffel equation for anisotropic porous media that includes the acoustic tensor Q, the solid-fluid interaction tensor C, and the permeability tensor K(ω). These tensors describe the elastic and viscous effects in the wave equation, and they all depend on the measurable fabric tensor, F. The modified Christoffel equation represents an eigenvalue problem with a sixth order characteristic equation and four non-zero roots. When the porosity φ is equal to zero, the model is reduced to that of a linear elastic solid and the Christoffel equation is obtained. When the porosity φ is equal to one, the model is reduced to the wave equation in a fluid. Also, this system reduces to the isotropic formulation developed by Biot when the fabric tensor is isotropic. Two eigenvalues represent the longitudinal wave modes P1 and P2 and the other two correspond to the shear wave modes S1 and S2. Such eigenvalues are complex valued, and describe the phase velocity and attenuation due to absorption of the four wave modes. Then, the poroelasticity theory was also extended to the case of an arbitrary phase direction (θ, ϕ) of wave propagation (Cardoso and Cowin, 2011). The advantage of that development is the ability to distinguish the role of fabric anisotropy in the predictions of phase and group velocities of the four wave modes propagating in porous media at any phase or ray direction.

In those two previous studies, the poroelasticity theory was only applied to the case of wave propagation in trabecular bone. That analysis was here extended here to many other anisotropic soft and hard tissues. Elastic constant and density values for the tissue matrix constituents and water were used in the poroelastic model to study the wave propagation in both soft and hard tissues. Only two independent variables (φ and F), one scalar and the other tensorial respectively, were used in the model to study the influence of material properties on both global and directional changes in the velocity and attenuation of the four wave modes generated in porous media. The collagen fibers in soft tissues and the mineralized matrix in hard tissues are responsible for the anisotropy of the solid tissue constituent through the fabric tensor in the model. The reported measurements in the literature were found to fall between the predicted values of fast wave velocity by the model.

Poroelasticity theory predicts the genesis of two longitudinal waves, however, the second wave, known as “slow wave”, has only been reported in hard tissues such as cancellous bone. We may speculate on two possible reasons why this has not been reported in soft tissues: first, because the predicted velocity of both waves (fast and slow) in soft tissues is very similar, which may result in superposition of both waves in the time domain, and second, because the attenuation of this slow wave may be too high to be actually measured. Interestingly, our numerical analysis suggests that both fast and slow waves may be generated in soft tissues, for instance, in tendons, which exhibit large acoustic anisotropy above the speed of sound in water. Careful experimentation is required to determine whether both fast and slow wave modes can be generated or not in soft tissues.

In hard tissues, the theoretical model predicted the high variability of fast and slow wave velocities observed in bovine and human bone in our experimental study. The development of the fabric-dependent anisotropic theory of propagation of quasi-waves in porous media (Cardoso and Cowin, 2011) was able to predict the high variability of fast and slow wave velocities observed in bovine and human bone in our experimental study. Figure 7 indicates that the fabric tensor measurement alone is able to drastically increase the model predictability on wave velocities from 53% to 86%. In other words, directional variability within a sample was effectively explained by the theoretical model after inclusion of the fabric; this directional variability could not be explained by the porosity only. The agreement between experimental and theoretical values indicates that despite the complexity added to the poroelastic theory, a tensorial variable describing the bone microstructure is required to explain the directional variability of the wave propagation with bone architecture. Therefore, the fabric tensor –a measure of bone microarchitecture– exhibited a role as important as the mass density in determining the acoustic properties of anisotropic porous bone samples.

Overall, the results from the present study demonstrate the ability of the proposed model to describe the acoustic behavior of the fast and slow wave velocities in both soft and hard tissues. The phase velocity depends on the architecture (porosity and fabric) and the composition of the medium (solid and fluid mass density, solid matrix elastic modulus, fluid bulk modulus and fluid viscosity). For given frequency and material parameter values, the behaviors of the fast and slow waves are governed by the extrinsic properties of the media: the porosity and fabric anisotropy. These theoretical predictions also corroborate our experimental observations that indicate that at high porosities the fast wave is mostly related to the propagation in the fluid constituent and the slow wave is highly related to the solid matrix structure.