Corneal topography from spectral optical coherence tomography (sOCT)

Abstract

We present a method to obtain accurate corneal topography from a spectral optical coherence tomography (sOCT) system. The method includes calibration of the device, compensation of the fan (or field) distortion introduced by the scanning architecture, and image processing analysis for volumetric data extraction, segmentation and fitting. We present examples of three-dimensional (3-D) surface topography measurements on spherical and aspheric lenses, as well as on 10 human corneas in vivo. Results of sOCT surface topography (with and without fan-distortion correction) were compared with non-contact profilometry (taken as reference) on a spherical lens, and with non-contact profilometry and state-of-the art commercial corneal topography instruments on aspheric lenses and on subjects. Corneal elevation maps from all instruments were fitted by quadric surfaces (as well as by tenth-order Zernike polynomials) using custom routines. We found that the discrepancy in the estimated radius of curvature from nominal values in artificial corneas decreased from 4.6% (without fan distortion correction) to 1.6% (after fan distortion correction), and the difference in the asphericity decreased from 130% to 5%. In human corneas, the estimated corneal radius of curvature was not statistically significantly different across instruments. However, a Bland-Altman analysis showed consistent differences in the estimated asphericity and corneal shape between sOCT topographies without fan distortion correction and the rest of the measurements.

1. Introduction

Optical coherence tomography (OCT) has become a widespread tool in various fields of medicine [1,2] particularly in ophthalmology, where its high resolution and non-invasiveness has allowed multiple applications in the retina and anterior segment of the eye [3–9]. However, the amount of quantitative information provided by anterior segment OCT is typically limited to axial distances between consecutive layers i.e. corneal thickness [10,11], anterior chamber depth [12,13] or anterior chamber angle [14], within the accuracy provided by axial resolution and exact knowledge of the refractive index of the tissue. Although the use of OCT as a pachymeter [15,16] and for optical biometry [17,18] is widespread, its capability to produce surface elevation maps, and therefore to be used as a corneal topographer, has only been limitedly exploited. Although several studies address the use of OCT to estimate corneal power [19,20], only a few recent papers explore the accuracy and perform validations of corneal topography and keratometry from OCT 3-dimensional imaging [8,21–23]. We have recently reported accurate surface topography in vitro using time-domain OCT [24], and the correction of optical distortion in anterior segment sOCT for quantitative 3-D imaging of the internal structures of the eye [25], and have demonstrated a method that takes advantage of the optical distortion in isolated crystalline lens sOCT images to reconstruct the 3-D gradient index profile of the lens [26,27]. Research efforts, however, do not seem to have been fully paralleled in commercial anterior segment OCT systems. For example, the latest release of a widespread commercially available anterior segment OCT (Visante Omni, by Carl Zeiss) has included a Placido ring topography for quantitative anterior corneal surface topography, rather than estimating corneal elevation from the OCT data.

One of the limitations of the most typical configuration of OCT systems is the presence of so-called fan (or field) distortion. The presence of this distortion in OCT was first reported by Westphal et al. [28] for non telecentric scanner. In general, the effect is related to the scanning architecture of most 3-D OCT systems [24,28–30], so that when imaging perfectly flat surfaces they appear curved. This phenomenon can be described as a combination of at least two possible effects: a) the architecture of the scanning system, which is primarily affected by the spatial separation of the mirrors, and b) design, position and alignment of the collimating lens in relation to the mirrors of the scanner. Therefore such images are not well represented in a Cartesian system of coordinates (x, y, z), but rather in (x_oct, y_oct, L), where L is the optical path along the ray and (x_oct, y_oct) are the angles (horizontal and vertical) of the scanner mirrors, which can be explicitly associated to the coordinates (origin and directional cosines) of rays entering the sample. This representation allows conversion from angular to spatial coordinates following relatively simple calibration.

OCT systems are designed to detect usually faint back-scattered light from tissue. However, both backscattered as well as back-reflected (from directional and specular reflections) light is detected, particularly for surfaces normal to the optical axis of the instrument, such as the corneal apex in anterior corneal imaging. The presence of back-reflected light results in saturation of the A-scan signals. Upon Fourier Transform, fully saturated A-scans appear as completely modulated white lines, whereas partially saturated A-scans give rise to replications and ghost signals. These effects produce additional distorting factors in the detected corneal surfaces from sOCT images, and may result in an artificial steepening of the estimated cornea. However, the consequences of these effects on the quantification of geometry of the surfaces have been generally miss-regarded.

Another practical limitation for quantification of in vivo sOCT is imposed by motion artifacts [31,32], which are associated to breath, pulsation [33], dynamics of the tear film [34], among others, and occur, even when forehead support or bite bars are used. In order to minimize the impact of motion artifacts, the common solution is to increase the acquisition speed [35]. A widespread solution in anterior segment OCT, also common to other imaging modalities such as Scheimpflug corneal topography, is the use of a meridional scanning configuration, instead of a denser rectangular scanning [19,20,22,25]. However, this approach assumes that the center of rotation is fixed and requires from radial interpolation, generating other sources of error. On the other hand, a dense, homogeneous sampling of the corneal elevation prevents from interpolation errors of radial or meridional sampling approaches.

In summary: (1) We provide a full experimental method for correction of fan distortion, which can be universally applied to any anterior segment OCT system. To our knowledge this is the first demonstration of the correction of fan distortion in real corneas using a system comparable to those used in clinics. (2) The study demonstrates for the first time the effect of fan distortion correction on surface asphericity (both on artificial surfaces and in vivo). (3) We report, to our knowledge, the first corneal topographic maps corrected from fan distortion in patient’s eyes, and a comparison to topographic maps obtained with state-of-the art clinical topography systems (Scheimpflug imaging and Placido-based videokeratography) in the same patients. (4) We present, to our knowledge, the first OCT topographic maps based on rectangular scanning, rather than meridional scanning. (5) Finally, we present image processing methods for reducing the effects of signal saturation in the corneal apex, as well as motion distortion reduction alternatives.

Although in this work the method is applied to the reconstruction of the anterior corneal surface, the methods also provide the ray equation data, which are necessary for the application of optical distortion correction algorithms to the internal surfaces of the eye [25]. The method can be generalized to any anterior segment OCT instrument.

2. Methods

2.1. Experimental sOCT setup

The sOCT system used in the measurements has been described in detail in previous publications [9]. The setup is based on a fiber-optics Michelson interferometer configuration with a superluminescent diode SLD (λ₀ = 840 nm, Δλ = 50 nm; Superlum, Ireland) as a light source and a spectrometer consisting of a volume diffraction grating and a 12-bit line-scan CMOS camera with 4096 pixels (Basler sprint spL4096-140k; Basler AG, Germany) as a detector. The horizontal and vertical scanning was produced by galvanometer optical scanners (Cambridge Technology Inc., USA), driven by an analog input/output card (National Instruments, USA). The distance between the centers of the scanning mirrors is 13.8 mm and the focal length of collimating lens is 75 mm. The effective acquisition speed is 25000 A-Scans/s, which optimized balance between speed and SNR. The axial range of the instrument is 7 mm in depth, resulting in a theoretical pixel resolution of 3.4 µm. The axial resolution predicted by the bandwidth of the superluminescent diode laser source is 6.9 μm.

2.2. Image processing, automatic segmentation and surface fitting

Anterior segment OCT systems are designed for imaging quasi-transparent media, as corneal and lens tissues, and therefore, their dynamic range is adapted for the very weak signals provided by the diffuse reflection of the ocular surfaces. Images of plastic surfaces, or even the cornea, typically show a “white” area corresponding to zones producing a specular or directional back-reflection. In sOCT systems saturation results in the images showing a repetitive structure along the “white” A-scans, as a result of the Fourier Transform. We implemented the following strategy to avoid the saturation, of the whole 3D scan acquisition: We reduced the amount of irradiance impinging the surface up to prevent the interference fringes (carrier) coded in the autocorrelation spectrum (envelope) from saturating the detection system. This procedure can be applied by shortening the exposure time of the CMOS camera or by lowering the radiant intensity from the autocorrelation spectrum of the reference arm to values below four times the detection range of the camera. This way, the maximum of the interference fringes placed at the maximum of the cross-correlation for the specular reflection is within the range of the camera. This allows separating the information of the specular-directional reflection area from the “white background”, as the artificial echoes introduced by the Fourier transform are reduced.

In a previous work [25] we presented a segmentation algorithm to extract the 3-D data from sOCT B-Scans. The current study incorporates important improvements for faster and more sensitive automatic segmentation of the surfaces. The algorithm can be summarized in six steps (Fig. 1 ): (1) Statistical thresholds are calculated based on a derivation of the Otsu’s [36] method. The statistical calculations are performed on individual A-Scans rather than on the B-Scans, which allows and adaptive treatment of the noise and signal levels of every A-Scan (see Fig. 1(a) and Media 1 ^{(2.1MB, AVI)} for a typical noisy raw B-scan) (2) Denoising algorithm. Morphological operators are used to evaluate and eliminate areas in the B-scan smaller than 10 pixels. (3) Detection of connected points in a neighborhood, identifying those belonging to a cluster >10 pixels in each B-scan (Fig. 1(b) and Media 2 ^{(811KB, AVI)} ) (4) Detection of connected points in a neighborhood in 3-D. (5) Identification of the boundaries of volumes, by performing a 3-D edge algorithm (extension to 3-D of Roberts algorithm in 2-D). This algorithm allows detecting the maximum intensity in each boundary region, allowing a multilayer segmentation (Fig. 1(c) and Media 3 ^{(633KB, AVI)} ). (6) Multilayer segmentation. The approach, based on boundary region identification (and not only maximum intensity), allows to automatically resolve very close layers of different reflectivity (Fig. 1(d) and Media 4 ^{(859.5KB, AVI)} ).

Fig. 1.

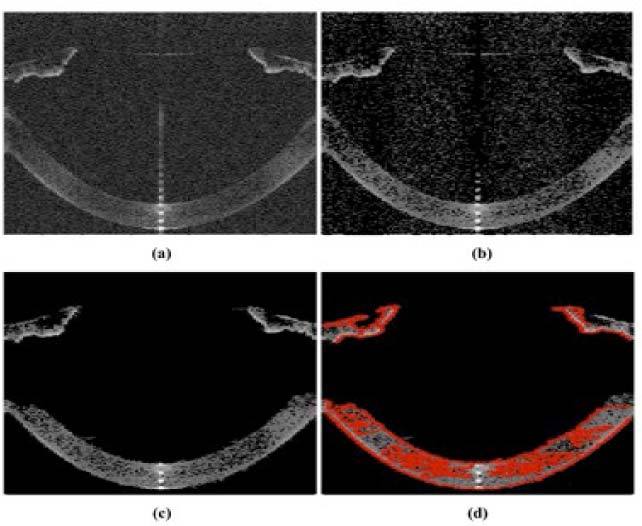
Single-frame excerpts from video recordings of the processing algorithms: a) Collection of original B-Scans, containing the data acquired from an in vivo healthy eye (Media 1 ^{(2.1MB, AVI)} ). b) Result of application of the statistical thresholding algorithm (Media 2 ^{(811KB, AVI)} ). c) Data after denoising image processing (Media 3 ^{(633KB, AVI)} ). d) Boundary detection in red (Media 4 ^{(859.5KB, AVI)} ).

3-D segmented surfaces corresponding to the layer identified as the anterior corneal surface are fitted to Zernike modal expansions (55 terms, tenth order) [37,38]. The method is implemented in an iterative procedure which allows further rejection of spurious points in the surface (Media 2 ^{(811KB, AVI)} ), by evaluating the local distance of every point with respect to the surface fitted to the Zernike modal expansion of 55 terms (tenth order). Points further than three times the standard deviation of the distances between the actual surface and the fitted surface are eliminated, and a new Zernike fitting is performed. The procedure is repeated until the fitted Zernike coefficients change less than 1% from the previous iteration. The final surfaces (Zernike fits) are also fitted by different quadrics (sphere or conicoids), using a nonlinear least mean square procedure [39–41].

We have developed a procedure that accounts for potential tilts of the surface, with two modes of operation: (1) The apex or center of the quadric is defined by the user. This mode is useful for comparison purposes across different topographers (where, for instance, the specular reflection can be used for reference in longitudinal measurements on patients following corneal treatment). In this case, tilt can be corrected using the information provided by the tilt Zernike coefficients, Z₁⁻¹ and Z₁¹. (2) The location of the apex is considered an additional variable to those defining the surface shape (radii of curvature, conic constants or eccentricity [41]). This mode is useful when the surfaces do not have a particular point that acts as a reference (i.e. in surface profilometry). The fitting process and correction of tilt is illustrated in Fig. 2 , for the first mode, considering the specular reflection as the reference Fig. 2(a), and after tilt correction and denoising through the Zernike fitting procedure described above (Fig. 2(b)). The points in blue represent the surface used for fitting, and the red points, the surface fitting to quadrics.

Fig. 2.

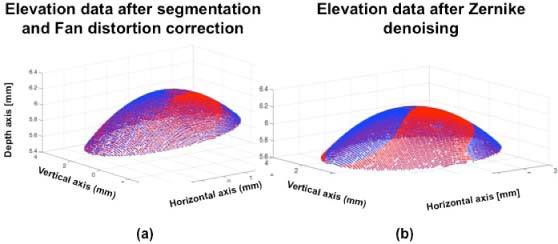
a) Elevation data (using the specular reflection as a reference) in blue and, the surface fitted to conicoid in red (note the tilt of the surface, well accounted by the fit). b) Surface fitting after tilt correction, and further denoising using Zernike fitting. Blue points are raw points used in the fitting and red points represent the fitted surface

2.3. Fan distortion measurement and correction: general considerations

We have previously reported on a method for hardware minimization and software correction of the residual fan distortion in a time-domain OCT system [24,42] which was applied to in vitro samples. A key step in the fan distortion correction is the estimation of the directional cosines at each point in the surface. The method relies on the assumption that the outgoing beam from single mode fibers can be described as TEM00 mode, and therefore following geometrical optics, the propagation of the beam can be described through their directional cosines.

Figure 3 shows a typical implementation of a sample arm for anterior segment OCT: A two mirror-scanner system, showing a certain separation between the mirror centers and the collimating lens. Simple ray tracing on this optical layout shows that the output directional cosines after the lens are not parallel to the optical axis. As it was demonstrated by Ortiz et al. [24], even when the lens is placed at the optimal position from the scanner the directional cosines are skew rays, with the geometry affecting not only the axial coordinate but also the lateral coordinates, since the optical scanner deflects the light in both, elevation and azimuth angles.

Fig. 3.

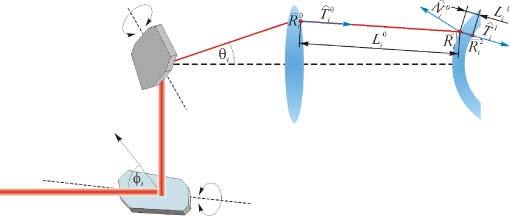
Illustration of a scanning system plus a collimation-condensing lens in an anterior segment OCT system. See text for details.

As a result of the separation between the scanning mirrors, an elliptical wavefront is formed. Therefore, rays in different orientations travel different distances, and as a consequence, the lateral coordinates of the OCT become ellipsoidal (not Eucledian), producing path differences between the ray that defines the optical axis of the system and the rest of rays.

In a previous work we made use of a confocal channel in the system to calibrate fan distortion [24]. However, that channel is not generally available. Therefore we developed an alternative method, which could be easily implemented for calibration any OCT system, and we applied it, in particular, to a custom-developed sOCT [9]. The method allows obtaining the axial distances that need to be added to each axial coordinate to compensate for the variable distances with respect to the optical axis at each location, as well as the transformation that must be performed to obtain lateral distances in Euclidean coordinates.

The procedure consists of collecting series of 3-D volumes (sOCT images) of a calibrated grid at different axial positions within the axial range of the device (7 mm). The grid was placed on a linear stage of 50 mm of travel path with micrometer accuracy. A 3-D volume was collected, every 0.5 mm.

The collected volumes were used to generate 2-D axial-integrated images [43] by simple addition of the intensity along each A-scan. Figure 4 (a) shows an example of an axially integrated image of the grid used in the calibration (taken 1 mm from the best focus).

Fig. 4.

(a) Axially integrated images of a grid used in the calibration (200x200 A-Scans, 11.25 wide system local units). (b) Automatic nodes identification (c) Vectorization of the node movement across the axial length

Each particular ray (and pixel in the image) is described by the local coordinates of the OCT x_oct and y_oct. We used the location of the nodes in the grid (crossing points between vertical and horizontal lines) to identify a set of 3-D coordinates in the system local coordinates, and relate them to the actual positions of the object in space. The Hough transform, in combination with circular and elliptical filters, was used to determine automatically the grid. The lines in the grid image were fitted by parabolic curves, and the nodes of the grids estimated from their intersections (Fig. 4 (b)). The parabolic fit also allowed us to establish the transformation of the system local coordinates into lateral Euclidean units for each point in the volume of interest. Also, since the nodes are labeled for each axial location of the grid, the axial Euclidean coordinates are also obtained. Figure 4 (c) represents the amount and direction of the shift of the nodes at the boundary positions of the axial range. The axial length for the voxel of the collected 3-D images was estimated to be 3.42 ± 0.01 µm.

Once the actual 3-D coordinates are estimated, the quantitative estimation of axial fan distortion was performed by 3-D sOCT imaging of a flat optical surface (mirror) along the axial range of the sOCT system (7 mm). The mirror was placed at the same axial positions used in the collection of grid images. Normality of the mirror with respect to the optical axis was ensured by a pan/tilt mount (within 8 mrad).

The corresponding magnitude of the fan distortion is the distance of one point expressed in local OCT coordinates with respect to the optical axis. This distance is subtracted (in OCT local coordinates) from the raw optical path difference of detected surfaces to obtain their actual position.

2.4. Experiments on artificial lens surfaces (spherical and aspheric)

Measurements were performed on a spherical lens of known geometry (27.91-mm of radius of curvature) and an aspheric PMMA surface. The nominal surface geometry of the spherical artificial lens (Edmund optics) was obtained from the Edmund® catalogue. The aspheric surface was obtained by ablating a PMMA cornea (of initially 12.7-mm radius of curvature) with a refractive surgery excimer laser (Technolas, Baush and Lomb), programmed with a standard algorithm to correct 6-D (on corneal tissue) over a 6-mm diameter optical zone [44,45]. The ablated surface was measured by non-contact profilometry (Sensofar PLu 2300 Software version 2300) which allows surface topographies with an axial resolution of 0.15 μm (for a 20 × microscope objective). 3-D elevation maps were obtained by evaluating the surface in a squared grid of 1157 points over a region of 15 mm for the spherical surface, and of 10 mm for the aspheric surface. In addition, the aspheric lens was measured using a Placido-based videokeratography (Humphrey Atlas model 990, Humphrey Instruments, San Leandro, CA, USA, for cornea). Finally, sOCT images were obtained of both the spherical and aspherical surfaces. Measurements were collected on a 15 × 15 mm zone, using 300 × 300 A-scans for the spherical lens, and on a 10 x10 mm zone for the aspheric lens, using 200 × 200 A-Scans, which resulted on a lateral resolution of 0.05 mm. The data were processed with and without the fan distortion correction. A total of 5 measurements were collected for each sample and device.

Elevation maps obtained for spherical surfaces (from profilometry, OCT, and OCT after fan distortion correction) were fitted by spherical surfaces, on a 6-mm diameter area. Elevation maps obtained for aspheric surfaces (from profilometry, corrected OCT and Placido-based videokeratography) were fitted by conicoids [39–41], on a 6-mm diameter (optical zone of the ablation). Difference maps were obtained subtracting OCT fitted topography maps from those obtained from the reference instruments. RMS (root mean square) of the difference map was used as a metric of the accuracy of the OCT anterior corneal topographic measurement.

For statistical analysis we applied an analysis of variance (ANOVA; general linear model for repeated measurements, with the data collected from different instruments the only factor). The evaluated data were the Zernike coefficients describing the surface (as proposed by Llorente et al. [46]), as well as radii and asphericities from the surface fitted data. Significant levels (ANOVA and pair wise comparison t-tests) were set at p<0.05. The statistical tests were performed using SPSS software (SPSS, Inc., Chicago, Illinois).

2.5. Experiments on human corneas in vivo

A total of 10 eyes from five human subjects participated in the experiment. The ages ranged from 24 to 38 years. The subjects were considered normal in a clinical ophthalmological examination. Refractions ranged between 0 to −4.75 D sphere and 0 to 1 D of cylinder. All protocols had been approved by Institutional Review Boards, and the subjects signed informed consents after the nature of the study had been explained, in accordance to the tenets of the declaration of Helsinki.

The subjects were aligned to the sOCT system by using the specular reflection of the cornea as a reference. Measurements were collected on a 10 × 12 mm zone, using 50 B-Scans composed by a collection of 360. In order to enhance the signal to noise ratio, 3 A-Scans in a B-Scan, were averaged, resulting in a final sampling of 50 × 120, which provides a spatial sampling interval of 0.1 mm for the horizontal direction and of 0.2 mm for the vertical direction. The corneal power exposure was 800 µW. Three-dimensional sOCT corneal images were collected in less than 0.8 seconds. This acquisition time was deemed as an appropriate compromise between resolution and presence of motion artifacts on control experiments on 20 subjects in which consecutive corneal images were obtained with decreasing acquisition times (0.5-2.0 sec). Five repeated images were collected per subject.

In addition to the sOCT measurements, corneal topographies were obtained from commercial Scheimpflug topography (Pentacam, Oculus Optikgeräte GmbH, Wetzlar, Germany) and Placido-based videokeratography (instrument of section 2.4). These instruments were used for comparison with state-of-the art clinical standards, not as gold-standard references. The 50-scan acquisition protocol was used in the Pentacam instrument. Each Pentacam measurement was collected in about 2 seconds, while the subject fixated foveally the built-in red fixation spot, and the corneal reflex of the fixation spot used as a reference. Each Placido-based videokeratography measurement was collected in about 300 ms. Alignment was achieved by centering the image of the reflected rings on the cornea with the corneal reflex. Five repeated sets of data were obtained per subject with each instrument.

Elevation data from all three instruments were fitted by Zernike polynomial expansions (up to the tenth order) using the algorithms described in Section 2.2, in order to remove noise. Quadrics (sphere and conicoid) were subsequently fitted to the elevation maps described by Zernikes. Radii of curvature (R) and asphericity (Q) were used to describe the surfaces. A variance analysis (ANOVA) was used to estimate the statistical significance of measurements from each instrument. A Bland-Altman test [47] was applied to evaluate the agreement across methods (OCT, Scheimpflug and Placido-based videokeratography), taking the Placido-based videokeratography as the reference. The SPSS software was used for statistical data analysis.

There are several ways in which the shape of corneal surfaces can be represented and quantified [39,48,49]. We selected the so-called “height representation” where the measured elevation is represented as the difference of corneal elevation data from the reference sphere (best fitted sphere estimated using nonlinear least squares algorithm) [50]. The corneal elevation maps are displayed in a square grid of 100 × 100 points (6-mm diameter), where warm colors depict points that are higher than the reference surface while cool colors designate lower points.

3. Results

3.1. Fan distortion

Figure 5 (a) shows the raw elevation map of flat optical surface obtained by the sOCT system (i.e. without fan distortion correction), by using a mesh of 300 x 300 A-Scans rastering a square zone of 19 system local coordinates width. The distortion of this surface is a direct measurement of the amount of residual fan distortion. As we had previously predicted [24], the residual fan distortion is constant and does not depend on the axial position of the sample. The measured peak-to-valley difference (fan distortion) in our sOCT is 96 μm in the horizontal direction and 24 μm in the vertical direction. This asymmetry is well predicted by simulations [24]. Figure 5 (b) shows the result of applying the algorithm for fan distortion correction to the sOCT images collected of a flat mirror placed on a holder mount.

Fig. 5.

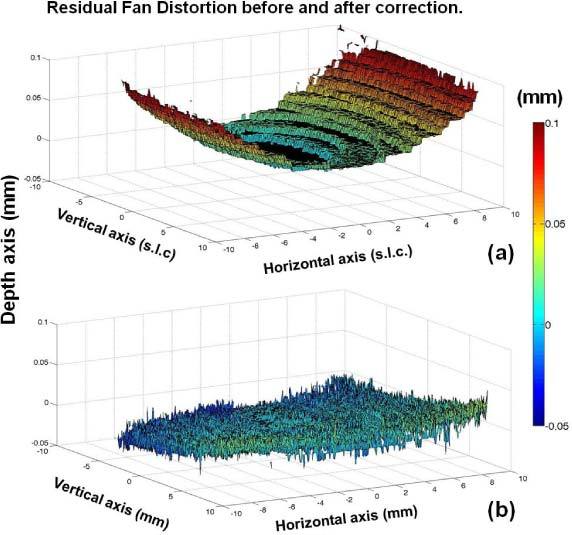
a) Map of residual fan distortion obtained from a flat optical surface with the sOCT system of the study. The surface is presented after segmentation of the image captured by the OCT and it is represented in system local coordinates (slc), except for the axial axis what it has been transformed into Euclidean coordinates for comparison purposes. b) Map of residual fan distortion after fan distortion correction.

3.2. Topographic measurements on artificial lens surface (spherical and aspheric)

Surface topographies from sOCT on a spherical lens and an ablated artificial cornea were compared to 3-D profilometric data, which were taken as a reference. Table 1 shows radii of curvature: nominal, and fits to profilometric and OCT data (average and standard deviation of repeated measurements). The radius of curvature from sOCT without fan distortion correction differs from profilometric data 3.9%, while after the fan distortion correction the difference decreases to 0.9%. The result of the variance analysis was that only statistically significant differences were found for the noncorrected sOCT measurement.

Table 1. Nominal and fitting parameters to surface elevation maps measured with different instruments (spherical surface).

Spherical surface	Nominal	Profilometry	OCT (without Fan distortion correction)	OCT (with Fan distortion correction)
Radius [mm]	27.91	27.78 ± 0.27	26.69 ± 0.11	28.03 ± 0.08

Figure 6 shows difference maps between sOCT and profilometric topography before (Fig. 6(a)) and after fan distortion correction (Fig. 6(b)) on spherical surfaces. The RMS error of the difference maps for the spherical surface decreases from 2.3 µm without fan distortion correction to 0.8 µm with fan distortion correction, for an area of 6-mm diameter. Figure 6 (c) shows relevant Zernike terms of the Zernike fit to the sOCT measurements (before and after correction of fan distortion), in comparison to profilometric measurements. Non-corrected sOCT surfaces show significant amount of astigmatism (Z22) that decreases dramatically with fan distortion correction (from 1.25 to −0.08 µm). Differences for this coefficient between non-corrected sOCT data and profilometry were statistically significant.

Fig. 6.

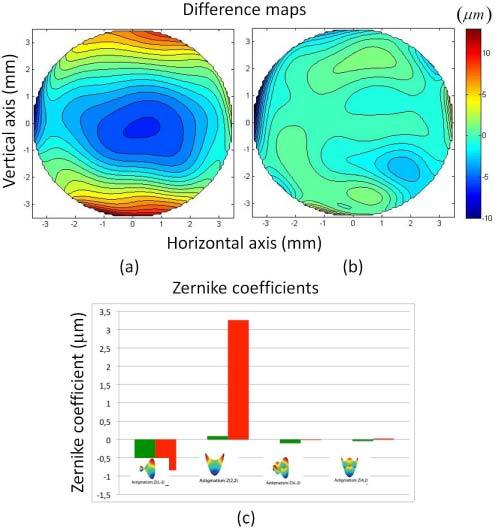
a) Difference map (sOCT elevation map – profilometric elevation map), without fan distortion correction. b) Difference map (sOCT elevation map – profilometric elevation map), with fan distortion correction, for a spherical surface. c) Second and fourth order astigmatism Zernike terms from a Zernike polynomial fit to the surfaces for sOCT topographies without fan distortion correction (red) and with fan distortion correction (green). Data in μm are averages across 5 repeated measurements for each instrument, and 6-mm diameter zones.

The geometrical aspects (radius and asphericity) of the conicoid fitting to the aspheric PMMA surface are summarized in Table 2 for the three instruments: Non-contact profilometer (taken as gold standard), Placido-based videokeratography, and sOCT without and with fan distortion correction. Even though Scheimpflug measurements were collected it was not possible use them, since the Pentacam software was not capable to produce reliable segmentation of the PMMA surface. Radii of curvature differed from profilometry by 0.8% for the Placido-based videokeratography, 4.6% for the sOCT without fan distortion correction (being statistically significantly different), and 1.6% for sOCT with fan distortion correction. Asphericities differed substantially across methods, as well the repeatability of the asphericity estimates from repeated measurements. Asphericities differed from profilometry by 65% for the Placido-disk topographer, 130% for the sOCT without fan distortion correction, and 5% for sOCT with fan distortion correction.

Table 2. Fitting parameters to surface elevation maps measured with different instruments (aspheric surface).

Aspheric surface	Profilometer	Placido-based videokerato.	sOCT (without Fan distortion correction)	sOCT (with Fan distortion correction)
Radius (mm)	8.53 ± 0.11	8.46 ± 0.01	8.92 ± 0.01	8.67 ± 0.00
Asphericity	−0.20 ± 0.25	−0.07 ± 0.08	0.47 ± 0.05	−0.21 ± 0.02

Figure 7 represents difference elevation maps (with respect to the non-contact profilometric maps) of the sOCT topography after fan distortion correction (Fig. 7(a)) and of the Placido-based videokeratography (Fig. 7(b)). The RMS error of the difference maps, for a 6-mm diameter area, was 2.6 µm for sOCT with correction and 5.6 µm for the Placido-based videokeratography. The differences with the profilometric topography (analyzed in terms of the Zernike coefficients) were not significant for neither instrument, although the differences for the sOCT tended to be smaller.

Fig. 7.

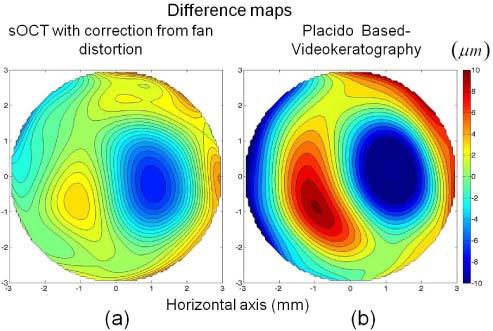
a) Difference map (OCT elevation map with fan distortion correction – profilometric elevation map). b) Difference map (Placido-based videokeratgoraphy elevation map – profilometric elevation map), for an aspheric surface. Data are for a 6-mm area (optical zone of the ablation).

3.3. Topographic measurements on human corneas in vivo

Corneal topographies were obtained on 10 eyes from 5 subjects from sOCT and commercial instruments. Tables 3 and 4 show radii and asphericities from conicoid fits to all corneas in a 6-mm diameter zone. Data are averages (and standard deviations) of 5 repeated measurements on each eye. Radii of curvature (Table 3) from sOCT without fan distortion measurements were systematically lower than those from sOCT measurements with fan distortion correction (2% on average). Discrepancies of the latter with respect to radii of curvature from Scheimpflug topography were between 1 and 2%, and from Placido-based videokeratography <1%. A variance analysis showed significant differences between the Placido-based videokeratography and Scheimpflug in S#1-OD, S#1-OS, S#2-OD and S#3_OD. Non-corrected sOCT data showed statistical differences compared to the other methods for S#4-OD. Corrected sOCT was statistically significantly different from other methods for S#1-OS. The Bland-Altmann plot for radii of curvature did not show any significant difference across instruments, providing a range of [-0.13, 0.05] for the comparison between Placido-based videokeratography and Scheimpflug, [-0.16, 0.16] for the sOCT without fan distortion correction, and [-0.09, 0.10] for the sOCT with fan distortion correction.

Table 3. Radii of curvature (from a conicoid fitting) of anterior corneal elevation maps measured with different instruments (10 eyes from 5 subjects).

Conicoid radius (mm)		Placido-based videokerato.	Scheimpflug	sOCT (without Fan distortion)	sOCT (with Fan distortion correction)
S#1	OD	8.16 ± 0.01	8.12 ± 0.02	8.23 ± 0.11	8.14 ± 0.02
	OS	8.18 ± 0.01	8.10 ± 0.02	8.10 ± 0.07	8.14 ± 0.01
S#2	OD	7.51 ± 0.04	7.45 ± 0.01	7.54 ± 0.03	7.53 ± 0.04
	OS	7.45 ± 0.03	7.45 ± 0.03	7.45 ± 0.01	7.46 ± 0.02
S#3	OD	7.59 ± 0.02	7.54 ± 0.01	7.54 ± 0.06	7.60 ± 0.02
	OS	7.53 ± 0.01	7.52 ± 0.03	7.47 ± 0.06	7.52 ± 0.01
S#4	OD	8.02 ± 0.11	7.90 ± 0.00	8.19 ± 0.04	8.09 ± 0.03
	OS	7.88 ± 0.09	7.83 ± 0.00	7.94 ± 0.03	7.89 ± 0.02
S#5	OD	7.50 ± 0.02	7.49 ± 0.02	7.54 ± 0.04	7.56 ± 0.06
	OS	7.52 ± 0.05	7.50 ± 0.03	7.51 ± 0.04	7.48 ± 0.05

Table 4. Asphericities (from a conicoid fitting) of anterior corneal elevation maps measured with different instruments (10 eyes from 5 subjects).

Asphericity		Placido-based videokerato.	Scheimpflug	sOCT (without Fan distortion)	sOCT (with Fan distortion correction)
S#1	OD	−0.12 ± 0.07	−0.02 ± 0.09	−0.22 ± 0.16	−0.13 ± 0.02
	OS	0.06 ± 0.11	−0.04 ± 0.15	−0.01 ± 0.12	−0.12 ± 0.09
S#2	OD	−0.13 ± 0.04	−0.19 ± 0.04	−0.04 ± 0.04	−0.07 ± 0.02
	OS	−0.18 ± 0.08	−0.10 ± 0.09	0.07 ± 0.01	−0.18 ± 0.01
S#3	OD	0.01 ± 0.08	−0.02 ± 0.01	−0.01 ± 0.08	−0.07 ± 0.02
	OS	−0.02 ± 0.07	−0.01 ± 0.07	0.01 ± 0.09	−0.03 ± 0.03
S#4	OD	−0.25 ± 0.11	−0.32 ± 0.00	−0.15 ± 0.05	−0.24 ± 0.03
	OS	−0.39 ± 0.00	−0.30 ± 0.02	0.07 ± 0.04	−0.34 ± 0.01
S#5	OD	−0.04 ± 0.09	0.01 ± 0.04	−0.04 ± 0.04	0.01 ± 0.04
	OS	−0.11 ± 0.04	0.02 ± 0.08	−0.06 ± 0.05	−0.12 ± 0.03

Asphericities (Table 4) from sOCT without fan distortion differed dramatically in comparison with the rest of the instruments (even changing signs), in consistency with the findings on the artificial aspheric surfaces. Only two eyes S#4-OS and S#5-OS show statistically significant differences between Scheimpflug and Placido-based videokeratography. When the sOCT without fan distortion correction was compared to the Placido-based videokeratography three eyes showed significant statistical differences (S#2-OD, S#2-OS and S#4-OS). In the case of the sOCT with fan distortion correction the only eye showing significant statistical difference was S#4-OS. The Bland-Altmann plot for asphericity showed relatively narrow limits of agreement comparing Placido-based videokeratography with Scheimpflug and sOCT with fan distortion correction ([-0.17, 0.21; Scheimpflug], [-0.19, 0.18; sOCT with fan distortion correction]). In the case of sOCT without fan distortion correction the limits of agreement in comparison with Placido-disk were higher [-0.21, 0.37].

Figure 8 shows topographic height maps from 4 eyes, obtained from Placido-based videokeratography, Scheimpflug and sOCT (without and with fan distortion correction). Difference maps are not shown, as none of the instruments is considered as a “gold standard”. All maps are presented on the same scale for each eye, and are averages of 5 repeated measurements. All data are represented over a 6-mm diameter zone, centered at the specular reflection for foveal fixation. The topographic maps were obtained by fitting the raw elevation maps to a tenth-degree Zernike expansion, relative to the best fitting sphere. The numbers below each map represent the average and standard deviation of the radius of curvature of best fitting sphere in mm.

Fig. 8.

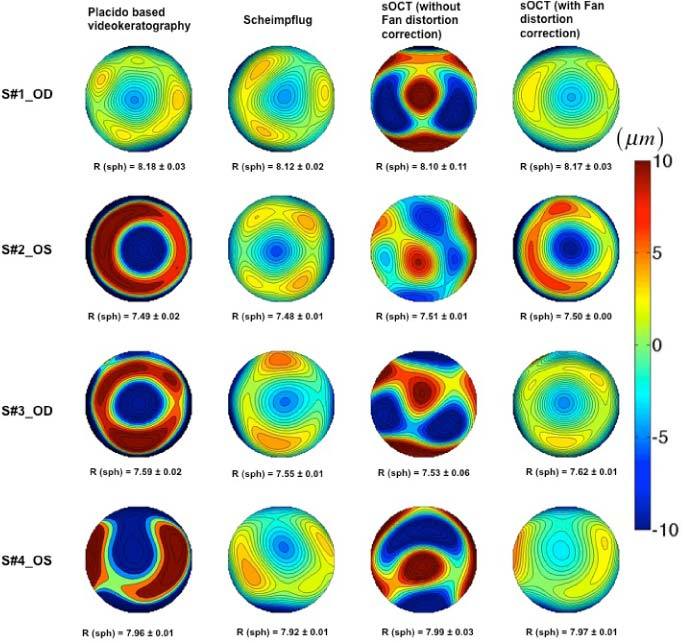
Corneal elevation maps obtained in 4 eyes obtained from different instruments (relative to the best fitting sphere). R = radii of curvature of the best fitting sphere (from fits to sphere quadrics).

4. Discussion

We have presented a method for correcting the distortion of OCT systems, due to the architecture of the sample arm. The calibration has been combined with new algorithms for denoising, segmentation and surface fitting, which have allowed automatic estimation of the surface topography. The presence of fan distortion and its correction in a non-telecentric scanning system was first reported by Westphal et al. [28]. In a previous study we presented theoretical predictions and measurements, as well as a method for correction of fan distortion in a time-domain OCT system provided with a confocal channel [28]. In this study, we have demonstrated that the sOCT corrected for fan distortion produces accurate topographic estimates of artificial surfaces, as compared to non-contact profilometric data. Correcting fan distortion has proved particularly critical for accurate estimates of asphericity. In fact, sOCT with fan distortion correction produced the closest estimates of asphericity with respect to the gold standard (non-contact profilometry) values than other commercial topographers (such as Placido-based videokeratography). A proper measurement of corneal asphericity is critical in clinical applications of corneal topography (refractive surgery, contactology, etc.).

Even though there are small statistically significant differences in terms of quadric parameters for the sOCT without correction, it is in terms of the topographic maps where differences are most notorious. The presence of astigmatism in the data prior to fan distortion correction is clearly observed in the measurements of artificial surfaces, where (unlike in real eyes) no other astigmatism arising from alignment or shape should be present.

Placido-based videokeratography, and to a less extent Scheimpflug imaging, are widely used clinically to measure the geometry of corneal surfaces. The high level of accuracy and precision of Placido-based videokeratography in measuring spherical and aspheric samples has been demonstrated in several studies [51,52]. We have recently reported on the accuracy of the Pentacam anterior and posterior corneal topography on artificial (plastic and hybrid porcine/plastic) eyes. Although the radii of curvature of the surfaces were retrieved within 98.3% accuracy [53] we did not attempt to explore the accuracy of the asphericity estimates. The repeatability of clinical instruments has also been studied. In general, Placido-based videokeratography showed higher repeatability due to its high-speed acquisition; however the posterior corneal surface or the geometry of the corneal apex cannot be measured [54]. Although some studies reported high repeatability in anterior corneal parameters in normal corneas measured with Pentacam [55–57], a recent study reported relatively high variability in the corneal elevation data obtained with this instrument [58]. The relative long acquisition times and the rotating slit scanning scheme may result in motion artifacts and changes in the center of slit rotation.

The relatively sparse information in certain dimensions (radially in Placido-based videokeratography, where the information in the 1-mm central region is lost, and the cornea is sampled radially, and meridionally in Scheimpflug, where the information is sampled only on 25-50 meridians) poses some limitations to these techniques. For example, the meridional pattern is not well suited in patients with irregularities with higher azimuthal frequencies [57].

In contrast, OCT allowed a more sensitive analysis of the geometrical shape of the corneal surface due to its larger axial and lateral resolution. In order to minimize the impact of motion artifacts, we decreased the acquisition times without compromising sampling density (>25000 A-Scans were used). The homogenous sampling pattern in the current study differs from that chosen in recent reports of OCT-based topography, where the information is collected in a series of meridians [19,20,22]. While this strategy is time-efficient and non-problematic in symmetric surfaces, it potentially encompasses similar limitations than those identified for Scheimpflug imaging (reduced sensitivity in the detection of asymmetries, dependence on the center of rotation, etc.). Optimizing both sampling density and sampling pattern will potentially contribute to more accurate corneal elevation reconstructions.

In summary, correction of fan distortion is important for accurate surface/corneal topography with OCT systems. Spectral OCT has the potential for becoming a system for state-of-the-art topography, and overcome the limitations of current standard topographic system. It is essential however to provide the systems with appropriate calibration tools, as well as automatic procedures for accurate detection and evaluation of the surfaces. Although the technique has been demonstrated on a laboratory-based OCT system, it can be easily extrapolated to other OCT systems.

5. Conclusions

We have presented a full experimental method for correction of fan distortion, which can be universally applied to any anterior segment OCT system. This method that allows achieving accurate corneal topographies from spectral anterior segment OCT. The method for correction has been combined with robust automatic image processing techniques. The sOCT topography after fan distortion correction has proved extremely accurate (compared to non-contact profilometry) on artificial lenses (less than 1% discrepancy for both radius of curvature and asphericity), and provided the most accurate estimate of surface asphericity. The statistical comparison of these corrected topographies with topographies from state-of-the art clinical topography systems represents a valuable contribution toward the development “All-OCT-based” topographic systems. Fan distortion correction (along with fast acquisition and powerful segmentation strategies) is essential to obtain reliable corneal elevation maps from sOCT in patients.