Recombination and the evolution of coordinated phenotypic expression in a frequency-dependent game

Abstract

A long standing question in evolutionary biology concerns the maintenance of adaptive combinations of traits in the presence of recombination. This problem may be solved if positive epistasis selects for reducing the rate of recombination between such traits, but this requires sufficiently strong epistasis. Here we use a model that we developed previously to analyze a frequency-dependent strategy game in asexual populations, to study how adaptive combinations of traits may be maintained in the presence of recombination when epistasis is too weak to select for genetic linkage. Previously, in the asexual case, our model demonstrated the evolution of adaptive associations between social foraging strategies and learning rules. We verify that these adaptive associations, which are represented by different two-locus haplotypes, can easily be broken by genetic recombination. We also confirm that a modifier allele that reduces the rate of recombination fails to evolve (due to weak epistasis). However, we find that under the same conditions of weak epistasis, there is an alternative mechanism that allows association between traits to evolve. This is based on a genetic switch that responds to the presence of one social foraging allele by activating one of two alternative learning alleles that are carried by all individuals. We suggest that such coordinated phenotypic expression by genetic switches offers a general and robust mechanism for the evolution of adaptive combinations of traits in the presence of recombination.

1. Introduction

Genetic recombination presents a problem for the emergence and maintenance of adaptive combinations of genetic traits in populations that reproduce sexually (Crow and Kimura, 1965). In an asexual population, adaptive combinations of traits may easily spread due to their relative selective advantage. However, in a sexually reproducing population successful combinations are faced with the additional challenge of segregation and recombination, which may initially facilitate their emergence, but may also break them apart and prevent their joint selective advantage from being realized. This problem is well recognized and thoroughly discussed in the study of the evolution of sex and recombination rates (for a recent review see Hadany and Comeron, 2008), and in the study of disruptive selection on multi-locus traits (Rueffler et al., 2006). One possible solution to this problem is that selection for favorable combinations of traits also selects for mechanisms that decrease the probability of recombination between them. This idea has often been studied within the framework of Nei's model of modifiers of recombination rates (Nei, 1967; 1969). The model includes a gene that modifies recombination rate between two other major genes that are under selection. The modifier gene does not have a direct effect on genotypic fitness; its success depends on its ability to produce offspring carrying good combinations of alleles at the two major genes.

The evolutionary dynamics of modifier genes were studied further and described by the “reduction principle” (Feldman, 1972; Feldman et al., 1980; Feldman and Liberman, 1986; Bergman et al., 1995). This principle states that when a population is at equilibrium and in a state of linkage disequilibrium (as a result of epistatic selection), a modifier allele introduced into the population will increase in frequency if it decreases the recombination rate. It is worth noting that although it is convenient to model the “modifier” as a gene, it does not have to be a real gene; the modifier model simply offers a mechanistic framework to explore the competition between genotypes that differ in their recombination rates. Such differences could be due to chromosomal insertions, deletions, inversions, or, indeed, external genetic regulation in the form of a modifier gene.

The modifier model has some limitations in explaining the prevalence of recombination in nature. For example, the evolution of reduced recombination rates may not be favored when epistatic selection is relatively weak (see Feldman et al., 1997), suggesting that combinations of traits with weak epistasis are bound to be broken up eventually despite the selective advantage they possess. In the course of a recent study (Arbilly et al., 2010), we identified such a case of weak epistasis and expand upon it here in studying the general problem of adaptive combinations and recombination. Our model illustrated that in asexual populations, different adaptive combinations of traits are likely to evolve and to co-exist in negatively frequency-dependent strategy games despite having only slight advantages over other trait combinations. More specifically, the model addressed the co-evolution of simple and complex learning rules and social foraging strategies. We simulated a population of social foragers engaged in a producer-scrounger game in which individuals can search for food independently (produce) or follow others in the group and join and utilize food that producers discovered (scrounge). The interaction between these producer and scrounger strategies results in a type of frequency-dependent selection that had been studied extensively in the past (reviewed by Giraldeau and Caraco, 2000; Giraldeau and Dubois, 2008). We studied the effect of this interaction on the evolution of the learning rules used by individuals to find food in their environment. We considered as complex a learning rule that allows representing, remembering and updating the value of four different patch types in the environment, and as simple a learning rule that merges the information about two similar patch types (of the four), and requires only two types to be represented in memory. Our analysis showed that when better food items are relatively rare, a tendency to search for food independently evolves an association with a complex learning rule, while a tendency to follow others evolves an association with a simple learning rule. The reason for these associations is that for complex learning to have an advantage, a large number of learning steps, normally not achieved by scroungers, is necessary. We demonstrated this result (Arbilly et al., 2010) in the absence of sexual reproduction and recombination, an assumption prevalent in most behavioral ecology models. In this type of model it is common to ignore genetic constraints and assume a “phenotypic gambit”, where the studied character is controlled by the simplest genetic system possible; traits are studied at the phenotypic level, and genetic constraints are assumed to have no effect on long-term evolution (Grafen, 1984; Hammerstein, 1998). Although this is a widely accepted approach, since our previous study demonstrated the evolution of trait combinations, it is natural to examine the most obvious challenge to these results: recombination.

Here, we first use our model (Arbilly et al., 2010) to address two important evolutionary questions: i) can the adaptive association between learning rules and social foraging strategies develop and be maintained in the presence of genetic recombination, and ii) at a recombination modifying gene, can an allele that reduces the recombination rate between the two target loci succeed? While these questions have been studied before under fluctuating epistasis (e.g. Charlesworth, 1976; Barton, 1995; Gandon and Otto, 2007), it is not clear that their predictions can be ascribed to a negatively-frequency dependent game in which fluctuations in epistasis are endogenous and stochastic as in the type of games studied here. In the first part of this paper we address these questions and show (i) recombination (even at a low rate) can easily break the adaptive association between learning rules and social foraging strategies, and (ii) a modifier allele that reduces the recombination rate fails to evolve. In the second part of the paper we explore an alternative mechanism for the evolution of adaptive combinations of traits, which is based on coordinated phenotypic expression. We propose a mechanism based on a genetic switch that responds to the presence of one of the two alternative social foraging alleles by activating one of the two alternative learning rules that are now assumed to be carried by all individuals. We show that under the same conditions that a modifier gene fails to evolve, such a genetic switch can evolve in spite of recombination, thus offering a potentially robust mechanism for the evolution of adaptive combinations of traits.

2. The model

Our earlier analysis of an asexual model (Arbilly et al., 2010) considered a wide range of parameters. In the current analysis we explore the evolution of positive linkage disequilibrium, which requires that some of the parameters take values for which linkage disequilibrium initially occurs (see further details below and Figure 2 in Arbilly et al., 2010).

2.1. The population

We simulated a population of n haploid agents. Each agent is defined by two genetic loci: a foraging strategy locus, F, which defines the agent's probability of applying the producer or scrounger strategy, and a learning rule locus, L, which determines the resolution at which the agent learns the environment when applying the producer strategy. All agents have the same lifespan, which is composed of J foraging steps executed simultaneously by all agents during a “producer-scrounger game” (see below); in line with our previous analysis (Arbilly et al., 2010), we use either J = 50 or J = 70. All agents end their lives at the end of the game and there is no overlap between generations. Fitness is determined according to the agents' accumulated payoff during the J steps of the game, and the top 50% of agents are then selected to reproduce. To simulate sexual reproduction the individuals selected for reproduction form pairs of haploid individuals that are allowed to recombine, and to create four haploid offspring per pair. Mutation rate μ for each locus is 1/n, and the population is followed through G generations. The simulated environment does not change (see below), but information about the environment is not transferred from one generation to the next. We can therefore assume that although individuals are engaged in a single game of J steps during their lifetimes, similar results would be expected for repeated games of J steps during each lifetime, as long as learning starts anew for each new game (i.e., repeated games are independent). The assumption that learning starts anew every generation may be realistic when the relevant cues for finding food change over time or when the environment changes.

2.2. The environment

The simulated environment consists of four food patches E₁, E₂, E₃, and E₄. The four patches are visually distinguishable from one another, but patches E₁ and E₂ have a common visual characteristic, for example, the same color, and so do patches E₃ and E₄; therefore, these can be viewed as E₁₂ and E₃₄, respectively (see illustration in Table 1). Each patch is represented by two parameters: the probability of finding food items in the patch, and the nutritional value of these items (see Table 1). The two parameters are set to be negatively correlated: while the patch that always provides a payoff has the lowest expected value, the patch in which obtaining a payoff is a rare event is the patch with the highest expected value. Simply put, the best food (the food with the highest nutritional value) is the least likely to be found. This environment presents organisms with a nontrivial learning task and is likely to be common in nature (valuable food items may be depleted sooner and become less common; e.g., Lewis, 1980; Kelrick et al., 1986; Price and Reichman, 1987; Edenius, 1991). To keep the simulation sufficiently simple, patch parameters remained constant throughout the game (no depletion during the game), and the environment had no spatial structure.

Table 1.

Food patches parameters and expected nutritional values. E₁₂ and E₃₄ represent perceptual unification of two patches based on a common visual cue (e.g. color or shape); the black square, black triangle, white circle and white pentagon demonstrate possible visual characteristics of the patches, which may cause perceptual unification based on color. The shapes are shown here for illustrative purposes only.

patch	E1	E2	E3	E4	E12	E34
parameter	■	▲	○	⌂	■ ▲	○ ⌂
Nutritional value	4	1.5	0.75	0.25
Probability of finding food	0.25	0.33	0.5	1
Expected value	1	0.5	0.375	0.25	0.75	0.313

2.3. Foraging strategy

The foraging strategy locus (F) determines the agent's probability of applying a producer strategy at each step of the producer-scrounger game described below (with the complementary probability of applying a scrounger strategy). We assume there are two alleles: F₁, whose carriers have a probability 1.0 of adopting a producer strategy, and F₂, whose carriers have a probability of 0.5 of applying the producer strategy and 0.5 of applying the scrounger strategy (i.e., to follow others). Thus carriers of the F₂ allele can also learn which food patch is most profitable and use this information in future steps, but they do so with probability one-half at each of the foraging steps (i.e., when they do not scrounge from others). The two probabilities of producing, defined by the two alleles (i.e. 1.0 and 0.5), were chosen in order to simulate a situation in which individuals differ considerably in their social foraging strategies but are still capable of using individual learning. Preliminary simulations have shown that bimodalities of this sort evolve as a result of the game even when multiple alleles coding for various probabilities are included in the simulation. The F₁ and F₂ alleles were assigned randomly with equal probability to the n individuals in the first generation.

2.4. Learning rules

Learning takes place only when an agent is applying the producer strategy. The value of the food item it has obtained (or zero in the case it has obtained no food) updates the agent's memory, and this information is used in the agent's subsequent producing steps to decide in which patch to search for food. As a typical memory updating rule we used the linear operator rule (McNamara and Houston, 1987; Bernstein et al., 1988; Beauchamp, 2000; Groβ et al., 2008; Eliassen et al., 2009), which is also known as the weighted return rule (March, 1996). For each patch it yields a weighted average of the most recently acquired payoff and previous payoffs, according to the equations:

$$M_{i,t+1}=\alpha M_{i,t}+(1-\alpha )Y_{i,t}t=1,2,\dots ,j$$

where M_i,t is the value of patch E_i in the agent's memory at step t, and {Y_i,t} is the updating scalar: Y_i,t equals the payoff obtained at step t if patch E_i had been visited at step t. Here α (0 ≤ α ≤ 1) is a memory factor describing the weight given to the agent's past experience as the most recent experience updates memory. Following our previous analysis (Arbilly et al., 2010), we use α = 0.5. Note that Y_i,t is the payoff obtained by the producer when it is alone at the food source, and it may be different from the payoff the producer eventually receives if joined by a scrounger (see game description below). For the first step, M_i,1 are set to the mean of all four patches' expected values (M_i,1 = 0.53 for all i).

Two learning rules were defined by the alleles at the learning rule locus. The first is a complex learning rule (allele L₁) that views the environment in full detail, as composed of the four food patches E₁, E₂, E₃, E₄. The second is a simple learning rule (allele L₂) that views the environment as composed of only two patches, E₁₂ and E₃₄. Note that with the complex learning rule, individuals can potentially learn to prefer the patch with the highest expected value (Table 1, patch E₁, expected value = 1.0), while with the simple learning rule they can at best learn to prefer the E₁₂ combination (with an expected value of 0.75). Thus, if applied successfully, complex learning should be better than simple learning. However, while both the complex and the simple learner do not sample the environment systematically, but choose a patch at each step based on their experience, a simple learner faces only two alternatives and will therefore receive a rough idea of the distribution among patches faster than a complex learner, who faces four alternatives. Therefore, complex learning is more likely to involve statistical sampling errors when the total number of learning steps is small. This cost of complex learning is inherent in the simulation and stems from the learning algorithm and the highly variable nature of the patches.

Including a third allele L₀ that results in no learning in the asexual model proved to be redundant (as it was always eliminated in the presence of L₁ and L₂ in games where J > 14) and henceforth we omit it from the model.

To account for the possibility that complex learning may be more costly than simple learning (in aspects not explicitly modeled in the simulation, such as physiology, processing time, and attention) a cost measured by the parameter γ was incurred by individuals carrying the complex learning allele (L₁). This cost was a fractional reduction by γ of the final cumulative payoff (after the J steps) to agents carrying the complex learning rule allele, L₁; in this analysis we use γ = 0.01, shown in the asexual model (Arbilly et al., 2010) to be affordable for the pure producer strategy F₁ (which, as a result, evolved an association with the complex learning rule L₁) but not for the part-time scrounger strategy F₂ (which, as a result, evolved an association with the simple learning rule L₂), in games of J = 50 and J = 70 steps.

2.5. Decision rule

When producing, the agents decide in which patch to forage based on the information they acquired and updated in the abovementioned learning process. We used the exponential (logit) response rule (following Ben-Akiva and Lerman, 1985; Busemeyer and Myung, 1992; Bereby-Meyer and Erev, 1998; Camerer and Ho, 1999), according to which patch E_i is chosen with a probability based on its relative weight in memory (M_Ex), using the expression:

$$p_{i,t+1}=\frac{e^{M_{i,t}}}{{\displaystyle \sum _{k=1}^4{e}^{M_{k,t}}}}.$$

Here p_i,t+1 is the probability of choosing patch E_i at step t+1. The above expression holds for complex learners (L₁ carriers) that distinguish between all four patches; simple learners (L₂ carriers) use the same expression but k goes from 1 to 2 (rather than from 1 to 4). Due to the nature of the learning rule and the high variability of the better patches, the value of the better patches in agents' memory is highly dynamic and often comes close to zero; with a simple ratio, this can drive agents to constantly choose the worst patches. The use of an exponential ratio, which keeps these values from zero, prevents such choice rigidness and allows more frequent sampling of seemingly less attractive patches (which may actually turn out to be the better patches) than a simple ratio.

2.6. The producer-scrounger game

As described above, a generation's lifespan is composed of either J = 50 or J = 70 steps; these values were chosen because they exhibited the clearest advantage to the F₁L₁ and F₂L₂ haplotypes, which in our earlier study (Arbilly et al., 2010) formed a consistent dimorphism in asexual populations.

Each step begins with a choice of foraging strategy (producing or scrounging) according to the agent's foraging allele (see above). Agents with the F₁ allele (they always search), or agents with the F₂ allele (they use the producer strategy with probability 0.5), choose a patch to forage in (based on the above learning and decision rules), and receive a payoff (or not) according to patch parameters described in Table 1. Agents with the F₂ allele that act as scroungers are then assigned to producers to simulate a scrounging process. We assume that at each step scroungers are able to distinguish successful producers from producers that failed to find food. All scroungers are assigned to one producer, and each assignment is random and independent. A producer in our game can be joined by only one scrounger, and the payoff is divided between the two agents; if more than one scrounger is assigned to one producer, only one of these scroungers will receive a payoff (a finder's share of half the payoff always goes to the searcher). This assumption is different from some other producer-scrounger models where a producer can be joined by many scroungers (see for example Beauchamp, 2000; Hamblin and Giraldeau, 2009). It is important to note, however, that this assumption does not change the negatively frequency-dependent dynamics of the game (Arbilly et al., 2010).

Simulation parameter and their meanings are summarized in Table 2.

Table 2.

Symbols used in the simulations and their descriptions.

Symbol	Description
F1	Foraging allele: pure producer (1.0 probability to apply producer strategy)
F2	Foraging allele: part-time scrounger (0.5 probability to apply producer strategy)
L0	Learning allele: non-learning
L1	Learning allele: complex learning rule
L2	Learning allele: simple learning rule
M1	Modifier of recombination allele: increasing recombination rate
M2	Modifier of recombination allele: decreasing recombination rate
S1	Learning switch allele: assigning learning rule at random
S2	Learning switch allele: assigning part-time scroungers with the complex learning mechanism, and pure producers with the simple learning mechanism
S3	Learning switch allele: assigning part-time scroungers with simple learning, and pure producers with complex learning
S4	Learning switch allele: assigning complex learning regardless of foraging genotype
S5	Learning switch allele: assigning simple learning regardless of foraging genotype
S*1	Foraging switch allele: assigning foraging strategy at random
S*2	assigning simple learners with the pure producer strategy, and complex learners with the part-time scrounger strategy
S*3	assigning simple learners with the part-time scrounger strategy, and complex learners with the pure producer strategy
S*4	assigning the pure producer strategy regardless of learning rule
S*5	assigning the part-time scrounger strategy regardless of learning rule
r	Recombination rate
r1	Recombination rate for parental genotype M1M2
r2	Recombination rate for parental genotype M1M2
r3	Recombination rate for parental genotype M2M2
R	Recombination rate between modifier locus and the foraging gene
n	Number of agents in the population
J	Number of steps in the game (equivalent to agents' lifespan)
G	Number of generations
μ	Mutation rate
γ	Cost of complex learning rule (% deducted from final cumulative payoff)
α	memory factor (weight of past events in memory when updating a new experience)

2.7. Model dynamics

The evolutionary dynamics of this model (Arbilly et al., 2010) are characterized by mild fluctuations in haplotype frequencies around an equilibrium point, maintained by the frequency-dependent game between pure producers (F₁) and part-time scroungers (F₂). In the asexual model, the ratio of allele frequencies was approximately 0.55:0.45 pure producers to part time scroungers, with fluctuations of up to ∼0.15 (Figure 3 in Arbilly et al., 2010). These fluctuations are caused by the combined effect of finite population size and the stochastic differences in fitness among individuals resulting from the variety of probabilistic processes described above. While theoretically a fixed ESS will be achieved in an infinite-size population, the goal of our agent-based simulation is to simulate a realistic scenario that includes stochastic and dynamic processes.

3. Co-evolution of learning rules and social foraging strategies in a sexually reproducing population

3.1. The effect of recombination

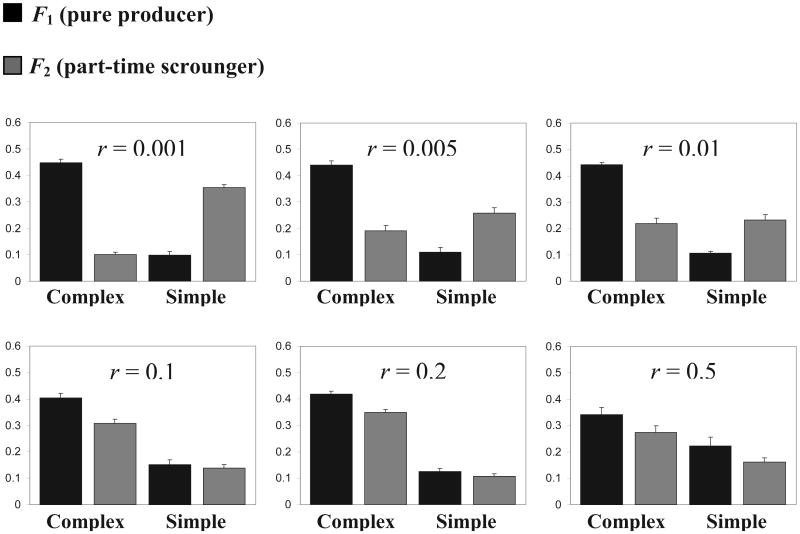
We initially investigated the evolutionary dynamics of our system with a fixed recombination rate r, the probability of recombination between the F₁/F₂ foraging gene and the L₁/L₂ learning gene (population size n = 300). We found that for any r > 0.005, the population fails to produce the dimorphism of the two adaptive haplotypes that we found with asexual reproduction (Arbilly et al., 2010). This can be seen in Figure 1, where a clear dimorphism dominated by the F₁L₁ and F₂L₂ haplotypes is seen only under a very low recombination rate, r = 0.001, and quickly disappears at higher recombination rates. It should be noted that even though for r = 0.005, some level of F₁L₁ and F₂L₂ dimorphism may appear in Figure 1, this is because the mean outcome of 10 runs is reported. But within each run, one or the other haplotype dominated without a stable dimorphism developing for the learning rule gene.

Figure 1.

Mean haplotype frequencies with standard errors under different fixed values of the recombination rate r. Black columns represent haplotypes associating the learning alleles L₁ (complex), and L₂ (simple) with the producer allele F₁, and grey columns represent their association with the part-time scrounger allele F₂. Mean frequency is calculated for generations 1001–2000 of 10 repeats for each parameter set. Generation lifespan is J = 70; results for means are qualitatively similar for J = 50.

Figure 1 also demonstrates that in the presence of genetic recombination, the lack of stable association between learning alleles and their compatible foraging alleles (whose frequencies are stabilized by the producer-scrounger game) allows the complex learning allele L₁ to increase in frequency. As a result, for r ≥ 0.1, most part-time scroungers (carriers of F₂) are applying the complex rather than the simple learning rule (see Figure 1). The reason for the increase in the frequency of L₁ is that, in the presence of recombination, the long-term fitness of the L₁ allele depends on the combined success of the F₁L₁ and F₂L₁ haplotypes (relative to the combined success of the F₁L₂ and F₂L₂ haplotypes). With a sufficiently large number of steps, e.g., J = 70, L₁-carrying haplotypes are the most successful. Reducing the number of steps to J = 50 resulted in the same phenomenon but in exactly the opposite direction, i.e. an increase in the frequency of the simple learning allele L₂ and its related haplotypes (data not shown). This is consistent with the effect of the number of steps on the success of the simple and complex learning rules that we observed in the asexual model (Arbilly et al., 2010).

3.2. Can linkage disequilibrium be maintained through the evolution of a modifier allele that reduces recombination rate?

Following previous work on the evolution of recombination rates under epistatic selection we asked how a recombination-modifying gene would evolve in our system. We modeled the modifier as a third gene, controlling the rate of recombination between the genes F₁/F₂ and L₁/L₂, which had two alleles: M₁ and M₂, where M₁ increased recombination rate and M₂ decreased it to 0 (i.e. complete linkage). The recombination rate r for a pair of reproducing individuals was determined by the combined parental genotype at the modifier locus. Parental genotype M₁M₁ set the recombination rate to r₁, M₁M₂ set the rate to r₂, and M₂M₂ set the rate to r₃ = 0. Without loss of generality we assume r₁ > r₃. We also tried the other possible relations: r₁ > r₂ > r₃, r₂ > r₁ > r₃, and r₁ > r₃ > r₂ > 0 (where the last is the only case in which M₂ did not decrease recombination rate to 0), and the results were qualitatively similar. The modifier gene itself was linked to one of the behavioral genes, chosen arbitrarily to be the foraging gene, with recombination rate R, which was fixed for all agents in the population.

We first examined the invasion of a population of n haploids all carrying allele M₂ (r = 0) by allele M₁ (coding for r > 0) through random mutation (μ = 1/n, as for the two behavioral genes). We also studied the opposite case where M₁ is fixed in the population and a mutant M₂ arises. The population had been set initially to either linkage equilibrium, positive linkage disequilibrium or negative linkage disequilibrium. It is important to note that the reduction principle applies when the population is in a state of equilibrium at linkage disequilibrium (Feldman and Liberman, 1986). In our simulation, however, the haplotype frequencies were highly dynamic and fluctuated continuously due to the effect of the negatively frequency-dependent selection in the producer-scrounger game and the stochastic outcomes of the learning process.

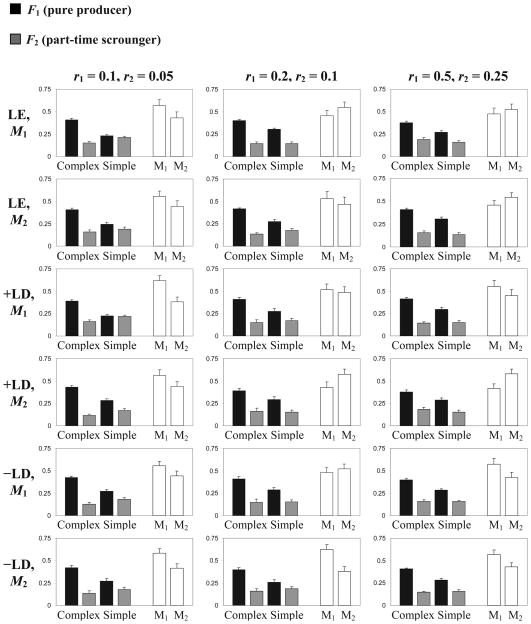
The results of these simulations are summarized in Figure 2, and are consistent across different initial conditions and different recombination rates induced by the modifier allele M₁. In all cases, the allele M₂, which confers complete linkage, did not reach fixation and its average frequency was usually below 0.6. As a result, a considerable amount of recombination took place, allowing the inferior haplotypes F₁L₂ and F₂L₁ to persist at substantial frequencies (0.13 – 0.19 and 0.23 – 0.31, respectively). Furthermore, similar to the results with a fixed recombination rate (Figure 1), the frequency of the complex learning allele L₁ was decoupled from that of the producer allele F₁, and with J = 70 steps L₁ increased in frequency, causing most part-time scroungers (carriers of F₂) to apply the complex rather than the simple learning rule. As in the case of a fixed recombination rate, reducing the number of steps to J = 50, resulted in the same phenomenon but in exactly the opposite direction, i.e. an increase in the frequency of the simple learning allele L₂ and its related haplotypes (not shown). With R > 0 (i.e. when the M locus and one of the behavioral loci were not completely linked) the results did not change. We also ran an additional 20 simulations with four types of M₁ alleles (r = 0.05, 0.1, 0.2, and 0.5) competing simultaneously with the complete linkage allele M₂. All five alleles started at equal frequency and the simulations ran for 2000 generations with μ = 1/1000, J = 70, and R = 0. The results were qualitatively similar to those presented in Figure 2: no persistent advantage for the complete linkage allele M₂ was detected and the population failed to produce the dimorphism of the two adaptive haplotypes that dominated the asexual population.

Figure 2.

Mean and standard error of behavioral haplotype and modifier allele frequencies in simulations, for different recombination rates and initial haplotype disequilibria. Black columns represent haplotypes associating the learning alleles L₁ (complex) and L₂ (simple) with the producer allele F₁, and grey columns represent their association with the part-time scrounger allele F₂. White columns represent the mean frequency of modifier alleles M₁ and M₂. Means are calculated for generations 1001–2000 of 10 repeats for each parameter set. r₁ and r₂, indicated at the top of each column of figures, are recombination rates for parental genotype M₁M₁ and M₁M₂, respectively (r₃, the recombination rate for parental genotype M₂M₂, is always zero). Initial haplotype patterns are indicated at the left of each row of figures: the recorded modifier allele (M) is the only modifier allele present in the population in the 1^st generation (while the other occurs by random mutation); LE – linkage equilibrium (all haplotypes at initial frequency of 0.25); +LD – positive linkage disequilibrium, F₁L₁ and F₂L₂ are each at initial frequency of 0.4 while F₁L₂ and F₂L₁ are each at initial frequency 0.1; −LD – negative linkage disequilibrium, F₁L₁ and F₂L₂ are each at initial frequency 0.1 while F₁L₂ and F₂L₁ are each at 0.4. All results are for simulations where J = 70, n = 300, μ = 1/n, γ = 0.01, and R = 0.

A modifier evolved successfully and linkage disequilibrium was maintained only in the special case where M₂ was dominant (and thus r₂ = r₃ = 0) and R, the recombination rate between the modifier and one of the behavioral genes was set to zero. These special conditions produced interesting dynamics that are described in some detail in the Appendix; in this special case, haplotypes carrying M₂ are protected from recombination and the population is effectively divided by the modifier genotype into two sub-populations that do not interbreed. Depending on initial conditions, carriers of M₂ that are associated with one of the adaptive combinations (i.e., F₁L₁ or F₂L₂) increase in frequency and take over either the producer fraction or the part-time scrounger fraction of the producer-scrounger game (almost all producers become F₁L₁M₂ or, alternatively, almost all part-time scroungers become F₂L₂M₂). The alternative foraging strategy can evolve an association with its compatible learning allele; recombination may occur in each case but will have no genetic effect (see Appendix). While this scenario is theoretically possible, there is little evidence that it can offer a general solution for the stability of trait combinations in nature.

3.3. Why does a modifier gene that reduces recombination rate fail to evolve?

The coexistence of M₁ and M₂ in Figure 2 may simply be explained by “mutation-drift” effects with no selective advantage of M₂ over M₁; the two alleles are subjected to genetic drift, but are maintained in the population by recurring mutations at the relatively high rate of μ = 1/n. We were able to confirm this explanation by re-running the simulations without any mutation at the M locus, and with initially equal frequencies of the alleles M₁ and M₂ (as well as of all alleles at the other two genes). In three sets of one hundred runs of 2000 generations, where the M₁ allele produced r₁ = 0.1, 0.2, or 0.5, the M₂ allele (coding for complete linkage) reached fixation in 55, 58, and 58 runs, respectively. In all other cases, the M₁ allele reached fixation. Altogether, these results suggest that although the M₂ allele is a bit more likely to reach fixation, its selective advantage is weak and effectively it does not allow the adaptive combinations to evolve.

As mentioned earlier, it is possible that the frequency-dependent fluctuations of the producer-scrounger game may violate the reduction principle's requirement for equilibrium with genetic linkage disequilibrium. As can be seen in our previous analysis (Figure 3 in Arbilly et al., 2010), the dynamic equilibrium between the foraging alleles F₁ and F₂ involves fluctuations of about 5–15% above and below the mean equilibrium level of the two strategies, and these fluctuations can easily last longer than 10 generations. While several studies have looked into the effect of a fluctuating environment on the evolution of modifiers of recombination, they studied it given explicit fitness functions (see Charlesworth, 1976; Barton, 1995; Gandon and Otto, 2007). Current theory does not make clear predictions for the effect of a dynamic equilibrium, as present in our model, on evolution of a recombination modifier. Although within each foraging strategy class it is still advantageous to be associated with a particular learning allele (i.e., F₁L₁ > F₁L₂, and F₂L₂ > F₂L₁) the temporal deviations from equilibrium that impose stronger selection on a particular foraging allele can give the inferior combination associated with this allele a relative advantage over the superior combination associated with the alternative foraging allele (i.e., F₁L₂ > F₂L₂ or F₂L₁ > F₁L₁). It is not clear, however, whether such temporal changes in the relative fitnesses of these haplotypes can explain the lack of success of the modifier allele M₂. To test this possibility we ran a set of simulations in which such dynamic fluctuations were prevented by maintaining the population at the long-term mean equilibrium frequencies. When selecting parents for a new generation, pure producer's (F₁) frequency was fixed at 0.55 and part-time scrounger's (F₂) at 0.45, regardless of their success relative to each other. Then a separate selection process was applied within the F₁ haplotypes (F₁L₁, F₁L₂), and within the F₂ haplotypes (F₂L₁, F₂L₂), allowing the two combinations with the learning alleles to compete within each social foraging class, and mutation and recombination to occur immediately after selection. The results (Figure 3) show no improvement in the success of the M₂ allele, thus excluding the frequency-dependent dynamic fluctuations as the cause for the failure of recombination reduction.

Figure 3.

Mean and standard error of haplotype and modifier allele frequencies in simulations where game fluctuations were stabilized. Initial frequencies of the behavioral alleles in the first generation were fixed at 0.55 for F₁ and 0.45 for F₂, and 0.5 for each of the learning alleles L₁ and L₂. While the frequencies of F₁ and F₂ remained constant (see text for further explanations), the frequencies of L₁ and L₂ from the second generation onward were determined by selection. The modifier allele (M) indicated at the left of each row of figures is the only modifier allele present in the population in the 1^st generation (while the other occurs by random mutation). Column colors, parameter values and calculation of means are as described in the legend to Figure 2.

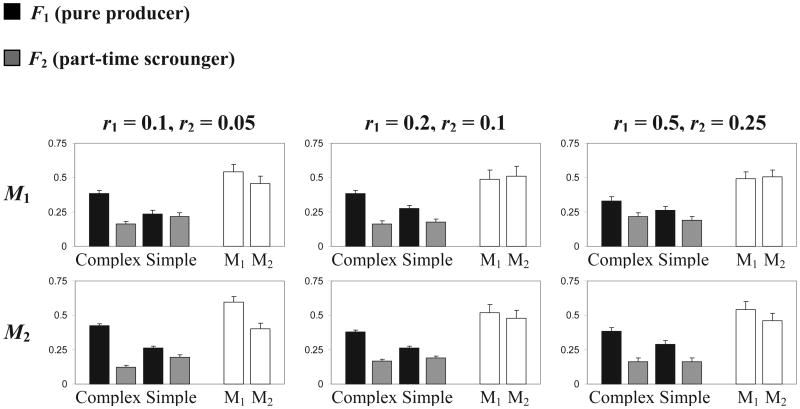
Additional simulations where the possibility of mutation in all loci was removed also failed to yield the anticipated dimorphism; all resulted in fixation of one of the learning alleles. This leaves us with weak selection as the most likely explanation; selection for neutral modifiers is known to be weak because its effect on fitness is indirect (see discussion by Feldman et al., 1997). Although the fitness advantage of the two adaptive haplotypes F₁L₁ and F₂L₂ was sufficiently high to allow their evolution in the absence of recombination (Arbilly et al., 2010), the same fitness advantage seems to be insufficient to generate the indirect selection required for a modifier allele to overcome drift and mutation. To test this possibility we ran another set of simulations where we artificially enhanced the fitness advantage of the adaptive combinations F₁L₁ and F₂L₂ by adding 3% to the fitness of each agent. Under these conditions, the modifier allele M₂ usually evolved successfully and linkage disequilibrium was maintained (see Figure 4).

Figure 4.

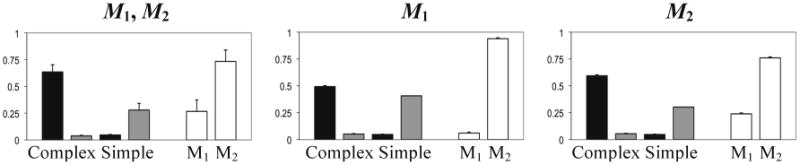
Mean and standard error of haplotype and modifier alleles frequencies in simulations with artificially added 3% fitness advantage to the haplotypes F₁L₁ and F₂L₂. Recombination rates for all figures are r₁ = 0.5, r₂ = 0.25, r₃ = 0. Behavioral haplotype (F/L) frequencies in the 1^st generation are 0.25 each. The modifier alleles present in the 1^st generation are indicated over the figures (where both alleles are recorded, they appear at a frequency of 0.5 each).Column colors, other parameter values and calculation of means are as described in the legend to Figure 2.

The conclusion drawn from the above analysis is that the evolution of adaptive trait combinations cannot be achieved through the evolution of genetic linkage when the fitness advantages of these combinations are not sufficiently high.

4. The evolution of coordinated phenotypic expression through a genetic switch

The above results prompted us to consider an alternative mechanism for the evolution of adaptive trait combinations under weak epistatic selection and in the presence of genetic recombination. This mechanism has already been suggested in some previous studies (e.g., Wolf et al., 2008b; Wolf et al., 2008a) but its evolution has not been studied explicitly. It is based on conditional expression of one trait in response to the presence of an allele coding for another trait. The idea is a simple extension of the principle of phenotypic plasticity, but instead of conditionally expressing one of two alternative alleles based on environmental cues, the expression is conditioned upon the individual's own genetic environment. Activation of one gene by the expression of another gene is wide-spread, especially in developmental processes (e.g., Capel, 1998, see also Carroll, 2005 for a review), and therefore biologically plausible.

We sought to investigate whether the foraging-learning compatible combinations could evolve and be maintained through the evolution of genetic switches for appropriate conditional expression. We used the same simulations of a sexually reproducing population with free recombination between all loci (r = 0.5), but added a new locus S with different possible alleles S₁ to S₅. These alleles act as genetic switches; they code for different conditional rules for expressing one gene in response to the presence of another gene. For this mechanism, however, we must assume that the conditionally expressed genes have both their alleles carried by the same individual and can therefore be conditionally expressed in response to the genetic switch. This requires that all agents have two loci for the conditionally expressed genes, and their haplotypes are composed of four loci, for example: “S₁ F₁ L₁ L₂ ” representing the social foraging gene F₁, the two learning alleles L₁ and L₂ (of which only one will be expressed), and the genetic switch allele S₁ that determines which learning rule will be expressed in response to the presence of F₁. This means that genetic linkage disequilibrium between the F and L genes is no longer possible; instead, the genetic switch coded by the S gene may generate a phenotypic association between the social foraging and the learning traits; that is a “phenotypic disequilibrium” (see also Arnold (1992) for related concepts). The assumption that all individuals carry the genes for the two learning rules requires some evolutionary justification. We suggest that such sets of alternative learning rules are likely to exist under a wide range of environmental conditions and could have evolved to serve various learning tasks. In fact, the two learning rules represented in our model as two distinct alleles may be operating in nature as a mechanism that may be adjusted to different levels (in response to either genetic, internal or external conditions). For example, it is conceivable that an increase in the level of attention can allow a forager to make finer distinctions between patches and therefore transform “simple learning” into “complex learning” (see Discussion).

Let us first consider the case where the allele at a single social foraging locus (F₁ or F₂) determines which of the two learning alleles will be expressed. The genetic switch in this case will be referred to as the “learning switch”, and it was modeled as a locus with five possible alleles:

• S₁ – assigns the learning rule at random

• S₂ – assigns to part-time scroungers the complex learning mechanism, and to pure producers with the simple learning mechanism (i.e. the wrong switch)

• S₃ – assigns to part-time scroungers the simple learning mechanism, and to pure producers the complex learning mechanism (i.e. the adaptive switch)

• S₄ – assigns complex learning regardless of foraging genotype

• S₅ – assigns simple learning regardless of foraging genotype

S₁ was designed to act as a control for the evolution of the other alleles, and in the initial population only S₁ was present. S₂, S₃, S₄ and S₅ were allowed to occur by random mutation (μ = 1/n, as in all genes in the simulation). S₄ and S₅ can also be viewed as representing the possibility that individuals carry only one of the learning alleles (either L₁ or L₂) because their complete inactivation of the alternative allele is practically equivalent to its absence from the genome. We ran simulations with both generation lifespan J of 50 and 70 steps.

At the second stage we considered the reverse case, where a single allele at the learning gene L determines which of the two alternative social foraging alleles carried by all individuals will be expressed. This genetic switch S* (denoting the foraging switch as opposed to the learning switch S), was also modeled as a locus with five alleles:

• S*₁ – assigns foraging strategy at random

• S*₂ – assigns to simple learners the pure producer strategy, and to complex learners the part-time scrounger strategy (i.e. the wrong switch)

• S*₃ – assigns to simple learners the part-time scrounger strategy, and to complex learners the pure producer strategy (i.e. the adaptive switch)

• S*₄ – assigns the pure producer strategy regardless of learning rule

• S*₅ – assigns the part-time scrounger strategy regardless of learning rule

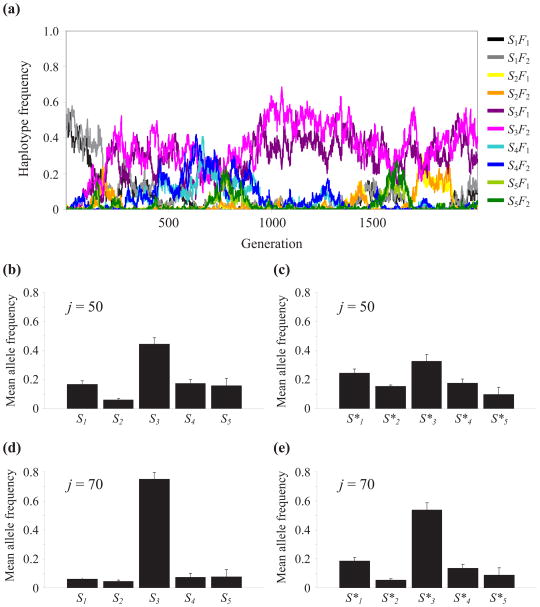
The simulation results are described in Figure 5; Figure 5a illustrates typical evolutionary dynamics of the adaptive learning switch S₃ under generation life span of J = 50 steps. It can be seen that after 1,000 generations, the two haplotypes S₃F₁ and S₃F₂ dominate the population, implying the successful evolution of the adaptive learning switch S₃ and stable expression of the F₁L₁ and F₂L₂ phenotypes, as in the asexual population. Figures 5b–d summarize the results of repeated simulations of the evolution of the learning and foraging switches under J = 50 and J = 70 learning steps and show that the adaptive switches S₃ and S*₃ generally prevailed. However, the evolution of the learning switch S₃ was more successful than the evolution of the foraging switch S*₃, and both genetic switches evolved further under J = 70 learning steps. The more successful evolution of both genetic switches under J = 70 learning steps is consistent with the stronger disruptive selection illustrated under these conditions (Arbilly et al., 2010, Figure 2). Simply put, the fitness advantage of the adaptive combinations is greater under J = 70, which generates stronger selection for the correct switch. It is clear from these results that the correct learning switch S₃ can succeed, thereby maintaining the stable association between foraging strategies and learning rules.

Figure 5.

(a) Example of evolutionary dynamics in a population carrying a learning switch gene S, generation lifespan J = 50. (b)–(e) Mean allele frequency (+standard error) of the genetic switch allele in generations 1000–2000, across 10 repeats of the simulation: (b) The learning switch with generation lifespan J = 50; (c) The foraging switch with generation lifespan J = 50; (d) The learning switch with generation lifespan J = 70; (e) The foraging switch with generation lifespan J = 70. Recombination rate between the two loci was 0.5. All populations started with the random switch S₁ or S*₁ at the switch locus and alternative switches arose by mutation.

The fact that the correct learning switch was more successful than the correct foraging switch is less intuitive because both switches generate exactly the same adaptive phenotypes (F₁L₁ and F₂L₂). However, as mentioned earlier, due to the frequency-dependent dynamics of the game, the foraging gene is also subject to oscillating selection that can sometimes make its inferior combination with a learning rule better than the superior combination of the competing foraging allele. As a result, while a foraging allele always benefits from expressing the correct learning rule (an expression controlled by the learning switch), a learning allele can occasionally increase in frequency when expressing the less compatible but temporarily better foraging strategy. Such cases may weaken the selection for the foraging switch relative to that acting on the learning switch and may explain the above results. Nonetheless, our results demonstrate that both genetic switches can evolve successfully and stabilize the adaptive trait combinations in spite of genetic recombination.

5. Discussion

Many behavioral strategies may be based on combinations of behavioral rules and are likely to be coded by more than a single gene. Yet, relying on a constructive simplification known as the “phenotypic gambit” (Grafen, 1984), evolutionary biologists frequently treat the evolution of such behavioral phenotypes as if they are coded by a single gene (Maynard Smith, 1978; Stephens and Krebs, 1986). In our previous paper (Arbilly et al., 2010) using this approach we found there is an advantage to the association of certain learning rules with certain social foraging strategies. By assuming complete linkage between the learning and the social foraging alleles we treated each combination as a single evolving gene. However, deeper understanding of evolutionary processes requires careful examination of such simplifying assumptions. In the present paper we showed that genetic recombination, even at a low rate, can easily break the adaptive association of learning and social foraging strategies, thus eliminating the dimorphism of producers that use complex learning and part-time scroungers that use simple learning. This led us to study the evolution of two mechanisms that might solve the problem of genetic recombination and stabilize the adaptive association of social and learning strategies. We found that a modifier gene that reduces the probability of recombination failed to evolve under the conditions tested by our model, but a mechanism that is based on a genetic switch for conditional expression would evolve successfully. To what extent can the results of our analysis be generalized?

The loss of dimorphism under genetic recombination is not surprising. In the absence of assortative mating or dominance, genetic recombination can prevent the evolution of genotypic bimodality (Waxman and Gavrilets, 2005). This also accords with a previous analysis of the long-term evolution of multilocus traits under frequency-dependent disruptive selection (although a somewhat different case from ours) by van Doorn and Dieckmann (2006), who found that genetic variation tends to concentrate at a single locus with a large phenotypic effect rather than to establish polymorphism at a number of loci that are subject to recombination.

Theoretically, recombination rates can be reduced through the evolution of a modifier allele (see introduction). However, it is well appreciated that selection for such modifiers is indirect and requires sufficiently strong epistatic selection (see Feldman et al., 1997). Evidently, epistasis in our model was not sufficiently strong for the evolution of such a modifier but was sufficiently strong for the evolution of a genetic switch. In light of these results, a genetic switch, which, unlike a modifier, consistently yields only the more compatible combinations, may offer a more general and robust mechanism for the evolution of trait combinations under weak epistasis and free recombination (and, more generally, for all cases where biased segregation of alleles is favored). This mechanism may be important for behavioral and learning strategies that frequently produce variable phenotypes differing only slightly in their mean fitness. In our study, for example, complex learning allowed the environment to be represented with twice the resolution of simple learning, but its fitness advantage over simple learning was strikingly small (see Figure 1b in Arbilly et al., 2010). Previous studies comparing the success of different learning rules also suggest that distinct learning rules may differ only slightly in their accumulated gains (March, 1996; Beauchamp, 2000; Groβ et al., 2008).

The coupling of two behavioral traits in the course of evolution is also quite relevant to the field of animal personalities (reviewed by Sih et al., 2004a; Sih et al., 2004b; van Oers et al., 2005; Bell, 2007; Sih and Bell, 2008). It is interesting that despite extensive evidence for correlations among behavioral traits in studies of animal personalities, the genetic mechanism underlying such correlated traits has remained unclear (see some discussion by van Oers et al., 2005; Penke et al., 2007). Recently, the problem of recombination that we have analyzed here was used by Massol and Crochet (2008) to question the validity of Wolf et al.'s theory for the evolution of animal personalities (Wolf et al., 2007). In reply to this criticism, Wolf et al. (2008b) suggested the idea of conditional expression or a “switching device” which is essentially the same as we propose in the present paper. Wolf et al. (2008a) also used conditional expression to circumvent the problem of recombination in further development of their theory, and suggest that this conditional expression be regarded as a representation of a norm of reaction (Max Wolf, personal communication). Conditional expression has in fact been implicitly assumed in many studies in evolutionary game theory, most notably in models of male-female conflict, as the parental investment conflict (e.g., Maynard Smith, 1977; Motro, 1994; Balshine-Earn and Earn, 1997; McNamara et al., 2000). Our work may be the first to explicitly model the evolution of such a mechanism and to illustrate its success under free recombination and weak epistatic selection. While the success of a genetic switch is intuitively plausible, our analysis also illustrates that its evolution in not obvious; despite generating exactly the same combinations of learning and social strategies, we showed that a foraging switch (expressing one of two foraging strategies based on the presence of a learning allele) was not as successful as a learning switch (expressing one of two learning strategies based on the presence of a foraging allele). As explained earlier, the effect of a genetic switch on fitness is determined through its interaction with the genes it expresses, and this is not independent of population dynamics.

How plausible is the genetic switch mechanism and how likely is it to occur? For clarity and concreteness we model the mechanism as a well defined switch that is coded by a separate gene. However, it is possible that a functional switch would emerge simply from either variant of the foraging gene activating only one of the learning alleles (and vice versa in the reverse switch case). Furthermore, the two learning alleles in the model may represent different expression levels of a single “learning gene”. There is evidence that such simple mechanisms are wide spread, and can generate great complexity (e.g. Graveley, 2001; Carroll, 2005; Wray, 2007).

Our previous analysis of the co-evolution between learning and social strategies led us to explore here the more general problem of how such co-evolution can result in stable association of compatible traits. The genetic switch modeled here represents a highly plausible solution that is consistent with empirical knowledge about gene regulation and expression (Carroll, 2005). It would be especially interesting to study further how genetic switches can evolve to express multi-locus combinations or generate cascade effects, and how their evolution or evolutionary constraints may explain empirical data on genetic networks and complex behaviors.

Highlights.

> We model sexual reproduction in a population of learning social foragers

> Asexual model resulted in LD between social foraging trait and learning rule trait

> We find the previously fitter trait combinations do not evolve under recombination

> A modifier of recombination rate does not maintain linkage between the two traits

> A genetic switch generating fit trait combinations by conditional expression evolves

Appendix

The case of a dominant modifier coding for complete linkage

Allele M₂, which eliminates recombination, can evolve successfully and linkage disequilibrium can be maintained in the special case where M₂ is dominant (and thus r₂ = r₃ = 0) and the recombination rate R between the modifier and one of the behavioral genes is zero. The conditions in this case produce interesting dynamics that are illustrated in Figure A. Because haplotypes carrying M₂ are protected from recombination, they increase in frequency when associated with one of the more adaptive combinations (i.e. L₁F₁ or L₂F₂). When such an increase, for example when F₁L₁M₂ becomes the dominant haplotype for producers (see example in Figure A1), not only is it better than F₁L₂ haplotypes but it is also protected from recombining with L₂ alleles. As a result, all F₁ alleles that are not strongly linked to L₁ (through linkage with M₂) are selected against. The M₁ allele could still invade the population and generate recombination but only among part-time scroungers (i.e. F₂L₁ and F₂L₂). Within this class, F₂L₂ always has some advantage and gradually increases in frequency. At this point, the recombination caused by M₁ becomes “silent recombination” since most pairs of haplotypes with combined genotype M₁M₁ are identical in their foraging-learning haplotype, which in this case is F₂L₂. Thus, the frequencies of M₁ and M₂ could still drift within the part-time scrounger class as neutral alleles (see Figure A1). Still, the frequency of M₁ within the fitter haplotypes F₁L₁ and F₂L₂ is much lower than within the other two haplotypes (see Figure A2).

Figure A.

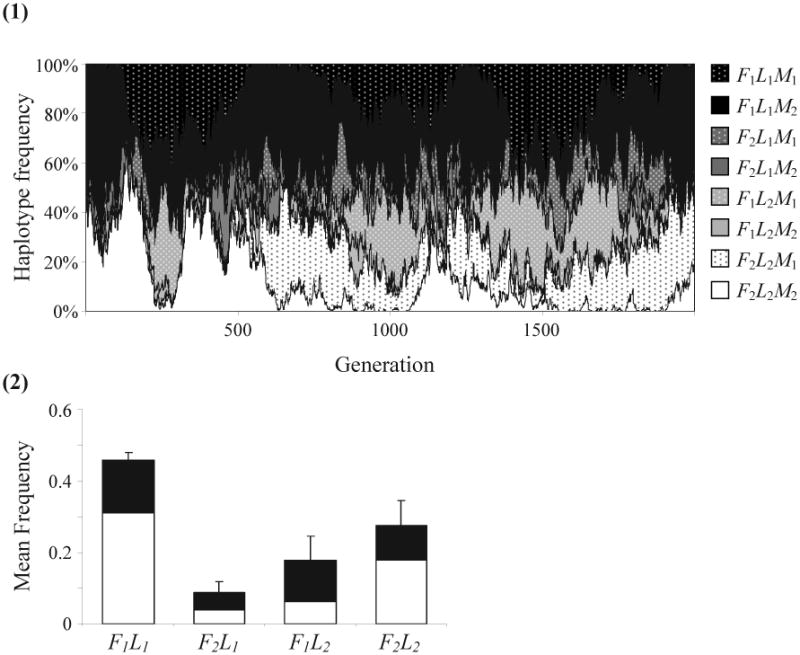
(Appendix). Maintenance of linkage disequilibrium in the special case of linkage dominance, n = 300, J = 70, γ = 0.01. Initial conditions: modifier allele eliminating recombination, M₂, is fixed, and the population is at positive linkage disequilibrium (F₁L₁ and F₂L₂ are at a frequency of 0.4 each, F₁L₂ and F₂L₁ are at a frequency of 0.1 each). (1) Haplotype frequencies throughout 2000 generations. The frequency of each haplotype at each generation is indicated by the area its color occupies on the Y axis. Haplotypes carrying the modifier allele M₁, which increases recombination, have the same background color as their linkage allele M₂ counterparts but with a dotted pattern. (2) Mean haplotype frequencies for generations 1001–2000, for 10 repetitions of the simulation. The white part of each bar represents the frequency of M₂, the modifier allele decreasing recombination rate within the behavioral haplotype, and the black part represents the frequency of M₁, the modifier allele increasing recombination rate.

It is important to note that linkage dominance does not completely protect the population from loss of linkage disequilibrium. While the producer-scrounger game is stable, and the ratio F₁:F₂ is relatively constant, the learning alleles L₁ and L₂ do not maintain a stable relationship. These alleles are not as frequency-dependent as the foraging alleles, and the advantage that each learning allele has over the other within each foraging strategy is very small and might not be realized in the sexual population.