Implementation of Time-Resolved Step-Scan Fourier Transform Infrared (FT-IR) Spectroscopy Using a kHz Repetition Rate Pump Laser

Abstract

Time-resolved step-scan Fourier transform infrared (FT-IR) spectroscopy has been shown to be invaluable for studying excited-state structures and dynamics in both biological and inorganic systems. Despite the established utility of this method, technical challenges continue to limit the data quality and more wide ranging applications. A critical problem has been the low laser repetition rate and interferometer stepping rate (both are typically 10 Hz) used for data acquisition. Here we demonstrate significant improvement in the quality of time-resolved spectra through the use of a kHz repetition rate laser to achieve kHz excitation and data collection rates while stepping the spectrometer at 200 Hz. We have studied the metal-to-ligand charge transfer excited state of Ru(bipyridine)₃Cl₂ in deuterated acetonitrile to test and optimize high repetition rate data collection. Comparison of different interferometer stepping rates reveals an optimum rate of 200 Hz due to minimization of long-term baseline drift. With the improved collection efficiency and signal-to-noise ratio, better assignments of the MLCT excited-state bands can be made. Using optimized parameters, carbonmonoxy myoglobin in deuterated buffer is also studied by observing the infrared signatures of carbon monoxide photolysis upon excitation of the heme. We conclude from these studies that a substantial increase in performance of ss-FT-IR instrumentation is achieved by coupling commercial infrared benches with kHz repetition rate lasers.

INTRODUCTION

Time-resolved infrared (IR) spectroscopy is a powerful method for the study of structural evolution, reaction mechanisms, photophysical properties, and transient excited states.^1–13 Two different approaches are most commonly used for acquiring time-resolved IR spectral data, distinguished by the method used for resolution of the IR spectrum. One is implemented using step-scan interferometry,^{1–10,14–16} whereas the other is based on spectral dispersion using either spectrally scanned single-wavelength detection or spectrally broadband multi-channel detection.^{12,13,17–20} In time-resolved experiments involving light initiation of a dynamic process, there are also two choices for obtaining time-resolved responses. One relies on use of a pulsed infrared laser as a probe, which follows the excitation pulse by a variable time delay. The other relies on use of a continuous infrared source, where the time response is measured using either electronic or optical gating of the continuous probe source.

The specific approach employed to obtain time-resolved IR spectra is generally dictated by practical considerations such as the nature and limitations of available infrared sources and detectors. Fundamentally different approaches are needed for ultrafast (<10⁻⁹ s) versus slower (>10⁻⁹ s) time scales due to the limited time response of IR detectors. For femtosecond and picosecond time scales, an optical pump–probe configuration is used, relying upon a short-pulse-laser excitation source and a similarly short-pulse-laser infrared probe. The time response of the measurement in this case is determined by the duration of the pump and probe pulses and the delay between the two, varied by changing the optical path. The infrared probes may contain up to several hundred cm⁻¹ of spectral width, and the time-response at each infrared wavelength is measured using dispersive methods coupled to either single-wavelength detectors or to multi-channel detection schemes, sometimes in combination with optical upconversion methods to transfer the infrared spectral information to more easily detected visible wavelengths. In contrast, for nanosecond and longer time scales, the most widely implemented methods rely upon step-scan Fourier transform infrared (ss-FT-IR) instrumentation. This time-resolved interferometric approach allows simultaneous full spectral interrogation with a free spectral range of 4000 cm⁻¹ or greater, where the time resolution is obtained by transient electronic sampling of a continuous wave (CW) black-body infrared source relative to the timing of the excitation light pulse.

Time-resolved ss-FT-IR provides the ability to measure transient infrared spectra over the entire spectral region of interest and over several decades of time. It has been widely applied to address scientific questions such as the mechanism of protein responses to light for photosynthetic and other light-activated proteins, the dynamics of charge transfer processes in inorganic molecules and materials, and the structure of molecular excited states. These and other areas of application have been described in an extensive body of scientific literature, including some recent reviews.^9,21

Despite the success of ss-FT-IR in these types of studies, however, there are some limitations that significantly restrict the application of ss-FT-IR. Perhaps the most severe of these limitations is that very long signal acquisition times are normally required in order to obtain excited-state spectra with reasonable signal-to-noise ratios. This limitation is largely a consequence of the fact that, to date, implementation of ss-FT-IR has relied upon coupling of step-scan interferometry with Q-switched, nanosecond-pulsed laser excitation sources that operate with a repetition frequency of, at most, a few tens of Hz. An interferogram will typically consist of at least a few thousand steps to achieve a useful spectral resolution and free-spectral range. Obtaining sufficient signal-to-noise to analyze very small spectral changes associated with excited-state processes can require averaging the results of hundreds of excitation laser pulses per step, or hundreds of thousands of pulses altogether. Thus, irrespective of the actual sequence of stepping and averaging, one finds that measuring transient spectra can require several hours or longer. During that time, significant issues may arise from long-term instabilities of both the sample and the instrument, often fundamentally limiting the signal-to-noise ratio that can be obtained and the types of scientific studies that can be performed.

The reason for this limitation is that until recently, the high per-pulse energies (~200 μJ/pulse) required for time-resolved ss-FT-IR experiments were only available from low repetition rate (~10 Hz) laser systems. Several practical considerations dictate the need for high per-pulse energy of the pump laser. The most commonly used pump laser has been a Q-switched Nd:YAG laser, whose fundamental emission at 1064 nm must be converted to a different wavelength to excite an electronic transition of interest. High per-pulse energies are required for nonlinear generation of the Nd:YAG harmonics (532, 355, or 266 nm) and for pumping dye lasers or nonlinear optical parametric oscillators to produce a range of pump wavelengths. Thus, irrespective of the needed pump pulse energy for any given experiment, simply generating light at desired pump wavelengths through nonlinear optical conversion processes requires the use of high per-pulse energy lasers. Further, in some cases, the photochemical process of interest is inefficient, and substantial pump pulse energies are actually required to achieve sufficient photochemical yields for a ss-FT-IR experiment. Compounding this latter issue, the IR probe beam from the FT-IR spectrometer cannot be focused very tightly (typical focal diameter is greater than 1 mm), meaning that the probe volume that must be excited by the laser is large, and therefore high per-pulse energies are required to generate significant excitation yields. Recent advances in laser technology (more efficient pumping schemes, intracavity harmonic generation, new laser materials) have led to the development of nanosecond pulsed lasers with high per-pulse energies (>100 μJ) that operate with repetition rates in the kHz regime.

A simple example illustrates the advantages of a high repetition rate laser as the pump source in a time-resolved ss-FT-IR experiment. Suppose that 4000 steps are needed per interferogram, and that 100 laser shots are needed per step to achieve a suitable signal-to-noise ratio. At 10 Hz operation, this scenario requires a minimum of 11.1 hours of data collection time (ignoring dead time associated with resetting the interferometer between scans and other instrument or data processing overhead). For a 4 kHz excitation source, this same experiment requires a minimum of 1.67 minutes. Further, in an ideal case, additional signal averaging would increase the signal-to-noise ratio by the square root of time (or square root of the number of excitation pulses), so relative to the original scenario, an order of magnitude improvement in signal-to-noise ratio could be achieved with 167 minutes, or less than three hours, of signal averaging.

Motivated by these considerations, we have explored the implementation of time-resolved ss-FT-IR spectroscopy with a kHz repetition rate pulsed laser source. Here we report a strategy for such implementation that is appropriate for obtaining excited-state spectra of molecular compounds, and we describe the details of the methodology for the particular laser and commercial FT-IR bench that we have employed. While the details of optimal implementation might vary depending on the choice of these commercial components and the types of studies to be performed, the general approach that we describe should be widely applicable. We do note that, in some cases, sample recovery times may be millisecond or longer, which, in principle, might limit usable excitation rates to less than kHz. However, even in these cases, the sample volume can often be replaced on the millisecond time scale by rapid flowing or sample cell translation, and these methods are widely used in kHz excitation rate transient absorption studies on the ultrafast time scale.²² To evaluate improvement in performance, we measure the excited-state infrared spectra of [Ru(bpy)₃]²⁺(bpy = bipyridine) and carbonmonoxy myoglobin (MbCO) and compare the signal-to-noise achieved here to that achieved in previous studies of the same compounds using lower repetition rate excitation sources. We have also demonstrated the applicability of kHz excitation rate ss-FT-IR to biological systems by measuring the excited-state photolysis of carbon monoxide from myoglobin. We conclude from these studies that a substantial increase in performance of ss-FT-IR instrumentation can indeed be achieved by coupling commercial infrared benches with kHz repetition rate lasers.

EXPERIMENTAL

Methods

The Ru(bpy)₃Cl₂ hexahydrate was purchased from Acros and dissolved in deuterated acetonitrile. Before use, the d-acetonitrile is dried using 5-Å molecular sieves to remove water. After preparation, the solution is processed by three freeze–pump–thaw cycles to remove much of the oxygen. The sample solution is then placed in a Wilmad IR cell with CaF₂ windows and a 0.1 mm spacer to define the path length. The cell is positioned in the external bench of the ss-FT-IR instrument and left under nitrogen in the purged box for at least 30 minutes before the measurements are performed.

Horse heart myoglobin (Mb) was purchased from Sigma. The myoglobin was dissolved in deuterated 100 mM potassium-phosphate buffer, pH* 7.4, where pH* denotes the uncorrected pH measurement of the D₂O solution. The enzyme was reduced by the addition of a small molar excess of sodium dithionite under a CO atmosphere to produce the MbCO complex. After the reduction, subsequent purification and concentration steps were carried out under a CO atmosphere. Dithionite was removed by passing the sample through a PD10 desalting column, equilibrated with the D₂O buffer. Diluted protein solution was concentrated using Centricon Amicon tubes with a 10 K cut-off membrane. Further concentration of the sample was achieved by evaporation under a stream of CO. The MbCO was placed between two CaF₂ windows with a 50 μm spacer and sealed with Apeizon vacuum grease.

Instrumentation

We use a Bio-Rad FTS-60 ss-FT-IR instrument in step-scan mode. The instrument is equipped with a home-built external bench. This choice of instruments dictates several of the details of our methodology. Many commercial instruments, including the Bio-Rad, are configured so that spectra can be measured either in conventional rapid-scan mode (with a continuously moving interferometer arm) or in step-scan mode. However, in the Bio-Rad instrument, the step-scan mode is actually achieved by synchronizing the second interferometer arm to the continuously scanning arm of a rapid-scan configuration, where for each “step”, the second interferometer arm is maintained at different fixed distance relative to the continuously scanning arm. To maintain this configuration, an active feedback mechanism is used that involves dithering the position of the second arm with a 16 kHz modulation and using the modulated intensity of a helium-neon laser reference signal to maintain the mirror separation between the two arms. This particular instrumental configuration leads to two important ramifications for the experiments described here. First, it is important to synchronize the excitation laser to the dither signal, so that dithering of the interferometer mirror does not add noise to the measured spectra. Second, the stability parameters associated with this interferometer configuration are likely different than for other configurations, so the optimization of operating regimes, discussed in more detail below, will also likely be different for different types of instruments, either home-built or commercial.

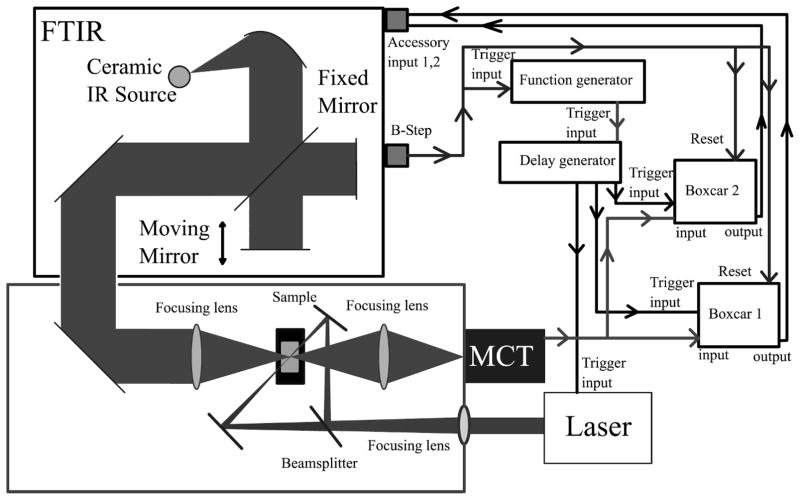
Figure 1 shows a diagram of the optical and electronic configuration of the time-resolved ss-FT-IR experiment. The excitation laser is a diode-pumped solid-state Q-switched Nd:YLF CrystaLaser operating at 351 (Model QL 351–500) or 527 nm (Model QL 527-1W0) and typically used at a repetition rate of 4 kHz. The laser is directed into the external infrared bench and is split into two beams of nearly equal power that are used in a counter-propagating geometry to excite the sample from both ends of the optical path. The sample concentration and path length are typically adjusted to provide an optical density of about 0.6 at the excitation wavelength, so the counter-propagating geometry leads to a significant improvement in the uniformity of excitation throughout the sample volume probed by the infrared beam compared to the situation with conventional single-direction excitation geometry. The excitation beam is focused by a 50 cm focal length lens to a diameter of approximately 3 mm, twice the 1.5 mm diameter of the infrared probe beam. Typical fluence of the excitation laser pulse at the sample is 5.7 mJ/cm².

Fig. 1.

Schematic of the nanosecond ss-FT-IR and the connectivity of the FT-IR. Data collection starts with an initiation signal from the FT-IR going to the function generator and providing a reset signal to the boxcar integration modules. The output from the function generator, described in the text, is passed through a delay generator, which sends pulses to the boxcars and laser. The homemade purged box contains the sample chamber, where the sample is excited from two sides. In the last step the boxcars send the data back to the FT-IR for acquisition and processing.

Under the conditions of our experiments, possible effects due to sample heating by the excitation pulse are minimal. An upper limit for the temperature rise associated with each pulse can be obtained using the sample volume, solvent heat capacity, and assuming that the entire per-pulse energy is absorbed. For the solvents used here, this estimate indicates a per-pulse temperature rise of ≈0.1–0.2 °C. Steady-state temperature increases can also be estimated. Sample cooling rates can be determined experimentally or calculated using heat transfer models and thermal diffusivity coefficients, with both methods providing cooling rates of a few milliseconds for ≈100 μm cell path lengths.²³ Thus, the steady-state temperature rise for the several kHz excitation conditions used here is no more than a few degrees Celsius. For example, a 4 kHz pulse repetition rate, a 5 ms cooling rate, and a 0.2 °C per-pulse temperature rise would lead to a steady-state temperature increase of ≈4 °C. Of course, even this small temperature rise could introduce small changes in the baseline of spectra due to temperature-dependent changes in the solvent reference. However, the sampling methods we describe below almost completely compensate for any small changes in steady-state temperature, because a reference sample is obtained just prior to each laser pulse. Thus, thermal effects in the measured time-resolved difference spectra are limited to those induced by the per-pulse temperature rise, which in our case is very small.

The external bench is contained within a Plexiglas chamber that is purged with dry nitrogen gas to remove water vapor. Typical spectral resolution is 1 cm⁻¹. The interferogram sampling was set to an under-sampling ratio of 2 (sampling at the reference HeNe laser frequency, collecting 7627 steps per scan) to achieve a free spectral range of 7901 cm⁻¹. The data were collected in multichannel step-scan mode with the two boxcars connected to unfiltered channel one and two. One of the boxcars is used to collect the reference and the second is used to collect the probe, as described in more detail below. After collecting the data, channel 1 (reference) was Fourier transformed using zero filling to 2ⁿ numbers and a triangle apodization, and the phase was saved. Channel 2 (probe) was Fourier transformed using zero filling and the triangle apodization and the phase from the reference. The infrared beam is focused onto the sample using a 15.2 cm focal length ZnSe lens (Fig. 1). For co-alignment of the ultraviolet and infrared optical beams, a ~1 mm diameter aperture is positioned on the ultraviolet beam and the infrared throughput is maximized through the same aperture. Effects of any spatial movement of the infrared probe arising from the moving interferometer mirrors are minimized by the use of a much larger excitation spot size relative to the size of the infrared probe. The infrared light is focused onto a detector using a 2.5 cm focal length KCl lens. The detector is a liquid nitrogen cooled, 20 MHz band width, pre-amplified HgCdTe photovoltaic detector (Kolmar, KMPV8-1-J1DC). This detector is determined to have a 15 ns rise time and is used in a dc-coupled configuration with sampling as described below. The detector’s chip size is 1 mm (linear dimension), which is found to be a good compromise between ease of alignment (favored by larger area) and a faster detector rise time (favored by smaller area).

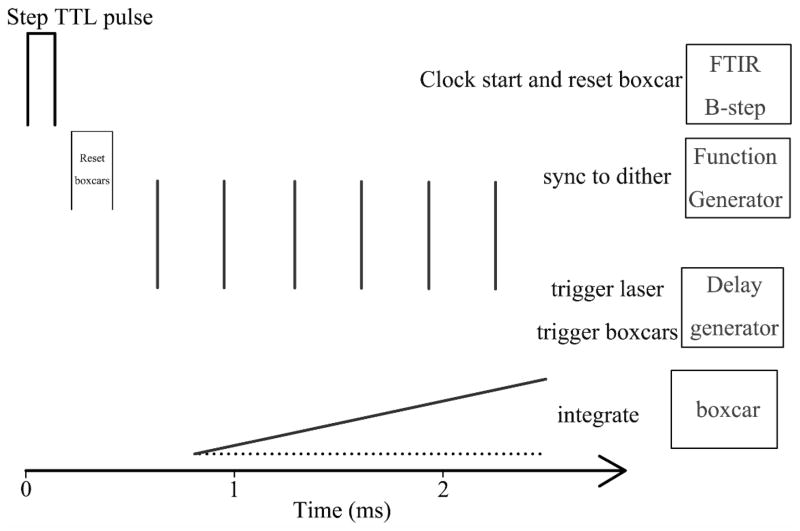
As noted previously, the interferometer output of the FTS-60 is modulated by a 16 kHz dither that is applied to one of the interferometer mirrors. To avoid this modulation appearing as added noise, the excitation laser pulses and sampling of the infrared signal must be phase-synchronized with the sinusoidal dither modulation. To achieve this synchronization (Fig. 2), the experiment is referenced to the master 16 kHz dither modulation signal provided by the step-scan FT-IR as the interferometer is stepped (B-step signal from the Bio-Rad bench). The step signal (a TTL pulse) is used for two purposes. It triggers a function generator (Stanford Research Model SR345) that produces a kHz pulse train of square waves, and it also provides a reset pulse for the boxcar integration modules. The kHz pulse train from the function generator, which can be adjusted in terms of repetition frequency and number of pulses, is passed to a delay generator. The delay generator is used to adjust the time of the initiation of the laser pulse train relative to the interferometer step (to allow for instrument settling time), while maintaining a fixed relationship between the kHz pulse train and the dithering modulation. Typically, the kHz pulse train is set to be at 4 kHz, though other choices are possible while noting that the pulse train must be at a frequency evenly divisible into the 16 kHz dither signal. This pulse train is used to trigger the Q-switched laser, leading to a series of optical excitation pulses, and is also used to trigger the boxcar integrators (Stanford Research Model SR-250) that sample, amplify, and average the infrared signal. The use of a Q-switched laser with low timing jitter between an external trigger signal and the light pulse is essential. This choice allows the laser to be actively triggered and to produce an excitation pulse that is fully synchronized with the interferometer dither modulation. An additional requirement for the present implementation is that the laser be stable when operated in an intermittent pulsed mode, where a burst of pulses is generated for each set of trigger signals from the delay generator, followed by dead time for sampling, the next interferometer step, and instrument settling.

Fig. 2.

A detailed illustration of the synchronization of the data collection at each step. The FT-IR produces a TTL pulse at each step of the interferogram, which is used to start the data collection. The pulse from the FT-IR is used to reset the boxcars and is input into a function generator. The function generator generates a burst of pulses triggered at a rate of 4 kHz (typically) and sent to the delay generator. The delay generator synchronizes the pulses to the 16 kHz dither frequency and triggers the laser and boxcars. The boxcars then sample, integrate, and exponentially average the infrared signal synchronized with the individual laser pulses. As described in the text, both a pre-pulse and a post-pulse sample are taken for each laser pulse. The averaged signal from each of the boxcars is provided to the FT-IR for processing.

For each laser excitation pulse, two infrared signals are measured by setting the sampling gates of the boxcar modules. One gate (reference signal) precedes the excitation pulse and the second (probe signal) is at a specific time delay following the pulse. For the experiments reported here, the timing of the boxcar gates is dictated by the known excited-state lifetimes of the species being examined.¹⁴ Thus, for Ru[bpy₃]²⁺ (excited-state lifetime of several hundred nanoseconds), the gate widths are set to 300 ns, and the pre-excitation-pulse gate is set to end within 200 ns of the laser pulse, while the onset of the post-excitation-pulse gate is set to coincide with the excitation laser pulse. The reference signal acquired prior to the excitation pulse corresponds to an unexcited sample, while the probe signal acquired during and following the pulse includes contributions from the fraction of sample that has been excited by the ultraviolet excitation pulse as well as the residual ground-state molecules. The signals acquired in the boxcar are subject to an analogue exponential averaging by the boxcar electronics (recall that each boxcar module is reset prior to the initiation of each laser pulse train following the interferometer step). The exponential averaging time is chosen to allow the average output of the boxcar to achieve its steady-state level prior to the end of the excitation pulse train and the next interferometer step. The average output of each boxcar module is provided as input to accessory input channels of the FTS-60 instrument and is sampled once per step with a time delay determined by the stepping frequency. For example, at a 200 Hz stepping rate, the data collection is done in the first two milliseconds, and the last three milliseconds are used for the reading of the channels by the interferometer. The FTS-60 instrument requires 3 ms for reading the channels in multichannel step-scan mode.

As previously described, collected interferograms are transformed using a fast Fourier transform algorithm with zero filling, which results in single beam intensity spectra. In all cases, prior to the experiment, a background spectrum of the solvent only is collected. The ground-state absorption spectrum of the sample is then generated relative to the solvent as A₁ = −log(I₁/I₀), where A₁ is the absorbance, I₁ is the intensity spectrum for the unexcited sample (i.e., the intensity spectrum measured using the pre-excitation-pulse sampling), and I₀ is the intensity spectrum of the solvent. Similarly, the absorption spectrum following excitation, A₂, is generated as A₂ = −log(I₂/I₀), where I₂ is the intensity spectrum measured following excitation (i.e., the intensity spectrum measured using the post-excitation-pulse sampling). Note that A₂ contains both ground-state and excited-state contributions, the former from unexcited molecules and the latter from the fraction of molecules that were excited and that remain in the excited state at the given delay time. A difference spectrum associated with the photo-excitation process, ΔA, is generated as ΔA = A₂ − A₁. Finally, an excited-state absorption spectrum, A_es, can be generated as A_es = ΔA +δA₁ = A₂ − (1 − δ)A₁. The value of δ is determined empirically to be that required to just remove negative features in ΔA, but in all cases is also in good agreement with the fractional excitation probabilities estimated from the experimental conditions, typically 0.1 or less. To improve signal-to-noise, either more excitation pulses can be averaged for each interferometer setting or multiple interferograms can be measured and averaged. Exploration of the overall instrument performance under various choices of these averaging parameters is described in the Results section.

RESULTS

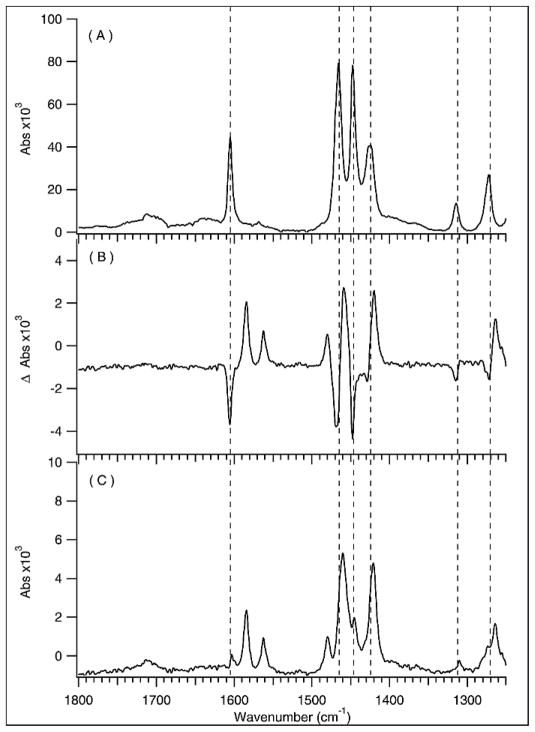
The ground- and excited-state FT-IR spectra of Ru[bpy₃]²⁺ are shown in Fig. 3. The excited-state data were acquired by averaging over 30 laser pulses per step, using 7627 steps in the interferogram, and averaging 10 spectra. The interferometer was stepped at 100 Hz. The ground-state spectrum, corresponding to A₁ in the discussion above, is shown in Fig. 3A. The difference spectrum, ΔA, is shown in Fig. 3B, and the reconstructed excited-state spectrum, A_es, is shown in Fig. 3C. To obtain A_es, (0.073 × A₁) was added to ΔA, which was found to remove the negative features in ΔA that correspond to bleach signals of the ground state without introducing any additional positive features. By comparing the photon density at 351 nm to the molecules in the probe volume, a 10% excitation probability is expected, which is close to the 7.3% experimentally achieved.

Fig. 3.

[Ru(bpy)₃]²⁺ was excited using 351 nm 20 ns pulses at 5.7 mJ/cm² of fluence. The FT-IR was operated at 100 Hz, collecting 10 spectra while averaging 30 pulses per step. (A) Ground-state absorption spectrum of [Ru(bpy)₃]²⁺. (B) The difference spectrum associated with photo-excitation of [Ru(bpy)₃]²⁺ graphed as laser on absorbance minus reference absorbance. (C) Excited-state spectrum obtained by adding 7.3% of the ground-state spectrum to the photo-excitation difference spectrum.

The minimal data acquisition time for these data was (#steps/spectrum)(1/Step Rate)(#spectra) = 762 s, or approximately 12.7 minutes (0.2 hours). In practice, due to interferometer cycling time and settling time per step, and most importantly, the need to acquire a high-quality spectrum of the solvent (I₀ in the discussion above), the total actual data acquisition time for the spectra shown was 50 minutes. The spectra shown correspond to a total averaging of 300 laser shots per interferometer setting. The signal-to-noise ratio achieved can be estimated from, for example, the data shown in Fig. 3B. Away from any real spectral features, the noise is found to be ≈1 × 10⁻⁴ absorbance units. Typical signal levels are ≈3 × 10⁻³ absorbance units, for a S/N ≈ 30. These results can be compared with a previously published study of Ru[bpy₃]²⁺ obtained using a 10 Hz excitation laser.¹⁴ In that study, similar signal-to-noise was achieved, albeit at much lower spectral resolution and reduced spectral coverage, making analysis and interpretation of the transient spectra more difficult. The total number of laser shots per interferometer point was 256, corresponding to a data acquisition time of more than 14 hours. Roughly speaking, this comparison indicates that for similar numbers of laser pulses, one obtains similar signal-to-noise, which is not an unexpected result. Further improvements in signal-to-noise could be obtained by additional averaging, and one would anticipate that the noise limit should decrease approximately as the square root of laser pulses. At low laser repetition rates, the previously discussed study is near the limit of what could be practically achieved due to long-term stability and sample degradation limitations. However, in our case, an additional factor of 2 in signal-to-noise could be expected simply by increasing data acquisition time by four times, to be on the order of a few hours at most (depending on the time needed to acquire a solvent spectrum of sufficiently high signal-to-noise). Thus, the implementation of step-scan time-resolved FT-IR with a kHz repetition rate laser source provides a tremendous advantage in terms of rapid data acquisition.

As an aside, the data shown in Fig. 3 represent the most spectrally resolved measurement of the excited-state infrared spectrum of Ru[bpy₃]²⁺ published to date. A few words concerning interpretation of these data are appropriate. A large body of previous experimental and theoretical work has established that excitation of this compound leads to a localized metal-to-ligand charge transfer excited state in which the Ru center is formally oxidized to Ru³⁺, while one bpy ligand is formally reduced to bpy^−.24–27 Thus, one could expect two new sets of vibrations in the excited-state infrared spectrum (with an intensity ratio of 2:1), which reports on the bpy ligands: (1) peaks associated with a reduced bipyridine and (2) peaks associated with a neutral bipyridine in the presence of the oxidized (Ru³⁺) center. However, the frequency shifts associated with the oxidation of the Ru center are quite small, having been previously measured by comparison of Ru[bpy₃]²⁺ to be at most a few cm^−1.25 Such small shifts and Ru[bpy₃]³⁺ may not always be evident in the excited-state spectra. On the other hand, the reduced bipyridine will likely demonstrate much larger shifts in infrared active peaks, and it is likely that most of the large features in the excited-state spectrum (Fig. 3C) correspond to the reduced bipyridine. Further assignment of the spectral peaks observed is not attempted here but will be the focus of subsequent investigations.

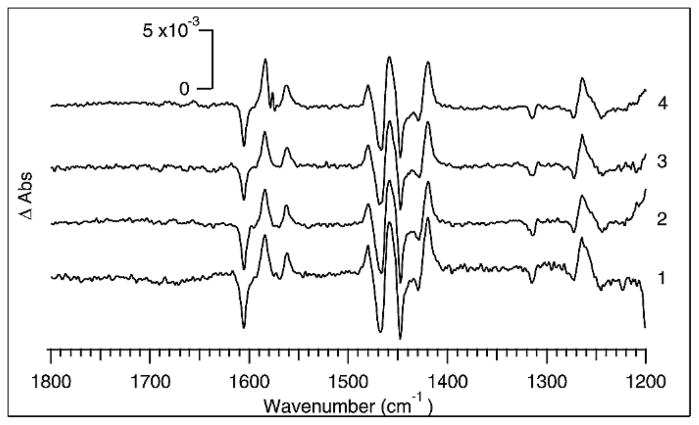
An interesting possibility enabled by the integration of high repetition rate laser sources with step-scan FT-IR is the ability to optimize the instrument’s performance by trading off the interferometer stepping rate versus the number of laser shots averaged per step. Thus, we have carried out a series of experiments in which the overall number of laser shots averaged per interferometer step are equal, but the scan rate of the interferometer is varied. The interferometer scan rate was varied between 200 Hz and 25 Hz. At each setting, nine laser pulses were averaged per interferometer step, and 33 scans were averaged to produce transient spectra that were the average of 297 excitation pulses. The results are shown in Fig. 4. For each scan of 7627 points, the time required is 38, 76, 152, and 305 seconds at 200, 100, 50, and 25 Hz, respectively. The slower stepping frequencies are then more susceptible to instrument drift during the scan than the higher frequencies. Such drift is caused, for example, by fluctuations in the infrared source or by temperature fluctuations that perturb the interferometer and is generally manifested as baseline irregularities. Perturbations to the baseline are clearly largest for the spectrum obtained at the 25 Hz stepping rate in Fig. 4, whereas the spectrum obtained at 200 Hz has the flattest baseline. For small signals, the baseline irregularities observed at lower stepping frequency can be the most significant noise source in the spectrum.

Fig. 4.

Photo-excitation difference spectra of [Ru(bpy)₃]²⁺ obtained using FT-IR scan rates from 200 to 25 Hz while collecting 297 total pulses for each spectrum. At (4) 200 Hz, (3) 100 Hz, (2) 50 Hz, and (1) 25 Hz the boxcars averaged 9 pulses per step and collected 33 scans. A burst of 9 pulses triggered the laser and boxcars. The per-pulse fluence was kept as close as possible to approximately 5.7 mJ/cm².

We have also investigated the use of kHz excitation rates to obtain time-resolved ss-FT-IR spectra of proteins. While we expected an improvement in performance of the experiment similar to the inorganic system, there are potential pitfalls with the application of kHz excitation rates in this case. Protein samples are susceptible to optical damage under pulsed laser illumination that leads to denaturation and even precipitation of the protein. Thus, one goal of this study was to determine whether protein samples are stable under the conditions required for kHz excitation rates (moderate per-pulse energy of ~100 μJ, but high average power, ~100 mW). Another goal was to investigate whether the slower recovery times of photo-excited protein samples would hinder data acquisition at kHz rates. Finally, we wanted to determine the improvement in the quality of time-resolved spectra of proteins obtained under these conditions.

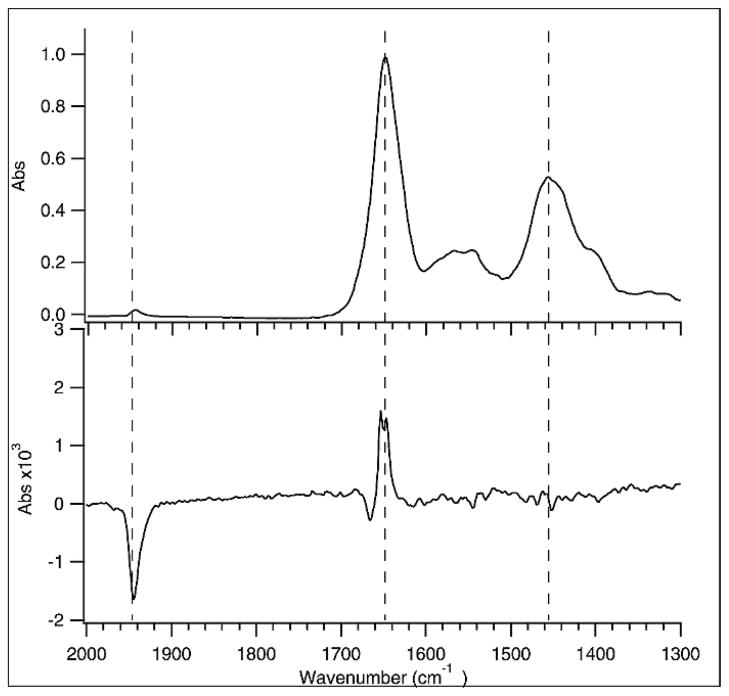
We chose to investigate the photolysis of carbon monoxide from carbonmonoxy myoglobin (MbCO) as a test case because this reaction has been thoroughly studied by time-resolved IR spectroscopy.^22,28–30 A frequency-doubled Nd:YLF laser operating at 527 nm is used to excite the MbCO, causing photodissociation of the CO from the heme and subsequent relaxation of the protein structure. The repetition rate of the laser was 1 kHz in order to accommodate the approximately millisecond rebinding lifetime of the photodissociated CO. Some steady-state population of photodissociated species might be generated under these conditions depending on the per-pulse excitation probability, the CO concentration (and hence the bimolecular recombination time), and the duration of each burst of excitation pulses. However, because of the sampling scheme used (see Experimental section), the only effect of any production of steady-state photodissociated population will be to reduce the size of the observed transient signal. The time-resolved ss-FT-IR spectrum obtained at 250 ns delay time shown in Fig. 5 was obtained using a MbCO concentration of 2.4 mM in D₂O solution and a laser fluence of 1.1 mJ/cm². The dominant feature in the spectrum is the bleach at 1944 cm⁻¹, corresponding to the loss of CO bound to heme in the ground state. We estimate that the photolysis yield under these excitation conditions is about 10%, based on the amplitude of the CO bleach. The measured yield is in good agreement with the calculated yield based on the pump beam energy and heme absorbance, indicating very little photo-degradation of the protein under these excitation conditions. We also saw no evidence of precipitated protein and no change in the FT-IR spectrum due to protein denaturation.

Fig. 5.

FT-IR spectra of 2.4 mM carboxy myoglobin in D₂O buffer using a 50 μm path length in a CaF₂ cell. The time-resolved FT-IR data were collected at an interferometer step rate of 100 Hz, with 7 pulses per step and averaging 120 scans. The laser was triggered at 1 kHz to allow the myoglobin to relax as much as possible before the next pulse was absorbed. (Top) Ground-state absorption spectrum. (Bottom) Difference spectrum of the photolysis upon excitation using 527 nm pulses with 1.11 mJ/cm² incident fluence. The boxcars were set to integrate the first 250 ns of infrared signal during and after the laser pulse.

Photodissociated CO is initially trapped in the “B” site within the heme pocket and gives rise to features near 2080 cm⁻¹, which are too weak to be observed under the conditions of this experiment. These features have only been observed at much higher protein concentrations, for which the protein amide vibrations become saturated. Under the present conditions, however, we obtain very high quality data for both the CO region and the protein backbone region, allowing us to simultaneously monitor the changes in ligation state of the heme and the coupled changes in protein conformation. Following CO photodissociation, the protein relaxes to accommodate the high-spin, 5-coordinate heme and free CO, producing changes to the amide I protein backbone vibrations between 1600 and 1700 cm⁻¹. We have already shown that the initial relaxation of the protein occurs on the picosecond timescale.²⁸ The observed ss-FT-IR spectrum is in good agreement with that observed at earlier times. We conclude that no further change occurs between the initial relaxation within 10 ps and the 250 ns timescale of the spectrum in Fig. 5. Clearly, it is possible to obtain high-quality time-resolved FT-IR spectra of proteins using a high repetition rate excitation laser without photo-degradation of the sample.

CONCLUSIONS

Step-scan FT-IR is a powerful tool for investigating excited-state structure and dynamics. However, previous implementations have been limited by the use of low repetition rate excitation sources. With such sources, very long data acquisition times of hours to days are required to achieve signal-to-noise ratios that provide useful information. We have demonstrated that nanosecond time-resolved step-scan FT-IR can be performed using a kHz pulsed laser source integrated with a commercial step-scan bench. This technological improvement leads to high-quality step-scan spectra in the mid-infrared region being obtained in minutes rather than hours and opens up the possibility of a wide range of new experiments. The new method developed has been demonstrated by measuring the excited-state spectra of Ru[bpy₃]²⁺ and MbCO as prototypical examples of transition metal complexes and photoactive proteins. In both cases, excited-state infrared spectra comparable to or better than previously published data have been obtained with data acquisition times that are a fraction of those previously required.

The configuration used for this work, which involves sampling a single time window in the excited-state decay process, is optimal for the case where one wishes to obtain a single excited-state spectrum at some fixed time following an excitation pulse. Such a situation is common when the lifetimes of photophysical processes are independently known, for example through other experiments such as time-resolved luminescence or time-resolved absorption experiments. In this case, what is desired from the step-scan FT-IR experiment is simply the structural information that can be obtained from infrared data. However, in other cases, one may wish to measure true time-resolved dynamics from the infrared experiment. Then the method presented here can easily be modified. One possibility would be simply to implement the above method for multiple experiments, each performed with a different setting of the time-delayed boxcar sampling gate. However, this approach would require significantly more experimental time. Alternatively, one could implement the experiment using digitization instrumentation to acquire the time-dependent waveform of the infrared signal, spanning both pre-excitation pulse and post-excitation pulse time windows, with waveform averaging across multiple laser shots at each step of the interferometer. We are currently exploring this strategy for obtaining high-quality transient infrared data with much reduced acquisition times relative to current methods.