How Crouch Gait Can Dynamically Induce Stiff-Knee Gait

Abstract

Children with cerebral palsy frequently experience foot dragging and tripping during walking due to a lack of adequate knee flexion in swing (stiff-knee gait). Stiff-knee gait is often accompanied by an overly flexed knee during stance (crouch gait). Studies on stiff-knee gait have mostly focused on excessive knee muscle activity during (pre)swing, but the passive dynamics of the limbs may also have an important effect. To examine the effects of a crouched posture on swing knee flexion, we developed a forward-dynamic model of human walking with a passive swing knee, capable of stable cyclic walking for a range of stance knee crouch angles. As crouch angle during stance was increased, the knee naturally flexed much less during swing, resulting in a ‘stiff-knee’ gait pattern and reduced foot clearance. Reduced swing knee flexion was primarily due to altered gravitational moments around the joints during initial swing. We also considered the effects of increased push-off strength and swing hip flexion torque, which both increased swing knee flexion, but the effect of crouch angle was dominant. These findings demonstrate that decreased knee flexion during swing can occur purely as the dynamical result of crouch, rather than from altered muscle function or pathoneurological control alone.

Introduction

Patients with cerebral palsy often experience difficulties during walking, which hampers their daily-life functioning. One important gait deviation in these patients is the occurrence of a ‘stiff-knee’ gait pattern, in which the knee of the swinging leg flexes much less than during typical human walking (Fig. 1a).21 In normal gait, the hip and knee are quickly flexed during pre-swing and initial swing, leading to forward progression of the swing leg and sufficient foot clearance. By contrast, a stiff-knee gait pattern leads to reduced foot clearance, foot dragging, frequent tripping, reduced step length, and reduced speed, and thereby limits functional performance. Stiff-knee gait has been reported to occur in 80% of ambulatory children with cerebral palsy,25 but its causes are yet unclear, making effective treatment difficult.

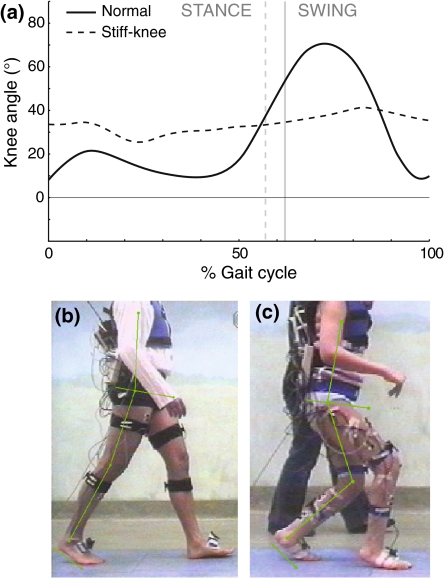
Figure 1.

(a) Example stiff-knee flexion–extension pattern (dashed line) compared to a normal knee angle during a stride (solid line). The stiff-knee gait pattern has an extremely limited dynamic range of motion and absence of appropriate knee flexion in the swing phase. Reproduced with permission from Sutherland and Davids21. (b, c) Examples of leg configuration at onset of push-off in normal and crouch gait, showing that knee angles can differ vastly, which may affect the progression of the leg into swing. Pictures are from a separate experimental study

Several potential causes of stiff-knee gait have been proposed in the literature. The cause most often mentioned is excessive activity in quadriceps muscles, especially in the rectus femoris, during swing16,18 or during pre-swing.1,6,7,17 Another potential cause is reduced or ineffective push-off of the trailing leg during double support, for example due to gastrocnemius weakness10 or due to toe-walking.9 Reduced hip flexion torque during (pre)swing has also been implicated as a possible cause.11,16,19

Stiff-knee gait often occurs in combination with excessive knee flexion during stance (crouch gait), which could also affect knee flexion during swing. In crouch gait, the knee is excessively flexed during stance and at the onset of push-off (Figs. 1b and 1c). Such a crouched leg positioning during push-off may influence the progression of the leg into swing, for example by influencing the swing leg dynamics, the effectiveness of push-off, or the distribution of energy between the trunk and the swing leg. However, there is still a limited understanding of the biomechanical factors that lead to adequate knee flexion in swing, and little is known about possible effects of a crouched posture.

Many studies on the causes of stiff-knee gait have used forward-dynamic simulation and induced acceleration techniques in complex musculoskeletal models to study the role of local muscle function during (pre)swing on swing leg knee flexion. These analyses have been performed using full body simulations6,19 or on the swing leg only, prescribing the pelvis motion in time.16 These studies yielded valuable insight into the role of individual muscle function on stiff-knee gait. However, the complexity of the models may also hamper a more conceptual understanding of the causes of stiff-knee gait.

A different approach to gain insight into human walking is to consider the passive dynamics of simplified conceptual models. Relatively simple dynamic models, i.e., with little or no actuation and simple geometry, can produce stable periodic walking motions.5,14,15 Such models have lent insight into the mechanics of normal human gait, such as the relationship between push-off and energy use.4,13 In robotics research, passive dynamics have been used to increase the efficiency and stability of walking machines.2 Although simple models do not cover all characteristics of human walking, they allow for thorough analysis of a basic set of parameters that influence gait. When cyclic motions are considered, the effect of parameter variations can be studied on the entire gait cycle for consecutive steps. This approach is aimed at revealing the inherent influence of passive dynamics on motion, which has meaningful consequences regardless of actuation or control.

The purpose of this study was to investigate possible dynamical causes of stiff-knee gait by thoroughly examining the effects of crouch, push-off strength, and hip torque on knee flexion during swing using a conceptually simple dynamic model of human gait.

Methods

Outline

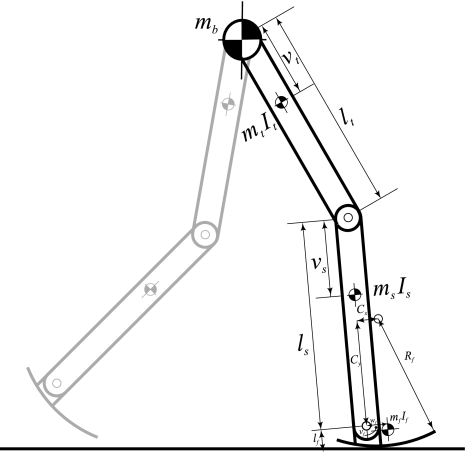
We developed a simplified model of the human body, as shown in Fig. 2, and used this model to perform forward-dynamic simulations of walking. The model had rigid knee and ankle joints in stance and a free, passively flexing and extending knee joint in swing. Human ankle push-off was modeled as an instantaneous push-off impulse under the trailing leg, just before contralateral heel strike. First, we studied the nominal behavior of the model when walking with straight legs during stance (‘upright model’) on level ground. Next, we simulated a range of crouch impairments by varying the knee extension limit of the model. We also investigated the effect of push-off magnitude, and of swing hip flexion torque, modeled as an inter-leg spring with varying stiffness. We evaluated the effects of crouch, push-off magnitude, and hip torque, as well as their interaction. The primary outcome measures were knee flexion and foot ground clearance during swing. An overview of the studies and outcome measures is given in Table 1, and further details are provided below.

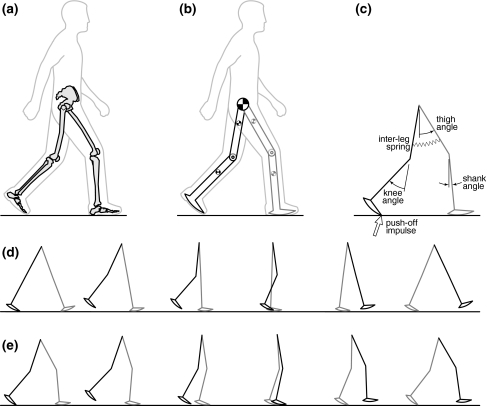
Figure 2.

(a, b) The model captures a simple representation of the human body as a set of rigid links and hinges. (c) We modeled ankle push-off as an instantaneous impulse and the effect of hip muscles as an inter-leg spring. See Appendix A1 for a detailed representation and parameter values. (d) Stick figures representing different phases during a step for upright and (e) crouch gait (22.5° knee flexion in stance)

Table 1.

Overview of studies performed

Study	Crouch angle (°)	Push-off magnitude (N s)	Hip spring stiffness (N m rad−1)
Nominal upright model	0	40	0
Crouch angle	0-max (28)	40	0
Push-off	0	min (16)-max (100)	0
Push-off × crouch angle	0-max	16-100	0
Hip torque	0	40	0-max (4.9)
Hip torque × crouch angle	0-max	40	0-max

Model Description

The model was similar to prior conceptually simple sagittal-plane models that have been used to study non-pathological gait.5,12,15 A detailed diagram of the model and a table of model parameters can be found in Appendix A1. Leg segments were modeled as rigid links with length, mass, and inertia based on average anthropometry of a group of male human subjects.22 For simplicity, the head, arms, and trunk were collectively modeled as a point mass of anthropomorphic magnitude, located at the hip. Hip and knee joints were modeled as frictionless hinges that allowed flexion and extension movements, and the knee could be locked at various angles. The ankles were always locked at 0°, such that the shank and foot formed one rigid body. Foot contact similar to that of human walking was provided by modeling the feet as arcs that rolled along the ground, with roll-over shape based on experimental values for humans.8 When the end of the arc shape (the “toe”) was reached, this point became the new contact point around which the foot rotated, similar to the metatarsophalangeal joint in humans.

Nominal Walking Simulation

We first simulated walking with a straight stance leg, qualitatively similar to normal human gait, as depicted in Fig. 2d. As with human walking, the motion consisted of a single support phase, in which the body was supported by one leg (the stance leg) while the other leg (the swing leg) swung forward; and a double support phase, in which the weight was transferred from one stance leg (the trailing leg) to the next (the leading leg). During single support, the knee of the stance leg was locked in full extension, so that the stance leg acted as a single inverted pendulum. The knee of the swing leg was free to move, so that it could passively flex and then extend, until it reached full extension. At full extension an instantaneous inelastic collision occurred (knee strike), and the knee was locked to prevent hyperextension. The double support phase began with an instantaneous push-off impulse applied under the trailing foot just before contralateral heel strike, and directed toward the hip. This impulse represented the ankle push-off that provides much of the positive work powering human walking23 and was the only energy input to the model. Immediately after push-off, heel strike of the leading leg with the floor was modeled as an instantaneous, perfectly inelastic collision. This collision represented the negative work typically performed by the leading leg during double support. Push-off magnitude for the nominal model was chosen so as to achieve a slow human walking speed approximating patient gait. The knee joints remained locked during push-off and collision, and were unlocked at the beginning of swing.

We derived equations of motion for the model and performed forward-dynamic simulations to produce cyclic gait. Equations of motion were derived using the TMT-method,20,24 described in detail in Appendix A.2–A.7. The equations of motion were solved forward in time by a numerical integration routine. We only considered periodic motions (limit cycles), in which the orientations and velocities of the body segments at the end of a step were identical to their values at the beginning of the step. This ensured that the results did not reflect transient behavior, which may be unsustainable and can confound comparisons of behavior across model parameters. We searched for periodic motions using a first order gradient search optimization, and assessed stability using Floquet analysis15 (Appendix A.8). All simulations were performed in MatLab^®.

Crouch Angle, Push-Off, and Hip Torque

We simulated a range of crouch gait impairments by varying the knee extension limit of the model, an example of which is shown in Fig. 2e. The knee angle of the stance leg (the ‘crouch angle’) was gradually increased from zero to the peak attainable value while keeping all other parameters constant. The knee of the swing leg was still free to move into flexion and then extension, but knee extension in terminal swing was limited to ensure that the knee angle at foot contact was equal to the prescribed crouch angle. For each crouch angle, we found a new periodic gait. For large crouch angles, periodic solutions either could not be found or were unstable (a common feature of limit cycle walking models at extreme parameter values) and such gaits were not considered.

We studied the effect of push-off impulse magnitude both independently and for interaction with crouch angle. We first varied the push-off impulse magnitude independently in the upright model, gradually decreasing and increasing the magnitude across the full range of values that yielded stable periodic gaits. We then varied both push-off and crouch angle simultaneously, finding stable periodic gaits for each possible combination.

Likewise, we evaluated the effect of adding a hip flexion torque in initial swing, first independently in the upright model and subsequently in combination with crouch angle. We modeled hip torque as a torsional spring acting between the stance leg and swing leg (Fig. 2c), representing the combined effect of muscles around the pelvis.3,12 This spring pulled the swing leg forward during initial swing, and slowed it down during terminal swing, without adding net energy to the system.

Outcome Measures

We evaluated the effects of crouch angle, push-off, hip torque, and their combinations on the main outcome measures: knee flexion and foot clearance in swing. These outcome measures were calculated for each periodic gait over the full range of attainable solutions. The increase in knee flexion during swing (ΔKFS) was used as a measure of ‘stiff-knee gait,’ and calculated as the peak knee flexion reached in swing minus the knee flexion at swing initiation (i.e., crouch angle) (Fig. 3). This captured two important aspects of swing knee flexion. First, ΔKFS is a measure of the angular displacement of the knee during swing, which is directly related to stiffness. Second, ΔKFS indicates the difference between the stance and swing leg knee angles, which is related to foot clearance. The other main outcome measure was foot clearance, calculated as the lowest position reached by any point of the foot during the middle portion of leg swing (defined as 60–90% of the gait cycle). We allowed the foot to pass through the floor without interference during this period, to avoid foot scuffing. The foot clearance could therefore be negative, a sign of inadequate swing leg behavior.

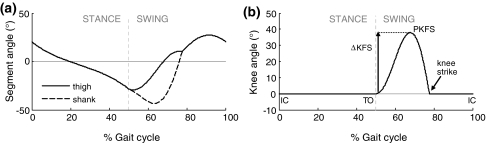
Figure 3.

(a) Thigh and shank segment angles, with respect to the vertical. The thigh angle is roughly equivalent to the hip angle in standard clinical gait analysis. (b) Knee joint angle for upright gait (0° stance knee flexion). Outcome measures included ΔKFS, the increase in knee flexion in swing, and PKFS, peak knee flexion during swing. IC denotes initial contact (heel strike), TO denotes toe-off

We also evaluated spatiotemporal and energy outcome measures for the main effects of crouch angle, push-off magnitude, and hip torque. We calculated speed, step frequency, and step length for each cyclic gait. Furthermore, we calculated the total amount of energy added during push-off, since an equally sized push-off impulse does not necessarily lead to identical energy input across gaits. We also calculated the distribution of this added energy between the swing leg and the rest of the body (trunk + stance leg). Similarly, we calculated the total amount of energy lost (which equals the energy added for steady-state periodic motions) and the distribution between energy lost at heel strike and energy lost at knee strike. These energy values were calculated as the changes in total (i.e., sum of potential and kinetic) energy of the segments.

Results

Increased crouch angle led to decreased knee flexion and decreased foot clearance for all push-off magnitudes and hip torques. Independently increasing push-off or hip torque led to increased knee flexion and foot clearance, but with smaller maximal effects.

Nominal Walking Simulation

The gait pattern of the upright model is depicted in Fig. 2d, while Fig. 3 shows the corresponding thigh, shank, and knee angles as a function of the gait cycle (stance + swing). Thigh and shank angles were measured with respect to the vertical, making the thigh angle similar to the hip angle in conventional gait analysis. In nominal upright gait the model walked at a speed of 0.85 m s⁻¹, a step frequency of 1.03 steps s⁻¹, and a step length of 0.83 m. ∆KFS (which is identical to peak knee flexion in the case of upright gait) was 38° and occurred relatively early in swing, at about one-third of the swing phase (Fig. 3b). Knee strike occurred at approximately 75% of the gait cycle. The swing foot cleared the ground during mid-swing by 2.2 mm, relatively little clearance compared to human gait.

Energy was added by the push-off impulse (10.2 J) and lost at knee strike (2.5 J) and heel strike (7.7 J) collisions. Approximately 25% of the energy added was distributed to the swing leg and 75% to the rest of the body.

Crouch Angle

An example of the crouch gait pattern is shown in Fig. 2e, which illustrates a single step with a mild crouch angle of 22.5° imposed on the stance knee. At this crouch angle, the model walked at a speed of 0.84 m s⁻¹, a step frequency of 1.06 steps s⁻¹ and a step length of 0.79 m, similar to upright gait. However, peak knee flexion was only 26.2°, leading to ΔKFS of only 3.7°, and foot clearance was −1.0 mm (which would mean foot scuffing for humans).

Crouch angles ranging from 0° to 28° could be imposed on the stance knee while keeping all other parameters constant and still allowing stable periodic motions. With crouch angles higher than 28° the model tended to fall forward over successive steps, partly due to the forward shift of the effective center of mass of the legs. As a result, the swing foot tended not to rise above the ground, so periodic gait patterns could not be achieved for larger crouch angles.

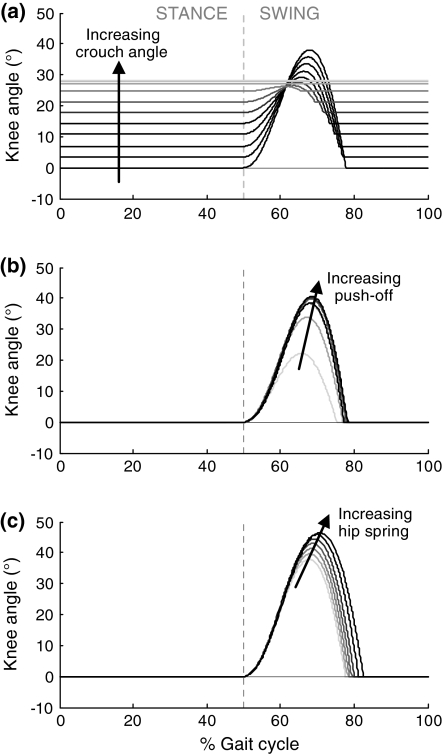
As crouch angle increased, knee flexion and foot clearance decreased while walking speed and energy distribution varied little (Fig. 4). As crouch angle was increased from 0° to 28°, ΔKFS decreased from 38° to 0° (Fig. 4a), resulting in a ‘stiff-knee’ gait pattern. This is illustrated in Fig. 5a, showing the knee angle as a function of the gait cycle for a number of increasing crouch angles. At higher crouch angles, no further knee flexion was achieved in swing and the knee remained effectively fixed during the entire stride. Figure 5a also shows that not only ΔKFS, but also the absolute peak knee flexion decreased with crouch angle, from 38° to 28°. Furthermore, the timing of both peak knee flexion and knee strike occurred earlier in the gait cycle. Reduced knee flexion in swing resulted in diminished foot clearance, which became negative at higher crouch angles (Fig. 4a).

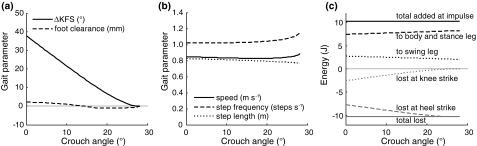
Figure 4.

The effect of crouch angle on (a) ΔKFS (the increase in knee flexion during swing) and foot clearance; (b) speed, step frequency, and step length; and (c) energy distribution. Data are from gaits with a push-off impulse size of 40 N s and no hip spring

Figure 5.

Knee angles as a function of the gait cycle for a number of (a) increasing levels of crouch gait, (b) increasing push-off magnitudes, and (c) increasing levels of hip spring stiffness

Speed, step frequency, and step length changed slightly with crouch angle (Fig. 4b). Speed first decreased slightly from 0.85 to 0.83 m s⁻¹ as crouch angle was increased from 0° to 18°, and then started to increase again, reaching 0.90 m s⁻¹ at 28° of crouch. Step frequency increased with crouch angle, going from 1.03 to 1.16 steps s⁻¹, while step length slightly decreased from 0.83 to 0.77 m.

The total energy added during push-off remained nearly constant with increasing crouch angle (Fig. 4c). The amount of energy distributed to the swing leg decreased by approximately 25% from 2.7 to 2.0 J. The energy lost at knee strike also decreased with crouch angle, going to zero at higher crouch angles.

Push-Off

The upright model could be stably powered by push-off magnitudes ranging from 16 to 100 N s. For weaker push-off, the propulsion was insufficient to achieve cyclic gait. The stance leg moved too slowly and the swing leg swung back before it could catch the fall of the stance leg. For stronger push-off, the model could reach cyclic solutions but became unstable.

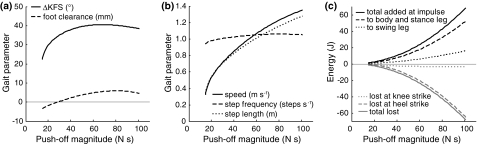
Greater push-off magnitude led to better knee flexion in swing and better foot clearance (Fig. 6a). ΔKFS ranged from 25° at a push-off magnitude of 16 N s, to 41° at a push-off magnitude of 70 N s. For greater push-off magnitudes, ΔKFS leveled off and started to decrease slightly. Peak knee flexion and knee strike occurred somewhat later in the gait cycle with increasing push-off magnitude (Fig. 5b).

Figure 6.

The effect of push-off magnitude on (a) ΔKFS (the increase in knee flexion during swing) and foot clearance; (b) speed, step frequency, and step length; and (c) energy distribution. Data are from gaits with 0° knee flexion and no hip spring

Speed and step length also increased with push-off magnitude (Fig. 6b). Speed increased up to 1.36 m s⁻¹, at a relatively large step lengths of up to 1.28 m. Step frequency increased only slightly with push-off magnitude. Naturally, the total energy added during push-off also increased with push-off magnitude (Fig. 6c). The distribution between swing leg and trunk plus stance leg remained relatively constant, at approximately 25 vs. 75%, while energy was increasingly lost at heel strike.

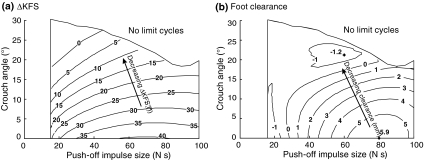
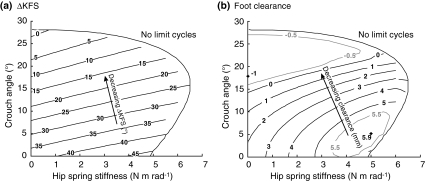
Push-off had a slight interaction with crouch angle, but did not affect ΔKFS and foot clearance as strongly (Fig. 7). As can be seen in Fig. 7a, ΔKFS decreased with increasing crouch angle for all push-off magnitudes. For low push-off magnitude and high crouch angles, ΔKFS was zero, indicating that no further knee flexion in swing occurred. Foot clearance also decreased with increasing crouch angle across push-off magnitudes (Fig. 7b). For low push-off magnitude and high crouch angles, the foot clearance was negative, indicating foot scuffing for humans.

Figure 7.

(a) Contour plot of ΔKFS (increase in knee flexion during swing) as a function of both push-off magnitude and crouch angle. (b) Contour plot of foot clearance as a function of both push-off magnitude and crouch angle. The single effect of crouch angle on ΔKFS and foot clearance (Fig. 4a) and the single effect of push-of magnitude on ΔKFS and foot clearance (Fig. 6a) each represent a cross section of these graphs. ΔKFS decreased with crouch angle for all push-off magnitudes, and foot clearance generally did as well

Hip Torque

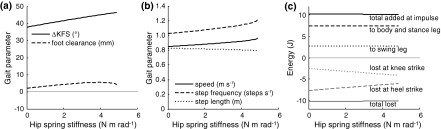
Inter-leg hip springs with stiffness ranging from 0 to 4.9 N m rad⁻¹ allowed for stable periodic motions. With greater spring stiffness, the swing leg moved too quickly, tending to result in the model falling forward, which prevented cyclic motions.

Hip torque generated by the inter-leg spring pulled the thigh of the trailing leg forward during initial swing, resulting in increased ΔKFS and improved foot clearance with increasing hip spring stiffness (Fig. 8a). Peak knee flexion occurred somewhat later in time with increasing stiffness, as did knee strike (Fig. 5c). Speed and step frequency increased slightly with hip spring stiffness, while step length slightly decreased (Fig. 8b). More energy was lost at knee strike and less at heel strike as hip torque was increased (Fig. 8c). The distribution of push-off energy to swing leg and body did not vary with hip torque.

Figure 8.

The effect of hip spring stiffness on (a) ΔKFS (increase in knee flexion during swing) and foot clearance; (b) speed, step frequency, and step length; and (c) energy distribution. Data are from gaits with 0° knee flexion and a push-off impulse size of 40 N s

Hip torque had a slight interaction effect with crouch angle, but did not affect ΔKFS as strongly (Fig. 9). ΔKFS decreased with increasing crouch angle for all hip spring stiffness values, and ΔKFS was more sensitive to changes in crouch angle than to hip spring stiffness (Fig. 9a). Foot clearance also generally decreased with increasing crouch angle across the range of hip spring stiffness, and became negative for low stiffness and high crouch angle (Fig. 9b). Hip torque did have a stronger effect on foot clearance than on ΔKFS, because it also affected the timing of peak knee flexion.

Figure 9.

(a) Contour plot of ΔKFS (increase in knee flexion in swing) as a function of hip spring stiffness and crouch angle. (b) Contour plot of foot clearance as a function of both hip spring stiffness and crouch angle. ΔKFS decreased with crouch angle for all hip spring stiffness values, and foot clearance generally did so as well

Discussion

The purpose of this study was to use a basic model of human walking to gain insight into passive dynamic factors which may affect knee flexion during leg swing among patients impaired by stiff-knee gait. We developed a dynamic walking model that performed stable cyclic gait, and used this model to study the effects of a crouched posture, push-off strength, and hip torque on knee flexion during swing. We found that by increasing the crouch angle, both the change in knee flexion during swing (ΔKFS) and peak knee flexion in swing decreased strongly, resulting in a stiff-knee gait pattern and reduced foot clearance. Increasing push-off magnitude or hip spring stiffness led to more knee flexion during swing, but the effect of crouch angle on ΔKFS and foot clearance remained.

The decrease in ΔKFS with increasing crouch angle can largely be explained by differences in gravitational effects on the leg segments at swing initiation and during the first part of swing. In the crouch model, the thigh of the trailing leg has a more vertical orientation during initial swing than in the upright model, while the shank has a more horizontal orientation (compare, for example, the leftmost configurations of Figs. 2d–2e). When considering the swing leg as a double pendulum, it can be seen that the knee of the trailing leg will tend to flex more at the onset of swing in the upright model than in the crouch model due to the effects of gravity. The gravitational force acting on the center of mass of the thigh has a larger moment arm relative to the hip axis in the upright model than in the crouch model and will tend to flex the hip more, simultaneously pulling the knee into flexion. Similarly, the gravitational force acting on the center of mass of the shank has a smaller moment arm relative to the knee in the upright model than in the crouch model, and therefore gravity counteracts the knee flexion less in the upright model.

As an illustration, we performed a pair of non-cyclic simulations to compare the relative importance of this gravitational effect to other factors such as hip motion. First we set the gravitational force on the swing leg to zero, while leaving the normal gravitational effects on the stance leg and body. We imposed the initial conditions for segment angles and velocities from both the upright and the crouch cyclic gait simulations at the onset of swing, and simulated forward in time. Without gravity, the swing leg did not swing forward anymore, and so motions similar to those in gait were not generated. However, starting from an upright posture led to only slight knee flexion, whereas starting from a crouch posture led to considerable knee flexion. Thus, without gravity on the swing leg, crouch angle had the opposite effect on swing knee flexion, which was outweighed by gravitational effects during cyclic walking. Next, we performed the opposite simulation experiment, i.e., passively swinging the leg in a gravitational field but without hip motion and with zero initial velocity. In this way, we removed possible effects of hip motion or initial velocity on knee flexion, so that we could study the effects of gravity in isolation. We started the simulation using initial positions (but not velocities) from the cyclic upright and crouch gaits. This yielded a similar decrease in ΔKFS with crouch angle as in cyclic walking, although with lower absolute peak knee flexion in all conditions. Although the effects of hip motion, initial velocities, and gravity are not linearly separable over the entire swing motion, these experiments help lend insight into their roles and indicate that gravitational effects were the main cause of the reduced ΔKFS with increased crouch.

Our results further showed that ΔKFS decreased with crouch angle even with increased push-off or hip torque. Although these factors also influenced knee flexion in swing, the passive dynamic effects of the crouch posture were always present, underlying other factors and influencing knee motion. The crouch effect was robust and remained a contributing factor, even with compensatory push-off or hip torques. Moreover, the imposed crouch angle had a larger influence on ΔKFS than push-off or hip torque, and the effect of crouch angle could not be neutralized by these factors in our model. This further emphasizes the relevance of crouch angle on swing leg knee flexion.

Foot clearance also generally worsened with increased crouch angle. Foot clearance did not change in direct proportion to ΔKFS, as shown by the difference between Figs. 7a and 7b, and between Figs. 9a and 9b. This is due to the fact that foot clearance is influenced by both the degree and the timing of knee flexion. With a crouched posture, peak knee flexion occurred early in swing (Fig. 5), and the knee was extending again at mid-swing, which resulted in foot scuffing. Since peak knee flexion occurred relatively early in swing in our model, foot clearance was limited in all simulations. However, in general foot clearance showed the same trend with increasing crouch angle as ΔKFS.

Speed, step length, and step frequency were slightly affected by increasing crouch angle (Fig. 4b), but did not significantly influence the effect of crouch on knee flexion. Since these parameters might also affect ΔKFS, a parallel set of simulations was performed in which crouch angle was increased while keeping speed, step length, and step frequency exactly constant (by appropriately adjusting the push-off and hip torque parameters). This resulted in nearly identical outcomes, in which the effect of crouch angle on ΔKFS was slightly enhanced.

Stronger push-off and hip torque both had a favorable effect on stiff-knee gait. ΔKFS and foot clearance generally improved when increasing push-off and hip torque. These findings are in agreement with previous studies showing that hip flexion moments in (pre)swing and push-off strength are factors that help progress the swing leg into flexion.6,10,16 Limited push-off power and hip flexion torque are thus important factors to consider in patients with stiff-knee gait. In the case of push-off, it is difficult to separate the influence of walking speed from the possible effects of adding energy to the swing leg. However, both of these strategies appear useful for mitigating a stiff-knee gait pattern.

Despite the effects of push-off and hip torque, the model in this study walked with limited speed and relatively long step length compared to human walking, similar to earlier simple dynamic walking models.3,14 However, these characteristics are typical of gait exhibited by patients with crouch or stiff-knee impairments. Whereas slow walking speed may be considered a limitation when studying unimpaired gait, these characteristics are relevant to the current study.

In our simulations, the push-off was directed toward the hip, in line with previous comparable model studies.3,4,12 In the crouch model the hip was somewhat lower and therefore the push-off impulse pointed slightly more forward compared to the upright model. All other things being equal, a more forward direction of the push-off impulse tends to flex the knee less in the ensuing swing (verified by an extra simulation in which only the push-off impulse direction was varied). However, the differences in push-off direction with crouch angle were small. We repeated the simulations with constant absolute push-off direction, and found nearly identical effects of crouch angle on ΔKFS and foot clearance.

Stiff-knee gait in patients with cerebral palsy is a complex problem in which many factors play a role. The use of a relatively simple model inevitably excludes several factors that are important in patient gait. One such factor is the knee flexion velocity at toe-off.1,6 In our model, the knee was locked during stance and during the instantaneous push-off and heel strike, resulting in zero knee flexion velocity at toe-off. Since no finite-time double support phase was included in our model, the influence of factors during this phase on knee flexion in swing could not be studied. For example, transfer of body weight from the trailing leg to the leading leg and joint torques during double support are likely to influence knee motion during swing. Similarly, joint torques about the knee during swing will obviously influence its motion as well.

Despite these simplifications, the result that passive knee flexion is lost at large crouch angles may have important consequences. Passive dynamics will impact swing leg behavior even in the presence of muscular activity or other more complex factors. Counteracting the decreased passive knee flexion and diminished foot clearance would require an active knee flexion torque during initial swing, especially in cases where push-off or hip flexion torques are low. This may be difficult or impossible for patients with impaired neuromuscular control. When possible, the additional muscle activity would still lead to increased mechanical work and energy use related to leg swing compared to walking with an extended stance leg.

The existing literature mainly emphasizes the role of local muscle functioning during pre-swing and swing as causes for the limited knee flexion in swing, showing that muscles such as rectus femoris and hip flexors can substantially affect knee flexion in swing.6,16,17 However, the present study showed that stiff-knee gait can also arise purely from differences in posture, and without any differences in swing leg actuation. This indicates that part of a stiff-knee gait pattern may result from uncontrolled dynamics of the system, rather than from deviations in muscle functioning or neurological control alone. In other words, the knee in ‘stiff-knee gait’ need not necessarily be ‘stiff’ at all. Specifically, patients walking in crouch may experience problems with knee flexion in swing due to the dynamics arising from their crouched posture. Our results suggest that for patients exhibiting combined crouch and stiff-knee gait patterns, reducing crouch during stance might also beneficially impact knee flexion during swing.

Appendix A: Supplementary Methods

A.1. Model Structure and Parameters

Figure A1 shows the detailed structure of the model used in this study. Parameters for this model are given in Table A1.

Figure A1.

Representation of the model. See Table A1 for abbreviations and parameter values

Table A1.

Parameter values for the model, as shown in Fig. A1

	Upper body b	Thigh t	Shank s	Foot f
Mass m (kg)	55.8	8.47	3.53	1.24
Moment of inertia I (kg m2)	0	0.21	0.07	0.01
Length l (m)	0	0.485	0.458	0.050
Vert. dist. CoM v (m)	0	0.210	0.198	0.015
Hor. offset CoM w (m)	0	0	0	0.050
Foot radius R (m)				0.30
x foot center C x (m)				0.05
y foot center C y (m)				0.25

m, I, l, and c of thigh and shank, and m of trunk and foot are based on Van Soest et al.23 foot radius is based on Hansen et al.8

A.2. Equations of Motion

The method used to derive the equations of motion for the model is derived from previous studies20,24 and based on the concept of virtual work. This method is called the ‘TMT-method,’ and the resulting equations are equal to those obtained with Lagrange’s method.

Starting with Newton’s second law, the sum of the forces must be equal to the mass times the accelerations:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \sum \mathbf{f} - \mathbf{M}\ddot{\mathbf{x}} = 0 $$\end{document} 1

In combination with ‘virtual velocity,’ this yields the virtual power equation:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \varvec{\delta} \dot{\mathbf{x}}\left\{ {\sum \mathbf{f} - \mathbf{M}\ddot{\mathbf{x}}} \right\} = 0 $$\end{document} 2

which says that the sum of the work done by all internal forces must be zero. This is true because all internal forces have opposite but equal reaction forces, delivering opposite and equal work, cancelling each other out for each instant in time.

First, a vector of global coordinates is defined, three for each segment:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \mathbf{x} = \left[ {x_{1} ,y_{1} ,p_{1} , \ldots ,x_{N} ,y_{N} ,p_{N} } \right]^{T} $$\end{document} 3

with x _i the x-coordinate of the center of mass of segment i; y _i the y-coordinate of the center of mass of segment i; p _i the orientation (angle) of segment i relative to global; and N the number of segments.

Next, a vector of generalized coordinates is defined, one for each degree of freedom:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \mathbf{q} = \left[ {p_{ 1} , \ldots ,p_{N} ,x_{\text{h}} ,y_{\text{h}} } \right]^{T} $$\end{document} 4

with p _i the angle of segment i relative to global, N the number of segments, and x _h and y _h the position of the hip joint.

We then express x as a function of the generalized coordinates by means of a kinematic transfer function F

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \mathbf{x} = \mathbf{F}\left( \mathbf{q} \right) $$\end{document} 5

Next, we define T as the partial derivatives matrix of x to q, so:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{T}} = {\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{q}}}}} $$\end{document} 6

Equation (6) is used in order to calculate the derivatives of x as a function of q, to input in our virtual power equation:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \dot{{\mathbf{x}}} = {\frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{q}}}}}{\frac{{\partial {\mathbf{q}}}}{{\partial {\mathbf{t}}}}} = {\mathbf{T}}\dot{\mathbf{q}} $$\end{document} 7

and, using the product rule:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \ddot{{\mathbf{x}}} = {\frac{{\partial {\mathbf{T}}}}{{\partial {\mathbf{t}}}}}\dot{{\mathbf{q}}} + {\mathbf{T}}{\frac{{\partial \dot{{\mathbf{q}}}}}{{\partial {\mathbf{t}}}}} $$\end{document} 8

We define:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{T}}_{2} = {\frac{{\partial {\mathbf{T}}}}{{\partial {\mathbf{q}}}}} $$\end{document} 9

Combining Eqs. (8) and (9) gives:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \ddot{{\mathbf{x}}} = {\mathbf{T}}_{2} \dot{{\mathbf{q}}}\dot{\mathbf{q}} + {\mathbf{T}}\ddot{\mathbf{q}} $$\end{document} 10

Now we go back to the virtual power Eq. (2), and fill in (7) and (10)

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \varvec{\delta} ({\mathbf{T}}\dot{\mathbf{q}})\left\{ {\sum {\mathbf{f}} - {\mathbf{M}}\left( {{\mathbf{T}}_{2} \dot{\mathbf{q}}\dot{\mathbf{q}} + {\mathbf{T}}\ddot{\mathbf{q}}} \right)} \right\} = 0 $$\end{document} 11

which has only generalized coordinates q. Equation (11) must be true for all virtual velocities, so for all \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \varvec{\delta} \dot{{\mathbf{q}}} $$\end{document}. Rearranging gives:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{T}}^{\text{T}} {\mathbf{MT}}\ddot{\mathbf{q}} = {\mathbf{T}}^{\text{T}} \sum {\mathbf{f}} - {\mathbf{T}}^{\text{T}} {\mathbf{MT}}_{2} \dot{\mathbf{q}}\dot{\mathbf{q}} $$\end{document} 12

Equation (12) can then be simplified by defining \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\bar{\mathbf{M}}} $$\end{document}, the reduced Mass matrix (hence the ‘TMT-method’):

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\bar{\mathbf{M}}} = {\mathbf{T}}^{\text{T}} {\mathbf{MT}} $$\end{document} 13

and \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\bar{\mathbf{f}}} $$\end{document} the reduced force vector which becomes, when adding Q as the generalized forces that are expressed directly in the coordinates of q (see Appendix A.6.)

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\bar{\mathbf{f}}} = {\mathbf{T}}^{\text{T}} \sum {\mathbf{f}} - {\mathbf{T}}^{\text{T}} {\mathbf{MT}}_{2} \dot{\mathbf{q}}\dot{\mathbf{q}} + {\mathbf{Q}} $$\end{document} 14

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{T}}^{\text{T}} {\mathbf{MT}}_{2} \dot{\mathbf{q}}\dot{\mathbf{q}} $$\end{document} represents the Coriolis forces, apparent forces resulting from accelerations of the system.

Adding (13) and (14) to (12) yields the simplified equation:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \bar{{\mathbf{M}}}\ddot{\mathbf{q}} = {\bar{\mathbf{f}}} $$\end{document} 15

This equation thus represents a ‘flying system’, i.e. it describes all joint constraints, but it does not yet include foot contact constraints. These are described in the next paragraph.

A.3. Constraint Equations

Now that we have the basic equations of motion, describing the system when no constraints are present, we need to add constraint equations d that describe the contact with the ground, as well as the locking of joints.

It is assumed that if the foot is in contact with the ground, it is fully fixed to its attachment point, so no sliding is allowed. Each foot rolls over the arc until it reaches the toe, and this toe is modeled as a hinge constraint.

The rolling arc foot constraint is defined in such a way that the lowest point of the arc of the foot is always in contact with the ground. The constraint is formulated so that this lowest point of the arc should be equal to the point of the foot in first contact with the ground plus the distance travelled over the arc of the foot. In formula:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{d}}_{\text{arc}} = {\mathbf{x}}_{\text{arc}} - \left[ {\begin{array}{l} {R \cdot \left( {p_{\text{f}} - p_{{{\text{fc}}1}} } \right) - x_{{{\text{c}}1}} } \hfill \\ 0 \hfill \\ \end{array} } \right] = 0 $$\end{document} 16

with x _arc the lowest point of the arc foot, which is in contact with the ground, R the foot radius, p _f the foot angle, p _fc1 the foot angle at first foot contact, and x _c1 the horizontal position of the bottom of the foot at first foot contact.

The toe constraint is modeled as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{d}}_{\text{toe}} = {\mathbf{x}}_{\text{toe}} - \left[ {\begin{array}{l} {x_{\text{c2}} } \hfill \\ 0 \hfill \\ \end{array} } \right] = 0 $$\end{document} 17

with x _toe the position of the toe and x _c2 the horizontal toe position at first toe contact.

Similar constraint equations are formulated to lock the ankle and knee joints:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ d_{\text{joint}} = p_{\text{d}} -p_{\text{p}} -p_{\text{c}} = 0 $$\end{document} 18

with p _d the angle of the distal segment, p _p the angle of the proximal segment, and p _c the constraint angle of the joint.

d can change for different phases of the gait cycle: only those constraints are modeled that describe the foot contacts and joint locks that are present in each gait phase. The derivatives of d can then be calculated as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \dot{{\mathbf{d}}} = {\frac{{\partial {\mathbf{d}}}}{{\partial {\mathbf{q}}}}}{\frac{{\partial {\mathbf{q}}}}{{\partial {\mathbf{t}}}}},\quad{\text{with}}\,{\mathbf{D}} = {\frac{{\partial {\mathbf{d}}}}{{\partial {\mathbf{q}}}}},\quad{\text{which}}\,{\text{gives:}}\,\dot{{\mathbf{d}}} = {\mathbf{D}}\dot{\mathbf{q}} = 0 $$\end{document} 19

and, similarly as above for \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \ddot{{\mathbf{x}}} $$\end{document}:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \ddot{{\mathbf{d}}} = {\mathbf{D}}_{2} \dot{\mathbf{q}}\dot{\mathbf{q}} + {\mathbf{D}}\ddot{\mathbf{q}},\quad{\text{with}}\,{\mathbf{D}}_{2} = {\frac{{\partial {\mathbf{D}}}}{{\partial {\mathbf{q}}}}} $$\end{document} 20

or:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{D}}\ddot{\mathbf{q}} = - {\mathbf{D}}_{2} \dot{\mathbf{q}}\dot{\mathbf{q}} $$\end{document} 21

Adding the constraint forces f _c to the general equation of motion and combining with the constraint equation gives:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left[ {\begin{array}{ll} {\mathbf{M}} & {{\mathbf{D}}^{{\mathbf{T}}} } \\ {\mathbf{D}} & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{ll} {\ddot{{\mathbf{q}}}} \\ {{\mathbf{f}}_{{\mathbf{c}}} } \\ \end{array} } \right]{\mathbf{ = }}\left[ {\begin{array}{ll} {{\bar{\mathbf{f}}}} \\ { - {\mathbf{D}}_{{\mathbf{2}}} \dot{\mathbf{q}}\dot{\mathbf{q}}} \\ \end{array} } \right] $$\end{document} 22

The equations of motion are solved forward in time by numerical integration using Matlab^® ODE23 function.

A.4. Event Detection

Figure 2d shows the gait phases of upright gait. Arbitrarily, the beginning of each stride is defined as toe-off of foot 2, thus the beginning of single support on leg 1. In the single stance phase, the model searches for the following events:

• Event 1: toe strike of the stance leg: the toe is reached while the foot is rolling over its arc shape.At this point the arc foot constraint is replaced by the toe constraint.

• Event 2: knee strike of the swing leg: knee angle crosses the prescribed stance leg knee angle. At this point the knee is locked by the knee constraint.

• Event 3: heel strike of the swing leg: the swing leg arc foot hits the floor. At this point an instantaneous push-off impulse is applied under the trailing leg (Appendix A.4.), followed by an instantaneous collision of the leading foot (Appendix A.5.).

• Event 4: foot lift of the stance leg: the force under the stance foot crosses zero and becomes negative. At this point the model tends to lift off and the simulation is stopped and discarded. This event usually only happens at (too) high speeds or unusual parameter combinations.

A.5. Impulsive Push-Off

At event 3, an instantaneous push-off impulse is applied under the rear foot. During this infinitely small time period, positions of the system are assumed to remain constant and only velocities change. It can be said that over a short interval of time, from t ⁻ (prior to impact) to t ⁺ (after impact), the equations of motion must be true:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \mathop {\lim }\limits_{t \to 0} \int\limits_{{t^{ - } }}^{{t^{ + } }} {{\mathbf{M}}\ddot{\mathbf{q}}} dt + \mathop {\lim }\limits_{t \to 0} \int\limits_{{t^{ - } }}^{{t^{ + } }} {{\mathbf{D}}^{\text{T}} {\mathbf{f}}} dt = \mathop {\lim }\limits_{t \to 0} \int\limits_{{t^{ - } }}^{{t^{ + } }} {{\bar{\mathbf{f}}}dt} $$\end{document} 23

The second term of (23) includes the constraint forces of the joints to be locked during impulse and the push-off impulse. The foot constraints are not included, as the leading leg has not yet touched the ground, and the trailing leg is allowed to come off the ground after the push-off impulse.

We can define the push-off impulse ρ _p as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \varvec{\rho}_{\text{p}} = \mathop {\lim }\limits_{t \to 0} \int\limits_{{t^{ - } }}^{{t^{ + } }} {{\mathbf{f}}_{\text{p}} } dt $$\end{document} 24

and the resulting impulses in the constraints:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \varvec{\rho}_{\text{c}} = \mathop {\lim }\limits_{t \to 0} \int\limits_{{t^{ - } }}^{{t^{ + } }} {{\mathbf{f}}_{\text{c}} } dt $$\end{document} 25

The second term in (23) can then be split into the known impulses applied under the trailing foot: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{D}}_{\text{p}}^{\text{T}} \varvec{\rho}_{\text{p}} $$\end{document} and the unknown resulting impulses in the joint constraints: \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{D}}_{\text{c}}^{\text{T}} \varvec{\rho}_{\text{c}} $$\end{document} with D _p describing the foot contact of the trailing leg where the push-off impulse is applied (based on d _arc or d _toe) and D _c the constraints to lock the joints.

The first term of (23), the change of momentum, is equal to:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \mathop {\lim }\limits_{t \to 0} \int\limits_{{t^{ - } }}^{{t^{ + } }} \bar{{\mathbf{M}}}\ddot{\mathbf{q}}dt = \bar{{\mathbf{M}}}\dot{\mathbf{q}}^{ + } - \bar{{\mathbf{M}}}\dot{\mathbf{q}}^{ - } $$\end{document} 26

The right hand site term in (23) goes to zero, since all forces other than the impulses are not infinitely high. Rewriting (23) then gives:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \bar{{\mathbf{M}}}\dot{\mathbf{q}}^{{\mathbf{ + }}} + {\mathbf{D}}_{\text{c}}^{{\mathbf{T}}} {\varvec{\uprho}}_{\text{c}} = \bar{{\mathbf{M}}}\dot{\mathbf{q}}^{ - } - {\mathbf{D}}_{\text{p}}^{{\mathbf{T}}} {\varvec{\uprho}}_{\text{p}} $$\end{document} 27

Combining (27) with the constraint equation yields the push-off impulse equations:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left[ {\begin{array}{ll} {{\bar{\mathbf{M}}}} & {{\mathbf{D}}_{\text{c}}^{{\mathbf{T}}} } \\ {{\mathbf{D}}_{\text{c}} } & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{l} {\dot{{\mathbf{q}}}^{\mathbf{+}} } \\ {\varvec{\rho}_{{\mathbf{c}}} } \\ \end{array} } \right]{\mathbf{ = }}\left[ {\begin{array}{ll} {\bar{{\mathbf{M}}}\dot{\mathbf{q}}^{ - } - {\mathbf{D}}_{\text{p}}^{{\mathbf{T}}} {\varvec{\rho}}_{\text{p}} } \\ {\mathbf{0}} \\ \end{array} } \right]. $$\end{document} 28

A.6. Impact Equations

Impact of the foot is modeled as a fully inelastic, instantaneous collision, after which the leading foot is fixed to the ground. Similarly, the knee strike in swing is modeled as an inelastic, instantaneous collision after which the knee joint is locked.The impact equation is comparable to the push-off Eq. (28). D ^T and ρ now include the (unknown) constraints and impulses of the joint constraints, as well as of the leading foot, since this foot is fixed to the ground after impact. Equation (27) then becomes:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\bar{\mathbf{M}}}\dot{\mathbf{q}}^{ + } + {\mathbf{D}}^{\text{T}} \varvec{\rho} = \bar{{\mathbf{M}}}\dot{\mathbf{q}}^{ - } $$\end{document} 29

Finally e can be defined as the restitution coefficient, the relative velocity after impact divided by the relative velocity before impact, with e = 1 if fully elastic and e = 0 if fully inelastic. For the general case of 0 ≤ e ≤ 1,

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ e = {\frac{{\dot{{\mathbf{d}}}^{ + } }}{{\dot{{\mathbf{d}}}^{ - } }}} = {\frac{{{\mathbf{D}}\dot{\mathbf{q}}^{ + } }}{{{\mathbf{D}}\dot{\mathbf{q}}^{ - } }}} $$\end{document} 30

Combining (29) and (30) yields the impact equations:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \left[ {\begin{array}{ll} {{\bar{\mathbf{M}}}} & {{\mathbf{D}}_{{}}^{{\mathbf{T}}} } \\ {{\mathbf{D}} } & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{l} {\dot{{\mathbf{q}}}^{ + } } \\ \varvec{\rho} \\ \end{array} } \right]{\mathbf{ = }}\left[ {\begin{array}{l} {\bar{{\mathbf{M}}}\dot{\mathbf{q}}^{ - } } \\ { - e{\mathbf{D}}\dot{\mathbf{q}}^{ - } } \\ \end{array} } \right] $$\end{document} 31

with \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ - e{\mathbf{D}}\dot{\mathbf{q}}^{ - } = 0 $$\end{document} for a fully inelastic impact.

A.7. Hip Spring

The hip spring is modeled as a joint moment Q _j, depending on inter-leg joint angle p _j:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ Q_{\text{j}} = - k\left( {p_{\text{j}} - p_{{{\text{o}},{\text{j}}}} } \right) $$\end{document} 32

with k the stiffness constant, and p _o the neutral joint angle, which is set to zero. Q _j is then expressed in the general coordinates q (segment angles) by a kinematic transfer.

A.8. Cyclic Motion and Stability Assessment

Cyclic motion is derived by comparing the state at the beginning and the end of one step. For this purpose a step function is defined as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{v}}_{n + 1} = {\mathbf{S}}\left( {{\mathbf{v}}_{n} } \right)\,{\text{with}}\,{\mathbf{v}} = \left( {{\mathbf{q}},\dot{{\mathbf{q}}}} \right) $$\end{document} 33

which is cyclic if:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{S}}\left( {{\mathbf{v}}_{\text{c}} } \right) = {\mathbf{v}}_{\text{c}} $$\end{document} 34

This cyclic limit cycle is searched for using a first-order gradient search method.

The stability of this cyclic initial state v _c, i.e., the ability of the model to go back to its cyclic motion if a small perturbation occurs, can then be determined by calculating the Jacobian J as the partial derivative of S to v. The state v _c + Δv ⁺ after a perturbation Δv can be quantified as:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\mathbf{v}}_{\text{c}} + \Updelta {\mathbf{v}}^{ + } = {\mathbf{S}}\left( {{\mathbf{v}}_{\text{c}} + \Updelta {\mathbf{v}}} \right) \approx {\mathbf{S}}\left( {{\mathbf{v}}_{c} } \right) + {\mathbf{J}}\Updelta {\mathbf{v}}\,{\text{with}}\,{\mathbf{J}} = {\frac{{\partial {\mathbf{S}}}}{{\partial {\mathbf{v}}}}} $$\end{document} 35

Thus:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \Updelta {\mathbf{v}}^{ + } = {\mathbf{J}}\Updelta {\mathbf{v}} $$\end{document} 36

For stability, Δv ⁺ < Δv for all small perturbations Δv. Therefore, the cycle is stable if all eigenvalues of J are <1.