Abstract
We present a combined quantum mechanics and molecular mechanics (QM/MM) study of the deep ultraviolet ππ* resonance Raman spectra of β-sheet amyloid fibrils Aβ34–42 and Aβ1–40. Effects of conformational fluctuations are described using a Ramachandran angle map (RAM), thus avoiding repeated ab-initio calculations. Experimentally observed effects of hydrogen deuterium exchange are reproduced. We propose that the AmIII band redshift upon deuteration is caused by the loss of coupling between Cα–H bending and N–D bending modes, rather than by peptide bond hydration.
I. Introduction
The structure and misfolding kinetics of amyloid fibrils are of considerable interest, due to their association with a number of neurodegenerative diseases.1–5 Detailed structural information at the molecular level should help monitor the fibrillation mechanism and kinetics. However, since amyloid fibrils are noncrystalline, aqueous insoluble protein aggregates, the applicability of traditional structural biology techniques such as X-ray crystallography and nuclear magnetic resonance (NMR) are limited.6
Deep UV resonance Raman spectroscopy (DUVRR, Figure 1) is a powerful tool for characterizing protein secondary structures, thanks to its sensitivity to the chemical environment of the peptide backbone.7–14 Vibrational spectra can provide specific information on protein secondary structures and folding dynamics. Unlike infrared (IR), Raman spectra of proteins do not overlap with those of water,7,9,10,15,16 making them more suitable for biological applications in aqueous environment. Deep ultraviolet (UV) photons (≤ 210 nm) excite the ππ* electronic transition of the protein backbone. As may be seen in Figure 2, the dominant Raman features are the amide I (AmI) band at 1600-1700 cm–1 (peptide C=O stretching modes); amide II (AmII) band at ~1500 cm–1 (in-phase N–H bending coupled to C–N stretching modes); amide III (AmIII) band at ~1200 cm–1 (out-of-phase N–H bending coupled to C–N stretching modes), and Cα–H/N–H bending modes at ~1400 cm–1 (Cα-H).7,9–13 The Cα–H bending mode mixes with the closely lying AmIII bands. This mixing depends on the Ramachandran angles along the peptide chain. Asher and coworkers had developed a family of sinusoidal empirical relationships between AmIII frequencies and the ψ angles for various peptide-peptide and peptide-water hydrogen bonding environments.12,14 The AmIII band of a protein can be decomposed into contributions from peptide bonds with specific ψ angles, which allows to use them for probing the secondary structure content of complex proteins.11,12,14
Figure 1.
The electronically resonant Raman scattering process.
Figure 2.
DUVRR spectra of of Ala-Ala (a) and Ala-Asp (b) dipeptides. Experimental10 (excitation wavelength 229 nm), direct ab-initio simulation, and simulation based on the Ramachandran angles map (RAM) are shown in black, red and blue lines. The Ramachandran angles (ϕ, ψ) are given in the parenthesis. In the RAM simulations, we used (-115,166) for Ala-Ala and (-115,176) for Ala-Asp.
DUVRR spectroscopy provides valuable conformational information on amyloid fibrils. Hydrogen-deuterium exchange (HX) can be used to study cross-β fibrils by comparative characterization.17 The peptide –NH is substituted by deuterium if exposed to D2O. However, peptide-peptide hydorgen bonding protects the –NH atoms from HX. A fibril core in the β-sheets dramatically reduces the HX rate due to the increased possibilities to form hydrogen bonds with surrounding carbonyl oxygen atoms from other residues. The change of DUVRR spectra upon HX is thus reduced by peptide-peptide hydrogen bonding. Combined with post-mortem hydrogen-deuterium exchange (HX), the Raman bands enhanced by electronic resonance can be well distinguished due to the loss of coupling of peptide N–H modes with other modes.11,18,19 Lednev and coworkers had found that the DUVRR spectra of antiparallel Aβ34–42 fibrils dissolved in H2O and D2O,11 change more substantially upon HX compared with those of parallel Aβ1–40. Conformational differences of parallel and antiparallel amyloid fibrils can thus be distinguished by this technique.11
In this paper, we perform a simulation of the effect of HX on the DUVRR spectra of Aβ1–40 and Aβ34–42. Details of the simulation of peptide bonds are given in Sec. II. The computational protocol for proteins which includes exciton effects are given in Sec. III. Simulation results of Aβ fibrils are presented and discussed in Sec. IV. We finally conclude in Sec. V.
Resonant ππ* Raman spectra of the peptide bond
The resonance Raman process (Figure 1) involves an electronic excitation from the ground electronic state and a de-excitation back to a vibrationally excited state in the ground electronic state. The differential Raman scattering cross section is,
| (1) |
where I0 and Ifi are the incident and outgoing wave intensities, respectively. ε0 is the permittivity, is the incident wave number and is the scattered wavenumber during the Raman process with initial and final states |i〉 and |f〉, respectively. The Raman process starts at |egμi〉, passes through an intermediate state |erνr〉, and ends in |egμf〉. |μ〉 and |ν〉 represent vibrational states in the ground and electronic states, respectively. The transition polarizability is given by:20
| (2) |
Here ω1 is the incident frequency, is the transition dipole operator, ωereg is the 0–0 transition energy between ground state |eg〉 and excited state er〉, and ωνrμi is the vibrational part of transition energy. Γerνr is the lifetime broadening of the intermediate vibronic state |erνr〉. Since only strongly allowed π – π* resonance transitions of peptide bonds are involved in the Raman process studied here, we neglect the Herzberg-Teller vibronic coupling and use Albrech's ‘A term’ to calculate the Raman intensities,21
| (3) |
where
| (4) |
is the electronic transition dipole moment, and 〈μ|ν〉 are the Franck-Condon (FC) integrals. We further neglect the difference in vibration frequencies in the ground and excited states and assume linearly displaced harmonic vibrations. The ground state vibrational Hamiltonian is,22
| (5) |
where ωj is the frequency of the j-th normal mode, and q̄j is its dimensionless coordinate centered around , which is related to the cartesian coordinates by
| (6) |
mj is the reduced mass of the j-th normal mode.23 The excited state Hamiltonian is,
| (7) |
The FC integrals depends on the displacement Δ between the potential energy surface minimas of ground and excited states, as shown in Figure 1, which can be evaluated from the potential energy gradient with respect to the dimensionless coordinate:
| (8) |
We had optimized the ground state geometry, hence ∂Eg/∂qj = 0 for all vibrational modes. Substituting Eq. (6) into Eq. (8), we have,
| (9) |
The normal modes are linear combinations of the atomic displacements q,
| (10) |
and the gradient with respect to atomic displacements (Hellman-Feynman forces). We can thus write the displacement as
| (11) |
here i runs over the 3N Cartesian coordinates of the system, lji is the elements of matrix L in Eq. (10). is the Hellman-Feynman force corresponding to the i-th deformation of the molecule in its electronic state |a〉.
Two methods are commonly used to calculate Δ. In the first, the excited state geometry is optimized and the displacements corresponding to each normal modes are calculated from the geometry deformation upon electronic excitation.24–26 In the second method, the excited state potential gradient instead of the geometry deformation is used to calculate the displacement.27–29 Excited state geometry optimization is expensive and is not generally implemented in standard quantum chemical packages. The excited gradient method used here avoids the optimization of excited state and usually yields reasonable agreement with experiment.27,28
The FC integrals in Eq. (16) were evaluated using the recurrence formula of Manneback,30
| (12a) |
| (12b) |
| (12c) |
The Gaussian 0931 package was used to optimize the ground state geometry configurations, performing frequency analysis and calculate excited state gradients, at the density functional theory (DFT) level with the PBE032–34 functional and the 6-311++G(d,p) basis set. The polarizable continuum model with conductor like solvations (CPCM)35,36 was used to perform the self consistent reaction field calculations to simulate the aqueous environment. The electronic transitions and excited state gradient were obtained by time-dependent density functional theory (TDDFT). We used the optimized ground state geometry configuration in the excited state calculations, and chose the electronic excited state with the largest transition intensity as the resonance electronic excitation. To correct for the systematic error in the density functional frequency calculations, we scaled all the vibrational frequencies by a factor of 0.97.37,38 Lifetime broadening of the intermediate state was taken to be 100 cm–1 in all calculations.
A protein is a chain of peptide bonds (P) each attached a side chain (R), as illustrated in Figure 3. DUVRR bands are sensitive to peptide secondary structures described by the Ramachandran dihedral angles. It is too expensive to perform repeated fully ab-initio calculations for large proteins. Glycine dipeptide (GLDP) is the simplest molecule that contains a ψ (N–Cα–C–N) angle and a ϕ (C–Cα–N–C) angle. We used a methylated derivative of GLDP, as shown in Figure 3(b), for modeling the excitations and vibrations of a single dipeptide unit. The displacement and DUVRR spectra were evaluated at the ab-initio level.
Figure 3.
(a) Schematic illustration of the protein chain; (b) The glycine dipeptide methylated derivative used to construct the RAM. Carbon (gray), nitrogen (blue), oxygen (red) and hydrogen (white) atoms.
Even though the Ramachandran angles are confined to narrow ranges for proteins with a specific tertiary structures, a large number of ψ and ϕ values are still required to describe a protein with tens of residues. Furthermore, hundreds of MD snapshots should be sampled to take structural fluctuation into account, which requires numerous GLDP models with specific dihedral angle values for the simulation. To reduce computational cost, we constructed a map between the dimensionless displacements and Ramachandran angles (Ramachandran angles map, RAM). Asher's group has illustrated that the Raman bands, especially the AmIII bands are strongly dependent sinusoidally on the ψ angles, but only slightly dependent on the ϕ angles.12 We therefore employed a finer (2 degree) grid to sample the ψ angles, and a coarser (5 degree) grid for ϕ. We used GLDP with nearest Ramachandran angles among the grid points to represent the corresponding segment in the protein. The RAM was constructed by evaluating the dimensionless displacements for each vibrational mode of GLDP for various dihedral angles. Side chain effects were neglected in the construction of RAM of the peptide backbone vibrations.
We had benchmarked the RAM for two dipeptides Ala-Ala (AA) and Ala-Asp (AD). Figure 2 compares the simulated DUVRR spectra with the 229 nm excited experiment10 on AA and AD crystal powder. The Ramachandran angles were obtained from X-ray crystal structures. Both AA and AD in their crystalline phase have β-strand like ψ angles. In the experimental spectra, the most prominent is the ~1245 cm–1 AmIII band, accompanied by a series weaker bands in the range 1330~1400 cm–1. The latter were assigned to Cα–H bending modes coupled with Cα–C stretching modes. The AmII (~1550 cm–1) and AmI (~1700 cm–1) bands are much weaker than the AmIII bands.
The RAM simulations (blue) and ab-initio simulations (red) of the two dipeptides clearly reproduce all the main experimental features, including the AmI, AmII and AmIII bands. The Ramachandran angles of AA crystal are (ϕ=-113, ψ=166), and for AD dipeptide they are (-113,176). As a consequence of the systematic error in DFT frequencies, the computed peak positions deviate from experiment. The most prominent peak in the dipeptide spectra arise from the AmIII bands and a weaker Cα–H band followed in the range 1350~1400 cm–1. The AmI and AmII bands are much weaker than AmIII.
The RAM simulated peak positions and relative intensities compare well with experiment in the range 1200–1700 cm–1. The agreement is not as good in the 1300~1330 cm–1 region, where Cα-C stretching modes have a considerable contribution. Ab initio spectra show weak peaks that are missed by the RAM simulation. This can be attributed to the Cα–C stretching modes, since the side chains attached on Cα were not taken into account in the construction of RAM.
III. DUVRR of proteins; Exciton effects
Structural fluctuations should be taken into account in the simulations of protein spectra. However, repeated ab-initio calculations are prohibitively expensive. High level ab-initio methods are limited to small molecules with tens of atoms. Molecular mechanics (MM) methods can handle large systems but are not able to describe the quantum effects involved in many chemical processes. The combination of ab-initio (quantum mechanics, QM) methods with MM methods has thus become widely used in the simulation of large biological system.39
Moreover, for large molecules, the number of degrees of freedom would be too high, and the potential energy surface might be too shallow to get a reliable energy minimized configuration. Therefore, we used geometry configurations extracted from molecular dynamics snapshots, which are usually different from the ab-initio lowest energy configurations. The ground state gradients in Eq. (8) do not generally vanish.
To calculate the deep UV ππ* transition of the protein backbone, we divided the protein chain into principal units as shown in Figure 3. The ground state vibrational wave function was factorized into the product of wave functions of each residue
| (13) |
where is the electronic ground state wave function of residue n, is the nuclear wave function with the lowest vibration quantum number of the j-th mode in the ground state of residue n, here we adopt the Born-Oppenheimer approximation that assumes the wave function of a system is the product of electronic part and nuclear part. It has been shown that vibronic coupling between adjacent peptide bonds is negligible.13,40,41 We thus approximated the vibronic excitations by the product of localized excited state of each chromophore,
| (14a) |
| (14b) |
The Frenkel exciton model within the Heitler-London approximation42,43 was employed to describe the vibronic excitations,
| (15) |
n runs over all the chromophores (peptide bonds) in the peptide chain. is the creation operator defined in Eq. (14b) and is its corresponding annihilation operator. The commutation relation of these oprators is Only the ππ* electronic transition of each unit is included in this Hamiltonian.
The ground state energy is taken as 〈g|H|g〉 = 0. The single vibronic excitation manifold energies can be evaluated by ab initio calculations,
| (16) |
here is the electronic excitation energy of the n-th peptide bond and represents the vibration part of the excitation correspond to the j-th mode in the n-th principal unit, which is described by a GLDP taken from our RAM. The off diagonal elements are
| (17) |
The electronic part of the resonance coupling between the m-th and n-th units is
| (18) |
which were evaluated by using the atomic frame technique.44 The Franck Condon (FC) integrals were evaluated using excited state gradient method by assuming linearly displaced vibrations.
The exciton wave functions were obtained by diagonalizing the Hamiltonian Eq. (15),
| (19) |
here denotes the wave function of the localized single exciton from |g0g〉 to |eνe〉 of the j-th mode on chromophore n. Cr is the r-th eigenvector of the exciton Hamiltonian, the corresponding eigenvalue ωr is the excitation energy of the exciton.
Note that we had divided the protein into principal units, where each pair of nearest residues is represented by the RAM. However, the electronic part of the exciton Hamiltonian is constructed from single peptide bonds as well as the side chains.44 We assume that the two peptide bonds contribute equally to the ππ* electronic transition in the GLDP molecule. Hence all the residues except the two terminals, contribute twice to Eq. (19). For systems with a large fibril core, the difference in the contribution from two terminal residues may be neglected.
It follows from Eq. (3) that the transition polarizability can be expressed in terms of the coupled exciton wave functions,
| (20) |
The coupling between localized peptide vibrational modes in the initial and final state |Ψi〉 and |Ψf〉 was neglected. We took the initial state |Ψi〉 as the ground state |g〉, this is justified for 1100~1800 cm–1 vibrations at 300K.
IV. Hydrogen–Deuterium Exchange in Aβ Fibrils
Before discussing the proton exchange of Aβ fibrils, a benchmark simulation of of H2O/D2O mixture is presented to illustrate isotope effects in DUVRR spectroscopy. The experimental spectra13 of pure H2O, pure D2O and 1:1 H2O/D2O mixture are presented in Figure 4(a). A weak peak at ~1554 cm–1 attributed to the stretching mode of residual atmospheric O2 appears in all the experimental spectra. The D2O OD bending band at ~1209 cm–1 does not overlap with any peptide backbone bands. The H2O OH bending band at ~1651 cm–1 may contributes to the C=O stretching band, but it was usually subtracted from the experimental spectra.10,11 The HOD bending (~1456 cm–1) mode in the H2O/D2O mixture overlaps with the N-D bending coupled to C-N stretching bands (AmII′ in Figure 6), which can not be avoided in the HX experiment.
Figure 4.
Comparison of calculated and experimental13 DUV Raman spectra of pure H2O, pure D2O and 1:1 H2O/D2O mixture at 204 nm excitation. The experimental 1560 cm–1 stretching band corresponds to atmospheric O2. The spectrum of 1:1 mixture was simulated by adding the contributions from H2O (25%), D2O (25%) and HOD (50%).
Figure 6.
Top row: Comparison of simulated (right) and experimental11 (left, excitation wavelength 197 nm) DUVRR spectra of Aβ34–42 (red lines) and Aβ1–40 (blue lines) fibrils in H2O; Bottom row: Same but in D2O.
The first electronic excited state in H2O is a HOMO-LUMO transition with a calculated excitation wavelength 164.31 nm, the higher excited states have excitation wavelength shorter than 135 nm. We thus only used the lowest excited state in the calculation of UVRR at 204 nm. The calculated displacements for H2O and D2O are 0.050 and 0.093, respectively. The larger displacement of D2O results in stronger Raman band.
The spectrum of the 1:1 H2O/D2O mixture was obtained by summing the contribution from 25% pure H2O, 25% D2O, and 50% HOD. The relative intensities only qualitatively agree with the experiments, this is because the experiment are conducted by 204 nm UV, which is not a resonance frequency. However, this benchmark illustrates that the intensity of Raman band should increase by deuterium substitution. In addition, the HOD bending mode may also be a reason of the stronger AmII′ band of protein after HX.
The Aβ34–42 and Aβ1–40 fibrils were simulated by MD in water with the CHARMM2245 force field and the TIP3P46 water model by using the NAMD47 package. An NPT ensemble, and periodic boundary conditions were employed to construct the dilute solution model, in which each residue only interacts with its surrounding water and probably with other residues in the same protein. The supercells are 48×28×40 Å3 for Aβ34–42 fibril and 92×82×75 Å3 for Aβ1–40 fibril to ensure there is no interaction between nearest images. All MD simulations start from a 10000 steps minimization followed by a 500 ps heating from 0 K to 310 K. The MD time step is 1 fs. 100 snapshots are taken every 1 ps from a 5 ns dynamics at 1 atm pressure and 310 K following a 2 ns equilibration. The ensemble of MD snapshots are used to simulate DUVRR spectra by weighting the total energy using Boltzmann distribution.
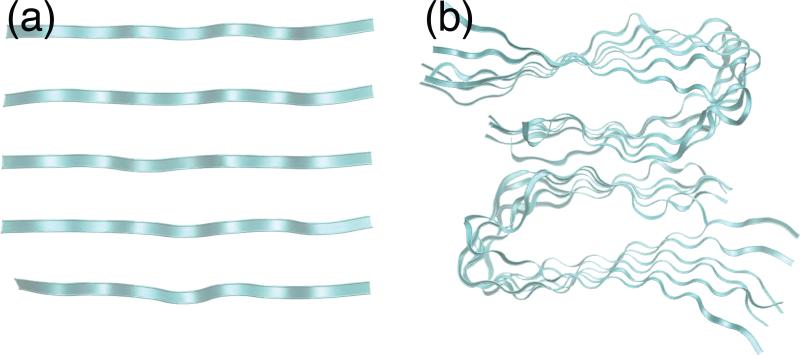
The antiparallel β-sheet Aβ34–42 fibril with the sequence LMVGGVVIA was constructed from the Aβ1–42 fibrils (PDB code: 2BEG),48 Figure 5(a) shows the ribbon structure of Aβ34–42 fibrils. The parallel β-sheet Aβ1–40 with the sequence DAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVV is taken from the NMR structure by Petkova et al.,1 since the conformation of residues D1–S8 is disordered, we only used the segment G9–V40 in our simulation.
Figure 5.
The structure of (a) Aβ34–42 fibrils and (b) residues G9–V40 of Aβ1–40.
Hydrogen-deuterium exchange substitutes –NH with –ND. However, the –NH atoms may be protected from HX by hydrogen bonding with carboxyl oxygen atoms of other residues either in or out of the same chain.50 By considering the tertiary folding of the two amyloid fibrils (Figure 5), we expect distinct difference in the HX dynamics of these systems: Due to the flat polymorph of Aβ34–42 fibrils, most –NH are expected to be exposed to solvent, resulting in substantial HX. In contrast, in the fibril core in Aβ1–40 fibrils, peptide-peptide hydrogen-bonding is highly probable, hence strong protection from HX is expected. To illustrate the change in DUVRR spectra upon HX, we show in Figure 7 the calculated spectra of Aβ34–42 fibrils with all –NH atoms deuterated. The main difference upon HX is the redshift of AmII band to AmII′ band, the AmII bands completely disappears in the fully deuterated fibrils, which implies that all the contribution of the residual AmII band after HX comes from protonated –NH atoms. The red shift of the AmII band is attributed to the loss coupling between N–D bending and Cα–H bending modes. At the same time, the intensity of N–H(D) bending bands (AmII → AmII′) dramatically increases upon HX, which is a consequence of isotopic effect and the contribution from residual HOD bending mode introduced by HX.
Figure 7.
Comparison of experimental11 (solid lines, excitation wavelength 197 nm) and simulated (dashed lines) DUVRR spectra of Aβ34–42 fibrils. The blue dashed line shows a fibril with all –NH atoms deuterated.
The experimental DUVRR spectra of Aβ34–42 and Aβ1–40 fibrils are displayed in the left column of Figure 6. In both the intensities of AmII band decrease upon HX, and a new AmII′ appear. However, it is obvious that the spectra of Aβ1–40 (blue lines) in H2O and D2O show much smaller differences than those of Aβ34–42 (red lines): the intensities of AmII and AmIII bands decrease less, and the intensity of new AmII′ band is much weaker. This implies that HX in Aβ1–40 is much lower than Aβ34–42.
We had used the following protocol to simulate hydrogen deuterium exchange in the DUVRR spectra. For each snapshot, we examined the hydrogen bonding environment for all –NH atoms. Using the optimized –NH···O=C hydrogen bond length in our ab-initio calculations, we assume a peptide-peptide hydrogen bond exists if the distance between –NH and carbonyl oxygen atoms does not greater than 1.85 Å. All –NH atoms in each snapshot were checked for the existence of hydrogen bonds. if there is no hydrogen bond between the –NH and carboxyl O atoms, we assume it was deuterated in D2O, and we use a deuterated RAM for the corresponding segment of the protein.
The Cα–H band is not visible in the spectra of Aβ34–42 in D2O. From our frequency analysis, we find that the Cα–H bending modes have a slight blueshift and may be masked by the strong AmII′ band. We also found a blueshift of Cα–H band in Aβ1–40 fibrils in Figure 6 that confirms our explanation of the change in the Cα–H band.
A small ~10 cm–1 redshift in the AmIII band is seen upon HX. From the experimental spectra of Figure 6, the AmIII bands of Aβ1–40 and Aβ34–42 in H2O appear to coincide but both redshift and decrease intensities with different degrees proportional to the HX rate in D2O. In contrast to the previously proposed peptide hydration mechanism,11 we argue that the redshift in the AmIII band may also be attributed to the loss of coupling between N–D bending with Cα–H bending and C–N stretching modes.The peptide bond hydration mechanism is based on the fact that the coexistence of peptide-water and peptide-peptide hydrogen bonding results in a redshift of AmIII peak about 5 cm–1.12 It implies that some of peptide bonds with only peptide-peptide hydrogen bond in H2O will also hydrogen bonding to water in D2O, and peptide hydration in Aβ34–42 is much more probable than that in Aβ1–40 when dissolved in D2O, which are less convincing. However, our simulations (Figure 7) show that for fully protonated and deuterated fibrils with the same peptide-water hydrogen bonding environments, there is a decreased intensity and a redshift of peak position of AmIII band, upon HX, which is a consequence of the loss of coupling. We thus propose that –NH deuteration induces the redshift in the AmIII band in Figure 6 and Figure 7. Deuteration of Aβ fibrils also decreases the intensities of AmIII bands, as shown in Figure 7, the three peaks in the range 1200–1350 cm–1 are dramatically weakened after HX. We believe that both the redshift and the decrease of intensities should account for the vanishing of the AmIII bands upon deuteration, as shown in Mikhonin and Asher's experiment.13
The change in the AmI band upon HX is well reproduced by our simulation shown in Figure 6. The weaker intensity of AmII′ band in our calculation can be attribute to that there is contribution from HOD bending mode in the experiment, but it was absent in the simulation. However, we encountered difficulties to fully reproduce the Cα–H and AmIII band peaks. It is obvious that the trend of change of these peaks coincides with experiment: The calculated peak positions agree well with the experiments, Cα–H band blueshifts and AmIII band redshifts. However, the intensities of both the two bands decrease upon HX. We believe that the reason for the deviation from experiment is the error in the DFT frequencies, which depend on the choice of functional and basis sets.38 We used the combination PBE0/6-311++G(d,p) for a reasonable description of high energy electronic excited states. The selected functional/basis set seems to overestimate the coupling between the Cα–H bending and C–N stretching modes.
V. Conclusions
We have developed a combined QM and MM protocol for simulating the deep UV resonance Raman spectra of amyloid fibrils. A number of snapshots were extracted from an MD trajectory to construct the ensemble for the simulation of fluctuation effects in biological systems. For each snapshot, we performed ab-initio resonance Raman calculations based on the Frenkel exciton model with the Heitler-London approximation. We have also constructed a map between excited state shift and Ramachandran angles, which can help future investigations of DRVRR spectroscopy of proteins.
Benchmarks for the dipeptides Ala-Ala and Ala-Asp illustrate that it is reasonable to neglect side chain effect in peptide backbone vibration and using GLDP to provide vibration information for the exciton model. These benchmarks also showed that the sampling density of the map is accurate enough to characterize protein secondary structure. The Benchmark on H2O/D2O mixture confirms the ability of our protocol to reproduce the effect of hydrogen-deuterium exchange in aqueous environment.
The effects of hydrogen-deuterium exchange which depends on the conformation of amyloid fibrils were simulated as well. All the main features of change in DUVRR spectra of Aβ34–42 and Aβ1–40 fibrils upon HX were reproduced in our calculations. We propose that the redshift of AmIII band after HX is a consequence of loss of coupling with Cα–H bending and N–D bending modes.
We note that the fibril cores of both systems have similar Ramachandran dihedral angles with short peptide microcrystals.49 Our ability to reproduce the main features of the DUVRR spectra of the two Aβ fibrils suggests that the structures employed in our simulation, which have similar Ramachandran angles with short peptide microscrystals, are consistent with those in the experiment. The success using dipeptide as principal unit to simulate DUVRR confirms the assumption that fibril core could be modeled by short peptide microcystals.49
Acknowledgements
We gratefully acknowledge the support of the National Institutes of Health (grants GM059230 and GM091364), the National Science Foundation (grant CHE-1058791), the Dept. of Energy (grants DE-FG02-04ER15571), and DARPA (grants UOFT-49606). We acknowledge the computational resource support from the GreenPlanet cluster at UCI (NSF Grant CHE-0840513). We wish to thank Dr. Alfonso Lam for helpful discussions.
References
- 1.Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. Proc. Natl. Acad. Sci. U.S.A. 2002;99:16742–16747. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Caughey B, Peter T, Lansbury J. Ann. Rev. Neurosci. 2003;26:267–298. doi: 10.1146/annurev.neuro.26.010302.081142. [DOI] [PubMed] [Google Scholar]
- 3.Rishton GM. Nature Chem. Bio. 2008;4:159. doi: 10.1038/nchembio0308-159. [DOI] [PubMed] [Google Scholar]
- 4.Strasfeld D, Ling Y, Gupta R, Raleigh D, Zanni M. J. Phys. Chem. B. 2009;113:15679–15691. doi: 10.1021/jp9072203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shim S-H, Gupta R, Ling Y, Strasfeld D, Raleigh D, Zanni M. Proc. Natl. Acad. Sci. U.S.A. 2009;106:6614–6619. doi: 10.1073/pnas.0805957106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chiti F, Dobson CM. Ann. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 7.Huang C, Balakrishnan G, Spiro TG. J. Raman Spectrosc. 2006;37:277–282. [Google Scholar]
- 8.Soldatova A, Ibrahim M, Olson J, Czernuszewicz R, Spiro T. J. Am. Chem. Soc. 2010;132:4614–4625. doi: 10.1021/ja906233m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ozdemir A, Lednev IK, Asher SA. Spectrochim. Acta Part A. 2005;61:19–26. doi: 10.1016/j.saa.2004.03.006. [DOI] [PubMed] [Google Scholar]
- 10.Mikhonin A, Ahmed Z, Ianoul A, Asher S. J. Phys. Chem. B. 2004;108:19020–19028. [Google Scholar]
- 11.Popova LA, Kodali R, Wetzel R, Lednev IK. J. Am. Chem. Soc. 2010;132:6324–6328. doi: 10.1021/ja909074j. [DOI] [PubMed] [Google Scholar]
- 12.Mikhonin AV, Bykov SV, Myshakina NS, Asher SA. J. Phys. Chem. B. 2006;110:1928–1943. doi: 10.1021/jp054593h. [DOI] [PubMed] [Google Scholar]
- 13.Mikhonin AV, Asher SA. J. Phys. Chem. B. 2005:3047–3052. doi: 10.1021/jp0460442. [DOI] [PubMed] [Google Scholar]
- 14.Asher SA, Ianoul A, Mix G, Boyden MN, Karnoup A, Diem M, Schweitzer-Stenner R. J. Am. Chem. Soc. 2001;123:11775–11781. doi: 10.1021/ja0039738. [DOI] [PubMed] [Google Scholar]
- 15.Cao W, Ye X, Georgiev G, Berezhna S, Sjodin T, Demidov A, Wang W, Sage J, Champion P. Biochem. 2004;43:7017–7027. doi: 10.1021/bi0497291. [DOI] [PubMed] [Google Scholar]
- 16.Champion P. Science. 2005;310:980–982. doi: 10.1126/science.1120280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu M, Shashilov V, Lednev IK. J. Am. Chem. Soc. 2007;129:11002–11003. doi: 10.1021/ja073798w. [DOI] [PubMed] [Google Scholar]
- 18.Kurouski D, Lauro W, Lednev IK. Chem. Commun. 2010;46:4205–4416. doi: 10.1039/b926758a. [DOI] [PubMed] [Google Scholar]
- 19.Oladepo S, Xiong K, Hong Z, Asher S. J. Phys. Chem. Lett. 2011;2:334–344. doi: 10.1021/jz101619f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Long DA. The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules. 1st ed. John Wiley & Sons Ltd; Chichester: 2002. [Google Scholar]
- 21.Albrecht AC. J. Chem. Phys. 1961;34:1476–1484. [Google Scholar]
- 22.Yan YJ, Mukamel S. J. Chem. Phys. 1986;85:5908–5923. [Google Scholar]
- 23.Wilson EB, Decius JC, Cross PC. Molecular Vibrations: The theory of infrared and Raman vibrational spectra. McGraw-Hill Book Company, Inc.; New York: 1955. [Google Scholar]
- 24.Peticolas WL, Rush T. J. Comput. Chem. 1995;16:1261–1270. [Google Scholar]
- 25.Markham LM, Mayne LC, Hudson BS, Zgierski MZ. J. Phys. Chem. 1993;97:10319–10325. [Google Scholar]
- 26.Gaff JF, Franzen S, Delley B. J. Phys. Chem. A. 2010;114:11681–11690. doi: 10.1021/jp103321x. [DOI] [PubMed] [Google Scholar]
- 27.Hudson BS, Markham LM. J. Raman Spectrosc. 1998;29:489–500. [Google Scholar]
- 28.Markham LM, Hudson BS. J. Phys. Chem. 1996;100:2731–2737. [Google Scholar]
- 29.Tsiper EV, Chernyak V, Tretiak S, Mukamel S. Chem. Phys. Lett. 1999;302:77–84. [Google Scholar]
- 30.Manneback C. Physica. 1951;17:1001–1010. [Google Scholar]
- 31.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, et al. Gaussian 09 Revision A.1. Gaussian Inc.; Wallingford CT: 2009. [Google Scholar]
- 32.Perdew JP, Burke K, Ernzerhof M. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 33.Perdew JP, Burke K, Ernzerhof M. Phys. Rev. Lett. 1997;78:1396. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 34.Amos RD. Chem. Phys. Lett. 1982;87:23–26. [Google Scholar]
- 35.Barone V, Cossi M. J. Phys. Chem. A. 1998;102:1995–2001. [Google Scholar]
- 36.Cossi M, Rega N, Scalmani G, Barone V. J. Comput. Chem. 2003;24:669–681. doi: 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
- 37.Scott AP, Radom L. J. Phys. Chem. 1996;100:16502–16513. [Google Scholar]
- 38.Merrick JP, Moran D, Radom L. J. Phys. Chem. A. 2007;111:11683–11700. doi: 10.1021/jp073974n. [DOI] [PubMed] [Google Scholar]
- 39.Hu H, Yang W. J. Mol. Struct. THEOCHEM. 2009;898:17–30. doi: 10.1016/j.theochem.2008.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mix G, Schweitzer-Stenner R, Asher SA. J. Am. Chem. Soc. 2000;122:9028–9029. doi: 10.1021/ja0039738. [DOI] [PubMed] [Google Scholar]
- 41.Bykov SV, Asher SA. J. Phys. Chem. Lett. 2010;1:269–271. doi: 10.1021/jz900117u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Frenkel J. Phys. Rev. 1931;37:1276. [Google Scholar]
- 43.Abramavicius D, Palmieri B, Voronine DV, Šanda F, Mukamel S. Chem. Rev. 2009;109:2350–2408. doi: 10.1021/cr800268n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jiang J, Abramavicius D, Bulheller BM, Hirst JD, Mukamel S. J. Phys. Chem. B. 2010;114:8270–8277. doi: 10.1021/jp101980a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.MacKerell AD, Bashford D, Bellott, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, et al. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 46.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 47.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kalé L, Schulten K. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lührs T, Ritter C, Adrian M, Riek-Loher D, Bohrmann B, Döbeli H, Schubert D, Riek R. Proc. Natl. Acad. Sci. U.S.A. 2005;102:17342–17347. doi: 10.1073/pnas.0506723102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sawaya MR, Sambashivan S, Nelson R, Ivanova MI, Sievers SA, Apostol MI, Thompson MJ, Balbirnie M, Wiltzius JJW, Mcfarlane HT, Madsen AØ, Riekel C, Eisenberg D. Nature. 2007;447:453–457. doi: 10.1038/nature05695. [DOI] [PubMed] [Google Scholar]
- 50.DeFlores LP, Tokmakoff A. J. Am. Chem. Soc. 2006;128:16520–16521. doi: 10.1021/ja067723o. [DOI] [PubMed] [Google Scholar]