Information analysis of posterior canal afferents in the turtle, Trachemys scripta elegans

Abstract

We have used sinusoidal and band limited Gaussian noise stimuli along with information measures to characterize the linear and non-linear responses of morpho-physiologically identified posterior canal (PC) afferents and to examine the relationship between mutual information rate and other physiological parameters Our major findings are: 1) spike generation in most PC afferents is effectively a stochastic renewal process, and spontaneous discharges are fully characterized by their first order statistics; 2) a regular discharge, as measured by normalized coefficient of variation (cv*), reduces intrinsic noise in afferent discharges at frequencies below the mean firing rate; 3) coherence and mutual information rates, calculated from responses to band limited Gaussian noise, are jointly determined by gain and intrinsic noise (discharge regularity), the two major determinants of signal to noise ratio in the afferent response; 4) measures of optimal non-linear encoding were only moderately greater than optimal linear encoding, indicating that linear stimulus encoding is limited primarily by internal noise rather than by non-linearities; 5) a leaky integrate and fire model reproduces these results and supports the suggestion that the combination of high discharge regularity and high discharge rates serves to extend the linear encoding range of afferents to higher frequencies. These results provide a framework for future assessments of afferent encoding of signals generated during natural head movements and for comparison with coding strategies used by other sensory systems.

1. Introduction

The vestibular system provides the brain with information about linear and angular head accelerations and head orientation with respect to gravity. This information is essential for control of eye position, posture and locomotion. Vestibular primary afferent neurons have traditionally been viewed as linear encoders whose response dynamics at low frequencies are adequately characterized by response gain and phase (reviewed by Lysakowski and Goldberg 2004). Vestibular primary afferents also have a spontaneous discharge whose regularity is considered to be an important physiological parameter (Goldberg 2000). The standard measure of discharge regularity is cv*, the coefficient of variation (cv) of the interspike interval (ISI) distribution extrapolated to a standard discharge rate (Goldberg 2000). Afferents with low cv* values are labeled regular and those with higher values are labeled irregular. In all animals investigated, cv* is correlated with afferent response dynamics in similar ways and is a major determinant of afferent sensitivity (Goldberg and Chatlani, 2009; reviewed by Goldberg 2000; Highstein et al. 2005). However, cv (or cv*) and other statistics of ISI distributions only characterize regularity on the time scale of the mean ISI. Higher order statistical structure in a spike train, such as serial correlations among ISIs or the recurrence of stereotypical ISI sequences, can influence discharge regularity on longer time scales. Indeed, recent studies have shown that serial ISI correlations can shape the spontaneous power spectrum and influence information transmission in electroreceptor primary afferents (Ratnam and Nelson 2000; Chacron et al. 2001; Neiman and Russell 2004). However, the role that such higher order structure might play in vestibular afferents is not well understood.

Natural auditory and visual signals tend to be highly structured, i.e., they are correlated across time or space. Consequently, much of the information extracted from natural signals is redundant, and the efficient encoding of natural signals by sensory neurons is likely to involve removal of this redundant information, resulting in neuronal signals that are statistically independent (Barlow 1961). Information theory has been a valuable tool in investigating the mechanisms by which sensory neurons are optimized for encoding the signals that occur in natural environments (Simoncelli and Olshausen 2001; Schwartz and Simoncelli 2001) because it provides a direct measure of the efficiency with which stimuli are encoded, and it also allows linear and non-linear stimulus encoding to be assessed independently (Borst and Theunissen 1999; Passaglia and Troy 2004; Chacron 2006)..

Turtles have become an important model system for the study of peripheral vestibular mechanisms (Bonsacquet et al. 2006; Boyer et al. 2004; Brichta et al. 1988, 2002.; Brichta and Goldberg 1996, 1998, 2000a,b; Cochran and Correia 1995; Goldberg and Brichta 2002; Holt et al. 2006a,b, 2007; Huwe and Peterson 1995; Moravec and Peterson 2004; Nam et al. 2007a,b; Rennie et al. 2004; Severinsen et al. 2003; Silber et al 2004; Rowe and Peterson 2004, 2006; Xue and Peterson 2006). The morphology and physiology of posterior canal (PC) afferents in the turtle, including their linear response dynamics to sinusoidal stimulation, have been well characterized (Brichta and Goldberg 2000a; 2000b). However, correlation analysis of spontaneous discharge and its relation to response properties and stimulus encoding are lacking. Although a theoretical consideration on information encoding in vestibular afferents has been presented by (Goldberg 2000), currently there is only one experimental study (Sadeghi et al. 2007) in which information metrics were applied to vestibular afferents. As part of a larger effort to determine if vestibular afferents are optimized to encode features of natural head movements in turtles, we have used a variety of information metrics to directly evaluate both linear and nonlinear stimulus encoding of Gaussian noise stimuli, and to evaluate the relationship between information measures and functionally significant morpho-physiological properties such as discharge regularity in the afferent population. Some of these results have been presented previously in abstract form (Rowe and Neiman 2005, 2007).

2. Results

2.1 Sample Statistics and Afferent Identification

Data were obtained from 272 afferents in 80 turtles. The range of cv values within this sample was 0.135 – 1.54. A subset of 198 of these afferents had spontaneous discharges with a mean ISI within the normalization range (20 – 100 msec) of our regression. Values of cv* at a standard ISI of 50 msec were calculated for this subset. Response gain and phase to sinusoidal stimulation was measured for 95 units, of which 51 were morphophysiologically identified on the basis of responses to efferent stimulation. Due to the long recording times required and the strict criteria we imposed to ensure good single unit isolation (see Methods, section 4.1), it was not possible to obtain all information metrics for all units. Specific numbers are given in the section for each metric.

2.2 Statistical properties of spontaneous discharge

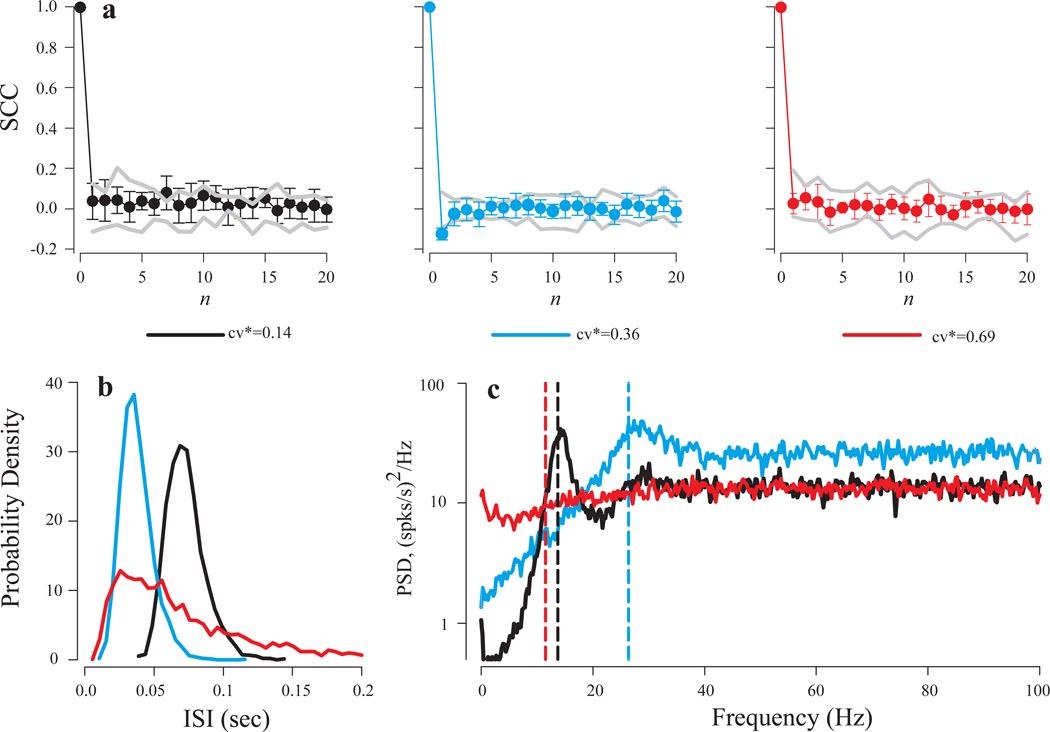
We assessed the presence of higher order structure in afferent spike trains, i.e., structure that cannot be characterized in terms of ISI distribution, in two ways. First, we examined serial correlation coefficients (SCCs) for 33 afferents from 10 turtles for which sufficiently long (3–10 min) recordings of spontaneous activity was recorded. The cv* values for this sample ranged from 0.15 to 0.68 (mean 0.37, SD ± 0.17). Average spontaneous discharge rate for this sample was 14.55 ± 8.82 spikes/s with a range of 0.40 – 41.15 spikes/s. Figure 1b shows ISI probability density distributions for three of these afferents with cv* values of 0.14 (black), 0.36 (blue) and 0.69 (red). As has been reported previously, small cv* values are associated with narrow ISI distributions. Serial correlograms for these three afferents are shown in Figure 1a. Gray lines indicate, for each afferent, the range of SCCs expected for a renewal process with the same ISI distribution created by randomly shuffling all ISIs. With 2 exceptions, serial correlograms for the afferents in this sample were within this range, and a Wilcoxon rank sum test established that the SCCs of the original data did not differ from those of the shuffled surrogates (Methods). The 2 exceptions, one of which is shown in Figure 1a (middle), both showed weak negative serial correlations at n=1.

Fig. 1.

Analysis of spontaneous discharge regularity of three PC afferents with cv* values of 0.69 (red lines), 0.36 (blue lines), and 0.14 (black lines). (a) Serial correlation coefficients (SCC) as a function of the number of intervening intervals (n). Gray lines show minimal and maximal values of SCCs for shuffled ISIs. Only the unit with cv*=0.36 showed significant serial correlation coefficient for n=1. (b) ISI distributions. (c) Power spectra. Afferents with lower cv* values showed clear peaks at the frequencies close to their mean firing rates (vertical dashed lines) and drop off sharply below the mean firing rate, indicating less intrinsic noise at the lower frequencies.

The second method was to calculate the spontaneous power spectral density (PSD) for each afferent in this sample and compare it to the power spectrum of a surrogate created by randomly shuffling all ISIs. PSDs for the same three afferents in Figure 1a and b are shown in Figure 1c. Vertical dashed lines indicate mean firing rates for each afferent. The spectra differ in that the most regular unit (black) displays a sharp peak at the mean firing rate, while the more irregular afferents have increasingly flat spectra. For the two afferents with relatively small cv* values (black and blue lines in Fig. 1c), the amplitude of their spontaneous PSDs, and thus the intrinsic noise level of the afferents, declines significantly, i.e., by at least an order of magnitude, at frequencies below the mean discharge rate. This effect was observed in afferents with cv* values < 0.4 (15 of 33). For all 33 afferents, the PSD was unaffected by randomly shuffling of ISIs, which suggests that the spectra are determined entirely by the ISI distribution. These results further indicate that spike generation can be characterized as a stochastic renewal process.

2.3 Responses to sinusoids

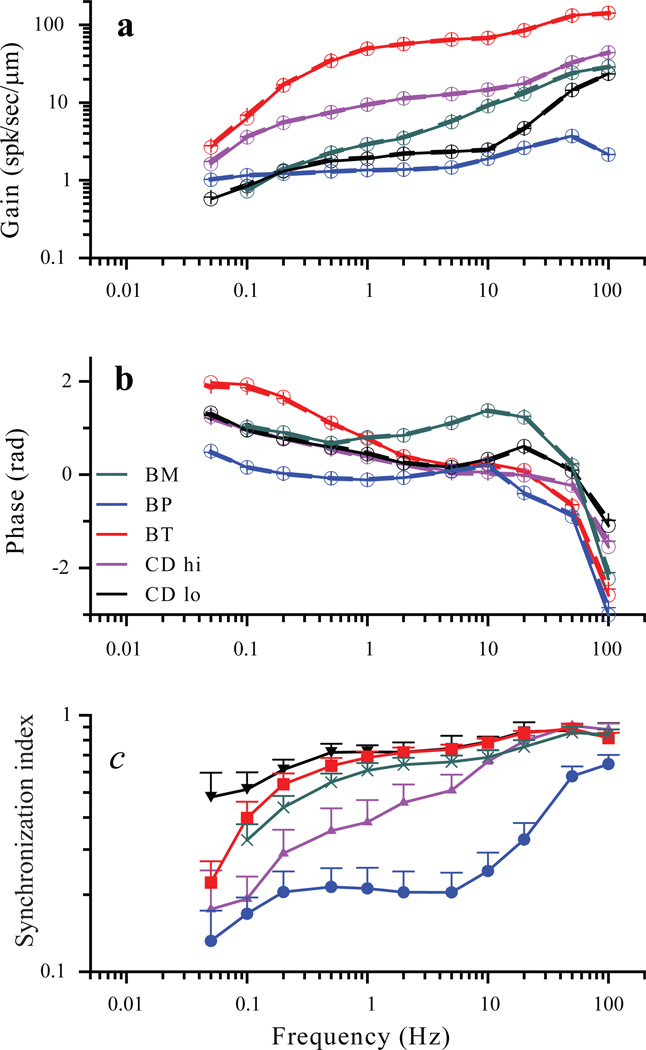
For the sample of 51 afferents morpho-physiologically identified by efferent responses (12 BT, 16 BP, 16 BM, 4 CD_Lo, 3 CD_Hi), average gains and phases of afferent responses to sinusoidal indentation of the posterior canal were similar to those reported for head rotation by Brichta and Goldberg (2000a) at comparable frequencies. Gain and phase plots for representative examples of each type are shown in Figure 2A and B. For all units, gain increases, and phase relative to peak indenter position decreases with increasing frequency. BT units had the highest gain and largest phase advance at low frequencies; BP units had the lowest gain and smallest phase advance. BM and CD units had intermediate properties. Responses for all units were nonlinear at frequencies above 10 – 20 Hz. The non-linearities were principally of two forms. The first was simple rectification, which manifested as 0 firing rate in the inhibitory half of the phase histograms, and as higher harmonics in the Fourier spectra. The second was a tendency to phase lock, which manifested as peaks in the phase histograms that were much narrower than one half cycle of the phase histogram, and as higher harmonics in the Fourier spectra. All categories of afferents exhibited phase locking at frequencies > 20 Hz. For all 51 afferents, the degree of phase locking at each frequency was quantified using the synchronization index (SI) (Fig. 2c). This measure increased with stimulus frequency, and at frequencies above 20 Hz was close to 1 for all afferent types except for BP units, whose SI values were less than 0.7.

Fig. 2.

Linear gain (a) and phase re peak excitatory indenter position (b) as a function of frequency for five morphologically distinct afferents. Values calculated from sinusoidal fits (circles) and values calculated from Fourier spectra (crosses) are virtually identical. c. Synchronization index for 5 groups of afferents (n= 12 BT, 16 BP, 16 BM, 4 CD_Lo, 3 CD_Hi). All groups show clear phase locking (SI values close to 1) at frequencies >10 Hz except for a BP units.

2.4 Responses to Gaussian noise

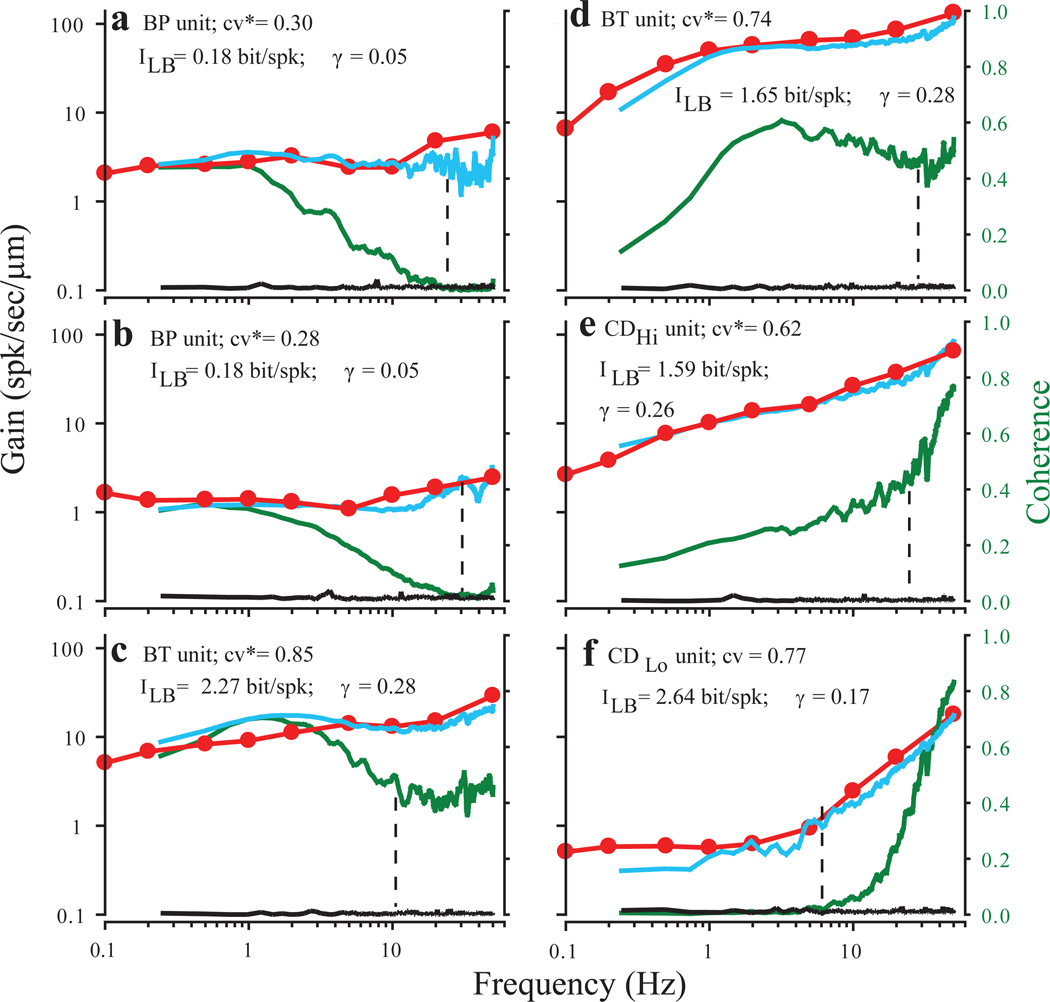
Response gains to Gaussian noise with a cutoff frequency of 50 Hz were analyzed for a sample of 51 afferents from 18 turtles. From this sample only 26 units, with the mean ISI within the normalization range for calculation of cv*, were included here. Representative examples are shown for 6 afferents in Figure 3 (blue lines). Gain values for the same units calculated from responses to single sinusoids are superimposed (red lines). Gain values calculated from responses to Gaussian noise were similar to those based on responses to single sinusoids over a wide range of indenter amplitudes (see figure legend). Stimulus-response (SR) coherence functions (green lines) represent linear information encoding rates for these units. Black lines are control coherence values calculated after randomly shuffling all spikes in the afferent responses. The afferents are arranged, a through f, in a continuum, from low pass through broad-band to high pass, in terms of their SR coherence functions. Broad-band afferents (c, d) have high gain and provide significant linear encoding across most of the frequency range. Their coherence functions parallel the shape of the gain curves at low frequencies but decline at high frequencies even though gain continues to increase. Thus, linear stimulus encoding is correlated with gain at low frequencies, but limited by intrinsic noise at high frequencies. For low-pass afferents (a, b), the decline of SR coherence at high frequencies is much more pronounced, reaching chance levels at frequencies near their spontaneous firing rate (vertical dashed lines) even though gain is relatively constant up to 50 Hz. These data indicate that for afferents with regular discharges, there is little or no linear stimulus encoding for stimulus frequencies above their spontaneous firing rate.

Fig. 3.

Comparison of linear gains and coherence functions for 6 PC afferents. All afferents were stimulated with Gaussian noise band limited to 50 Hz. In each panel (a–f), gain calculated from responses to Gaussian noise are shown in blue, gain for the same afferent measured from responses to sinusoidal indentation in red, and coherence between the Gaussian stimulus and the afferent response in green. Note that coherence axis is linear. The black lines are coherence values from the same data sets, but calculated after randomly shuffling all the ISIs in the response, preserving ISI distributions, but eliminating any higher order structure. They provide an estimate of coherence values that would be obtained by chance for any particular data set. Mean spontaneous firing rates are indicated by vertical dashed lines. All units were identified on the basis of responses to efferent stimulation. For each unit cv*, lower bound information estimate (I_LB), and coding fraction (γ) are also shown. Peak-to-peak sinusoidal indenter amplitudes and Gaussian noise SD, respectively, were (in µm) 3.5 and 2.07 in a, 16.7 and 4.64 in b, 7 and 2.1 in c, 1.5 and 0.5 in d, 3.5 and 1.03 in e, and 16 and 4.6 in f.

Hi-pass afferents (e,f) have coherence values that are close to chance levels below their spontaneous firing rate, indicating there is little or no linear encoding at low frequencies, even though they have measurable gains at those frequencies comparable to those of other afferents that do encode these frequencies (a,b). Coherence functions rise steeply above the mean firing rate, suggesting that these units are able to linearly encode higher frequencies.

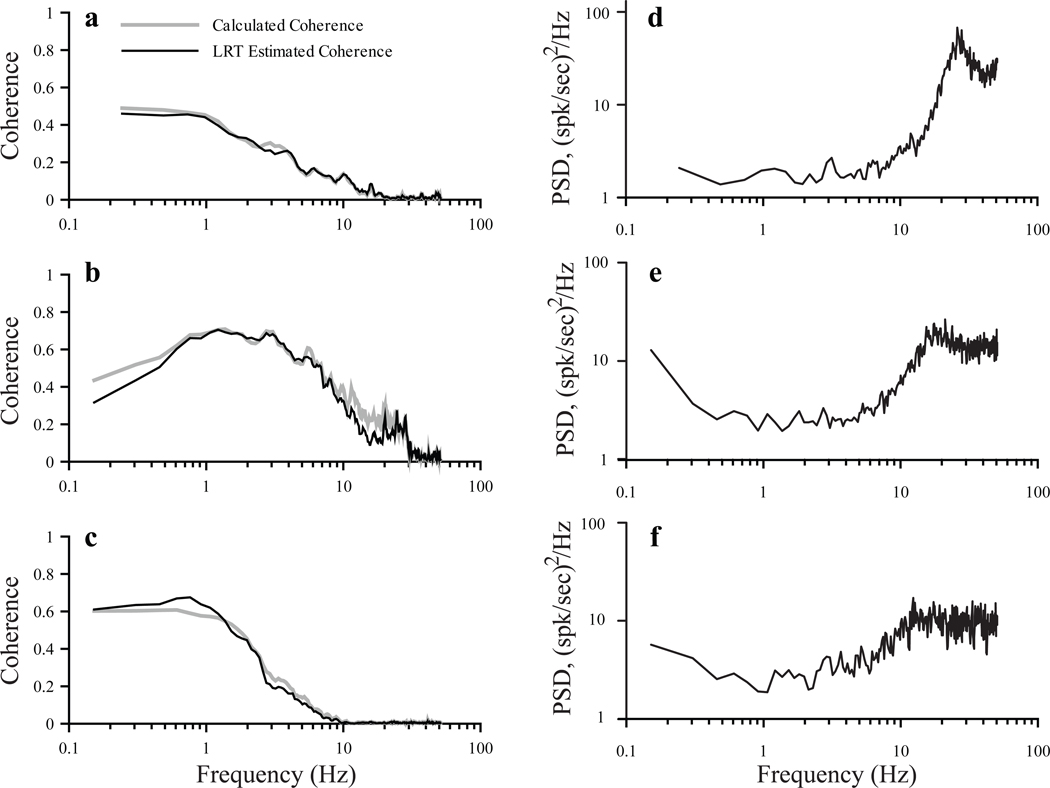
To better understand the role of spontaneous activity in shaping the SR coherence function and thus linear stimulus encoding, we compared calculated SR coherence functions with those estimated on the basis of linear response theory (LRT) as described in Methods. The results for three afferents are shown in Figure 4a–c. The close correspondence between calculated and approximated SR coherence functions within the stimulus band (0 – 50 Hz in A, 0 – 30 Hz in B and 0 – 10 Hz in C) suggests that the shapes of the coherence functions in Figure 3 can be influenced by both gain and internal noise (spontaneous PSD). As an example, the SR coherence function for the regular afferent in Fig. 3a is replotted in Figure 4a, along with estimated SR coherence. The PSD for this afferent, calculated from 10 min of spontaneous activity, is shown in Fig. 4d. The discrepancy between the flat shape of the gain curve and low pass SR coherence function (Fig. 3a) is clearly due to the increased spectral power at frequencies above 10 Hz (Fig. 4d). Lower spectral power at frequencies < 10 Hz results in high SR coherence, while higher power at frequencies > 10 Hz combined with low gain (Fig. 3a), results in SR coherence values at chance levels. Similarly, for the other two units in Figure 4 (b,e and c,f), whose gain curves were relatively flat (not shown), amplitude of spontaneous PSD was inversely related to SR coherence values, with maximum coherence at frequencies where PSD magnitude was lowest. Thus, both gain and internal noise play important roles in shaping SR coherence and linear encoding profiles.

Fig. 4.

Comparison of calculated coherence functions (A–C, grey lines) with those estimated based on linear response theory (a–c, black lines) and spontaneous power spectra (D–F) for 3 afferents with cv* values of 0.3 (a,d), 0.32 (b,e) and 0.335 (c,f). Calculated SR coherence in A is re-plotted from Figure 3A. Units were stimulated with Gaussian noise band limited to 50 Hz (a), 30 Hz (b) and 10 Hz (c). Intensities (Gaussian SD) were 2.07 (a), 6.47 (b), and 6.63 (c).

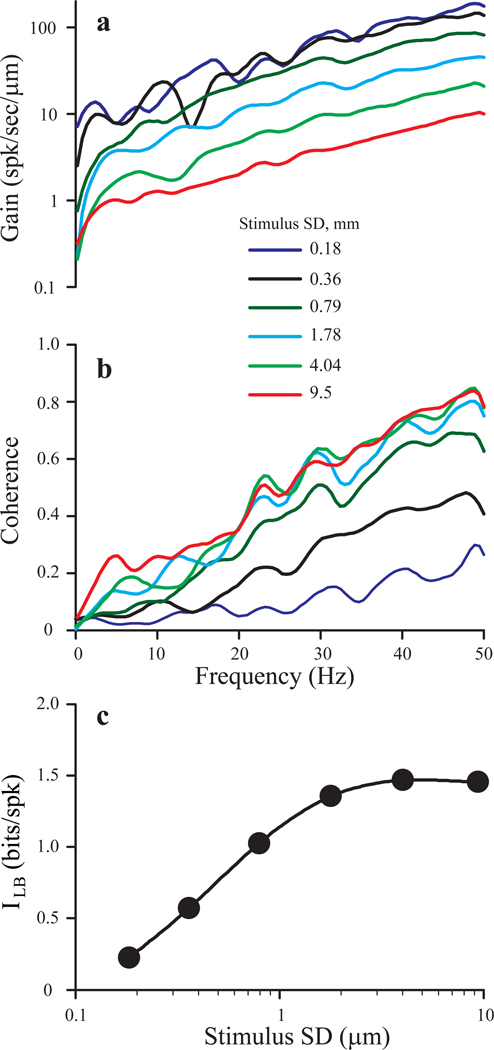
Gain and coherence of responses to Gaussian noise both changed in characteristic ways with increases in stimulus amplitude (standard deviation or SD). Figure 5 illustrates these relationships for an afferent stimulated with 50 Hz Gaussian noise at six different stimulus amplitudes. At the lowest intensities (SD = 0.18, 0.36 µm), responses were linear, i.e., gain was independent of stimulus amplitude (Fig. 5a). Nevertheless, coherence values (Fig, 5b) and information rates (Fig. 5c) both increased markedly. This behavior is consistent with the linear response approximation of Eq.(3). At higher stimulus SDs, responses became non-linear: gain values decreased as stimulus amplitude increased, while coherence values and information rates saturated. The frequency dependence of gain did not change significantly over the entire range of intensities (Fig. 5a). This pattern of dependence of gain and coherence on stimulus strength was observed in 4 other afferents in our sample, regardless of their overall sensitivity.

Fig. 5.

Effect of stimulus strength on gain (a), coherence (b), and lower bound of mutual information rate, I_LB (c) for an afferent stimulated with 50 Hz bandwidth Gaussian noise (stimulus SD indicated in the figure legend). The afferent was a BM unit with moderately high gain and a cv* value of 0.47.

2.5 Information rates

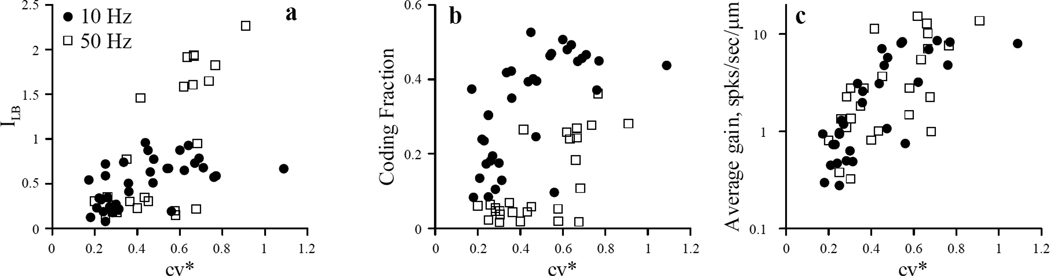
For the sample of 26 afferents stimulated with Gaussian noise with a bandwidth of 0.1–50 Hz, the average lower bound information rate estimate, I_LB, calculated from SR coherence functions, was 0.83±0.75 bits/spike (range 0.13 – 2.23 bits/spike). For a sample of 34 afferents stimulated with Gaussian noise with a bandwidth of 0.1–10 Hz, average I_LB was 0.52 ± 0.25 bits/spike (range, 0.08 – 0.96 bits/spike), which was not significantly different from the value obtained with the 50Hz bandwidth (Wilcoxon matched pairs test,, z-value=−0.90, p=0.37). Average coding fraction was 0.12 ± 0.11 (range 0.02 – 0.36) for the 50 Hz bandwidth and 0.32±0.14 (n=34, range 0.08 – 0.53) for the 10 Hz bandwidth. This difference was statistically significant ((Wilcoxon matched pairs test, z-value=−3.67, p=2× 10⁻⁴). Both I_LB and the coding fraction were positively correlated with cv* (Fig. 6 a,b). For afferents stimulated by 10Hz noise, the Spearman correlation coefficient, ρ, was 0.53 (p=2×10⁻³) between cv* and I_LB, and 0.65 (p=9×10⁻⁵) between cv* and the coding fraction. For the sample stimulated with 50Hz noise, the correlation coefficients were 0.61 (p=10⁻³) between cv* and I_LB, and 0.50 (p=0.012) between cv* and the coding fraction. Presumably these positive correlations between information metrics and cv* were due to higher values of gain observed for less regular units (Goldberg, 2000; see also Fig. 6 c).

Fig.6.

Lower bound of mutual information rate (I_LB) (a), coding fraction (b) and average gain (c) versus cv* for two samples of afferents stimulated with 50 Hz (n=26, grey squares) or 10 Hz (n=34, black circles) bandwidth Gaussian noise. Gain values were averaged over the 0.1 –10 Hz range for both samples.

Reliability of PC afferent responses to repeated segments of Gaussian frozen noise was studied in 19 units with cv* values ranging from 0.17 to 1.32. All units in this sample showed poor reliability (average 0.14 ± 0.07, range, 0.04 to 0.27) and significant spike timing jitter (average 66.7 ± 26.3 msec, range 14.6 to 110 msec). The units with the highest reliability were those with little or no spontaneous activity (CD_lo), resulting in significant correlations between cv* and the reliability: the Spearman correlation coefficient ρ was 0.58 (p=0.009). However, there were no significant correlations between cv* and spike timing jitter (ρ = −0.07, p=0.81). These results indicate that precise spike timing played little or no role in stimulus encoding.

2.6 Non-linear Response Dynamics

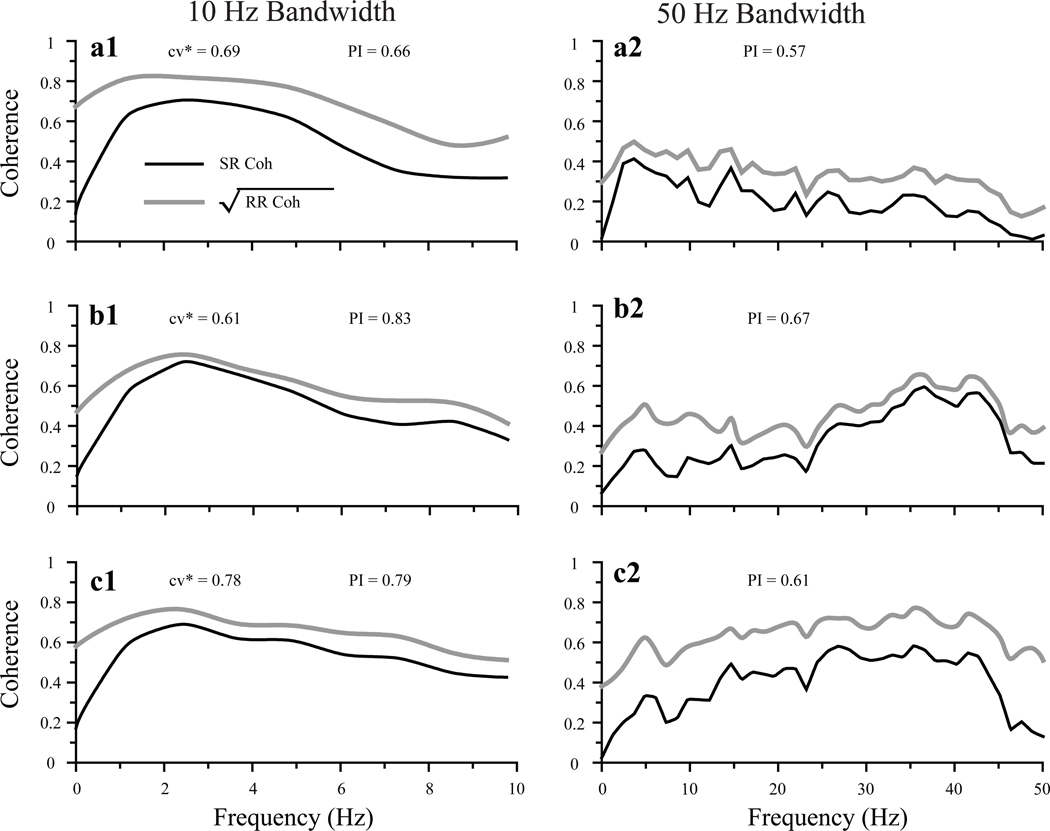
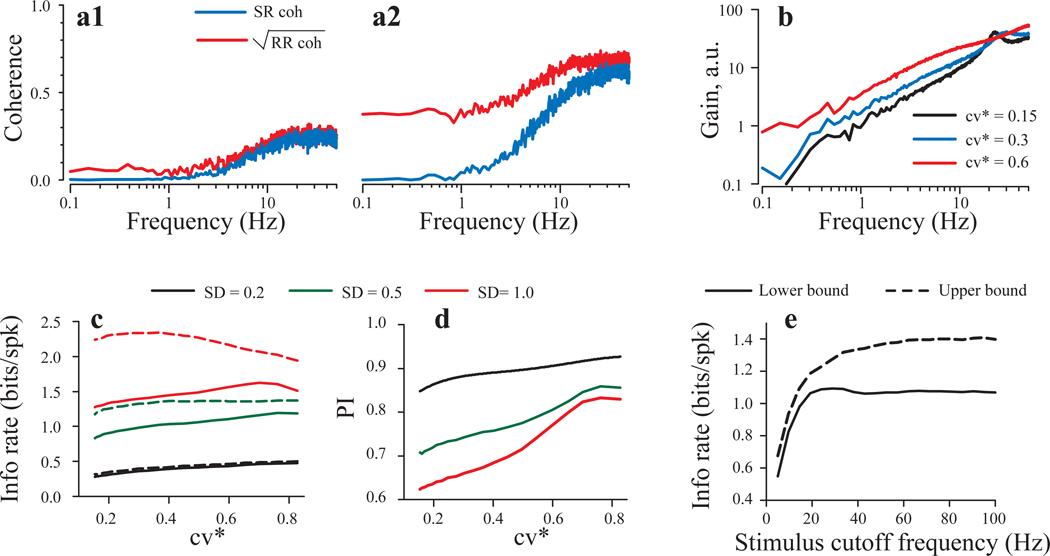
Low values of SR coherence can result either from nonlinearities in stimulus transduction or from noise. To examine which of these two factors limit SR coherence (and hence linear stimulus encoding) in PC afferents, we measured response-response (RR) coherence between successive responses to identical noise segments, whose bandwidth was set at 10 or 50 Hz. Total power in the stimuli was held constant. RR coherence sets a theoretical upper limit for mutual information, i.e., it quantifies the structure in the spike train that is produced by the stimulus regardless of whether the encoding is linear or non-linear. Thus, large differences between SR and RR coherence indicate significant non-linear encoding, while small differences suggest that linear encoding is limited by noise. RR coherence values were moderately greater than SR coherence values at frequencies higher than 2 Hz regardless of stimulus bandwidth (Figure 7). For Gaussian noise band limited to 10 Hz, the average value of PI, which is a measure of the relative effectiveness of linear encoding (see Methods), was 0.69 ± 0.14 (range: 0.4 – 0.92) for a sample of 10 bouton afferents. Similar values of PI were obtained when the bandwidth of the Gaussian noise was extended to 50 Hz (mean PI, 0.64 ± 0.18; range, 0.38 – 0.96) (Table 2). These values of PI indicate that low SR coherence values were largely due to noise rather than to nonlinearities. Nevertheless, some units showed substantial differences between SR and RR coherences at low frequencies (< 2 Hz), indicating that significant non-linear encoding may be present at the frequencies that dominate normal vestibular signals.

Fig. 7.

SR (black lines) and square root of RR coherence (grey lines) for stimuli of 10 and 50 Hz bandwidths for three different units (a–c). Afferents were stimulated with 10 identical 30 s segments of Gaussian noise band limited to 10 (left column) or 50 (right column) Hz. Total stimulus power was held constant. Stimulus intensities (Gaussian SD) were 5.28 µm in a1, 5.08 µm in a2, 2.79 µm in b1, 2.08 µm in b2, 0.9 µm in c1, and 0.85 µm in c2. Values of performance index (PI) and cv* are indicated. Units a and b were BM units; unit c was a BT unit.

Table 2.

Information measures for samples of PC afferents stimulated with Gaussian noise at 2 different bandwidths. Means and standard deviations (in parentheses) are given for each measure. Mean value of cv* for the sample was 0.56 (0.15). Lower bound estimates, I_LB, are calculated from SR coherence functions; upper bound estimates, I_UB, from RR coherence functions. Both are given in bits/s as well as bits/spike. All information measures except the PI index and the coding fraction clearly increased as stimulus bandwidth increased, indicating that afferents are encoding the higher frequencies. At both 10 Hz and 50 Hz, 60–70% of the information in the spike train was linearly encoded. I_LB; lower bound estimates.

Freq.	N	ILB, bits/s	ILB, bits/spike	IUB, bits/s	IUB, bits/spike	PI index	Coding fraction
10 Hz	10	7.14 (3.55)	0.63 (0.33)	11.01 (5.18)	1.00 (0.57)	0.69 (0.15)	0.25 (0.11)
50 Hz	10	16.9 (12.1)	1.17 (0.53)	30.01 (21.78)	2.17 (1.39)	0.64 (0.18)	0.11 (0.06)

2.7 Modeling

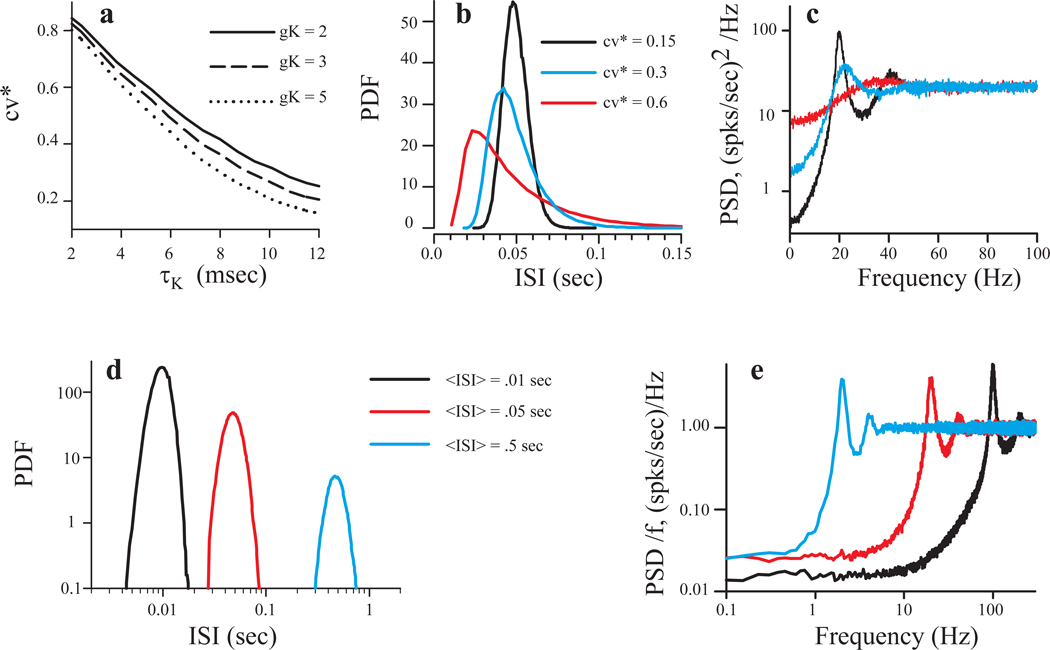
Parameters such as discharge rate and regularity are difficult to manipulate independently, and their role in stimulus encoding must be inferred from statistical analyses of population results (e.g., Brichta and Goldberg, 2000a). In order to more systematically investigate their contribution as well as the origin of afferent non-linearities, we used a leaky integrate and fire model in which these and other parameters could be manipulated independently. In the model, background discharge was created by spontaneous synaptic events, which followed Poisson statistics (Methods). Thus, the stochastic nature of the discharge resulted solely from fluctuations of the synaptic current. The current underlying the after-hypolarizing potential (AHP) was the major factor controlling the variability of interspike intervals (Smith and Goldberg 1986): an increase in AHP time constant (τ_K) and/or its strength (g_K) resulted in lower cv* values and a more regular spike train (Fig. 8a). The mean firing rate was kept constant at 20 spikes/s by the appropriate tuning of the threshold voltage, V_T. As observed in afferent recordings (Fig.1b), more regular spontaneous firing was characterized by narrower distributions of ISIs (Fig. 8b, black and blue lines) and well expressed peaks in the power spectra (Fig. 8c, cf Fig. 1c). Increasing the strength of the AHP current also lowered spectral power at low frequencies (Fig. 8c, black and blue lines), reducing intrinsic noise and allowing more regular units to better encode frequencies below their mean firing rate by increasing signal to noise ratio (SNR) at those frequencies. The effect of the mean firing rate on spontaneous discharge regularity is shown in Fig. 8 d and e, where the cv* was kept constant (cv* = 0.165) while the mean firing rate was varied by changing values of V_T and τ_K. As mean ISI increases, ISI probability density functions (PDF) maintain a constant relative width (cv*), while the height of PDF decreases (Fig. 7d). As expected, shorter ISIs (higher firing rates) extend the range of low frequencies for which PSD values are reduced (Fig. 8e), suggesting that afferents with higher firing rates are better suited for uniform linear encoding over a wider frequency range.

Fig. 8.

Spontaneous dynamics of the model. In panels a – c, the AHP time constant, τ_K was varied while the mean firing rate was fixed at 20 spikes/s by tuning the threshold voltage V_T, keeping other parameters constant. a: cv* versus AHP time constant for indicated values of AHP strength (g_K). b: Probability density of spontaneous ISIs for indicated values of cv*. c: Power spectral density (PSD) of spontaneous discharges for the units in panel B. Panels d and e, illustrate the ISI probability density and spontaneous discharge PSD for three different mean firing rates at a fixed cv value of 0.165. The PSD values in E were normalized to the mean firing rate.

SR and RR coherences are shown in Fig. 9a for a model unit with a cv* of 0.6 stimulated with band limited noise (f_c = 50 Hz) at two stimulus amplitude levels (a1, a2). For both coherences, the frequency dependence was largely determined by the gain profile of the model unit. For low stimulus amplitudes (Fig. 9 a1), SR and RR coherences were similar across the entire frequency range, indicating that the response of the model is essentially linear. At the higher stimulus amplitude (Fig. 9 a2), RR coherence is increased across the frequency range, but SR coherence is increased only for middle and high frequencies, resulting in large differences between SR and RR coherence at low frequencies. Thus, at large stimulus intensities nonlinear encoding, the difference between SR and RR values, becomes significant and the lower bound of the mutual information rate (SR coherence) underestimates the true mutual information rate.

Fig. 9.

Model results for stimulation with Gaussian noise band limited to 50 Hz. Model parameters are shown in Table 1. In all simulations, the mean spontaneous firing rate was fixed at 20 spikes/s. a: SR coherence (blue lines) and the square root of RR coherence (red lines) for a model unit with cv = 0.6, for two values of stimulus strength; SD =0.3 (A1) and SD = 1 (A2). b: Gain for the 50 Hz band limited noise with the strength SD = 0.5 and three values of cv (a.u. stands for arbitrary units). c: lower bound (solid lines) and upper bound (dashed lines) estimates of mutual information rates versus cv for the three values of stimulus intensity. d: performance index PI versus cv for the same data as in panel b. e: lower bound (solid lines) and upper bound (dashed lines) estimates of mutual information rates versus the cutoff frequency for a model unit with cv = 0.5 (stimulus intensity, SD = 0.5).

According to the LRT, Eq.(3), the SR coherence is determined jointly by the gain and the PSD of the spontaneous activity. In the model, the increase in cv* is accompanied by a parallel increase in the gain (Fig. 8b) (Smith and Goldberg, 1986), and thus an increase in coherence. On the other hand, irregular units exhibit a higher level of low frequency internal noise (Fig. 8c,e), which decreases SR coherence. Consequently, the lower bound estimates of mutual information rate show only slight increases with increasing cv* (solid lines in Fig. 9c). Figure 9c also illustrates that mutual information rate shows a strong dependence on stimulus intensity, presumably because of the increased SNR. At low stimulus intensities (Fig. 9c, black lines), the values of lower and upper bound estimates of mutual information rate are close, but at higher intensities (Fig. 9c, green and red lines), the difference between the lower and upper bound estimates increases with increasing stimulus intensity. Significantly, for the stronger stimuli (green and red lines) the difference between I_LB and I_UB is greater for model units with lower cv*. This is illustrated further in Fig. 9d, where the performance index, PI, which reflects the ratio of SR/RR (see Methods), is shown as a function of cv* for the three values of stimulus amplitude. The PI decreases as stimulus intensity increases, as expected, but also increases with increasing cv*, indicating a greater degree of linear encoding for irregular units. Presumably, this is due to the linearizing effect of noise in irregular units as discussed in (Sadeghi et al. 2007), in addition to the higher gain seen in irregular units (Fig 9b).

Finally, figure 9e shows the influence of stimulus frequency bandwidth on the encoding properties of model units. The stimulus variance was kept constant, as it was in experiments. While the lower bound of the mutual information rate (solid line) increases and then saturates for 20 f_c > Hz, the upper bound (dashed line) continues to grow (cf, Fig. 9c). Thus, the proportion of nonlinear stimulus encoding increases as the frequency band is extended.

3. Discussion

We have used sinusoidal and band limited Gaussian noise stimuli to characterize the linear and non-linear responses of posterior canal (PC) afferents and to examine the relationship between mutual information rate and other physiological parameters such as gain and discharge regularity. Our major findings are: 1) spike generation in most PC afferents is a stochastic renewal process, so that spontaneous discharges are fully characterized by their first order statistics and lack any higher order statistical structure such as serial ISI correlations; 2) a regular discharge, as measured by normalized coefficient of variation (cv*), reduces intrinsic noise in afferent discharges at frequencies below the mean firing rate. This effect is evident at cv* values as high as 0.3; 3) coherence and mutual information rates, calculated from responses to band limited Gaussian noise, are jointly determined by gain and intrinsic noise (discharge regularity), the two parameters that are the major determinants of signal to noise ratio in the afferent response (Figs. 3, 4); 4) for Gaussian stimuli, nonlinearities were manifested as differences between SR and RR coherences. The relatively small magnitude of these differences, and the fact that RR coherence values are significantly <1, indicate that linear stimulus encoding is limited primarily by intrinsic discharge noise rather than nonlinearities; 5) a leaky integrate and fire model reproduces these experimental results and supports the suggestion that the combination of high discharge regularity and high discharge rates serves to extend the linear encoding range of afferents to higher frequencies (Fig. 8c,e).

In terms of coherence measures and linear encoding (Figure 3), PC afferents form a clear continuum from low pass units that only encode frequencies below their mean firing rate, to high pass units that only encode frequencies above their mean firing rate. In between these extremes are broad band units that encode a range of frequencies spanning their mean firing rates. Low pass units are predominantly of the BP group, and high pass units are predominantly of the CD_lo group. Because of their low gains, BP and CD are thought to be involved signaling large amplitude voluntary head movements (Brichta and Goldberg 2000b), and the present results suggest that they encode distinctly different frequency components of these movements; low frequency sustained components are encoded by BP units and high frequency transients are encoded by CD_lo units. Broad band units are predominantly of the BT group, but also include CD_hi and some BM units. BT units have higher gains, which has led to the suggestion that they signal small amplitude movements associated with postural sway (Brichta and Goldberg 2000b). The frequency spectra of these movements are not known, but the broad band encoding of BT units suggests that there may be a more uniform frequency distribution for passive movements than for volitional movements.

3.1 Determinants of mutual information

Lower bound estimates of mutual information between the stimulus and spike train are calculated from the SR coherence of responses to Gaussian noise. In order to relate measures of mutual information to more traditional measures, such as linear gain, it is important to establish that measures based on noise stimuli are comparable to those based on responses to deterministic stimuli like sinusoids. Our results demonstrate, for individual afferents, that gain calculated from responses to single sinusoids does indeed closely match gain calculated from responses to Gaussian noise over comparable range of frequencies, even when the stimulus intensities for the two regimes are not matched (Figure 3). Our results also indicate that, for individual afferents, the shape of the SR coherence function is related not only to linear gain, but also to the shape of the afferent’s spontaneous discharge power spectrum, which reflects intrinsic noise (Figure 4). This demonstrates directly that the background noise in the afferent spike train is an important determinant of afferent information capacity, and that a significant advantage of a regular discharge, which reduces noise at frequencies below the spontaneous firing rate, is enhanced information capacity at these low frequencies. The ability to evaluate the interactions among these parameters for individual afferents is important because the parameter values can vary significantly, even within defined categories of afferents, and especially across preparations, and group averages can obscure important correlations.

The only previous study that has used information measures to study vestibular afferents was that of Sadeghi et al. (2007), whose results also demonstrate that a regular afferent discharge rate can improve SNR and linear encoding for frequencies below an afferent’s spontaneous discharge rate. However, further comparisons are complicated by inter-specific differences. For example, Sadeghi et al. (2007) categorized the afferents in their sample as regular or irregular depending on whether their cv* values were < or ≥ 0.15, respectively, and this is typical of studies of vestibular afferents in primates and other mammals (e.g., Hullar et al., 2005; Baird et al., 1988; Ramachandran and Lisberger 2006; reviewed by Goldberg 2000). Pigeons (Dickman and Correia 1989) and toadfish (Boyle and Highstein 1990) have also been reported to have substantial numbers of regular afferents, with cv or cv* values below 0.1. In our sample of turtle posterior canal afferents, however, nearly all values of cv* were ≥ 0.15 and would have be categorized as irregular by mammalian criteria. Among identified BP units, the most regular category in turtles, cv* values were as high as 0.3. Nevertheless, many of these afferents were sufficiently regular that low frequency noise in their spontaneous discharge was reduced and low frequency signal transmission enhanced as a result of the improvement in signal to noise ratio.

In turtles, as in other animals, cv* values decrease as firing rate increases for individual afferents, and it is possible that the absence of highly regular afferents in turtles is related to the lower discharge rates of BP afferents (10–50 spikes/sec). However, it is important to note that within this range of firing rates, there is a rather wide range of cv* values (Brichta and Goldberg, 2000a, Fig. 2). A similar situation occurs in mammals (Baird et al. 1988, Figure 1), toadfish (Boyle and Highstein 1990, Figure 1), and pigeons (Dickman and Correia 1989, Figure 2). This suggests that spontaneous discharge rate and regularity are best regarded as independent parameters whose influence on stimulus encoding should be evaluated separately. The most regular afferents do not appear to provide any linear encoding at frequencies above their mean firing rate. Thus, increasing the spontaneous discharge rate of regular afferents may serve to extend their linear encoding range of to higher frequencies.

Central vestibular neurons also vary in discharge regularity, and there is evidence that the variation is correlated with other functional features (reviewed by Goldberg 2000). However, the regularity of discharges observed in central neurons is apparently never as pronounced as that of afferents and appears to be the result of intrinsic mechanisms similar to those postulated in afferents, since central neurons receive a mixture of regular and irregular afferent input (reviewed by Goldberg 2000). Thus, regularity in central neurons is unlikely to be related to the representation of any specific signal component encoded in afferent inputs, and may instead function more generally to increase SNR and enhance the linear encoding of low frequency stimuli in the same way that we are suggesting for afferents.

3.2 Linear vs. non-linear encoding

SR coherence values less than 1 do not necessarily indicate the presence of non-linear encoding in afferents, since the reduction can also be due to noise. Response-response (RR) coherence values, however, include any non-linear encoding that is present. Comparison of SR and RR coherence functions for turtle posterior canal afferents (Figure 7) reveals clear differences especially at low frequencies. However, the performance index (PI), which characterizes the overall adequacy of optimal linear encoding, was 64–70%, and RR coherence values were well below their maximum value of 1. This suggests that it is primarily internal noise rather than the presence of nonlinearities that limits the lower bound estimate of mutual information rate. Nevertheless, PI values of 64 – 70% indicate that some nonlinear decoding may be needed to extract all of the information from afferent spike trains. For comparison, PI values for electroreceptor afferents of weakly electric fish have been estimated to be 86 % (Chacron 2006).

Within our sample, spike timing did not appear to be a significant factor in stimulus encoding. This was evident from the low values of RR coherence and reliability measures that we observed, and from the fact that the addition of ±2–5 msec spike time jitter had little or no effect on values of mutual information rates. In contrast, Sadeghi et al. (2007) recently reported in primates that ±2 msec spike time jitter significantly reduced a linear coding fraction for regular vestibular afferents and suggested that those afferents encode information based on a timing code. This interpretation rests on the assumption that the jitter does not affect estimates of firing rate, i.e., that the time scale for determining firing rate is long relative to the jitter. If, on the other hand this time scale is shorter, e.g., close to the mean ISI, the results of the jitter analysis could also be interpreted in terms of a rate code. Indeed, it has been previously suggested that one consequence of increased discharge regularity is to shorten the time required to determine firing rate (Goldberg, 2000). For an afferent with a mean ISI of 10 msec and cv* of 0.05, such as those observed in primates, the standard deviation (SD) of its ISI distribution is 0.5 msec. ISI jitter of ±2 msec (4 SDs) for such an afferent is a large amount of noise that could significantly interfere with linear encoding. The extremely regular afferents observed in mammals, with cv* values < 0.05, are similar to stable limit cycle oscillators with small amounts of intrinsic noise, whose response to weak stimuli can be characterized as linear even though the stimulus is encoded in terms of spike times (Ermentrout et al 2007; Schleimer and Stemmler 2009). The linear response approximation Eq.(3) is still applicable, since the system’s gain G (f) is related to the phase response curve of the oscillator, which determines the sensitivity of its phase to external stimuli (Ermentrout et al 2007; Schleimer and Stemmler 2009). For regular PC afferents in turtles, with mean ISIs ≥ 50 msec and cv* values > 0.1, intrinsic noise levels may already be sufficient to prevent encoding in terms of precise spike times, so that addition of ±2–5 msec jitter (0.4 – 1 SD) had no significant effect on the mutual information rate. In any case, a coding scheme based on spike time precision that is intrinsic to the neuron is different than a scheme based on spike time precision that is imposed by a stimulus and that produces precise and reliable neuron responses to particular stimulus features (Nemenman et al. 2008).

The low level of non-linear encoding we observed is different than what has been reported for visual and auditory pathways. The comparison with vision is particularly instructive, since the temporal bandwidths of the visual and vestibular systems are comparable. The temporal bandwidth of human vision, for example, ranges from 5 – 60 Hz depending on mean luminance levels (Woodhouse and Barlow 1982). Nevertheless, spike timing precision on a sub-millisecond scale in visual neurons has been shown to be important in efficiently encoding natural visual stimuli, even though natural stimuli have correlation times that are two orders of magnitude greater (Nemenman et al. 2008), and the spontaneous activity of visual neurons is irregular by criteria employed in vestibular studies. This suggests that the lack of any dependence of stimulus encoding on precise spike timing in turtle PC afferents was not simply a consequence of their relatively high cv* values.

The greater reliance of posterior canal afferents on linear encoding may instead reflect the relatively low dimensionality and simple statistical structure of the signals these afferents must encode compared with those encoded by visual and auditory neurons. Natural images and sounds have a complex correlational structure, and recent evidence indicates that the non-linearities present in visual and auditory neurons are necessary for the removal of redundant information and the creation of an efficient neural code. The statistics of natural vestibular signals has never been examined for any species, but they are likely to be simpler, and so may require little or no non-linear encoding in the periphery.

3.3 Modeling

We modified a stochastic leaky integrate and fire (LIF) model to include a separate potassium conductance to represent the AHP current (Smith and Goldberg 1986; Liu and Wang 2001). Input to the model involved modulation of the rate of quantal synaptic events whose properties and release statistics matched those measured for PC afferents by Holt et al. (2006). The difference between regular and irregular afferents measured experimentally could readily be reproduced in the model by manipulating only the size or duration of the AHP current (Figs. 8 and 9). Nevertheless, the use of a single conductance to represent the AHP is almost certainly an oversimplification, and various other conductances in the afferent terminal may well play a role in encoding hair cell signals into spike sequences (Wang 1998; Liu and Wang 2001; reviewed by Bean 2007; Eatock, et al. 2008).

The modeling results supported our experimental results that SR coherence, a measure of optimal linear encoding, is shaped by both the gain and spontaneous activity (internal noise). In our simulations, we mimicked units whose gain values increased with stimulus frequency. This, in combination with the significant low frequency noise in the spontaneous activity of irregular units, led to low coherence values at low frequencies (Fig. 9). The model also displayed predominantly linear stimulus encoding at low stimulus amplitudes, but increasingly non-linear encoding at higher stimulus amplitudes and wider frequency bands (Fig. 9). We note that in our simulations, RR coherence values were significantly < 1, and the PI index was > 60% even for strong stimuli, which is similar to experimental results (Fig. 5; Table 2) and supports our conclusion that optimal linear encoding is limited mainly by internal noise rather than nonlinearities.

4. Materials and Methods

4.1 General

Experiments were performed in an in vitro preparation of red-eared turtles, Trachemys (Pseudemys) scripta elegans (10–13 cm carapace length). Turtles were sacrificed by decapitation, and further dissection was done in a bath of oxygenated turtle Ringer’s solution. After removal of the dorsal cranium, the brainstem was transected at the meso-thalamic junction, and the rostral portions discarded. A small hole was drilled in the bone overlying the posterior canal, approximately 2–3 mm from the posterior ampulla, to allow placement of a mechanical probe on the posterior semicircular duct. The head was then placed in a humidified recording chamber that was continuously infused with mixture of 95% O₂/5% CO₂. All procedures have been approved by the Ohio University IACUC (protocol number L01-35)

Afferent spikes were recorded with glass micropipettes filled with 2M NaCl and having electrical impedances of 50–100 MΩ. These high impedance electrodes were used to ensure that recordings came from single afferents. Spike waveforms were continuously monitored on an oscilloscope to ensure good single unit isolation. Spike amplitudes ranged from 1–20 mv against a background electrode noise of 50–100 µv. Since multiple waveforms were never observed, spike or waveform discrimination software was never required or used. ISI distributions were examined for all units and always revealed clear refractory periods, further confirming that recordings were not contaminated by multiple afferents. The electrodes were inserted into the posterior division of the VIIIth nerve along the antero-dorsal margin (Brichta and Goldberg, 2000a). Signals from the electrodes were amplified, digitized at 10 kHz, and stored for offline analysis using Spike2 software™ (Cambridge Electronic Design, CED). Values are stated as mean ± SD. Matlab™ Statistics Toolbox™ was used for statistical tests.

4.2 Stimulation

Stimuli were applied via mechanical indentation of the posterior semicircular duct. Previous work on turtle PC afferents has demonstrated that the relationship between spontaneous discharge regularity, as characterized by cv*, and response dynamics is the same for both mechanical indentation and rotational stimuli (Holt et al. 2006). A mechanical probe, consisting of a 1 mm glass rod tapered to a ~250 µm diameter tip, was placed on the surface of the exposed posterior duct and initially advanced to a baseline indentation of 30–35 µm. The probe was mounted on a piezoelectric indenter (Burleigh, IPZ 100), and motion of the probe was controlled by voltages applied to the indenter. Stimuli consisted of multiple cycles of single sinusoids, ranging in frequency from .01 to 100 Hz and band-limited Gaussian noise with cutoff frequencies of either 10 or 50 Hz. For sinusoids, peak-to-peak indentation amplitude varied from 1.4 to 19 .7 µm (mean, 10.5 µm), and for each afferent, amplitude was adjusted to produce an unrectified sinusoidal response to low frequency (0.1 or 0.5 Hz) stimuli. The stimulus protocol used for all afferents presented each frequency for a fixed number of cycles that ranged from 2 at 0.01 Hz to 200 at 100 Hz. Gaussian noise stimuli were delivered in single long (typically 10 minute) segments for purposes of calculating lower bound information estimates (see below), or in a series of short (5–30 sec) segments for calculating upper bound information estimates. For each unit, a stimulus amplitude was chosen that elicited a clear response, but with minimal modulation of firing rate. The standard deviation (SD) of Gaussian noise stimuli ranged from 0.5 to 5.1 µm (mean, 3.4 µm) for the 50 Hz bandwidth and from 0.7 to 6.6 µm (mean, 4.47 µm) for the 10 Hz bandwidth, depending on the sensitivity of each unit. For some units, the influence of stimulus strength on response properties was examined by presenting a sequence of 120 sec segments of 50 Hz Gaussian noise, where the SD for successive segments varied from 0.18 to 9.5 µm. All stimulus waveforms were presented using CED hardware and Spike2 software. Movement of the probe was monitored by an in-line low voltage displacement transducer (LVDT; Schaevitz, DC-050).

4.3 Afferent Identification

Afferents were identified on the basis of cv*, responses to efferent stimulation, and responses to periodic mechanical indentation, following the classification scheme established by Brichta and Goldberg (2000a,b). In this scheme, five groups are distinguished. The primary distinction is between calyx bearing (CD) afferents, including both afferents with pure calyx terminals and dimorphic terminals (those with a mixture of calyx and bouton endings), and afferents with pure bouton terminals. Among CD afferents, a further distinction is made between those with high (>5 spikes/sec) spontaneous discharge rates (CD_hi) and those with low (<5 spikes/sec) discharge rates (CD_lo). Bouton afferents are subdivided into those with terminals located near the torus (BT), those with terminals near the planum (BP), and those with terminals near the middle of the each hemicrista (BM).

Efferent fibers were stimulated with cathodal current pulses delivered via a stainless steel microelectrode placed on the axon bridge spanning the anterior and posterior divisions of the VIII^th nerve. The reference electrode was placed in the middle ear cavity. Stimulus parameters were 20 pulses at 200 Hz, 100 µsec duration, 50–100 µA amplitude. For each afferent data set collected, the stimulus artifacts produced by the efferent stimulation were recorded and stored. The artifacts present in afferent responses to efferent stimuli were removed offline by subtracting these stored waveforms.

4.4 Data Analysis

Data analyses were performed offline using custom software programmed in Matlab™. Spontaneous Discharge Regularity. Values of the coefficient of variation (cv), defined as cv = std (ISI)/〈ISI〉 were estimated from 10–60 second stationary segments of spontaneous discharge. Since cv varies with the mean ISI, we also calculated cv*, an estimate of cv at a standard mean ISI of 50 msec, using a power law regression, cv(t) = a(t) · cv*^b(t), where the coefficients a (t) and b (t) are determined empirically as described by Goldberg et al. (1984). Some units (~20%) in our sample had mean ISI values outside the normalization range for calculating cv* (20 – 100 msec). Where possible, values of cv* for these units were calculated from ISI distributions constructed from 5 sec segments of activity near the peaks and troughs of the response to .01 Hz sinusoidal stimulus. Units for which cv* could not be calculated were not included in any analyses relating discharge regularity to other parameters.

In order to evaluate discharge regularity on time scales longer than mean ISI, we calculated serial correlations and power spectra. These were estimated from 3 – 10 min segments of spontaneous discharge, for which firing rate was stationary through the entire segment. Serial correlation coefficients (SCC) are second order statistics derived from normalized auto correlation functions of spike trains that do measure patterns in ISI sequences. SCCs (ρ) for ISIs (I_k) that are separated by n intervening intervals, were calculated as ${\rho }_n=\frac{\langle I_k{I}_{k+n}\rangle -{\langle I_k\rangle }^2}{\text{var}(I)}$, where n ranged from 0–50 intervals, and the brackets 〈 〉 indicate averaging over k = 1, …, M consecutive intervals (Cox and Lewis 1966). SCC values range from +1 to −1. A spike train with statistically independent ISIs constitutes a renewal stochastic point process in which SCCs are zero for all n ≠ 0. In order to test whether SCCs differed significantly from 0 we used the procedure of Ratnam and Nelson (2000). A sequence of ISIs was partitioned into non-overlapping segments, each containing 500 intervals, and SCCs were calculated for each segment. Intervals within each segment were then randomly shuffled to eliminate serial correlations, and a second set of SCCs were calculated for the shuffled segments. A Wilcoxon rank sum test with a significance level α = 0.01 was used to judge whether the SCCs for the original and shuffled segments were statistically different.

Power spectra were calculated as in Gabbiani and Koch (1998); each spike train was represented as a sequence of delta functions centered at the spike times, $x(t)={\displaystyle \sum _{k=1}^N}\delta (t-t_k)-r$, where t_k are the spike times, N is the number of spikes in the recorded data, and r is the mean firing rate. The delta functions were approximated by rectangular pulses with a height of 1/ Δt, where Δt is the sampling interval of .001 sec. The power spectra of these sequences was calculated by averaging fast Fourier transforms (FFTs) of x (t) from overlapping windows, each 4096 or 8192 sampling intervals wide, using a Hamming window. For each sequence, a control power spectrum was also calculated after randomly shuffling all ISIs. For a renewal process, the power spectrum is uniquely defined by the distribution of interspike intervals (Cox and Lewis 1966), and random shuffling of the ISIs, which preserves their first order statistics, does not alter the power spectrum. Thus, changes in the power spectrum after shuffling ISIs indicate that spike generation is not a renewal process, and that successive ISIs are not independent.

Linear Response Properties

Linear components of afferent responses were assessed with both sinusoidal and Gaussian noise stimuli. For sinusoidal stimuli, the gain and phase of afferent responses were measured in two ways. In the first method, phase histograms were constructed for responses at each frequency and fitted with a sine function. The mean-to-peak amplitude of the fitted function was normalized by indenter excursion to yield a measure of gain in units of spikes/sec/µm of indentation. The phase of the fitted function was measured relative to the outermost position of the indenter, which corresponds to peak head velocity (Rabbit et al. 1995). In the second method, the spike sequence recorded across all cycles of each frequency was sorted into 8192 consecutive bins. An FFT was applied to the resulting histogram, and the amplitude and phase at the input frequency were extracted.

To characterize the linear response components of PC afferents with broad band Gaussian noise, afferents were stimulated with long, 120 – 500 s, noise segments. System gain was calculated as

$$G(f)=|P_{\mathit{\text{sx}}}(f)|/P_{\mathit{\text{ss}}}(f),$$ (1)

where P_ss (f) is the power spectral density (PSD) of the stimulus, s (t), and P_sx (f) is the cross-spectral density of the stimulus and the spike train (Bendat and Piersol 2000; Chacron et al., 2005; Sadeghi et al. 2007). The stimulus-response (SR) coherence function is a normalized cross-correlation measure in the frequency domain varying from 0 to 1 (Bendat and Piersol 2000):

$$C_{\mathit{\text{SR}}}(f)=|P_{\mathit{\text{sx}}}(f){|}^2/[P_{\mathit{\text{ss}}}(f)P_{\mathit{\text{xx}}}(f)],$$ (2)

where P_xx (f) is the PSD of the stimulus driven spike train. Coherence values of 1 indicate that a system is linear and deterministic. Coherence values less than 1 indicate the existence of noise and/or nonlinearities in stimulus transmission. The frequency dependence of SR coherence may be distinct from gain (Sadeghi et al 2007), and for a weak stimulus it is strongly influenced by the PSD of spontaneous firing (Chacron et al 2005). To confirm the co-dependence of SR coherence on gain and the PSD of spontaneous afferent discharge, we employed linear response theory (LRT), which can also be applied to nonlinear systems if the stimulus is small (Hänggi and Thomas 1982) as it was in our experiments. In LRT, the PSD of a system perturbed by a small stimulus can be approximated as $P_{\mathit{\text{xx}}}(f)=P_{\mathit{\text{xx}}}^0(f)+|G(f){|}^2{P}_{\mathit{\text{ss}}}(f),\text{ where }{P}_{\mathit{\text{xx}}}^0(f)$ is the PSD of the unperturbed system, and G (f) is referred to as linear susceptibility. Similarly, the SR coherence can be approximated (Neiman et al. 1997; Chacron et al. 2005) as,

$$C_{\mathit{\text{SR}}}(f)=1-\frac{P_{\mathit{\text{xx}}}^0(f)}{P_{\mathit{\text{xx}}}^0(f)+|G(f){|}^2{P}_{\mathit{\text{ss}}}(f)}.$$ (3)

In our analysis, $P_{\mathit{\text{xx}}}^0(f)$ is the PSD of spontaneous afferent discharge (internal noise) and G (f) is the gain. Eq. (3) indicates that within the framework of LRT, SR coherence is determined by both gain and the PSD spontaneous activity (internal noise). Coherence approaches its maximum value of 1 as $P_{\mathit{\text{xx}}}^0(f)\to 0$, and for values of $P_{\mathit{\text{xx}}}^0(f)>0$, coherence increases as gain increases. Comparison of calculated coherence from Eq. (2) with estimated coherence from Eq. (3), can help assess the separate contributions of gain and internal noise to the encoding properties of afferents.

Information Rates

Broad band Gaussian noise stimuli were also used to estimate information transmission by afferents using a linear reconstruction method (Bialek et al. 1991; Gabbiani and Koch 1998; Gabbiani and Metzner 1999; Wessel et al. 1996). This method estimates the information contained in linearly reconstructed Gaussian stimulus and sets the lower bound of mutual information rate, $I_{\mathit{\text{LB}}}=-{\displaystyle \underset{0}{\overset{f_c}{\int }}}{\text{log}}_2\left[1-C_{\mathit{\text{SR}}}(f)\right]\mathit{\text{df}}$ (in bits/s), where f_c is the cutoff frequency of the stimulus. To control for the heterogeneity in mean firing rates among vestibular afferents, we also expressed the mutual information rate in units of bits/spike by dividing the lower bound estimate by the mean firing rate of the afferent during noise stimulation. The quality of reconstruction is measured by the coding fraction, $\gamma =1-\sqrt{\text{var}(n)/\text{var}(s)}$, where var(n) and var(s) are variances of reconstruction noise and stimulus, respectively (Gabbiani and Koch 1998). The coding fraction varies from 0 (no encoding) to 1 (perfect encoding).

Reliability of PC afferent responses, a measure of variability in response for a fixed stimulus, was characterized in terms of responses to repeated presentations (K = 10 – 50) of identical 5, 15, or 30 sec segments of Gaussian noise band limited to 10 Hz. We used a reliability measure proposed by Schreiber et al. (2003) in which each response was convolved with a Gaussian filter of 1 msec width giving K response time series, r_i (t), where i = 1, …, K and t runs from 0 (onset of the stimulus) to T (duration of the stimulus segment). We then calculated a normalized cross correlation function between all pairs of responses as

$$R_c(\tau )=\frac{2}{K(K-1)}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{j=k+1}^K}\frac{\langle r_k(t)r_j(t+\tau )\rangle }{\text{std }(r_k)\text{ std }(r_j)},$$

where angular brackets represent averaging over the stimulus duration, and std (r) is the standard deviation of a response. The magnitude of R_c (τ) at zero lag (τ = 0) serves as a measure of reliability, while the width of the peak at τ = 0, defined by the level where R_c (τ) declines to 1/e of its maximum value, characterizes the amount of spike timing jitter across trials. Perfectly reliable neurons, with stereotypical responses and spikes aligned perfectly across trials, produce a delta-shaped cross-correlation with zero width and a magnitude of 1 at τ = 0. At the opposite extreme, completely uncorrelated responses result in R_c (τ) = 0.

Non-Linear Response Properties

To quantify phase locking in PC afferents, we calculated a synchronization index (SI), also known as vector strength as $\mathit{\text{SI}}={\left[{\langle \text{cos}(2\pi f_0{t}_k)\rangle }^2+{\langle \text{sin}(2\pi f_0{t}_k)\rangle }^2\right]}^{1/2}$, where the average is taken over spike times (Mardia and Jupp 1999). The synchronization index varies from 0, when the phase distribution is uniform, to 1, when spikes are perfectly locked to the stimulus resulting in a single delta peak in the phase distribution.

Nonlinear neural responses to broad-band Gaussian stimulation are often characterized in terms of higher order Wiener kernels (Marmarelis and Marmarelis 1978; DiCaprio 2003). However, effective linear coding is possible even for systems that respond non-linearly (Metzner et al. 1998). In order to assess whether a linear encoding model was adequate for PC afferents, we used an approach proposed recently by Roddey et al. (2000) (see also Chacron (2006)). In this method, a neuron is stimulated with a repeated sequence of K identical noise segments (frozen noise) as in the assessment of reliability above. The variability of successive responses is characterized in terms of response – response (RR) coherence, which can be viewed as a frequency domain representation of the normalized cross-correlation between pairs of responses in the sequence. RR coherence is calculated as $C_{\mathit{\text{RR}}}(f)=\frac{{\left|\frac{2}{(K-1)K}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{j<k}}{P}_{\mathit{\text{kj}}}(f)\right|}^2}{{\left[\frac{1}{K}{\displaystyle \sum _{k=1}^K}{P}_{\mathit{\text{kk}}}(f)\right]}^2}$, where P_kj (f) are cross-spectra between k-th and j-th responses in the sequence, P_kk (f) is the power spectral density of k-th response. RR coherence characterizes response variability that cannot be accounted for by the stimulus. Like SR coherence, RR coherence is a normalized quantity ranging from 0 (no correlations across responses) to 1 (stereotypical responses). RR coherence sets an upper bound for the performance of an optimal nonlinear model and satisfies the following inequality, $C_{\mathit{\text{SR}}}\le \sqrt{C_{\mathit{\text{RR}}}}$. Large differences between SR coherence and the square root of RR coherence indicate that a linear encoding model may not be appropriate. RR coherence is clearly related to the normalized cross-correlation function used for assessment of reliability. For a perfectly reliable response, RR coherence is 1 over the whole frequency domain, which corresponds to a delta-peak in the normalized cross correlation, R_c (τ). Any finite width of the peak in R_c (τ) at τ = 0 will correspond to a finite frequency band in RR coherence with a cutoff frequency reciprocal to that width. We stimulated PC afferents with either a few (4–10) 30 sec segments of frozen noise or a larger number (20–50) of 5 sec segments, and then estimated SR and RR coherences as described above. The cutoff frequency of the noise stimulus was varied from 10 to 50 Hz to study the effect of nonlinearities at a range of frequencies. To quantify the adequacy of the optimal linear encoding model, we calculated a performance index (PI) (Chacron 2006) as the average ratio of SR coherence to square root of RR coherence in the frequency band of the stimulus, $\mathit{\text{PI}}=\frac{1}{f_c}{\displaystyle \underset{0}{\overset{f_c}{\int }}}\frac{C_{\mathit{\text{SR}}}(f)}{\sqrt{C_{\mathit{\text{RR}}}(f)}}\mathit{\text{df}}$. The maximal value of this measure is 1 and corresponds to encoding that is 100% linear. Small values of PI indicate high levels of non-linear encoding. Stimulation with repeated segments of Gaussian noise also allows an estimation of an upper bound of the mutual information rate as $I_{\mathit{\text{UB}}}={\displaystyle \underset{0}{\overset{f_c}{\int }}}{\text{log}}_2\left[1+\frac{P_{\overline{R}\overline{R}}(f)}{\sqrt{P_{\overline{\mathit{\text{nn}}}}(f)}}\right]\mathit{\text{df}}$, where P_R̄R̄ (f) is the power spectrum of the average response to all presentations and $P_{\overline{\mathit{\text{nn}}}}(f)$ is the power spectrum of the deviations of individual responses from the average response (Borst and Theunissen 1999).

4.5 Modeling

A generalized stochastic leaky integrate and fire (LIF) model with an adaptation current was used to simulate the response properties of PC afferents to Gaussian noise stimuli. The model was based on the after-hyperpolarization (AHP) model of Smith and Goldberg (1986), and included a time-dependent potassium conductance to mimic the AHP current. The membrane potential V is given by

$${\tau }_M\frac{\mathit{\text{dV}}}{\mathit{\text{dt}}}=-(V-V_R)-{\tilde{g}}_K(t)(V-V_K)-{\tilde{g}}_S(t)(V-V_S),$$ (4)

where τ_M is the membrane time constant, V_R is the resting potential, V_K is the potassium equilibrium potential, and V_S is the synaptic equilibrium potential. All conductances are normalized to the leak conductance and are thus dimensionless. The model produces a spike whenever V (t) reaches a threshold value, V_T, after which the voltage is reset to V_R. The first term in the right hand side of Eq.(4) is the leak current. The second term represents the AHP current, with the time dependent potassium conductance, g̃_K (t), given by

$$\frac{d{\tilde{g}}_K}{\mathit{\text{dt}}}=-\frac{{\tilde{g}}_K}{{\tau }_K}+\delta (V-V_T),$$ (5)

where τ_K is the time constant, and δ is the Dirac delta function. Eq. (5) is solved with the initial condition, g̃_K (t = 0) = g_K. Thus, whenever a spike occurs (V = V_T), the potassium conductance undergoes a step-like increase followed by an exponential decay, ${\tilde{g}}_K(t)=g_K\text{ exp }\left(-\frac{t\text{'}}{{\tau }_K}\right)$, where t' is time after a spike. The third term is the synaptic current, produced by input from hair cells. The time-dependent synaptic conductance, g̃_S (t), was simulated in quantal form as a train of miniature EPSPs (mEPSPs), each represented by an alpha function centered at release times, t_i, and governed by Poisson statistics with the rate, λ, as described by Holt et al. (2006);

$${\tilde{g}}_S(t)=g_S{\displaystyle \sum _i}\alpha (t-t_i),\alpha (t)=\mathrm{\Theta }(t){\beta }^{2}t\text{ exp }(-\beta t),$$ (6)

where Θ is the Heaviside (step) function, g_S sets the synaptic strength, and β sets the shape (duration) of each mEPSP. To simulate spontaneous activity, the synaptic quantal rate was constant, λ = λ₀. To simulate afferent responses to mechanical indentation, the rate was modulated by a time dependent waveform,

$$\lambda (t)=({\lambda }_0+\sigma y(t))\mathrm{\Theta }({\lambda }_0+\sigma y(t)),$$ (7)

where σ is the magnitude of a Gaussian signal, y (t), with zero mean and a unit standard deviation. To account for the high frequency gain enhancement of irregular PC afferents, we preprocessed the stimulus, x (t), with a high pass filter as in Sadeghi et al. (2007). The modulated input to Eq.(7) was calculated as y (t) − x_A (t), where x (t) is the original band-limited noise (the same band-limited Gaussian noise used for afferent stimulation), x_A (t) is low pass filtered noise. Low pass filtering is given by ${\tau }_A\frac{{\mathit{\text{dx}}}_A}{\mathit{\text{dt}}}=-x_A+x$, where τ_A sets the cutoff frequency. The standard deviation of y (t) was normalized to 1. Equations (4) and (5) were integrated numerically using a Euler explicit scheme with a constant time step of 0.05 msec.

Several model parameters contribute to the regularity of spontaneous discharge (Smith and Goldberg 1986): quantal rate and size of mEPSPs, the time constant of the AHP current, τ_K, the initial AHP conductance, g_K, and the threshold voltage, V_T. In our numerical simulations we manipulated the parameters of the AHP current (τ_K and g_K) to vary afferent response properties. Since altering these parameters resulted in changes of both the mean firing rate and cv, we adjusted the threshold voltage V_T to maintain the mean ISI at 50 msec, leaving the rest of parameters unchanged, so that additional normalization to cv* values was unnecessary. The parameters for synaptic current (quantal rate, λ, and characteristic rate of the alpha function, β) were taken from Holt et al. (2006). Other parameters of the model were taken from (Smith and Goldberg 1986) and tuned to reproduce the spontaneous activity of PC afferents. Values for all model parameters are summarized in Table 1. Two rectifying nonlinearities were inherent in the model. The first is at the level of synaptic transmission; large inhibitory stimuli reduce the rate of synaptic events, λ, to zero. The second is in the process of spike generation, since it is impossible to have a negative firing rate.

Table 1.

Model parameter values used in simulations

τM	1 ms
VR	0 mV
VK	− 30 mV
VS	70 mV
VT	4 – 10 mV (varied to reach spontaneous rate of 20 Hz)
gK	3 – 5 (varied)
τK	2 – 12 ms (varied)
σ	0.1 – 2 (varied)
λ0	850 s−1
β	750 s−1
gS	0.12
τA	20 ms