Organization of Anti-Phase Synchronization Pattern in Neural Networks: What are the Key Factors?

Abstract

Anti-phase oscillation has been widely observed in cortical neural network. Elucidating the mechanism underlying the organization of anti-phase pattern is of significance for better understanding more complicated pattern formations in brain networks. In dynamical systems theory, the organization of anti-phase oscillation pattern has usually been considered to relate to time delay in coupling. This is consistent to conduction delays in real neural networks in the brain due to finite propagation velocity of action potentials. However, other structural factors in cortical neural network, such as modular organization (connection density) and the coupling types (excitatory or inhibitory), could also play an important role. In this work, we investigate the anti-phase oscillation pattern organized on a two-module network of either neuronal cell model or neural mass model, and analyze the impact of the conduction delay times, the connection densities, and coupling types. Our results show that delay times and coupling types can play key roles in this organization. The connection densities may have an influence on the stability if an anti-phase pattern exists due to the other factors. Furthermore, we show that anti-phase synchronization of slow oscillations can be achieved with small delay times if there is interaction between slow and fast oscillations. These results are significant for further understanding more realistic spatiotemporal dynamics of cortico-cortical communications.

1. Introduction

Dynamical activity of the neural systems in the brain is characterized by collective oscillatory activity over a broad range of frequencies, showing complex spatiotemporal pattern formations (Gusnard and Raichle, 2001; Corbetta and Shulman, 2002; Buzsáki, 2006). These complicated patterns are related to cognitive process (Engel et al., 2001; Fries, 2005), so as to provide wonderful objects for research in order to properly understand the information processing in the brain. The mechanisms underlying these spatiotemporal patterns are consist of at least two components. One component refers to the background, which is a type of spontaneous pattern formation, not necessarily related to a state of cognition in evidence. This pattern is organized basing on the fact that in the absence of cognitive tasks, neurons still keep on firing and sending information to their neighbors. The other component refers to the pattern induced by some cognitive tasks, which is organized basing on the background one (Dosenbach et al., 2006; Ouyang et al., 2011). It is therefore of fundamental importance to gain insight into the organization of the background pattern formation for better understanding how brain realize its cognitive functioning.

The neuronal networks in the brain are very complex in topological structure (Hilgetag et al., 2000; Hilgetag and Kaiser, 2004; Sporns et al., 2004; Bassett and Bullmore, 2006; Hagmann et al., 2008; Bonifazi et al., 2009; Bullmore and Sporns, 2009). On such complex networks, even if in the absence of any external stimuli, the dynamical patterns could be very complicated under the condition of spontaneous communications among the dynamical nodes (Newman, 2003; Boccaletti et al., 2006; Arenas et al., 2008; Yuan et al., 2008). The two simplest patterns are in-phase (zero time lag) and anti-phase oscillations. In-phase pattern means that the neurons fire simultaneously. Long-distance in-phase synchronization is believed to benefit for the integration of separated functions performed in different regions, which has been a topic of great interests (Engel et al., 1991b; Roelfsema et al., 1997; Rodriguez et al., 1999; Varela et al., 2001; Wang et al., 2006; Vicente et al., 2008). Differently, anti-phase pattern means that certain areas of the brain normally increase activity, when others decrease activity. Anti-phase pattern can be considered as the simplest case, where two regions can be distinguished from each other from the viewpoint of dynamics, so that the mechanism underlying the anti-phase patterns is quite useful for deeper understanding the formation of functional regions. In neuronal networks, such anti-phase patterns have been widely observed in experiments (Greicius et al., 2003; Fox et al., 2005; Fox and Raichle, 2007; Mantini et al., 2007; Shmueli et al., 2007; Vincent et al., 2007; Lewis et al., 2009). Actually, during attentional tasks, the pattern of different areas of functional networks can usually show two opposite types of responses that increase (Cabeza and Nyberg, 2000; Corbetta and Shulman, 2002) or decreases activity (Gusnard and Raichle, 2001; Simpson et al., 2001), so as to organize a type of anti-phase pattern. An anti-phase oscillation is also observed during the rest state (Greicius et al., 2003; Fox et al., 2005; Mantini et al., 2007). For example, it was demonstrated by using functional magnetic resonance imaging (fMRI) method that spontaneous blood oxygen level-dependent signal during rest fluctuates slowly with a small frequency and is highly organized into anti-phase pattern (Fox et al., 2005). Even during sleep, similar phenomena have also been observed that some regions increase activities meanwhile some other regions decrease activities (Kaufmann et al., 2006; Horovitz et al., 2009). Anti-phase oscillation patterns have also been found in anesthetized monkeys (Vincent et al., 2007), meaning that they do not necessarily reflect a state of consciousness. These patterns are experimentally found to oscillate at various bands of frequencies, e.g., the cardiac rate (Shmueli et al., 2007) or even much slower (<0.1 Hz; Mantini et al., 2007). The anti-phase pattern in the absence of task is a type of background one organized by the spontaneous cortico-cortical communication dynamics, and the intrinsic dynamical reasons for the organization of the anti-phase pattern in the absence of overt task performance may have some relationship to that typically seen during attentional tasks.

In dynamical systems, the organization of anti-phase oscillation pattern has usually been considered relating to the time-delays in coupling, which is consistent with the real neuronal networks in the brain, where communication between neurons are carried out by propagation of action potentials from one neuron to the network neighbors through neuronal axons, with finite velocity (Swadlow, 1985, 2000). This finite velocity leads to conduction delays, which can reach up to many tens of milliseconds. Some of the unmyelinated axons can generate a delay time as large as 300 ms. Furthermore, cortical architectures are hierarchical modular networks with several characteristics: (1) The distances between neurons within a module are usually shorter than that in different modules (Achard and Bullmore, 2007; Bullmore and Sporns, 2009); Consequently, the delay time is most likely smaller within modules. (2) The connection densities are usually larger within modules (Hilgetag et al., 2000; Hilgetag and Kaiser, 2004; Achard and Bullmore, 2007; da F Costa et al., 2007), which may impact on synchronization within and between the modules. (3) Inhibitory couplings usually form local connections (Albus and Wahle, 1994; Bosking et al., 1997; Battaglia et al., 2007). As a result, inhibitory coupling likely exists more within modules.

These important structural factors may influence the pattern formation of neural networks significantly. In a recent theoretical study (Deco et al., 2009), it is shown that the anti-phase patterns can emerge from noise-driven transitions between different multistable cluster synchronization states, with a two-community network structure. In the study, impact of different factors of the time delay and the modularity is mixed. However, to elucidate which characteristics is crucial for the origin of anti-phase patterns is actually a significant problem.

In this work, we investigate the anti-phase oscillation pattern organized on a two-module network of either neuron cell model or neural mass model and study the key factors among the conduction delay times, the connection densities, and the coupling types (excitatory or inhibitory). Our results show that delay times and coupling types can play key roles in this organization, but connection densities cannot. In an excitatory coupled neuronal systems, the role of delay time is similar to a classical case of coupled phase oscillators. A delay time close to half-period can induce anti-phase pattern between two neuronal modules. However, this is not a necessary condition, since we further reveal that if there exist an interaction between low and fast oscillations, small delay time can contribute to the organization of anti-phase pattern in slow oscillation, which could be especially relevant to those experimentally observed anti-phase synchronization of very small frequencies. The investigation is significant for understanding more complicated spatiotemporal pattern formations in the brains organized by cortico-cortical communication dynamics.

2. Materials and Methods

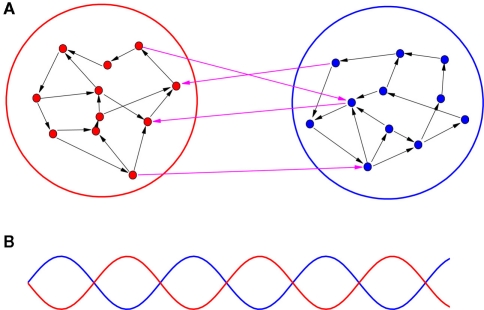
To study the key factors for the organization of an anti-phase pattern between cortices, we analyze the dynamical behaviors of both coupled neuron cells model and coupled neural mass model on a two-module network. As schematically demonstrated in Figure 1A, a part of cortex is modeled by a module, and the communication between cortices is represented by the time-delayed interaction between modules. By changing several important factors, we aim to elucidate the conditions for supporting an anti-phase oscillation between modules, as illustrated in Figure 1B. Within each module, the collective behaviors of the oscillators should show a macroscopic rhythmic oscillation. In the simplest case, these oscillators within each module arrive at a relatively high degree of coherence with small phase shifts (approximate in-phase oscillation).

Figure 1.

A schematic demonstration of an anti-phase oscillation organized on a two-module network. (A) The network is divided into two modules. Several factors are different within-module and between modules, including conduction delays, connection densities, and coupling types (excitatory or inhibitory). (B) Illustration of anti-phase oscillation between modules. The lines stand for some kinds of collective behaviors within each module, e.g., total firing rate, total synaptic current, etc.

The factors we will study in the following include conduction delay times, connection densities, and coupling types (excitatory or inhibitory). In the brain, the nodes (nerve cells or cortices) are connected in different distances. Generally speaking, long-distance connections contribute to integrating the functions of different areas and short-distance connections can save the connection costs. According to experimental results, the nodes within-module usually have much shorter distance than those between modules (Achard and Bullmore, 2007; Bullmore and Sporns, 2009), so that we can suppose that the conduction delays are usually smaller within modules. On the other hand, it has been reported that some long-distance conduction delays may not be too large in myelinated axons (Waxman, 1980), which is also believed to be significant for the integration of the functions. We will study systematically how the synchronization pattern changes when the delays within and between modules are varied.

The second factor is the connection densities. In the brain networks, there are much more short-distance connections than long-distance ones. In this work, the word module is used with broader meanings to allow us change various factors within and between modules, however, in the usual sense, the concept of module is based on the connection densities (Hilgetag et al., 2000; Clauset et al., 2004; Hilgetag and Kaiser, 2004; Newman and Girvan, 2004; Newman, 2006; Achard and Bullmore, 2007; da F Costa et al., 2007). Denser connections within a module and sparser connections between modules may be significant for performing some particular functions by the modules while maintaining communication between modules, allowing both functional segregation and integration. The modularity has been shown to impact on synchronization of oscillators without considering delays (Arenas et al., 2006, 2008; Gómez-Gardeñes et al., 2010; Zhao et al., 2011). However, its role in organizing the anti-phase pattern between modules in the presence of heterogeneous delays is not known. This issue is a very important open problem. In experiments, functional networks are usually detected by some coherent activities (Scannell et al., 1999; Hilgetag and Kaiser, 2004), and anti-phase pattern could be the simplest case that the coherent activity within one module can be distinguished from another. A deep understanding of the impact of connection densities in organizing anti-phase pattern is useful to elucidate the role of modularity in organizing functional networks in the brain.

The third factor refers to the coupling types. In the brain, there coexist excitatory and inhibitory neurons. They have different numbers, distributions, and connected distances in brains (Albus and Wahle, 1994; Bosking et al., 1997; Battaglia et al., 2007), so that the distributions of excitatory and inhibitory connections are also different within-module and between modules. The competition and balance of excitation and inhibition has profound effects on the collective dynamics of neural network, such as the emergence of slow oscillations (Wang et al., 2011). Therefore, the type of coupling may also contribute to the organization of anti-phase patterns in cortical communication.

When these factors are taken into consideration, we can simplify some other settings in our model. We consider a directed random network of N/2 nodes for each module. We assume that the connection probability k_in and time-delays τ_in are uniform for connections within the modules. Likewise, they are also uniform for the connections between modules and are denoted as k_out and τ_out, respectively. The ratios of the number of excitatory links to the number of all links within and between modules are represented as Φ_in and Φ_out, respectively. In the brain, the overall ratio is about Φ = 0.8, while in our model we assume it is a tunable parameter.

After the analysis of this simplified model, we will also study the impact of distributed delay times using a realistic cortical network of visual system of macaque monkey, where the delay time is assumed to depend on the distance between the functional regions.

2.1. Neuron cell model

We first study the dynamical behaviors with pulse-coupled integrate-and-fire (IAF) neuron model on each node. Each module may represent a local neuronal circuit from two distant, but connected cortical regions. The IAF model is described as

$$\frac{d{V}_j}{dt}=I_d-V_j+{\displaystyle \sum _i}{K}_{ij}\delta \left(t-t_{i,k}^s-{\tau }_{ij}\right),$$ (1)

where V_j is the membrane potential of the jth neuron. Whenever the membrane potential of a neuron crosses a spiking threshold V_th, an action potential is generated and the membrane potential is reset to the resting potential V_r. $t_{i,k}^s$ is the time of the kth spike sent by neuron i. It takes a delay time τ_ij for the spike to propagate to the neuron j. τ_ij = τ_in when the two neurons are from the same module and τ_ij = τ_out otherwise. K_ij is the connectivity matrix, and K_ij = 0 means there is no link from neuron i to neuron j. Otherwise, K_ij are given a value common for all i and a positive (negative) K_ij represents that the presynaptic neuron i is excitatory (inhibitory). The dc current I_d is set that the neurons keep on spontaneous firing.

While investigating the aforementioned three factors, we respectively change the conduction delays (τ_in ≠ τ_out; k_in = k_out; and Φ_in = Φ_out = 100%), connection densities (k_in ≠ k_out; τ_in = τ_out; and Φ_in = Φ_out = 100%), and nerve type. In the third case, where we investigate the factor of coupling types, we change 20% neurons to inhibitory ones in each module. The output links of these inhibitory neurons only link to the neighbors within each module, so that we get Φ_in = 80% ≠ Φ_out = 100%, τ_in = τ_out, and k_in = k_out.

2.2. Neural mass model

We can consider a model representing the cortical network of higher hierarchy compared to the neuronal networks in subsection 2.1. In almost all cortical regions, there is a basic neural circuit composed of a pyramidal cell receiving excitatory input from extrinsic afferent systems and spiny cells and inhibitory input from interneurons. Neural mass model (Wendling et al., 2000; Zhou et al., 2007) has been developed based on such basic micro-circuits to describe mean activity of the cortical networks. The dynamics are described by average membrane potential v and spike density S of three subpopulations: excitatory pyramidal cells, excitatory and inhibitory interneurons. A network of coupled neural mass oscillators is described by the following equations,

$$\begin{array}{rcll}{\ddot{v}}_0^i\left(t\right)& =AaS\left[v_1^i\left(t\right)-v_2^i\left(t\right)\right]-2a{\stackrel{°}{v}}_0^i\left(t\right)-a^2{v}_0^i\left(t\right),& & \text{(2)}\\ {\ddot{v}}_1^i\left(t\right)& =Aa\left\{I_0+\sum _{j=1,\dots ,N}{g}_{ij}S\left[v_1^j\left(t-{\tau }_{ij}\right)-v_2^j\left(t-{\tau }_{ij}\right)\right]\right.& & \\ & \left.+C_{2}S\left(C_1{v}_0^i\left(t\right)\right)\right\}-2a{\stackrel{°}{v}}_1^i\left(t\right)-a^2{v}_1^i\left(t\right)+{\eta }_i\left(t\right),& & \text{(3)}\\ {\ddot{v}}_2^i\left(t\right)& =Bb\left\{C_{4}S\left[C_3{v}_0^i\left(t\right)\right]\right\}-2b{\stackrel{°}{v}}_2^i\left(t\right)-b^2{v}_2^i\left(t\right),& & \text{(4)}\end{array}$$

where the spike density is related to the potential by the sigmoid function

$$S\left(v\right)=2e_0/\left(1-e^{r\left(v_{0-v}\right)}\right),$$ (5)

where 2e₀ is the maximum firing rate, r₀ is the post-synaptic potential corresponding to a firing rate of e₀ and r is the steepness of the sigmoid. Here C₁ and C₂, C₃ and C₄ are the average number of synaptic contacts, for the excitatory and inhibitory synapses, respectively. The superscript i is the serial number of the population. η_i(t) represents independent background white noise. τ_ij is the time delay from the population j to the population i. When the population i and j belong to the same module, τ_ij = τ_in; otherwise, τ_ij = τ_out. g_ij Is the coupling strength, where a positive g_ij is equivalent to an average excitatory effect and a negative g_ij to an average inhibitory effect. In numerical simulations, we use very small g_ij, so that the frequency of coupled oscillators does not have a big difference from that of a single oscillator.

This model can generate either delta or alpha oscillation, depending on the injected dc current I₀. The spatiotemporal patterns are very complicated, depending not only on system parameters but also on initial states, so that we use an anti-phase pattern with some noise perturbation as the initial state for numerical simulations in order to investigate the role of important factors in persisting this pattern.

We use a set of typical system parameters as in Wendling et al. (2000): A = 3.25 mV, B = 22 mV, a = 100 s⁻¹, b = 50 s⁻¹, C₁ = 135, C₂ = 108, C₃ = 33.75, C₄ = 33.75, r₀ = 6 mV, e₀ = 2.5 s⁻¹, and r = 0.56 mV⁻¹. In our simulation, we set I₀ = 115 mA for the delta oscillation and I₀ = 180 mA for the alpha oscillation.

2.3. Synchronization index

In the following, we define the in-phase and anti-phase synchronization index in order to evaluate the anti-phase patterns. First we define the oscillatory phase ψ of a single neural mass oscillator j. Here we use a definition generalized from Pikovsky et al. (2001):

$${\psi }^j\left(t\right)=2\pi \frac{t-t_0^j}{T},$$ (6)

where T is the oscillation period and $t_0^j$ is the first time that the output of the jth oscillator $v_1^j-v_2^j$ arrives at its maximum value. Such a definition can also be applied to the oscillations in the neuron cell model. The order parameter within modules, ${Ƶ}_{1,2}$, can be defined as

$${Ƶ}_{1,2}={\langle e^{i{\psi }^j\left(t\right)}\rangle }_{N/2},$$ (7)

where the subscripts 1,2 denote the two modules, and ${⟨\cdot ⟩}_{N∕2}$ means averaging within a module and over long time.

The in-phase index ϑ_in within modules can be defined as

$${\vartheta }_{in}=\frac{\left|{Ƶ}_1\right|+\left|{Ƶ}_2\right|}{2},$$ (8)

so that ϑ_in = 1 when an ideal in-phase pattern is achieved within modules and ϑ_in = 0 when it is a zero-coherence state.

The anti-phase index ϑ_an between modules is defined as

$${\vartheta }_{an}=1-\frac{\left|{Ƶ}_1+{Ƶ}_2\right|}{\left|{Ƶ}_1\right|+\left|{Ƶ}_2\right|},$$ (9)

so that ϑ_an = 1 when a perfect anti-phase pattern is achieved between modules and ϑ_an = 0 vise verse. If within a module, the oscillations are incoherence, ϑ_in ≈ 0, and the collective behavior is merely some fluctuations. In order to avoid such irrelevant case, we only define ϑ_an when ϑ_in > 0.1.

3. Results

3.1. Effect of delay time

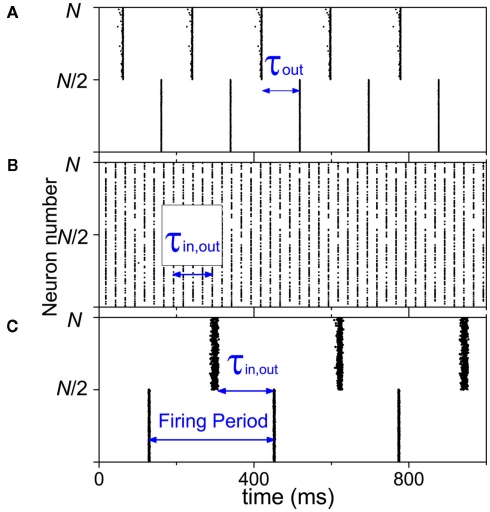
In the neuron cell model, when we select reasonably different delay times for the connections within-module and between modules, anti-phase pattern can be achieved between the two modules. The precondition is that in-phase pattern has to be achieved within each module. An example can be seen in Figure 2A, where the delay time between module is τ_out = 100 ms, and the delay time within each module is τ_in = 2 ms. The other two parameters, the density and ratio of excitatory coupling, is the same within and between modules. The existence of an anti-phase synchronization is robust to these parameters. Therefore, the delay time can be a key factor in organizing the anti-phase pattern.

Figure 2.

Dynamics of two-module networks with neuron cell models. (A) Delay times are different within-module τ_in = 2 ms and between modules τ_out = 100 ms; k_in = k_out = 0.6; and Φ_in = Φ_out = 100%. (B) Connection densities are different within-module k_in = 1 and between modules k_out = 0.2; τ_in = τ_out = 100 ms; and Φ_in = Φ_out = 100%. (C) 20% neurons are changed to be inhibitory and the outputs of them only link to the neighbors within modules; Φ_in = 80%, Φ_out = 100%, τ_in = τ_out = 150 ms, and k_in = k_out = 0.3.

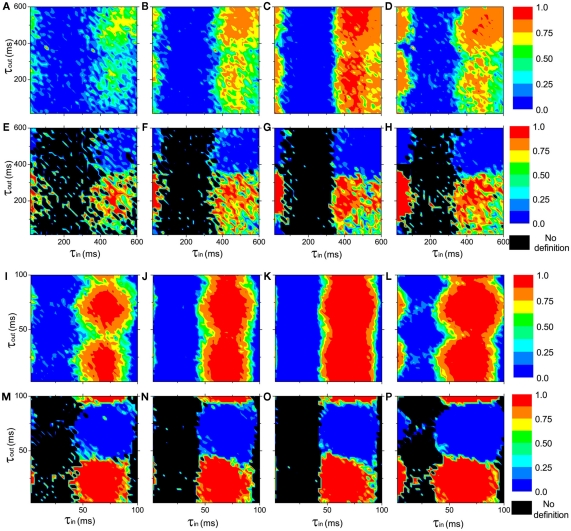
In the neural mass model, we can get similar conclusion. With I₀ = 115 mA, a single oscillator oscillates at about 1.5 Hz in the delta band. We use excitatory couplings, i.e., positive g_ij. Numerical results show that conduction delays also play a key role in the persistence of the anti-phase patterns between modules and in-phase patterns within modules, as shown in Figures 3A–H, where the pronounced anti-phase pattern mainly persists in two regions: the delays within a module τ_in ∼ 0 and the delays between modules τ_out are around 200 ms, and τ_in are around 500 ms and τ_out are around 200 ms. The latter one has a larger region than the former one. This situation, i.e., the delay time between distant modules can be significantly smaller than those within the module, is unlikely to be realistic, though we can simulate it in the model. When we change the input current to I₀ = 180 mA, the frequency of a single oscillator comes to the alpha band, around 11 Hz. The numerical results are shown in Figures 3I–P, which are similar to those in Figures 3A–H. The most prominent difference is that the time scale is only about 1/7 of the Figures 3A–H, noting the frequency in Figures 3I–P is about 7 times of that in Figures 3A–H.

Figure 3.

The in-phase synchronization index ϑ_in within a module and the anti-phase synchronization index ϑ_an between the modules as functions of the delay times τ_in and τ_out at different connection densities in networks of coupled neural mass oscillators (Eqs 2–4). (A–D) and (I–L): the in-phase synchronization index ϑ_in in color scale. (E–H) and (M–P): the anti-phase synchronization index ϑ_an in color scale. ϑ_an is not defined when ϑ_in < 0.1, represented by black region. Upper panel (A–H): I₀ = 110 mA, the neural mass oscillators oscillate at about 1.5 Hz in the delta band. Lower panel (I–P): I₀ = 180 mA, the neural mass models oscillate at about 11 Hz in the alpha band. The connections densities of the networks are: (A,E,I,M), k_in = k_out = 0.3; (B,F,J,N), k_in = 0.6, k_out = 0.3; (C,G,K,O), k_in = 0.9, k_out = 0.3; (D,H,L,P), k_in = k_out = 0.6.

3.2. Effect of connection density

In neuron cell model, no matter how we change the connection densities within-module and between modules, if other factors are homogeneous, the anti-phase pattern never emerges. An example is shown in Figure 2B. Therefore, the connection density is not a key factor in organizing the anti-phase pattern. However, in the neural mass model, we can see that, though anti-phase pattern cannot be found when delay times are homogeneous (τ_in = τ_out, the diagonal of each panel of Figure 3) the parameter region of τ_in and τ_out for anti-phase pattern are different, depending on connection densities. It means that the connection density also play an important role in maintaining the stability of the anti-phase pattern in the presence of noise perturbation, if τ_in and τ_out are different.

Previously, it has been found that the connection densities have impacts on the synchronization properties of a network (Arenas et al., 2006, 2008; Gómez-Gardeñes et al., 2010; Zhao et al., 2011). The collective behaviors of nodes within a module are easier to be established since the interactions within a module is stronger (connection density is higher) than that between modules. Intuitively, the connection density probably has an impact on the organization of anti-phase pattern. In this work, we clarify that the connection density actually impact on the stability rather than the existence of an anti-phase pattern. With higher connection densities within or between the modules, the anti-phase attractors are stabilized in a broader parameter region of the delay time.

3.3. Effect of inhibitory coupling

At last, when we change 20% neurons to inhibitory type in each module, anti-phase oscillation may also be observed if the inhibitory synaptic current is sufficient large, as shown in Figure 2C. This result also depends on the coupling strength (synaptic current). Under the condition τ_in = τ_out and k_in = k_out, in order to achieve the anti-phase pattern between modules, a good match of coupling strength with τ_in,out, k_in,out and Φ_in,out is required. In the example we show in Figure 2C, τ_in,out = 150 ms, k_in,out = 0.3, Φ_in = 80%, Φ_out = 100%, and the inhibitory coupling strength is ten times of the excitatory coupling strength. The balance of excitation and inhibition in neural network with large inhibitory coupling is realistic in biological neural networks, since inhibitory synapses are in general closer to the neuron cell body (soma; Buzsáki, 2006). These results also indicate that in the organization of an anti-phase oscillation pattern in cortex, the coupling types can be a key factor. The mechanism is that the inclusion of inhibitory coupling may generate slow oscillations within the module, which will be discussed in more detail later.

3.4. Analysis

Given a pair of oscillators ɸ₁(t) and ɸ₂(t), with time-delayed coupling, their phase difference is defined as Δɸ = ɸ₁ − ɸ₂. The stability of in-phase and anti-phase patterns versus delay time becomes clear when the evolution of Δɸ can be approximately written in the following linearized form:

$$\frac{d\Delta \varphi }{dt}=\left\{\begin{array}{cc}G\left(2\pi \gamma \tau \right)\Delta \varphi ,\hfill & \Delta \varphi \sim 0\hfill \\ G\left(2\pi \gamma \tau +\pi \right)\left(\Delta \varphi -\pi \right),\hfill & \Delta \varphi \sim \pi \hfill \\ \hfill \end{array}\right.,$$ (10)

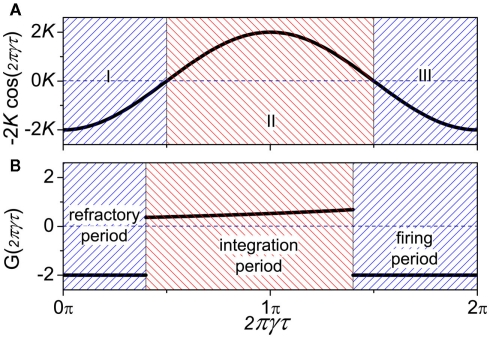
where γ is the oscillatory frequency, τ is the delay time of the coupling and G is a periodic function with period 2π. In such a case, stability analysis theory can give the conclusion that when G(2πγτ) < 0, the in-phase pattern (Δɸ = 0) is stable and when G(2πγτ + π) < 0, the anti-phase pattern (Δɸ = π) is stable. Furthermore, for some given values of delay time τ, if both G(2πγτ) and G(2πγτ + π) are negative, the in-phase and the anti-phase pattern coexist in this parameter region; and whether the in-phase or anti-phase pattern will be achieved depends on the initial conditions.

For example, in the case of classical coupled phase oscillators:

$$d{\phi }_{1,2}\left(t\right)∕dt=2\pi \gamma +Ksin\left[{\phi }_{2,1}\left(t-\tau \right)-{\phi }_{1,2}\left(t\right)\right],$$ (11)

where K is the coupling strength, G(2πγτ) takes the form G(2πγτ) = −2K cos(2πγτ). The function −2K cos(2πγτ) (K > 0) versus 2πγτ is shown in Figure 4A. When 2πγτ < π/2 or 2πγτ > 3π/2, G(2πγτ) < 0, and G(2πγτ + π) > 0, so that the in-phase pattern is stable. When π/2 < 2πγτ < 3π/2, G(2πγτ) > 0, and G(2πγτ + π) < 0, the anti-phase pattern is stable.

Figure 4.

Comparison of function G(2πγτ) between (A) coupled phase oscillators (K > 0) and (B) coupled neuron cells systems.

In the following, we show that anti-phase synchronization in coupled neuron systems can be understood using coupled phase oscillators, with mathematical details presented in Appendix. The collective behaviors of coupled neuron cells are basis for the spatiotemporal pattern formations in neuron networks. In the simplest case where a pair of neuron cells are pulse-coupled together $\left(K_{12}=K_{21}=\tilde{K}\right),$ the phase shift between them is determined by the delay time, coupling strength, and the initial conditions (Ernst et al., 1998). We can define the phase of an IAF cell as:

$${\phi }^j\left(t\right)=2\pi \frac{t-t_0^j}{T},$$ (12)

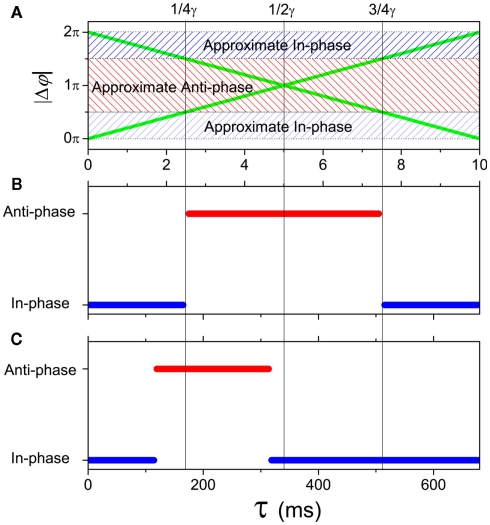
where $t_0^j$ is the time when the jth neuron fires for the first time. The membrane potential V(t) then can be expressed as a function of the phase V(φ). Actually, from Mirollo and Strogatz (1990), an IAF cell is usually described as a phase oscillator in this way. In the case of a pair of cells with small excitatory coupling, the phase difference |Δφ| = |φ₁ − φ₂| equals to the time delay τ or 2π − τ (Ernst et al., 1998), so that a delay time approximated to half of the period can induce an apparent anti-phase oscillation pattern. This case in shown in Figure 5A. It looks different when compared to the classical phase oscillator in Figure 5B. However, there is similarity between a pair of pulse-coupled IAF model and a pair of coupled phase oscillators model: when τ approximates to 0 or 1/γ, the phase difference is small (in-phase or approximate in-phase), whereas when τ approximates to 1/2γ, the phase difference is big (anti-phase or approximate anti-phase). This similarity actually has deeper significance in understanding key role of delay time in organizing the anti-phase pattern in neuron networks, as we will show shortly.

Figure 5.

In-phase and anti-phase attractors. (A) A pair of coupled IAF oscillators described by Eq. 1 (green lines); (B) a pair of coupled phase oscillators described by Eq. 11 (K > 0); (C) a pair of coupled neuron mass oscillators described by Eqs 2–4.

Let us consider a system with two populations of cells. Within each population, neurons are coupled together so that they fire orderly; and between the populations, the phase difference between pairs of neurons corresponds to the phase difference of the oscillations of the two populations. This is the simplest case where the interaction between neuron cells can map to the interaction between neuron populations. In this case, we can show (see Appendix) that the phase difference can be described by the same form as in Eq. 10, where the function G(2πγτ) is piece-wise, satisfying:

$$G\left(2\pi \gamma \tau \right)\left\{\begin{array}{c}<0,2\pi \gamma \tau \in refractoryperiod\hfill \\ >0,2\pi \gamma \tau \in integrationperiod\hfill \\ <0,2\pi \gamma \tau \in firingperiod\hfill \\ \hfill \end{array}\right.,$$ (13)

as shown in Figure 4B. When the neuron receives a spike, if V(φ) increases to a new value $V\left(\phi \right)+\tilde{K},$ the neuron is in the integration period, (φ ∈ integration period); if V(φ) increases to V_th where the neuron fires a spike, it is in the firing period, (φ ∈ firing period); and if V(φ) remains at the value V_r, it is in the refractory period, (φ ∈ refractory period). More details about the function G can be obtained in the Appendix. These three periods are qualitatively similar to the three regions I, II, and III in coupled phase oscillators with K > 0 in Figure 4A. The above analysis can therefore explains the relationship of the organizations of anti-phase pattern between coupled neuronal systems and coupled phase oscillators, so as to understand the key role of the delay time.

In a pair of coupled neural mass oscillators, the dynamical behaviors versus delay time will be more similar to the case of coupled phase oscillators. We show an example in Figure 5C. Compared to the coupled phase oscillators, the region for anti-phase pattern is smaller and shifts to smaller τ in coupled neural mass oscillators. This result has influence on the organization of the anti-phase pattern on the two-module networks. For example, in each panel of Figure 3, the region with high values of the in-phase index ϑ_in and anti-phase index ϑ_an is smaller in size at small τ_in than that of large τ_in.

To organize the anti-phase oscillation pattern between modules, highly coherent oscillation (approximate in-phase synchronization) has to be achieved within modules, or otherwise there would not be macroscopic oscillations of the population except for some fluctuations. From the above analysis, we know that a suitable delay time between modules τ_out is very important. The delay time within modules τ_in should be small enough (or close an integer times of the period) to allow the oscillators within modules have small phase difference, so that the oscillators within each module may exhibit the approximate in-phase pattern. For pulse-coupled neuron networks, in the extreme case, all the neurons within a module fire simultaneously, and the interaction between modules is equal to the interaction between a pair of neurons as analyzed by Ernst et al. (1998). The delay time between modules approximating to half of the period can induce this anti-phase pattern. In network of neural mass models, the dynamics is more similar to the coupled phase oscillators, though the attractors are more complex, depending on the initial conditions. Therefore, different delay times within and between modules can be a key factor for anti-phase synchronization.

The connection density does not play an important role as the delay times. In the network of coupled neuron cells with homogeneous delay time τ and excitatory coupling, high-coherence collective oscillation can only be achieved when τ = nT where T is the firing period of the neurons (e.g., n = 4 in Figure 2B). Supposing that the neurons in the first module fire, after time τ, the signal transfer to the second module, inducing firing of the neurons in the second module. At the same time, the neurons in the first module also fire because of the relationship between the delay time and the firing period, so that only in-phase oscillation is observed. In this case, changing the connection density within and between modules cannot organize an anti-phase pattern. However, connection densities also have impact on the anti-phase pattern. Neuronal network is complicated in dynamics, where multiple attractors usually coexist, and network connection matrix is very important for the stability of an attractor (Memmesheimer and Timme, 2006). Connection densities play a very important role in the stability of an existing anti-phase pattern, though changing connection densities cannot influence the existence of an anti-phase pattern. Specially, in the network of neuron cell model, under the condition of suitable delay times and other parameters for anti-phase pattern, if the connection density is not suitable to stabilize this pattern robustly, this pattern is still difficult to achieve. For example, if k_in is small, anti-phase pattern can be only achieved by using the initial condition very close to this attractor. Otherwise, with random initial conditions, the neurons will fire randomly without achieving in-phase and anti-phase synchronization. For the network of neural mass model, other attractors can also coexist with the anti-phase synchronization. Comparing the Figures 3E–H or the Figures 3M–P, one can notice that, even in these simulations we use the same initial conditions, under the noise perturbations, the parameter regions of anti-phase pattern are not the same with different k_in or k_out. In this case, the connection density can play an important role in preserving the anti-phase pattern.

The other key factor is the inhibitory coupling. When inhibitory couplings are added within modules, the firing patterns can be altered. Compared to the case of totally excitatory coupling, Brunel and Wang (2003) have ever shown that in the presence of inhibitory coupling, an oscillatory behavior at the population level can happen among the neurons. The period of the collective oscillations is determined by several parameters of the excitatory and inhibitory synapses. Given an oscillation period, a suitable delay time τ approximating to half of the period can induce an anti-phase pattern, similar to the case of a pair of coupled neuron cells when the oscillations within-module is highly coherent. In the example we show in Figure 2C, the period is about 320 ms, and the delay time is 150 ms. Therefore, the role of inhibitory couplings in anti-phase synchronization is that they induce emergent oscillations with periods fitting to delay times between modules.

3.5. Interaction between high and low frequencies

The analysis in the previous section shows that the time delay approximating to 1/4γ < τ < 3/4γ contributes to the anti-phase patterns for oscillations with frequency γ for dominant excitatory couplings between modules. Collective activity in the brain oscillates in a quite wide range of frequencies. The conduction delays between neurons in different cortex are usually tens of milliseconds which can support anti-phase synchronization of oscillations with a period of hundreds milliseconds if the oscillations are narrow-banded. In reality, the anti-phase oscillations can be much slower (sometime slower than 0.1 Hz), corresponding to the delay times several orders of magnitude larger than the conduction delays. A crucial question is whether the relatively small delay times of neuronal communications can contribute to the slow anti-phase patterns? Our analysis using a simple mathematical model show that this is possible if there exists an interaction between slow and fast oscillations.

Supposing the signal measured from a cortical region is a function of two variables δ and α as H(δ,α), where δ and α respectively denote the phase of slow and fast oscillations. We describe the evolution of them as coupled phase oscillators

$$\begin{array}{llll}{\stackrel{·}{{\displaystyle \delta }}}_{1,2}\left(t\right)& =2\pi {\gamma }_{\delta }& & \\ & +I_{\delta }\left[{\delta }_{1,2}\left(t\right),{\delta }_{2,1}\left(t-\tau \right),{\alpha }_{1,2}\left(t\right),{\alpha }_{2,1}\left(t-\tau \right)\right],& & \text{(14)}\\ {\stackrel{·}{{\displaystyle \alpha }}}_{1,2}\left(t\right)& =2\pi {\gamma }_{\alpha }& & \\ & +I_{\alpha }\left[{\delta }_{1,2}\left(t\right),{\delta }_{2,1}\left(t-\tau \right),{\alpha }_{1,2}\left(t\right),{\alpha }_{2,1}\left(t-\tau \right)\right],& & \text{(15)}\end{array}$$

where γ_δ and γ_α represent their intrinsic frequencies and the subscripts 1 and 2 indicate two cortical regions. The question now can be specified as: can the anti-correlated population activities be observed between these two regions in δ band, if the conduction delay τ has the same order as 1/γ_α, and τ < 1/4γ_δ.

If there is no interaction between high-frequency and low-frequency oscillations, the system will be reduced to two coupled oscillators in the δ and α bands separately, very similar to that of Eq. 11. In this case, anti-phase synchronization cannot be realized for the slow oscillations with τ < 1/4γ_δ. Therefore, if the anti-correlation pattern organized in low-frequency band is induced by small time-delays, there must be an interaction between high-frequency and low-frequency oscillations.

We use an example in the following to demonstrate this mechanism, where we take the interaction terms as

$$\begin{array}{rcll}{I}_{{\delta }_{1,2}}& =Ksin\left({\delta }_{2,1}\left(t-\tau \right)-{\delta }_{1,2}\left(t\right)\right)cos\left({\alpha }_{2,1}\left(t-\tau \right)-{\alpha }_{1,2}\left(t\right)\right),& & \text{(16)}\\ I_{{\alpha }_{1,2}}& =Ksin\left({\alpha }_{2,1}\left(t-\tau \right)-{\alpha }_{1,2}\left(t\right)\right)cos\left({\delta }_{2,1}\left(t-\tau \right)-{\delta }_{1,2}\left(t\right)\right),& & \text{(17)}\end{array}$$

with positive coupling strength K > 0. This is one of the simplest cases where the interaction between high-frequency [cos(α_2,1(t − τ) − α_1,2(t))] has influence on the interaction between low-frequency oscillations [sin(δ_2,1(t − τ) − δ_1,2(t))], and vise versa. Using new variables u = δ + α and v = δ − α, we can separate the system into two pairs of coupled phase oscillators with frequencies γ_δ + γ_α and γ_δ − γ_α, respectively,

$$\begin{array}{rcll}{\stackrel{·}{u}}_{1,2}\left(t\right)& =2\pi \left({\gamma }_{\delta }+{\gamma }_{\alpha }\right)+Ksin\left(u_{2,1}\left(t-\tau \right)-u_{1,2}\left(t\right)\right),& & \text{(18)}\\ {\stackrel{·}{v}}_{1,2}\left(t\right)& =2\pi \left({\gamma }_{\delta }-{\gamma }_{\alpha }\right)+Ksin\left(v_{2,1}\left(t-\tau \right)-v_{1,2}\left(t\right)\right).& & \text{(19)}\end{array}$$

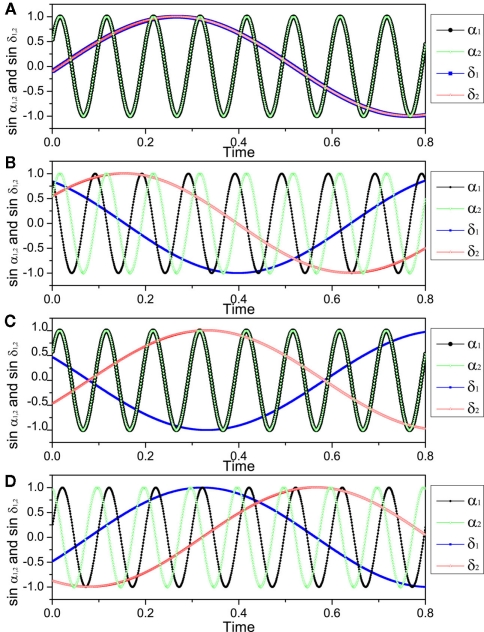
Now the conditions for in-phase and anti-phase synchronization of these new oscillators become clear. Since δ = (u + v)/2 and α = (u − v)/2, we can obtain the phase differences of the original fast oscillations α_1,2 and slow oscillations δ_1,2. We can identify several important values of the delay τ. The results are summarized in Table 1. All of τ_0,1,2,3,4 have the same order of 1/γ_α, and are smaller than 1/4γ_δ when γ_δ is much smaller than γ_α. Notably, there is a region (τ₂, τ₃), the slow oscillations δ₁ and δ₂ can show anti-phase oscillation. Examples of numerical simulation are shown in Figure 6.

Table 1.

Phase difference of α_1,2 and δ_1,2.

Δɸ\τ	(τ0, τ1)	(τ1, τ2)	(τ2, τ3)	(τ3, τ4)
α1 − α2	0	π/2	0	−π/2
δ1 − δ2	0	π/2	π	π/2

τ₀ = 0; τ₁ = 1/4(γ_δ + γ_α); τ₂ = 1/4(γ_δ − γ_α); τ₃ = 3/4(γ_δ + γ_α); τ₄ = 3/4(γ_δ + γ_α).

Figure 6.

The pattern of slow and fast oscillations in the presence of time-delays, described by Eqs. (16) and (17). Parameters are K = 0.02, γ_α = 10, γ_δ = 1, so that τ₁ = 0.025 × 10/11, τ₂ = 0.025 × 10/9, τ₃ = 0.075 × 10/11, τ₄ = 0.075 × 10/9. (A) τ = 0.005 ∈ (τ₀, τ₁), α₁ − α₂ = δ₁ − δ₂ = 0; (B) τ = 0.025 ∈ (τ₁, τ₂), α₁ − α₂ = δ₁ − δ₂ = π/2; (C) τ = 0.05 ∈ (τ₂, τ₃), α₁ − α₂ = 0, δ₁ − δ₂ = π; (D) τ = 0.075 ∈ (τ₃, τ₄), α₁ − α₂ =  − π/2, δ₁ − δ₂ = π/2.

In the real cortex system, the interactions between high and low-frequency oscillations will not be as simple as the model shown in Eqs. (16) and (17). Furthermore, some of the anti-phase patterns of cortical dynamics are investigated by using indirect methods, e.g., fMRI studies (Fox et al., 2005), where the underlying mechanism of slow oscillation is quite complicated and is not yet clearly understood. Nevertheless, this part of discussion provides an understanding of principle that it is possible to obtain anti-phase pattern in very slow-frequency band with a relative smaller delay time if there is the interaction between high and low frequencies oscillations. Moreover, in the presence of these interactions, more types of patterns can emerge in addition to in-phase and anti-phase oscillations, e.g., the pattern of π/2 phase difference (see Table 1; Figure 6). It is therefore expected that more complex pattern formations can organize in the time delay environments when the interactions among different frequency bands are entangled in a complicated manner. Our research is of fundamental meaning for further understanding the complex pattern formations organized within cortico-cortical communications.

4. Discussions

4.1. In-phase synchronization within modules

When we show the organization of an pattern which is anti-phase between modules and in-phase synchronization within modules, the analysis is made basing on that in-phase has been organized within modules. The dynamics between modules is then similar to a pair of coupled neuron cells or coupled phase oscillators (Eq. 11). In other words, in our analysis, in-phase pattern within-module is a precondition for the organization of anti-phase pattern between modules.

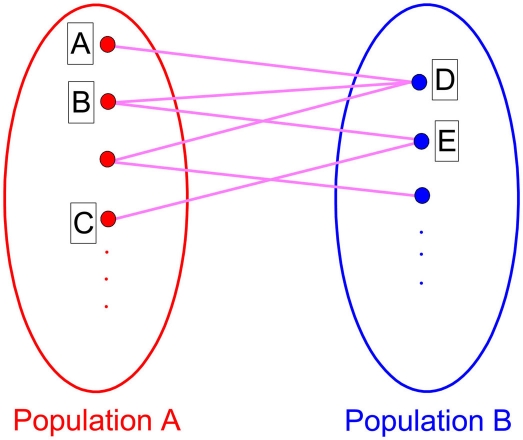
However, when two neurons without direct connections are coupled to the third intermediary one, each fires in anti-phase with the third one, the two neurons can achieve in-phase firing. Such a case can be also observed on a neuronal network. As shown in Figure 7, the network is divided into two populations; within each population, there is no connection among neurons, but between populations, neurons are randomly coupled with suitable delay times for anti-phase firings. On this network, neuron A and B can achieve in-phase because they have common input from neuron D and both of them are anti-phase to neuron D. The neurons D and E can achieve in-phase because of the common input from neuron B. This mechanism can finally make all the neurons within one population fire in-phase, even for those without a common input, like the neurons A and C. In such a case, anti-phase between the two populations forms a precondition for the organization of in-phase pattern within each population in the presence of delay times. This case is therefore different from what we have analyzed where the connection density is usually higher within modules than between modules. In a real neuronal network, the two populations presented in Figure 7 will not be defined as a module in term of connectivity. Including interaction within such a population does not necessarily enhance in-phase synchronization, so that if there exist interactions within populations, especially when the delay time and coupling type are the same as those between the populations, the in-phase pattern could be destroyed.

Figure 7.

A network structure where in-phase pattern within population can be induced by anti-phase between populations when there is no interaction between neurons within the populations.

Generally speaking, the mechanism, where anti-phase between populations is precondition for in-phase within populations, is more appropriate to describe the case where two populations are indirectly coupled by the third intermediary one. This situation is perhaps relevant for understanding in-phase synchronization between distant cortical regions (Vicente et al., 2008); the mechanism, where in-phase within modules is precondition for anti-phase between modules, is more relevant for understanding the organization of anti-phase pattern between two coupled cortical regions.

4.2. Under tasks

We have analyzed important factors in the spontaneous organization of anti-phase patterns without external stimuli. Actually, this kind of anti-phase pattern can also be organized under tasks. From the traditional viewpoint, the task-induced anti-phase pattern often referrs the coexistence of both the areas of task-increased activity and task-decreased activity (Broyd et al., 2009). Our analysis can also shed some lights on this task-induced anti-phase pattern phenomenon.

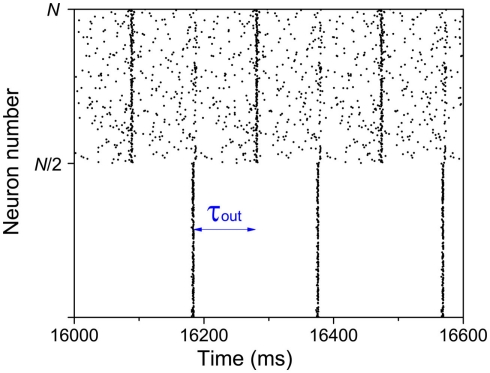
If we suppose that one of the modules is forced to be in-phase synchronization by external signal, rather than spontaneous organized, a suitable delay time may also be a key factor in inducing an anti-phase pattern between modules. We give a simple example in Figure 8. A number (N = 1000) of IAF neurons are coupled together with excitatory synapses. In the absence of external input, these neurons fire randomly, with a set of parameters k_in = k_out = 0.05 and τ_in = τ_out = 100 ms. We add an external input to the first module (1 → N/2), to force the neurons in this modules fire nearly simultaneously every 200 ms, mimicking a firing pattern induced by some tasks. Since the delay time τ_out = 100 ms, after 100 ms, the membrane potentials of the neurons in the second module are increased, so that a large fraction of them fire simultaneously at that time. Even though the neurons in the second module still show a relatively random firing pattern, anti-phase oscillation can be observed between modules. However, if the delay time does not approximate to half of the period of the external input, such an anti-phase pattern cannot be observed.

Figure 8.

Anti-phase pattern when the neurons in the first module are forced to fire every 200 ms. τ_out = 100 ms.

This simple mathematical mechanism can help us understand some observations in neuron systems. Previous studies showed that approximate in-phase patterns (or long-distance spatial coherence) can be observed in slow-wave sleeping states, anesthetized states, or under tasks. Anti-phase patterns are also found in these states. Regardless whether the in-phase pattern in each module is self-organized (e.g., resting state) or induced by external signals (under some tasks), the in-phase patterns within cortex make the cortico-cortical communication dynamics much similar to the time-delayed coupled phase oscillators, showing anti-phase pattern with suitable delay times. There is a precondition that the in-phase synchronization is achieved within modules, which may bridge the understanding of the common characteristics of cortical dynamics in slow-wave sleeping states, anesthetized states, or under tasks.

4.3. Diversity in network connectivity and delays

All the above analysis is made basing on the conditions that the delay times and connection densities are uniform within each module or between modules. However, in the real cortical networks, none of them is uniform. In the following, we discuss some results on network with diverse connectivity and delays, and show that delay time is still a key factor but the connected density is not as important in organizing in-phase and anti-phase patterns.

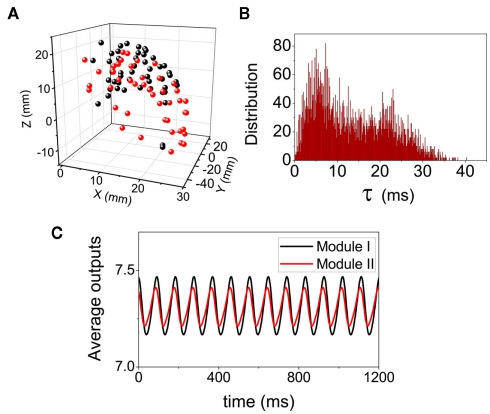
We use the cortico-cortical network among the visual areas of monkey (Kötter, 2004; Kaiser and Hilgetag, 2006). Basing on network connectivity, this network can be put into two modules (da F Costa et al., 2007), and the connection densities are much higher within each module than that between modules. The spatial position of the mass-center of these cortical areas (network nodes) are shown in Figure 9A, where the black and red colors represent different modules. We simulate the dynamics of the network by putting a neural mass oscillator on each node. The delay times are introduced by a conduction velocity assumed to be common for all the links. Therefore, the delay times are non-uniform, proportional to the Euclidean distances between different pairs of areas. In the simulations we cannot find anti-phase synchronization between the two modules. Even if we start with an anti-phase pattern with some noise perturbation as the initial conditions, this pattern cannot be preserved on this network. For very large velocity, the delay times approximate to zero, and the whole network can preserve a highly coherent (in-phase) state. On the other hand, when the velocity is in the biologically reasonable range, the delay times have a broad distribution from zero to a value comparable to the period of the neural mass oscillator (Figure 9B), the phase differences among oscillators distribute randomly in (−π, π). Even though the average values of the output from each module show some small macroscopic oscillation, they do not show anti-phase pattern between the two modules (Figure 9C). These results confirm again that the formation of densely connected modules cannot induce an anti-phase pattern between them. In the real visual cortex, cells tend to fire simultaneously when activated by related features of a visual stimulus (Gray et al., 1989; Engel et al., 1991a; Castelo-Branco et al., 2000; Tiesinga et al., 2008), though this network has two modules.

Figure 9.

Dynamical pattern on the cortical network of Macaque visual system. (A) The spatial positions of the network nodes. (B) The distributions of the delay time τ when the conduction velocity is set as a biological reasonable value 2.4 mm/ms. (C) The average values of the output $v_1^j-v_2^j$ within each modules.

Anti-phase induced by inhibitory coupling

The above analysis is basing on the case that the coupling between modules is dominantly excitatory. If the coupling is inhibitory, the results of coupled neural mass oscillators can be roughly predicted from Eq. 11, where a negative K stands for a negative coupling, so that we can expect that anti-phase pattern emerges when the delay time τ is around zero. Our simulations of a pair of coupled neuron mass oscillators confirmed that, anti-phase pattern emerges with zero τ, whereas in-phase pattern emerges when the delay is close to half of the oscillation period.

In neuronal systems, the inhibitory neurons and the non-symmetry of the inhibitory connections can induce pronounced competition of activity among neuron pools. Competition dynamics broadly exists in neuronal system (Laurent et al., 2001; Levi et al., 2005; Mazor and Laurent, 2005; Moldakarimov et al., 2005; Rollenhagen and Olson, 2005; Komarov et al., 2009a; Szücs et al., 2009), which may play important roles in neuronal functions, e.g., the integration between low-frequency and high-frequency oscillations (Rabinovich et al., 2006). This type of dynamics also has a relationship to anti-phase pattern from a generalized viewpoint. For example, in the well-known n-competitor neuronal system (Komarov et al., 2009a,b), each population activity may achieve its peak value sequently. If in this case, n can be degenerated to 2, the dynamics degenerates to the anti-phase oscillation pattern. Therefore, it is significant to get insight into the organization of anti-phase pattern for better understanding the organization of more complicated competition dynamics in the brain.

To summarize this part of discussion, when the coupling is inhibitory between modules, delay time can also be a key factor in the organization of anti-phase oscillation. The difference from the case of excitatory coupling is that anti-phase between modules require a small delay (or close to a period) between modules.

Conclusion

We investigate the anti-phase oscillation pattern organized on two-module networks with both neuron cell model and neuron mass model in time delay environments, among other factors. The time-delays and the coupling types (excitatory and inhibitory) can be key factors for organizing the patterns of in-phase within modules and anti-phase between modules, but the connection densities are not as crucial though the stability is influenced by the network connectivity. Our analysis shows that important understanding of the anti-phase synchronization in neural networks can be obtained by the classical coupled phase oscillators. The anti-phase patterns organized in real cortical networks are more complicated. Furthermore, some of them are investigated by using indirect methods, e.g., fMRI studies. It is possible that anti-phase pattern in the signals of these indirect measurements can reflect some kinds of anti-phase pattern in cortical dynamics. However, it is still an open problem how they are related. Our analysis in this work provides a clear understanding of the key factors in the organization of the anti-phase pattern on a two-module neuronal network, which is of importance for gaining insight into the mechanisms underlying the dynamics, no matter how this anti-phase pattern is expressed in the measurement signals. These results are significant for further understanding the formation of more complex spatiotemporal patterns and functional networks in the brain, and the bridge between the anti-phase patten in the measurement signals and the anti-phase pattern organized on the neuronal network need to be meticulously constructed in the further studies.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

Analysis of phase difference in pulse-coupled neuronal network

The phase of an IAF cell can be defined as:

$${\phi }^j\left(t\right)=2\pi \frac{t-t_0^j}{T},$$ (A1)

where $t_0^j$ is the time when the jth neuron fires for the first time. The potential V then have the properties V(φ = 0) = V_r, V(φ = 2π) = V_th, dV/dΦ > 0, and d²V/dΦ² < 0. For two coupled neurons, when a neuron receives an action potential from the other one, its phase will has an increment $\tilde{\phi },$

$$\tilde{\phi }=g\left({\phi }_{1,2}\right)-{\phi }_{1,2},$$ (A2)

where the function g(φ) is

$$g\left(\phi \right)=V^{-1}\left(min\left[V\left(\phi \right)+\tilde{K},V_{th}\right]\right),$$ (A3)

and V⁻¹ is the inverse function of V(φ). The phase difference of these two neurons Δφ = φ₁ − φ₂ therefore follows

$$\frac{d\Delta \phi }{dt}=\left\{\begin{array}{cc}g\left(2\pi \gamma \tau +\Delta \phi \right)-2\pi \gamma \tau -\Delta \phi ,\hfill & {\phi }_2=2\pi \gamma \tau \hfill \\ & \\ -g\left(2\pi \gamma \tau -\Delta \phi \right)+2\pi \gamma \tau -\Delta \phi ,\hfill & {\phi }_1=2\pi \gamma \tau \hfill \\ & \\ 0,\hfill & otherwise\hfill \\ \hfill \end{array}\right..$$ (A4)

It means that only when φ₂ = 2πγτ or φ₁ = 2πγτ, its value is non-zero. In the following, we assume it has non-zero values all the time, which means that the coupling effect always takes place. We can write this evolution of Δφ in the following form:

$$\begin{array}{llll}\frac{d\Delta \phi }{dt}& =g\left(2\pi \gamma \tau +\Delta \phi \right)-2\pi \gamma \tau -\Delta \phi -g\left(2\pi \gamma \tau -\Delta \phi \right)& & \\ & +2\pi \gamma \tau -\Delta \phi .& & \text{(A5)}\end{array}$$

This situation describes such a system that the neuron system is divided into two populations; within each population, nerve cells are coupled together so that they fire orderly; and between these populations, the phase difference between the paired nerve cells corresponds to the phase difference of the oscillations of the two populations. In this case, the evolution of Δφ can be written as

$$\frac{d\Delta \varphi }{dt}\approx \{\begin{array}{ll}2g^{\prime }\left[\left(2\pi \gamma \tau \right)-1\right]\Delta \varphi ,\hfill & \Delta \varphi \sim 0\hfill \\ 2g^{\prime }\left[\left(2\pi \gamma \tau +\pi \right)-1\right]\left(\Delta \varphi -\pi \right),\hfill & \Delta \varphi \sim \pi \hfill \end{array},$$ (A6)

where g′(φ) = dg(φ)/dΦ. We therefore get G(2πγτ) = 2g′[(2πγτ) − 1], so that one can understand the role of delay time τ in coupled neuronal systems as in the coupled phase oscillators.

In the following we will show that the expression of g(φ) in Eq. A2 can generate a similar performance of G(2πγτ) versus τ to the case in coupled phase oscillators when we consider another factor existing in real neuronal systems, the refractory period.

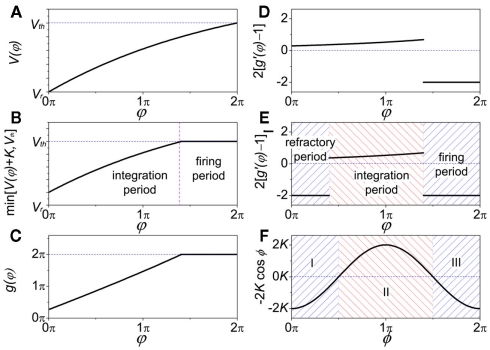
The properties dV/dΦ > 0 and d²V/dΦ² < 0 (Figure A1A) are the basis for the analysis in the following. When the neuron receives a spike, if V(φ) increases to $V\left(\phi \right)+\tilde{K},$ we call that the neuron is located in the integration period; if V(φ) increases to V_th, it is located in the firing period, as shown in Figure A1B. Therefore, we get

$$g\left(\phi \right)=\left\{\begin{array}{cc}{V}^{-1}\left[V\left(\phi \right)+\tilde{K}\right],\hfill & integrationperiod\hfill \\ 2\pi ,\hfill & firingperiod\hfill \\ \hfill \end{array}\right.,$$ (A7)

as shown in Figure A1C. Since $\tilde{K}>0,$ we get

$$g^{\prime }\left(\phi \right)\left\{\begin{array}{cc}>1,\hfill & integrationperiod\hfill \\ =0,\hfill & firingperiod\hfill \\ \hfill \end{array}\right.,$$ (A8)

as shown in Figure A1D. On the other hand, if the refractory period is taken into consideration, $V\left(\phi \right)+\tilde{K}=V_r$ is a constant during this period, so that g(φ) = 0 and g′(φ) = 0. We can therefore express 2[g′(φ) − 1] as

$$2\left[g^{\prime }\left(\phi \right)-1\right]\left\{\begin{array}{cc}<0,\hfill & refractoryperiod\hfill \\ >0,\hfill & integrationperiod\hfill \\ <0,\hfill & firingperiod\hfill \\ \hfill \end{array}\right.,$$ (A9)

as shown in Figure A1E. These three periods are similar to the three cases labeled as I, II, and III in Figure A1F for coupled phase oscillators with K > 0. The above analysis can therefore explain the relationship of the organizations of anti-phase pattern between coupled neuronal systems and coupled phase oscillators, so as to understand the key role of the delay time.

Figure A1.

Comparison of function G(φ) in coupled neuron systems and G(φ) in coupled phase oscillators. When analyzing the role of delay time τ in the stability of in-phase pattern, the value of G(2πγτ) is vital; when referring to anti-phase pattern the value of G(2πγτ + π) is vital. (A) In IAF oscillator V(φ) versus φ; (B) $min\left[V\left(\phi \right)+\tilde{K},V_{th}\right]$ versus φ; (C) g(φ) versus φ; (D) 2[g′(φ) − 1] versus φ; (E) 2[g′(φ) − 1] versus φ when refractory period is defined (the same form as Figure 4B); (F) in coupled phase oscillators, −2K cosφ versus φ when K > 0 (the same form as Figure 4A).