Seizure Prediction: Methods

Abstract

Epilepsy, one of the most common neurological diseases, affects over 50 million people worldwide. Epilepsy can have a broad spectrum of debilitating medical and social consequences. Although antiepileptic drugs have helped treat millions of patients, roughly a third of all patients have seizures that are refractory to pharmacological intervention. The evolution of our understanding of this dynamic disease leads to new treatment possibilities. There is great interest in the development of devices that incorporate algorithms capable of detecting early onset of seizures or even predicting them hours before they occur. The lead time provided by these new technologies will allow for new types of interventional treatment. In the near future, seizures may be detected and aborted before physical manifestations begin. In this chapter we discuss the algorithms that make these devices possible and how they have been implemented to date. We also compare and contrast these measures, and review their individual strengths and weaknesses. Finally, we illustrate how these techniques can be combined in a closed-loop seizure prevention system.

1. Introduction

Epilepsy is one of the most common and devastating neurologic diseases, afflicting over 50 million individuals worldwide. Seizure control with antiepileptic drugs decreases morbidity and mortality associated with this disease and remains the mainstay of treatment for most epilepsy patients. Despite the tremendous progress in the development of antiseizure medications and devices over the last five decades, at least 30% of all epilepsy cases remain refractory to current therapeutics. One of the most disabling aspects of epilepsy is the apparent unpredictability of seizures. Even brief episodes of staring or impairment of consciousness can be life-threatening, especially if they occur while the person is driving, swimming, climbing heights, or alone. The embarrassment of seizures often leads to social isolation and a loss of sense of well being.

For almost 50 years, epileptic seizures were believed to begin abruptly with no warning even though patient reports indicate periods when seizures are more likely to occur though they cannot specify a precise day or time [35]. Long-term EEG recordings from patients, advancements in computer technology, digital EEG technology, and storage allowed investigators to study the EEG with specifically employed mathematical tools in an attempt to identify changes or precursors to EEG or behavioral seizure onset [9]. In one of the most important works from the early 1970's, Viglione and colleagues showed that seizures may develop over longer time scales [48]. Similar evidence from hemodynamic studies performed in individuals with temporal lobe epilepsy showed a significant increase in blood flow within the epileptic hippocampus several minutes before seizure onset [3, 50].

Over the past 25 years, numerous seizure prediction algorithms have emerged from several centers throughout the world [31]. Nearly all published seizure prediction studies have been retrospective [32]. In other words, despite the existence of many published seizure prediction algorithms, no Class 1 evidence of clinical usefulness (prospective, blinded, and randomized) exists. This important limitation is one of the major drawbacks in the science of seizure prediction and stems in part to the lack of availability of long-term and uniform EEG recording, and rigorous statistical testing about the specificity and sensitivity of each method. Nevertheless, despite these limitations, an early seizure warning system has many potential benefits for the patient. Advanced seizure warning could allow patients or caregivers to take action and thereby minimize their risk of injury. Depending on its configuration, an automatic seizure warning system could be made to trigger pharmacological intervention in the form of fast-acting drugs or electrical stimulation. This would be a significant breakthrough because this intermittent, on-demand treatment system could replace the dependency on daily anticonvulsant treatment. Seizure prediction techniques could conceivably be coupled with treatment strategies aimed at interrupting the process even before a seizure begins to develop. The use of on-demand release of a short-acting drug or electrical stimulation during the preictal state could reduce side effects from treatment with antiepileptic drugs, such as sedation and clouded thinking. Furthermore, such systems could conceivably reduce morbidity and mortality, as well as greatly improve the quality of life for people with epilepsy. From a basic science perspective, the identification of a preictal state would greatly contribute to our understanding of the pathophysiological mechanisms that generate individual seizures and epilepsy.

In this review, we go over the dynamic aspects of epilepsy and the most widely used quantitative EEG approaches used in the science of seizure prediction. The available seizure prediction algorithms, as well as their potential use and limitations are presented.

2. Methods

“Epileptic seizure prediction” is the identification of a time when seizures are probably approaching and without a priori knowledge of the exact time in which they will occur [47]. Frequency-based methods, nonlinear dynamics (Chaos), and statistical analysis of EEG signals are the most common quantitative EEG techniques employed to forecast seizures [6]. The majority of the state-of-the-art techniques used to predict an epileptic seizure involves linearly or nonlinearly transforming the signal using one of several mathematical measures, and subsequently using the measure toward trying to predict the seizure based off the output of the measure. These systems include some purely mathematical transformations, such as the Fourier transform, or some class of machine learning techniques, such as artificial neural networks, or some combination of the two. Most of the measures are calculated from EEG epochs of ~20 seconds in a moving window analysis to include observation (interictal), preseizure, and seizure periods (Figure 1). Some measures also require pre-processing and filtering of the EEG epochs. All of these methods will be an appropriate determination of the nonseizure (interictal) from the seizure (ictal) period. Therefore, an area of important research is in defining the actual seizure onset time since the so called seizure prediction horizon will directly depend on when the seizure actually started.

Figure 1.

Ten second EEG trace showing the critical time window for EEG based seizure prediction. A is the time of earliest EEG change associated with the seizure (green bar); B is the unequivocal EEG seizure onset (blue bar); C is the time of earliest clinical change (red bar). The prediction horizon (black box) is the time from the processing window to the unequivocal EEG onset of the seizure.

This section reviews the measures that are commonly used to describe EEG time-series, some of which have been employed for prediction of seizures as reported in the literature [9]. The majority of these techniques use some type of time-series analysis method to detect seizures offline. Time-series analysis of an EEG falls into one of the following two groups: Univariate or multivariate mathematical measures.

2.1 Univariate Measures

Univariate time-series analyses are time-series analyses that consist of a single observation recorded sequentially over equal time increments. Some examples of univariate time-series are the price of a company's stock, daily fluctuations in humidity levels, and single-channel EEG recordings. Time is, of course, an implicit variable in the time-series. Information on the start time and the sampling rate of the data collection allows for the representation of the univariate time-series graphically as a function of time over the entire duration of data recording. The amplitude value of the recorded EEG signal sampled in the form of a discrete time-series x (t) x (ti) x (iΔt), (i = 1, 2, …, N and Δt is the sampling interval) can also be encoded through the amplitude and the phase of the subset of harmonic oscillations over a range of different frequencies. Time-frequency methods specify the map that translates between these representations.

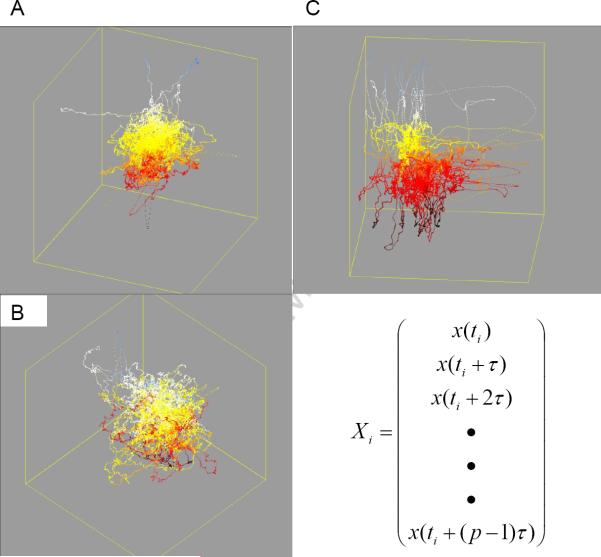
EEG analysis using univariate measures uses a single recording site. Linear univariate measures characterize the EEG time-series in terms of the amplitude and phase information. For purposes of characterizing the state and dynamics of the system, nonlinear univariate measures are employed. Nonlinear univariate methods start by characterizing the system state at a given moment in time. The so-called system state is described by a point in m-dimensional space called the state or phase space where m is the embedding dimension (Figure 2). The system dynamics determines how the system evolves over time [6].

Figure 2.

Space state embedding. An example of a state space computed from a single channel of EEG showing changes in the state space during a seizure. A is the interictal space state. B is the 10-second preseizure space state. C is the seizure space state. p is the embedding dimension of the state space; t is the time delay for the construction of the state space [(x,y,x,ẋẍ)].

In this section, we describe univariate linear methods most commonly used for seizure prediction. Common to each method is that they require the stationarity of the time-series. This implies that the statistical parameters (mean and standard deviation) of the process do not change with time, which for seizures is probably not true.

2.1.1 Short-term Fourier transform

Calculation of the power spectrum of one or more channels of the EEG provides the basis for one of the more widely used techniques for predicting an epileptic seizure. The core hypothesis is that the EEG signal, when partitioned into its component periodic (sine/cosine) waves, has a signature that varies between the ictal and the interictal states. To detect this signature, the Fourier transform of the signal is analyzed to find the frequencies that are most prominent (in amplitude) in the signal. Indeed, applying time-frequency analysis to seizure EEG activity is a good method to help to identify the source of epileptic seizures [4]. However, despite the correlation between the power spectrum and ictal activity, the power spectrum itself is usually not used as a stand-alone detector of a seizure or seizure precursor. It is typically coupled with some other time-series prediction technique or machine learning method.

The Fourier transform is a generalization of the Fourier series, breaking up any time-varying signal into its frequency components of varying magnitude. Any time-varying signal can be represented as a summation of sine and cosine waves of varying magnitudes and frequencies [49]. The Fourier transform is represented with the power spectrum which has a value for each harmonic frequency. This indicates how strong that frequency is in the given signal. The magnitude of this value is calculated by taking the modulus of the complex number that is calculated from the Fourier transform for a given frequency (|F(κ)|). When using the short-term Fourier transform, the assumption is made that the signal is stationary for some small period of time, T_s. The Fourier transform is then calculated for segments of the signal of length T_s. The short-term Fourier transform at time t gives the Fourier transform calculated over the segment of the signal lasting from τ -T_s.) to t. The length of T_s determines the resolution of the analysis since there is a trade-off between time and frequency resolution. A short T_s yields better time resolution, but it limits frequency resolution. The converse is also true. A long T_s increases the frequency resolution while decreasing the time resolution of the output. As described below, wavelet analysis can overcome this limitation, and offers a tool that can maintain both time and frequency resolution.

2.1.2 Accumulated energy

With this method, a running average of energy is computed from the EEG time-series [8]. Although this method has shown some promise in terms of identifying EEG seizure precursors under very specific conditions, results appear not to be consistent across datasets [12, 21, 23].

2.1.3 Autocorrelation and autoregressive modeling

Identification of a preictal period was achieved by employing autocorrelation methods between values of the EEG signal at different time points [29, 32]. The decorrelation time is computed as a as a function of the time difference with the first zero-crossing representing the decorrelation time [32]. Using autoregressive modeling techniques, preictal changes have been reported [37, 39]. The linear modeling of a time-series assumes that each value of the series depends only on a weighted sum of the previous values of the same series and “noise”. The main assumption in linear modeling is the stationarity of the signal. So, for non-stationary signals like EEG, one needs to segment it into stationary parts.

2.1.4 Discrete wavelet transforms

Wavelet transforms follow the principle of superposition, like Fourier transforms, and assume EEG signals are composed of various elements from a set of parameterized basis functions. As discussed earlier, Fourier transforms are limited to sine and cosine wave functions. In contrast, wavelets must meet other mathematical criteria, which allow the basic functions to be far more general than simple sine/cosine waves. The use of wavelets makes it substantially easier to approximate choppy signals with sharp spikes, than the Fourier transform. The reason for this is that sine and cosine waves have infinite support (i.e., stretch out to infinity in the time domain), making it difficult to approximate a spike. Wavelets can have finite support, so a spike in the EEG signal can be easily estimated by changing the magnitude of the component basis functions. For instance, discrete wavelets will break up any time-varying signal into smaller uniform functions, known as the basic functions. The basic functions are created by scaling and translating a single function of a certain form, known as the mother wavelet. In the case of the Fourier transform, the basic functions used are sine and cosine waves of varying frequency and magnitude. Since a cosine wave is just a sine wave translated by π/2 radians, the mother wavelet is the since wave in the case of the Fourier transform. For a wavelet transform, the basic functions are more general. The only requirements for the basis is that the functions are both complete and orthonormal under the inner product. The wavelet basis is very similar to the Fourier basis, with the exception that the wavelet basis can be finite. In a wavelet transform the basic functions can be defined over a certain window and zero everywhere else. As long as the family of functions defined by scaling and translating the mother wavelet is orthonormally complete, that family of functions can be used as the basis. With the Fourier transform, the basis is made up of sine and cosine waves that are defined over all values of x where −∞ < x <∞.

Wavelets and short-term Fourier transforms also serve as the foundation for other measures such as entropy. The spectral entropy method calculates some feature based on the power spectrum. Entropy was first used in physics to describe the amount of disorder in a thermodynamic system. Shannon extended its application to information theory in the late 1940s to address the entropy for a given probability distribution [41]. Entropy is a measure of how much information can be learned from the occurrence of a random event. Unlikely events yield more information than events that are very probable. For spectral entropy, the power spectrum is a probability distribution. Spectral entropy allows us to calculate the amount of information there is to be gained from learning the frequencies that make up the signal. Since nonstationary signals need to be accounted for when the Fourier transform is used, the short-term Fourier transform is employed to calculate the power spectrum over small parts of the signal rather than the entire signal itself. The spectral entropy is an indicator of the number of frequencies that make up a signal. A signal made up of many different frequencies (white noise, for example) would have a uniform distribution and therefore yield high spectral entropy. Conversely, a signal made up of a single frequency would yield low spectral entropy.

Wavelets have been applied to subdural electrocorticogram (ECoG) signals in an attempt to predict seizures. In one report, the authors first partitioned the ECoG signal into seizure and nonseizure components using a wavelet-based filter [34]. The filter did not specifically predict seizures. It flagged any increase in power or shift in frequency, regardless of cause (a seizure, an interictal epileptiform discharge, or merely normal activity). After the filter decomposed the signal down into its components, it was passed through a second filter that tried to isolate the seizures from the other events. The algorithm's median filter (2 sec) suppressed most interictal epileptiform discharges while power increases in “normal” activity were not “flagged” as seizures. Although this method did not predict electrographic onset, very short-term predictions of clinical seizure onset of 15 s or longer of were identified [34].

2.1.5 Statistical moments

These methods provide information about the amplitude and distribution of the EEG time-series. Even when a cumulative distribution function for a random variable cannot be determined, it is possible to describe an approximation to the distribution of this variable using moments and functions of moments [51]. Statistical moments provide information about the distribution of the amplitude of a given signal. In general, the statistical moments are taken about the mean. The first statistical moment is the mean of the distribution being considered, also known as the kth central moment. The second moment about the mean is the variance. The third moment about the mean provides the skew, which indicates the amount of asymmetry in that distribution. The fourth moment about the mean is the kurtosis, which shows the degree of peakedness of that distribution. These methods have been used to distinguish between the interictal and ictal states [37]. The absolute value of the skewness |μ3| was used for seizure prediction. However, it was not able to reproducibly predict a seizure by detecting the state change from interictal to preictal [37]. Nevertheless, statistical moments may prove valuable for early seizure detection in recordings with large amplitude seizures [7].

2.1.6 Correlation dimension

The correlation dimension, correlation density, and Kolmogorov entrophy are measures that are based on the concept of the correlation integral. These measures can be calculated from the state space representation of the EEG time-series. Changes in the state space over time can be used to describe the evolution of a seizure (Figure 2). The correlation dimension is computed from the state space embedding of the EEG time-series. This measures assumes that the probability that any two randomly chosen points of the state space exist within a given relative distance [10, 42]. The correlation dimension distinguishes random signals from deterministic time-series [10]. Accordingly, this measure can provide an approximation of the dimensionality of the state space. Human ECoG time-series studies indicate that the correlation dimension drops significantly just prior to seizure onset [19]. However, as with other nonlinear methods, results have not been reproducible and statistical validation is lacking [11, 32].

2.1.7 Correlation density

This is a closely related measure to the correlation dimension and is determined calculating the correlation integral for a fixed radius. A combination of time spatial embedding and time delays is applied to the EEG. As with the correlation dimension, the ability to predict seizures by employing the correlation density as been has been met with mixed results [26, 27].

2.1.8 Kolmogorov entropy

The Kolmogorov entropy gives a measure about the uncertainty of future states of the system over time. This measure has been applied to EEG time-series from children undergoing ECoG epilepsy evaluation. In a small dataset, results indicate that the Kolmogorov entropy may be useful in identifying EEG preseizure states [46]. Again, these results have not been prospectively evaluated.

2.1.9 Dynamical similarity index

Dynamical similarity index purportedly can track spatiotemporal changes in brain dynamics minutes in advance of an impending seizure. The measure is computed by phase space reconstruction of the EEG time-series by using time intervals between two positive zero-crossings and the measure of the dynamical similarity between the reference and test windows, respectively, using the cross correlation integral. Although one study demonstrated the utility of this index in identifying preseizure states [20], these initial results have not been reproducible in other studies [5, 52].

2.1.10 Loss of recurrence and local flow

The degree of nonstationarity can be determined by computing the frequency distribution of time distances under stationary conditions with respect to each reference point. In a nonstationary system, an increase deviation from this distribution is observed because of an absence of distant time indices in the neighborhood of the reference [36]. The loss of recurrence quantifies the degree of nonstationarity in a time-series. This loss of recurrence has been employed toward determining with predictability of an impending seizure [30].

2.1.11 Lyapunov exponent

EEG signals are extremely complex, with statistical properties depending on both time and space [for reviews, see 9, 22]. EEG signals contain numerous properties of non-linear systems, such as the existence of limit cycles (alpha activity, ictal activity), instances of bursting behavior (during light sleep), jump phenomena (hysteresis), amplitude-dependent frequency behavior (the smaller the amplitude the higher the EEG frequency), and existence of frequency harmonics (e.g., under photic driving conditions). Therefore, the epileptogenic brain may embody elements of a nonlinear system. Several researchers have suggested that the EEG of the epileptic brain is a nonlinear signal with deterministic and possibly even chaotic properties [13, 20, 24, 30]. Lopes da Silva and colleagues proposed two scenarios of how a seizure might evolve [22]. First, a seizure could be caused by a sudden and abrupt state transition, in which case it would not be preceded by detectable dynamic changes in the EEG. This scenario would be conceivable for the initiation of seizures in primary generalized epilepsy. Second, this transition could be a gradual change or a cascade of changes in dynamics, which could in theory be detected and even predicted. In recent years, several studies have demonstrated experimental evidence that temporal lobe epileptic seizures are preceded by changes in dynamic properties of the EEG signal. Indeed, several nonlinear time-series analysis tools have yielded promising results in terms of their ability to reveal preictal dynamic changes essential for actual seizure anticipation. Therefore the hypothesis is that seizure is considered to be a transition from a chaotic state to an ordered state in the dynamic system. The theory is that patients may go through a preictal transition minutes to hours before a seizure occurs, and this so-called preictal state can therefore be characterized by the various dynamical measures described below.

The Lyapunov exponent is a nonlinear measure of the average rate of divergence/convergence of two neighboring trajectories in a dynamic system and is dependent on the sensitivity of initial conditions [25]. This dynamical measure has been employed toward identifying preictal changes in EEG datasets collected from humans undergoing evaluation with ECoG for epilepsy surgery [13,14]. Lyapunov exponents are estimated from the equation of motion describing the time evolution of a given dynamic system [1]. In the absence of the equation of motion describing the trajectory of the dynamic system, Lyapunov exponents are determined from observed scalar time-series data, x(t_n) = x(n δt), where δt, where δt is the sampling rate for the data acquisition. In this case, the goal is to generate a higher dimensional vector embedding of the scalar data x(t) that defines the state space from which the scalar EEG data is derived. Heuristically this is done by constructing a higher dimensional vector x_i from the data segment x(t) of given duration T, with τ defining the embedding delay used to construct a higher dimensional vector x from x(t) and d is the selected dimension of the embedding space and t_i is the time instance within the period [T - (d - 1)τ]. Geometrical theorem states that for an appropriate choice of d > d_min, x_i provides a faithful representation of the phase space for the dynamical systems from which the scalar time-series was derived [43]. A suitable practical choice for d, the embedding dimension can be derived from the false nearest neighbor algorithm. Furthermore, a suitable prescription for selecting the embedding delay τ is given in Abarbanel [1]. From x_i a most stable short term estimation of the largest Lyapunov exponent can be performed referred to as “short term largest Lyapunov exponent” (STL_max) [13]. The estimation L of STL_max is obtained where δx_ij(0) = x(t_i) − x(t_j) is the displacement vector, defined at time points t_i and t_j and δx_ij(Δt) = x(t_i + Δt) − x(t_j + Δt) is the same vector after time Δt. N is the total number of local STL_max that will be estimated within the time period T of the data segment, where T = NΔt + (d-1)τ. A decrease in the Lyapunov exponent indicates a transition to a more ordered state (Figure 3). This general approach has been employed toward identifying an EEG precursor by employing the Lyapunov exponents with varying success. By report, when the correct sites were chosen, the preictal transition was seen in >91% of the seizures [14]. However, these results have been refuted by utilizing a paradigmatic chaotic system [17, 18]. These studies suggest that both finite-time statistical fluctuations and noise can fundamentally hinder the predictive power of Lyapunov exponents computed from the EEG time-series. Nevertheless, efforts to statistically validate this method through a prospective, data out-of-sample, class 1 approach, are currently underway.

Figure 3.

Display of entrainment of two sites prior to a left onset temporal lobe seizure with the left temporal depth electrode (LTD3, black trace) within the seizure focus and the left scalp mandibular surface electrode (MN1, red trace) nearby. The short-term-maximum Lyapunov Exponent (STLmax) was calculated in overlapping 10.24 minutes windows. The convergence between the sites occurs approximately 25 minutes before the onset of the EEG seizure (B).

2.2 Multivariate Measures

In this section, we describe the multivariate linear and nonlinear methods most commonly used for seizure prediction. Multivariate time-series analyses, which are time-series analyses that consist of more than one observation recorded sequentially over time. Multivariate time-series analyses are used to assess the interaction between the different components of the system under consideration. Examples include records of stock prices and dividends, concentration of greenhouse gases and global temperature, and multichannel scalp EEG, invasive brain depth electrodes, or ECoG subdural brain recordings. Time again is an implicit variable.

Some of the most commonly used measures for EEG time series analyses will be discussed in the following sections. The linear and nonlinear univariate measures that operate on single channel recordings of EEG data will be reviewed first. Then some of the most commonly utilized multivariate measures that operate on more than a single channel of EEG data will be described. Then techniques representative of the different approaches used in seizure prediction will be discussed. Time frequency analysis, nonlinear dynamics, signal correlation (synchronization), and signal energy are very broad domains and could be examined in a number of ways. Here we review a subset of techniques, examine each, and discuss their underlying principles and uses for seizure prediction.

EEG signals can be conceptualized as a series of numerical values (voltages) over time and space (gathered from multiple electrodes), called a multivariate time series. The standard methods for time-series analysis (e.g., power analysis, linear orthogonal transforms, and parametric linear modeling) not only fail to detect the critical features of a time-series generated by an autonomous (no external input) nonlinear system, but may incorrectly depict the series as random noise [33]. In the case of a complex multidimensional, nonlinear system such as the EEG time-series, we do not know, or cannot measure, all of the relevant variables. This problem is not insurmountable and can be overcome mathematically. The variables in a dynamic system must be related over time. Thus, by analyzing individual variables (e.g., voltage) over time, we can also obtain information about the important dynamic features of the whole system. By analyzing more than one variable over time, we can follow the dynamics of the interactions of different parts of the system under investigation, creating a more complete picture of the system as a whole. Neuronal networks can generate numerous activities, some of which are characterized by rhythmic or quasi-rhythmic signals. These activities may be reflected in the corresponding EEG local field potentials. Essential features of these networks are that variables of the network have both a strong nonlinear range and complex interactions. Therefore, they are referred to as nonlinear systems with complex dynamics. Small changes in the control parameters and/or the initial conditions have profound effects on the characteristics of the dynamics. For this reason, real neuronal networks behave like nonlinear complex systems and can display changes between states such as small amplitude, quasi-random fluctuations and large amplitude, rhythmic oscillations. Such dynamic state transitions have been postulated to occur in the brain during the transition between interictal and epileptic seizure states [28].

Multivariate analysis assesses multiple channels of EEG simultaneously. This approach is used to consider the interactions between the channels and how they correlate rather than looking at channels individually. This is useful since there is often some interaction (e.g., synchronization) between different regions of the brain leading up to a seizure. Of the techniques discussed in the following sections, the simple synchronization measure and the lag synchronization measure are bivariate measures, which only consider two channels at a time and define how those two channels correlate. Another method which employed nonlinear deterministic dynamics assumes that the generation of a seizure follows nonlinear deterministic stochastic dynamics by comparing interictal with ictal epileptogenetic zones, respectively [2, 16, 30]. For instance, when two different systems are identical except for a shift by some time lag, τ, they are said to be lag synchronized [38]. Lag synchronization has been employed and results indicate a preseizure state based on evidence on a decrease in synchronization in human epileptic ECoG recordings [29]. In this study, the normalized cross correlation function was used to calculate the similarity of two signals. Results yielded a value between 0 and 1, indicating the similarity between two signals. When the normalized cross correlation function produced a value close to 1 for a given τ, then the signals were considered to be lag synchronized by a phase of τ.

The remaining metrics take all of the EEG channels into account simultaneously. This is achieved by using a dimensionality reduction technique called principal component analysis (PCA). PCA takes a dataset in a multidimensional space, finds the most prominent dimensions in that dataset, and then linearly transforms the original dataset to a lower dimensional space using the most prominent dimensions from the original dataset. PCA may be used as an early seizure detection/prediction technique itself [28]. It is also used as a screening tool to extract the most important dimensions from a data matrix containing pairwise correlation information for all EEG channels, as is the case with the correlation structure.

2.2.1 Simple synchronization measure

It is well known that areas of the brain synchronize with one other during certain events. During seizures abnormally large amounts of highly synchronous activity are seen, either focally or in a more generalized pattern. It has been suggested this activity may begin hours before the initiation of a seizure. The autoregressive measure of synchrony is derived from a multichannel model of the EEG where each point is described as a linear combination of the previous values from all selected channels. Quiroga and colleagues suggested a multivariate method to calculate the synchronization between two EEG channels [45]. This method first defines certain “events” for a pair of signals. Once the “events” have been defined, this method then counts the number of times the “events” in the two signals occur within a specified amount of time (τ) of each other [45]. The total count is then divided by a normalizing term equivalent to the maximum number of events that could be synchronized in the signals. For two discrete EEG channels x_i and y_i, i = 1, … N, where N is the number of points making up the EEG signal for the segment considered, event times are defined as $t_i^x$ and $t_i^y$ (i = 1, …, m_x; j = 1, …, m_y). Any change can be defined as an event, however, events should be chosen so that the events appear simultaneously across the signals when they are synchronized. An event is defined as a local maximum over a range of K values [45]. In other words, the i^th point in signal x would be an event if x_i > x_{i ± k}, k = 1, …, K. τ, which is the time within which events from x and y must occur in order to be considered synchronized, must be less than half of the minimum inter-event distance. Otherwise, a single event in one signal could be considered to be synchronized with two different events in the other signal. Finally, the number of events in x that appear shortly (within a defined time, τ) after an event in y is counted. Similarly the number of events in y that appear shortly after an event in x can also be defined. This would be denoted c^τ(y|x). With these two values, the synchronization measure Q_τ can be calculated as follows:

$$Q_{\tau }=\frac{c^{\tau }(x\mid y)+c^{\tau }(y\mid x)}{\sqrt{m_x{m}_y}}$$

The metric is normalized so that 0 ≤ Q_τ ≤ 1and Q_τ is 1 if and only if x and y are fully synchronized (always have corresponding events within τ). Although this measure seems highly intuitive for prediction of seizures, results indicate that synchronization measures do not identify preictal EEG changes unless information about postictal changes in closely clustered seizures was available [15].

2.2.2 Correlation Structure

Another method of seizure analysis is to evaluate the correlation over all of the recorded EEG channels. First, a correlation is defined over the given channels. In order to define the correlation matrix, a segment of the EEG signal is assessed for a given window of specified time. The EEG signal is then normalized by channels within this time window. Given m channels, the correlation matrix, C is defined as $C_{ij}=\frac{1}{w_j}{\sum }_{\mathit{tew}}{\mathit{EEG}}_i\left(t\right)\cdot {\mathit{EEG}}_j\left(t\right)$ where w_l specifies the length of the given window w and EEG_i is the i^th channel. EEG_i has also been normalized to have 0 mean and a specified unit variance [22]. C_ij will yield a value of 0 when EEG_i and EEG_j are uncorrelated, a value of 1 when they are perfectly correlated, and a value of −1 when they are perfectly anti-correlated. The correlation matrix is symmetrical since C_ij = C_ji. In addition, C_ii = 1 for all values of i since any signal will be perfectly correlated with itself. It follows that the trace of the matrix (Σ C_ii) will always equal the number of channels (m).

The simplified representation of the correlation matrix is based on the eigen values of the matrix. The eigenvalues determine which dimensions of the original matrix have the highest correlation. When the eigenvalues (λ₁, λ₂, …, λ_m) are sorted so that λ₁ ≤ λ₂ ≤ … ≤ λ_max, they can then be used to produce a spectrum of the correlation matrix C [40]. This spectrum is sorted by intensity of correlation and used to track how the dynamics of all m EEG channels are affected when a seizure occurs.

2.2.3 Phase Correlation

Measurement of phase synchrony can be based on spectral coherence. These methods include amplitude and phase information, as well as detection of maximal values, after filtering. Weakly coupled nonlinear equations are phase locked, but the amplitudes vary chaotically and are mostly uncorrelated. Tass [44] proposes using two indices to characterize the strength of synchronization, one based on Shannon entropy and one based on conditional probability. Therefore, the degree of deviation of the relative phase distribution from a uniform phase distribution can be quantified. The previously described techniques approach the problem of detecting and predicting seizures from a traditional time-series prediction perspective. In all such cases, the EEG signal is merely signal that has predictive content embedded in it. The goal is to transform the signal using various mathematical techniques to reveal this predictive content. The fact that an EEG signal is generated in a particular biological context, and is representative of a particular physical aspect of the system, is immaterial in these techniques.

2.2.4 Autoregressive measures of synchrony

The autoregressive measure of synchrony is derived from a multichannel model of the EEG. In this model, each point is described as a linear combination of the previous values from all selected channels. The best fit of this model to the EEG shows how good the model is fitted for each EEG time-series. In the setting of a higher degree of synchrony between EEG channels, a better fit is thought to occur [15]. However, with use of this measure, no significant preictal changes were reported unless the postictal changes were also taken into account [15].

2.2.5 Short-term largest Lyapunov exponent T-index

STLmax measures were measured across multiple EEG time-series channels and a so called dynamical entrainment was observed by using the T-index derived from a paired t-test for comparison of means. The authors report a good predictive power with a relatively low false prediction rate. The dynamical entrainment is defined as a measure indicating `entrainment between critical brain recording electrode sites [13]. However, these findings have not been subjected to class 1 validation [32]. Also, as mentioned earlier, finite-time statistical fluctuations and noise may fundamentally confound the EEG time-series derived Lyapunov exponents predictive power [17, 18].

2.2.6 Phase synchronization

The degree to which two signals are phase locked during a time period is called phase synchronization. In intracranial EEG data, this measure has shown its power to discriminate transient synchronization. During the interictal period, measures of mean phase coherence indicate that the level of synchronization is pathologically increased [29]. Specific states of brain synchronization have been identified both in advance of an impending seizure and around the epileptogenic zone [20].

3. Conclusion

Epilepsy is a dynamic disease, characterized by numerous types of seizures, syndromes and presentations. This has led to a wide array of ictal and interictal EEG records to analyze. To understand these signals, investigators have begun employing various signal processing techniques, including both univariate and multivariate tools. Even with these tools, the richness of the datasets has meant that these techniques have had limited success in predicting seizures. These limitations may in part stem from our lack of understanding about the mechanism leading to seizures. In many cases, the initial success of a particular measure has been difficult to replicate because the first set of trials was the victim of overtraining. Thus far, no measure has been able to reliably and repeatedly predict seizures with a high level of specificity and sensitivity. While the lines between seizure prediction, early detection, and detection can sometimes blur, it is important to note they do comprise three distinct and different questions. Seizure prediction seeks to tease out minute changes in the preictal EEG signal. The tools that are able to detect one of these minor fluctuations often fall short when trying to replicate their success in even slightly altered conditions. When coupled with the proper type of therapeutic intervention (e.g., chemical stimulation or directed pharmacological delivery) seizure warning algorithms could usher in a new era of epilepsy treatment. The various techniques presented in this chapter need to be continually studied, refined, and combined. They should be tested on standard datasets in order for their results to be accurately compared. After full development, techniques should be tested on out-of-sample datasets to determine their effectiveness in a clinical setting.