Extensive linkage disequilibrium and parallel adaptive divergence across threespine stickleback genomes

Abstract

Population genomic studies are beginning to provide a more comprehensive view of dynamic genome-scale processes in evolution. Patterns of genomic architecture, such as genomic islands of increased divergence, may be important for adaptive population differentiation and speciation. We used next-generation sequencing data to examine the patterns of local and long-distance linkage disequilibrium (LD) across oceanic and freshwater populations of threespine stickleback, a useful model for studies of evolution and speciation. We looked for associations between LD and signatures of divergent selection, and assessed the role of recombination rate variation in generating LD patterns. As predicted under the traditional biogeographic model of unidirectional gene flow from ancestral oceanic to derived freshwater stickleback populations, we found extensive local and long-distance LD in fresh water. Surprisingly, oceanic populations showed similar patterns of elevated LD, notably between large genomic regions previously implicated in adaptation to fresh water. These results support an alternative biogeographic model for the stickleback radiation, one of a metapopulation with appreciable bi-directional gene flow combined with strong divergent selection between oceanic and freshwater populations. As predicted by theory, these processes can maintain LD within and among genomic islands of divergence. These findings suggest that the genomic architecture in oceanic stickleback populations may provide a mechanism for the rapid re-assembly and evolution of multi-locus genotypes in newly colonized freshwater habitats, and may help explain genetic mapping of parallel phenotypic variation to similar loci across independent freshwater populations.

1. Introduction

The field of evolutionary genetics has been revolutionized over the past 40 years by a better understanding of proximate genetic mechanisms, and an influx of molecular data. Population genetic studies can now be performed with increasing precision using a battery of genetic markers, and genetic variance in quantitative traits can now be linked to genomic regions using linkage mapping and genome-wide association studies. Despite this advance, evolutionary genetics has largely focused on one or a small number of discrete loci, much as it has since the Modern Synthesis in the 1930s [1,2]. Relatively few loci are typically used to infer demographic parameters or map complex traits in natural populations of most organisms.

However, genes are not islands, and exist as members of genomic communities united by strong interactions. Here, we consider the genomic architecture of evolving populations, which we define as the genome-wide distribution and covariation of loci and genomic regions important for adaptation and reproductive isolation. Genetic covariation quantified by linkage disequilibrium (LD) among loci can be genomically localized or stretched across chromosomes [3–5]. Evolutionary genetics has long recognized the potential for genomic architecture to alter evolutionary trajectories. Many models of speciation include an important role for LD among loci [6–8], such as alleles for male traits and female preferences in pre-zygotic models [9,10] or Bateson–Dobzhansky–Mueller incompatibility loci in post-zygotic models [11,12]. Adaptation may be facilitated by co-adapted gene complexes, which are multi-locus genotypes favoured by selection [13–19].

What conditions could maintain these genomic architecture patterns? Early empirical work was limited, although protein electrophoresis studies showed little LD in natural populations [20,21], suggesting that genomic architecture would be unimportant for evolution except in rare cases. Furthermore, theoretical work showed that in single randomly mating populations, recombination is very effective at breaking down LD patterns unless loci are tightly linked and selection is very strong [22,23]. On the other hand, proximate genetic mechanisms, such as variation in recombination rates or segregating chromosomal inversions, can facilitate local LD across neighbouring loci [14,24–28]. In addition, theoretical work predicts that if selection maintains differences in allele frequencies at two or more loci in different populations, gene flow between populations will result in significant LD at both local and more long-distance scales [29–33]. With the technological advent of modern population genomics [34,35], in which dozens of individuals can be assayed at thousands of genetic markers, we can now resolve these issues empirically by directly studying genomic architecture at a fine scale in natural populations [36–40].

Recent population genomic studies of adaptive radiations [41–47] and incipient speciation [48] in non-model organisms have already shown that genomes are much more dynamic and structured than was expected based upon previous theory, and that significant heterogeneity in genetic divergence and LD across genomes may be important for speciation [49–51]. In particular, ‘genomic islands of divergence’, which are regions that exhibit significantly greater divergence than expected under neutrality and potentially cover multiple genes [28,50,52–55], have been identified in a number of organisms. Genomic islands can promote speciation by causing the non-random association of alleles that might be important for both pre- and post-zygotic isolation [53]. To explain this type of genomic architecture, models of selective sweeps via hitchhiking [56–58] have been modified for metapopulation scenarios in which differential selection is occurring in alternative environments, with appreciable gene flow among the populations [54,59]. This process has been labelled ‘divergence hitchhiking’ to differentiate it from hitchhiking via single selective sweeps [28].

To understand the importance of genomic architecture for adaptive divergence and speciation, we must define the patterns of LD across natural populations that span the species boundary [60]. An evolutionary model system for this work is the threespine stickleback (Gasterosteus aculeatus). Across coastal regions of the Northern Hemisphere, oceanic stickleback have repeatedly given rise to freshwater populations that have diverged in numerous traits. In some cases, this diversification has led to the formation of new species [61–65]. These speciation events in stickleback correspond to significant environmental differences, such as salinity and temperature variation between ocean and freshwater habitats, or benthic and limnetic niches in fresh water [63,66–75]. Research has progressed rapidly in defining the genetic basis of some evolving traits in freshwater stickleback [62,76–78], including variation in armour, coloration and craniofacial attributes, among others [79–84]. In laboratory crosses, genetic variation in these traits has been attributed to a relatively small number of genomic regions [80,81,84–89]. Across independently evolved populations, the same genomic regions [90], major loci [84] and in some cases the same alleles [80], have been associated with similar derived phenotypes, implying that independent evolution at the population level repeatedly uses the same alleles from the standing genetic variation [89–93].

These recent findings about the genetic basis of evolving stickleback traits suggest that the genomic architecture of oceanic populations may influence adaptive trajectories and speciation [90,94–96]. The traditional ‘source-sink’ model for stickleback divergence has been represented as a bottlebrush phylogeny, in which large, genetically diverse and panmictic oceanic populations provide the raw material for evolution in ephemeral freshwater populations through unidirectional gene flow from oceanic to freshwater populations [97]. An alternative model, suggested by recent results, is of a metapopulation with significant bidirectional gene flow, in which alleles for adaptive divergence may persist longer than the populations themselves [92]. Importantly, the bottlebrush and metapopulation scenarios will lead to very different genomic architectures. Under the bottlebrush phylogeny model, the expectation is that LD should be low in the large, panmictic oceanic populations, which are less subject to recent selective sweeps and environmental shifts. In addition, LD should be more extensive in freshwater populations owing to selective sweeps in recently colonized habitats [5,21–23,98–100]. In contrast, the metapopulation model predicts significant LD in both freshwater and oceanic populations. Differential selection between the two environments would increase genetic differentiation at selected loci, while bidirectional gene flow would result in short-term LD among these loci in each population and reduce differentiation across the rest of the genome [29–33]. In both scenarios, both local and long-distance LD might be augmented by a combination of population structure established in allopatry, segregating chromosomal rearrangements and epistatic selection [5].

To assess the genomic basis of parallel adaptation, we recently performed a genome-wide scan of independently derived stickleback populations in Alaska using restriction-site associated DNA (RAD) sequencing [90]. We found numerous genomic regions exhibiting parallel signatures of selection, with a surprisingly large number of regions in which the alleles were clearly identical by descent. The goal of the present paper is to describe the patterns of local and long-distance LD in both freshwater and oceanic populations of stickleback, and to associate it with patterns of recombination rate variation across the genome. As expected, we find significant patterns of LD in freshwater populations. Surprisingly, we also find significant local and long-distance LD in the oceanic populations, even though no differentiation exists across oceanic populations for most of the neutral regions of the genome. Our data support a metapopulation model of stickleback adaptive radiation, rather than the bottlebrush phylogeny model. Our findings suggest that genomic architecture in the form of LD, maintained in a metapopulation with divergent selection, may play a critical role in facilitating parallel adaptation. More broadly, our findings highlight the use of population genomic analyses of non-model species, even those as well studied as stickleback, for understanding the origin of species better.

2. Methods

(a). Linkage disequilibrium in natural populations

To assess LD in divergent natural populations, we re-analysed data on five populations of threespine stickleback in Alaska from Hohenlohe et al. [90]. These five populations include three freshwater (Bear Paw Lake (BP), Boot Lake (BL) and Mud Lake (ML)), representing three independent colonizations of freshwater habitats, and two oceanic habitats (Rabbit Slough (RS) and Resurrection Bay (RB)) [90]. Twenty individuals were collected from each population, RAD-sequenced and genotyped at all single-nucleotide polymorphisms (SNPs; for methodological details see earlier studies [87,90]). Because genetic differentiation is very low between the two oceanic populations (F_ST = 0.0076, with no genomic regions of substantial differentiation [90], we combined these two populations into a single oceanic sample for several of the analyses. To allow comparison with data from the laboratory intercross (described below), we focus primarily on comparisons between this combined oceanic population and BL, but full analyses on all five individual populations are discussed and presented as electronic supplementary material.

We filtered the list of SNPs to bi-allelic loci with minor allele frequency ≥ 0.1 across all populations combined, resulting in 2433 SNPs spread across the genome. Of these, 2241 were on the 21 assembled linkage groups (LGs), ranging from 57 (LG V) to 198 (LG IV) SNPs per LG, with an average density of 1 per 178 kb. We further removed any individuals that were genotyped at fewer than 67 per cent of loci, in order to provide high confidence in the inference of haplotype phase. This resulted in variable sample size of individuals across populations (BP, 12; BL, 12; ML, 20; RB, 18; RS, 14). Because these data are drawn from short-read next-generation sequencing, they consist of diploid genotypes at each locus for each individual with no direct haplotype phase information. We inferred haplotype phase and imputed missing genotypes using the program fastphase [101]. This technique uses a hidden Markov model of local haplotype assignment along each chromosome, allowing for either a block-like or gradually decaying LD structure.

To assess haplotype structure, we calculated two statistics that reflect the decay of LD along the length of each chromosome. Both of these measures are based on extended haplotype homozygosity (EHH; [102]). At each distance x from a given locus, EHH estimates the probability that any two randomly chosen haplotypes in the population are identical over the entire distance x. The first measure that we used, integrated haplotype homozygosity (iHH; [103]), is the integral under the EHH curve for each SNP; thus each locus has its own iHH value, and iHH can be plotted as a continuous distribution along the genome. This measure is often used to detect recent selective sweeps that increase the local extent of LD around a selected locus [35]. The second measure of LD, cross-population EHH (XP-EHH; [98]), is the natural log of the ratio between iHH from two different populations at each locus. Genomic regions that deviate from the expected value of XP-EHH = 0 may reflect a recent selective sweep in one or both populations. Using the phased SNP data from above, we calculated iHH within each of the five populations and the combined oceanic population, and we calculated XP-EHH between each freshwater population and the combined oceanic population.

We examined patterns of long-distance LD using the pair-wise measure D′. Within and between LGs, we constructed matrices of D′ values for each pair-wise SNP comparison within each population. The statistic D′ is the non-random association D between alleles at the two loci, normalized by the maximum value that D could take given the allele frequencies [5]. D′ ranges from 0 (no association) to 1 (complete LD). To assess the significance of long-distance LD, we compared elevated values against the empirical genome-wide distribution of D′ values between different LGs within each population. Observed patterns of long-distance LD were consistent between D and D′, so that we focus our discussion below on D′.

(b). Genomic patterns of recombination

We examined rates of recombination along the stickleback genome in an F₂ cross between the freshwater BL population and the oceanic RS population. A single individual was taken from two different laboratory lines that were originally derived from each population, but have been maintained in the laboratory for several generations, to make a parental cross. Two F₁ full-sib individuals were crossed to create an F₂ family. Because blocks of LD were expected to be relatively large, we did not require the density of markers typically produced by traditional RAD sequencing. Instead, we used a modification of RAD sequencing to genotype 87 F₂ individuals, along with the parental and F₁ generations. Genomic DNA from each individual was digested with both SbfI and EcoRI restriction endonucleases and the resulting fragments were ligated to a unique, barcoded adapter with an overhang complementary to SbfI and a second adapter with an overhang complementary to EcoRI. Thirty-six F₂ samples were ligated to SbfI adapters identical to those used by Hohenlohe et al. [90]. The remaining F₂ and the F₁ and parental samples were ligated at a later time to shortened SbfI adapters with 6 nucleotide barcodes constituted from these oligos:

P1 Top: ACACTCTTTCCCTACACGACGCTCTTCCGATCTxxxxxxTGC*A

P1 Bottom: 5Phos/xxxxxxAGATCGGAAGAGCGTCGTGTAGGGAAAGAGTGT

where x denotes barcode nucleotides.

The modified P1 adapters require the use of a long PCR primer:

5′-AATGATACGGCGACCACCGAGATCTACACTCTTTCCCTACACGACGCTCTTCCGATC*T-3

The second (P2) adapter was similar to that used by Hohenlohe et al. [90] except that it was modified to have an EcoRI overhang instead of a T overhang. The modified P2 was assembled from these oligos:

Top: 5′Phos/A*ATTAGATCGGAAGAGCGGTTCAGCAGGAATGCCGAGACCGATCAGAACAA3′

Bottom: 5′CAAGCAGAAGACGGCATACGAGATCGGTCTCGGCATTCCTGCTGAACCGCTCTTCCGATC*T3′.

The differences among adapters are not functionally significant, and are due to slight improvements to the protocol that occurred throughout the course of the data generation. After ligation, DNA was multiplexed in five batches containing 12, 12, 12, 15 and 36 samples each (except the DNA of F₁ parents and P₀ grandparents, which were each treated separately), and size-fractionated by gel electrophoresis. A size fraction was selected that contained only the subset of the genome for which an SbfI and an EcoRI cut site lie within 470–670 bp of each other.

The libraries for these 91 individually barcoded fish were run in three single-end sequencing lanes on an Illumina Genome Analyzer II. We derived a reliable set of genotyped markers by applying a number of conservative filters to putative SNPs. First, we aligned raw reads to the stickleback genome using bowtie [104], removing any reads that mapped with equal numbers of mismatches to multiple genomic locations. We removed tags that were predicted to be duplicates within four mismatches in the 60 bp read length based on the observed RAD sites in the stickleback reference genome sequence. Within each individual, we removed data for all tags with less than 30X depth of coverage (although results were nearly identical when this threshold was reduced to 5X), and we considered only RAD tags that passed all of these filters in at least 20 individuals. At each nucleotide position in each individual, we calculated the likelihood of each of the 10 possible unordered diploid genotypes using the multinomial sampling model described earlier [90], with the addition of a prior distribution on the sequencing error rate, ε, which was uniform from 0.001 to 0.01. This prior distribution is based upon our experience of average per-nucleotide error rate produced by our Illumina sequencer.

Next-generation sequencing techniques involve unavoidable sampling variance across alleles, loci and individuals, in addition to sequencing and PCR errors, and thus wide variation in the uncertainty of each genotype call. To account for these factors, we applied a hidden Markov model to assign a probability of parental ancestry to each SNP marker in each F₂ individual [105–107]. We assembled a list of 584 markers for which the maximum-likelihood genotype in each individual (as described above) produced a minor allele frequency of at least 0.1. At each of these markers, we modelled the emission probabilities for the three possible ancestral states (i.e. homozygous BL, heterozygous or homozygous RS) by considering all possible genotype combinations among the parents, F₁, and the focal F₂ individual. The composite likelihood of each genotype combination was calculated by multiplying the likelihoods of each genotype in a combination across all five individuals. The majority of genotype combinations are uninformative or impossible; likelihoods of these combinations contribute equally to all states [105,106]. We considered informative genotype combinations only to be those that were fixed for alternative alleles in the two parents, and the composite likelihoods of these genotype combinations were summed to calculate the emission probability for each ancestry state at each marker. We used the re-scaling technique of Rabiner [106] to maintain computational precision. We assumed the transition probability t to be constant across the genome and found its maximum-likelihood value over the whole dataset (t = 4.4 × 10⁻⁸, equivalent to 4.4 cM Mb⁻¹); the likelihood function of t was relatively smooth and unimodal. To calculate recombination rates below, we assigned one of the three ancestry states to a given locus if its marginal posterior probability exceeded 0.8.

We modelled recombination in a Bayesian framework. We set as a prior distribution on recombination rate r a beta distribution with parameters α = β= 0.5, which is a non-informative prior, scaled to the recombination rate r across 1 Mb. We then estimated cM Mb⁻¹ in a 100 kb sliding window across each LG, using the simple Morgan mapping function, d = r. Within each window, the number of opportunities for recombination (n) is twice the number of individuals genotyped over the window. The observed number of recombination events is k. If a marker pair exhibiting a recombination event spanned multiple 100 kb windows, fractional values of k were assigned proportionally to the physical distance between the markers that overlapped each window. The posterior estimate for recombination rate is thus 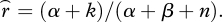We calculated the 95 per cent Bayesian credible interval by taking the 2.5 and 97.5 per cent quantiles of a beta distribution with parameters (α + k) and (β + n − k).

3. Results

(a). Haplotype structure

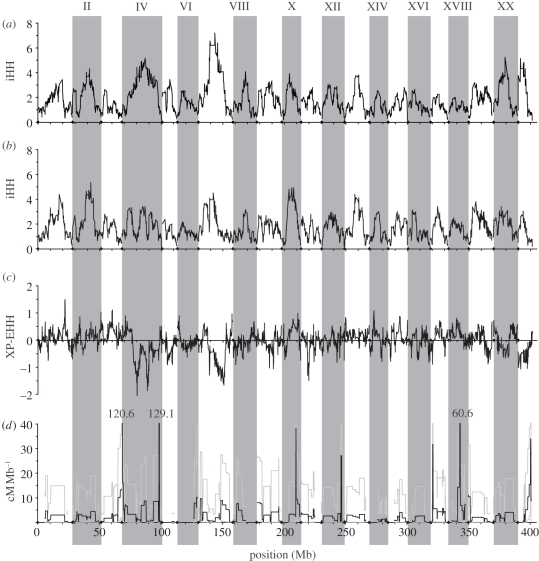
The extent of haplotype structure and decay of LD varies across the stickleback genome in both the oceanic and freshwater populations (figure 1a,b; electronic supplementary material, figure S1). Most LGs exhibit declining iHH values towards the chromosome ends, and the oceanic and freshwater populations correspond in many regions of elevated iHH (e.g. LG I). There is some correspondence between previously identified significant peaks of population differentiation, inferred to be caused by divergent selection between oceanic and freshwater populations, and differences between the two populations in extent of LD. For instance, we [90] previously identified peaks of significant freshwater–oceanic differentiation on LGs I, IV, VII and XI. The largest deviations of XP-EHH from its expected neutral value of 0 lie precisely at these genomic regions (figure 1c; electronic supplementary material, figure S2). However, for all but LG I, the trend is in the opposite direction from the expectation. Negative values of XP-EHH on LGs IV, VII and XI indicate greater extent of LD in the ocean than in the freshwater population, contrary to the expectation that selective sweeps should be more recent and leave a stronger signature of LD in the freshwater populations.

Figure 1.

Genomic distributions of haplotype structure and recombination rates. Vertical grey shading and Roman numerals at the top indicate the 21 linkage groups (LGs; unassembled scaffolds not shown). (a) Integrated haplotype homozygosity (iHH), a measure of the decay of LD from a locus, within the combined oceanic population. Units of iHH are megabases (integral under the EHH curve; see text for details). (b) iHH in the freshwater population Boot Lake (BL). (c) Cross-population extended haplotype homozygosity (XP-EHH) comparing the oceanic with BL populations. Positive values indicate larger values of LD in BL, and negative values indicate larger values in the ocean. (d) Recombination rate estimated from an oceanic by freshwater F₂ cross using a hidden Markov model. Grey lines indicate upper and lower boundaries of the Bayesian 95 per cent credible interval. Three apparent peaks of recombination greater than 40 cM Mb⁻¹, most likely the result of chromosomal rearrangements relative to the reference genome sequence, have been truncated in this plot; the height of these peaks in cM Mb⁻¹ is given above each one.

(b). Recombination rates

We estimated recombination rate from an F₂ laboratory cross derived from two of the same stickleback populations (RS and BL). The total genetic map size of the genome (not including unassembled scaffolds) is 1013 cM, for a genome-wide average of 2.53 cM Mb⁻¹, which aligns well with previously published estimates of recombination rates in stickleback [88]. The distribution of recombination rates across the stickleback genome exhibits large regions of background levels of recombination (approx. 1–4 cM Mb⁻¹), punctuated by several narrow regions of very high apparent recombination (figure 1d). In some cases, correspondence can be observed between apparent recombination hotspots and regions of reduced iHH in natural populations (e.g. on LGs XVII, XXI). It is likely that many of the large peaks actually represent chromosomal rearrangements relative to the reference genome sequence, but this hypothesis remains to be tested. Given our stringent filtering and the statistical approach of the hidden Markov model, which requires high confidence in a series of genotype calls to infer a transition between ancestral states, these cannot be easily attributed to genotyping error or misalignment to the reference genome.

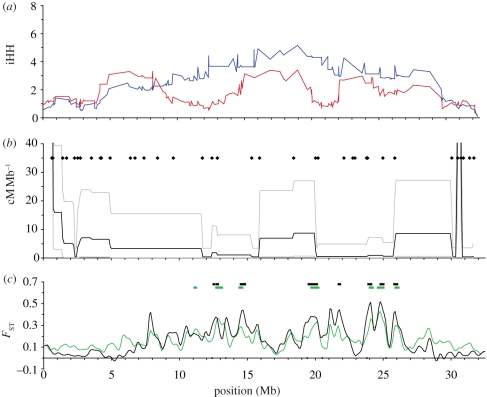
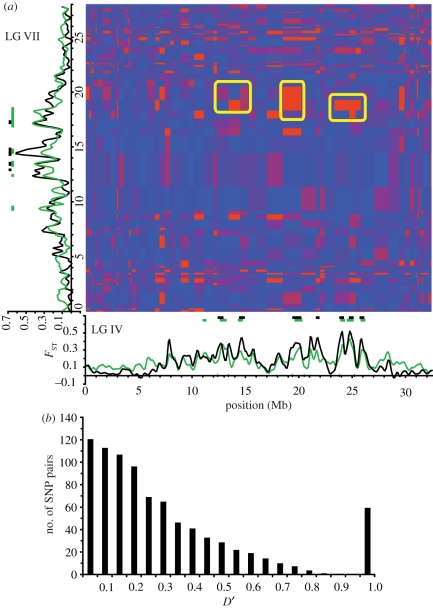
The relationships among recombination rate, LD, and differentiation between ocean and freshwater populations can be observed in more detail on two LGs: IV and VII (figures 2 and 3). On LG IV, the oceanic population is characterized by a single region of elevated LD covering nearly the entire chromosome (figure 2a). In contrast, the freshwater population exhibits three broad regions of elevated LD, broken by regions of reduced iHH. These areas of lower LD do not appear to be the result of recombination rate variation, as estimated in our laboratory cross between oceanic and freshwater parents (figure 2b). However, regions of reduced recombination on LG IV do align with broad, previously identified regions implicated in parallel adaptation, one at approximately 13 Mb and a pair at approximately 20 Mb and 24.5 Mb (figure 2c) [87,90,108]. Again, contrary to expectations from a recent selective sweep in fresh water, LD is reduced rather than elevated at these points in the freshwater compared with the oceanic population.

Figure 2.

Haplotype structure, recombination and differentiation along LG IV. (a) iHH in the oceanic (blue) and BL (red) populations. (b) Recombination rate in an F₂ cross. Black dots represent the location of markers used. Grey lines indicate the upper and lower boundaries of a Bayesian 95 per cent credible interval about the estimate. Two extreme peaks in apparent recombination rate are truncated (see figure 1). (c) Population differentiation between BL and the combined oceanic population (black), and between all three freshwater populations and the oceanic population (green). Bars above the plot indicate regions of p < 10⁻⁵ bootstrap significance (see Hohenlohe et al. [90] for details).

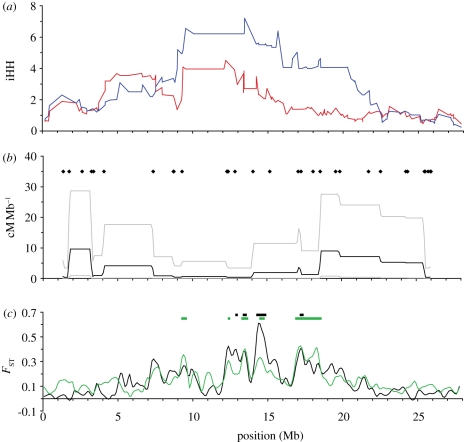
Figure 3.

Haplotype structure, recombination and differentiation along LG VII. All details as in figure 2.

On LG VII, again the extent of LD is higher in the oceanic than in the freshwater population (figure 3a). In this case, a broad region of reduced recombination rate in the centre of the chromosome corresponds both to a region of elevated LD within both freshwater and oceanic populations (figure 3b), and also to a cluster of peaks of population differentiation between them (figure 3c).

We tested whether the relationship between reduced recombination rate and elevated population differentiation was a genome-wide pattern by correlating recombination rate in 100 kb windows with F_ST averaged across roughly equally sized kernel smoothing windows [90]. Across the entire genome, there is a slight but statistically significant negative correlation between recombination rate and population differentiation (electronic supplementary material, figure S3). This holds both for differentiation between the focal populations BL and RS (ρ = −0.090; p < 10⁻⁵) and overall differentiation between oceanic and freshwater populations (ρ = −0.065; p < 10⁻⁴). Such a relationship between population divergence and recombination rate, particularly in the context of chromosomal inversion polymorphisms that can reduce recombination, has been predicted by theory and observed in other taxa [109,110].

(c). Long-distance linkage disequilibrium

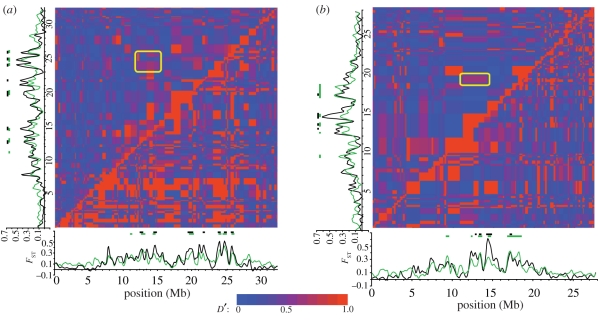
The pattern of long-distance LD on LG IV in the freshwater population reflects the three broad regions of elevated iHH (figure 4a). These broad regions also exhibit relatively high levels of long-distance LD across the chromosome, so that much of LG IV in the freshwater population appears locked in association by LD. By contrast, long-distance LD is generally much lower on LG IV in the oceanic population (figure 4a).

Figure 4.

Long-distance LD and population differentiation on (a) LG IV and (b) LG VII. Pair-wise LD among loci, measured as D′, estimated in the combined oceanic (above the diagonal) and freshwater Boot Lake (below the diagonal) populations. The yellow rectangle highlights a region of potential long-distance LD between two genomic regions previously implicated in adaptation to fresh water. Differentiation between oceanic and freshwater populations, adapted from Hohenlohe et al. [90], is shown along the bottom and side. The black line compares the oceanic populations with BL, and the green line compares the oceanic populations with three independently derived freshwater populations including BL. Bars above the plot indicate regions of p < 10⁻⁵ bootstrap significance (see Hohenlohe et al. [90] for details). A key to the colour scheme for D′ is shown at the bottom.

Nonetheless, there is evidence for LD in the oceanic population between genomic regions previously linked to divergent selection at approximately 13 Mb and at approximately 24–25 Mb (figure 4a; electronic supplementary material, figure S4a). At the peak of this pair-wise association, D′ = 0.61. The total genetic distance between these genomic regions estimated from the recombination data above is 36.2 cM, approaching free recombination. The putative adaptive region centred at approximately 13 Mb also exhibits complete long-distance LD (D′ = 1.0) with another region at approximately 16–17.5 Mb, which actually exhibits low levels of population differentiation between ocean and fresh water. Genetic distance is just 3.3 cM between these regions.

On LG VII, both the oceanic and freshwater populations exhibit scattered pairs of chromosomal regions that are associated in LD (figure 4b; electronic supplementary material, figure S4b). In both populations, the two previously identified major peaks of adaptive differentiation at approximately 14–15 Mb and at approximately 16–18 Mb appear in LD: D′ = 0.60 in the ocean, and D′ = 1.0 for one pair of SNPs in fresh water. Genetic distance between these regions is 5.4 cM. As with LG IV, however, several pairs of widely spaced loci that have not been implicated in population differentiation also show long-distance LD. Thus, distant genomic islands, whether or not they play a role in adaptive divergence, are associated with each other in LD.

Finally, and perhaps most surprisingly, there is evidence for LD among adaptive genomic regions across chromosomes. In the combined oceanic population, all three previously identified peaks of population differentiation on LG IV show high LD (D′ = 1.0) with a region including, or just adjacent to, the second peak on LG VII (figure 5a). These regions of inter-chromosome LD are also evident within each of the two oceanic populations considered separately (electronic supplementary material, figure S5). Roughly, 6 per cent of all between-chromosome SNP pairs show a long-distance LD of D′ = 1.0 (figure 5b).

Figure 5.

(a) Long-distance LD between LGs IV and VII in the combined oceanic population. Plots of population differentiation (F_ST) on the left and the bottom are as in figure 4 (adapted from Hohenlohe et al. [90]). Three areas of pair-wise LD between previously identified adaptive genomic regions are highlighted by yellow rectangles. (b) Histogram of D′ values for all inter-chromosomal pairs of SNPs in the combined oceanic population. Labels on the horizontal axis represent the upper limit of bins of width 0.05. The three areas highlighted in (a) occupy the far right bin at D′ = 1.0.

4. Discussion

(a). Extensive linkage disequilibrium supports a metapopulation model of the stickleback adaptive radiation

Using a novel application of next-generation sequencing technology (RAD-seq [111]), we have produced the first systematic description of LD patterns across the threespine stickleback genome in both ancestral oceanic and derived freshwater populations. High levels of both local and long-distance LD exist in populations from each habitat. As is expected under strong directional selection after invasion by colonists from the ocean, the freshwater populations do show extensive LD. The traditional conceptual model for stickleback evolution is one of a bottlebrush phylogeny [97], which represents a stable core of large and genetically diverse oceanic populations surrounded by short branches of freshwater populations. In this model, gene flow is unidirectional from oceanic to freshwater populations, which quickly diverge before going extinct. Because of their ephemeral nature, the freshwater populations have traditionally been thought to matter little for the long-term evolution of the stickleback system.

Surprisingly, we found that some blocks of LD were larger and more pronounced in the oceanic populations than in fresh water. This result is unexpected under the bottlebrush model because no evidence of population structure or non-random mating exists for the ocean populations, and they also have very large effective population sizes (N_e), both of which should lead to low levels of LD. One hypothesis for local intra-chromosomal LD is that genomic rearrangements are segregating in the oceanic populations at high enough frequencies to cause the observed LD patterns [25,26]. In addition, gene flow from freshwater to oceanic populations may explain patterns of LD across chromosomes as a result of admixture, and also may be a driving factor in the evolution of the stickleback system. Although individually each freshwater population may be relatively insignificant as a source of alleles, in the aggregate, the thousands of freshwater populations may be a much more important source of genetic variation in the ocean than previously envisioned. This will be particularly true if the same genotypes are selected independently in different freshwater populations providing a large ‘meta-pool’ of alleles for gene flow back into the ocean.

The bottlebrush model was already endangered by the finding that a single clade of alleles at one locus (Eda) was linked to loss of lateral plates in most (but not all) freshwater populations across the Northern Hemisphere [80]. In light of this result, Schluter & Conte [92] proposed the ‘transporter hypothesis’ that freshwater alleles return to the ocean and persist at low frequency, and are then selected to high frequency in newly colonized freshwater habitats, reassembling multi-locus freshwater genotypes. Independent selection on low-frequency alleles at many different loci alone may facilitate such a rapid, parallel reassembly. The presence of LD, in the context of divergent selection and gene flow between the habitats, would provide an enhanced mechanism for the transporter model. Even a relatively low level of LD among freshwater alleles at multiple loci in the ocean would greatly increase the probability of parallel reuse of multiple cassettes of alleles and genomic regions in the adaptation to fresh water.

(b). Recombination rate variation suggests the presence of important chromosomal features

The genome-wide recombination frequency patterns that we generated from an F₂ mapping cross produced from one ocean and one freshwater parent demonstrated only a weak association between recombination rates and LD. The relatively low genome-wide average (2–4 cM MB⁻¹) is periodically punctuated by very high levels of recombination within very narrow genomic windows, similar to findings in other organisms [112–116]. These results have been attributed to structural features such as sequence motifs that increase local recombination rate [117], and this may be the case in stickleback as well.

An alternative hypothesis is that these apparent peaks of recombination are the artefacts of segregating chromosomal features, and may be marking, for example, the breakpoints of inversions or translocations that differ between the cross and the reference genomes. Conversely, areas of reduced recombination in our data may reflect chromosomal rearrangements segregating between the two parents in our cross. Such genomic features may be important for stickleback genomic and phenotypic evolution by suppressing recombination; multiple rearrangements along a chromosome may suppress recombination over a very large region. For example, we had previously found that a large number of genetic markers spread across nearly the entire length of LG IV are associated with the stickleback lateral plate phenotype [87], and we subsequently showed that these align with three major signatures of natural selection [90]. We add to this story by showing that two regions of reduced recombination align with these three signatures of selection, and that two peaks of extremely high apparent recombination punctuate the ends of LG IV. These features may reflect segregating chromosomal rearrangements in natural populations, which could help synthesize findings from previous stickleback research. If multiple loci on LG IV are contributing to the lateral plate phenotype, and are linked in chromosomal blocks, this may provide an explanation of why the loss of lateral plates segregated in an apparently Mendelian fashion in nearly all of our laboratory crosses from these Alaskan populations [84], whereas intermediate phenotypes are seen in different populations from this same region of Alaska. In the ongoing work, we are directly testing for the presence of chromosomal rearrangements segregating within and between each of these populations.

(c). Genome architecture may influence parallel phenotypic evolution in stickleback

In addition to the patterns on LG IV, several observed LD blocks encompass genomic regions that contain either major quantitative trait loci (QTL) or signatures of selection in several other regions of the genome. Both local and long-distance LD cover LG IV and LG VII, chromosomes that contain the genes Eda and Pitx1. These loci are involved in the development of lateral plates and pelvic structure, respectively, and have been implicated in the repeated evolutionary loss of these phenotypes in natural populations [80,81,84,86,87]. We have previously found evidence that large portions of these chromosomes are subject to directional selection in freshwater habitats [90]. Importantly, the extent of LD is much greater for both of these linkage groups in the ocean than in fresh water. This result suggests that the oceanic populations are not simply repositories of freshwater alleles at low frequency because of slight gene flow, but that in the ocean, strong and perhaps epistatic selection occurs against the freshwater alleles.

Under the metapopulation model, long-lived alleles (such as Eda) in genomic regions could repeatedly experience freshwater and oceanic environments over millennia. In this case, genomic regions contributing to adaptations in either environment, and which would be identified as major QTL in mapping crosses, may be the consequence of multiple compensatory or augmenting mutations that occur on the background of old LD blocks [118,119]. For example, the nearly Mendelian inheritance observed for major locus alleles on LG IV and LG VII in Alaskan populations may be the product of numerous independent mutations that are now associated in oceanic and freshwater linkage blocks. This interpretation is similar to what had previously been described as ‘co-adapted gene complexes’, as well as newer ideas concerning ‘genomic islands of divergence’. This pattern complicates the question of whether evolution proceeds by small or large steps. In the stickleback system, contemporary parallel evolution would involve selection on complex alleles that had been assembled as a series of smaller effect mutations in the dynamic metapopulation [118–122].

The pattern of long-distance LD across linkage groups requires further explanation, as free recombination will occur among chromosomes. The genomic regions subject to divergent selection, and therefore most differentiated between populations, should exhibit the strongest patterns of LD soon after introgressive hybridization, but this LD should decay rapidly over time with independent assortment of chromosomes. Inter-chromosome translocations or transmission ratio distortion [123] could play a role in long-distance LD and need to be investigated in these populations. An additional hypothesis is epistasis for fitness among these loci, which could prolong the lifespan of LD [15,124,125]. This hypothesis is supported by the observation that only some of the pairs of adaptive genomic regions exhibit elevated long-distance LD (e.g. only one of the two major adaptive regions on LG VII shows LD with the adaptive regions on LG IV). If long-distance LD were purely the result of gene flow among differentiated populations with divergent selection, one would expect roughly equal levels of long-distance LD among all most highly differentiated genomic regions. The combination of metapopulation structure with additive and epistatic selection may offer the best explanation for these long-distance LD patterns, and determining the relative roles of each will be an active area of research in stickleback and similar systems.

(d). Stickleback genomic architecture and ecological speciation

Although studies of genomic architecture are in their infancy in stickleback, our results already have consequences for studies of the genomics of speciation in stickleback. The majority of research on stickleback speciation has focused on benthic–limnetic species pairs in British Columbia [9,69,126–133]. In addition to differences in mate preferences, benthic–limnetic stickleback exhibit environmentally determined post-zygotic isolation in the form of selection against individuals with intermediate phenotypes [129,134]. Gene flow occurs at low levels among these species, and it will be interesting to determine how LD patterns (if they exist) compare with those we have identified in the more allopatric Alaskan populations.

We do not know whether the oceanic and freshwater stickleback that we examined should be considered members of differentiated populations or incipient species. However, some studies of reproductive isolation have been performed between ocean and freshwater stickleback [63,135]. These studies have discovered preferences (particularly based on size) as well as differences in phenology for anadromous and freshwater stickleback that breed in the same lakes, both of which may be important for pre-zygotic isolation [72]. Because of the combination of population structure and fitness landscape, comparisons of oceanic and freshwater stickleback may be ideal for studying the earliest stages of speciation mediated via divergence hitchhiking. As noted by Via in this volume [136], our previous work on signatures of selection in these populations fits a model of divergence hitchhiking. Many species may have similar metapopulation structures. For example, numerous species of plants and animals have recolonized newly opened habitats after glaciers receded from the last glacial maximum. It is interesting to note that our blocks of LD are quite large, and are similar to patterns described in this volume for whitefish [137,138] and aphids [136], but contrast markedly with the findings of Strasburg et al. [139] from a review of plant systems and Heliconius butterflies [140]. A focus of future work should be explaining the variance in the scale of genomic architecture across these systems. Theory suggests that the size of genomic islands is sensitive to the precise combination of demographic, fitness and genomic parameters [59,141]. For example, the strength of selection and the episodic nature of gene flow in systems like stickleback might lead to larger LD blocks, but more consistent gene flow in some plant systems may lead to slower growth in LD and smaller islands.

The observations of genomic architecture in stickleback populations indicate mechanisms for post-zygotic isolation between ocean and freshwater stickleback. The patterns of local, and in particular long-distance, LD suggest that genetic incompatibilities could result in viability selection against hybrids through the breaking up of co-adapted gene complexes. In addition, the recombination rate variation highlights the potential for chromosomal incompatibilities during the production of gametes in hybrids. Unpublished data from our laboratory indicate that the survivorship of embryos from crosses between ocean and freshwater fish are often lower than survivorship in crosses within populations and habitat types, supporting this hypothesis. We anticipate that a very active area of future research using stickleback will be examining the role of genomic architecture in the maintenance of correlations among alleles that are important for speciation.

5. Conclusion

Oceanic and freshwater stickleback populations have long been used for studies of the genetic architecture of phenotypic evolution. Here, we present data on substantial local and long-distance LD, and variation in recombination rate, that suggest that evolution in this system occurs in the context of bidirectional gene flow between differentiated populations adapting to alternative fitness optima. A metapopulation experiencing divergent selection, combined with genetic interactions like epistasis and chromosomal features, may lead to significant evolution of co-adapted gene complexes. Our results suggest that the genomic islands of divergence in oceanic and freshwater stickleback may be associated as an archipelago of adaptive genomic regions, and that this may facilitate rapid phenotypic divergence and contribute to incipient reproductive isolation between these two forms.