Establishment of new mutations under divergence and genome hitchhiking

Abstract

Theoretical models addressing genome-wide patterns of divergence during speciation are needed to help us understand the evolutionary processes generating empirical patterns. Here, we examine a critical issue concerning speciation-with-gene flow: to what degree does physical linkage (r < 0.5) of new mutations to already diverged genes aid the build-up of genomic islands of differentiation? We used simulation and analytical approaches to partition the probability of establishment for a new divergently selected mutation when the mutation (i) is the first to arise in an undifferentiated genome (the direct effect of selection), (ii) arises unlinked to any selected loci (r = 0.5), but within a genome that has some already diverged genes (the effect of genome-wide reductions in gene flow for facilitating divergence, which we term ‘genome hitchhiking’), and (iii) arises in physical linkage to a diverged locus (divergence hitchhiking). We find that the strength of selection acting directly on a new mutation is generally the most important predictor for establishment, with divergence and genomic hitchhiking having smaller effects. We outline the specific conditions under which divergence and genome hitchhiking can aid mutation establishment. The results generate predictions about genome divergence at different points in the speciation process and avenues for further work.

1. Introduction

Speciation is a fundamental process responsible for creating the great diversity of life on the Earth. In general, speciation involves the splitting of one reproductive community (or genotypic cluster) of organisms into two [1,2]. Conceptualizing speciation in this manner leads to a basic research programme: in order to understand speciation, one must understand how genetically based barriers to gene flow (i.e. reproductive isolation) evolve between populations. Much progress has been made on discerning the importance of different factors and traits (including ecological adaptation) generating reproductive isolation [3–6]. In addition, progress has been made in identifying and characterizing individual ‘speciation genes’ contributing to reproductive isolation, and, in particular, genes causing intrinsic post-zygotic isolation in hybrids [1,7–11].

In contrast, we lack a good understanding of how these speciation genes are embedded and arrayed within the genome, and thus of how genomes evolve collectively during population divergence [12]. Thus, major questions remain about the genomic architecture of speciation and how this architecture either facilitates or impedes further divergence, especially for populations in the formative stages of speciation. Generally speaking, our empirical and theoretical understanding of the genomics of speciation is still largely dominated by what Ernst Mayr described as ‘beanbag thinking’ of the action of individual genes [13,14]. There are exceptions where interactions among multiple loci have been considered, e.g. the ‘snow-ball’ effect for the accumulation of the number of post-zygotic incompatibilities through time [15–17]. However, in general, studies of speciation genes have been restricted to examining one or a few independent loci [11]. These beanbag approaches have worked well enough so far because, until recently, empirical studies were limited to such a gene-centred focus. But as represented by the articles in this issue, we are now capable of rapidly scanning large portions of the genome of both model and non-model organisms for differentiation [18–21]. Consequently, genomic theories need to be developed if we want to move the field of evolutionary genomics away from descriptive studies of patterns of divergence towards a more predictive framework that tackles the causes and consequences of genome-wide patterns.

In this regard, an important consideration is the geographical context of speciation, specifically, whether gene flow accompanied the divergence process and at what point in time it occurred. Gene flow is important, because strictly allopatric population divergence, be it via selection or genetic drift, proceeds unfettered by the homogenizing effects of migration [17]. Thus, the extent of genetic linkage and recombination among genes relative to the strength of selection is not a major constraint on divergence in complete allopatry. Although much has been learned about specific reproductive barriers and individual speciation genes from studying allopatric taxa [1], it is difficult to ascribe any special significance to a particular genetic change in such systems. Genomic architecture is less relevant to speciation in allopatry, as divergence across the genome is inevitable.

In contrast, physical linkage relationships and recombination rates among genes, along with levels of gene flow and the strength of selection, are critical considerations with respect to divergence-with-gene-flow speciation, where gene flow constantly introduces the wrong combination of genes into a local population [17,22–24]. These considerations apply when speciation is initiated in the face of gene flow, as well as when some divergence initially occurs in allopatry and then a period of secondary contact and gene flow follows, although the dynamics might be somewhat different between the two scenarios [25–27]. Here, we are primarily interested in the question of population divergence initiated with gene flow. The implications of our findings, however, also apply to instances of hybrid zones formed following secondary contact. But in these cases, further information is needed on patterns of genome architecture prior to secondary contact to accurately equate how the different evolutionary processes we describe contribute to further differentiation upon secondary contact. For example, clustering of adaptive mutations may potentially be more commonly maintained following secondary contact than when built de novo in sympatry. This is an interesting avenue for future studies.

Some classic work in shaping the theory of speciation-initiated-with-gene-flow was done by Joseph Felsenstein in a paper entitled ‘Skepticism to Santa Rosalia: or why are there so few kinds of animals’ [28]. This insightful paper developed the term ‘selection–recombination antagonism’ to describe how recombination breaks up associations between selected loci and other reproductive isolation loci, impeding genetic divergence across the genome. The implication was that there are theoretical constraints for speciation-with-gene-flow; unless genes involved in assortative mating were tightly linked to those affecting habitat performance (or a single gene had pleiotropic effects on both) [29]—considered unlikely possibilities—little progress may be made towards speciation. The results led to a perspective that if speciation is initiated in the face of gene flow, it would probably necessitate building from a few areas of the genome where several genes under strong divergent selection fortuitously resided in close linkage. The most recent offshoots of this perspective are the concepts of ‘genomic islands of speciation’ and ‘divergence hitchhiking’ (hereafter ‘DH’) [30–33], which we discuss below.

However, several aspects of Felsenstein's model, which he readily discussed, were not meant to be biologically realistic, but rather to highlight general points about selection–recombination antagonism. For example, if assortative mating is based on habitat preference rather than differentially choosing mates in a common mating pool [34,35], or if the same allele causes assortative mating in both populations, the selection–recombination antagonism can be alleviated [28]. Moreover, if selection is strong and migration not completely random between populations, a degree of disequilibrium is established between performance genes even in the absence of genetically based habitat choice and physical linkage among loci [22,34–37]. These considerations lead to the idea that multifarious selection affecting multiple loci across the genome could also kick start speciation-with-gene-flow [38–40]. In this case, widespread selection could potentially reduce gene flow to the extent that divergence could build up or be maintained across the genome.

Empirically, the reduction in effective gene flow owing to selection can result in positive associations among population pairs between levels of adaptive phenotypic or ecological divergence (a proxy for the strength of selection) and neutral genetic differentiation [41–46]. This pattern has been referred to as ‘isolation-by-adaptation’ (IBA), which is analogous to ‘isolation-by-distance', but reductions in gene flow arise from increasing adaptive divergence, rather than increasing physical distance [18,47]. Here, we define the term ‘genome hitchhiking’ (hereafter ‘GH’) to describe the process by which genetic divergence across the genome is facilitated, even for loci unlinked to those under selection, by the global reductions in gene flow that selection causes genome-wide. This process, unlike DH, does not invoke a role for physical linkage, and can result in IBA across the genome. A key question therefore is how quickly, in terms of the number and strength of loci under divergent selection, do two populations reach a point where GH becomes a significant factor in facilitating the accumulation of new mutations.

Along these lines, our article has five main goals: (i) to outline the processes of DH and GH and discuss how they can facilitate genomic divergence for speciation-initiated-with-gene-flow, (ii) to review past theory on the effects of both forms of hitchhiking on equilibrium levels of genetic divergence for neutral sites linked to those under selection, (iii) to report new theoretical findings concerning hitchhiking and the establishment of new, beneficial mutations, (iv) to generate explicit predictions concerning when we expect DH and GH to be most effective and how their relative importance is expected to vary across stages of the speciation process, and (v) to clearly outline what types of further studies need to be conducted to build a more complete understanding of the genomic architecture of speciation.

(a). Genomic islands and divergence hitchhiking

To aid thinking about divergence in the genome, evolutionary biologists have developed the metaphor of ‘genomic islands of divergence’, where a genomic island is any gene region, be it a single nucleotide or an entire chromosome, which exhibits significantly greater differentiation than expected under neutrality [18]. The metaphor thus draws parallels between genetic differentiation observed along a chromosome and the topography of oceanic islands and the contiguous sea floor to which they are connected. Following this metaphor, sea level represents the threshold above which observed differentiation is significantly greater than expected by neutral evolution alone. Thus, an island is composed of both directly selected and linked (potentially neutral) loci above sea-level expectation. Factors such as physical proximity between selected and other loci, rates of recombination and strength of selection each affect the height and the size of genomic islands. Under this metaphor, the few genes under or physically linked to loci experiencing strong divergent selection can diverge, whereas gene flow will homogenize the remainder of the genome, resulting in isolated genomic islands (but see [48,49]).

The verbal theory of DH posits that physical linkage to divergently selected loci greatly facilitates the formation of genomic islands of relatively large size, making it easier for speciation in the face of gene flow to occur than previously thought [30,31]. The premise is that divergent selection reduces interbreeding between populations in different habitats [30,31,50]. This reduces inter-population recombination, and even if recombination occurs, selection reduces the frequency of immigrant alleles in advanced generation hybrids [17]. This reduction in effective gene flow might allow large regions of genetic differentiation to build up in the genome around the few loci subject to divergent selection. The idea rests on the assumption that a site under divergent selection will create a relatively large window of reduced gene flow (and hence recombination) around it, enhancing the potential to accumulate differentiation at linked sites. Notably, islands may successively build in primary or secondary contact situations.

(b). Genomic continents and genome hitchhiking

As an alternative to DH on a few loci, selection acting on many loci distributed throughout the genome, as documented in many genome scans [18,51], could drive speciation [40,52,53]. This process also produces variable patterns of genomic divergence owing to differences among loci in selection intensities, linkage relationships and recombination rates. However, in the case of selection on many loci, genomic regions displaying weaker differentiation may not all be neutrally evolving, but rather represent regions more weakly affected by selection. In this case, many loci are diverged beyond neutral, ‘sea-level’ expectations such that genomes differ by many ‘archipelagoes’ or even ‘continents’ of divergence. We stress that the island versus continent views represent ends of a continuum, rather than mutually exclusive hypotheses. For example, continents can be conceptualized as large islands with variable topography (e.g. mountain tops and lowland continental plains all above neutral sea level). The process of GH could generate continents of divergence, with selection on many loci across the genome lowering effective gene flow to the point that divergence across the genome is facilitated.

(c). Empirical patterns from genome scans: islands or continents?

Empirical genome scan studies have provided evidence for the island view of divergence ([18]; for review [32,54]). In contrast, evidence for more widespread divergence is rarer (but see [51,55]). However, this may stem from strong limitations in relying on genome scans alone for detecting selection. Genome scans conducted without complementary selection experiments and mapping studies can be biased towards supporting an island view because, inevitably, only the most diverged regions will be identified as statistical outliers (but see [55]). Other loci affected by selection, but more weakly, will go unnoticed and be considered part of the mostly ‘undifferentiated’ and neutral genome. In short, although empirical genome scans have usefully identified candidate regions strongly affected by divergent selection, they cannot readily detect weaker selection. Observational genome scans, although a good starting point, therefore have certain limitations for discerning the proportion of the genome affected by selection. In contrast, direct experimental measurements of selection on the genome might be able to detect both weak and strong selection, and, thus, in concert with genome scans may help determine the fraction of the overall genome affected by selection.

Michel et al. [52] conducted an experimental test of the genomic islands hypothesis in the apple and hawthorn host races of Rhagoletis pomonella, a model for sympatric ecological speciation. Contrary to expectations, they reported numerous lines of evidence for widespread divergence and selection throughout the Rhagoletis genome, with the majority of loci displaying latitudinal clines, associations with adult eclosion time, within-generation responses to selection in a manipulative over-wintering experiment and host differences in nature despite substantial gene flow (4–6% per generation). The results, coupled with linkage disequilibrium analyses, provide field-based and experimental evidence that divergence was driven by selection on numerous independent genomic regions, suggesting that ‘continents’ of multiple differentiated loci, rather than isolated islands of divergence, can characterize even the early stages of speciation. Their results also illustrate continental topography. The divergence observed throughout the Rhagoletis genome was clearly more accentuated in some regions, such as those harbouring chromosomal inversions. A final point is that standard outlier analyses in this same study were consistent with the genomic island hypothesis: only two independent genomic regions were detected as statistical outliers between the host races. Thus, experimental data and biological information on gene flow in nature were critical for detecting weaker yet widespread divergence across the genome. Until further such studies emerge, it will be impossible to know if genomic continents are the exception, or the norm.

These considerations lead to a number of theoretical questions. How numerous, and how large, are regions of divergence in the genome expected to be? How clustered or dispersed are divergent regions? How might the answers to these questions depend upon how far speciation has proceeded? Under what conditions, and thus at what point in the speciation process, does GH become important for speciation? Here, we review past theory and report new theoretical results that begin to answer these questions.

(d). Expectations at equilibrium

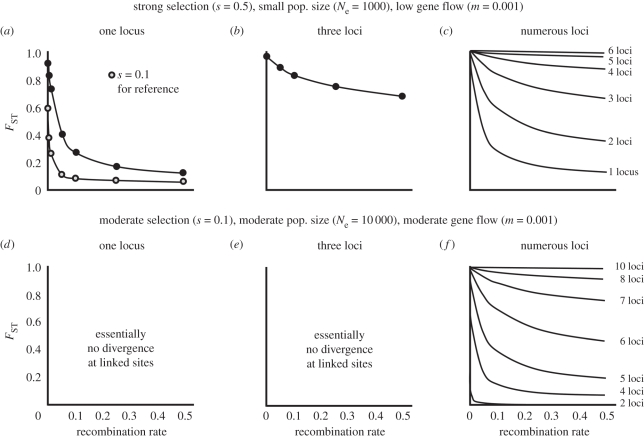
Feder & Nosil [46] developed the beginnings of a theory of DH and GH with respect to patterns of neutral differentiation expected to accumulate around a gene subject to divergent ecological selection between populations (figure 1). They used a combination of analytical and simulation approaches to expand the single-locus models of Charlesworth et al. [56] to any number of loci under selection and to a wider range of parameter values. Feder & Nosil [46] considered two demes subject to divergent selection and exchanging migrants at a gross rate m and quantified the ability for reduced gene flow surrounding selected sites to generate and maintain neutral differentiation at regions of increasing recombination distance from the selected site. The strength of selection, recombination rate between neutral and selected loci, gross migration rate and numbers of loci under selection were varied. Selection against immigrant alleles resulted in the effective migration rate being lower than the gross migration rate [57–60]. Thus, for each set of parameter values and different genomic regions, the effective migration rate was calculated, and then converted to F_ST at mutation/drift equilibrium using standard population genetic formulae. The results allowed visualization of the decay of F_ST along a chromosome as one moves away from a divergently selected site.

Figure 1.

(a–f) A summary of previous theory on equilibrium levels of neutral genetic differentiation under DH and GH. Shown are equilibrium levels of divergence (F_ST) at neutral sites linked at various recombination distances to a locus under divergent selection. DH can generate and maintain regions of neutral differentiation extending away from a selected site, but only under certain conditions. Note that when numerous, unlinked loci in addition to the original site are also under selection, genome-wide divergence can occur via GH such that genomic islands are erased (e.g. in (c) compare scenarios with one to three loci to those with four to six loci under selection); pop., population. Reproduced with permission from Feder & Nosil [46]. Copyright © John Wiley and Sons Inc.

The main finding of Feder & Nosil [46] was that DH around a single locus can generate large regions of neutral differentiation under some conditions, but that these conditions are somewhat limited (figure 1). For a single locus under selection, regions of neutral differentiation do not extend far along a chromosome away from a selected site unless selection is strong and both effective population size and migration rate are low (e.g. N_e = 1000 and m = 0.001; compare figure 1a and d). Even just a modest increase in N_e or m to levels generally considered more in keeping with speciation-with-gene-flow (e.g. 10 000 and 0.01, respectively) greatly diminishes neutral differentiation around a selected gene (figure 1d) [46]. When multiple loci are considered, regions of differentiation can be larger (figure 1b, c and f). However, with many loci under selection, effective migration rates become so low that genome-wide divergence occurs via GH and isolated regions of divergence are erased (i.e. the whole genome becomes Pangaea, a super-continent of differentiation; figure 1b, c and f). What is therefore required for DH to be important is that effective gene flow is significantly reduced locally in the genome without being substantially reduced globally. Feder & Nosil [46] examined equilibrium levels of divergence at neutral sites linked to those under selection. Here, we investigate the seminal issue of the roles that direct selection, DH and GH play for facilitating the establishment of newly arisen divergently selected mutations (i.e. new mutations that are favoured in one habitat, but selected against in the other).

2. Methods

(a). Computer simulations

We used computer simulations to estimate the probability that a new mutation conferring a fitness tradeoff between habitats became established to differentiate populations (in a similar manner, we previously examined how chromosomal inversions can evolve to distinguish populations [27]). To do this, we broke down the process into the three major components affecting the probability of establishment representing: (i) selection acting directly on the new mutation itself uninfluenced by selection on any other gene in the genome (i.e. the mutation arose in a completely undifferentiated genome; ‘noH’ refers to no hitchhiking hereafter), (ii) when the new mutation was unlinked (r, the recombination distance = 0.5) to one or more other loci in the genome under divergent selection (GH), and (iii) when the new mutation was linked at varying recombination distances to another locus in the genome experiencing divergent selection (DH).

Comparing probabilities among these three sets of conditions allowed us to partition the effects of direct selection on the new mutation itself, GH and DH in contributing to the establishment of mutations in populations diverging with gene flow (figures 2 and 3). Specifically, the estimated probability of establishment of a new mutation in the absence of other genes in the genome experiencing divergent selection represents the effect of the gene itself divorced from either form of hitchhiking (see noH in figures 2 and 3). Subtracting the estimated probability of establishment of a new mutation on its own (noH) from that of a locus unlinked to any genes(s) under divergent selection allowed quantification of the effect to which GH facilitates the establishment of the new mutation and fosters speciation (figure 3). Likewise, subtracting the estimated probability of establishment of a new unlinked mutation from that for a mutation linked to a gene (r < 0.5) under divergent selection allowed quantification of the effect of DH on the probability of mutation establishment (figure 3). We use the term establishment, rather than fixation, because with divergence-initiated-with-gene-flow, a new mutation never becomes differentially fixed between populations. Migration will always introduce at least a few disfavoured alleles into a population in each generation. However, it is still possible that a new mutation can rise to very high frequency in the population in which it is favoured provided that the selection coefficient s is much greater than the effective migration rate. Estimating the establishment probability for a new mutation is therefore somewhat different from the standard population genetic analysis of estimating the probability of fixation within a population divorced from gene flow.

Figure 2.

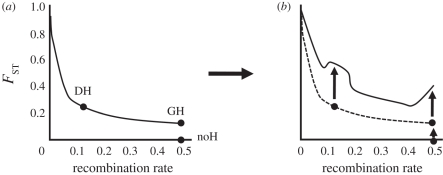
Schematic depiction of different scenarios for the establishment of a new mutation. In all cases, black dots represent genomic locations where new mutations arise. (a) If the mutation is the first to arise, in a completely undiverged genome, it receives no aid in establishment from hitchhiking effects (noH). This can be thought of as the baseline probability of establishment of the mutation all on its own. The establishment of the mutation might be facilitated in two ways. First, establishment might be facilitated by DH if the new mutation arises in physical linkage to a locus already diverged via selection. Second, establishment might be facilitated by GH if the new mutation arises unlinked to any selected loci, but within a genome that has some diverged loci. (b) Divergence before (dashed line) versus after (solid line) establishment of the new mutations.

Figure 3.

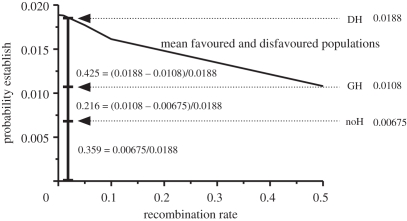
Partitioning the probability of establishment for a new mutation into relative contributions owing to noH, GH and DH (see figure 2 and main text for abbreviations). Shown is an example with conditions favourable for DH with a high migration rate (m) = 0.1, strong selection on the initially diverged locus (s_o = 0.5), selection on the new mutation less than the migration rate (s_n = 0.05) and tight linkage (r = 0.001) between the already selected locus and new mutation. Given are the probabilities of establishment for the mutation alone (0.00675), for the new mutation unlinked to the previously existing selected locus (0.0108), and for the new mutations at various recombination distances from r = 0.5 to r = 0.001 to the selected locus (dark line = mean for the new mutation arising in the favoured and disfavoured populations). For r = 0.001, the probability of establishment for a new mutation under these conditions equals 0.0188. Based on these values, the relative contributions to establishment are 35.9% for the new mutation on its own, 21.6% for the GH effect and 42.5% for DH. Thus, even under these favourable conditions with very tight linkage, there is a less than two times increase for the effect of DH on the establishment of a new mutation above that for GH and the effect of the mutation on its own in the absence of linkage (0.0188/0.0108 = 1.74).

We used discrete generation, two-deme population genetic computer simulations written in Matlab for a diploid, hermaphroditically reproducing organism to estimate the probabilities of establishment of a new mutant A allele conferring a habitat-related fitness tradeoff occurring at a designated locus 1 (i.e. we determined how often the new mutant A allele would be retained by selection versus lost by genetic drift). As described in detail in the electronic supplementary material, we varied parameter values for symmetric migration rates (m) between populations, recombination rates (r) between loci, selection strength (s) and number of loci (n_loci) under divergent selection. Selection strength itself was varied for two types of loci: already established loci (designated s_o for ‘original’) and a new mutation (s_n for ‘new’). We examined a range of selection strengths (s = 0.5–0.01) and migration rates (m = 0.1–0.001) which we considered to have the greatest realism for speciation-initiated-with-gene-flow. The simulations assumed multiplicative fitness interactions between loci with no epistasis and a life cycle in which divergent selection followed migration between populations and occurred prior to mating. Although the general qualitative nature of our conclusions will not change, we leave it to further work to explore the quantitative consequences of epistasis, dominance (we assumed partial dominance of fitness) and unequal population sizes.

Simulations were begun with the frequencies of the alleles at all loci besides the designated locus 1 receiving the new mutation in selection–migration balance between populations. This was accomplished by starting the simulations with frequencies of the A and a alleles at all loci in populations 1 and 2 equal to 0.5 and in linkage equilibrium with one another. The frequency of the a allele was set equal to 1.0 for locus 1. We then ran the simulation until the change in allele frequencies between generations for all loci became equal to 0 (within the limit of computational precision). For this initial phase of establishing selection–migration balance, the simulations were purely deterministic (i.e. driven by natural selection) and there was no stochastic process (i.e. genetic drift) affecting allele frequencies.

After attaining selection–migration balance, a new mutant A allele was introduced into locus 1 at a randomly chosen gamete in either population 1 or 2. The mutant gamete was then combined with a randomly chosen non-mutant gamete in the population to form a diploid zygote and the fate of the new mutant A allele followed until it was either lost or retained. The total probability for the establishment of a new mutant A allele in population 1 was calculated as the mean of 100 000 simulation runs introducing the new A mutation into population 1 and 100 000 simulation runs introducing the new A mutation into population 2. These values therefore represent the estimated probability that a given new A allele mutation at locus 1 occurring anywhere in the two diverging populations will become established in population 1.

In the simulations, individuals migrated from population 1 into population 2 and from population 2 into population 1 at rate m. Population densities were assumed to be independently regulated in the two demes (i.e. soft selection), with a total of n₁ and n₂ zygotes (newborn offspring) produced in each population in each generation (for the current study, n₁ was set equal to n₂ in all the simulations). We considered a life cycle with selection following migration and preceding mating (newborn offspring > dispersal between populations > viability selection within populations > recombination/meiosis in parents > random mating and fusion of gametes separately within each population > next generation of zygotes in populations). We then followed the fate of the new mutant A allele at locus 1 until it was either lost or retained as a polymorphism (see below for criteria used to determining establishment for the mutant A allele).

After the introduction of the new mutant allele A at locus 1, stochastic processes affecting alleles were entered into the simulations in the migratory and reproductive phases of the life cycle. Following meiosis and recombination, gametes were randomly drawn from the gene pools of populations 1 and 2 and separately combined to form the n₁ and n₂ diploid zygotes in populations 1 and 2, respectively, constituting the next generation. After this, a proportion of m₁₂ of the newborn offspring in population 1 was randomly assigned to migrate to population 2 and 1 − m₁₂ to remain in population 1. The reverse was true for offspring in population 2, with relative proportions of migration and residency being m₂₁ and 1 − m₂₁, respectively. The simulations were run varying the parameter values, as outlined in detail in the electronic supplementary material. In short, 100 000 trials were performed for each combination of parameter values separately introducing the new A mutant allele into population 1 (where it was favoured) and population 2 (where it was selected against).

The new mutant allele A at locus 1 was considered lost if its frequency dropped to 0 in both populations 1 and 2. The A allele was considered to become established in a stochastic simulation run if the frequency of the allele exceeded a predetermined threshold level in population 1. For a given set of parameter values, the threshold frequency for allele A in population 1 was determined through analysis of a deterministic selection model without genetic drift (i.e. simulations conducted without random selection of genotypes for migration and of gametes for zygote formation). Specifically, we set the threshold as the frequency when the ratio of the expected change in the frequency of the A allele in population 1 between generations under the deterministic model divided by the standard deviation for the expected change in frequency under a random sampling, drift process, as determined by a binomial distribution with population size n₁, first became equal to 0.5. Through stochastic computer simulations and analytical approaches, we found that once this threshold frequency was attained, there was a low probability (<0.5 × 10⁻⁴) of the A allele decreasing in frequency in the next 100 generations in population 1. We therefore considered that when the A allele reached this threshold frequency, it had become established as a polymorphism.

The eventual expected equilibrium frequencies for the A allele polymorphism in populations 1 and 2 were determined through deterministic simulations by running the simulations until the change of frequency of the A allele between generations in the two populations became equal to 0 (again, to the limit of computational precision). Notably, we report establishment probability for new mutations when they arise in the habitat they are favoured in, disfavoured in and averaged across the two. As discussed in the electronic supplementary material, we compared our simulation results with analytical predictions for the probability of an establishment of a new mutation described by Yeaman & Otto [61] and Yeaman & Whitlock [62]. Important differences between the simulation and analytical results, which highlight the need for the simulation approach, are discussed below and in the electronic supplementary material.

3. Results

(a). General result

Our most general result was that the largest effects on the establishment of a new mutation usually stemmed from the tension between the migration rate and the strength of selection on the mutation itself, and not from physical linkage to a pre-existing locus differentiating populations or from GH. The exceptions were when selection coefficients were less than the migration rate between populations (s < m) and when multiple loci were under strong selection.

(b). Single locus diverged prior to new mutation

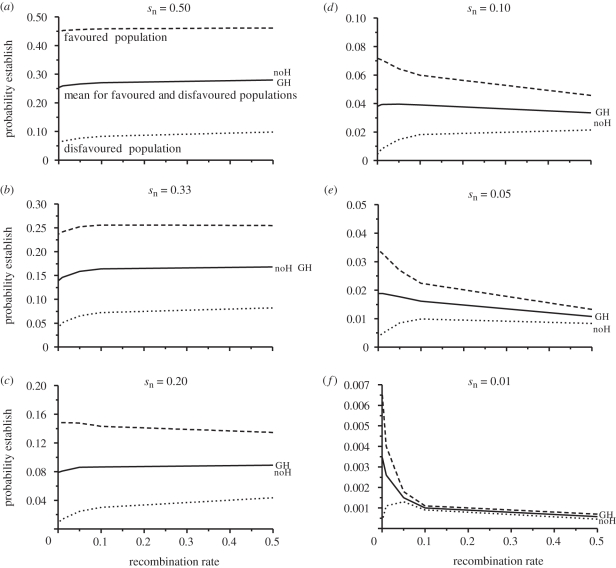
In our simulation runs for a single pre-diverged locus, the stronger that selection was favouring a new mutation, the higher the probability was for its establishment (figure 4), a result previously shown analytically by Yeaman & Otto ([61], see also [63]). With selection acting directly on the new mutation of the order of or greater than the migration rate, DH did not greatly enhance the probability of establishment of the mutation. Indeed, under these conditions, DH could actually hinder, rather than facilitate the establishment of new mutations (compare regions of low versus high recombination in figure 5a–c). This occurred for two reasons. First, when a new mutation arose in a favourable environment but in the occasionally maladapted genotype, it was doomed if it was too tightly linked and could not recombine away from the disfavoured allele. Second, when a new mutation arose in the population in which it was disfavoured, tight linkage hindered its ability to disassociate from this genetic background and establish itself in the alternative population where it was favoured. Since half of all new mutations are expected to occur in the population in which they are disfavoured (given equal-sized populations), tight linkage can have a net negative effect on establishment. The balance between the enhancing and impeding effects of linkage is depicted in figure 5 by comparing the dashed (favoured population) and stippled (disfavoured population) lines.

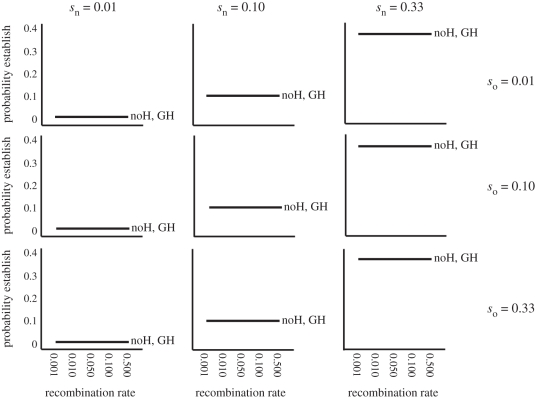
Figure 4.

The effects of selection strength on the probability of establishment of new mutations; s_n is the strength of selection on a new mutation and s_o is the strength of selection on an originally pre-diverged locus. The strength of selection acting directly on mutations was of greater importance for establishment than either DH or GH, as evidenced by the fact that the probability of establishment of a new mutation was similar when: (i) it is the first and only mutation to arise in an undifferentiated genome (no hitchhiking is noH, probability of establishment denoted at r = 0.50), (ii) it arises in physical linkage to a locus already diverged via selection (DH is the probability of establishment for each recombination rate represented by the solid line in each panel), and (iii) it arises unlinked to any selected loci, but within a genome that has a single locus already diverged (GH is probability of establishment denoted at r = 0.50). In essence, noH = DH = GH. Results are shown for m = 0.001. Highly comparable results were observed when migration rates were higher (see electronic supplementary material).

Figure 5.

(a–f) The effects of varying selection strength from very strong (s_n = 0.5) to weak (s_n = 0.01) on the probability of establishment of a new mutation linked at various recombination distances to an original locus under very strong divergent selection (s_o = 0.5). Probabilities of establishment are given for conditions of high migration rate (m = 0.1) for a new mutation arising in the favoured population (dashed line), in the disfavoured population (stippled line) and the mean for the favoured and disfavoured populations together (solid line). Also shown are the baseline probabilities of establishment for a new mutation on its own not influenced by selection on any other loci in the genome (noH) and when the new mutation was unlinked (r = 0.5) to the other locus in the genome under divergent selection (GH). Note that the probabilities for the favoured and disfavoured populations tend to counterbalance one another, especially when selection on the new mutation is not lower than the migration rate, reducing the effect of DH in facilitating mutation establishment.

Nonetheless, DH sometimes promoted mutation establishment above and beyond what occurred for loci unlinked to pre-diverged loci. This occurred, for example, in cases when the strength of selection on a new mutation was a little below the rate of gene flow between populations, and the initially diverged locus was also under strong selection (e.g. s = 0.05 versus m = 0.1; figure 5e). However, this effect at most approached only two times that of GH in the absence of physical linkage (figure 5e). Moreover, for any appreciable DH to occur, divergent selection on the initially diverged locus needed to be strong and at least around twice the migration rate (see electronic supplementary material, figure S1).

Divergence hitchhiking also played a role when the strength of selection on a new mutation was much lower than the gene flow rates, and the initially diverged locus was also under strong selection (e.g. when s = 0.01 versus m = 0.10 in figure 5f). In such cases, a new mutation linked to a diverged locus exhibited up to six times the establishment probability of unlinked loci (figure 5f). However, the new mutation needed to be fairy tightly linked to the already diverged locus to show a marked effect (approx. r < 0.03; figure 5f). Moreover, the absolute probabilities of establishment in these circumstances were low (approx. 0.002–0.0035; figure 5f) and, consequently, the effects on population divergence would be slight, unless numerous such small effect mutations were to establish. The extent to which the distribution of new mutations is skewed towards generating beneficial alleles with small fitness effects could therefore influence the significance of DH.

Analytical approximations for the probability of establishment of new mutations in the habitat that they were favoured in were generally in agreement with the simulation results. Concordance between the analytical approximations and computer simulations was greatest when migration rates were low and selection was strong. Concordance was reduced under high migration rates, where the simplifying assumptions of the analytical approximations become violated and they overestimate the significance of linkage for mutation establishment (see electronic supplementary material, figure S2 and data for details). This overestimation could have contributed to an enhanced historical appreciation for the role of linkage in speciation-with-gene-flow.

(c). Multiple loci diverged prior to new mutation

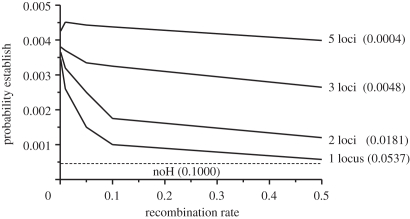
Increasing the number of loci under strong selection (s = 0.5) increasingly flattened the curves for the mean probabilities of establishment of a new, slightly beneficial mutation (s = 0.01; figure 6). As a consequence, recombination distance, and hence DH, became a less important factor for the establishment of any one specific new mutation as the number of background loci under selection increased. However, with increasing numbers of loci, the chances that a new mutation will fortuitously occur in close proximity to a locus under divergent selection proportionately increases. Thus, DH could still contribute to speciation.

Figure 6.

The effect of increasing numbers of unlinked loci in the genome each under very strong divergent selection (s_o = 0.5) on the probability of establishment of a new mutation under weak selection (s_n = 0.01) relative to the migration rate (m = 0.1). Shown are the results for the mean probabilities of establishment of a new mutation averaged across the favoured and disfavoured populations when one, two, three and five loci are under very strong divergent selection. Also given in parentheses are the effective migration rates (m_e) for a neutral unlinked locus in the genome estimated by the method of Feder & Nosil [46] for when no, one, two, three and five loci are already under very strong divergent selection.

As expected and in contrast to DH, the role that GH plays in establishing new mutations increased with additional loci (figure 6). This is because as the number of loci under divergent selection through the genome increases, the genome-wide effective gene flow rate between populations will reduce ever closer to zero. As this happens, populations will increasingly evolve as if they are allopatric, resulting in the mean probability of establishment for a new mutation across populations elevating to approximately s/2 regardless of linkage (mean probability = (the probability of establishment in the favoured habitat + the probability of establishment in the disfavoured habitat)/2 = (s + 0)/2 = s/2; where s is the relative fitness advantage of the favoured homozygote with partial dominance in heterozygotes). At this point for new mutations with small s, GH will dominate and DH will play a minor role in aiding mutation establishment. For figure 6 with weak selection of s = 0.01 acting on a new mutation, the upper bound for the probability of establishment is 0.005. When as few as three loci are under very strong divergent selection (s = 0.5) in the genome and with a migration rate of m = 0.1, the probabilities of establishment for new weakly selected mutations (s = 0.01) become similar across the range of recombination distances to selected loci (the curve is flattening). With five loci under strong disruptive selection, the upper bound for the probability of establishment of a new mutation is approached regardless of linkage. Simply put, with three loci, the weak selection coefficient of s = 0.01 acting on the new mutation becomes greater than the genome-wide effective migration rate (m_e ∼ 0.0049 for a neutral gene based on the simulation methods of Feder & Nosil [46]) and with five loci it is much greater (m_e ∼ 0.0004).

In this regard, it is important to understand that the effects of DH on reducing effective gene flow only begin to be fully realized in F₂ and in backcross progeny of mixed ancestry. This is because it is the first generation in which recombination begins to integrate introgressing genes into the chromosomes of the resident population. Consequently, reduced recombination between a new mutation and a linked, already diverged locus increases divergent selection against this block of genes—relative to if they were unlinked—in F₂ and backcross progeny and reduces the effective migration rate locally in the genome. However, this general delay means that in systems where selection follows migration, two rounds of genome-wide divergent selection occur (one on migrants and one on F₁ hybrids) regardless of linkage, thereby generating GH before the largest effects of DH occur (if mating follows migration, then one round of selection occurs on F₁ hybrids). As a result, GH rather than DH may often be the primary mechanism facilitating the establishment of new mutations, resulting in a more even accumulation of adaptive changes across the genome. Most importantly, our simulations imply that the transition to a strong role for GH can occur relatively quickly with respect to the number of differentiated loci.

4. Discussion

We presented here new theoretical results concerning the probability that new mutations establish to differentiate populations undergoing divergence-with-gene flow. We find that the strength of selection acting directly on a new mutation is an important predictor of establishment, with both DH and GH having smaller effects in comparison. Thus, the implication of Felsenstein's [28] selection–recombination antagonism for a somewhat narrow window for DH to act around a selected site may be closer to reality than has been recently argued [30,31,33]. However, we also show that this does not preclude divergence-with-gene-flow occurring readily based on the selective advantage of new favourable mutations. Moreover, both DH and GH can affect mutation establishment under some conditions. In particular, with just a few loci under strong selection, diverging populations can rapidly transit into a phase where linkage becomes relatively unimportant for new mutations to establish and IBA occurs genome-wide. In this regard, it is important to realize that the effects of GH act immediately on migrants and F₁ hybrids, while the primary consequences of DH in reducing effective migration locally in the genome are more delayed until the F₂ and backcross generation. Thus, divergent selection against migrants and their immediate offspring, when moderately strong, can readily help in generating genome-wide differentiation and IBA without the need to wait for the boosting effects of DH in second-generation hybrids [45]. Furthermore, the conditions previously shown by Feder & Nosil [46] to be conducive for neutral differentiation to accumulate around strongly selected sites owing to DH (e.g. low migration rate) are those in which new, divergently selected mutations will establish genome-wide regardless of linkage. Low m means that not just strongly selected genes, but many mutations of modest to low fitness value can come to differentiate taxa throughout the genome, resulting in more limited consequences for DH in speciation. Thus, our collective results generate predictions about genomic divergence at different points in the speciation process and avenues for further theoretical work, which we discuss below.

(a). Differential importance of various processes across the speciation continuum

The process of population differentiation is often an extended one, whereby divergence occurs along a continuum ranging from continuous variation, to ecotype and race formation, speciation and post-speciation divergence [53,64–66]. As divergence proceeds along this continuum, levels of gene flow become lower. The collective theoretical results presented above generate predictions about the importance of different processes in promoting genetic divergence at different points in the speciation continuum.

During the earliest stages of non-allopatric speciation, if levels of gene flow are high, our results predict that individual loci directly subject to strong divergent selection will diverge relatively independently from other loci in the genome. As divergence of these strongly selected loci reduces the effective rate of recombination and gene flow between populations, the conditions for divergence of other loci become relaxed [30,31,46,67]. It is during these intermediate, but not very initial, stages of speciation that DH could be important, with loci tightly linked to the few genes which have already diverged now able to differentiate owing to reduced gene flow surrounding selected sites. In particular, DH will be most important when selection strength on new mutations is when weak compared with the migration rate. If selection is of the order of or stronger than migration, DH is not required for genetic divergence. Thus, rather than being critical for speciation, DH is best thought of as potentially supplying a fortuitous push towards divergence when new mutations of lesser effect on fitness happen to occur near previously diverged loci. We note, however, that Yeaman & Whitlock [61] recently showed that under prolonged periods of stabilizing selection in patches with different optima, slight advantages owing to DH can potentially result in the evolution of genetic architectures with tighter clustering of locally adaptive alleles, with alleles or linkage groups of major effect replacing multiple alleles or linkage groups of more minor effect (i.e. over time, genomic archipelagos and continents shrink in size but grow in height). Also, chromosomal rearrangements that capture locally favourable combinations of genes could contribute to facilitating increased divergence for certain regions of the genome owing to reduced recombination within inverted regions ([27,68], but see [69]). Finally, if the mutation process is skewed towards producing new alleles of minor effect, then DH could also be more important.

The situation is different as speciation progresses and multiple loci become diverged and genome-wide effective gene flow is more substantially reduced (i.e. population divergence proceeds to stages ever more analogous to those for allopatric demes). Here, GH can strongly facilitate further divergence and speciation. Over time, divergence and, in particular, GH will facilitate a build-up of reproductive isolation, creating ever more favourable conditions for loci with modest and weak effects to differentiate throughout the genome. As the process proceeds, associations between loci become stronger, eventually expanding to genome-wide linkage disequilibrium and widespread genomic divergence. Our theoretical results imply that this transition to genome-wide IBA can occur relatively rapidly with respect to the number of loci experiencing strong selection. Whether this occurs rapidly in time is a separate issue. In sum, speciation-with-gene-flow will likely involve selection acting directly on loci, physical linkage and linkage disequilibrium between unlinked loci, but with differential importance of each across the speciation continuum. Indeed, work on Heliconius butterflies at different points in the speciation continuum documented trends very similar to those suggested above [70].

(b). Future theoretical work: genome structure and standing genetic variation

Future theoretical studies could focus on three major issues. First, one can imagine that genome structure, for example the size and number of chromosomes, will affect patterns of genomic divergence during speciation, but little work to date has explicitly examined this. For example, with fewer and smaller chromosomes (with respect to recombination), it should be more common for multiple locally adapted mutations to occur in tighter physical linkage, or in regions of low recombination such as in the proximity of centromeres. Thus, future models should vary genome structure and recombination rate variation across chromosomes. In a similar vein, the distribution of beneficial alleles can be explored with respect to the interaction of the mutation process in specific ecologically relevant traits. In the current study, we implicitly assumed that mutations of both small and large fitness effect were possible. However, as populations increasingly adapt to divergent ecological selection pressures, they may approach more optimal phenotypes and finer adaptive changes associated with mutations of smaller effect may predominate (unless of course environmental conditions are constantly changing for populations) [71]. With such models, further insight will emerge into how the structure and organization of genomes and the mutation spectrum affect speciation.

Second, initial adaptation to a new habitat might often stem from pre-existing rather than new mutational variation [72,73]. If selective sweeps stem from new mutations, then divergence can initially be elevated across relatively large regions of the chromosome, especially if selection is strong and the sweep occurred rapidly and recently in the past. In contrast, with standing genetic variation, recombination has already been acting for some time to break up associations between selected and neutral genomic regions. Thus, sweeps from standing variation can reduce the magnitude of neutral differentiation surrounding selected sites relative to that observed for new mutations, resulting in ‘soft sweeps’ [74–76]. Adaptation from standing variation will also occur quickly following shifts to new habitats, as there is no waiting time for beneficial new mutations to occur. However, in very large populations, the distinction between adaptation from standing variation versus new mutations can become blurred, because multiple new mutations can arise readily and contribute to adaptation very early in the divergence process [76–79]. Most work on selective sweeps has focused on patterns within a population, and thus models considering pairs of populations experiencing divergent selection pressures are needed to discern expected patterns of differentiation produced by sweeps for speciation-with-gene-flow.

Third, secondary contact between populations at various levels of divergence is commonplace and genomic architecture is surely important in these situations. Our results primarily describe the establishment of new mutations in the context of differentiation initiated in the face of gene flow. Thus, further work is needed to resolve the types of architectures likely established during initial allopatry and maintained after secondary contact to determine how this might affect the roles that direct selection, DH and GH play in establishing new mutations following introgression. For example, in allopatry, the selection–recombination antagonism of Felsenstein [28] is weak or non-existent. Hence, performance and assortative mating genes can become alternately fixed between populations regardless of linkage prior to contact, potentially creating genome architectures conducive to GH. In addition, the clustering of adaptive mutations may be more commonly maintained following secondary contact and introgression than when built de novo in sympatry. This could be especially true for tightly linked groups of weakly divergently selected alleles. Clustering was observed to varying degrees in several of the articles in this special issue [69,79,80]. Finally, genetic interactions between genomic regions resulting in hybrid incompatibilities may also play greater roles in cases of allopatry and secondary contact than when divergence is initiated-with-gene-flow. Further theory and empirical data are therefore needed to extend our current findings to address the consequences of past biogeography, and non-equilibrium dynamics in general, for the genomics of speciation-with-gene-flow.

(c). Future empirical work: ‘experimental genomics’

As noted earlier, observational genome scans are biased towards inferring that selection acts only on the few most differentiated outlier regions. In contrast, properly designed and replicated experiments can detect weak selection on less-differentiated regions. Some cutting-edge experiments of this type have now been conducted in the laboratory using microbes [80–82], but these do not address reproductive isolation or speciation in natural populations. Until large experiments are conducted measuring selection on the genome directly in nature, it will be impossible to resolve how many gene regions diverge during speciation. We argue that ‘experimental genomics’ will provide much insight into the mechanisms and genomic basis of speciation. Such studies are now needed to test, and refine, the theoretical results discussed here.