Oscillations in joint synchrony of reproductive hormones in healthy men

Abstract

Negative-feedback (inhibitory) and positive-feedforward (stimulatory) processes regulate physiological systems. Whether such processes are themselves rhythmic is not known. Here, we apply cross-approximate entropy (cross-ApEn), a noninvasive measurement of joint (pairwise) signal synchrony, to inferentially assess hypothesized circadian and ultradian variations in feedback coupling. The data comprised simultaneous measurements of three pituitary and one peripheral hormone (LH, FSH, prolactin, and testosterone) in 12 healthy men each sampled every 10 min for 4 days (5,760 min). Ergodicity, due to the time series stationarity of the measurements over the 4 days, allows for effective estimation of parameters based upon the 12 subjects. Cross-ApEn changes were quantified via moving-window estimates applied to 4-day time series pairs. The resultant ordered windowed cross-ApEn series (in time) were subjected to power spectrum analysis. Rhythmicity was assessed against the null hypothesis of randomness using 1,000 simulated periodograms derived by shuffling the interpulse-interval hormone-concentration segments and redoing cross-ApEn windows and spectral analysis. By forward cross-ApEn analysis, paired LH-testosterone, LH-prolactin, and LH-FSH synchrony maintained dominant rhythms with periodicities of 18–22.5, 18, and 22.5 h, respectively (each P < 0.001). By reverse (feedback) cross-ApEn analysis, testosterone-LH, testosterone-prolactin, and testosterone-FSH synchrony cycles were 30, 18, and 30–45 h, respectively (each P ≤ 0.001). Significant 8- or 24-h rhythms were also detected in most linkages, and maximal bihormonal synchrony occurred consistently at ∼0400–0500. Collectively, these analyses demonstrate significant ultradian (<24 h), circadian (∼24 h), and infradian (>24 h) oscillations in pituitary-testis synchrony, wherein maximal biglandular coordination is strongly constrained to the early morning hours.

physiological systems operate by coupling diverse signals through specific pathways (processes) (8, 12, 13). Pathophysiology typically results in pathway disruption, which is reflected in altered forward (amplification) and/or reverse (inhibition) control of overall output. Examples include autonomous endocrine tumors with reduced feedback responses, resulting in sustained increases in hormone secretion (9), transpubertal adaptations in pituitary-gonadal coordination (39), and aging-associated adaptations of pathway-specific orderliness (29, 31). Experimental methods have often entailed agonist and inhibitor experiments, including studies after in vitro separation of cell types (5, 35, 40). However, physical separation of otherwise integrated components definitionally disrupts regulatory linkages.

A well-established, model-free metric for examining signal disruption on the basis of irregularity or complexity is the approximate entropy (ApEn) measurement (19). ApEn quantifies and discriminates subtle erosion of pattern reproducibility in system output captured as time series. In numerous biological applications, and for diverse classes of theoretical mathematical models, ApEn identifies small changes in sequential regularity of time series that correspond to changes in underlying system state (19, 27, 30, 41). A bivariate analog of ApEn, cross-ApEn, quantifies joint synchrony of paired signals and is thus applicable to coupled data sets from (possibly very complicated) networks (30). Cross-ApEn is able to distinguish insidious disruption of pathway fidelity (e.g., pituitary-adrenal and pituitary-gonadal coupling) in aging individuals (29, 42). Moreover, the application of directional (A→B vs. B→A) cross-ApEn permits appraisal of primarily forward vis-à-vis reverse pathway changes in health, disease, aging, and development without disturbing the underlying system (16, 17).

Although circadian, ultradian, and other rhythms are well established for mean-level variations in hormonal dynamics, virtually nothing is known about the temporal variation of the dynamics per se. Since the study of the dynamics of hormonal secretory patterns has elucidated much toward our understanding of both physiology and pathophysiology of endocrine systems (5, 8, 35, 36), it would seem most appropriate and important to attempt to evaluate the nature of temporal variations in signal dynamics themselves. The present data set, consisting of pituitary-testis data from 4 days of intensive sampling of four hormones at 10-min intervals, provides a nearly unprecedented opportunity to test the postulate that forward/reverse pathway integration varies in both a basic circadian (∼24-h rhythmic) and an ultradian (rhythm with <24-h period) fashion.

METHODS

Subjects.

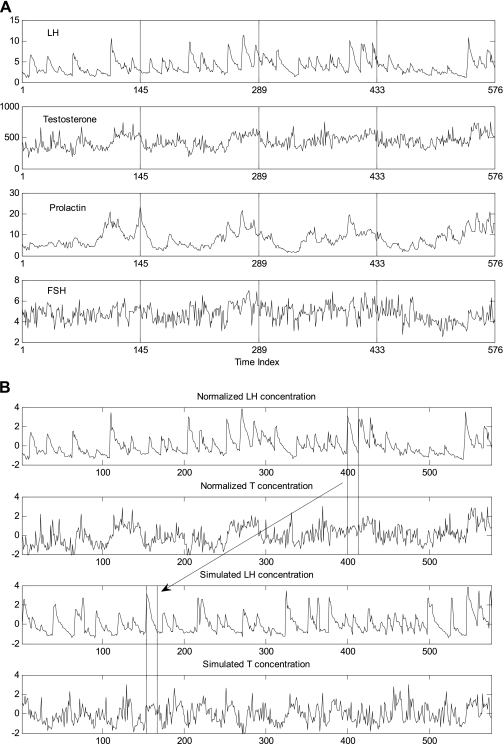
The present analyses were applied to archival LH, FSH, and prolactin data reported earlier (14), where only univariate ApEn was assessed. Matching testosterone time series have not been described previously. In brief, 12 healthy men provided written informed consent approved by the Institutional Review Board at the Mayo Clinic, Rochester, MN. Blood was sampled from normal men every 10 min for 4 days without interruption (total blood loss: 510 ml). Three regular meals were served daily at 0800, 1200, and 1700, and room lights were turned off at 2230. Room lights were turned on at 0700, and sampling began at 0800. Subjects had lavatory access and were allowed to ambulate in the room, but they were not allowed to exercise vigorously or smoke. LH, FSH, testosterone (T) and prolactin were assayed in each of the 576 samples in each of the 12 volunteers (except for FSH, which was assayed in 11 volunteers). There were no adverse events. Figure 1A illustrates the time series data of one man.

Fig. 1.

A: 4-day (5,760-min, x-grid at 8 AM) record of 10-min LH, testosterone (T), prolactin, and FSH concentrations (top to bottom) in 1 subject (21-yr-old man). B: 4-day, 10-min LH and T paired profiles (top 2 rows) and resampled LH interpulse intervals concomitantly with T (bottom 2 rows). The starting and ending points of 1 LH interpulse interval concomitantly with T are identified by vertical lines. Note the location shift of this piece of 2-dim data. Data are z-score transformations (SDs with zero mean and unit SD).

Overview of analysis.

The data consisted of 12 subjects, with each subject having measurements taken every 10 min for 4 days (576 observations). In some contexts 12 subjects is a small sample, whereas in others it isn't necessarily so. For instance, in time series one typically observes a single time-evolving sequence of dependent observations, the values being from one subject in a population. Based upon the property of ergodicity, one is able to estimate the parameters for the population from the single subject's time series. In that setting, although there would be but one subject, the degrees of freedom are on the order of the number of observations. This is the basis for time series and spectral analysis. Ergodicity occurs in time series under the conditions of strict stationarity for which the time dependencies die out sufficiently quick. One perspective for a time series is that it consists of a large number of oscillations with random amplitudes and phases. It is this perspective that is the basis for the estimation of the ultradian/circadian/infradian rhythms of the present study. For many of the calculations of the present study, the estimates are based upon the time series for each of the 12 subjects, e.g., the power spectrum for each subject and the cross-ApEn calculations. We then pool these estimates over the 12 subjects, with each estimate having a large number of degrees of freedom. By so pooling the 12 estimates, large statistical power is achieved by the population estimates based upon the 12 subjects. Hence, from the time series perspective, although we only have 12 subjects, there are a large number of degrees of freedom that result in highly accurate estimates for each subject. To identify circadian (and other) rhythms, one needs data that consist of multiple days. At the same time, one must sample sufficiently fast so as to be able to detect pulse times and to estimate secretion rates. Thus, the present data, sampled every 10 min for 4 days, were ideal, and the large number of observations (576) per subject more than compensates for the relatively small sample size of 12 subjects.

Proper application of cross-ApEn, as for virtually all statistical measurements, is to relatively stationary or steady-state epochs. However, here the primary point of our study is to examine the potential temporal variation in feedback and feedforward signal exchange, e.g., to assess diurnal or ultradian adaptations in network and pathway function. Accordingly, to ensure proper interpretability in statistical comparisons, we require that cross-ApEn be applied to relatively stationary epochs and thus to relatively short windowed blocks of data. The two-step procedure of first evaluating cross-ApEn relatively locally in time, and then secondly sliding the underlying local windows along the entirety of the 4-day records, produces a statistically valid means to evaluate temporal changes in bihormonal synchrony, which often correspond to changes in associated feedback and feedforward interactions.

Analysis of joint synchrony (cross-ApEn) variations over 4 days.

To test the hypothesis that LH feeds forward onto T (LH-T) in a rhythmic manner, we calculated the periodogram of a moving-window cross-ApEn (MVcross-ApEn; details are shown below). In the appendix, definitions of ApEn, moving-window ApEn (MVApEn), and MVcross-ApEn are provided for completeness. To this end, we first standardized (performed z-score transformation of) the series of LH and T concentrations so that LH and T patterns could be compared with respect to relative reproducibility. Next, we calculated MVcross-ApEn(T LH), defined as LH→T feedforward synchrony, with parameters m = 1, r = 0.2, and w = 36, where m is the pattern vector length, r is the pattern similarity threshold [expressed as a percentage of the whole (n = 576 data) series SD], and w is the window size in MVcross-ApEn. Specifically, we normalized each series so that SD = 1 and then computed MVcross-ApEn using r = 0.2. Note that MVcross-ApEn is based on 36 points (details are given in MVcross-ApEn), but r is defined on the basis of all 576 points. MVcross-ApEn (T LH) yields a series of ordered cross-ApEn values, which can be viewed as a time series, and its periodogram is calculated. The postulate is that MVcross-ApEn exhibits rhythmic changes that can be assessed from the periodogram, thus denoting systematic variations in two-hormone synchrony over the 4-day interval. The same concept was used for LH→prolactin and LH→FSH feedforward pairs. This analysis was applied also to the reverse direction for T→LH, T→prolactin, and T→FSH, which are termed here as feedback pathways (periphery to pituitary).

To evaluate which frequencies in the periodogram showed a power that could not be explained by chance alone, we performed a resampling procedure whereby we shuffled (resampled) interpulse-interval segments (details are given below) in the original concentration data, creating simulated series (Fig. 1B; note that in this figure the interpulse interval at 400 is shuffled to 155 in the simulated series). Pulse onsets, and thereby the intervening concentration segments, were identified initially using a previously described pulse detection method (15). It is important that interpulse-interval segments are shuffled, and not at all possible time points; in the former, the null hypothesis will be stationary processes but without the cross-ApEn rhythm. If all points are shuffled, the null hypothesis is an independent and identically distributed random (i.e., “white noise”) process; this is inappropriate because the observed data is obviously not iid. To obtain accurate empirical P values, the resampling process was repeated to generate a null set of 1,000 simulated 4-day time series for each LH-containing pair and each subject. For each such simulated series, we calculated MVcross-ApEn and the periodogram of MVcross-ApEn. The 1,000 simulated (randomly derived) periodograms were used to construct a cumulative frequency distribution from which to compute an empirical P value for the strongest rhythmic cycle in the authentic data. Given a group of k subjects, we obtained such a P value for each subject and each hormone pair also for the mean of each group for each hormone pair. Then we used Fisher's method to combine the k P values to get an overall chi-square measurement of group significance by −2 × ∑_i[ln(p_i)], I = 1, . . . ,k. The overall (group effect) P value was obtained from the chi-square distribution, with degree of freedom 2 × k.

To assess the difference (in terms of the significance of the dominant period) between two pathways, for example, LH→T vs. LH→FSH, we transformed the corresponding P values in each subject to z-scores and applied the two-sample Kolmogorov-Smirnov (KS) test (z-scores of LH→T vs. z-scores of LH→FSH) or a matched-pair t-test (matched by subject). One can also plot the empirical cumulative frequency distribution of the z-scores to visualize the difference (figures not included).

Periods of special interest (24 and 8 h) were examined by Fourier analysis to determine the amplitude and clock time of peak bihormonal synchrony. We also assessed the difference (over all periods) between two pathways by comparing the shape of their group mean spectrum. The nonparametric method of comparing cumulative periodograms by Diggle and Fisher (4) was applied (details are given below).

Cross-ApEn.

ApEn was developed as a quantification of irregularity in sequences and time series data motivated by both application needs (19) and fundamental questions within mathematics (27, 30). Two input parameters, a block or run length m and a tolerance window r, must be specified to compute ApEn. Briefly, ApEn measures the logarithmic probability that blocks or templates of length m that are close (within r) for m contiguous observations remain close (within the same tolerance width r) on the next incremental comparisons. The ApEn calculation provides a single nonnegative number, which is an ensemble estimate of relative process randomness wherein larger ApEn values denote greater irregularity, and smaller values to more instances of recognizable patterns or features in data. It has been widely applied to hormonal data such as these (7, 24, 29).

Analogously, cross-ApEn quantifies joint pattern synchrony between two time series (20, 30); the formal mathematical definition of cross-ApEn is given in Ref. 29. As for ApEn, it is a two-parameter family of statistics, with m and r taking the same meaning as in the ApEn setting, Cross-ApEn measurements, within tolerance r, the (conditional) regularity or frequency of v-patterns similar to a given u-pattern of window length m. It is typically applied to standardized u and v time series. Greater asynchrony indicates fewer instances of (sub)pattern matches, quantified by larger cross-ApEn values. For the studies below, we calculate cross-ApEn values for all data sets applying widely utilized and validated parameter values m = 1 and r = 20% of the SD of the specified time series. Previous evaluations, including both theoretical model-based analysis (19, 25, 26, 29) and numerous diverse applications (16, 17, 29, 33, 37), demonstrate that the input parameters indicated above produce good reproducibility for cross-ApEn for time series of the lengths considered herein. In particular, the SD of cross-ApEn is less than or equal to 0.06 for virtually all processes analyzed for the present data lengths. This establishes the model independence for cross-ApEn; i.e., it assures robust qualitative inferences across diverse model configurations. In effect, the choices for m and r are made to insure that the conditional frequencies that underlie the cross-ApEn specification are reasonably estimated from the input data time series. For much smaller r values or larger m values than those utilized herein, one usually achieves poor conditional frequency estimates (i.e., statistical replicability is compromised), whereas for larger r values, too much detailed system probabilistic information is lost (collapsed into coarser agglomerations).

ApEn and cross-ApEn evaluate both dominant and subordinant patterns in data; notably, they can detect changes in underlying episodic behavior not reflected in peak occurrences or amplitudes or even subtler, more insidious changes in instances in which no apparent features, e.g., pulses or spikes, are readily identifiable (28). Additionally, ApEn and cross-ApEn are robust to noise and artifacts and are scale and translation independent. Importantly, changes in ApEn and cross-ApEn have been shown mathematically to correspond to mechanistic inferences concerning subsystem autonomy, feedback, and coupling in very distinct model settings (22, 28, 38).

Elsewhere (9), we provide a detailed stepwise description of the ApEn calculation, accompanied by several figures, that should enhance the visual understanding of the ApEn and cross-ApEn calculations. A recent study of paired ACTH-cortisol dynamics in Cushing's disease (33) further illustrates cross-ApEn quantification (specifically, Fig. 1) in Ref. 33, with greater ACTH-cortisol secretory asynchrony in the diseased subject compared with the control.

In Ref. 7, we provide a theoretical basis for understanding why ApEn and cross-ApEn provide a more general and robust measurement of feature persistence than do linear correlation and spectral measurements, either univariate or bivariate. Descriptively, correlation and spectral measurements assess the degree of matching or recurring features (characteristic subblocks) at fixed spectral frequencies, whereas the ApEn formulation implicitly relaxes the fixed frequency mandate in evaluating recurrent feature matching. Thus both ApEn and cross-ApEn provide a sharper measurement of equidistribution and asynchrony and can identify subtle yet persistent pattern recurrences in both data and models that the aforementioned alternatives fail to do (18, 29).

MVcross-ApEn.

A moving-window version of cross-ApEn was implemented to capture changes in local synchrony over time, i.e., a local time inhomogeneity of the underlying network interactions. The calculation is dynamic in providing a series of cross-ApEn values, since the calculation window is shifted en bloc in 10-min (1-sample) increments across the 4-day paired hormone data. For example, consider two time series, X = (x_i) and Y = (y_i), I = 1, . . . ,N, and window size 36 samples. MVcross-ApEn values are calculated on the basis of every 36 consecutive pairs (series A and series B) of data points. The first cross-ApEn value depends on ([x₁,y₁], . . . , [x₃₆,y₃₆]), and the second cross-ApEn value depends on ([x₂,y₂], . . . , [x₃₇,y₃₇]). In general, the jth cross-ApEn, 1 ≤ j ≤ n − 36 + 1, is calculated from data ([x_j,y_j], . . . , [x_{36 + j − 1},y_{36 + j − 1}]). Thus, in MVcross-ApEn, each cross-ApEn_j is calculated using only a local region of contiguous data in the 4-day paired time series data.

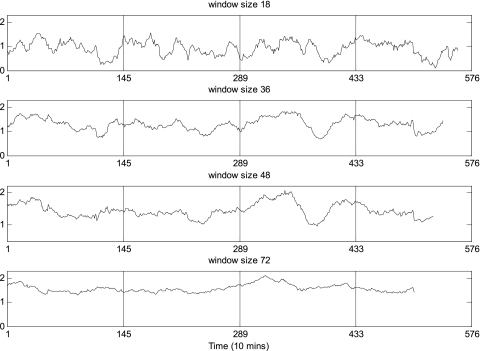
Window size 36 (6 h) was chosen after estimates were compared for 18 (3 h), 36 (6 h), 48 (8 h), and 72 (12 h). This reflects a balance between statistical and probabilistic concerns (19). Smaller windows lose power, and larger series lose discrimination. A window size of n = 18 was too small for the current data set because there were some unreliably small cross-ApEn values due to lack of matches (nonreplicability), whereas a window size of n = 72, although statistical very stable, was sufficiently coarse to most effectively detect more rapid ultradian rhythms. The patterns of the MVcross-ApEn series with window sizes of 36 and 48 were qualitatively quite similar. Figure 2 presents the LH-T cross-ApEn time series with the four different choices of window size in a subject.

Fig. 2.

Illustrative profiles of moving-window (MV)cross-ApEn values of LH-T with window sizes of 18, 36, 48, and 72 in a healthy man of 21-yr-old (x-grid at 8 AM).

Periodogram.

A power spectrum, or periodogram, was used to determine the amplitudes of frequencies of periodic variations in the cross-ApEn time series. The goal was to quantify periodic components in the presence of noise. A peak in the periodogram indicates an important contribution to variance of the frequency (or frequencies) near the value that corresponds to the peak.

Power vs. frequency (no. of cycles/5,410 min) is plotted in the periodogram. Power is calculated as scaled square of the fast Fourier transformation of the time series. The length (period) of a cross-ApEn cycle (in min) for the present 4-day (5,760 min) data [created from 576 separate 10-min concentrations using a moving 36-point (360 min) window] is 5,410 min/no. of cycles. Power was construed as significant when the value of the true observations exceeded 95% of the values of the 1,000 random samples of the interpulse-interval sequence of the time series. To summarize the results from all men, we also calculated the mean periodogram by averaging the power over all men at each frequency and analogously 1,000 mean periodograms of the random resamples to get the P value.

Resampling interpulse concentration segments.

To obtain empirical P values of the significance of a power, we broke the original time series (hormone concentrations) into pieces according to a vector of pulse onset times (15) and resampled the pieces to get a new process comprising randomly reordered pulse times as follows: given process X and its pulse onset times I, decompose X into pieces P = (p_i) according to I, e.g., I = (9, 53, 120, 300), then P = [(x₁, . . . ,x₉), (x₁₀, . . . ,x₅₃), (x₅₄, . . . ,x₁₂₀), (x₁₂₁, . . . ,x₃₀₀)]; resample I according to process X [e.g., I_X = (53, 300, 120, 9)], and use I_x to resample pieces of P to get P*, e.g., P* = [(x₁₀, . . . ,x₅₃), (x₁₂₁, . . . ,x₃₀₀), (x₅₄, . . . ,x₁₂₀), (x₁₀, . . . ,x₅₃)].

Given processes X and Y and pulse times I_X of X, define P_X and P_Y by I_X. Treat P_x and P_y as a two-dim process, and resample paired pieces of P_X and P_Y to get P*_X and P*_Y simultaneously.

Again, as stated above, it is important that interpulse interval segments are shuffled and pieced back together to produce a shuffled series and not a shuffling of all time points. Roughly speaking, the end of one pulse interval and the starting of another is very much like a renewal process. The segments of a hormonal concentration profile that are closest to being independent are the interpulse intervals.

Comparison of periodograms.

We compare the shape of two periodograms by comparing their normalized cumulative periodograms (4). The details of the analytical procedure are illustrated by the following example.

We compare the two periodograms of moving block Cross-ApEn series LT (LH→T) and LF (LH→FSH). Let I_LT(ω_j) and I_LF(ω_j), j = 1, . . . , [(541 − 1)/2] be the power of corresponding cross-ApEn series at frequency ω_j (j cycles/5,410 min), and 541 is the length of the cross-ApEn series.

Calculate the normalized cumulative periodograms, denoted as F_LT(ω_j) and F_LF(ω_j), j = 1 . . . 270 as F_LT(ω_j) = ∑_{i = 1 to j} I_LT(ω_i)/∑_{i = 1 to 270} I_LT(ω_i) and F_LF(ω_j) = ∑_{i = 1 to j} I_LF(ω_i)/∑_{i = 1 to 270} I_LF(ω_i).

Calculate the KS difference as d = sup_j∣F_x (ω) − F_y (ω)∣, j = 1, . . . ,270.

Randomly interchange I_LT(ω_j) and I_LF(ω_j) for j = 1, . . . ,270, to get I*_LT(ω) and I*_LF(ω) and then calculate F*_LT(ω), F*_LF(ω) and their KS difference d*.

Repeat step 3 1,000 times, and calculate the total number of those d* at least as large as d and divide by 1,000 to get the significance probability.

RESULTS

Twelve men participated and completed all 4 days of 10-min blood sampling without interruption. One subject did not have sufficient serum to permit FSH measurements. The median (range) age and body mass index were 33 (18–75) yr and 26 (21–29) kg/m², respectively. Deconvolution analysis of the uninterrupted 4-day LH time series in the 12 subjects yielded (per 4 days) 50 (42–67) LH secretory bursts, rapid- and slow-phase LH half-lives (min) of 22 (6.5–25) and 90 (71–119), an LH secretory burst mode (min) of 15 (12–20), basal and pulsatile LH secretion (IU·l⁻¹·4 days⁻¹) of 143 (64–289) and 198 (125–315), mass per burst (IU/l) of 3.6 (2.3–7.2), and γ (a regularity term): 2.7 (2.1–3.2), for which values > unity denote greater regularity of the Weibull process than a Poisson process.

Cross-ApEn values without windowing were determined first. These are single values calculated over all 4 days (576 data points) for six physiologically relevant pairs. Since cross-ApEn values are asymptotically normal under broadly valid assumptions, Table 1 gives the mean ± SE (n = 11, 12) cross-ApEn (and the median) for the pairwise (LH, FSH, prolactin, and T) combinations studied here. By paired parametric testing, feedback cross-ApEn values were higher (denoting lower joint pattern synchrony) than feedforward cross-ApEn values: T-LH cross-ApEn > LH-T cross-ApEn (P < 0.01), T-PRL > LH-PRL (P < 0.01), and T-FSH > LH-FSH (P < 0.01). The descending rank order of joint synchrony was LH-PRL (maximal synchrony and lowest cross-ApEn) > LH-T = LH-FSH > T-FSH > T-LH = T-PRL.

Table 1.

Bivariate cross-ApEn of physiologically paired LH, PRL, FSH, and T concentrations measured 576 times over 4 days

Cross-ApEn	Means ± SE	Median
Feedforward
LH-T	1.8298 ± 0.0366	1.8145
LH-prolactin	1.6262 ± 0.0615	1.6460
LH-FSH*	1.8469 ± 0.0354	1.7984
Feedback
T-LH	2.1700 ± 0.0331	2.1573
T-PRL	2.1957 ± 0.0332	2.2114
T-FSH*	2.0551 ± 0.0306	2.0916

Data are means ± SE and median (n = 12 except for FSH, where n = 11). ApEn, approximate entropy; T, testosterone; PRL, prolactin. Feedforward denotes pituitary-gonadal or pituitary-pituitary coupling, whereas feedback denotes gonadal-pituitary coupling (methods).

^*One FSH series was incomplete.

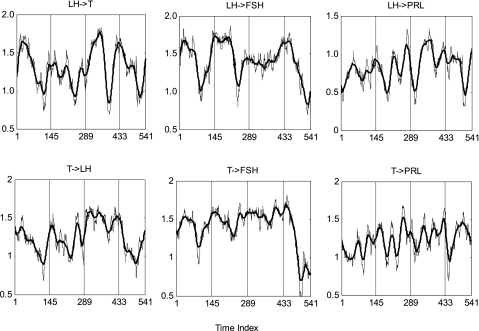
To test the hypothesis that joint synchrony varies over time, windowed cross-ApEn (1, 0.2, 36) was evaluated repeatedly in 10-min increments across the 4 days in each subject for all 6 hormone pairs. Figure 3 shows cross-ApEn time series of LH-T and all other hormone pairs for one subject. The total number of successive cross-ApEn values is 541 (spanning 5,410 min or ∼90 h) in each series, reflecting the window size and original series length.

Fig. 3.

Illustrative profile of MVcross-ApEn (x-grid at 8 AM) with window size 36 (6-h) values for LH-T, LH-prolactin, and LH-FSH feedforward synchrony and T-LH, T-prolactin, and T-FSH feedback synchrony in a healthy 21-yr-old man. The lighter continuous curve is unsmoothed, whereas the darker continuous curve is smoothed (flattened somewhat) by a 23-point moving average.

Simulated random cross-ApEn time series were obtained by shuffling the multivariate process by LH (for feedforward) and the T (for feedback) interpulse segments of the original concentration data 1,000 times each. This produced 1,000 (random) cross-ApEn time series each containing 541 estimates for each subject (n = 12 or 11) and each hormone pair (n = 6). Fourier analysis (power spectrum estimation) was then performed on the authentic cross-ApEn series derived from the unshuffled hormone pair and on the 1,000 randomly generated cross-ApEn time series. This allowed direct comparison of each authentic cross-ApEn power spectrum (plot of squared amplitude against frequency) with the distribution of 1,000 random cross-ApEn power spectra (periodograms) in the 12 subjects.

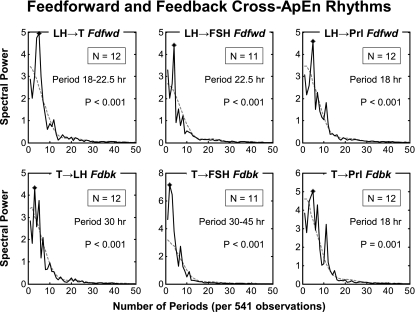
At each frequency, a mean power spectrum was calculated by averaging individual spectra and can be compared with its randomly shuffled counterparts to get a significance measurement. Figure 4 depicts the results of six cross-ApEn power spectrum analyses. Each of the six graphs in this figure presents the mean power spectra (mean periodograms) of one hormone pair. The solid (irregular) curve gives the mean spectrum for the authentic (unshuffled) cross-ApEn series and the dashed (smoother) curve the 95% limit for the random series. The x-axis defines the number of cycles (frequency) per 5,410 min (or ∼90 h) and the y-axis the strength of the periodic signal. Period length (h) of the dominant cycle detected in the cross-ApEn time series is listed below the rectangles. The P value within each graph designates the probability of observing the detected dominant cycle in 1,000 shuffled pairs. The periodicities with the greatest power (each P ≤ 0.001) were 18–22.5 (LH-T), 22.5 (LH-FSH), and 18 h (LH-PRL) for feedforward and 30 (T-LH), 30–45 (T-FSH), and 18 h (T-PRL) for feedback, suggesting mainly circadian (nearly 24 h) and ultradian (more than 1 cycle/24 h) rhythms.

Fig. 4.

Mean periodograms (over n periodograms, where n is the number of men) of LH-T, LH-FSH, and LH-prolactin feedforward synchrony and T-LH, T-FSH, and T-prolactin feedback synchrony. Periodograms determined in healthy men of cross-ApEn using the original (unshuffled) time series (solid curve) and the 95% limit for shuffled (randomly resampled 1,000 times for each man) time series (dashed curve). The length of primary periodicity is given in hours, and the P value is estimated from the cumulative frequency distribution of the 1,000 randomly generated mean periodogram amplitudes (methods).

The periods with the greatest power (primary period) for each subject and each pair of hormones are summarized in Table 2. Those periods are not necessarily the same across subjects for a given hormone pair synchrony. For the null hypothesis of no significant periodicities of cross-ApEn in the cohort as a whole, chi-square values were 89 (22 df), 104 (24 df), and 115 (24 df) for LH-FSH, LH-prolactin, and LH-T (each P < 10⁻⁶), and pooled z-scores were 6.8, 7.4, and 8.1, respectively (each P < 10⁻⁶). Chi-square values for T feedback cross-ApEn cycles were comparable at 80 (24 df) for T-LH, 110 (22 df) for T-FSH, and 112 (24 df) for T-prolactin (each P < 10⁻⁶ vs. chance periodicities). Corresponding cohort-defined z-scores were comparably significant, namely 5.9, 7.9, and 7.8 (each P < 10⁻⁵).

Table 2.

Summary of strongest periods of cross-ApEn time series

	Feedforward			Feedback
	LH→T (n = 12)	LH→PRL (n = 12)	LH→FSH (n = 11)	T→LH (n = 12)	T→PRL (n = 12)	T→FSH (n = 11)
25% (h)	30.1	22.5	90.2	45.1	25.8	40.1
Median (h)	22.5	18.0	30.1	30.1	20.0	30.1
75% (h)	18.0	18.0	22.5	22.5	12.9	22.5
Chi2 (df)	115 (24)	104 (24)	89 (22)	80 (24)	112 (24)	110 (22)
z-Score (P value)	8.1 (<10−8)	7.4 (<10−7)	6.8 (<10−6)	5.92 (<10−5)	7.83 (<10−7)	7.89 (<10−7)
Dominant*	18.0–22.5	18.0	22.5	30.1	18.0	30.1–45.1

^*Dominant period is determined from the mean spectrum of each cohort.

Although most of the primary periods are detectable (P < 0.05) for each subject and each synchrony, their level of significance may differ across the distinct synchronies. We compared synchronies by their levels of the significance of the primary periods (Table 3). P values were first transformed to z-scores, with a higher score corresponding to a higher level of significance. By paired t-test (P = 0.008) and by the KS test (P = 0.002) of the z-scores, the primary period of LH-T feedforward variation is more significant than that of the T-LH feedback variation in joint synchrony. In addition, primary T-FSH cross-ApEn rhythms are generally more significant than primary T-LH rhythms (P = 0.018, paired t-test; P = 0.016, KS test). Primary T-prolactin periods are more significant than primary T-LH feedback synchrony by t-test (P = 0.05) or by post hoc nonparametric testing (P = 0.01).

Table 3.

Testing the differences between hormone synchronies via levels of significance of primary periods

	Paired t-Test > (Over z-Scores)	KS Test < (Over z-Scores)
LH-T vs. LH-FSH	0.1639	0.1410
LH-T vs. LH-PRL	0.2902	0.4255
LH-PRL vs. LH-FSH	0.4551	0.2819
T-FSH vs. T-LH	0.0182	0.0162
T-PRL vs. T-LH	0.0541	0.0095
T-FSH vs. T-PRL	0.3739	0.2997
LH-T vs. T-LH	0.0076	0.0023
T-FSH vs. LH-F	0.0710	0.1884
T-PRL vs. LH-PRL	0.3324	0.4255

KS, Kolomogrov-Smirnov.

Significant (P < 0.05) ranges of periodicities, which include 24 h (∼4 cycles/541 observations), were disclosed for all linkages except T→LH (where 3 and 5 cycles/541 observations are significant). Significant 8-h periodicities (∼11–12 cycles/541 observations) were obtained for all linkages except (LH→FSH). Cosine regression is illustrated in Fig. 5, and phase results are tabulated in Table 4. These show maximum synchrony at 0400–0500 for many 24-h rhythms and for most 8-h rhythms.

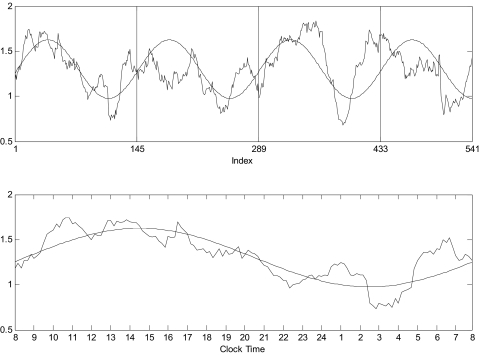
Fig. 5.

Cosine fit of the 24-h period of LH→T cross-ApEn profile in a 21-yr-old man. The unsmoothed curve is the MVcross-ApEn(T∣LH) profile, and the smoothed curve is the cosine fit. Top: the fit over all observations (5,410 min, x-grid at 8 AM). Bottom: the look of the fit of the 1st day of the 4 days with the x-axis clock time.

Table 4.

Most synchronous time and amplitude

Phase	LH→T	LH→FSH	LH→PRL	T→LH	T→FSH	T→PRL
24-h Cycle (3.7569 cycles/541 obs)
50%	3.7860, 3:47	3.8397, 3:50	6.9186, 6:55	5:5244, 5:31	4.2320, 4:14	6.6694, 6:40
IQR	2:25–4:39	2:35–4:51	5:30–9:46	4:01–5:58	3:07–5:08	5:48–10:06
Amplitude
Median	0.2383	0.1673	0.1480	0.2070	0.1676	0.1394
Means ± SD	0.2208 ± 0.0803	0.1861 ± 0.0708	0.1496 ± 0.0669	0.1991 ± 0.0670	0.1743 ± 0.0716	0.1292 ± 0.0452
8-h Cycle (11.2708 cycles/541 obs)
Median	4.6307, 4:38	5.1776, 5:11	3.5868, 3:35	4.8129, 4:49	4.4809, 4:29	4.0405, 4:02
IQR	4:00–5:18	4:37–5:45	2:52–3:46	4:35–5:31	3:32–5:12	3:10–5:28
Amplitude
Median	0.0580	0.0594	0.0681	0.0726	0.0658	0.0983
Means ± SD	0.0596 ± 0.0302	0.0500 ± 0.0277	0.0676 ± 0.0327	0.0765 ± 0.0299	0.0657 ± 0.0286	0.0939 ± 0.0447

IQR, interquartile range.

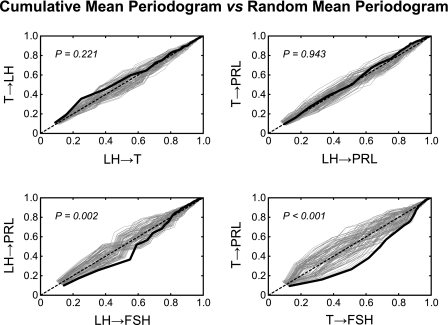
To visually compare the shapes of the mean spectra of hormone pairs, we created Fig. 6 by plotting the normalized cumulative mean periodogram of the first hormone pair vs. the normalized cumulative mean periodogram of the second hormone pair. The cumulative periodogram was normalized so that the range was 0 to 1. If the two periodograms are identical, the black solid curve should fall along the equal line of identity (black dashed line). The gray dashed curves create an envelope of the black solid curve by plotting its analog, using the randomly interchanged data. A black solid curve falling outside of the envelope corresponds to a significant difference between the two hormone pairs. If the x-axis denotes the measurement of the first series and the y-axis denotes that of the second one, a black solid curve significantly below the equal line indicating the power spectrum of the first is shifted to lower frequency compared with that of the second one. Roughly speaking, the relative power (compared with higher frequencies) of the low frequencies is greater in the first series.

Fig. 6.

Cumulative mean periodogram comparison of LH-T vs. T-LH, LH-prolactin vs. T-prolactin, LH-FSH vs. LH-prolactin, and T-FSH vs. T-prolactin. The solid black curve is from the true mean periodograms; the gray dash curves are generated from shuffled periodograms. The dashed black line is the equal-angle line, which represents an ideal case of 2 identical cumulative periodograms.

Four comparisons are presented in Fig. 6, and the P values of all nine comparisons are listed in Table 5. Four were found to be significantly different: LH→T vs. LH→FSH (P = 0.033), LH→T vs. LH→PRL (P = 0.028), LH→FSH vs. LH→PRL (P = 0.002), and T→FSH vs. T-PRL (P < 0.001). The power spectrum of LH→FSH was shifted to lower frequencies compared LH→T and LH→PRL. LH→T was shifted to lower frequencies compared with LH→PRL. The shape of T→FSH power spectrum was shifted to lower frequencies compared with T→PRL. Note that this method allowed us to compare the shape of the periodograms, and thus the comparison is over a combination of all periods.

Table 5.

Testing the differences between the shape of mean periodograms of hormone synchronies

Pairs	CP vs. CP ≠ (Over Mean Periodograms)
LH-T vs. LH-FSH	0.0328
LH-T vs.LH-PRL	0.0282
LH-PRL vs.LH-FSH	0.0017
T-FSH vs.T-LH	0.3809
T-PRL vs.T-LH	0.5819
T-FSH vs.T-PRL	<0.0001
LH-T vs.T-LH	0.2209
T-FSH vs.LH-F	0.5937
T-PRL vs. LH-PRL	0.9434

CP, cumulative periodograms.

DISCUSSION

The present analyses unveil for the first time that quantifiable synchrony of reproductive hormonal linkages varies considerably across the day and night. This is true for both 24- and 8-h rhythms and for almost all bihormonal pathways studied here. We repeated the analysis using partial data (2.24 days with 323 data points, starting at 2 PM on the 1st day); the 24-h rhythm was still detected in all pathways, and the 8-h rhythm was detected in LH-PRL and T-PRL pathways. The consistency of these findings is remarkable and suggests entrainment of reproductive hormonal networks by the suprachiasmatic nucleus and other Zeitgebers. The phase analysis using full data showed that maximal synchrony occurs at ∼0400–0500 in most linkages. Maximal regularity of hormonal linkages just prior to awakening may reflect a physiological process that partly regulates or is influenced by the sleep-wake transition. The exact relationship between paired hormone coordination and sleep or circadian pacemakers could potentially be assessed if sleep-wake cycles were desynchronized from circadian time. Although substantial knowledge of circadian clock function is available in other physiological contexts (3), whether the rhythms that we have observed are energy responsive and temperature compensated, as observed in animal models (1, 2), will require further elucidation.

A strength of the cross-ApEn approach is that complete system specification or a full network model is not necessary to certify the statistical validity of changes in ApEn (or cross-ApEn) with concomitant changes in joint synchrony and thereby the network function (22). This work also introduces an empirical estimator of random feedforward relationships, e.g., LH-T cross-ApEn, calculated repeatedly after (LH concentration) pulse segments were resampled (performing 1,000 random permutations on the original pulse onset-defined intervals). The empirically constructed cumulative frequency distribution was used to estimate the probability of the authentic cross-ApEn rhythm arising from chance LH-T pattern similarities in each of the 12 subjects. By this construction, the cohort-defined z-score for the probability of falsely rejecting the null hypothesis of no cross-ApEn rhythms was estimated as z = 8.1 (P < 10⁻⁸). Likewise, for LH-FSH and LH-prolactin, group z-scores were z = 6.8 (P < 10⁻⁶) and z = 7.4 (P < 10⁻⁷). Thus, according to this estimation strategy, joint hormone feedforward (pituitary-gonad and pituitary-pituitary) synchrony exhibits remarkable nonrandom rhythmicity over a 4-day interval. The individual factors supervising these changes will require further study, including such entities as food intake, exercise, sleep, and stress.

The present data show that bivariate hormone synchrony oscillates in an infradian (periodicity >24 h) fashion in normal individuals for T-LH and T-FSH feedback. The latter rhythm was foreshadowed in a rat model of T-induced nycthemeral FSH cycles (Fig. 2 in Ref. 10). Moreover, androgens are capable of modifying the master circadian pacemaker (11). Whether infradian rhythms in feedforward synchrony exist with periodicities exceeding 4 days (5,760 min) cannot be ascertained from our data (which is only 4 days in length). Important infradian rhythms operate in a variety of physiological systems (43, 44), but precisely how they relate to the basic feedback and feedback synchrony cycles discovered here is not yet known.

Forward cross-ApEn oscillated at a median ultradian (>1 cycle/24 h) periodicity of 18 h in the case of LH-prolactin synchrony. Whether such joint synchrony arises from prolactin's feedback effects on the hypothalamus (34) or from intrapituitary gonadotrope-lactotrope interactions is not yet known (37).

Caveats include the relatively small cohort size (12 subjects), which is more than sufficiently compensated by the degrees of freedom resulting from the 2,308 separate hormone measurements in each person, restriction of analyses initially to men, the limitation of sampling only every 10 min for 4 days, and the ultimate need to appraise whether feedback rhythms are free running, Zeitgeber entrainable, and temperature compensated. The methods presented here should offer an analytical platform for pursuing such studies, including in other feedback systems such as cellular and molecular networks. The requirement is that relevantly paired signals be monitored frequently without biological coupling being disrupted and that sufficient data be obtained to capture several cycle lengths.

In conclusion, reproductive hormone homeostasis, evaluated at the level of bivariate signaling pathways, proceeds by way of infradian, circadian, and ultradian dynamics. If verified further, these outcomes introduce a new basis for experimental and model-based investigations of feedback/feedforward regulation in health, premorbidity, disease, and aging.

Perspectives and significance.

Endocrine glands communicate with each other and with remote target tissues via intermittent signal exchange (6, 12, 13, 40). Whereas parametric models of single hormone signals are widely utilized in the endocrine literature, modeling the joint dynamics of more than one hormone (e.g., the pituitary and target gland hormones together) is not well developed. This is due mainly to the fact that biological interactions are typically nonlinear, and the modeling of nonlinear dynamics imposes severe technical limitations. Linear methods such as auto- and cross-correlations will not necessarily detect nonlinear interactions (29). Hence, methods such as cross-ApEn, which can detect nonlinear relationships without requiring explicit modeling of the nonlinear structure, are important (21, 23, 32). This concept was used to show, for the first time, that the dynamics of hormonal secretory patterns follow circadian and ultradian patterns with maximal bihormonal synchrony at about 0400–0500 just before waking. The magnitudes of the observed changes across the 24-h day are similar to those observed in many other nycthemeral rhythms. Feedforward linkages were uniformly more synchronous than feedback linkages among reproductive hormones. The consistency of these findings suggests broader relevance to other classical (hypothalamopituitary-end organ) hormonal networks and introduces the need to conduct experiments at a strictly consistent time of day, to evaluate bihormonal regulatory complexity in other physiological contexts, and to explore pathophysiological disruption and molecular bases of underlying mechanisms.

GRANTS

This work was supported in part via Center for Translational Science Activities Grant No. 1-UL-1-RR-024150 from the National Center for Research Resources (Rockville, MD) and by AG-031763 and DK-050456 (Metabolic Studies Core of the Minnesota Obesity Center) from the National Institutes of Health (Bethesda, MD).

DISCLOSURES

The authors have nothing to disclose. ^{. . .}

APPENDIX: DEFINITIONS OF ApEn AND MOVING-WINDOW VERSIONS

ApEn can be defined for a deterministic or stochastic real-valued sequences of finite length and for an infinite real-valued sequence, assuming the limit exists. Let m be a positive integer and r a positive real value. Let x_t = {u_t}, t = 1, . . . ,N, be a sequence of length n. Define x_t = [u, . . . ,u_{t + m}] for t = 1, . . . ,N − m, and the distance between x_t and x_s as the maximum difference in their respective components:

$$d_{m+1}(x_t,x_s)=\max \left\{\left|u_t-u_s\right|,.\; .\; .,\left|u_{t+m}-u_{s+m}\right|\right\}.$$

If d_{m + 1}(x_t,x_s) ≤ r, the two segments of length m + 1 are said to be close. The basis of ApEn and cross-ApEn is the quantification of the predictability of future values based upon the past. For a given x_t, the fraction that is close is

$$C_t^{m+1}(r)=\#\{s|d_{m+1}(x_t,x_s)\le r\}/(N-m).$$

Let

$${\Phi }^{m+1}(r)=\frac{{\displaystyle \sum _{t=1}^{N-m}\log C_t^{m+1}(r)}}{N-m},$$

and similarly

$${\Phi }^m(r),\text{with}ApEn(N,m,r)={\Phi }^m(r)-{\Phi }^{m+1}(r).$$

In C_t^{m + 1}(r) above, x_t is being compared with all possible x_s, s = 1, . . . , N − m.

In the present study, we are interested in moving-window versions, where we will define the window length via a parameter w; the window at time t, 1 ≤ t ≤ N − m − w, is the set of times s such that 0 ≤ s − t ≤ w. To define MVApEn, let

$$C_t^{(w,m+1)}(r)=\#\{s|d_{m+1}(x_t,x_s)\le r,0\le s-t\le w\}/(w+1)=\frac{{\displaystyle \sum _{s=t}^{t+w}{I}_{\{d_{m+1}(x_t,x_s)\le r\}}}}{w+1},$$

where I is an indicator function. Once the C_t^{w,m + 1}(r) is constructed, the construction of MVApEn is analogous to that of ApEn(N,m,r) above. In the moving-window versions, only times s close to t are allowed. To define MVcross-ApEn, suppose that {u_t} and {v_t} are two sequences of length N, t = 1, . . . ,N. Let x_t = [u, . . . ,u_{t + m}] and y_t = [v_t, . . . ,v_{t + m}] for t = 1, . . . ,N − m. In general, there are two cross-ApEn statistics, depending on whether v or u is the template for comparisons. Define as follows:

$$C_t^{(w,m+1)}(r)(v|u)=\#\{s|d_{m+1}(x_t,y_s)\le r,0\le s-t\le w\}/(w+1)=\frac{{\displaystyle \sum _{s=t}^{t+w}{I}_{\{d_{m+1}(x_t,y_s)\le r\}}}}{w+1}$$

$$C_t^{(w,m+1)}(r)(u|v)=\#\{s|d_{m+1}(y_t,x_s)\le r,0\le s-t\le w\}/(w+1)=\frac{{\displaystyle \sum _{s=t}^{t+w}{I}_{\{d_{m+1}(y_t,x_s)\le r\}}}}{w+1}$$

Once the C_t^{(w,m + 1)}(r)(v|u) and C_t^{(w,m + 1)}(r)(u|v) are defined, the construction of the MVcross − ApEn(v u) and the MVcross − ApEn(u|v) proceeds exactly as in that of the MVApEn.